-附录一 泄水建筑物水力设计计算公式

新版水力学常用计算公式-新版.pdf1、明渠均匀流计算公式：Q=A ν=AC RiC=n 1R y （一般计算公式）C=n 1R 61（称曼宁公式）2、渡槽进口尺寸(明渠均匀流)z ：渡槽进口的水位降（进出口水位差）ε：渡槽进口侧向收缩系数，一般ε＝0.8～0.9b ：渡槽的宽度（米）h ：渡槽的过水深度（米）φ：流速系数φ＝0.8～0.953、倒虹吸计算公式：Q=mA z g 2(m 3/秒）4、跌水计算公式：5、流量计算公式：Q=A ν式中Q ——通过某一断面的流量，m 3／s ；ν——通过该断面的流速，m ／hA ——过水断面的面积，m 2。

6、溢洪道计算1）进口不设闸门的正流式开敞溢洪道（1）淹没出流：Q ＝εσMBH 23＝侧向收缩系数×淹没系数×流量系数×溢洪道堰顶泄流长度×溢洪水深23（2）实用堰出流：Q=εMBH 23gZ 2bh Q ＝跌水水力计算公式：Q ＝εmB 2/30g 2H ，式中：ε—侧收缩系数，矩形进口ε＝0.85～0.95；，B —进口宽度（米）；m —流量系数=侧向收缩系数×流量系数×溢洪道堰顶泄流长度×溢洪水深232）进口装有闸门控制的溢洪道（1）开敞式溢洪道。

Q ＝εσMBH 23＝侧向收缩系数×淹没系数×流量系数×溢洪道堰顶泄流长度×溢洪水深23（2）孔口自由出流计算公式为Q=M ωH=堰顶闸门自由式孔流的流量系数×闸孔过水断面面积×H 其中：ω=be 7、放水涵管(洞)出流计算1）、无压管流Q=μＡ02gH =流量系数×放水孔口断面面积×02gH 2）、有压管流Q ＝μＡ02gH =流量系数×放水孔口断面面积×02gH 8、测流堰的流量计算——薄壁堰测流的计算1）三角形薄壁测流堰，其中θ＝90°，即自由出流：Q ＝1.4H 25或Q ＝1.343H 2.47（2-15）淹没出流：Q ＝（1.4H 25）σ（2-16）淹没系数：σ＝2)13.0(756.0H h n +0.145（2-17）2）梯形薄壁测流堰，其中θ应满足tan θ＝41，以及b ＞3H ，即自由出流：Q ＝0.42b g 2H 23＝1.86bH 23（2-18）淹没出流：Q ＝（1.86bH 23）σ（2-19）淹没系数：σ＝2(23.1）H h n -0.127（2-20) 9、水力发电出力计算N=9.81HQ η式中N ——发电机出力，kW ；H ——发电毛水头，m ，为水库上游水位与发电尾水位之差，即H=Z 上-Z 下；Q ——发电流量，m 3／s ；η——发电的综合效率系数（包括发电输水管的水头损失因素和发电机组效率系数），小型水库发电一般为0.6—0.7。

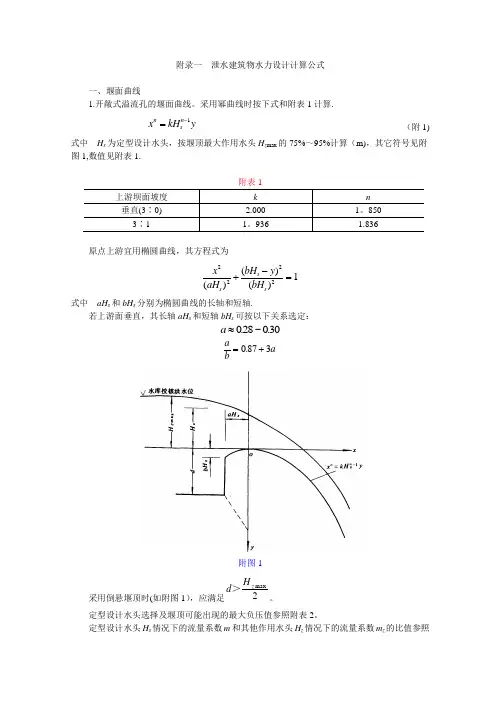
附录一 泄水建筑物水力设计计算公式一、堰面曲线1.开敞式溢流孔的堰面曲线。

采用幂曲线时按下式和附表1计算.x kH y n s n =-1 （附1)式中 H s 为定型设计水头，按堰顶最大作用水头H z max 的75%～95%计算（m)，其它符号见附图1,数值见附表1.附表1上游坝面坡度 k n 垂直(3∶0) 2.000 1。

850 3∶11。

9361.836原点上游宜用椭圆曲线，其方程式为x aH bH y bH s s s 22221()()()+-=式中 aH s 和bH s 分别为椭圆曲线的长轴和短轴.若上游面垂直，其长轴aH s 和短轴bH s 可按以下关系选定：a ≈028030.~.ab a =+0873.附图1采用倒悬堰顶时(如附图1），应满足2maxz H d ＞。

定型设计水头选择及堰顶可能出现的最大负压值参照附表2。

定型设计水头H s 情况下的流量系数m 和其他作用水头H z 情况下的流量系数m z 的比值参照附表3。

2.设有胸墙的堰面曲线。

当校核情况下最大作用水头H z max（孔口中心线上)与孔口高(D)的比值5.1max＞DHz时；或闸门全开时仍属孔口泄流,即可按下式计算:sHxy224ϕ=（附2)式中H s——定型设计水头，一般取孔口中心线至水库校核洪水位的水头的75％～95％；ϕ——孔口收缩断面上的流速系数,一般取ϕ=0.96；若孔前设有检修闸门槽时取ϕ=0.95。

其余符号参照附图2。

附图2原点上游可用单圆，复式圆或椭圆曲线，与胸墙底缘通盘考虑。

若5.12.1max＜＜DHz时，应通过试验决定。

H s/H z max0。

75 0。

775 0.80 0。

825最大负压值(m）0.5H s0。

45H s0。

4H s0.35H sH s/ H z max0.85 0.875 0。

90 0.95 1.0 最大负压值（m) 0。

3H s0。

25H s0.2H s0.1H s0。

挡土墙泄水管计算公式
首先，我们需要明确挡土墙的结构和泄水管的类型。

一般来说，挡土墙主要由墙身和基础组成，而泄水管则分为不同的型号和规格。

我们需要确定泄水管的数量和位置。

根据挡土墙的设计图纸，我们可以计算出每个泄水管的尺寸和数量。

一般来说，泄水管的高度和宽度可以根据墙身的高度和宽度来确定，而泄水管的数量则取决于墙身的面积和泄水管的位置。

在确定了泄水管的尺寸和数量之后，我们可以根据以下公式进行计算：
π·r²·h+π·(r+d)²·h-π·r²·d=墙身面积，其中，π为圆周率，r为半径，h为高度，d为直径。

具体来说，这个公式的作用是将墙身面积按照泄水管的数量分配到每个泄水管的位置上。

同时，我们还需要考虑到墙身和泄水管的实际情况，例如泄水管的材质、厚度等因素。

还需要注意一些细节问题。

例如，泄水管的数量和位置应该根据实际情况进行调整，以确保墙身的稳定性和泄水效果。

同时，泄水管的型号和规格应该根据墙身的实际情况进行选择，以确保能够满足墙身的排水需求。

为了确保计算结果的准确性，我们需要考虑到一些可能的影响因素。

例如，墙身的坡度、土壤的湿度、地质条件等都可能对泄水管的数量和位置产生影响。

因此，在进行计算时，我们需要对实际情况进行充分的调研和分析，以确保最终的计算结果能够满足实际需求。

总之，挡土墙泄水管计算公式可以帮助我们确定泄水管的尺寸、数量和位置，确保墙身的稳定性和排水效果。

在实际应用中，我们需要根据实际情况进行充分的调研和分析，以确保最终的计算结果能够满足实际需求。

B——引渠段底宽度（m）；
（注：绿色为一次输入数据）20.40
v 0——引渠段行进流速（m/s）； 2.86
H——堰上水深（m）；
（注：红色为对比输入数据）8.70
g——重力加速度，可采用9.81（m/s 2）；9.81H 0——计入行进流速水头的堰上水深（m）；9.12h e ——孔口高度（m）； 3.50 ——孔流流速系数，可采用0.95～1.0；0.98r——胸墙底圆弧半径（m）；
0.20
计算系数，可由公式（A.0.3-4）计算求得，该公式适用于0<r/h e <0.25
0.160
孔流垂直收缩系数，可按公式（A.0.3-3）计算求得；
0.732
孔流流量系数，可按公式（A.0.3-2）计算求得或由表A.0.3-1查得；
0.602 ——孔流淹没系数，可由表A.0.3-2查得；
1.000B 0——闸孔总净宽（m），可按公式（A.0.3-1）计算求得。

18.00Q——假拟过闸流量（m 3/s）；507.56
Q——过闸流量（m 3/s）；
507.56
对于平底闸，当为孔流时，闸孔总净宽可按公式（A.0.3-1）～（A.0.3-4）计算（计
算示意图见图A.0.3）《水闸设计规范》SL265-2001ϕ'σH
h e '1'εϕεμ-
=⎥⎥
⎦
⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-+
=
2
111
'H h e λεe
h r 16718
.24.0=
λ30
02H g m B Q σε=。

厂房泄压面积计算公式厂房泄压面积计算是在工程设计中非常重要的一项计算工作。

厂房泄压面积指的是在厂房内发生事故时，通过厂房的泄压装置所泄出的气体或液体的面积。

泄压面积的计算对于保障人员的安全以及减少财产损失具有重要意义。

厂房泄压面积的计算公式是一个基本的公式，可以通过该公式来计算泄压装置的面积。

该公式的计算结果可以作为设计厂房泄压装置的依据。

厂房泄压面积计算公式如下：A = Q / (Cd * √(2 * δ * P / ρ))其中，A为泄压面积；Q为泄压装置流量；Cd为泄压装置的流量系数；δ为泄压装置出口径向长度；P为泄压装置出口压力；ρ为泄压装置出口密度。

在使用该公式进行泄压面积计算时，需要明确以下几个参数的取值：1. 泄压装置流量Q：泄压装置流量是指单位时间内泄压装置泄出的气体或液体的体积。

该参数的取值需要根据具体的设计要求和事故情况进行确定，通常可以通过工程经验或者模拟计算得到。

2. 泄压装置的流量系数Cd：流量系数Cd是衡量泄压装置流量特性的一个参数，是由泄压装置的结构和设计参数决定的。

对于不同类型的泄压装置，Cd的取值也不同。

在实际工程中，可以通过试验或者参考相关标准来确定泄压装置的流量系数。

3. 泄压装置出口径向长度δ：泄压装置出口径向长度是指泄压装置出口径向方向上的长度。

该参数的取值需要根据实际情况进行确定，一般可以通过泄压装置的设计图纸或者实际测量得到。

4. 泄压装置出口压力P：泄压装置出口压力是指泄压装置出口处的气体或液体的压力。

该参数的取值需要根据实际情况进行确定，可以通过压力传感器或者其他测量设备进行测量。

5. 泄压装置出口密度ρ：泄压装置出口密度是指泄压装置出口处的气体或液体的密度。

该参数的取值需要根据实际情况进行确定，可以通过密度计或者其他测量设备进行测量。

通过以上参数的取值，可以使用厂房泄压面积计算公式来计算泄压装置的面积。

计算结果可以作为设计厂房泄压装置的依据，确保在发生事故时能够及时有效地泄压，保障人员的生命安全和财产的安全。

目次前言1 范围2 引用标准3 总则4 术语、符号5 重力坝布置6 坝体结构和泄水建筑物型式7 泄水建筑物的水力设计8 结构计算基本规定9 坝体断面设计10 坝基处理设计11 坝体构造12 坝体防裂及温度控制13 观测设计附录A (标准的附录) 堰面曲线、堰面压力及反弧段半径附录B (标准的附录) 坝身泄水孔体型设计附录C (标准的附录) 水力设计计算公式附录D (标准的附录) 坝基、坝体抗滑稳定抗剪断参数值附录E (标准的附录) 实体重力坝的应力计算公式附录F (标准的附录) 坝基深层抗滑稳定计算附录G (标准的附录) 坝体温度和温度应力计算条文说明1 范围本规范规定了重力坝的布置、结构计算、设计原则、温度控制和观测等技术要求。

本规范适用于水利水电大、中型工程岩基上的1、2、3级混凝土重力坝的设计，4、5级混凝土重力坝设计可参照使用。

对于坝高大于200m的混凝土重力坝设计，应作专门研究。

22引用标准33下列标准所包含的条文，通过在本标准中引用而构成本标准的条文。

在标准出版时，所示版本均为有效。

所有标准都会被修订，使用本标准的各方应探讨使用下列标准最新版本的可能性。

GB50199—94 水利水电工程结构可靠度设计统一标准 GB50201—94 防洪标准DL／T5039—95 水利水电工程钢闸门设计规范DL／T5057—1996水工混凝土结构设计规范DL5073—1997 水工建筑物抗震设计规范DL5077—1997 水工建筑物荷载设计规范DL／T5082—1998水工建筑物抗冰冻设计规范SD105—82 水工混凝土试验规程SD303—88 水电站进水口设计规范SDJ12—1978 水利水电枢纽工程等级划分及设计标准(山区、丘陵区部分) (试行) 及补充规定SDJ336—89 混凝土大坝安全监测技术规范(试行) SL48—94 水工碾压混凝土试验规程3 总则3.0.1 本规范是根据GB50199规定的原则制定的。

溢洪道设计规范篇一：水利工程设计水利工程设计（下）安徽省设计院总工程师骆克斌4.2 输水、泄水建筑物《强制性条文》共引入《溢洪道设计规范》SL253-2000共5条，其中有关布置方面1条，水力学2条，边坡稳定1条，基础防渗1条。

4.2.1 溢洪道1 溢洪道布置2 水力学问题3 边坡稳定问题4 基础防渗处理1 溢洪道布置SL253-2000第2.1.10条规定，当溢洪道靠近坝肩布置时，其布置及泄流不得影响坝肩及岸坡的稳定。

在土石坝枢纽中，当溢洪道靠近坝肩时，与大坝连接的接头、导墙、泄槽边墙等必须安全可靠。

2 水力学问题1）堰面压力设计标准针对溢洪道中特殊的水力学问题，规范第3.3.5条对实用堰堰顶附近堰面压力提出应满足下列规定：（1）对于常遇洪水闸门全开情况，堰面不应出现负压；（2）对于设计洪水闸门全开情况，堰顶附近负压值不得大于0.03Mpa；（3）对于校核洪水闸门全开情况，堰顶附近负压值不得大于0.06Mpa。

2 水力学问题2）水流空化数SL253-2000第3.7.2条规定，溢洪道各部位的水流空化数σ应大于该处体形的初生空化数σ1。

3 边坡稳定问题《强制性条文》引入该规范中第5.1.4条规定，溢洪道的边坡必须保持稳定,对可能失稳的边坡应采取适当的处理措施。

对地质条件复杂的高边坡尚应进行专门的研究及边坡监测设计。

对易风化掉块，易软化或抗冲能力低的稳定边坡也应进行相应的防护。

4 基础防渗处理《强制性条文》引入该规范第5.4.2条规定，防渗和排水设施的布设应满足下列要求：1）具有可靠的连续性和足够的耐久性。

2）防渗帷幕不得设置在建筑物底面的拉力区。

4.2.2 水工隧洞1 综述2 隧洞布置3 洞内水流流态的要求4 水工模型试验问题5 高流速水工隧洞的空化6 水工隧洞衬砌与裂缝控制7 不衬砌和采用喷锚衬护的水工隧洞8 灌浆和防渗1 综述水工隧洞包括发电引水隧洞、尾水隧洞、灌溉和供水隧洞、泄洪隧洞、排水隧洞、施工导流隧洞等。

水力计算公式选用水力计算是指通过水力学原理和公式来计算液体在管道、河道等流动过程中的各种参数和特性。

水力计算公式是水力学研究的基础，能够用来预测流体的流速、压力、流量等参数，对水利工程的设计和运行具有重要意义。

下面介绍几种常用的水力计算公式及其选用情况。

1.流量计算公式流量是指单位时间通过其中一截面的液体体积，常用的流量计算公式有：流量计算公式为：Q=A×v，其中Q为流量，A为流动截面的横截面积，v为流速。

该公式适用于对流量有明确要求的场合，如管道流量、水库泄洪流量等。

2.流速计算公式流速是指单位时间内通过其中一截面的液体速度，常用的流速计算公式有：流速计算公式为：v=Q/A，其中v为流速，Q为流量，A为流动截面的横截面积。

该公式适用于需要计算流速的情况，如河流流速、管道流速等。

3.压力计算公式压力是指液体对单位面积所产生的压力，常用的压力计算公式有：压力计算公式为：P=γh，其中P为压力，γ为液体的密度，h为液体的压力高度。

该公式适用于计算液体的静态压力，如水塔的压力、泵站的压力等。

4.速度计算公式速度是指液体在流动过程中的速度，常用的速度计算公式有：速度计算公式为：v=√(2gh)，其中v为速度，g为重力加速度，h为液体的压力高度。

该公式适用于计算液体的速度，如水流速度、潜流速度等。

5.阻力计算公式阻力是指液体在流动过程中由于各种因素的作用而产生的阻碍力，常用的阻力计算公式有：阻力计算公式为：f=KLRV^2/2g，其中f为阻力，K 为阻力系数，L为流动的长度，R为流动的半径，V为流体的速度，g为重力加速度。

该公式适用于计算流动中的阻力，如管道流动阻力、水泵阻力等。

在选用水力计算公式时，需要根据具体情况进行考虑。

首先要了解需要计算的参数，并根据参数的性质选择相应的计算公式。

其次要考虑计算公式的适用范围和精度，以及参数的测量方法和所需数据的可获取性。

最后还要结合实际应用需求，选择合适的计算公式进行计算和分析。

水工隧洞水力计算水工隧洞水力计算的内容，一般有：泄流能力计算、水头损失计算、绘制压坡线（有压流）、水面线的计算（无压流）。

1、泄流能力水工隧洞泄流能力计算，分有压流和无压流两种情况。

实际工程中，多半是根据用途先拟定隧洞设置高程及洞身断面和孔口尺寸，然后通过计算校核其泄流量。

若不满足要求，再修改断面或变更高程，重新计算流量，如此反复计算比较，直至满意为止。

（1）有压流的泄流能力有压流的泄流能力按公式（1）计算：02gH A Q μ= (1)式中Q ——泄流量；μ——流量系数；A ——隧洞出口断面面积；g ——重力加速度。

g H H 2200υ+=式中 H ——出口孔口静水头； g220υ——隧洞进口上游行近流速水头。

流量系数μ随出流条件不同而略有差异，自由出流和淹没出流分别按公式（2）和公式（3）计算：∑∑???? ??+???? ?+=222211i j i j j j A A R C gl A A ζμ (2) ∑∑ ??+???? ??+???? ??=2222221i I I i J j A A R C gl A A A A ζμ (3)式中 A ——隧洞出口断面面积；A 2——隧洞出口下游渠道过水断面面积；ζj ——局部水头损失系数；A j ——与ζj 相应流速之断面面积；L i 、A i 、R i 、C i ——某均匀洞段之长度、面积、水力半径和谢才系数。

上述泄流能力计算公工适用于有压泄水隧洞，对发电的有压引水隧洞，其过流能力决定于机组设计流量，即流量为已知，要求确定洞径。

（2）无压流的泄流能力无压泄水隧洞的洞身底坡常大于临界坡度，洞内水流呈急流状态，其泄流能力不受洞长影响，而受进口控制，若进口为深孔有压短管，仍可按公式(2)和公式(3)计算，而忽略其沿程水头损失（根号中的最后一项）。

表孔堰流进口的斜井式无压隧洞，其泄流能力由堰流公式计算：2/302H g mB Q ε= (4) 式中ε——侧收缩系数；m ——流量系数；B ——堰顶宽度（m ）；H 0——包括行近流速水头g 220υ的堰顶水头。

长距离输水管道水力计算公式的选用1． 常用的水力计算公式：供水工程中的管道水力计算一般均按照均匀流计算，目前工程设计中普遍采用的管道水力计算公式有:达西（DARCY ）公式：gd v l h f 22**=λ（1）谢才（chezy ）公式：i R C v **= （2）海澄－威廉（HAZEN-WILIAMS ）公式：87.4852.1852.167.10dC lQ h h f ***= （3） 式中h f ------------沿程损失，mλ―――沿程阻力系数 l ――管段长度，md-----管道计算内径，mg----重力加速度，m/s 2C----谢才系数 i----水力坡降； R ―――水力半径，mQ ―――管道流量m/s 2v----流速 m/sC n ----海澄――威廉系数其中大西公式，谢才公式对于管道和明渠的水力计算都适用。

海澄－威廉公式影响参数较小，作为一个传统公式，在国内外被广泛用于管网系统计算。

三种水力计算公式中 ，与管道内壁粗糙程度相关的系数均是影响计算结果的重要参数。

2． 规范中水力计算公式的规定3． 查阅室外给水设计规范及其他各管道设计规范，针对不同的设计条件，推荐采用的水力计算公式也有所差异，见表1：表1 各规范推荐采用的水力计算公式4． 公式的适用范围： 3．1达西公式达西公式是基于圆管层流运动推导出来的均匀流沿程损失普遍计算公式，该式适用于任何截面形状的光滑或粗糙管内的层流和紊流。

公式中沿程阻力系数λ值的确定是水头损失计算的关键，一般采用经验公式计算得出。

舍维列夫公式，布拉修斯公式及柯列勃洛克（C.F.COLEBROOK ）公式均是针对工业管道条件计算λ值的著名经验公式。

舍维列夫公式的导出条件是水温10℃，运动粘度1.3*10-6 m 2/s,适用于旧钢管和旧铸铁管,紊流过渡区及粗糙度区.该公式在国内运用教广. 柯列勃洛可公式)Re 51.27.3lg(21λλ+∆*-=d (Δ为当量粗糙度,Re 为雷诺数)是根据大量工业管道试验资料提出的工业管道过渡区λ值计算公式,该式实际上是泥古拉兹光滑区公式和粗糙区公式的结合,适用范围为4000<Re<108.大量的试验结果表明柯列勃洛克公式与实际商用圆管的阻力试验结果吻合良好,不仅包含了光滑管区和完全粗糙管区,而且覆盖了整个过渡粗糙区,该公式在国外得到及为广泛的应用.布拉修斯公式25.0Re 316.0=λ是1912年布拉修斯总结光滑管的试验资料提出的,适用条件为4000<Re<105,一般用于紊流光滑管区的计算. 3.2 谢才公式该式于1775年由CHEZY 提出,实际是达西公式的一个变形,式中谢才系数C 一般由经验公式y e R n C *=1计算得出,其中61=y 时称为曼宁公式,y 值采用)1.0(75.013.05.2---=n R n y (n 为粗糙系数)公式计算时称为巴浦洛夫斯基,这两个公式应用范围均较广.就谢才公式本身而言,它适用于有压或无压均匀流动的各阻力区,但由于计算谢才系数C 的经验公式只包括反映管壁粗糙状况的粗糙系数n 和水力半径R,而没有包括流速及运动年度,也就是与雷诺数Re 无关,因此该式一般仅适用于粗糙区.曼宁公式的适用条件为n<0.02,R<0.5m;巴浦洛夫斯基公式的适用条件为0.1m ≤R ≤3m;0.011≤n ≤0.04.3.3 海澄-威廉公式是在直径≤3.66m 工业管道的大量测试数据基础上建立的著名经验公式,适用于常温的清水输送管道,式中海澄-威廉系数Ch 与不同管材的管壁表面粗糙程度有关.因为该式参数取值简单,易用,也是得到广泛应用的公式之一.此公式适用范围为光滑区至部分粗糙度区,对应雷诺数Re 范围介于104-2*106.通过对各相关规范所推荐计算公式的比较,除混凝土管仍然推荐采用谢才公式外,其它管材大多推荐采用达西公式.在新版《室外给水设计规范》中取消舍维列夫公式的相关条文,笼统采用达西公式,但未明确要求计算λ值采用的经验公式.由于舍维列夫公式是建立在对旧钢管及旧铸铁管研究的基础上,然而现在一般采用的钢或铸铁材质管道,内壁通常需进行防腐内衬,经过涂装的管道内壁表面均比旧钢管,旧铸铁管内壁光滑得多,也就是Δ值小得多,采用舍维列夫公式显然也就会产生较大得计算误差,该公式得适用范围相应较窄.经过内衬得金属管道采用柯列勃洛克公式或谢才公式计算更为合理.PVC-U,PE 等塑料管道,或者内衬塑料得金属管道,因为其内壁Δ值很低,一般处于0.0015-0.015,管道流态大多位于紊流光滑区,采用适用光滑区得布拉修斯公式以及柯列勃洛克公式一般均能够得到与实际接近得计算结果.因此, 《埋地硬聚氯乙稀给水管道工程技术规程》及《埋地聚乙稀给水管道工程技术规程》中对塑料管道水力计算公式均是合理得且与《室外给水设计规范》并不矛盾. 海澄-威廉公式可以适用于各种不同材质管道得水力计算,其中海澄-威廉系数Ch 得取值应根据管材确定.对于内衬水泥砂浆或者涂装有比较光滑得内防腐涂层得管道,其海澄-威廉系数应该参考类似工程经验参数或者实测数据,合理取用.因此,无论采用达西公式,谢才公式或者海澄-威廉公式计算,不同管材得差异均表现在 管内壁表面当量粗糙程度得不同上,各公式中与粗糙度相关系数得取值是影响计算结果得重要因素.值得一提得是,同种材质管道由于采用不同得加工工艺,其内表面得粗糙度也可能有所差异,这一因素在设计过程种也应重视(常用管材得粗糙度系数参考值见表2) 表2 常见管材粗糙度相关系数参考值5.管径对选择计算公式得影响 根据雷诺数计算公式vVdRe ,雷诺数与流速v,管径d 成正比,与运动粘度成反比,因此对应管道得不同设计条件应对所使用计算公式得适用范围进行复核.保证计算得准确性.大多说供水工程得设计按照水温10℃,运动粘度1.3*10-5 m 2/s 得条件考虑,因此雷诺数实际受流速及管道口径得影响.以塑料管道为例,在正常设计流速范围条件下,管道内径大于100mm 时,虽然管道仍然处于紊流光滑区,但其雷诺数Re>105,也就是说已经超出了布拉修斯公式得适用范围,而且误差大小与雷诺数成正比.对PVC-U 管,采用布拉修斯公式与柯列勃洛克公式对比计算,当管内径为500mm ,流速1.5 m/s 时,采用布拉修斯公式得出得水力坡降比柯列波列克得结果低11%以上.采用《埋地硬聚氯乙稀给水管道工程技术规程》推荐得修正公式与柯式对比计算,修正公式计算结果,小口径管偏安全,中等口径与柯式符合较好,大口径管得负误差达5%以上.因此笔者认为,大口径塑料管或采用塑料内衬管不宜采用布拉修斯公式计算,而更宜于采用如柯列波洛克公式等适用条件更宽得其它经验公式,或应通过试验等对其进行修正.与上述情况类似,采用谢才公式计算时,如果管道内径大于2m 时则不采用曼宁公式计算谢才系数.如果采用巴甫洛夫斯基公式,其适用管径可以达到12m,对一般输水工程管道已完全足够了.海澄-威廉公式的数据基础是WILLIAMS 和HAZEN 在大量工业管道现场或试验测量或得的.该公式因为简单易用,被广泛运用在管网水力计算中,国内外不少管道水力计算软件均采用该公式编制.由此可见,对于口径大于2m 得管道应尽量避免采用海澄-威廉公式计算以策安全.6.值得提出得是,上述所有水力计算公式中采用得管径均为计算内径,各种管道均应采用管道净内空直径计算,对于采用水泥砂浆内衬得金属管道应考虑内衬层厚度得影响.大口径管道计算应尽量避免采用海澄-威廉公式,建议采用柯列勃洛克公式计算,大量试验结果证明该公式计算结果与实际工业管道符合性好,水力条件适用范围广,虽然运用该式需要进行多次迭代计算才能得到λ值,较为麻烦,不过运用计算机简单编程既能方便地得到较为准确地结果,手工计算时也可以通过查表或者查询蓦迪图辅助计算.。

《防洪标准》（GB50201-94）特大型工矿企业 一等工程设计：100年一遇校核：200年一遇《堤防工程设计规范》（GB50286-98）堤防工程一级堤防工程的安全超高值：不允许越浪的工程， 1.00m 1、2级的堤顶超高值不应低于2.00m堤顶超高按下式计算：Y=R+e+A其中：Y ：堤防超高；R ：波浪爬高；e ：风雍水面高度；A ：安全超高。

波浪爬高计算：最大风壅水面高度按下式计算：式中：K—综合摩阻系数，取3.6×10-6；W—计算风速，（取24m/s ）D—风区长度，取1500m ；H m —水域的平均水深0.6m ；β—计算风向与坝轴线法线的夹角（度）。

计算时，假设风向与坝轴线垂直，即cosβ＝1。

平均波浪爬高按以下公式计算：式中──累积频率为p 的波浪爬高（m ）；──斜坡的糙率及渗透性系数；──经验系数，1.30；──爬高累积频率换算系数； ｍ──斜坡坡率，ｍ＝ctgα，α为斜坡坡角（度）；──堤前波浪的平均波高（m ）； Ｌ──堤前波浪的波长（m ）。

波浪的平均波高和平均波长高按以下公式计算： β=cos gH 2D KW e m 2L H m K K K R p v p 21+=∆pR ∆K VK p K H ⎪⎪⎩⎪⎪⎨⎧⎢⎢⎣⎡⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛=0245.027.0227.013.00018.07.013.0V gd th V gF th V gd th v H g 5.0239.1⎪⎪⎭⎫ ⎝⎛=V H g V gT 45.3min 168⎪⎪⎭⎫ ⎝⎛=V T g V gt 式中　H──平均波高（m ）； T──平均波周期（s ）； V──计算风速，17（m ／s ）； F──风区长度，400（m ）； ｄ──水域的平均水深，5（m ）； ｇ──重力加速度，9.81；──风浪达到稳定状态的最小风时（s ）。

经计算，风壅高度0.18m ，波浪爬高为0.20m ，合计0.38m 。

附录一泄水建筑物水力设计计算定律泄水建筑物是指在危急情况下，为了保护人员安全和减少财产损失而特别设计的建筑物。

为了确保泄水建筑物的设计合理和安全可靠，需要进行水力设计计算。

水力设计计算是根据一定的物理原理和定律，通过计算得出泄水建筑物的设计参数和尺寸。

以下是几个常用的水力设计计算定律。

1.布努利定律布努利定律是水力学中的基本定律，它描述了理想流体在流动过程中的能量守恒关系。

布努利定律的数学表达式为：P + ρgh + 1/2ρv² = 常数其中，P为流体的压强，ρ为流体的密度，g为重力加速度，h为流体的重心高度，v为流体的速度。

布努利定律适用于理想流体在流动过程中速度、压强和高度之间的相互关系。

2.库伯定则库伯定则是根据努西二次定律推导出的，它描述了流体在管道中的流动状态。

库伯定则的数学表达式为：Q=A·v其中，Q为单位时间内通过管道的流量，A为管道的横截面积，v为流体的速度。

库伯定则说明了在稳定流动状态下，管道的流量与管道横截面积和流体速度之间存在着确定的关系。

3.空气动力学定律空气动力学定律适用于泄水建筑物中空气流动的计算。

空气动力学定律描述了空气在流动过程中的压强和速度之间的关系。

根据空气动力学定律，可以计算出泄水建筑物中空气流量和压力的大小。

4. stoppy模型stoppy模型是一种常用的泄水建筑物水力设计计算模型，它基于实验数据和理论分析，可以较准确地预测泄水建筑物的性能。

stoppy模型可以计算出泄水建筑物的泄水能力、排水时间等参数，从而为泄水建筑物的设计提供参考。

总之，水力设计计算是泄水建筑物设计的重要组成部分。

通过应用布努利定律、库伯定则、空气动力学定律和stoppy模型等水力设计计算定律，可以确保泄水建筑物的设计合理、安全可靠。

在实际设计中，还需要考虑材料的耐久性、结构的稳定性等因素，以满足泄水建筑物的使用要求。

第五章泄水建筑物体型和轮廓尺寸选定的水力设计第一节堰坝水流与堰型问题任何水利枢纽都有泄洪建筑物,为安全计,其泄流方式多采用表孔堰流。

枢纽中的拦河坝为混凝土坝时，常将一段拦河坝布置成溢流坝；拦河坝为土石坝时，一般须布置河岸溢洪道。

本节先以高溢流坝和河岸开敞式正槽溢洪道的控制堰为对象，讨论其体型选择和轮廓尺寸布置的有关水力学问题。

一、溢洪道控制堰堰型及其水力特性作为溢洪道的控制堰,其体型、尺寸和布置方式是溢洪道泄流能力的决定性因素。

不同的泄流能力，洪水期可能出现的水库最高洪水位和相应要求的坝高不同，因此，控制堰的设计是否合理，直接关系到枢纽布置方案的优劣。

这里我们仅从水力学观点分析一些主要堰型的水力持性。

控制堰在平面上可呈直线或曲线.一般大体积混凝土溢流坝、河岸正槽溢洪道都常将堰顶轴线布置为直线;溢流拱坝坝顶为曲线。

河岸溢洪道也有采用曲线堰顶布置的，如墨西哥式溢洪道，主要用于山区小型水库无闸门控制的溢洪道。

控制堰的水力特性很大程度上取决于沿水流向垂直剖面的形态，剖面形态不同，其水力特性、适用条件也不同.对于实用堰，首先应确定是非真空堰还是真空堰，是高堰还是低堰。

非真空堰与真空堰的区别，在于是否依赖堰顶附近水流底部的适当负压(真空度)来保证运行工况的泄流能力；高堰与低堰的区别，在于堰的上游堰高与堰顶运行水头之比是否足够大．从而使堰的泄流能力不再受此相对堰高的影响。

大部分溢流坝或溢洪道，为减免负压可能导致的有害后果，常采用非真空剖面堰，溢流坝通常属高堰；河岸溢洪道的控制堰既可能是高堰，也可能是低堰。

在实际工程中，适当控制堰顶负压值的真空剖面堰也不乏先例。

（一)非真空实剖面高堰非真空实用堰的堰型选择原则，应以其能在较大的堰顶水头变化范围内有较大的流量系数，且堰面不产生危害性负压为标准。

这使人易于想到，实用堰堰顶曲线可按薄壁堰自由溢流水舌下缘进行构制。

早在1888年，巴赞(Bazin)首次用上述原则得到了巴赞实用堰剖面，认为沿该堰面溢流将不产生负压。

泄水口水力计算9．3．1 泄水口的水力计算，应包括依据设计流量和截流要求确定泄水口的尺寸和布设间距等内容。

9．3．2 在纵坡坡段上的开口式泄水口，设计泄水量应根据开口长度L i、低凹区的宽度B w、下凹深度h a以及过水断面的纵向坡度i z和横向坡度i h确定，如图9．3．2所示。

可利用附录C中图C-1～图C-6查取截流率（Q0/Q c）后，按过水断面泄水能力Q c确定其设计泄水量Q0，泄水口开口长度、下凹区宽度和下凹深度取值应根据喇叭口的形状和尺寸确定。

图9．3．2 开口式泄水口周围的水流状况1-拦水带或缘石；2-低凹区条文说明在纵坡坡段上，开口式泄水口的截流率主要随开口长度的增加而增大，也同开口处是否设置低凹区有关。

低凹区越宽，下凹深度越大，截流量便越大。

由于计算公式较烦琐，因此，本规范推荐采用诺模图的形式，并列出了几种常用开口长度和低凹区尺寸组合条件下的截流率计算用图（见附录C）。

9．3．3 在凹形竖曲线底部的开口式泄水口的设计泄水量，应按泄水口处的水深和泄水口的尺寸确定。

1 开口处设有低凹区，当开口处的净高h0大于或等于由图9．3．3-1确定的满足堰流要求的最小高度h m时，可利用图9．3．3-2确定开口的泄水量Q0或最大水深h i。

图9．3．3-1 开口式泄水口满足堰流要求的最小开口高度h m计算图图9．3．3-2 开口处净高h0大于或等于h m时开口的泄水量Q0或最大水深h i计算图 2 不设低凹区时可按式（9．3．3-1）确定其泄水量Q0。

（9．3．3-1）3 当开口处水深h i超过净高h0的1．4倍时，可按式（9．3．3-2）确定其泄水量Q0。

Q0＝13．14h0L i（h i－0．5h0）（9．3．3-2）条文说明在凹形竖曲线底部，表面水由前后两个方向向下流入泄水口。

水流进入泄水口的状态，同该处的水深有关。

当水深低于泄水口的孔口高度（即拦水带或缘石高度）时，水流呈堰流状态。

而当水深淹没开口，超过1．4倍孔口高度时，水流呈孔口流状态。