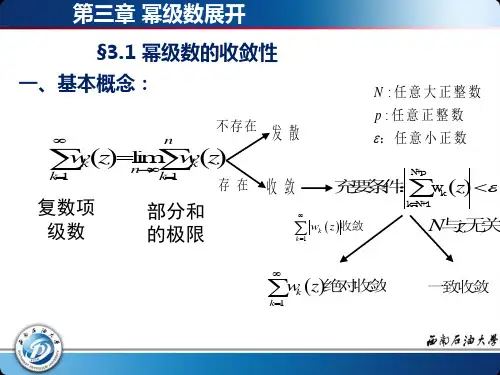
幂级数展开法部分分式展开法围线积分法——留数法自学
- 格式:ppt
- 大小:474.50 KB
- 文档页数:11



数学物理方法_第三章_幂级数展开幂级数展开是数学物理中常用的一种方法,它是通过使用幂级数来表示一个函数,从而方便对函数进行近似计算和分析。
在许多问题中,幂级数展开可以简化计算的复杂性,帮助我们更好地理解问题的本质。
幂级数是一个无穷级数,形式为:f(x)=a0+a1(x-x0)+a2(x-x0)^2+a3(x-x0)^3+...其中,a0、a1、a2...是常数系数,x0是展开点。
幂级数展开可以将一个任意函数表示成一个级数,进而通过截断级数的方式来近似求解。
这种展开方法在物理学和工程学中得到广泛应用。
幂级数展开的理论基础是泰勒级数展开,泰勒级数展开是幂级数展开的一个特殊情况。
泰勒级数展开是指将任意可导函数在其中一点x0附近展开成幂级数。
泰勒展开的前n+1项可以用n阶导数来表示,形式如下:f(x)=f(x0)+f'(x0)(x-x0)+f''(x0)(x-x0)^2/2!+f'''(x0)(x-x0)^3/3!+...+f^n(x0)(x-x0)^n/n!+...幂级数展开的应用非常广泛,它在数学、物理、工程学和计算机科学中都有着重要的地位。
以下是幂级数展开的几个典型应用:1.函数逼近幂级数展开是一种有效的函数逼近方法。
通过截断幂级数,我们可以用其前几项来近似计算函数的值。
这对于高阶函数和复杂函数来说是非常有用的,因为我们可以通过截断级数来减少计算的复杂性。
2.微分方程的求解使用幂级数展开的方法可以求解一些特定的微分方程。
对于一些微分方程,无法找到解析解,但通过将解展开成幂级数的形式,可以将微分方程转化为代数方程,从而求得解的逼近解。
3.近似计算幂级数展开是一种常用的近似计算方法。
通过截取幂级数的前几项,我们可以将一个复杂的函数近似成一个简单的形式,从而方便我们进行数值计算。
4.解析几何的研究在解析几何中,幂级数展开是研究曲线和曲面的重要工具。
通过展开曲线或曲面,我们可以对其性质进行分析和计算,帮助我们更好地理解几何问题。

1引言函数的幕级数展开在高等数学中有着重耍的地位,在研究泵级数的展开之 前我们务必先研究一下泰勒级数,因为泰勒级数在幕级数的展开屮有着重要的地 位。
一般情况,我们用拉格朗日余项和柯西余项来讨论幕级数的展开,几乎不用 积分型余项来讨论,今天我们的研究中就有着充分的体现。
2泰勒级数泰勒定理指出:若函数/在点兀。
的某个邻域内存在直至斤阶的连续导数,则/(x) = /(x 0) + /(x 0)(x-x 0) + /(x Q )^X这里心(兀)=。
((兀-兀)〃)称为皮亚诺型余项。
如果增加条件“/(X )有H + 1阶连续 导数”,那么心(0还可以写成三种形式(柯西余项) (积分型余项) 如果在(1)中抹去余项心(X ),那么在兀。
附近/可用(1)式中右边的多项式来近似代 替。
如果函数/在兀=兀0处有任意阶的导数,这吋称形式为:的级数为函数/在x 0的泰勒级数,对于级数(2)是否能够在X 。
附近确切地表达/, 或说/在心泰勒级数在心附近的和函数是否就是/,这是我们现在耍讨论的问 题。
下面我们先看一个例子:例1山由于函数/(%)= \ 八,心 °,(拉格朗日余项)心。
)+广(%)(-切+%(—订+・・・+匚糾 (兀一兀0)+…(2)= 广“+1)[兀+0(兀_观卄(]_0)〃 (兀_观)〔0, x = 0,在x = x0处的任何阶导数都为0,即/叫0) = 0/= 1,2,…,所以/在x = 0处的泰勒级数为:C C 0 2 . 0 “0 + 0 • X H X + -------- ------- X+…,2! nl显然,它在(- oo,+oo)上收敛,且其和函数S(X)= 0,由此看到对一切* 0都有/(X)H S(X),这说明具有任意阶导数的函数,其泰勒级数并不是都收敛于函数本身,只有lim R n (x) = 0HT8时才能够。
在实际应用上主要讨论在勺=0的展开式。
这时(2)也可以写成刑)+以乩+皿宀…+创乩"+…,1! 2! /1!称为麦克劳林级数。