恒高教育七年级数学上册11正数和负数
- 格式:ppt
- 大小:1.38 MB
- 文档页数:17

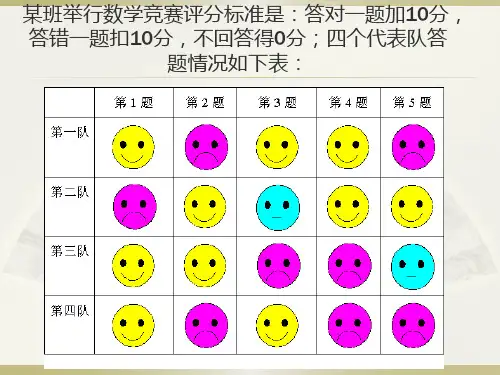
1.1正数和负数知识要点:1.大于0的数叫正数.小于0的数叫负数.一个数前面的“ +号叫做它们的符号・“ + ”号通常省略不写.2.0既不是正数也不是负数.3.如果一个问题中出现相反意义的量,我们可以用正数和负数分別表示它们.温馨提示:1•判断一个数是正是负,不能仅仅看其前面的符号.2.0既不是正数也不是负数.方法技巧:1.用正负数表示相反意义的量时,应先找到基准量,再规定相反意义的量屮的一个为正,则另一个为负.2.寻找一列数的规律时,通常从符号、与去掉符号后的数字两个方面入手分别寻找规律.2 51、在 T, +7, 0, 一一,二中,负数有()316A、1个B、2个C、3个D、4个专题一用正负数表示相反意义的量2、“牛牛”饮料公司的一种饮料包装上有"500±30mL”字样,其中500表示标准容量是500mL, +30表示最多不超过30mL,那么_30表示___________________________________3、近期,某市“曼菲庄园”生产的蓝裁包装纸箱上标明蓝館的质量为5鳥爲千克,如果这箱蓝裁重4. 98千克,那么这箱蓝莓质量_______ 标准.(填“符合”或“不符合”)4、“佳佳”超市2017年下半年的营业额与2016年同月营业额相比的增长率如下:月份7 8 9 10 11 12比上年同一1.8 0 0.2 -1.5 0.3 0.4月增长(%)请问:(1)“佳佳”超市2017年下半年的营业额与2016年同月营业额相比,哪儿个月是增氏的?(2)2017年7月和2016年10月比上年同月增长率是负数,表示什么意思?(3)2017年下半年与2016年下半年同月份相比营业额没有增长的是哪儿个月?5、一种商品的标准价格是200元,但随着季节的变化,商品的价格可浮动±10%,想-•想.(1)±10%的含义是什么?(2)请你计算出该商品的最高价格和最低价格;(3)如果以标准价格为基准,超过标准价记“ + ”,低于标准价记“一”,该商品价格的浮动范圉又可以怎样表示?6、王老师是七年级(1)班数学老师,王老师先拿出一支新买的2B铅笔,请5位同学估计这只铅笔的长度,并把它们的估计的值写在了黑板上,如图所示:下图是王老师让学生用刻度尺测量这支铅笔的图片:(单位:厘米):(1)请读出这支铅笔的长度,再以它为基准,大于这个值的规定为正,小于这个值的为负,用正、负数表示五位同学对这支铅笔的估计出的五个数。

新人教版七年级上册数学11正数和负数教案人教版义务教育教科书◎数学七年级上册1.1正数和负数内容简介1.《正数和负数》是人教版义务教育教科书七年级数学第一章第一节.2.“正数与负数”是“有理数”一章的第一节课,引入负数是实际的需要,也是学好后续内容的需要.本节先回顾数的产生和发展,然后通过引言中温度、产量增长率、收支情况的实例,引出负数,进而给出正数与负数的描述性定义并进一步介绍正负数在实际生活中的应用.学情分析1.学生已经学过了正整数、正分数和零的知识,即正有理数及“”的知识,还学过用字母表示数的知识,这些都是研究本节内容的基础.2.负数是一个比较抽象的概念,为了让学生能比较容易理解负数,要多采用从学生的生活实际出发,让学生理解由于知识面的不断扩大,引入负数的必要性.教学目标1.借助生活中的实例,感受引入负数的必要性,认识到数的产生和发展离不开生活和生产的需要.2.知道什么是正数和负数,并会用正、负数表示实际问题中的数量.3.理解数“”表示的量的意义.4.体会数学符号与对应的思想,用正、负数表示具有相反意义的量的符号化方法.5.通过本节课的研究,培养观察、想象、归纳与概括的能力.6.通过正负数的研究,渗透对立、统一的辩证思想.教学重点1.知道什么是正数和负数.2.理解数“”表示的量的意义.教学难点理解负数、数“”表示的量的意义.教学策略1.通过师生共同活动,创设问题情景,展示一些在实际生活中出现“负数”应用的图片,激发学生对新知识的兴趣,引入“负数”.2.通过学生主动研究和研讨,让学生自己完成对负数概念的引入.3.课前把学生分成几个研究小组,培养学生主动研究与合作研究的能力.教学资源1.教具:电脑、PPT课件(或相应图片)、投影仪.2.学具:地图册等.1教师备课系统──多媒体教案3.多媒体教室.教学时数2课时.2人教版义务教育教科书◎数学七年级上册第1课时教学内容1.1正数和负数.教学目标1.整理前两个学段学过的整数、分数(包括小数)的知识,掌握正数和负数的概念.2.能区分两种相反意义的量,会用符号表示正数和负数.3.体验数学发展的一个重要原因是生活实际的需要,激发学生研究数学的兴趣.教学重点两种相反意义的量.教学难点正确区分两种相反意义的量.教学过程一、设置情境引入课题上课开始时,教师应经由进程详细的例子,扼要申明在前两个学段我们已经学过的数,并由此请学生斟酌:糊口中仅有这些“以前学过的数”够用了吗?下面的例子仅供参考.师:今天我们已经是七年级的学生了,我是你们的数学老师.下面我先向你们做一下自我介绍,我的名字是XXX,身高1.76米,体重74.5千克,今年33岁.我们的班级是七(1)班,有50个同学,其中男同学有27个,占全班总人数的54%……问题1:老师刚才的介绍中呈现了几个数?分别是什么?你能将这些数按以前学过的数的分类方法进行分类吗?学糊口动:斟酌,交流师:以前学过的数,实际上主要有两大类,分别是整数和分数(包括小数).问题2:在生活中,仅有整数和分数够用了吗?请同学们看课本(观察本节前面的几幅图中用到了什么数,让学生感触感染引入负数的需要性)并斟酌讨论,然后进行交流.(也可以出示气象预报中的气温图,地图中表示地形上下地形图,工资卡中存取钱的记录页面等)学生交流后,教师归结:以前学过的数已经不够用了,有时分需要一种前面带有“-”的新数.二、分析问题探究新知问题3:前面带有“-”(负)号的新数我们应怎样命名它呢?为什么要引入负数呢?通常在日常生活中我们用正数和负数分别表示怎样的量呢?3教师备课系统──多媒体教案发起教师以本章引言中的实例加以申明.这些问题都必需要求学心理解.教师可以用多媒体出示这些问题,然后师生交流.也可以让学生浏览本章引言中的实例,并斟酌上面的问题.明确:上述问题中,表示温度、产量增长率、收支情况时,既要用到数3,1.8%,3.5等,还要用到数-3,-2.7%,-4.5,-1.2等,它们的实际意义分别是:零下3摄氏度,减少2.7%,支出4.5元,亏空1.2元.我们知道,像3,1.8%,3.5这样大于的数叫做正数.像-3,-2.7%,-4.5,-1.2这样在正数前加符号“-”(负)号的数叫做负数.有时,为了明确表达意义,在正数前面也加上“+”(正)号.夸大:用正、负数表示实际问题中具有相反意义的量,而相反意义的量包含两个要素:一是它们的意义相反,如向东与向西,支出与支出;二是它们都是数量,而且是同类的量.三、举一反三思惟拓展经过上面的讨论交流,学生对为什么要引入负数,对怎样用正数和负数表示两种相反意义的量有了初步的理解,教师可以要求学生举出实际生活中类似的例子,以加深对正数和负数概念的理解,并开拓思维.问题4:请同学们举出用正数和负数表示的例子.问题5:你是怎样理解“正整数”、“负整数”、“正分数”和“负分数”的呢?请举例说明.四、实例练训练深化认识教科书第3页例题.例(1)一个月内,XXX体重增长2 XXX,XXX体重减少1 XXX,XXX体重无变化,写出他们这个月的体重增长值.(2)某年,下列国家的商品进口总额比上年的变化情况是:美国减少6.4%,德国增长1.3%,法国减少2.4%,英国减少3.5%,意大利增长0.2%,中国增长7.5%.解:(1)这个月XXX体重增长2 XXX.XXX体重增长-1 kg,XXX体重增长0 XXX.(2)六个国家这一年商品进出口总额的增长率是:美国-6.4%,德国1.3%,法国-2.4%,英国-3.5%,意大利0.2%,中国7.5%.五、小结围绕下面两点,以师生共同交流的方式进行.1.由于实际问题中存在着相反意义的量,以是要引入负数,这样数的范围就扩展了.4人教版义务教育教科书◎数学七年级上册2.正数就是以前学过的以外的数(或在其前面加“+”),负数就是在以前学过的以外的数前面加“-”.本课作业:教科书第5页题1.1第1,2,4,5题.本课评析密切联系糊口实际,创设进修情境.本课是有理数的第一节课时.引入负数是数的范围的一次重要扩展,学生脑筋中关于数的结构要做重大调整(其实是一次知识的顺应进程),而负数相对于以前的数,对学生来说显得更抽象,因此,这个观点其实不是一下就能建立的.为了接受这个新的数,就必需对原本的数的结构进行收拾整顿.负数的发生主要是由于原本的数不够用了(不能正确简洁地表示数量),书本的例子或图片中呈现的负数就是让学生去感触感染和体验这一点.使学生接受糊口生产实际中的确存在着两种相反意义的量是本课的教学难点,以是在教学中可以多举几个这方面的例子,而且所举的例子又应该吻合学生的年龄和思惟特性.当学生接受了这个事实后,引入负数(为了区分这两种相反意义的量)就是顺理成章的事了.这个教学设计突出了数学与实际糊口的紧密联系,使学生体会到数学的应用价值,表现了学生自主进修、合作交流的教学理念,书本中的图片和例子都是糊口生产中常见的事实,学生容易接受,以是应该让学生自己看书、进修,而且勉励学生讨论交流,教师作适当引导便可以了.第2课时教学内容1.1正数和负数.教学目标1.经由进程对数“”的意义的探讨,进一步理解正数和负数的观点.2.利用正负数正确表示相反意义的量(规定了指定方向变化的量).3.进一步体验正负数在生产生活实际中的广泛应用,提高解决实际问题的能力,激发研究数学的兴趣.教学重点正确理解和表示向指定方向变化的量.教学难点深化对正负数概念的理解.教学进程一、知识回顾深化理解回顾:上一节课我们知道了在实际生产和生活中存在着两种不同意义的量,为了区分这两种量,我们用正数表示其中一种意义的量,那么另一种意义的量就用负数来表示.这就是说:数的范围扩大了(数有正数和负数之分).那么,有没有一种既不是正数5教师备课系统──多媒体教案又不是负数的数呢?问题1:有没有一种既不是正数又不是负数的数呢?学生思考并讨论.(数既不是正数又不是负数,是正数和负数的分界,是基准.这个道理学生其实不容易理解,可视学生的讨论情况作些开导和引导,下面的例子供参考.)例如:在温度的表示中,零上温度和零下温度是两种不同意义的量,通常规定零上温度用正数来表示,零下温度用负数来表示.那么某一天某地的最高温度是零上7℃,最低温度是零下5℃时,就应该表示为+7℃和-5℃,这里+7℃和-5℃就分别称为正数和负数.那末当温度是零度时,我们应该怎样表示呢?(表示为℃),它是正数还是负数呢?由于零度既不是零上温度也不是零下温度,以是,既不是正数也不是负数。