5 回转器 电路仿真

利用运算放大器构成回转器电路的研究电22 王明轩2012010905 电22 李自帅2012010916 摘要：回转器是基本的电路元件之一，它在电力处理和信号处理电路中具有广泛的应用。

本文以采用运算放大器实现回转器的电路为例，讨论了回转器的端口特性及其性质，并运用Multisim对分析结果进行了仿真验证。

关键词：回转器运算放大器仿真一、背景介绍回转器(Gyrator)的是现代网络理论中使用的一种双口电阻元件，其元件符号如图所示：回转器(gyrator)是一种具有电阻倒换或电感与电容倒换性质的二端口元件，由特勒根提出并加以命名的基本电路元件。

目前，回转器已做成IC模块供用户使用，是无电感滤波器中的重要元件。

它在信号处理和元件转换中具有独特的作用。

课上学习回转器过程中，对其“回转”功能（尤其是可以将电容转变为电感应用在集成电路中）产生浓厚兴趣。

因此选取课本上所给的由运算放大器构成的回转器电路结合仿真进行研究，电路如右图所示。

二、原始电路分析1.理论分析（1）回转器的实现电路如下：由运放的“虚短”和“虚断”可得：由电阻的串联可知：故：，故类似的，可以求出：故：满足回转器的参数矩阵，及实现了回转器的要求。

（2）利用回转器实现电容到电感的回转。

在电路的又端口接一个电容原件C，此时有：由回转器的特性方程可得：可以令C便实现了电容到电感的回转。

2.仿真验证仿真过程中，令所有R=1kΩ，电源内阻rr=500Ω。

（1）直流特性令负载RL=1k Ω，连接仿真电路如图：R7进行直流扫描分析其回转功能，输出值即为U2/I1、 U1/I2,结果如图：可见当电压绝对值在一定范围内时，这两个比值绝对值都恒定在1k Ω附近，符合理论分析的回转器回转特性。

如果输入电压绝对值过大或过小，运放不再工作在线性工作区，回转特性无法实现。

（2）交流特性及将电容“回转”为电感的功能。

输入换为交流电源，并将负载换为10μF 电容，仿真电路如图：进行交流分析，输出量为输入电压和电流，结果如图由其相频特性曲线可看出在中频段时，电流领先电压约为90°，即实现了由电容回转为电感的功能。

五级数模转换电路原理及设计方案一、五级数模转换电路的原理1.比较器：比较器是将模拟信号与参考电平进行比较的电路。

当输入信号大于参考电平时，比较器输出高电平；当输入信号小于参考电平时，比较器输出低电平。

2.积分器：积分器是通过对输入信号进行积分，将模拟信号转换为电压值。

积分器的输出电压与输入信号的积分成正比。

3.控制电路：控制电路控制比较器和积分器的工作方式。

它将比较器的输出和积分器的输出进行比较，并根据比较结果来控制比较器和积分器的工作。

1.将输入信号与参考电平输入到比较器中进行比较。

2.如果输入信号大于参考电平，比较器输出高电平；如果输入信号小于参考电平，比较器输出低电平。

3.将比较器的输出输入到积分器中进行积分。

4.根据比较器的输出和积分器的输出，控制比较器和积分器的工作。

5.重复以上步骤，将模拟信号逐渐转换为数字信号。

二、五级数模转换电路的设计方案1.确定比较器的参数：根据输入信号的幅值和参考电平确定比较器的输入电压范围。

2.确定积分器的参数：根据输入信号的频率和积分时间确定积分器的电容和电阻值。

3.选择合适的控制电路：根据比较器和积分器的输出确定合适的控制电路。

4.进行电路仿真：利用仿真软件进行电路仿真，验证电路的设计方案。

5.制作五级数模转换电路：根据电路的设计方案，进行电路的布线和焊接。

6.调试电路：对电路进行调试，检查电路是否正常工作。

7.进行测试和优化：对电路进行测试，根据测试结果进行电路的优化。

总结：五级数模转换电路是一种将模拟信号转换为数字信号的电路。

它通过比较器、积分器和控制电路实现模拟信号到数字信号的转换。

设计五级数模转换电路需要确定比较器和积分器的参数，选择适合的控制电路，并进行电路仿真、制作、调试和优化。

五级数模转换电路能够将连续变化的模拟信号转换为离散的数字信号，实现数字系统的处理和分析。

五、运放实现回转器仿真实验一、电路课程设计目的1、了解回转器的基本特性及其运放实现；2、掌握回转器参数的测试方法，了解回转器的应用。

二、仿真电路设计原理回转器的概念是B.D.H.Tellegen 于1948年提出的。

六十年代由L.P .Huelsman 及B.A.Sheei 等人用运算放大器及晶体管电路实现。

回转器是一种二端口器件。

它的电流与电压的关系为I 1=gU 2I 2= - gU 1或写成U 1= -rI 2 U 2=rI1式中g 和r =1g分别称为回转电导和回转电阻，简称回转常数。

用矩阵形式可表示为⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡212100U U g g I I 或⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡212100I I rr U U 若在回转器2—2′端口接以负载阻抗Z L ，则在1—1′端口看入的输入阻抗为LL in Z rI Z I r U I r rU rII rI I U Z 22222222212111/=--=-=-=-==如果负载阻抗Z L 在1—1′端口，则从2—2′端口看入的等效阻抗为LL in Z rI Z I r U I r rU rI I U Z 211211211222/==-=-==由上可见，回转器的一个端口的阻抗是另一端口的阻抗的倒数(乘上一定比例常数)，且与方向无关(即具有双向性质)。

利用这种性质，回转器可以把一个电容元件“回转”成一个电感元件或反之。

例如在2—2′端口接入电容C ，在正弦稳态条件下,即1L Z j Cω=，则在1－1′端口看入的等效阻抗为eg Lin L j C r j rZ rZ ωω====22211式中：L r C eg =2为1—1′端口看入的等效电感。

同样，在1—1′端接电容Ｃ，在正弦稳态条件下，从2—2′看进去的输入阻抗Ｚin2为eg in L j C j r Cj I I r U I r rU rI I rI I U Z ωωω=⋅=⋅-⋅-=⋅-=-===211211211212221式中：Ｌeg ＝r 2C 。

南京航空航天大学仿真实验报告课程名称电路实验与实践实验名称基于PSpice的回转器实验仿真班级姓名惠琦学号实验组别同实验者实验日期实验地点评定成绩审阅老师一、实验目的1.加深对回转器特性的认识，并对其实际应用有所了解。

2.研究如何用运算放大器构成回转器，并学习回转器的测试方法。

二、实验原理1.回转器是理想回转器的简称，它能将一端口上的电压（电流）“回转“成另一端口上的电流（电压）。

端口变量之间的关系为：I1=gU2 或u1=-ri2I2=-gU1 u2=ri1式中：r、g 为回转系数，r 为回转电阻，g 为回转电导。

2.两个负阻抗变换器实现回转器：用电阻接入时:Rin=1/(g2RL)一般情况:Zin=1/(g2ZL)回转电导:g=1/R三、实验仿真软件OrCAD PSpice仿真实验报告纸四、实验步骤1.测回转电导 g：实物实验步骤：回转器输入端接信号发生器，调得 US=1.5V（有效值），输出端接负载电阻 RL=200Ω，分别测 U1，U2，I1，求 g。

仿真步骤：原理图如下，搭建如图原理图并运行仿真，观察并记录 U1，U2，I1，求回转电导g。

2.记录不同频率下 U1、I1 的相位关系：实物实验步骤：回转器输出端接电容，C 分别取 0.1μ F、0.22μ F，用示波器观察 f 分别为 500Hz、1000Hz 时 U1 和 I1 的相位关系。

仿真步骤：原理图如下，其中电压源为VSIN（适合暂态分析），分析设置中选择暂态分析Transient，取合适的时间，用标记Mark功能标记 U1 和I1（实际标记的是采样电阻旁的电压），对 C 分别取 0.1μ F、0.22μ F，对f分别取500Hz、1000Hz（在VSIN中修改FREQ参数），进行暂态分析，观察并记录波形。

仿真实验报告纸3.测由模拟电感组成的并联谐振电路的 Uc~f 幅频特性：实物实验步骤：取 C1=0.1μ F 经回转器成为模拟电感，另取 C=0.22μ F，则f0=1.073kHz,符合要求。

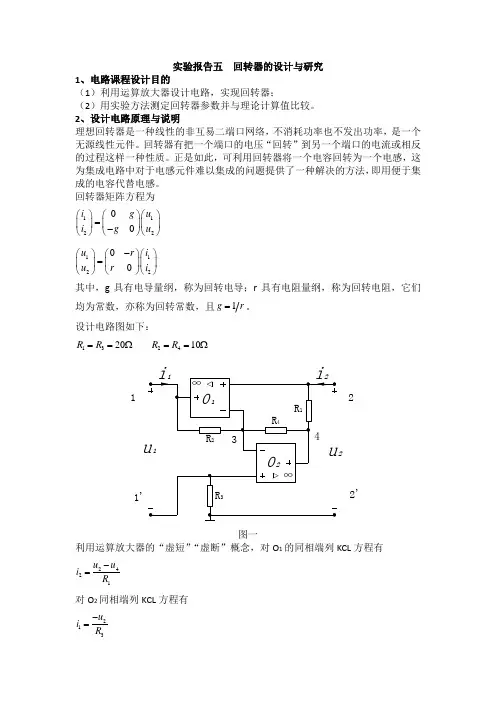
实验报告五 回转器的设计与研究1、电路课程设计目的（1）利用运算放大器设计电路，实现回转器；（2）用实验方法测定回转器参数并与理论计算值比较。

2、设计电路原理与说明理想回转器是一种线性的非互易二端口网络，不消耗功率也不发出功率，是一个无源线性元件。

回转器有把一个端口的电压“回转”到另一个端口的电流或相反的过程这样一种性质。

正是如此，可利用回转器将一个电容回转为一个电感，这为集成电路中对于电感元件难以集成的问题提供了一种解决的方法，即用便于集成的电容代替电感。

回转器矩阵方程为112200i u g i gu ⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭112200u i r u r i -⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭其中，g 具有电导量纲，称为回转电导；r 具有电阻量纲，称为回转电阻，它们均为常数，亦称为回转常数，且1g r =。

设计电路图如下：1320R R ==Ω 2410R R ==Ω121'2'图一利用运算放大器的“虚短”“虚断”概念，对O 1的同相端列KCL 方程有2421u u i R -=对O 2同相端列KCL 方程有213u i R -=又流过R 2和R 4的电流相同有12424u u u R R -=故42112R i u R R =写成矩阵形式为31122412100R i u i u R R R ⎛⎫-⎪⎛⎫⎛⎫⎪=⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪⎝⎭当1234R R R R =时，即满足回转器的条件，矩阵形式为3112231010R i u i u R ⎛⎫-⎪⎛⎫⎛⎫ ⎪= ⎪ ⎪⎪⎝⎭⎝⎭ ⎪⎝⎭回转电导31g R =，回转电阻3r R =。

现取1320R R ==Ω，2410R R ==Ω，故0.05g s =，20r =Ω。

3、电路课程设计仿真内容与步骤及结果（1）在1-1’ 端口接入电源，在2-2’ 端口接入10Ω电阻，测量I 1 I 2 U 2；图二1212200.6u i ==Ω21 5.999200.3u i -=≈Ω （2）在2-2’ 端口接入电源，在1-1’ 端口接入10Ω电阻测量I 2 I 1 U 1；图三125200.25u i ==Ω 2110200.5u i --==Ω-（3）测量回转器将电感回转为电容的特性；图四波形图为图五电流超前电压，表现出电容的特性。

. . . .南京航空航天大学电路实验报告回转器电路设计姓名：李根根学号：031220720目录一、实验目的……………………………………………………………………………………….2二、实验仪器……………………………………………………………………………………….2三、实验原理……………………………………………………………………………………….2四、实验要求……………………………………………………………………………………….3五、用pspice软件进行电路仿真并分析……………………………………………..….5六、实验内容………………………………………………………………………………………9七、实验心得………………………………………………………………………….….….…..11八、附件（Uc – f图） (12)一、实验目的1．加深对回转器特性的认识，并对其实际应用有所了解。

2．研究如何用运算放大器构成回转器，并学习回转器的测试方法。

二、实验仪器1．双踪示波器2．函数信号发生器3．直流稳压电源4．数字万用表5．电阻箱6．电容箱7．面包板8．装有pspice软件的PC一台三、实验原理1．回转器是理想回转器的简称。

它是一种新型、线性非互易的双端口元件，其电路符号如图所示。

其特性表现为它能够将一端口上的电压（或者电流）“回转”成另一端口上的电流（或者电压）。

端口变量之间的关系为I1 = gu2 u1 = -ri2I2 = gu1 u2 = ri1式子中，r，g称为回转系数，r称为回转电阻，g称为回转电导。

2．两个负阻抗变换器实现回转器图中回转电导为:四、实验要求先利用pspice软件进行电路仿真，（提示：仿真时做瞬态分析，信号源用Vsin ，做频率分析时，信号源用VAC）然后在实验室完成硬件测试：1．用运算放大器构成回转器电路（电路构成见实验教材p216图9-24，其中电阻R 的标称值为1000Ω），测量回转器的回转电导。

仿真实验五 回转器的研究一、 实验目的：1、了解回转器的基本电特性及其运算放大器实现办法。

2、掌握回转器参数的测试方法并了解其应用。

二、 实验原理：理想回转器是一种线性的非互易二端口网络，如下图所示为回转器的电路模型：作为理想的二端口网络，其端口电流、电压关系可表示为：1221i gu i gu =⎧⎨=-⎩ 或写为：2112u ri u ri =⎧⎨=-⎩其中，g 具有电导量纲，称为回转电导；r 具有电阻量纲，称为回转电阻，他们均为常数，亦称为回转常数，且1g r =。

用矩阵形式表示上面的方程，写为112211220000i u g i g u u i r u r i ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦-⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ 因为12211221,Z Z Y Y ≠≠，所以理想回转器是非互易的，不满足互易定理。

根据理想回转器的端口方程，可作出用受控源表示回转器的电路模型，01U 02U 由上述方程可计算理想回转器的总功率为：()()112212210p u i u i u gu u gu =+=+-=上式说明，理想回转器既不消耗功率也不发出功率，因此它是一个无源线性元件。

同时由上述方程又可看出，回转器有把一个端口的电压“回转”到另一个端口的电流或相反的过程这样一种性质。

正是如此，可利用回转器将一个电容回转为一个电感，这为集成电路中对于电感元件难以集成的问题提供了一种解决办法，即用便于集成的电容代替电感。

如在上图的输出端接一负载阻抗2Z 则输入阻抗i Z 为：212221222111i I U g Z g Z I gU U g I ∙∙∙∙∙∙-====⎛⎫- ⎪⎝⎭上式中，当2Z →∞（端口2开路），0i Z →（端口1短路），当20Z →（端口2短路），i Z →∞（端口1开路）。

如故取21Z j Cω=，则2i C Z j g ω=j L ω=，可见2CL g=。

称回转器的这种性质为阻抗倒置性。

利用运算放大器构成回转器的电路及其应用马纪梅【摘要】Gyrator is an ideal linear passive multiterminal component, which is widely used in power, signal processing and element conversion. This paper takes a gyrator realization using operational amplifiers as an example to analyze the gyrator's characteristics. It is verified that two gyrators in cascade can be an ideal transformer through Multisim simulation experiment. Based on the impedance conversion characteristic of gyrator, the paper puts an emphasis on introducing the application of gyrator to implement low-frequency oscillatory easily, to measure power transformer wire-wound DC resistance combined with bridge type measurement circuit according to the characteristic of high inductance and low resistance of transformer. Hence concrete and practical circuits are offered in this paper.%回转器是一种理想线性无源的多端元件,它在电力、信号处理及元件转换中具有广泛的应用.本文以运算放大器实现回转器的电路为基础,讨论了回转器的端口特性及其阻抗变换性质,通过实际测量验证了本文所设计的回转器实现方案可行.通过Multisim仿真实验验证了两个回转器级联可以实现理想变压器,扩展了回转器的应用.基于回转器的阻抗变换特性,重点介绍了回转器在方便实现频率低于1Hz的振荡电路中的应用；并针对电力变压器大电感与小电阻的特点,配合桥式测量电路,提出利用回转器测量直流电阻的测试方法,大大缩短了测量时间.同时设计了具体应用电路,以供参考.【期刊名称】《河北工业大学学报》【年(卷),期】2012(041)004【总页数】4页(P23-26)【关键词】回转器;阻抗变换;变压器;低频振荡;直流电阻测试【作者】马纪梅【作者单位】河北工业大学电气工程学院,天津300130【正文语种】中文【中图分类】TM130 引言回转器是一种具有电阻倒换或电感与电容倒换性质的二端口元件，由特勒根提出并加以命名的基本电路元件.现有的电路教材中，大多只介绍了回转器的定义和端口特性，没有专门的物理器件组成的介绍[1]，在教学过程中比较抽象，学生不易理解，影响了对其的应用开发.本文给出了由运算放大器构成回转器的实现电路，推导了回转器的阻抗变换特性，重点介绍了回转器方便实现理想变压器、低频振荡电路和测量电力变压器绕组直流电阻等方面的应用.1 回转器的实现电路回转器可以依据其不同的等效电路模型采取不同的实际电路器件加以实现，采用运算放大器实现回转器的电路如图1所示，运算放大器为JRC 4558D.由图1所设定的电流参考方向，可列写下面几个方程，对端子1有对运放A2有将式 (2)代入式 (1)得同理对2端子列写基尔霍夫电流方程，可得回转器端口的电压电流方程可表示为理论上但由于电阻有误差，实际运算放大器也非理想元件，只能做到图1 回转器电路Fig.1 Gyrator circuit2 回转器阻抗变换特性回转器具有阻抗变换特性，即可以将电感和电容元件、电阻和电导元件互相转换，这一特性使大电感的实现和电路的集成化变得简单方便.回转器的电路符号和阻抗变换的等效电路图如图2所示.图2中将式 (6)代入式 (5)中，得图2 回转器阻抗变换的等效电路Fig.2 Theequivalentcircuitof gyrator's impedance conversion由式 (7)可知，1端口处可等效为一个等效电感和等效电阻相串联的组合，其中回转器可以起到阻抗变换的作用.按图1实际制作回转器，实测回转电阻为.以图2为基础，将端口2的电导器件去掉，只接入一1F电容，端口1串联信号发生器和一个的限流电阻，信号发生器输出正弦波，频率按表一数据调节，输出幅值5 V不变，分别测量和限流电阻电压幅值及其相位关系，由示波器可知相位超前相位90°，端口1为感性负载，不同的电源频率与对应模拟电感值如表一所示，从表中看出模拟电感理论值和测量值基本一致，表明由图1实际制作回转器的方案可行.表1 不同频率下对应模拟电感值Tab.1 The simulated inductance of differentworking frequency频率/Hz 1/V /V 1= -1/mA 电感理论值 eq/H eq= eq-eq/H 100 0.30 5.10 51.0 0.963 0.0260 200 0.59 5.07 50.70.963 0.0360 300 0.91 5.02 50.2 0.963 0.0010 400 1.2 4.96 49.6 0.963 0.000 500 1.49 4.89 48.9 0.963 0.0020电感测量值 eq/H 0.937 0.927 0.962 0.963 0.9613 回转器的应用3.1 回转器级联构成变压器将两个回转电导分别为和的回转器级联起来，如图3所示.则整个二端口网络的传输参数为[2]而理想变压器的传输参数为图3 2个回转器级联图Fig.3 The circuitof two gyrators in cascade比较式 (8)和式 (9)可知，变比，选取合适的和可得到理想的变比，即通过两个回转器的级联可以组成实用的变压器.对时利用Multisim进行仿真 [3]，取，按照图3进行仿真，其中回转器由图1组成，输入，输出，仿真变比=100.001，与理论值一致.3.2 回转器在振荡电路中的应用利用回转器的阻抗变换特性，使极低频的正弦波振荡器的实现变的简单、方便[4].将合适的电容接入回转器，可以得到大数值、低损耗的模拟电感.利用回转器实现振荡频率低于1 Hz的电路图如图4所示.其中由回转器（虚线框部分）变换而得的模拟大数值电感与电容组成并联谐振回路.运放A3是振荡器的输出级，为电压跟随器，使负载与谐振回路隔离，输出信号由电阻和分压后经运放A4隔离放大，反馈至谐振电路，用来补偿谐振回路的能量损耗，使振荡持续稳定.图4 低频正弦波振荡器Fig.4 Low-frequency oscillatory network根据图4中标称的电阻值模拟电感.因此理论振荡频率由式 (10)计算为0.16Hz.实际搭建电路，实测振荡频率为0.15Hz，与理论值相符.3.3 回转器在测量电力变压器绕组直流电阻中的应用电力变压器绕组直流电阻测试是变压器产品、半成品试验和出厂试验中的重要测试项目，通过该项目试验可以检查绕组焊接质量、确定绕组的平均温升等[5].电力变压器的绕组具有大电感（数百至数千亨）、微电阻的特性（0.001～1），其固有的时间常数较大，因此采用传统的电桥法或直流压降法测量往往需要较长的时间才能达到平衡，快速测量较难[6].利用回转器的阻抗变换特性，可以将电力变压器绕组大电感与小电阻的串联模型转变为小电容与小电导并联模型，从而为快速测试变压器绕组直流电阻创造了条件.由回转器构成的实用测量电力变压器绕组直流电阻的电路图如图5所示.图中虚框内为回转器，以及节点①与地之间的等效电阻构成桥式测量电路，待测变压器绕组为组成的等效电路，其中为变压器绕组直流电阻值，当时检流计指针指向零，电桥处于平衡状态，因此，变压器绕组直流电阻即为的值.此电路测试电力变压器直流电阻范围为0～100.例如，某企业生产的容量为800 kVA的S9系列、初级侧电压为10 kV、次级侧电压为0.4 kV的电力变压器，高压绕组在25℃时的直流电组值为0.452 1，电感量为177.95H，时间常数经图5电路中回转器变换后的等效电容，等效电阻，时间常数.可见，时间常数缩短了20多倍，大大节省了测试时间.图5 实测电路图Fig.5 Practicalcircuitdiagram本文所介绍的几种电路在理论和实践上都得到了证明，电路结构比较简单，仅仅靠改变电阻的阻值便可改变设计参数，得到具有不同回转参数的回转器，如果采用电位器，便可制成可变电容和可变电感，既做到了电容、电感的微型化，又使实际调试变得十分简单、方便.因此，近几年此种技术获得了广泛的应用和发展.但由于实际运算放大器并非理想，所模拟出来的电容、电感亦受到一定量值及频带的限制，因此，在采用任何一种模拟电路进行设计时，都要充分考虑.参考文献：[1]白慧珍，王宝珠，张惠娟.电路理论基础 [M].北京：中国科学技术出版社，2004.[2]何善福，张峰.回转器的实验设计与Multisim仿真分析 [J].实验室研究与探索，2011，30（3）：45-48.[3]王连英.基于Multisim 10的电子仿真实验与设计 [M].北京：北京邮电大学出版社，2009.[4]田社平，陈洪亮.利用运算放大器构成回转器的电路及其仿真测量 [J].电气电子教学学报，2008，30（2）：67-69.[5]张海龙，关根志，周金.全自动变压器绕组直流电阻快速测量仪 [J].高压电器,2008，44（6）：574-577.[6]刘占荣，姜俊莉，刘振伶.电力变压器绕组直流电阻的测试和分析 [J].华中电力.2009，22（5）：29-31.。