北师大版八年级下册数学第一章《证明(二)》知识点及习题

北师大版八年级下册数学重难点突破知识点梳理及重点题型巩固练习《三角形的证明》全章复习与巩固(提高)【学习目标】1.经历回顾与思考的过程，深刻理解和掌握定理的探索和证明.2.结合具体实例感悟证明的思路和方法，能运用综合、分析的方法解决有关问题.3.能正确运用尺规作图的基本方法作已知线段的垂直平分线和角的平分线，以及绘制特殊三角形.【知识网络】【要点梳理】要点一、等腰三角形1.三角形全等的性质及判定全等三角形的对应边相等，对应角也相等.判定：SSS、SAS、ASA、AAS、HL.2.等腰三角形的判定、性质及推论性质：等腰三角形的两个底角相等（等边对等角）判定：有两个角相等的三角形是等腰三角形（等角对等边）推论：等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合（即“三线合一”）3.等边三角形的性质及判定定理性质定理：等边三角形的三个角都相等，并且每个角都等于60°；等边三角形的三条边都满足“三线合一”的性质；等边三角形是轴对称图形，有3条对称轴.判定定理：有一个角是60°的等腰三角形是等边三角形；三个角都相等的三角形是等边三角形.4.含30°的直角三角形的边的性质定理：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.要点诠释：等边三角形是中考中常考的知识点，并且有关它的计算也很常见，因此对于等边三角形的特殊数据要熟记于心，不如边长为a 的等边三角形他的高是2a ，面积是24；含有30°的直角三角形揭示了三角形中边与角的关系，打破了以往那种只有角或边的关系，同时也为我们学习三角函数奠定了基础.要点二、直角三角形1.勾股定理及其逆定理定理：直角三角形的两条直角边的平方和等于斜边的平方.逆定理：如果三角形两边的平方和等于第三边的平方，那么这个三角形是直角三角形.2.命题与逆命题命题包括题设和结论两部分；逆命题是将原命题的题设和结论交换位置得到的；正确的逆命题就是逆定理.3.直角三角形全等的判定定理定理：斜边和一条直角边对应相等的两个直角三角形全等（HL ）要点诠释：①勾股定理的逆定理在语言叙述的时候一定要注意，不能说成“两条边的平方和等于斜边的平方”，应该说成“三角形两边的平方和等于第三边的平方”.②直角三角形的全等判定方法，还有SSS,SAS,ASA,AAS,一共有5种判定方法. 要点三、线段的垂直平分线1.线段垂直平分线的性质及判定性质：线段垂直平分线上的点到这条线段两个端点的距离相等.判定：到一条线段两个端点距离相等的点在这条线段的垂直平分线上.2.三角形三边的垂直平分线的性质三角形三条边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等.3.如何用尺规作图法作线段的垂直平分线分别以线段的两个端点A 、B 为圆心，以大于12AB 的长为半径作弧，两弧交于点M 、N ；作直线MN ，则直线MN 就是线段AB 的垂直平分线.要点诠释：①注意区分线段的垂直平分线性质定理和判定定理,注意二者的应用范围；②利用线段的垂直平分线定理可解决两条线段的和距离最短问题.要点四、角平分线1.角平分线的性质及判定定理性质：角平分线上的点到这个角的两边的距离相等；判定：在一个角的内部，且到角的两边的距离相等的点，在这个角的平分线上.2.三角形三条角平分线的性质定理性质：三角形的三条角平分线相交于一点，并且这一点到三条边的距离相等.3.如何用尺规作图法作出角平分线要点诠释：①注意区分角平分线性质定理和判定定理,注意二者的应用范围；②几何语言的表述，这也是证明线段相等的一种重要的方法.遇到角平分线时，要构造全等三角形.【典型例题】类型一、能证明它们么1. 如图，△ACD 和△BCE 都是等腰直角三角形，∠ACD=∠BCE=90°，AE 交CD 于点F ，BD 分别交CE 、AE 于点G 、H ．试猜测线段AE 和BD 的数量和位置关系，并说明理由．【思路点拨】由条件可知CD=AC ，BC=CE ，且可求得∠ACE=∠DCB ，所以△ACE ≌△DCB ，即AE=BD ，∠CAE=∠CDB ；又因为对顶角∠AFC=∠DFH ，所以∠DHF=∠ACD=90°，即AE ⊥BD ．【答案与解析】猜测AE=BD ，AE ⊥BD ；理由如下：∵∠ACD=∠BCE=90°，∴∠ACD+∠DCE=∠BCE+∠DCE ，即∠ACE=∠DCB ，又∵△ACD 和△BCE 都是等腰直角三角形，∴AC=CD ，CE=CB ，∵在△ACE 与△DCB 中，,AC DC ACE DCB EC BC =⎧⎪∠=∠⎨⎪=⎩∴△ACE ≌△DCB （SAS ），∴AE=BD ， ∠CAE=∠CDB ；∵∠AFC=∠DFH ，∠FAC+∠AFC=90°，∴∠DHF=∠ACD=90°，∴AE ⊥BD ．故线段AE 和BD 的数量相等，位置是垂直关系.【总结升华】主要考查全等三角形的判定，涉及到等腰直角三角形的性质及对顶角的性质等知识点．举一反三：【变式】将两个全等的直角三角形ABC 和DBE 按图1方式摆放，其中∠ACB=∠DEB=90°，∠A=∠D=30°，点E落在AB上，DE所在直线交AC所在直线于点F．（1）求证：AF+EF=DE；（2）若将图1中的△DBE绕点B按顺时针方向旋转角α，且0°＜α＜60°，其它条件不变，请在图2中画出变换后的图形，并直接写出你在（1）中猜想的结论是否仍然成立；（3）若将图1中的△DBE绕点B按顺时针方向旋转角β，且60°＜β＜180°，其它条件不变，如图3．你认为（1）中猜想的结论还成立吗？若成立，写出证明过程；若不成立，请写出AF、EF与DE之间的关系，并说明理由．【答案】（1）证明：连接BF（如下图1），∵△ABC≌△DBE（已知），∴BC=BE，AC=DE．∵∠ACB=∠DEB=90°，∴∠BCF=∠BEF=90°．∵BF=BF，∴Rt△BFC≌Rt△BFE．∴CF=EF．又∵AF+CF=AC，∴AF+EF=DE．（2）解：画出正确图形如图2.（1）中的结论AF+EF=DE仍然成立；（3）证明：连接BF ，∵△ABC ≌△DBE ，∴BC=BE ，∵∠ACB=∠DEB =90°，∴△BCF 和△BEF 是直角三角形，在Rt △BCF 和Rt △BEF 中，,BC BE BF BF=⎧⎨=⎩ ∴△BCF ≌△BEF ，∴CF=EF ；∵△ABC ≌△DBE ，∴AC=DE ，∴AF=AC+FC=DE+EF ．类型二、直角三角形2. 下列说法正确的说法个数是（ ）①两个锐角对应相等的两个直角三角形全等，②斜边及一锐角对应相等的两个直角三角形全等，③两条直角边对应相等的两个直角三角形全等，④一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等．A.1B.2C.3D.4【思路点拨】根据全等三角形的判定方法及“HL”定理，判断即可；【答案】C.【解析】A 、三个角相等，只能判定相似；故本选项错误；B 、斜边及一锐角对应相等的两个直角三角形，符合两三角形的判定定理“AAS”；故本选项正确；C 、两条直角边对应相等的两个直角三角形，符合两三角形的判定定理“SAS”；故本选项正确；D、一条直角边和另一条直角边上的中线对应相等的两个直角三角形，首先根据“HL”定理，可判断两个小直角三角形全等，可得另条直角边相等，然后，根据“SAS”，可判断两个直角三角形全等；故本选项正确；所以，正确的说法个数是3个．故选C．【总结升华】直角三角形全等的判定，一般三角形全等的判定方法都适合它，同时，直角三角形有它的特殊性，作为“HL”公理就是直角三角形独有的判定方法，使用时应该抓住“直角”这个隐含的已知条件．3.（2016•南开区一模）问题背景：在△ABC中，AB、BC、AC三边的长分别为、、，求这个三角形的面积．小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．（1）请你将△ABC的面积直接填写在横线上；（2）若△ABC三边的长分别为、、2（m＞0，n＞0，且m ≠n），运用构图法可求出这三角形的面积为．【思路点拨】（1）是直角边长为1，2的直角三角形的斜边；是直角边长为1，3的直角三角形的斜边；是直角边长为2，3的直角三角形的斜边，把它整理为一个矩形的面积减去三个直角三角形的面积；（2）结合（1）易得此三角形的三边分别是直角边长为m，4n的直角三角形的斜边；直角边长为3m，2n的直角三角形的斜边；直角边长为2m，2n的直角三角形的斜边．同样把它整理为一个矩形的面积减去三个直角三角形的面积可得．【答案与解析】解：（1）S△ABC=3×3﹣×1×2﹣×2×3﹣×1×3=；（2）构造△ABC如图所示，S△ABC=3m×4n﹣×m×4n﹣×3m×2n﹣×2m×2n=5mn．故答案为：（1）3；（2）5mn．【总结升华】此题主要考查了勾股定理应用，利用了数形结合的思想，通过构造直角三角形，利用勾股定理求解是解题关键，关键是结合网格用矩形及容易求得面积的直角三角形表示出所求三角形的面积进行解答．类型三、线段垂直平分线4. 如图，在锐角△ABC中，AD、CE分别是BC、AB边上的高，AD、CE相交于F，BF的中点为P，AC的中点为Q，连接PQ、DE．（1）求证：直线PQ是线段DE的垂直平分线；（2）如果△ABC是钝角三角形，∠BAC＞90°，那么上述结论是否成立？请按钝角三角形改写原题，画出相应的图形，并给予必要的说明．【思路点拨】（1）只需证明点P、Q都在线段DE的垂直平分线上即可．即证P、Q分别到D、E的距离相等．故连接PD、PE、QD、QE，根据直角三角形斜边上的中线等于斜边的一半可证；（2）根据题意，画出图形；结合图形，改写原题．【答案与解析】（1）证明：连接PD、PE、QD、QE．∵CE⊥AB，P是BF的中点，∴△BEF是直角三角形，且PE是Rt△BEF斜边的中线，∴PE=12 BF．又∵AD⊥BC，∴△BDF是直角三角形，且PD是Rt△BDF斜边的中线，∴PD=12BF=PE，∴点P在线段DE的垂直平分线上．同理可证，QD、QE分别是Rt△ADC和Rt△AEC斜边上的中线，∴QD=12AC=QE，∴点Q也在线段DE的垂直平分线上．∴直线PQ垂直平分线段DE．（2）当△ABC为钝角三角形时，（1）中的结论仍成立．如图，△ABC是钝角三角形，∠BAC＞90°．原题改写为：如图，在钝角△ABC中，AD、CE分别是BC、AB边上的高，DA与CE的延长线交于点F，BF的中点为P，AC的中点为Q，连接PQ、DE．求证：直线PQ垂直且平分线段DE．证明：连接PD，PE，QD，QE，则PD、PE分别是Rt△BDF和Rt△BEF的中线，∴PD=12BF，PE=12BF，∴PD=PE，点P在线段DE的垂直平分线上．同理可证QD=QE，∴点Q在线段DE的垂直平分线上．∴直线PQ垂直平分线段DE．【总结升华】考查了线段垂直平分线的判定和性质、直角三角形斜边上的中线等于斜边的一半等知识点，图形较复杂，有一定综合性，但难度不是很大．举一反三：【变式】在△ABC中，AB=AC，AB的垂直平分线交AB于N，交BC的延长线于M，∠A=40度．（1）求∠M的度数；（2）若将∠A的度数改为80°，其余条件不变，再求∠M的大小；（3）你发现了怎样的规律？试证明；（4）将（1）中的∠A改为钝角，（3）中的规律仍成立吗？若不成立，应怎样修改．【答案】（1）∵∠B=12（180°-∠A）=70°∴∠M=20°（2）同理得∠M=40°（3）规律是：∠M的大小为∠A大小的一半，证明：设∠A=α，则有∠B=12（180°-α）∠M=90°-12（180°-α）=12α.（4）不成立.此时上述规律为：等腰三角形一腰的垂直平分线与底边相交所成的锐角等于顶角的一半．类型四、角平分线5. 如图，△ABC中，∠A=60°，∠ACB的平分线CD和∠ABC的平分线BE交于点G．求证：GE=GD．【思路点拨】连接AG，过点G作GM⊥AB于M，GN⊥AC于N，GF⊥BC于F．由角平分线的性质及逆定理可得GN=GM=GF，AG是∠CAB的平分线；在四边形AMGN中，易得∠NGM=180°-60°=120°；在△BCG中，根据三角形内角和定理，可得∠CGB=120°，即∠EGD=120°，∴∠EGN=∠DGM，证明Rt△EGN≌Rt△DGM（AAS）即可得证GE=GM．【答案与解析】解：连接AG，过点G作GM⊥AB于M，GN⊥AC于N，GF⊥BC于F．∵∠A=60°，∴∠ACB+∠ABC=120°，∵CD，BE是角平分线，∴∠BCG+∠CBG=120°÷2=60°，∴∠CGB=∠EGD=120°，∵G是∠ACB平分线上一点，∴GN=GF，同理，GF=GM，∴GN=GM，∴AG是∠CAB的平分线，∴∠GAM=∠GAN=30°，∴∠NGM=∠NGA+∠AGM=60°+60°=120°，∴∠EGD=∠NGM=120°，∴∠EGN=∠DGM，又∵GN=GM，∴Rt△EGN≌Rt△DGM（AAS），∴GE=GD．【总结升华】此题综合考查角平分线的定义、三角形的内角和及全等三角形的判定和性质等知识点，难度较大，作辅助线很关键．举一反三：【变式】（2015春•澧县期末）如图：在△ABC中，∠C=90°AD是∠BAC的平分线，DE⊥AB 于E，F在AC上，BD=DF；证明：（1）CF=EB．（2）AB=AF+2EB．【答案】证明：（1）∵AD是∠BAC的平分线，DE⊥AB，DC⊥AC，∴DE=DC，∵在Rt△DCF和Rt△DEB中，∴Rt△CDF≌Rt△EBD（HL）．∴CF=EB；（2）∵AD是∠BAC的平分线，DE⊥AB，DC⊥AC，∴CD=DE．在△ADC与△ADE中，∵精品文档用心整理∴△ADC≌△ADE（HL），∴AC=AE，∴AB=AE+BE=AC+EB=AF+CF+EB=AF+2EB．资料来源于网络仅供免费交流使用。

北师大版初二数学下册重点知识梳理汇总，期末高分必备！GUIDE导读初二数学下册知识点（※表示重点部分）第一章 三角形的证明※知识点1 全等三角形的判定及性质判定定理简称判定定理的内容 性质 SSS 三角形分别相等的两个三角形全等全等三角形对应边相等、对应角相等 SAS 两边及其夹角分别相等的两个三角形全等 ASA 两角及其夹边分别相等的两个三角形全等 AAS 两角分别相等且其中一组等角的对边相等的两个三角形全等※知识点2 等腰三角形的性质定理及推论内容 几何语言 条件与结论等腰三角形的性质定理 等腰三角形的两底角相等。

简述为：等边对等角在△ABC 中，若AB=AC ，则∠B=∠C 条件：边相等，即AB=AC 结论：角相等，即∠B=∠C 推论 等腰三角形顶角的平分线、底边上的中线及底边上的高线互相垂直，简述为：三线合一在△ABC ，AB=AC ，AD⊥BC，则AD 是BC 边上的中线，且AD 平分∠BAC 条件：等腰三角形中一直顶点的平分线，底边上的中线、底边上的高线之一 结论：该线也是其他两线 ※等腰三角形中的相等线段：1.等腰三角形两底角的平分线相等2.等腰三角形两腰上的高相等3.两腰上的中线相等4.底边的中点到两腰的距离相等※知识点3 等边三角形的性质定理内容性质定理 等边三角形的三个内角都相等，并且每个角都等于60度解读【要点提示】1）等边三角形是特殊的等腰三角形。

它具有等腰三角形的一切性质2）等边三角形每条边上的中线、高线和所对角的平分线“三线合一” 【易错点】所有的等边三角形都是等腰三角形，但不是所有的等腰三角形都是等边三角形※知识点4 等腰三角形的判定定理内容 几何语言 条件与结论等腰三角形的判定定理 有两个角相等的三角形是等腰三角形，简述为：等校对等边 在△ABC 中，若∠B=∠C 则AC=BC 条件：角相等，即∠B=∠C 结论：边相等，即AB=AC解读 【注意】对“等角对等边”的理解仍然要注意，他的前提是“在同一个三角形中”拓展 判定一个三角形是等腰三角形有两种方法（1）利用等腰三角形；（2）利用等腰三角形的判定定理，即“等角对等边”※知识点5 反证法概念 证明的一般步骤反证法在证明时，先假设命题的结论不成立，然后推导出与定义、基本事实、已有定理或已知条件相矛盾的结果，从而证明命题的结论一定成立，这种证明方法称为反证法（1）假设命题的结论不成立（2）从这个假设出发，应用正确的推论方法，得出与定义、基本事实、已有定理或已知条件相矛盾的结果（3）由矛盾的结果判定假设不正确，从而肯定原命题正确解读【要点提示】（1）当一个命题涉及“一定”“至少”“至多”“无限”“唯一”等情况时，由于结论的反面简单明确，常常用反证法来证明 （2）“推理”必须顺着假设的思路进行，即把假设当作已知条件，“得出矛盾”是指推出与定义、基本事实、已有定理或已知条件相矛盾的结果第二章 一元一次不等式与一元一次不等式组一. 不等关系※1. 一般地,用符号“<”(或“≤”), “>”(或“≥”)连接的式子叫做不等式※2. 准确“翻译”不等式,正确理解“非负数”、“不小于”等数学术语.非负数 <===> 大于等于0(≥0) <===> 0和正数 <===> 不小于0非正数 <===> 小于等于0(≤0) <===> 0和负数 <===> 不大于0二. 不等式的基本性质※1. 掌握不等式的基本性质,并会灵活运用：(1) 不等式的两边加上(或减去)同一个整式，不等号的方向不变，即：如果a>b,那么a+c>b+c, a-c>b-c.(2) 不等式的两边都乘以(或除以)同一个正数，不等号的方向不变，即：如果a>b,并且c>0,那么ac>bc，(3) 不等式的两边都乘以(或除以)同一个负数，不等号的方向改变，即：如果a>b,并且c<0,那么ac<bc,※2. 比较大小：(a、b分别表示两个实数或整式)一般地：如果a>b，那么a-b是正数；反过来，如果a-b是正数，那么a>b；如果a=b，那么a-b等于0；反过来，如果a-b等于0，那么a=b；如果a<b，那么a-b是负数；反过来，如果a-b是正数，那么a<b；即：a>b <===> a-b>0a=b <===> a-b=0a<b <===> a-b<0三. 不等式的解集：※1.能使不等式成立的未知数的值，叫做不等式的解；一个不等式的所有解，组成这个不等式的解集；求不等式的解集的过程，叫做解不等式。

一、选择题1．如图，点A 为MON ∠的角平分线上一点，过A 点作一条直线分别与MON ∠的边OM ON 、交于,B C 两点，点P 为BC 的中点，过P 作BC 的垂线交OA 的延长线于点D ，连接DB DC 、，若130MON ∠=︒，则BDC ∠=（ ）A ．70︒B ．60︒C ．50︒D ．40︒2．如图，在ABC 中，4AB AC ==，ABC ∠和ACB ∠的平分线交于点E ，过点E 作//MN BC 分别交AB 、AC 于M 、N ，则AMN 的周长为（ ）A ．12B ．4C ．8D ．不确定 3．下列各组线段a 、b 、c 中不能组成直角三角形的是（ ） A ．a ＝7，b ＝24，c ＝25B ．a ＝4，b ＝5，c ＝6C ．a ＝3，b ＝4，c ＝5D ．a ＝9，b ＝12，c ＝15 4．下列几组数能作为直角三角形三边长的是（ ） A ．3，4，6 B ．1，1，3 C ．5，12，14 D ．5，25，5 5．如图，在△ABC 中，∠ACB ＝90°，BE 平分∠ABC ，DE ⊥AB 于点D ．若∠A ＝30°，AE ＝10，则CE 的长为（ ）A ．5B ．4C ．3D ．26．下面说法中正确的是（ ）A ．ABC ∆中BC 边上的高线，是过顶点A 向对边所引的垂线B ．ABC ∆中BC 边上的高线，是过顶点A 向对边所引的垂线段C ．三角形的角平分线不是射线D ．等腰三角形的对称轴和底边上的高线、中线以及顶角的平分线，互相重合7．如图，点123,,,A A A A ，…在同一直线上，111122223,,AB A B A B A A A B A A ===，3334A B A A =，……，若B 的度数为x ，则1n n n A B A +∠的度数为（ ）A ．()111802n x -︒-B ．()11802n x ︒-C ．()111802n x +︒-D ．()211802n x +︒-8．如图，在OAB 和△OCD 中，OA OB =，OC OD =，OA OC >，40AOB COD ∠=∠=︒，连接AC ，BD 交于点M ，连接OM ．下列结论：①AC BD =；②40AMB ∠=︒；③OM 平分BOC ∠；④MO 平分BMC ∠． 其中一定正确的为（ ）A ．①②③B ．①②④C ．①③④D ．②③④ 9．如图，ABC 中，AB AC =，BD DC =，若80BAC ∠=︒，AD AE =，则CDE∠的度数为（ ）A ．40°B ．30°C ．20°D ．10°10．如图，直线a ，b 相交形成的夹角中，锐角为52°，交点为O ，点A 在直线a 上，直线b 上存在点B ，使以点O ，A ，B 为顶点的三角形是等腰三角形，这样的点B 有（ ）A ．1个B ．2个C ．3个D ．4个 11．如图，ABC 是等边三角形，BD 是中线，延长BC 至E ，使CE CD =，则下列结论错误．．的是（ ）A ．30CED ∠=︒B ．120∠=︒BDEC ．DE BD = D ．DE AB = 12．如图，A ，B 两点在正方形网格的格点上，每个方格都是边长为1的正方形，点C 也在格点上，且ABC 为等腰三角形，在图中所有符合条件的点C 的个数为（ ）A ．7B ．8C ．9D ．10二、填空题13．如图，在ABC 中，AB AC =，AD 平分BAC ∠，PD 垂直平分AB 连接BD 并延长，交边AC 于点E ．若BCE 是等腰三角形，则BAC ∠的度数为________．14．如图，在ABC 中，ABC ∠和ACB ∠的平分线相交于点O ，过点O 作//EF BC 交AB 于E ，交AC 于F ，过点O 作OD AC ⊥于D ，有下列结论：①EF BE CF =+；②点O 到ABC 各边的距离相等；③1902BOC A ∠=+∠︒；④()12AD AB AC BC =+-．其中正确的结论是______（把你认为正确结论的序号都填上）．15．在平面直角坐标系中，一块等腰直角三角板如图放置，其中(2,0)A ，(0,1)B ，则点C 的坐标为_______．16．等腰三角形周长为20，一边长为4，则另两边长为______．17．如图，OA ，OB 分别是线段MC 、MD 的垂直平分线，MD ＝5cm ，MC ＝7cm ，CD ＝10cm ，一只小蚂蚁从点M 出发，爬到OA 边上任意一点E ，再爬到OB 边上任意一点F ，然后爬回M 点，则小蚂蚁爬行的最短路径的长度为_____．18．如图，AD 是△ABC 的平分线，DF ⊥AB 于点F ，DE ＝DG ，AG ＝16，AE ＝8，若S △ADG ＝64，则△DEF 的面积为 ________．19．如图，线段AB ，BC 的垂直平分线l 1，l 2相交于点O ，若∠B ＝50°，则∠AOC ＝_____．20．如图，D 是等边三角形ABC 外一点，3AD =，2CD =，则BD 的最大值是________________．三、解答题21．如图，ABC ，其中AC BC >．（1）尺规作图：作AB 的垂直平分线交AC 于点P （要求：不写作法，保留作图痕迹）； （2）若8,AB PBC =的周长为13，求ABC 的周长；（3）在（2）的条件下，若ABC 是等腰三角形，直接写出ABC 的三条边的长度．22．在平面直角坐标系中，已知()30A -,，()0,3B ，点C 为x 轴正半轴上一动点，过点A 作AD BC ⊥交y 轴于点E ．（1）如图①，若点C 的坐标为()2,0，试求点E 的坐标；（2）如图②，若点C 在x 正半轴上运动，且3OC <，其它条件不变，连接OD ，求证：OD 平分ADC ∠；（3）若点C 在x 轴正半轴上运动，当AD CD OC -=时，求OCD ∠的度数．23．如图，在ABC ∆中，80ABC ACB ∠=∠=︒，D 是AB 上一点，且AD BC =，//DE BC 且DE AC =.连接AE ，CE ，CD ．（1）求AED ∠的度数；（2）证明：ACE ∆是等边三角形；（3）求ECD ∠的度数．24．如图，在平面直角坐标系中，直线AB 经过点A （﹣2，3），B （4，0），交y 轴于点C ；（1）求直线AB 的关系式；（2）求△OBC 的面积；（3）做等腰直角三角形PBC ，使PC ＝BC ，求出点P 的坐标．25．如图，等边△ABC 中，点E 在AB 上，点D 在CB 的延长线上，且ED=EC ． （1）如图①，点E 为AB 的中点，求证：AE=DB ．（2）如图②，点E 在边AB 上时，AE DB （填：“＞”，“＜”或“=”）．理由如下：过点E 作EF ∥BC ，交AC 于点F （请你完成以下解答过程）．（3）在等边△ABC 中，点E 在直线AB 上，点D 在直线BC 上，且ED=EC ．若AB=1，AE=2时，直接写出CD 的长．26．已知：如图，在ABC 中，,90AC BC ACB =∠=︒，D 是AB 延长线上一点，过点C 作CE CD ⊥，使CE CD =，连结,BE DE ．（1）求证：AD BE =．（2）求DBE ∠的度数．（3）连结AE ，若ADE 是等腰三角形，1AB =，求DE ．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】过D 作DE ⊥OM 于E ，DF ⊥ON 于F ，求出∠EDF ，根据角平分线性质求出DE=DF ，根据线段垂直平分线性质求出BD=CD ，证Rt △DEB ≌Rt △DFC ，求出∠EDB=∠CDF ，推出∠BDC=∠EDF ，即可得出答案．【详解】解：如图：过D 作DE ⊥OM 于E ，DF ⊥ON 于F ，则∠DEB=∠DFC=∠DFO=90°，∵∠MON=130°，∴∠EDF=360°-90°-90°-130°=50°，∵DE⊥OM，DF⊥ON，OD平分∠MON，∴DE=DF，∵P为BC中点，DP⊥BC，∴BD=CD，在Rt△DEB和Rt△DFC中，DB DC DE DF=⎧⎨=⎩，∴Rt△DEB≌Rt△DFC（HL），∴∠EDB=∠CDF，∴∠BDC=∠BDF+CDF=∠BDF+∠EDB=∠EDF=50°．故选：C．【点睛】本题考查了全等三角形的性质和判定，角平分线性质，线段垂直平分线性质的应用，能正确作出辅助线是解此题的关键，注意：线段垂直平分线上的点到线段两个端点的距离相等，角平分线上的点到角的两边的距离相等．2．C解析：C【分析】由角平分线的定义和平行线性质易证△BME和△CNE是等腰三角形，即BM＝ME，CN＝NE，由此可得△AMN的周长＝AB+AC．【详解】解：∵∠ABC和∠ACB的平分线交于点E，∴∠ABE＝∠CBE，∠ACE＝∠BCE，∵MN//BC，∴∠CBE＝∠BEM，∠BCE＝∠CEN，∴∠ABE＝∠BEM，∠ACE＝∠CEN，∴BM＝ME，CN＝NE，∴△AMN的周长＝AM+ME+AN+NE＝AB+AC，∵AB＝AC＝4，∴△AMN的周长＝4+4＝8．故选C．【点睛】本题考查了等腰三角形的判定与性质，平行线的性质，熟记各性质是解题的关键． 3．B解析：B【分析】根据判断三条线段是否能构成直角三角形的三边，需验证两小边的和的平方是否等于最长边的平方，分别对每一项进行分析，即可得出答案；【详解】A 、222724=25+ ，能构成直角三角形；B 、22245=416+≠ ，不能构成直角三角形；C 、22234=5+ ，能构成直角三角形；D 、222912=225=15+，能构成直角三角形；故选：B ．【点睛】本题考查了勾股定理的逆定理，用到的知识点是已知△ABC 的三边满足222+=a b c ，则△ABC 是直角三角形；4．D解析：D【分析】要能作为直角三角形三边长，需验证两小边的平方和等于最长边的平方．【详解】解：A 、32+42≠62，不符合勾股定理的逆定理，不是直角三角形，不符合题意；B 、12+12≠2，不符合勾股定理的逆定理，不是直角三角形，不符合题意；C 、52+122≠142，不符合勾股定理的逆定理，不是直角三角形，不符合题意；D 2+（2＝52，符合勾股定理的逆定理，是直角三角形，符合题意； 故选：D ．【点睛】本题考查了勾股定理的逆定理：已知△ABC 的三边满足a 2+b 2=c 2，则△ABC 是直角三角形． 5．A解析：A【分析】先根据含30°角的直角三角形的性质求出DE ＝5，再根据角平分线的性质求出CE ＝DE ＝5即可．【详解】解：∵DE ⊥AB ，∴∠ADE ＝90°，在Rt △ADE 中，∠A ＝30°，AE ＝10，∴DE ＝12AE ＝5，∵BE平分∠ABC，DE⊥AB，∠ACB＝90°，∴CE＝DE＝5，故选：A．【点睛】本题考查的是角平分线的性质、含30°角的直角三角形的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．6．C解析：C【分析】从三角形的一个顶点向底边作垂线，垂足与顶点之间的线段叫做三角形的高．三角形一个内角的平分线与这个内角的对边交于一点，则这个内角的顶点与所交的点间的线段叫做三角形的角平分线．三角形一边的中点与此边所对顶点的连线叫做三角形的中线．据此分析判断即可．【详解】解：A．ABC∆中BC边上的高线，是过顶点A向对边所引的垂线段，原说法错误，故本选项不符合题意；B．当∠B或∠C是钝角时，过A不存在到线段BC的垂线，故本选项说法错误，不符合题意；C．三角形的角平分线就是三角形的内角平分线与这个内角的对边的交点与这个内角的顶点之间的线段，故本选项正确，符合题意；D．对称轴是直线，不能与线段重合，本故选项说法错误，不符合题意；故选：C．【点睛】本题主要考查了三角形的角平分线、中线以及高线，三角形有三条中线，有三条高线，有三条角平分线，它们都是线段．7．C解析：C【分析】根据等腰三角形的性质和三角形外角的性质进行求解计算【详解】解：∵在△ABA1中，∠B=x，AB=A1B，∴∠BA1A=1802x︒-，∵A1A2=A1B1，∠BA1A是△A1A2B1的外角，∴∠A1B1A2=∠A1A2B1=12∠BA1A=21180180222x x︒-︒-⨯=；同理可得，∠A2B2A3=∠A2A3B2=12∠A1B1A2=231180180222x x︒-︒-⨯=；∴∠A n B n A n +1=()111802n x +︒- 故选：C ．【点睛】 本题考查的是等腰三角形的性质及三角形外角的性质，准确识图，找出规律是解答此题的关键．8．B解析：B【分析】由SAS 证明△AOC ≌△BOD 得出∠OCA=∠ODB ，AC=BD 即可判断①；由全等三角形的性质得出∠OAC=∠OBD ，由三角形的外角性质得：∠AMB+∠OAC=∠AOB+∠OBD ，得出∠AMB=∠AOB=40°，即可判断②；作OG ⊥MC 于G ，OH ⊥MB 于H ，则∠OGC=∠OHD=90°，由AAS 证明△OCG ≌△ODH （AAS ），得出OG=OH ，由角平分线的判定方法得出MO 平分∠BMC ，即可判断④；由∠AOB=∠COD ，得出当∠DOM=∠AOM 时，OM 平分∠BOC ，假设∠DOM=∠AOM ，由△AOC ≌△BOD 得出∠COM=∠BOM ，由MO 平分∠BMC 得出∠CMO=∠BMO ，推出△COM ≌△BOM ，得OB=OC ，而OA=OB ，所以OA=OC 即可判断③；【详解】∵ ∠AOB=∠COD=40°，∴∠AOB+∠AOD=∠COD+∠AOD ，即∠AOC=∠BOD ，在△AOC 和△BOD 中，OA OB OC ODAOC BOD =⎧⎪=⎨⎪∠=∠⎩， ∴△AOC ≌△BOD （SAS ），∴∠OCA=∠ODB ，AC=BD ，故①正确；∴∠OAC=∠OBD ，由三角形的外角性质得：∠AMB+∠OAC=∠AOB+∠OBD ，∴∠AMB=∠AOB=40°，故②正确；作OG ⊥MC 于G ，OH ⊥MB 于H ，如图所示：则∠OGC=∠OHD=90°，在△OCG和△ODH中OCA ODBOGC OHD OC OD∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△OCG≌△ODH（AAS），∴OG=OH，∴MO平分∠BMC，故④正确；∵∠AOB=∠COD，∴当∠DOM=∠AOM时，OM平分∠BOC，假设∠DOM=∠AOM，∵△AOC≌△BOD∴∠COM=∠BOM，∵MO平分∠BMC∴∠CMO=∠BMO，在△COM和△BOM中，COM BOMOM OMCMO BMO∠∠⎧⎪=⎨⎪∠=∠⎩，∴△COM≌△BOM（ASA）∴OB=OC，∵OA=OB，∴OA=OC与OA＞OC矛盾，故③错误；故选：B．【点睛】本题考查了全等三角形的判定与性质，三角形的外角性质，角平分线的判定等知识，证明三角形全等是解题的关键；．9．C解析：C【分析】根据已知可求得∠DAC及∠ADE的度数，根据∠CDE=90°-∠ADE即可得到答案．【详解】解：∵AB＝AC，BD=DC∴ AD⊥BC（等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合）∴∠ADC=90°，∵∠BAC＝80°，∴∠BAD＝∠DAC＝ 80°÷2=40°（等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合），∵AD＝AE，∴∠ADE＝（180°−40°）÷2=70°，∴∠CDE＝∠ADC-∠ADE=90°-70°=20°，故答案为：C.【点睛】本题主要考查了等腰三角形的性质，三角形内角和定理，掌握等腰三角形的性质，三角形内角和定理是解题的关键.10．D解析：D【分析】以点O 、A 、B 为顶点的等腰三角形有3种情况，分别为OA OB =，OA AB =，OB AB =，从这三方面考虑点B 的位置即可．【详解】解：如图所示，①当OA OB =时，以点O 为圆心，OA 为半径作圆，与直线b 在O 点两侧各有一个交点，此时B 点有2个；②当OA AB =时，以点A 为圆心，OA 为半径作圆，与直线b 有另外一个交点，此时B 点有1个；③当OB AB =时，作OA 的垂直平分线，与直线b 有一个交点，此时B 点有1个， 综上，B 点总共有4个，故选：D ．【点睛】本题考查了等腰三角形的判定，两条边相等的三角形为等腰三角形，因此要注意分类讨论，由每种情况的特点选择合适的方法确定点B 是解题的关键．11．D解析：D【分析】因为△ABC 是等边三角形，又BD 是AC 上的中线，所以有∠ADB ＝∠CDB ＝90°，且∠ABD ＝∠CBD ＝30°，∠ACB ＝∠CDE ＋∠DEC ＝60°，又CD ＝CE ，可得∠CDE ＝∠CED ＝30°，所以就有∠CBD ＝∠DEC ，即DE ＝BD ，∠BDE ＝∠CDB ＋∠CDE ＝120°.由此得出答案解决问题．【详解】解：∵△ABC 是等边三角形，∴∠ABC=∠ACB＝60°，∵BD是AC上的中线，∴∠ADB＝∠CDB＝90°，∠ABD＝∠CBD＝30°，∵∠ACB＝∠CDE＋∠DEC＝60°，又CD＝CE，∴∠CDE＝∠CED＝30°，∴∠CBD＝∠DEC，∴DE=BD，∠BDE＝∠CDB＋∠CDE＝120°，故ABC均正确．故选：D．【点睛】此题考查等边三角形的性质，等腰三角形的性质等知识，注意三线合一这一性质的理解与运用．12．B解析：B【分析】分两种情况：①AB为等腰三角形的底边；②AB为等腰三角形的一条腰；画出图形，即可得出结论．【详解】解：如图所示：①AB为等腰三角形的底边，符合条件的点C的有5个；②AB为等腰三角形的一条腰，符合条件的点C的有3个．所以符合条件的点C共有8个．故选：B．【点睛】此题考查了等腰三角形的判定，熟练掌握等腰三角形的判定是解题的关键，注意数形结合的解题思想．二、填空题13．45°或36°【分析】设∠BAD=∠CA D=α根据三角形内角和定理和三角形外角的性质表示∠EBC∠BEC和∠C再分三种情况讨论即可【详解】解：∵AD平分∴设∠BAD=∠CAD=α∵AB=AC∴∠AB解析：45°或36°．【分析】设∠BAD=∠CAD=α，根据三角形内角和定理和三角形外角的性质表示∠EBC、∠BEC和∠C ，再分三种情况讨论即可．【详解】解：∵AD 平分BAC ∠，∴设∠BAD=∠CAD=α，∵AB=AC ，∴∠ABC=∠C=1802902αα︒-=︒-， ∵PD 垂直平分AB ，∴AD=BD ， ∴∠ABD=∠BAD=α,∠EBC=∠ABC-∠ABE=902α︒-，∴∠BEC=∠ABE+∠BAC=3α,当BE=BC 时，∴∠BEC=∠C ，即903αα︒-=，解得22.5α=︒，∴245BAC α∠==︒；当BE=CE 时，∠EBC=∠C ，此时E 点和A 点重合，舍去；当BC=CE 时，∴∠EBC=∠BEC ，即9023αα︒-=，解得18α=︒，∴236BAC α∠==︒，故答案为：45°或36°．【点睛】本题考查三角形外角的性质，等腰三角形的性质，三角形内角和定理,垂直平分线的性质．掌握方程思想，能正确表示相关角是解题关键．14．①②③④【分析】由在△ABC 中∠ABC 和∠ACB 的平分线相交于点O 根据角平分线的定义与三角形内角和定理即可求得③正确；由平行线的性质和角平分线的定义得出△BEO 和△CFO 是等腰三角形得出EF=BE+解析：①②③④【分析】由在△ABC 中，∠ABC 和∠ACB 的平分线相交于点O ，根据角平分线的定义与三角形内角和定理，即可求得③1902BOC A ∠=+∠︒正确；由平行线的性质和角平分线的定义得出△BEO 和△CFO 是等腰三角形得出EF=BE+CF 故①正确；由角平分线的性质得出点O 到△ABC 各边的距离相等，故②正确；由角平分线定理与三角形面积的求解方法，即可求得④根据求得答案，即可得到④正确．【详解】解：∵在△ABC 中，∠ABC 和∠ACB 的平分线相交于点O ，∴∠OBC=12∠ABC ，∠OCB=12∠ACB ，∠A+∠ABC+∠ACB=180°， ∴∠OBC+∠OCB=90°12-∠A ，∴∠BOC=180°-（∠OBC+∠OCB）=90°+1∠A；故③正确；2∵在△ABC中，∠ABC和∠ACB的平分线相交于点O，∴∠OBC=∠OBE，∠OCB=∠OCF，∵EF∥BC，∴∠OBC=∠EOB，∠OCB=∠FOC，∴∠EOB=∠OBE，∠FOC=∠OCF，∴BE=OE，CF=OF，∴EF=OE+OF=BE+CF，故①正确；过点O作OM⊥AB于M，作ON⊥BC于N，连接OA，∵在△ABC中，∠ABC和∠ACB的平分线相交于点O，∴点O到△ABC各边的距离相等，故②正确．∴AM=AD，BM=BN，CD=CN，∵AM+BM=AB，AD+CD=AC，BN+CN=BC，∴AD=1（AB+AC-BC）故④正确，2故答案为：①②③④．【点睛】此题考查了角平分线的定义与性质，等腰三角形的判定与性质．此题难度适中，解题的关键是注意数形结合思想的应用．15．【分析】如图过点C作CH⊥x轴于H证明△AHC≌△BOA（AAS）可得结论【详解】解：如图过点C作CH⊥x轴于H∵∠AHC=∠CAB=∠AOB=90°∴∠BAO+∠CAH=90°∠CAH+∠ACH=解析：(3,2)【分析】如图，过点C作CH⊥x轴于H．证明△AHC≌△BOA（AAS），可得结论．【详解】解：如图，过点C作CH⊥x轴于H．∵∠AHC=∠CAB=∠AOB=90°，∴∠BAO+∠CAH=90°，∠CAH+∠ACH=90°，∴∠ACH=∠BAO ，在△AHC 和△BOA 中，AHC AOB ACH OAB AC AB ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AHC ≌△BOA （AAS ），∴AH=OB ，CH=OA ，∵A （2，0），B （0，1），∴OA=CH=2，OB=AH=1，∴OH=OA+AH=3，∴C （3，2）．故答案为：（3，2）．【点睛】本题考查等腰直角三角形的性质，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．16．88【分析】从等腰三角形的腰为长为4与等腰三角形的底边为4两种情况去分析求解即可求得答案【详解】解：若等腰三角形的腰为长为4设底边长为x 则有x+4×2=20解得：x=12此时三角形的三边长为4412解析：8，8【分析】从等腰三角形的腰为长为4与等腰三角形的底边为4两种情况去分析求解即可求得答案．【详解】解：若等腰三角形的腰为长为4，设底边长为x ，则有x+4×2=20，解得：x=12，此时，三角形的三边长为4，4，12，∵4+4＜12，∴不可以组成三角形；若等腰三角形的底边为4，设腰长为x ，则有2x+4=20，解得：x=8，∵4+8＞8，∴可以组成三角形；∴三角形的另两边的长分别为8，8．故答案为：8，8．【点睛】本题考查等腰三角形的定义和性质，利用分类讨论思想解题是关键．17．10cm 【分析】根据轴对称的性质和线段的垂直平分线的性质即可得到结论【详解】解：设CD 与OA 的交点为E 与OB 的交点为F ∵OAOB 分别是线段MCMD 的垂直平分线∴ME ＝CEMF ＝DF ∴小蚂蚁爬行的路径解析：10cm【分析】根据轴对称的性质和线段的垂直平分线的性质即可得到结论．【详解】解：设CD 与OA 的交点为E ，与OB 的交点为F ，∵OA 、OB 分别是线段MC 、MD 的垂直平分线，∴ME ＝CE ，MF ＝DF ，∴小蚂蚁爬行的路径最短＝CE+EF+DF=CD ＝10cm ，故答案为：10cm ．【点睛】本题考查了轴对称的性质-最短路径的问题，线段的垂直平分线的性质，解题的关键是熟练掌握知识点．18．16【分析】过点D 作于H 先利用三角形的面积公式计算出DH=8再利用角平分线的性质得到DF=DH=8接着证明得到证明得到利用等线段代换得到于是求出EF 的长然后根据三角形的面积公式计算即可【详解】过点D解析：16【分析】过点D 作DH AC ⊥于H ，先利用三角形的面积公式计算出DH=8，再利用角平分线的性质得到DF=DH=8，接着证明Rt DEF DGH △≌Rt △得到EF HG =，证明Rt ADF △≌Rt △ADH 得到AF AH =，利用等线段代换得到EF AG HG AE =--，于是求出EF 的长，然后根据三角形的面积公式计算即可【详解】过点D 作DH AC ⊥于H ，64S =△ADG ，16AG =1642AG DH ∴⨯⨯= 8DH ∴= AD 是ABC 的平分线，,DF AB DH AC ⊥⊥8DF DH ==∴在Rt DEF △和Rt DGH △中DE DG DF DH =⎧⎨=⎩\ ∴Rt DEF △≌Rt DGH △EF HG ∴=同理可得Rt ADF △≌Rt △ADHAF AH ∴=168EF AF AE AH AE AG HG AE EF =-=-=--=--4EF ∴=11481622DEF S EF DF ∴=⨯⨯=⨯⨯=△ 【点睛】本题考查了角平分线的性质，全等三角形的判定和性质，熟练掌握角平分线的性质，全等三角形的判定定理是解题关键．19．100°【分析】根据线段垂直平分线的性质和等边对等角可得∠OBA=∠A ∠OBC=∠C 根据三角形外角的性质可得∠AOP=∠A+∠ABO=2∠ABO ∠COP=∠C+∠CBO=2∠CBO 再利用角的和差即可 解析：100°【分析】根据线段垂直平分线的性质和等边对等角可得∠OBA=∠A ，∠OBC=∠C ，根据三角形外角的性质可得∠AOP=∠A+∠ABO=2∠ABO ，∠COP=∠C+∠CBO=2∠CBO ，再利用角的和差即可得出∠AOC ．【详解】解：如图，连接BO 并延长至P ，∵线段AB、BC的垂直平分线l1、l2相交于点O，∴OA=OB，OB=OC，∴∠OBA=∠A，∠OBC=∠C，∵∠AOP=∠A+∠ABO=2∠ABO，∠COP=∠C+∠CBO=2∠CBO，∴∠AOC=∠AOP+∠COP =2(∠ABO+∠CBO)=2∠ABC=100°，故答案为：100°．【点睛】本题考查了线段垂直平分线的性质：垂直平分线垂直且平分其所在线段；垂直平分线上任意一点，到线段两端点的距离相等．也考查了等腰三角形的性质．20．5【分析】将AD顺时针旋转60°得连结可得AD=DD′=AD′可证△ABD′≌△ACD（SAS）可得BD′=CD由BD′+DD′≥BD当BD′D三点在一线时BD最大BD最大=BD′+DD′=5【详解解析：5【分析】将AD顺时针旋转60°，得AD'，连结BD'，可得AD=DD′=AD′，可证△ABD′≌△ACD （SAS），可得BD′=CD，由BD′+DD′≥BD，当B、D′、D三点在一线时，BD最大，BD最大=BD′+DD′=5．【详解】解：∵将AD顺时针旋转60°，得AD'，连结BD'，则AD=DD′=AD′，∴△ADD′是等边三角形，又∵等边三角形ABC，∴∠BAC=∠D AD'，∴∠BAD′+∠D′AC=∠CAD+∠D′AC=60°，∴AB=AC，AD′=AD，∴△ABD′≌△ACD（SAS），∴BD′=CD，∴BD′+DD′≥BD，当B、D′、D三点在一线时，BD最大，BD最大=BD′+DD′=CD+AD=2+3=5．故答案为：5．．【点睛】本题考查三角形旋转变换，等边三角形判定与性质，掌握三角形旋转变换的性质，等边三角形判定与性质，用三角形三边关系确定B、D′、D共线是解题关键．三、解答题21．（1）画图见解析；（2）△ABC的周长=21；（3）AB=8，AC=8，BC=5．【分析】（1）根据垂直平分线的作法作出图形即可；（2）根据垂直平分线的性质可得AP=BP，从而得出AC+BC的值，再根据AB=8，即可求得△ABC的周长；（3）分两种情况进行讨论即可．【详解】解：（1）如图所示：即PQ为所求；；（2）如图所示：∵AB 的垂直平分线交AC 于点P ，∴PA =PB ，∵△PBC 的周长为13，∴PB +PC +BC =13，∴PA +PC +BC =13，即AC +BC =13，∴△ABC 的周长=AB +AC +BC =8+13=21；（3）∵AC ＞BC ，∴分两种情况，①AC =AB =8时，BC =21-AC -BC =21-8-8=5；②BC =AB =8时，AC =21-AB -BC =21-8-8=5，∵AC ＞BC ，∴不合题意舍去；综上所述，若△ABC 是等腰三角形，△ABC 的三条边的长度为AB =8，AC =8，BC =5．【点睛】本题是三角形综合题目，考查了线段垂直平分线的性质、等腰三角形的性质、尺规作图、三角形周长等知识．本题综合性强，熟练掌握等腰三角形的性质和线段垂直平分线的性质是解题的关键．22．（1）点E 的坐标为（0，2）；（2）见解析；（3）60OCD ∠=︒【分析】（1）先根据ASA 判定△AOE ≌△BOC ，得出OE=OC ，再根据点C 的坐标为（2，0），得到OC=2=OE ，进而得到点E 的坐标；（2）先过点O 作OM ⊥AD 于点M ，作ON ⊥BC 于点N ，根据△AOE ≌△BOC ，得到S △AOE =S △BOC ，且AE=BC ，再根据OM ⊥AE ，ON ⊥BC ，得出OM=ON ，进而得到OD 平分∠ADC ；（3）在DA 上截取DP=DC ，连接OP ，根据SAS 判定△OPD ≌△OCD ，再根据三角形外角性质以及三角形内角和定理，求得∠PAO=30°，进而得到∠OCB=60°．【详解】解：（1）如图①，∵AD ⊥BC ，BO ⊥AO ，∴∠AOE=∠BDE=90︒，又∵∠AEO=∠BED ，∴∠OAE=∠OBC ，∵A （-3，0），B （0，3），∴OA=OB=3，在△AOE 和△BOC 中，90AOE BOC OA OB OAE OBC ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩， ∴△AOE ≌△BOC(ASA)，∴OE=OC ，又∵点C 的坐标为（2，0），∴OC=2=OE ，∴点E 的坐标为（0，2）；（2）如图②，过点O 作OM ⊥AD 于点M ，作ON ⊥BC 于点N ，∵△AOE ≌△BOC ，∴S △AOE =S △BOC ，且AE=BC ，∵OM ⊥AE ，ON ⊥BC ，∴OM=ON ，∴OD 平分∠ADC ；（3）如图所示，在DA 上截取DP=DC ，连接OP ，∵∠PDO=∠CDO ，OD=OD ，在△OPD 和△OCD 中，DP DC PDO CDO OD OD =⎧⎪∠=∠⎨⎪=⎩，∴△OPD ≌△OCD(SAS)，∴OC=OP ，∠OPD=∠OCD ，∵AD-CD=OC ，∴AD-DP=OP ，即AP=OP ，∴∠PAO=∠POA ，∴∠OPD=∠PAO+∠POA=2∠PAO=∠OCB ，又∵∠PAO+∠OCD=90°，∴3∠PAO=90°，∴∠PAO=30°，∴∠OCB=60°．【点睛】本题主要考查了全等三角形的判定与性质，角平分线的判定定理以及等腰直角三角形的性质的综合应用，解决问题的关键是作辅助线构造全等三角形，运用全等三角形的性质进行求解．23．（1）20AED ∠=︒；（2）见解析；（3）70ECD ∠=︒．【分析】（1）根据三角形内角和定理可得∠BAC=20°，根据平行线得性质可得∠ADE=∠ABC ，利用SAS 可证明△ABC ≌△EAD ，根据全等三角形得性质可得∠AED=∠BAC=20°；（2）根据全等三角形得性质可得AE=AB ，由等角对等边可得AB=AC ，即可证明AE=AC ，根据等腰三角形得性质可得∠ADE=∠EAD=80°，可得∠CAE=60°，即可证明△ACE 是等边三角形；（3）由（2）可知∠AEC=60°，即可得出∠DEC 的度数，根据等腰三角形得性质即可得答案．【详解】（1）∵80ABC ACB ∠=∠=︒，∴∠BAC=180°-2∠ACB=20°，∵//DE BC ，∴ADE ABC =∠∠，ABC ACB ∴∠=∠，ADE ACB ∴∠=∠∴在ABC ∆和EAD ∆中BC AD ADE ACB AC DE =⎧⎪∠=∠⎨⎪=⎩，ABC EAD ∴∆≅∆，20AED BAC ∴∠=∠=︒．（2）由（1）知：ABC EAD ∆≅∆，AE AB ∴=，80EAD ABC ∠=∠=︒∵80ABC ACB ∠=∠=︒∴AB AC =，AE AC ∴=，∵∠BAC=20°，802060CAE ∴∠=︒-︒=︒，ACE ∴∆是等边三角形.（3）ACE ∆是等边三角形，60CEA ∴∠=︒，∵∠AED=20°，602040CED ∴∠=︒-︒=︒，ED AC EC ==，EDC ∴∆为等腰三角形，18040702ECD ︒-︒∴∠==︒． 【点睛】本题考查全等三角形的判定与性质、平行线的性质及等边三角形的判定与性质，熟练掌握相关性质及定理是解题关键．24．（1）122y x =-+；（2）4OBC S =；（3）P 为（2，6）或（-2，-2） 【分析】（1）设直线AB 的解析式为：y kx b =+，把点A （-2，3），B （4，0）即可得到结论； （2）由（1）知点C 的坐标为（0，2），利用三角形面积直接求解即可；（3）分①当点P 在直线BC 上方，②当点P 在直线BC 下方两种情况讨论，利用全等三角形的判定和性质求解即可．【详解】（1）设直线AB 的解析式为：y kx b =+， 把点A （-2，3），B （4，0）代入得，2340k b k b -+=⎧⎨+=⎩，解得：122 kb⎧=-⎪⎨⎪=⎩，∴直线AB的关系式为：122y x=-+；（2）由（1）知：点C的坐标为（0，2），∴OB=4，OC=2，∴△OBC的面积为：11OB OC42422OBCS=⨯=⨯⨯=；（3）①当点P在直线BC上方时，过P作PE⊥y轴于E，如图：∵△OBC是等腰直角三角形，且PC=BC，∴∠PCB=90︒，∴∠PCE+∠EPC =90︒，∠PCE+∠OCB =90︒，∴∠EPC =∠OCB，在△EPC和△OCB中，90PEC COBEPC OCBPC BC∠=∠=︒⎧⎪∠=∠⎨⎪=⎩，∴△EPC≅△OCB，∴EC=OB=4，EP=OC=2，∴点P的坐标为（2，6），②当点P在直线BC下方时，过P1作P1F⊥y轴于F，如图：同理可证1FPC OCB≅，∴FC=OB=4，P1F=OC=2，∴点P1的坐标为（-2，2），综上，点P的坐标为（2，6）或（-2，2）．【点睛】本题考查了待定系数法求一次函数的解析式，等腰直角三角形的性质，正确的作出图形，利用数形结合是解题的关键．25．（1）见解析；（2）=，理由见解析；（3）1或3【分析】（1）根据等腰三角形的三线合一得到CE为∠ACB的平分线，证明BD=BE，等量代换证明结论；（2）过点E作EF∥BC，交AC于点F，证明△DBE≌△EFC，根据全等三角形的性质证明；（3）分点E在AB的延长线上和点E在BA的延长线上两种情况，根据全等三角形的性质解答．【详解】（1）证明：∵△ABC为等边三角形，点E为AB的中点，∴CE为∠ACB的平分线，∴∠BCE=12∠ACB=12×60°=30°．∵ED=EC，∴∠D=∠DCE=30°，∵∠ABC=60°，∠D+∠DEB=∠ABC，∴∠DEB=30°，∴BD=BE，∵AE=BE，∴AE=BD；（2）解：AE=BD，理由如下：如图，过点E作EF∥BC，交AC于点F，∵△ABC为等边三角形，∴∠ACB=∠ABC=60°，∵EF∥BC，∴∠AEF=∠ABC=∠AFE=∠ACB=60°，∴△AEF为等边三角形，∴AB=AC，∴BE=CF，∴∠DBE=∠EFC=120°，在△DBE和△EFC中，DE EC DBE EFC BE FC =⎧⎪∠=∠⎨⎪=⎩，∴△DBE ≌△EFC （SAS ），∴EF=DB ，∵AE=EF ，∴AE=DB ；故答案为：=；（3）当点E 在BA 的延长线上时，如图③，作EF ∥BC 交CA 的延长线于F ，则△AEF 为等边三角形，∴AF=AE=EF=2，∠BEF=60°，∴∠CEF=60°+∠BEC ，∵∠EDC=∠ECD=∠B+∠BEC=60°+∠BEC ，∴∠CEF=∠EDB ，在△CEF 和△EDB 中，603CEF EDB F B EB CF ∠=∠⎧⎪∠=∠=︒⎨⎪==⎩，∴△CEF ≌△EDB （AAS ），∴BD=EF=2，∴CD=BD-BC=1，当点E 在AB 的延长线上时，如图，作EF ∥BC 交AC 的延长线于F ，则△AEF 为等边三角形，∴AF=AE=EF=2，∠AEF=60°，∴∠CEF=60°-∠AEC ，∵∠D=∠ECD=∠ABC+∠AEC=60°+∠AEC ，∴∠CEF=∠D ，在△CEF 和△EDB 中，601CEF D F DBE EB CF ∠=∠⎧⎪∠=∠=︒⎨⎪==⎩，∴△CEF ≌△EDB （AAS ），∴BD=EF=2，∴CD=BD+BC=3，综上所述，CD=1或3．【点睛】本题考查了等边三角形的性质、三角形全等的判定和性质，掌握全等三角形的判定定理和性质定理是解题的关键．26．（1）见解析；（2）90°；（3【分析】（1）用SAS 证明△ACD ≌△BCE ，即可得到结论；（2）根据全等三角形的性质得到∠EBC=∠BAC=45°，可得∠DBE ；（3）分DA=DE ，DA=AE ，DE=AE ，三种情况根据等腰三角形的性质求解．【详解】解：（1）∵CE ⊥CD ，∴∠DCE=90°=∠ACB ，∴∠ACB+∠BCD=∠DCE+∠BCD ，即∠ACD=∠ECB ，∴在△ACD 和△BCE 中，AC BC ACD ECB CD CE =⎧⎪∠=∠⎨⎪=⎩，∴△ACD ≌△BCE （SAS ），∴AD=BE ；（2）由（1）可知：△ACD ≌△BCE ，∴∠EBC=∠BAC=45°，∴∠DBE=180°-∠EBC-∠ABC=90°；（3）∵△ADE 是等腰三角形，若DA=DE ，则∠DAE=∠DEA ，∵∠DAC=∠DEC ，∴∠CAE=∠CEA，∴AC=EC，∵AC≠EC，∴DA≠DE；若DA=AE，∵∠EBA=90°，∴AE＞BE，∵△ACD≌△BCE，∴AD=BE，∴AE≠AD；若DE=AE，∵EB⊥AD，AE=DE，∴B是AD中点，∴AD=2AB=2BD=1，∵△ACD≌△BCE，∴BE=AD=2，由（2）可知：∠DBE=90°，∴DE=225+=；BE DB综上：DE的值为5．【点睛】本题考查了全等三角形的判定和性质，等腰三角形的性质，解题的关键是注意分类讨论，灵活运用等腰三角形的性质．。

注意：要证明一条线为一个线段的垂直平分线，应证明两个点到这条线段的距离相等且这两个点都在要求证的直线上才可以证明通常来说，垂直平分线会与全等三角形来使用。

垂直平分线的性质：线段垂直平分线上的点到这条线段的两个端点的距离相等。

巧记方法：点到线段两端距离相等。

可以通过全等三角形证明。

垂直平分线的尺规作法方法之一：(用圆规作图)1、在线段的中心找到这条线段的中点通过这个点做这条线段的垂线段。

2、分别以线段的两个端点为圆心，以大于线段的二分之一长度为半径画弧线。

得到两个交点(两交点交与线段的同侧)。

3、连接这两个交点。

原理：等腰三角形的高垂直平分底边。

方法之二：1、连接这两个交点。

原理：两点成一线。

等腰三角形的性质：1、三线合一 ( 等腰三角形底边上的高、底边上的中线、顶角平分线相互重合。

)2、等角对等边(如果一个三角形，有两个内角相等，那么它一定有两条边相等。

)3、等边对等角(在同一三角形中，如果两个角相等，即对应的边也相等。

)垂直平分线的判定①利用定义.②到一条线段两个端点距离相等的点，在这条线段的垂直平分线上.(即线段垂直平分线可以看成到线段两端点距离相等的点的集合)例1．如图，已知：在△ABC中，∠C=90°∠A=30°，BD平分∠ABC交AC于D.求证：D在AB的垂直平分线上.分析：根据线段垂直平分线的逆定理，欲证D在AB的垂直平分线上，只需证明BD=DA即可.证明：∵∠C=90，°∠A=30°（已知），∴∠ABC=60°（Rt△的两个锐角互余）又∵BD平分∠ABC（已知）∴∠DBA=1/2∠ABC=30°=∠A∴BD=AD（等角对等边）∴D在AB的垂直平分线上（和一条线段两个端点距离相等的点，在这条线段的垂直平分线上）.例2．如图，已知：在△AB C中，AB=AC，∠BAC=120°，AB的垂直平分线交AB于E，交BC于F。

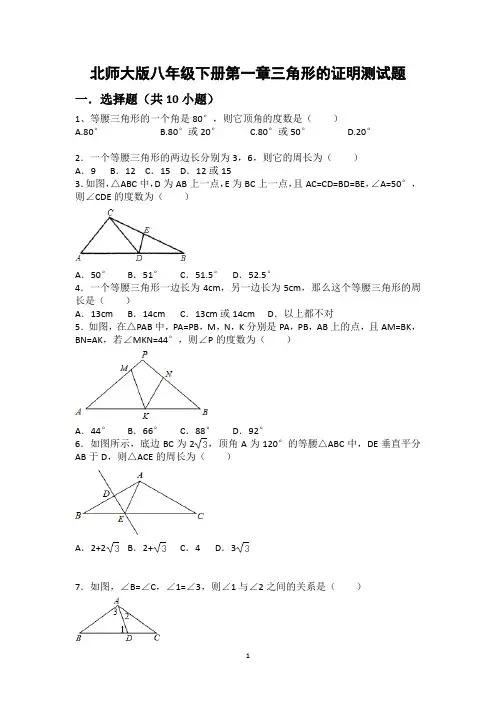
北师大版八年级下册第一章三角形的证明测试题一．选择题（共10小题）1、等腰三角形的一个角是80°，则它顶角的度数是（）A.80°B.80°或20°C.80°或50°D.20°2．一个等腰三角形的两边长分别为3，6，则它的周长为（）A．9 B．12 C．15 D．12或153．如图，△ABC中，D为AB上一点，E为BC上一点，且AC=CD=BD=BE，∠A=50°，则∠CDE的度数为（）A．50°B．51°C．51.5°D．52.5°4．一个等腰三角形一边长为4cm，另一边长为5cm，那么这个等腰三角形的周长是（）A．13cm B．14cm C．13cm或14cm D．以上都不对5．如图，在△PAB中，PA=PB，M，N，K分别是PA，PB，AB上的点，且AM=BK，BN=AK，若∠MKN=44°，则∠P的度数为（）A．44°B．66°C．88°D．92°6．如图所示，底边BC为2，顶角A为120°的等腰△ABC中，DE垂直平分AB于D，则△ACE的周长为（）A．2+2B．2+C．4 D．37．如图，∠B=∠C，∠1=∠3，则∠1与∠2之间的关系是（）A．∠1=2∠2 B．3∠1﹣∠2=180°C．∠1+3∠2=180° D．2∠1+∠2=180°8．如图在等腰△ABC中，其中AB=AC，∠A=40°，P是△ABC内一点，且∠1=∠2，则∠BPC等于（）A．110°B．120°C．130°D．140°9．如图，在△ABC中，AB=AC，BD=CE，BE=CF，若∠A=50°，则∠DEF=（）A．55°B．60°C．65°D．70°10．如图所示，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且S△ABC=4cm²，则S阴影等于（）A．2cm²B．1cm²C．cm²D．cm²二．填空题（共5小题）11．等边三角形是一个轴对称图形，它有______条对称轴．12．等腰三角形一腰上的高与另一腰的夹角为48°，则该等腰三角形的底角的度数为______．13．在等腰△ABC中，AB=AC，AC腰上的中线BD将三角形周长分为15和21两部分，则这个三角形的底边长为______.14．等腰三角形的一个内角为70°，它一腰上的高与底边所夹的度数为______．15．如图，已知：∠MON=30°，点A1、A2、A3 在射线ON上，点B1、B2、B3…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形，若OA1=a，则△A6B6A7的边长为______．三．解答题（共8小题）16．如图，在△ABC中，AB=AC，AD是BC边上的中线，AE⊥BE于点E，且BE=．求证：AB平分∠EAD．17．如图，已知AC⊥BC，BD⊥AD，AC与BD交于O，AC=BD．求证：△OAB是等腰三角形．18．如图，已知△ABC中，AB=BD=DC，∠ABC=105°，求∠A，∠C度数．19．如图，在△ABC中，AB=AC，AB的垂直平分线交AB于点N，交BC的延长线于点M，若∠A=40°．（1）求∠NMB的度数；（2）如果将（1）中∠A的度数改为70°，其余条件不变，再求∠NMB的度数；（3）你发现∠A与∠NMB有什么关系，试证明之．20．如图，在△ABC中，AD平分∠BAC，BD⊥AD，垂足为D，过D作DE∥AC，交AB于E．求证：△BDE是等腰三角形．21．如图，在△ABC中，AD平分∠BAC，点D是BC的中点，DE⊥AB于点E，DF ⊥AC于点F．求证：△ABC是等腰三角形．22．如图，在△ABC中，AB=AC，AD是BC边上的中线，BE⊥AC于点E．求证：∠CBE=∠BAD．23．如图，在△ABC中，AB=AC，D是BC上任意一点，过D分别向AB，AC引垂线，垂足分别为E，F，CG是AB边上的高．（1）当D点在BC的什么位置时，DE=DF？并证明．（2）DE，DF，CG的长之间存在着怎样的等量关系？并加以证明：（3）若D在底边BC的延长线上，（2）中的结论还成立吗？若不成立，又存在怎样的关系？北师大版八年级下册第一章三角形的证明测试题参考答案与试题解析一．选择题（共10小题）1、等腰三角形的一个角是80°，则它顶角的度数是（）【解答】解：①80°角是顶角时，三角形的顶角为80°，②80°角是底角时，顶角为180°﹣80°×2=20°，综上所述，该等腰三角形顶角的度数为80°或20°．故选B．2．一个等腰三角形的两边长分别为4，8，则它的周长为（）A．12 B．16 C．20 D．16或20【解答】解：①当4为腰时，4+4=8，故此种情况不存在；②当8为腰时，8﹣4＜8＜8+4，符合题意．故此三角形的周长=8+8+4=20．故选C．3．如图，△ABC中，D为AB上一点，E为BC上一点，且AC=CD=BD=BE，∠A=50°，则∠CDE的度数为（）A．50°B．51°C．51.5°D．52.5°【解答】解：∵AC=CD=BD=BE，∠A=50°，∴∠A=∠CDA=50°，∠B=∠DCB，∠BDE=∠BED，∵∠B+∠DCB=∠CDA=50°，∴∠B=25°，∵∠B+∠EDB+∠DEB=180°，∴∠BDE=∠BED=（180°﹣25°）=77.5°，∴∠CDE=180°﹣∠CDA﹣∠EDB=180°﹣50°﹣77.5°=52.5°，故选D．4．一个等腰三角形一边长为4cm，另一边长为5cm，那么这个等腰三角形的周长是（）A．13cm B．14cm C．13cm或14cm D．以上都不对【解答】解：当4cm为等腰三角形的腰时，三角形的三边分别是4cm，4cm，5cm符合三角形的三边关系，∴周长为13cm；当5cm为等腰三角形的腰时，三边分别是，5cm，5cm，4cm，符合三角形的三边关系，∴周长为14cm，故选C5．如图，在△PAB中，PA=PB，M，N，K分别是PA，PB，AB上的点，且AM=BK，BN=AK，若∠MKN=44°，则∠P的度数为（）A．44°B．66°C．88°D．92°【解答】解：∵PA=PB，∴∠A=∠B，在△AMK和△BKN中，∴△AMK≌△BKN，∴∠AMK=∠BKN，∵∠MKB=∠MKN+∠NKB=∠A+∠AMK，∴∠A=∠MKN=44°，∴∠P=180°﹣∠A﹣∠B=92°，故选：D．6．如图所示，底边BC为2，顶角A为120°的等腰△ABC中，DE垂直平分AB于D，则△ACE的周长为（）A．2+2B．2+C．4 D．3【解答】解：过A作AF⊥BC于F，∵AB=AC，∠A=120°，∴∠B=∠C=30°，∴AB=AC=2，∵DE垂直平分AB，∴BE=AE，∴AE+CE=BC=2，∴△ACE的周长=AC+AE+CE=AC+BC=2+2，故选：A．7．如图，∠B=∠C，∠1=∠3，则∠1与∠2之间的关系是（）A．∠1=2∠2 B．3∠1﹣∠2=180°C．∠1+3∠2=180° D．2∠1+∠2=180°【解答】解：∵∠1=∠3，∠B=∠C，∠1+∠B+∠3=180°，∴2∠1+∠C=180°，∴2∠1+∠1﹣∠2=180°，∴3∠1﹣∠2=180°．故选B．8．如图在等腰△ABC中，其中AB=AC，∠A=40°，P是△ABC内一点，且∠1=∠2，则∠BPC等于（）A．110°B．120°C．130°D．140°【解答】解：∵∠A=40°，∴∠ACB+∠ABC=180°﹣40°=140°，又∵∠ABC=∠ACB，∠1=∠2，∴∠PBA=∠PCB，∴∠1+∠ABP=∠PCB+∠2=140°×=70°，∴∠BPC=180°﹣70°=110°．故选A．9．如图，在△ABC中，AB=AC，BD=CE，BE=CF，若∠A=50°，则∠DEF=（）A．55°B．60°C．65°D．70°【解答】解：∵AB=AC，∴∠B=∠C，在△DBE和△ECF中，∴△DBE≌△ECF（SAS），∴∠EFC=∠DEB，∵∠A=50°，∴∠C=（180°﹣50°）÷2=65°，∴∠CFE+∠FEC=180°﹣65°=115°，∴∠DEB+∠FEC=115°，∴∠DEF=180°﹣115°=65°．故选：C．10．如图所示，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且S△ABC=4cm2，则S阴影等于（）A．2cm2 B．1cm2 C．cm2 D．cm2【解答】解：根据三角形的面积公式，知：等底等高的两个三角形的面积相等．即有：S阴影=S△BCE=S△ABC=1cm2．故选：B．二．填空题（共10小题）11．等边三角形是一个轴对称图形，它有 3 条对称轴【解答】解：等边三角形是轴对称图像，它有三个顶点，所以对应3条对称轴故答案为：312．等腰三角形一腰上的高与另一腰的夹角为48°，则该等腰三角形的底角的度数为69°或21°．【解答】解：分两种情况讨论：①若∠A＜90°，如图1所示：∵BD⊥AC，∴∠A+∠ABD=90°，∵∠ABD=48°，∴∠A=90°﹣48°=42°，∵AB=AC，∴∠ABC=∠C=（180°﹣42°）=69°；②若∠A＞90°，如图2所示：同①可得：∠DAB=90°﹣48°=42°，∴∠BAC=180°﹣42°=138°，∵AB=AC，∴∠ABC=∠C=（180°﹣138°）=21°；综上所述：等腰三角形底角的度数为69°或21°．故答案为：69°或21°．13．在等腰△ABC中，AB=AC，AC腰上的中线BD将三角形周长分为15和21两部分，则这个三角形的底边长为16或8．【解答】解：∵BD是等腰△ABC的中线，可设AD=CD=x，则AB=AC=2x，又知BD将三角形周长分为15和21两部分，∴可知分为两种情况①AB+AD=15，即3x=15，解得x=5，此时BC=21﹣x=21﹣5=16；②AB+AD=21，即3x=21，解得x=7；此时等腰△ABC的三边分别为14，14，8．经验证，这两种情况都是成立的．∴这个三角形的底边长为8或16．故答案为：16或8．14．等腰三角形的一个内角为70°，它一腰上的高与底边所夹的度数为35°或20°．【解答】解：在△ABC中，AB=AC，①当∠A=70°时，则∠ABC=∠C=55°，∵BD⊥AC，∴∠DBC=90°﹣55°=35°；②当∠C=70°时，∵BD⊥AC，∴∠DBC=90°﹣70°=20°；故答案为：35°或20°．15．如图，已知：∠MON=30°，点A1、A2、A3 在射线ON上，点B1、B2、B3…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形，若OA1=a，则△A6B6A7的边长为32a ．【解答】解:∵△A1B1A2是等边三角形∴∠B1A1A2＝60°，A1B1＝B1A2＝A1A2∵∠MON=30°∴∠OB1A1=30°（三角形的一个外角等于和它不相邻的两个外角和∠OB1A1=∠B1A1A2－∠MON）∴OA1=A1B1（等边对等角）∴OA1=A1A2=a同理，根据∠MON=∠OB2A2，可得：A2A3=A2B2=OA1＋A1A2=2A1A2=2a同理，可推出：A3A4=2A2A3=4a同理，可推出：A4A5=2A3A4=8a同理，可推出：A5A6=2A4A5=16a同理，可推出：A6A7=2A5A6=32a 即题目所求另外我们不难发现，第n个（△A1B1A2为第一个）等边三角形的边长为AnAn+1=(2^n-1)a 注：2的n-1次方倍的a三．解答题（共8小题）16．如图，在△ABC中，AB=AC，AD是BC边上的中线，AE⊥BE于点E，且BE=．求证：AB平分∠EAD．【解答】证明：∵AB=AC，AD是BC边上的中线，∴BD=BC，AD⊥BC，∵BE=BC，∴BD=BE，∵AE⊥BE，∴AB平分∠EAD．17．如图，已知AC⊥BC，BD⊥AD，AC与BD交于O，AC=BD．求证：△OAB是等腰三角形．【解答】证明：∵AC⊥BC，BD⊥AD∴∠D=∠C=90°，在Rt△ABD和Rt△BAC中，，∴Rt△ABD≌Rt△BAC（HL），∴∠DBA=∠CAB，∴OA=OB，即△OAB是等腰三角形．另外一种证法：证明：∵AC⊥BC，BD⊥AD∴∠D=∠C=90°在Rt△ABD和Rt△BAC中∴Rt△ABD≌Rt△BAC（HL）∴AD=BC，在△AOD和△BOC中，∴△AOD≌△BOC（AAS），∴OA=OB，即△OAB是等腰三角形．18．如图，已知△ABC中，AB=BD=DC，∠ABC=105°，求∠A，∠C度数．【解答】解：∵AB=BD，∴∠BDA=∠A，∵BD=DC，∴∠C=∠CBD，设∠C=∠CBD=x，则∠BDA=∠A=2x，∴∠ABD=180°﹣4x，∴∠ABC=∠ABD+∠CDB=180°﹣4x+x=105°，解得：x=25°，所以2x=50°，即∠A=50°，∠C=25°．19．如图，在△ABC中，AB=AC，AB的垂直平分线交AB于点N，交BC的延长线于点M，若∠A=40°．（1）求∠NMB的度数；（2）如果将（1）中∠A的度数改为70°，其余条件不变，再求∠NMB的度数；（3）你发现∠A与∠NMB有什么关系，试证明之．【解答】解：（1）∵在△ABC中，AB=AC，∠A=40°，∴∠ABC=∠ACB=70°，∵AB的垂直平分线交AB于点N，交BC的延长线于点M，∴MN⊥AB，∴∠NMB=90°﹣∠ABC=20°；（2）∵在△ABC中，AB=AC，∠A=70°，∴∠ABC=∠ACB=55°，∵AB的垂直平分线交AB于点N，交BC的延长线于点M，∴MN⊥AB，∴∠NMB=90°﹣∠ABC=35°；（3）∠NMB=∠A．理由：∵在△ABC中，AB=AC，∴∠ABC=∠ACB=，∵AB的垂直平分线交AB于点N，交BC的延长线于点M，∴MN⊥AB，∴∠NMB=90°﹣∠ABC=∠A．20．如图，在△ABC中，AD平分∠BAC，BD⊥AD，垂足为D，过D作DE∥AC，交AB于E．求证：△BDE是等腰三角形．【解答】解：（1）∵AD平分∠BAC，DE∥AC，∴∠EAD=∠CAD，∠EDA=∠CAD，∴∠EAD=∠EDA，∵BD⊥AD，∴∠EBD+∠EAD=∠BDE+∠EDA∴∠EBD=∠BDE，∴DE=BE，∴△BDE是等腰三角形．21．如图，在△ABC中，AD平分∠BAC，点D是BC的中点，DE⊥AB于点E，DF ⊥AC于点F．求证：△ABC是等腰三角形．【解答】证明：∵AD平分∠BAC，DE⊥AB于点E，DF⊥AC于点F，∴DE=DF，在Rt△BDE和Rt△CDF中，，∴Rt△BDE≌Rt△CDF（HF），∴∠B=∠C，∴△ABC为等腰三角形．22．如图，在△ABC中，AB=AC，AD是BC边上的中线，BE⊥AC于点E．求证：∠CBE=∠BAD．【解答】证明：∵AB=AC，AD是BC边上的中线，BE⊥AC，∴∠CBE+∠C=∠CAD+∠C=90°，∠CAD=∠BAD，∴∠CBE=∠BAD．23．如图，在△ABC中，AB=AC，D是BC上任意一点，过D分别向AB，AC引垂线，垂足分别为E，F，CG是AB边上的高．（1）当D点在BC的什么位置时，DE=DF？并证明．（2）DE，DF，CG的长之间存在着怎样的等量关系？并加以证明：（3）若D在底边BC的延长线上，（2）中的结论还成立吗？若不成立，又存在怎样的关系？【解答】解：（1）当点D在BC的中点时，DE=DF，理由如下：∵D为BC中点，∴BD=CD，∵AB=AC，∴∠B=∠C，∵DE⊥AB，DF⊥AC，∴∠DEB=∠DFC=90°，在△BED和△CFD中，∴△BED≌△CFD（AAS），∴DE=DF．（2）DE+DF=CG．证明：连接AD，则S△ABC=S△ABD+S△ACD，即AB•CG=AB•DE+AC•DF，∵AB=AC，∴CG=DE+DF．（3）当点D在BC延长线上时，（1）中的结论不成立，但有DE﹣DF=CG．理由：连接AD，则S△ABD=S△ABC+S△ACD，即AB•DE=AB•CG+AC•DF∵AB=AC，∴DE=CG+DF，即DE﹣DF=CG．同理当D点在CB的延长线上时，则有DE﹣DF=CG，说明方法同上．。

北师大版八年级数学下册第一章（证明）练习题1.下列图形中，可以由其中一个图形通过平移得到的是 ( )A. B. C. D. 2.列命题中，其逆命题不成立的是（ ）A ．同旁内角互补，两直线平行B ．如果三角形的三边长 a ，b ，c 满足 a 2+b 2=c 2，那么这个三角形是直角三角形C ．如果两个实数相等，那么它们的平方相等D ．角平分线上的点到角两边的距离相等3. 等腰三角形的两边长分别为3和6，则这个等腰三角形的周长为( )A ．12B ．15C ．12或15D ．184.如图，在△ABC 中，BC ＝5，∠A ＝80°，∠B ＝70°，把△ABC 沿RS 的方向平移到△DEF 的位置，若CF ＝4，则下列结论中错误的是( )A. BE ＝4B. ∠F ＝30°C. AB ∥DED. DF ＝55．如图，在△ABC 中，AB ＝AC ，∠A ＝36°，BD 是AC 边上的高，则∠DBC 的度数是( )A ．18°B ．24°C ．30°D ．36°第4题 第5题 第6题 第7题 第8题6．如图，在△ABC 中，∠C ＝90°，AC ＝3，∠B ＝30°，点P 是BC 边上的动点，则下列选项中AP 长不可 能是( )A ．3.5B ．4.2C ．5.8D ．77．如图，在△ABC 中，BD 平分∠ABC ，BC 的垂直平分线交BC 于点E ，交BD 于点F ，连接CF .若∠A ＝60°，∠ABD ＝24°，则∠ACF 的度数为( )A ．48°B ．36°C ．30°D ．24°8．如图，在△ABC 中，∠C ＝90°，∠B ＝30°，以点A 为圆心，任意长为半径画弧分别交AB ，AC 于点M和N ，再分别以M ，N 为圆心，大于12MN 的长为半径画弧，两弧交于点P ，连接AP 并延长交BC 于点D ， 则下列说法中正确的个数是( )①AD 是∠BAC 的平分线②∠ADC ＝60°；③点D 在AB 的垂直平分线上；④S △DAC ∶S △ABC ＝1∶3.A. 1 B ．2 C ．3 D ．49．要判定两个直角三角形全等，下列说法正确的有（ ）①有两条直角边对应相等；②有两个锐角对应相等；③有斜边和一条直角边对应相等；④有一条直角边和一个锐角相等；⑤有斜边和一个锐角对应相等；⑥有两条边相等．A．①③④⑤B．①③⑤C．①③④⑤⑥D．①③④10．如图，已知∠MON＝30°，点A1，A2，A3，…在射线ON上，点B1，B2，B3，…在射线OM上，△A1B1A2，△A2B2A3，△A3B3A4，…均为等边三角形，若OA1＝1，则△A6B6A7的边长为()A．6 B．12 C．32 D．6411．一个等腰三角形有一角是70°，则其余两角分别为.12．在用反证法证明命题“三角形中必有一个内角小于或等于60° ”时，首先应该假设这个三角形中_ _.13．有下列三角形：①有两个角等于60°；②有一个角等于60°的等腰三角形；③三个外角(每个顶点处各取一个外角)都相等的三角形；④一腰上的中线也是这条腰上的高的等腰三角形．其中是等边三角形的有．(填序号)14. “垂直于同一条直线的两条直线互相平行”的逆命题是，这是一个(填“真”或“假”)命题．15．已知点A的坐标为(1,3)，点B的坐标为(2,1)．将线段AB沿某一方向平移后，点A的对应点的坐标为(−2,1)．则点B的对应点的坐标为．16．如图，在Rt△ABC中，∠C＝90°，AD平分∠CAB，CD＝3，AB＝12，则△ABD的面积为.第16题第17题第18题第19题第20题17．如图，∠A=15°，AB=BC=CD=DE=EF，则∠MEF=________．18．如图，将一长方形纸片ABCD折叠，使两个顶点A，C重合，折痕为FG.若AB＝4，BC＝8，则△ABF 的面积为___ __．19．如图，△ABC中，∠C=90°，∠A=30°，AB的垂直平分线交AC于D，交AB于E，CD=2，则AC=________．20．如图,在平面直角坐标系中,点A,B的坐标分别为(1,0),(4,0),点C在第一象限内,且∠CAB=90°,BC=6.将△ABC沿x轴向右平移,当点C落在直线y=√3x-2√3上时,线段BC扫过的面积为.21. 如图所示，在平面直角坐标系中，每个小方格的边长是1，把△ABC先向右平移4个单位，再向下平移2个单位，得到△A′B′C′．（1）在坐标系中画出△A′B′C′，并写出△A′B′C′各顶点的坐标．（2）求出△A′B′C′的面积.22.如图，OA⊥OB，OA＝45海里，OB＝15海里，我国某岛位于O点，我国渔政船在点B处发现有一艘不明国籍的渔船，自A点出发沿着AO方向匀速驶向该岛所在地O点，我国渔政船立即从B处出发以相同的速度沿某直线去拦截这艘渔船，结果在点C处截住了渔船．(1)请用直尺和圆规作出C处的位置；(2)求我国渔政船行驶的航程BC的长.23.如图，在△ABC中，AD平分∠BAC，交BC于点D，EF∥AD，交AC于点E，交BA的延长线于点F. 求证：△AEF为等腰三角形.24．如图，为了测出某塔CD的高度，在塔前的平地上选择一点A，用测角仪测得塔顶D的仰角为30°，在A，C之间选择一点B(A，B，C三点在同一直线上)．用测角仪测得塔顶D的仰角为75°，且AB间的距离为40 m.(1)求点B到AD的距离；(2)求塔高CD.(结果用根号表示)25. 如图，已知E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，C，D是垂足，连接CD，且交OE于点F.（1）求证：OE是CD的垂直平分线；（2）若∠AOB＝60°，请你探究OE，EF之间有什么数量关系？并证明你的结论．26.在△ABC中，点E，点F分别是边AC，AB上的点，且AE＝AF，连接BE，CF交于点D，∠ABE＝∠ACF．（1）求证：△BCD是等腰三角形．（2）若∠A＝40°，BC＝BD，求∠BEC的度数．27. 如图，在△ABC中，∠C＝90°，AD平分∠BAC，DE⊥AB于点E，点F在AC上，且BD＝DF．（1）求证：CF＝EB；（2）请你判断AE、AF与BE之间的数量关系，并说明理由．28．如图，在△ABC中，AB＝BC，BE⊥AC于点E，AD⊥BC于点D，∠BAD＝45°，AD与BE交于点F，连接CF.(1)求证：BF＝2AE；(2)若CD＝2，求AD的长．29. 已知:如图所示,△ABC是边长为6 cm的等边三角形,动点P、Q同时从A、B两点出发,分别在AB、BC 边上匀速移动,它们的速度分别为v P=2 cm/s,v Q=1 cm/s,当点P到达点B时,P、Q两点同时停止运动,设点P 的运动时间为t s.(1)当t为何值时,△PBQ为等边三角形?(2)当t为何值时,△PBQ为直角三角形?。

《第1章三角形的证明》一、选择题1．如果三角形的三个内角度数比为1：1：2，则这个三角形为（）A．锐角三角形B．钝角三角形C．非等腰直角三角形D．等腰直角三角形2．下面命题不正确的是（）A．两个内角分别是50°和65°的三角形是等腰三角形B．两个外角相等的三角形是等腰三角形C．一个外角的平分线平行于一边的三角形是等腰三角形D．两个内角不相等的三角形不是等腰三角形3．下列选项中，可以用来证明命题“若a2＞1，则a＞1”是假命题的反例是（）A．a=﹣2 B．a=﹣1 C．a=1 D．a=24．反证法证明“三角形中至少有一个角不小于60°”先应假设这个三角形中（）A．有一个内角小于60° B．每个内角都小于60°C．有一个内角大于60°D．每个内角都大于60°5．如图，在△ABC中，AB=AC，E是AB的中点，以点E为圆心，EB为半径画弧，交BC于点D，连接ED并延长到点F，使DF=DE，连接FC，若∠B=70°，则∠F 的度数是（）A．40 B．70 C．50 D．456．如图所示的正方形网格中，网格线的交点称为格点．已知A、B是两格点，如果C也是图中的格点，且使得△ABC为等腰三角形，则点C的个数是（）A．6 B．7 C．8 D．97．如图，一艘海轮位于灯塔P的南偏东70°方向的M处，它以每小时40海里的速度向正北方向航行，2小时后到达位于灯塔P的北偏东40°的N处，则N处与灯塔P的距离为（）A．40海里B．60海里C．70海里D．80海里二、填空题8．如图所示，在△ABC中，AB=AC，点D、E在BC边上，∠ABD=∠DAE=∠EAC=36°，则图中共有等腰三角形的个数是．9．如图，在△ABC中，∠B与∠C的平分线交于点O，过点O作DE∥BC，分别交AB、AC于点D、E．若AB=5，AC=4，则△ADE的周长是．10．如图，AD是△ABC的边BC上的高，由下列条件中的某一个就能推出△ABC 是等腰三角形的是．①∠BAD=∠ACD；②∠BAD=∠CAD；③AB+BD=AC+CD；④AB﹣BD=AC﹣CD．三、解答题11．证明题：如图所示，在△ABC中，AB=AC，∠APB≠∠APC，求证：PB≠PC．12．如图，在△ABC中，AB=AC，AD是高，AM是△ABC外角∠CAE的平分线．（1）用尺规作图方法，作∠ADC的平分线DN；（保留作图痕迹，不写作法和证明）（2）设DN与AM交于点F，判断△ADF的形状．（只写结果）13．已知∠AOB及其内部一点P，试讨论以下问题的解答：（1）如图①，若点P在∠AOB的平分线上，我们可以过P点作直线垂直于角平分线，分别交OA、OB于点C、D，则可以得到△OCD是以CD为底边的等腰三角形；若点P不在∠AOB的平分线上（如图②），你能过P点作直线，分别交OA、OB于点C、D，得到△OCD是等腰三角形，且CD是底边吗？请你在图②中画出图形，并简要说明画法．（2）若点P不在∠AOB的平分线上（如图③），我们可以过P点作PQ∥OA，并作∠QPR=∠AOB，直线PR分别交OA、OB于点C、D，则可以得到△OCD是以OC为底的等腰三角形．请你说明这样作的理由．（3）若点P不在∠AOB的平分线上，请你利用在（2）中学到的方法，在图④中过P点作直线分别交OA、OB于点C、D，使得△OCD是等腰三角形，且OD是底边．保留画图的痕迹，不用写出画法．《第1章三角形的证明》参考答案与试题解析一、选择题1．如果三角形的三个内角度数比为1：1：2，则这个三角形为（）A．锐角三角形B．钝角三角形C．非等腰直角三角形D．等腰直角三角形【考点】三角形内角和定理．【分析】由三角形的三个内角度数比为1：1：2，可设三角形的三个内角分别为：x，x，2x，然后由三角形的内角和等于180°，即可得方程：x+x+2x=180°，解此方程即可求得答案．【解答】解：∵三角形的三个内角度数比为1：1：2，∴设三角形的三个内角分别为：x，x，2x，∴x+x+2x=180°，解得：x=45°，∴三角形的三个内角度数分别为：45°，45°，90°．∴这个三角形为等腰直角三角形．故选：D．【点评】此题考查了三角形的内角和定理．此题比较简单，解题的关键是根据三角形的三个内角度数比为1：1：2，设三角形的三个内角分别为：x，x，2x，利用方程思想求解．2．下面命题不正确的是（）A．两个内角分别是50°和65°的三角形是等腰三角形B．两个外角相等的三角形是等腰三角形C．一个外角的平分线平行于一边的三角形是等腰三角形D．两个内角不相等的三角形不是等腰三角形【考点】等腰三角形的判定．【分析】认真阅读各选项，结合各选项提供的已知条件及等腰三角形的定义可得．【解答】解：A、第三个角180°﹣50°﹣65°=65°，有两等角的三角形是等腰三角形，正确；B、外角相等，则对应的内角也相等，有两等角的三角形是等腰三角形，正确；C、利用两直线平行，内错角相等，同位相等，可知，另外的两内角也相等，有两等角的三角形是等腰三角形，正确；D、两个内角不相等的三角形可能是等腰三角形，错误．故选D．【点评】本题考查了等腰三角形的判定；找出各选项的正误是正确解答本题的关键．3．下列选项中，可以用来证明命题“若a2＞1，则a＞1”是假命题的反例是（）A．a=﹣2 B．a=﹣1 C．a=1 D．a=2【考点】反证法．【分析】根据要证明一个结论不成立，可以通过举反例的方法来证明一个命题是假命题．【解答】解：用来证明命题“若a2＞1，则a＞1”是假命题的反例可以是：a=﹣2，∵（﹣2）2＞1，但是a=﹣2＜1，∴A正确；故选：A．【点评】此题主要考查了利用举例法证明一个命题错误，要说明数学命题的错误，只需举出一个反例即可这是数学中常用的一种方法．4．反证法证明“三角形中至少有一个角不小于60°”先应假设这个三角形中（）A．有一个内角小于60° B．每个内角都小于60°C．有一个内角大于60°D．每个内角都大于60°【考点】反证法．【专题】证明题．【分析】此题要运用反证法，由题意先假设三角形的三个角都小于60°成立．然后推出不成立．得出选项．【解答】解：设三角形的三个角分别为：a，b，c．假设，a＜60°，b＜60°，c＜60°，则a+b+c＜60°+60°+60°，即，a+b+c＜180°与三角形内角和定理a+b+c=180°矛盾．所以假设不成立，即三角形中至少有一个角不小于60°．故选B．【点评】此题考查的知识点是反证法，解答此题的关键是由已知三角形中至少有一个角不小于60°假设都小于60°进行论证．5．如图，在△ABC中，AB=AC，E是AB的中点，以点E为圆心，EB为半径画弧，交BC于点D，连接ED并延长到点F，使DF=DE，连接FC，若∠B=70°，则∠F 的度数是（）A．40 B．70 C．50 D．45【考点】全等三角形的判定与性质；等腰三角形的判定与性质．【分析】由题意可得EB=ED，根据等边对等角的性质，易得∠B=∠EDB=∠ACB，即可得EF∥AC，又由AE=BE，根据平行线等分线段成比例定理，可得BD=CD，然后利用SAS即可证得△EBD≌△CFD，即可得∠F=∠BED．【解答】解：∵以点E为圆心，EB为半径画弧，交BC于点D，∴EB=ED，∴∠EDB=∠B=70°，∴∠BED=180°﹣∠B=∠BDE=40°，∵AB=AC，∴∠ACB=∠B，∴∠EDB=∠ACB，∴EF∥AC，∵E是AB的中点，即BE=AE，∴BD=CD，在△EBD和△FCD中，，∴△EBD≌△FCD（SAS），∴∠F=∠BED=40°．故选A．【点评】此题考查了全等三角形的判定与性质、等腰三角形的性质以及平行线的判定与性质．此题难度适中，注意掌握数形结合思想的应用，注意理解题意．6．如图所示的正方形网格中，网格线的交点称为格点．已知A、B是两格点，如果C也是图中的格点，且使得△ABC为等腰三角形，则点C的个数是（）A．6 B．7 C．8 D．9【考点】等腰三角形的判定．【专题】分类讨论．【分析】根据题意，结合图形，分两种情况讨论：①AB为等腰△ABC底边；②AB为等腰△ABC其中的一条腰．【解答】解：如上图：分情况讨论．①AB为等腰△ABC底边时，符合条件的C点有4个；②AB为等腰△ABC其中的一条腰时，符合条件的C点有4个．故选：C．【点评】本题考查了等腰三角形的判定；解答本题关键是根据题意，画出符合实际条件的图形，再利用数学知识来求解．数形结合的思想是数学解题中很重要的解题思想．7．如图，一艘海轮位于灯塔P的南偏东70°方向的M处，它以每小时40海里的速度向正北方向航行，2小时后到达位于灯塔P的北偏东40°的N处，则N处与灯塔P的距离为（）A．40海里B．60海里C．70海里D．80海里【考点】等腰三角形的判定与性质；方向角；平行线的性质．【专题】应用题．【分析】根据方向角的定义即可求得∠M=70°，∠N=40°，则在△MNP中利用内角和定理求得∠NPM的度数，证明三角形MNP是等腰三角形，即可求解．【解答】解：MN=2×40=80（海里），∵∠M=70°，∠N=40°，∴∠NPM=180°﹣∠M﹣∠N=180°﹣70°﹣40°=70°，∴∠NPM=∠M，∴NP=MN=80（海里）．故选：D．【点评】本题考查了方向角的定义，以及三角形内角和定理，等腰三角形的判定定理，理解方向角的定义是关键．二、填空题8．如图所示，在△ABC中，AB=AC，点D、E在BC边上，∠ABD=∠DAE=∠EAC=36°，则图中共有等腰三角形的个数是6．【考点】等腰三角形的判定与性质．【分析】由在△ABC中，AB=AC，点D、E在BC边上，∠ABD=∠DAE=∠EAC=36°，根据等腰三角形的性质与三角形内角和定理，易求得各角的度数，继而求得答案．【解答】解：∵在△ABC中，AB=AC，∠ABD=36°，即△ABC是等腰三角形，∴∠C=∠B=36°，∴∠BAC=108°，∵∠DAE=∠EAC=36°，∴∠BAD=36°，∴∠BAD=∠B=36°，∠EAC=∠C=36°，∴△ABD，△ACE是等腰三角形，∴∠ADE=∠AED=∠DAC=∠BAE=72°，∴△ADE，△ABE，△ACD是等腰三角形．故答案为：6．【点评】此题考查了等腰三角形的性质与判定．此题难度不大，注意掌握数形结合思想的应用．9．如图，在△ABC中，∠B与∠C的平分线交于点O，过点O作DE∥BC，分别交AB、AC于点D、E．若AB=5，AC=4，则△ADE的周长是9．【考点】等腰三角形的判定与性质；平行线的性质．【专题】压轴题．【分析】由在△ABC中，∠B与∠C的平分线交于点O，过点O作DE∥BC，易证得△DOB与△EOC是等腰三角形，即DO=DB，EO=EC，继而可得△ADE的周长等于AB+AC，即可求得答案．【解答】解：∵在△ABC中，∠B与∠C的平分线交于点O，∴∠DBO=∠CBO，∠ECO=∠BCO，∵DE∥BC，∴∠DOB=∠CBO，∠EOC=∠BCO，∴∠DBO=∠DOB，∠ECO=∠EOC，∴OD=BD，OE=CE，∵AB=5，AC=4，∴△ADE的周长为：AD+DE+AE=AD+DO+EO+AE=AD+DB+EC+AE=AB+AC=5+4=9．故答案为：9．【点评】此题考查了等腰三角形的判定与性质、角平分线的定义以及平行线的性质．此题难度适中，注意证得△DOB与△EOC是等腰三角形是解此题的关键，注意掌握数形结合思想与转化思想的应用．10．如图，AD是△ABC的边BC上的高，由下列条件中的某一个就能推出△ABC 是等腰三角形的是②③④．①∠BAD=∠ACD；②∠BAD=∠CAD；③AB+BD=AC+CD；④AB﹣BD=AC﹣CD．【考点】等腰三角形的判定与性质．【专题】压轴题．【分析】可根据等腰三角形三线合一的性质来判断①②是否正确；③④要通过作等腰三角形来判断其结论是否成立．【解答】解：应添加的条件是②③④；证明：②当∠BAD=∠CAD时，∵AD是∠BAC的平分线，且AD是BC边上的高；则△ABD≌△ACD，∴△BAC是等腰三角形；③延长DB至E，使BE=AB；延长DC至F，使CF=AC；连接AE、AF；∵AB+BD=CD+AC，∴DE=DF，又AD⊥BC；∴△AEF是等腰三角形；∴∠E=∠F；∵AB=BE，∴∠ABC=2∠E；同理，得∠ACB=2∠F；∴∠ABC=∠ACB，即AB=AC，△ABC是等腰三角形；④△ABC中，AD⊥BC，根据勾股定理，得：AB2﹣BD2=AC2﹣CD2，即（AB+BD）（AB﹣BD）=（AC+CD）（AC﹣CD）；∵AB﹣BD=AC﹣CD①，∴AB+BD=AC+CD②；∴①+②得：，2AB=2AC；∴AB=AC，∴△ABC是等腰三角形故答案为：②③④．【点评】此题主要考查的是等腰三角形的判定和性质；本题的难点是结论③的证明，能够正确的构建出等腰三角形是解答③题的关键．三、解答题11．证明题：如图所示，在△ABC中，AB=AC，∠APB≠∠APC，求证：PB≠PC．【考点】反证法．【专题】证明题．【分析】运用反证法进行求解：（1）假设结论PB≠PC不成立，PB=PC成立．（2）从假设出发推出与已知相矛盾．（3）得到假设不成立，则结论成立．【解答】证明：假设PB≠PC不成立，则PB=PC；∵在△ABP和△ACP中，，∴△ABP≌△ACP，∴∠APB=∠APC；与∠APB≠∠APC相矛盾．因而PB=PC不成立，则PB≠PC．【点评】解此题关键要懂得反证法的意义及步骤．12．如图，在△ABC中，AB=AC，AD是高，AM是△ABC外角∠CAE的平分线．（1）用尺规作图方法，作∠ADC的平分线DN；（保留作图痕迹，不写作法和证明）（2）设DN与AM交于点F，判断△ADF的形状．（只写结果）【考点】等腰三角形的判定与性质；作图—基本作图．【专题】作图题．【分析】（1）以D为圆心，以任意长为半径画弧，交AD于G，交DC于H，分别以G、H为圆心，以大于GH为半径画弧，两弧交于N，作射线DN，交AM 于F．（2）求出∠BAD=∠CAD，求出∠FAD=×180°=90°，求出∠CDF=∠AFD=∠ADF，推出AD=AF，即可得出答案．【解答】解：（1）如图所示：（2）△ADF的形状是等腰直角三角形，理由是：∵AB=AC，AD⊥BC，∴∠BAD=∠CAD，∵AF平分∠EAC，∴∠EAF=∠FAC，∵∠FAD=∠FAC+∠DAC=∠EAC+∠BAC=×180°=90°，即△ADF是直角三角形，∵AB=AC，∴∠B=∠ACB，∵∠EAC=2∠EAF=∠B+∠ACB，∴∠EAF=∠B，∴AF∥BC，∴∠AFD=∠FDC，∵DF平分∠ADC，∴∠ADF=∠FDC=∠AFD，∴AD=AF，即直角三角形ADF是等腰直角三角形．【点评】本题考查了作图﹣基本作图，等腰三角形的性质和判定的应用，主要培养学生的动手操作能力和推理能力，题目比较典型，难度也适中．13．已知∠AOB及其内部一点P，试讨论以下问题的解答：（1）如图①，若点P在∠AOB的平分线上，我们可以过P点作直线垂直于角平分线，分别交OA、OB于点C、D，则可以得到△OCD是以CD为底边的等腰三角形；若点P不在∠AOB的平分线上（如图②），你能过P点作直线，分别交OA、OB于点C、D，得到△OCD是等腰三角形，且CD是底边吗？请你在图②中画出图形，并简要说明画法．（2）若点P不在∠AOB的平分线上（如图③），我们可以过P点作PQ∥OA，并作∠QPR=∠AOB，直线PR分别交OA、OB于点C、D，则可以得到△OCD是以OC为底的等腰三角形．请你说明这样作的理由．（3）若点P不在∠AOB的平分线上，请你利用在（2）中学到的方法，在图④中过P点作直线分别交OA、OB于点C、D，使得△OCD是等腰三角形，且OD是底边．保留画图的痕迹，不用写出画法．【考点】作图—应用与设计作图；角平分线的性质；等腰三角形的判定．【分析】（1）作∠AOB的平分线，过P点作角平分线的垂线，分别交角的两边OA、OB于点C、D，则△OCD是以CD为底边的等腰三角形；（2）根据PQ∥OA，得出∠QPR=∠OCD，进而得出OD=CD，即可得出答案；（3）作QP∥DO，再作∠ODR=∠O，即可得出答案．【解答】解：（1）能．画法：作∠AOB的平分线，过P点作角平分线的垂线，分别交角的两边OA、OB 于点C、D，则△OCD是以CD为底边的等腰三角形，如图①．（2）∵PQ∥OA，∴∠QPR=∠OCD，又∵∠QPR=∠AOB，∴∠OCD=∠AOB．∴OD=CD．即△OCD是以OC为底的等腰三角形．（3）如图②．【点评】此题主要考查了基本作图角平分线的性质等知识；作角平分线是正确解答本题的关键．。

1等腰三角形知识点1等腰三角形的性质定理等腰三角形的性质定理：等腰三角形的两个底角相等(简述为等边对等角)•1 — 1 所示，在△ ABC 中，T AB = AC ,：/ B = Z C • 定理的证明：取BC 的中点D ，连接AD •AB AC(已知),•/ BD CD(中点定义),•••△ ABDN ACD(SSS).AD AD(公共边),•/ B =/ C(全等三角形的对应角相等 ).定理的作用：证明同一个三角形中的两个内角相等. 拓展等腰三角形还具有其他性质. (1)等腰直角三角形的两个底角相等，都等于 45(2) 等腰三角形的底角只能是锐角，不能是钝角或直角，但顶角可以是锐角、钝角或直角. K(3) 等腰三角形的三边关系：设腰长为 a ，底边长为b ,则 v a . 2(4) 等腰三角形的三角关系：设顶角为/A ，底角为/B ，/C ，则/ A = 180°—/ B — / C = 180° 180°— 2 / C .知识点2等腰三角形的性质定理的推论推论1:等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合 (简称“三线合一”(1) 用符号语言表示为：如图 1 — 3所示，① 在△ ABC 中，T AB = AC ，/ 1 = / 2，• AD 丄BC . BD = DC ; ② 在△ ABC 中，T AB = AC ，AD 丄 BC ，•/ 1 = / 2，BD = DC ; ③ 在△ ABC 中，T AB = AC ，BD = DC ，•/ 1 = / 2，AD 丄 BC . (2) 推论1的证明.① 在△ ABC 中，T AB = AC ，/ 1 = / 2，AD = AD ， • △ ABD ◎△ ACD(SAS).• BD = DC ，/ ADB =/ ADC = 90°.： AD 丄 BC .用符号语言表).②在△ ABC 中，T AD 丄BC，：/ ADB =/ ADC = 90°.•/ AB= AC,： / B = Z C .又AD = AD Rt △ ADB 也Rt △ ADC(AAS).•••/ 1 = / 2, BD = CD .③在△ ABC 中，T AB = AC, AD = AD, BD = CD ,•△ ABD ◎△ ACD(SSS)•/ 1 = / 2,/ ADB = / ADC = 90°,「. AD 丄BC.⑶推论1的作用：证明角相等、线段相等或垂直91 1 2推论2:等边三角形的三个角都相等，并且每个角都等于60° .(1) 用符号语言表示为：如图 1 -4所示，在厶ABC 中，T AB= BC = AC，•/ A=/ B =/ C = 60°.(2) 推论2的证明：•/ AB= AC，• / B = / C .•/ AB= BC，•/ A =/ C .• •/ A=/ B=/ C.又•••/ A+ / B+ / C= 180。

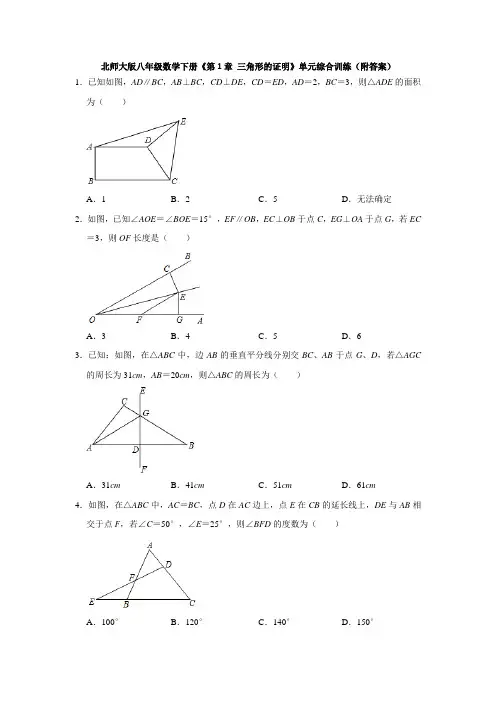
北师大版八年级数学下册《第1章三角形的证明》单元综合训练（附答案）1．已知如图，AD∥BC，AB⊥BC，CD⊥DE，CD＝ED，AD＝2，BC＝3，则△ADE的面积为（）A．1B．2C．5D．无法确定2．如图，已知∠AOE＝∠BOE＝15°，EF∥OB，EC⊥OB于点C，EG⊥OA于点G，若EC ＝3，则OF长度是（）A．3B．4C．5D．63．已知：如图，在△ABC中，边AB的垂直平分线分别交BC、AB于点G、D，若△AGC 的周长为31cm，AB＝20cm，则△ABC的周长为（）A．31cm B．41cm C．51cm D．61cm4．如图，在△ABC中，AC＝BC，点D在AC边上，点E在CB的延长线上，DE与AB相交于点F，若∠C＝50°，∠E＝25°，则∠BFD的度数为（）A．100°B．120°C．140°D．150°5．已知在平面直角坐标系xOy中，O（0，0），A（4，3）点B在x轴或y轴上移动，若O、A、B三点可构成等腰三角形，则符合条件的B点有（）A．9个B．8个C．7个D．6个6．如图，△ABC中，AD⊥BC交BC于D，AE平分∠BAC交BC于E，F为BC的延长线上一点，FG⊥AE交AD的延长线于G，AC的延长线交FG于H，连接BG，下列结论：①∠DAE＝∠F；②∠DAE＝（∠ABD﹣∠ACE）；③S△AEB：S△AEC＝AB：AC；④∠AGH＝∠BAE+∠ACB，其中正确的结论有（）个．A．1B．2C．3D．47．如图，Rt△ABC中，∠ACB＝90°，∠ABC＝30°，AC＝6，D是线段AB上一个动点，以BD为边在△ABC外作等边△BDE．若F是DE的中点，则CF的最小值为（）A．6B．8C．9D．108．如图，给定由10个点（任意相邻两点距离为1）组成的正三角形点阵，在其中任意取三个点，以这三个点为顶点构成的正三角形的个数是（）A．12B．13C．15D．179．如图，△ABC是等边三角形，P是三角形内任意一点，D、E、F分别是AC、AB、BC边上的三点，且PF∥AB，PD∥BC，PE∥AC．若PF+PD+PE＝a，则△ABC的边长为（）A．a B．a C．a D．a10．一副三角板如图摆放，点F是45°角三角板ABC的斜边的中点，AC＝4．当30°角三角板DEF的直角顶点绕着点F旋转时，直角边DF，EF分别与AC，BC相交于点M，N．在旋转过程中有以下结论：①MF＝NF：②四边形CMFN有可能为正方形；③MN长度的最小值为2；④四边形CMFN的面积保持不变；⑤△CMN面积的最大值为2．其中正确的个数是（）A．2B．3C．4D．511．如图，在△ABC中，∠B＝30°，∠C＝45°，AE⊥BC于点E，AB的垂直平分线交BC 于点D，交AB于点F，若BD＝6，则CE的长为（）A．2B．2C．3D．312．如图，∠C＝90°，AC＝10，BC＝5，AX⊥AC，点P和点Q从A点出发，分别在线段AC和射线AX上运动，且AB＝PQ，当点P运动到AP＝，△ABC与△APQ全等．13．如图，BE和CE分别为△ABC的内角∠ABC和外角∠ACD的平分线，BE⊥AC于点H，CF平分∠ACB交BE于点F，连接AE，则下列结论：①∠ECF＝90°；②AE＝CE；③∠BFC＝90°+∠BAC；④∠BAC＝2∠BEC；⑤∠AEH＝∠BCF，正确的为．14．如图，在△ABC中，AB＝AC，∠A＝50°，AB的垂直平分线分别交AC和AB于点D 和E，那么∠DBC＝度．15．已知等腰三角形的两边长分别为x和y，且x和y满足|x﹣3|+（y﹣1）2＝0，则这个等腰三角形的周长为．16．在△ABC中，∠B＝50°，当∠A为时，△ABC是等腰三角形．17．如图，已知P、Q是△ABC的边BC上的两点，且BP＝QC＝PQ＝AP＝AQ，则∠BAC ＝．18．如图，直线l∥m，等边△ABC的顶点B在直线m上，边BC与直线m所夹锐角为20°，则∠1的度数为．19．已知a、b、c是△ABC的三边的长，且满足a2+2b2+c2﹣2b（a+c）＝0，则此三角形的形状为．20．如图，六边形ABCDEF的六个内角都等于120°，若AB＝BC＝CD＝3cm，DE＝2cm，则这个六边形的周长等于cm．21．∠α＝24°24'＝°，若∠α是一个直角三角形的其中一个锐角，则另一个锐角是°．22．如图，在△ABC和△DCB中，∠A＝∠D＝90°，AC＝BD，AC与BD相交于点O．（1）求证：△ABC≌△DCB；（2）△OBC是何种三角形？证明你的结论．23．如图，BD、CD分别平分∠ABC、∠ACB，过点D作直线分别交AB、AC于点E、F，若AE＝AF，BE＝4，CF＝2，回答下列问题：（1）证明：ED＝FD；（2）试找出∠BDC与∠A的数量关系，并说明理由；（3）求EF的长．24．如图△ABC中，AB，AC的垂直平分线分别交BC于D，E，垂足分别是M，N．（1）若BC＝10，求△ADE的周长．（2）若∠BAC＝100°，求∠DAE的度数．25．如图，△ABC中，AB＝AC，DE垂直平分AC，若∠A＝30°，求∠BCD的度数．26．如图，已知在△ABC中，AC＝BC＝AD，∠CDE＝∠B，求证：△CDE是等腰三角形．27．如图，在△ABC中，AB＝AC，∠BAC＝36°，BD是∠ABC的平分线，交AC于点D，E是AB的中点，连接ED并延长，交BC的延长线于点F，连接AF，求证：（1）EF⊥AB；（2）△ACF为等腰三角形．28．如图，点M，N分别在正三角形ABC的BC，CA边上，且BM＝CN，AM，BN交于点Q．求证：∠BQM＝60°．29．如图，已知∠AOB＝60°，点P在边OA上，点M、N在边OB上．（1）若∠PNO＝60°，证明△PON是等边三角形；（2）若PM＝PN，OP＝12，MN＝2，求OM的长度．30．如图，等边△ABC中，点D在延长线上，CE平分∠ACD，且CE＝BD．说明：△ADE是等边三角形．31．如图1，直线PQ⊥直线MN，垂足为O，△AOB是直角三角形，∠AOB＝90°，斜边AB与直线PQ交于点C．（1）若∠A＝∠AOC＝30°，则BC BO（填“＞”“＝”“＜”）；（2）如图2，延长AB交直线MN于点E，过O作OD⊥AB，若∠DOB＝∠EOB，∠AEO ＝α，求∠AOE的度数（用含α的代数式表示）；（3）如图3，OF平分∠AOM，∠BCO的平分线交FO的延长线于点R，∠A＝36°，当△AOB绕O点旋转时（斜边AB与直线PQ始终相交于点C），问∠R的度数是否发生改变？若不变，求其度数；若改变，请说明理由．参考答案1．解：过D作BC的垂线交BC于G，过E作AD的垂线交AD的延长线于F，∵∠EDF+∠FDC＝90°，∠GDC+∠FDC＝90°，∴∠EDF＝∠GDC，于是在Rt△EDF和Rt△CDG中，，∴△DEF≌△DCG，∴EF＝CG＝BC﹣BG＝BC﹣AD＝3﹣2＝1，所以，S△ADE＝（AD×EF）÷2＝（2×1）÷2＝1．故选：A．2．解：∵∠AOE＝∠BOE＝15°，EC⊥OB于点C，EG⊥OA于点G，∴CE＝EG＝3，∵EF∥OB，∴∠COE＝∠OEF＝15°∴∠EFG＝15°+15°＝30°，∠EOF＝∠OEF，∴OF＝EF＝2EG＝2×3＝6．故选：D．3．解：∵DG是AB的垂直平分线，∴GA＝GB，∵△AGC的周长为31cm，∴AG+GC+AC＝BC+AC＝31cm，又AB＝20cm，∴△ABC的周长＝AB+AC+BC＝51cm，故选：C．4．解：∵△ABC中，AC＝BC，∠C＝50°，∴∠ABC＝（180°﹣50°）＝65°，∵∠ABC是△BEF的外角，∴∠BFE＝∠ABC﹣∠E＝65°﹣25°＝40°，∴∠BFD＝180°﹣40°＝140°，故选：C．5．解：分三种情况说明：①以点O为圆心，OA长为半径画圆，与x轴、y轴有4个交点，这4个交点分别与点O、A构成4个等腰三角形；②以点A为圆心，OA长为半径交x轴和y轴的正半轴有2个点，这2个交点分别与点O、A构成2个等腰三角形；③作OA的垂直平分线交x轴和y轴的正半轴有2个点，这2个交点分别与点O、A构成2个等腰三角形；综上所述：符合条件的B点有：4+2+2＝8（个）．故选：B．6．解：如图，AE交GF于M，①∵AD⊥BC，FG⊥AE，∴∠ADE＝∠AMF＝90°，∵∠AED＝∠MEF，∴∠DAE＝∠F；故①正确；②∵AE平分∠BAC交BC于E，∴∠EAC＝，∠DAE＝90°﹣∠AED，＝90°﹣（∠ACE+∠EAC），＝90°﹣（∠ACE+），＝（180°﹣2∠ACE﹣∠BAC），＝（∠ABD﹣∠ACE），故②正确；③∵AE平分∠BAC交BC于E，∴点E到AB和AC的距离相等，∴S△AEB：S△AEC＝AB：CA；故③正确，④∵∠DAE＝∠F，∠FDG＝∠FME＝90°，∴∠AGH＝∠MEF，∵∠MEF＝∠CAE+∠ACB，∴∠AGH＝∠CAE+∠ACB，∴∠AGH＝∠BAE+∠ACB；故④正确；故选：D．7．解：如图所示，连接BF，∵等边△BDE中，F是DE的中点，∴BF⊥DE，BF平分∠DBE，∴∠DBF＝30°，即点F在∠DBE的角平分线上运动，∴当点D在CF上时，∠CFB＝90°，根据垂线段最短可知，此时CF最短，又∵∠ABC＝30°，∴∠CBF＝60°，∵Rt△ABC中，∠ACB＝90°，∠ABC＝30°，AC＝6，∴BC＝AC＝6，∴Rt△BCF中，CF＝BC×sin∠CBF＝×＝9，故选：C．8．解：如图所示，边长为1的正三角形共有1+3+5＝9个，边长为2的正三角形共有3个，边长为3的正三角形共有1个，边长为的正三角形有2个，红颜色和蓝颜色的两个三角形，综上可知：共有9+3+1+2＝15个，故选：C．9．解：延长EP交BC于点G，延长FP交AC于点H，如图所示：∵PF∥AB，PD∥BC，PE∥AC，∴四边形AEPH、四边形PDCG均为平行四边形，∴PE＝AH，PG＝CD．又∵△ABC为等边三角形，∴△FGP和△HPD也是等边三角形，∴PF＝PG＝CD，PD＝DH，∴PE+PD+PF＝AH+DH+CD＝AC，∴AC＝a；故选：D．10．解：①连接CF，∵F为AB中点，AC＝BC，∠ACB＝90°，∴AF＝BF＝CF，CF⊥AB，∴∠AFM+∠CFM＝90°．∵∠DFE＝90°，∠CFM+∠CFN＝90°，∴∠AFM＝∠CFN．同理，∵∠A+∠MCF＝90°，∠MCF+∠FCN＝90°，∴∠A＝∠FCN，在△AMF与△CNF中，∵，∴△AMF≌△CNF（ASA），∴MF＝NF．故①正确；②当MF⊥AC时，四边形MFNC是矩形，此时MA＝MF＝MC，根据邻边相等的矩形是正方形可知②正确；③连接MN，当M为AC的中点时，CM＝CN，根据边长为4知CM＝CN＝2，此时MN最小，最小值为2，故③错误；④当M、N分别为AC、BC中点时，四边形CDFE是正方形．∵△ADF≌△CEF，∴S△CEF＝S△AMF∴S四边形CDFE＝S△AFC．故④正确；⑤由于△MNF是等腰直角三角形，因此当DM最小时，DN也最小；即当DF⊥AC时，DM最小，此时DN＝BC＝2．∴DN＝DN＝2 ；当△CEF面积最大时，此时△DEF的面积最小．此时S△CMN＝S四边形CFMN﹣S△FMN＝S△AFC﹣S△DEF＝4﹣2＝2，故⑤正确．故选：C．11．解：连接AD，如图：∵AB的垂直平分线交BC于点D，∴AD＝BD＝6，∵在△ABC中，∠B＝30°，∴∠BAD＝∠B＝30°，∴∠ADE＝∠B+∠BAD＝60°．∵AE⊥BC于点E，∴∠AED＝90°，∴∠DAE＝30°，∴DE＝AD＝3，∴AE＝＝3，∵∠C＝45°，∴△AEC为等腰直角三角形，∴EC＝AE＝3，故选：D．12．解：∵AX⊥AC，∴∠P AQ＝90°，∴∠C＝∠P AQ＝90°，分两种情况：①当AP＝BC＝5时，在Rt△ABC和Rt△QP A中，，∴Rt△ABC≌Rt△QP A（HL）；②当AP＝CA＝10时，在△ABC和△PQA中，，∴Rt△ABC≌Rt△PQA（HL）；综上所述：当点P运动到AP＝5或10时，△ABC与△APQ全等；故答案为：5或10．13．解：∵CF平分∠ACB，CE平分∠ACD，∴∠ACF＝∠ACB，∠ACE＝∠ACD，∴∠ECF＝∠ACF+∠ACE＝（∠ACB+∠ACD）＝90°，故①正确；∵BE平分∠ABC，BE⊥AC，∴∠ABE＝∠CBE，∠BHA＝∠BHC＝90°，∴∠BAH+∠ABE＝90°，∠ACB+∠EBC＝90°，∴∠BAC＝∠BCA，∴AB＝BC，∵BE⊥AC，∴AH＝CH，∴EA＝EC，故②正确；∵∠BFC＝180°﹣（∠FBC+∠FCB）＝180°﹣（∠ABC+∠ACB）＝180°﹣（180°﹣∠BAC）＝90°+∠BAC，故③正确；设∠ACE＝∠ECD＝x，∠ABE＝∠EBC＝y，则有，可得∠BAC＝2∠BEC，故④正确，∵EA＝EC，BE⊥AC，∴∠AEB＝∠BEC，∵∠FCH+∠ACE＝90°，∠ACE+∠BEC＝90°，∴∠FCH＝∠BEC＝∠AEB，∵∠ACF＝∠BCF，∴∠AEH＝∠BCF，故⑤正确．故答案为：①②③④⑤．14．解：∵AB＝AC，∠A＝50°，∴∠ABC＝∠C＝65°，∵DE是AB的垂直平分线，∴DA＝DB，∴∠ABD＝∠A＝50°，∴∠DBC＝∠ABC﹣∠ABD＝15°．故答案为：15．15．解：∵|x﹣3|+（y﹣1）2＝0，∴x＝3，y＝1．当腰长为3时，三边长为3、3、1，周长＝3+3+1＝7；当腰长为1时，三边长为3、1、1，1+1＜3，不能组成三角形．故答案为：7．16．解：①∠B是顶角，∠A＝（180°﹣∠B）÷2＝65°；②∠B是底角，∠B＝∠A＝50°．③∠A是顶角，∠B＝∠C＝50°，则∠A＝180°﹣50°×2＝80°，∴当∠A的度数为50°或65°或80°时，△ABC是等腰三角形．故答案为：50°或65°或80°．17．解：∵BP＝QC＝PQ＝AP＝AQ，∴△APQ为等边三角形，△ABP为等腰三角形，△AQC为等腰三角形，∴∠P AQ＝∠APQ＝∠AQP＝60°，在△ABP和△CAQ中，∴△ABP≌△ACQ，∴∠QAC＝∠B＝∠APQ＝30°，同理：∠BAP＝30°，∠BAC＝∠BAP+∠P AQ+∠QAC＝30°+60°+30°＝120°．故答案为：120°18．解：如图所示，过点C作直线n∥m，在直线m上取一点D，∵直线l∥m，∴l∥m∥n，∴∠1＝∠2，∠3＝∠CBD＝20°，∵△ABC为等边三角形，∴∠ACB＝60°，∴∠2+∠3＝60°，∴∠2＝60°﹣∠3＝60°﹣20°＝40°，∴∠1＝40°．故答案为：40°．19．解：由已知条件a2+2b2+c2﹣2b（a+c）＝0化简得，（a﹣b）2+（b﹣c）2＝0∴a﹣b＝0，b﹣c＝0即a＝b，b＝c∴a＝b＝c故答案为等边三角形．20．解：分别作直线AB、CD、EF的延长线和反向延长线使它们交于点G、H、P，如图所示：∵六边形ABCDEF的六个角都是120°，∴六边形ABCDEF的每一个外角的度数都是60°，∴△APF、△BGC、△DHE、△GHP都是等边三角形，∴GC＝BC＝3cm，DH＝DE＝EH＝2cm，∴GH＝3+3+2＝8（cm），F A＝P A＝PG﹣AB﹣BG＝8﹣3﹣3＝2（cm），EF＝PH﹣PF﹣EH＝8﹣2﹣2＝4（cm）．∴六边形的周长为2+3+3+3+2+4＝17（cm）；故答案为：17．21．解：∠α＝24°24'＝24.4°，90°﹣24.4°＝65.6°，故答案为24.4°，65.6°．22．证明：（1）在△ABC和△DCB中，∠A＝∠D＝90°AC＝BD，BC为公共边，∴Rt△ABC≌Rt△DCB（HL）；（2）△OBC是等腰三角形∵Rt△ABC≌Rt△DCB∴∠ACB＝∠DCB∴OB＝OC∴△OBC是等腰三角形23．（1）证明：过D点分别作DG⊥BC，DK⊥AB，DH⊥AC，垂足分别为G，K，H，如图，∴∠EKD＝∠FHD＝90°，∵BD平分∠ABC，CD平分∠ACB，∴DK＝DG＝DH，在△EKD和△FHD中，，∵AE＝AF∴∠AEF＝∠AFE，∴△EKD≌△FHD（AAS），∴ED＝FD；（2）解：∠BDC＝90°+∠A．理由如下：∵BD平分∠ABC，CD平分∠ACB，∴∠DBC＝∠ABC，∠DCB＝∠ACB，∴∠DBC+∠DCB＝（∠ABC+∠ACB），∵∠BDC+∠DBC+∠DCB＝180°，∴∠BDC+（∠ABC+∠ACB）＝180°，∵∠A+∠ABC+∠ACB＝180°，∴∠ABC+∠ACB＝180°﹣∠A，∴∠BDC+（180°﹣∠A）＝180°，∴∠BDC＝90°+∠A；（3）解：如图，∵BD，CD分别平分∠ABC，∠ACB，∴∠1＝∠2，∠3＝∠4，∵∠2+∠7+∠4＝180°，∠5+∠6+∠7＝180°，∴∠2+∠4＝∠5+∠6，即∠1+∠3＝∠5+∠6，∵∠AEF＝∠AFE，∴∠1+∠5＝∠3+∠6，∴∠5＝∠3，∠1＝∠6，∴△BED∽△CED，∴ED：CF＝BE：DF，∵DE＝DF，则ED2＝CF⋅BE＝2×4＝8，则ED＝，∴EF＝2ED＝．24．解：（1）∵AB、AC的垂直平分线分别交BC于D、E，垂足分别是M、N，∴AD＝BD，AE＝CE，∴△ADE的周长＝AD+DE+AE＝BD+DE+CE＝BC＝10．（2）∵∠BAC＝100°，∴∠B+∠C＝180°﹣∠BAC＝80°，∵AD＝BD，AE＝CE，∴∠BAD＝∠B，∠CAE＝∠C，∴∠BAD+∠CAE＝80°，∴∠DAE＝∠BAC﹣（∠BAD+∠CAE）＝100°﹣80°＝20°．25．解：∵DE垂直平分AC，∴DA＝DC，∴∠DCA＝∠A＝30°，∵AB＝AC，∴∠B＝∠ACB，∵∠A+∠B+∠ACB＝180°，∴∠ACB＝（180°﹣30°）÷2＝150°÷2＝75°，∴∠BCD＝∠ACB﹣∠DCA＝75°﹣30°＝45°．∴∠BCD的度数为45°．26．证明：∵∠ADE+∠CDE+∠BDC＝180°，∠BCD+∠B+∠BDC＝180°，∠CDE＝∠B，∴∠ADE＝∠BCD，∵AC＝BC，∴∠A＝∠B，在△ADE和△BCD中，，∴△ADE≌△BCD（ASA），∴DE＝CD，∴△CDE是等腰三角形．27．证明：（1）∵AB＝AC，∠BAC＝36°，∴∠ABC＝72°，又∵BD是∠ABC的平分线，∴∠ABD＝36°，∴∠BAD＝∠ABD，∴AD＝BD，又∵E是AB的中点，∴DE⊥AB，即FE⊥AB；（2）∵FE⊥AB，AE＝BE，∴FE垂直平分AB，∴AF＝BF，∴∠BAF＝∠ABF，又∵∠ABD＝∠BAD，∴∠F AD＝∠FBD＝36°，又∵∠ACB＝72°，∴∠AFC＝∠ACB﹣∠CAF＝36°，∴∠CAF＝∠AFC＝36°，∴AC＝CF，即△ACF为等腰三角形．28．证明：∵BM＝CN，BC＝AC，∴CM＝AN，又∵AB＝AC，∠BAN＝∠ACM，∴△AMC≌△BNA，则∠BNA＝∠AMC，∵∠MAN+∠ANB+∠AQN＝180°∠MAN+∠AMC+∠ACB＝180°，∴∠AQN＝∠ACB，∵∠BQM＝∠AQN，∴∠BQM＝∠AQN＝∠ACB＝60°．29．解：（1）∵∠AOB＝60°，∠PNO＝60°，∴∠OPN＝60°，∴∠PON＝∠PNO＝∠OPN，∴△PON是等边三角形；（2）作PH⊥MN于H，如图，∵PM＝PN，∴MH＝NH＝MN＝1，在Rt△POH中，∵∠POH＝60°，∴∠OPH＝30°，∴OH＝OP＝×12＝6，∴OM＝OH﹣MH＝6﹣1＝5．30．证明：∵△ABC为等边三角形，∴∠B＝∠ACB＝60°，AB＝AC，即∠ACD＝120°，∵CE平分∠ACD，∴∠ACE＝∠DCE＝60°，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS），∴AD＝AE，∠BAD＝∠CAE，又∵∠BAC＝60°，∴∠DAE＝60°，∴△ADE为等边三角形．31．解：（1）∵△AOB是直角三角形，∴∠A+∠B＝90°，∠AOC+∠BOC＝90°，∵∠A＝∠AOC＝30°，∴∠B＝∠BOC＝60°∴△BOC是等边三角形，∴BC＝BO故答案为：＝；（2）∵OD⊥AB，∠AEO＝α，∴∠DOE＝90°﹣α，∵∠DOB＝∠BOE，∴∠BOE＝＝（90°﹣α）＝45°﹣α，∴∠AOE＝∠AOB+∠BOE＝90°+45°﹣＝135°﹣；（3）∠R的度数不变，∠R＝27°．理由如下：设∠AOM＝β，则∠AOC＝90°﹣β，∵OF平分∠AOM，∴∠FOM＝∠RON＝，∴∠COR＝∠CON+∠RON＝90°+，∵∠OCB＝∠A+∠AOC＝36°+90°﹣β＝126°﹣β，∵CR平分∠BCO，∴∠OCR＝＝63°﹣，∴∠R＝180°﹣（∠OCR+∠COR）＝180°﹣63°+﹣90°﹣＝27°，∴∠R的度数不变，∠R＝27°。