一种快速的椭圆形窗口的裁剪算法
- 格式:pdf
- 大小:148.12 KB
- 文档页数:3

实验题目:实验三图形裁剪算法1.实验目的:理解区域编码(Region Code,RC)设计Cohen-Sutherland直线裁剪算法编程实现Cohen-Sutherland直线裁剪算法2.实验描述:设置裁剪窗口坐标为:wxl=250;wxr=850;wyb=250;wyt=450;裁剪前如下图所示:裁剪后结果为:3.算法设计:Cohen-Sutherland 直线裁剪算法:假设裁剪窗口是标准矩形,由上(y=wyt)、下(y=wyb)、左(x=wxl)、右(x=wxr)四条边组成,如下图所示。
延长窗口四条边形成 9个区域。
根据被裁剪直线的任一端点 P(x,y)所处的窗口区域位置,可以赋予一组4位二进制区域码C4C3C2C1。
编码定义规则:第一位C1:若端点位于窗口之左侧,即 X<Wxl,则 C1=1,否则 C1=0。
第二位C2:若端点位于窗口之右侧,即 X>Wxr,则 C2=1,否则 C2=0。
第三位C3:若端点位于窗口之下侧,即 Y<Wyb,则 C3=1,否则 C3=0。
第四位C4:若端点位于窗口之上侧,即 Y>Wyt,则 C4=1,否则 C4=0。
裁剪步骤:1. 若直线的两个端点的区域编码都为0,即 RC1|RC2=0(二者按位相或的结果为0,即 RC1=0 且RC2=0),说明直线两端点都在窗口内,应“简取”。
2. 若直线的两个端点的区域编码都不为0,即 RC1&RC2≠0(二者按位相与的结果不为0,即 RC1≠0且 RC2≠0,即直线位于窗外的同一侧,说明直线的两个端点都在窗口外,应“简弃”。
3. 若直线既不满足“简取”也不满足“简弃”的条件,直线段必然与窗口相交,需要计算直线与窗口边界的交点。
交点将直线分为两段,其中一段完全位于窗口外,可“简弃”。
对另一段赋予交点处的区域编码,再次测试,再次求交,直至确定完全位于窗口内的直线段为止。
4. 实现时,一般按固定顺序左(x=wxl)、右(x=wxr)、下(y=wyb)、上(y=wyt)求解窗口与直线的交点。

weiler-atherton多边形裁剪算法weileratherton多边形裁剪算法,又称为weiler-atherton算法,是一种用于对多边形进行裁剪的算法。
它可以被用于计算机图形学中的裁剪任务,如可视化、图像处理和计算机辅助设计等领域。
本文将详细介绍weileratherton多边形裁剪算法的原理、步骤和实现方法。
1. 算法原理:weileratherton多边形裁剪算法是基于边界点的引入和处理的。
该算法将两个多边形相互之间进行裁剪,并生成裁剪结果。
算法使用四个边界点集合,分别为输入多边形的边界点集合(输入多边形顶点经过一系列处理得到),裁剪多边形的外部边界点集合和内部边界点集合,以及裁剪结果的边界点集合。
2. 算法步骤:weileratherton多边形裁剪算法的具体步骤如下:(1) 初始化:创建输入多边形的边界点集合、裁剪多边形的外部边界点集合和内部边界点集合,并将输入多边形的边界点添加至外部边界点集合中。
(2) 遍历输入多边形的每条边:对于输入多边形的每条边,判断其与裁剪多边形的相交情况。
(3) 相交情况处理:若相交情况为内部相交或外部相交,则根据交点生成新的内部边界点,并添加至相应的边界点集合中。
(4) 构造裁剪结果:根据输入多边形的边界点集合和裁剪多边形的内部边界点集合,生成裁剪结果的边界点集合。
(5) 根据边界点集合构造裁剪结果:根据裁剪结果的边界点集合,绘制裁剪结果多边形。
3. 算法实现:weileratherton多边形裁剪算法的实现可以使用编程语言来完成。
一种常用的实现方法是通过遍历输入多边形的每个边,利用线段与裁剪多边形的边界的相交情况判断是否产生交点,并根据交点生成新的边界点。
具体的实现步骤如下:(1) 初始化输入和裁剪多边形的边界点集合。
(2) 遍历输入多边形的每条边,对于每条边,判断其与裁剪多边形的每条边的相交情况。
(3) 根据相交情况,判断是否生成交点,如果有生成交点,则根据交点生成新的边界点,并添加至相应的边界点集合中。

中间区段法裁剪
中间区段法裁剪(Middle Segment Clipping)是计算机图形学
中一种常用的二维裁剪算法,主要用于裁剪直线和多边形等图形。
中间区段法裁剪的基本思想是:首先确定裁剪窗口的边界,并将其等分为上、下、左、右四个方向的区段。
接着,根据裁剪窗口与图形在平面上的相对位置关系,决定各个区段是否需要进行裁剪。
最终,根据裁剪结果进行图形的显示或丢弃。
具体裁剪过程如下:
1. 确定裁剪窗口的边界:左边界(Xmin)、右边界(Xmax)、上边界(Ymin)和下边界(Ymax)。
2. 以直线为例,对于每一条线段,根据起点(P1)和终点
(P2)的位置关系,判断其是否需要进行裁剪。
3. 首先根据P1和P2的水平位置关系判断是否在裁剪窗口的
左右区段内。
若在同一区段内,则根据垂直位置关系进一步判断是否在裁剪窗口的上下区段内。
若在裁剪窗口内,则直接保留该线段。
若跨越区段边界,则根据裁剪窗口与线段的交点计算新的起点和终点,并进行裁剪。
4. 根据裁剪结果进行线段的显示或丢弃。
中间区段法裁剪的优点是相对简单、高效,适用于直线和多边形等较简单的图形。
缺点是无法处理曲线和复杂图形的裁剪。
在实际应用中,可以与其他裁剪算法结合使用,以实现更复杂的图形裁剪效果。

剪纸剪椭圆形的最简单方法
剪纸剪椭圆形的最简单方法是使用定圆法。
以下是具体步骤:
1. 准备一个纸张和一把剪刀。
2. 将纸张对折,确保两边完全对齐。
3. 从对折的边上开始,用剪刀沿着纸张边缘剪出一个半圆形。
4. 将剪下的半圆形打开,你会得到一个圆形。
5. 将纸张再次对折,确保两边完全对齐。
6. 从对折的边上开始,用剪刀沿着纸张边缘剪出一个更小的半圆形。
7. 将剪下的半圆形打开,你会得到一个椭圆形。
这种方法可以保证剪下的椭圆形是对称的,而且非常简单易行。
记得要小心使用剪刀以避免意外伤害。


自学裁剪100例公式自学裁剪公式是学习裁剪技术的基础,掌握了这些公式,可以帮助我们更好地理解裁剪的原理和技巧,提升我们的裁剪技能。
本文将介绍100个常用的自学裁剪公式,通过逐步思考和举例说明,帮助你掌握这些公式。
一、裁剪公式的基础知识在开始介绍具体的裁剪公式之前,我们先来了解一些基础知识。
裁剪公式是通过数学计算来确定裁剪点和线段的位置,以实现准确、精细的裁剪效果。
了解以下几个概念对于理解后续的裁剪公式非常重要:1. 坐标系:裁剪过程中需要使用坐标系来确定点的位置。
常用的坐标系有笛卡尔坐标系和极坐标系。
在笛卡尔坐标系中,x轴和y轴垂直,以原点为基准,用(x, y)表示点的位置;在极坐标系中,以原点为基准,用(r, θ)表示点的位置,其中r表示点到原点的距离,θ表示点与正方向x轴的夹角。
2. 裁剪窗口:裁剪窗口是一个定义了裁剪区域的矩形。
在裁剪时,只有位于裁剪窗口内的图形部分会被显示,位于裁剪窗口外的部分会被裁剪掉。
通常,裁剪窗口的左下角坐标为(w_min_x, w_min_y),右上角坐标为(w_max_x, w_max_y)。
3. 裁剪对象:裁剪对象是指需要进行裁剪操作的图形。
常见的裁剪对象包括线段、多边形、圆等。
二、裁剪公式的具体应用下面我们将具体介绍100个常用的自学裁剪公式,并结合示例进行说明。
这些公式涵盖了不同类型的裁剪对象,帮助你了解裁剪技术的全貌。
1. 线段裁剪公式:- Cohen-Sutherland裁剪算法- Liang-Barsky裁剪算法2. 多边形裁剪公式:- Sutherland-Hodgman裁剪算法- Weiler-Atherton裁剪算法3. 圆裁剪公式:- 椭圆裁剪算法4. 曲线裁剪公式:- Bezier曲线裁剪算法5. 文本裁剪公式:- 文本溢出裁剪算法以线段裁剪公式为例,我们来演示Cohen-Sutherland裁剪算法的应用。
这个算法将线段裁剪为窗口内的可见部分。
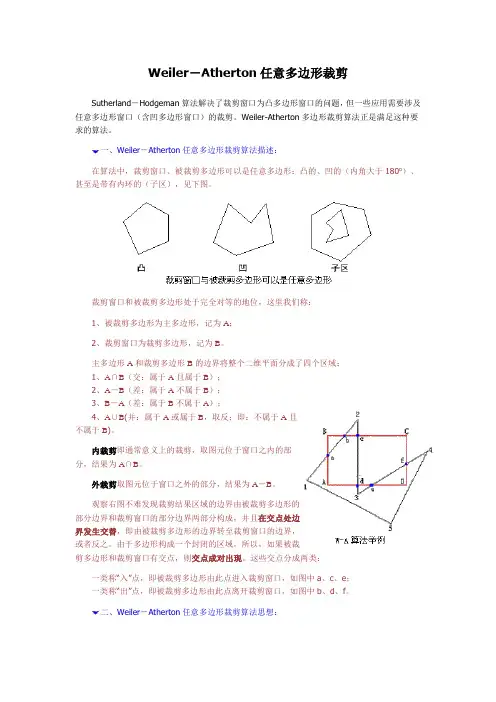
Weiler-Atherton任意多边形裁剪Sutherland-Hodgeman算法解决了裁剪窗口为凸多边形窗口的问题,但一些应用需要涉及任意多边形窗口(含凹多边形窗口)的裁剪。
Weiler-Atherton多边形裁剪算法正是满足这种要求的算法。
一、Weiler-Atherton任意多边形裁剪算法描述:在算法中,裁剪窗口、被裁剪多边形可以是任意多边形:凸的、凹的(内角大于180o)、甚至是带有内环的(子区),见下图。
裁剪窗口和被裁剪多边形处于完全对等的地位,这里我们称:1、被裁剪多边形为主多边形,记为A;2、裁剪窗口为裁剪多边形,记为B。
主多边形A和裁剪多边形B的边界将整个二维平面分成了四个区域:1、A∩B(交:属于A且属于B);2、A-B(差:属于A不属于B);3、B-A(差:属于B不属于A);4、A∪B(并:属于A或属于B,取反;即:不属于A且不属于B)。
内裁剪即通常意义上的裁剪,取图元位于窗口之内的部分,结果为A∩B。
外裁剪取图元位于窗口之外的部分,结果为A-B。
观察右图不难发现裁剪结果区域的边界由被裁剪多边形的部分边界和裁剪窗口的部分边界两部分构成,并且在交点处边界发生交替,即由被裁剪多边形的边界转至裁剪窗口的边界,或者反之。
由于多边形构成一个封闭的区域,所以,如果被裁剪多边形和裁剪窗口有交点,则交点成对出现。
这些交点分成两类:一类称“入”点,即被裁剪多边形由此点进入裁剪窗口,如图中a、c、e;一类称“出”点,即被裁剪多边形由此点离开裁剪窗口,如图中b、d、f。
二、Weiler-Atherton任意多边形裁剪算法思想:假设被裁剪多边形和裁剪窗口的顶点序列都按顺时针方向排列。
当两个多边形相交时,交点必然成对出现,其中一个是从被裁剪多边形进入裁剪窗口的交点,称为“入点”,另一个是从被裁剪多边形离开裁剪窗口的交点,称为“出点”。
算法从被裁剪多边形的一个入点开始,碰到入点,沿着被裁剪多边形按顺时针方向搜集顶点序列;而当遇到出点时,则沿着裁剪窗口按顺时针方向搜集顶点序列。

一、名词解释:计算机图形学、图象处理、模式识别、计算几何、凸多边形、种子填充算法、窗口、视区、光顺性、拟合、多项式插值、小挠度曲线、图形变换、齐次坐标系、凸包、*轮廓线、*等值线、图形的翼边表示、ER模型、图形消隐、*本影、*半影、用户坐标系、规范化设备坐标系、构造、约束技术、二、选择题1、计算机图形学与计算几何之间的关系是( )。
A)学术上的同义词B)计算机图形学以计算几何为理论基础C)计算几何是计算机图形学的前身D).两门毫不相干的学科2、计算机图形学与计算机图象学的关系是( )。
A)计算机图形学是基础,计算机图象学是其发展B)不同的学科,研究对象和数学基础都不同,但它们之间也有可转换部分C)同一学科在不同场合的不同称呼而已D)完全不同的学科,两者毫不相干3、触摸屏是( )设备。
A)输入B)输出C)输入输出D)既不是输入也不是输出4.计算机绘图设备一般使用什么颜色模型?( )A)RGB;B)CMY;C)HSV ;D)HLS5.计算机图形显示器一般使用什么颜色模型?( )A)RGB;B)CMY;C)HSV ;D)HLS6.分辨率为1024×1024的显示器各需要多少字节位平面数为24的帧缓存?( )A)512KB;B)1MB;C)2MB ;D)3MB7.哪一个不是国际标准化组织(ISO)批准的图形标准?( )A)GKS;B)PHIGS;C)CGM ;D)DXF8.下述绕坐标原点逆时针方向旋转a角的坐标变换矩阵中哪一项是错误的? ( )| A B || C D |A) cos a; B)sin a; C)sin a; D)cos a9、在多边形的逐边裁剪法中,对于某条多边形的边(方向为从端点S到端点P)与某条裁剪线(窗口的某一边)的比较结果共有以下四种情况,分别需输出一些顶点.请问哪种情况下输出的顶点是错误的?( )A)S和P均在可见的一侧,则输出S和P.B)S和P均在不可见的一侧,则输出0个顶点.C)S在可见一侧,P在不可见一侧,则输出线段SP与裁剪线的交点.D)S在不可见的一侧,P在可见的一侧,则输出线段SP与裁剪线的交点和P.10、在物体的定义中对边的哪条限制不存在? ( )A) 边的长度可度量且是有限的B) 一条边有且只有两个相邻的面C) 一条边有且只有两个端点D) 如果一条边是曲线,那么在两个端点之间不允许曲线自相交11.下述哪一条边不是非均匀有理B样条(NURBS)的优点? ( )A) NURBS比均匀B样条能表示更多的曲面B) 对于间距不等的数据点,用NURBS拟合的曲线比用均匀B样条拟合的曲线更光滑C) NURBS提供的权控制方法比用控制点更能有效的控制曲线的形状D) 使用NURBS可以提高对曲面的显示效率12.透视投影中主灭点最多可以有几个? ( )A) 0; B)1; C)2; D)313*.在面片的数量非常大的情况下哪一个消隐算法速度最快? ( )A) 深度缓存算法(Z-Buffer)B) 扫描线消隐算法C) 深度排序算法(画家算法)D) 不知道14*.下面关于深度缓存消隐算法(Z-Buffer)的论断哪一条不正确? ( )A) 深度缓存算法并不需要开辟一个与图像大小相等的深度缓存数组B) 深度缓存算法不能用于处理对透明物体的消隐C) 深度缓存算法能并行实现D) 深度缓存算法中没有对多边形进行排序15.在用射线法进行点与多边形之间的包含性检测时,下述哪一个操作不正确? ( )A) 当射线与多边形交于某顶点时且该点的两个邻边在射线的一侧时,计数0次B) 当射线与多边形交于某顶点时且该点的两个邻边在射线的一侧时,计数2次C) 当射线与多边形交于某顶点时且该点的两个邻边在射线的两侧时,计数1次D) 当射线与多边形的某边重合时,计数1次16*、扫描消隐算法在何处利用了连贯性(相关性Coherence)?(1)计算扫描线与边的交点;(2)计算多边形在其边界上的深度;(3)计算多边形视窗任意点处的深度值;(4)检测点与多边形之间的包含性。


计算机图形学的裁剪算法
计算机图形学的裁剪算法是图形学的一种重要算法,它的基本思想是将一个完整的几何图形(如线段、多边形、圆圈等)按照指定的裁剪窗口(矩形)进行裁剪,只保留在窗口内的部分,而把窗口外的部分抛弃掉。
由于裁剪算法的应用非常广泛,像图形显示系统、图形设备接口(GDI)和图形处理器(GPU)等都广泛使用裁剪算法。
计算机图形学的裁剪算法可以分为两种:2D裁剪算法和
3D裁剪算法。
2D裁剪算法是基于二维空间的,它将一个几何
图形投影到一个平面上,然后按照指定的窗口裁剪;而3D裁
剪算法是基于三维空间的,它将一个几何图形投影到一个三维空间,然后按照指定的窗口裁剪。
2D裁剪算法的基本步骤如下:首先,将要裁剪的几何图
形投影到平面上;其次,计算出投影后的几何图形以及裁剪窗口之间的交点;最后,将裁剪窗口内的部分保留,而把窗口外的部分抛弃掉。
3D裁剪算法的基本步骤如下:首先,将要裁剪的几何图
形投影到三维空间;其次,计算出投影后的几何图形以及裁剪窗口之间的交点;最后,将裁剪窗口内的部分保留,而把窗口外的部分抛弃掉。
计算机图形学的裁剪算法在图形处理中有着重要的作用,它不仅能够有效减少图形处理时间,而且还可以节约存储空间。
此外,它还可以有效提高图形处理效率,提高图形显示效果。
但是,它也存在着一定的局限性,比如,当几何图形的运动变得复杂时,它就会变得费时费力,这就对性能产生了一定的影响。
总之,计算机图形学的裁剪算法是图形学的重要算法,它的应用非常广泛,在图形处理中有着重要的作用。
虽然它也存在着一定的局限性,但是它仍然是一种有效的图形处理算法。

一种有效的圆形窗口线裁剪算法任洪海;张飞侠【摘要】根据线段两端点相对于圆形窗口的可能位置讨论裁剪结果.当两端点都在圆形窗口之外时,通过圆切线斜率与线段斜率的比较,及点区域判别来判断线段与窗口的相交情况.在确定线段与圆形窗口有交点的情况下,应用参数化形式求交运算,简化求交方程的构造.实验结果表明,新算法显著提高了裁剪效率.%The result of clipping is discussed according to possible positions for both endpoints of a line segment in relation to circular window. The intersection is determined by comparing the slope of the tangent with the slope of the line segment and the ingenious region detection about the point when both endpoints of the line segment are outside of the circular window. Simplify the intersection equation by means of the intersection calculation with the parametric form when the intersection actually happens. The experimental results show that the new algorithm further improves the clipping efficiency.【期刊名称】《图学学报》【年(卷),期】2011(000)005【总页数】5页(P74-78)【关键词】计算机应用;圆形窗口线裁剪;斜率比较;区域判别【作者】任洪海;张飞侠【作者单位】大连交通大学软件学院计算机图形学教研室,辽宁大连,116052;辽宁对外经贸学院信息技术系,辽宁大连,116052【正文语种】中文【中图分类】TP391线裁剪是计算机图形学中的一个基本操作。
第1篇一、实验目的本次实验旨在深入理解并掌握裁剪算法的基本原理,通过编程实现Cohen-Sutherland算法和Liang-Barsky算法,对图形进行窗口裁剪,从而提高图形处理效率,优化显示效果。
二、实验环境1. 开发环境:Visual Studio 20192. 编程语言:C++3. 图形库:OpenGL三、实验内容1. 理解裁剪算法的基本原理;2. 实现Cohen-Sutherland算法;3. 实现Liang-Barsky算法;4. 对图形进行窗口裁剪,并展示裁剪效果。
四、实验过程1. 理解裁剪算法的基本原理裁剪算法是计算机图形学中的一个重要技术,用于将一个图形或图像中不需要的部分去除,只保留需要的部分。
常见的裁剪算法有Cohen-Sutherland算法、Liang-Barsky算法等。
Cohen-Sutherland算法是一种编码线段裁剪算法,通过将线段端点相对于窗口的位置进行编码,判断线段是否与窗口相交,从而实现裁剪。
Liang-Barsky算法是一种参数化线段裁剪算法,通过计算线段参数,判断线段是否与窗口相交,从而实现裁剪。
2. 实现Cohen-Sutherland算法(1)定义窗口边界首先,定义窗口边界,包括左边界、右边界、上边界和下边界。
(2)编码线段端点将线段端点相对于窗口的位置进行编码,编码规则如下:- 如果端点在窗口内,则编码为0;- 如果端点在窗口左侧,则编码为1;- 如果端点在窗口右侧,则编码为2;- 如果端点在窗口上方,则编码为4;- 如果端点在窗口下方,则编码为8。
(3)判断线段是否与窗口相交将线段两端点的编码进行异或运算,如果结果为0,则线段与窗口相交;否则,线段与窗口不相交。
(4)裁剪线段如果线段与窗口相交,则根据端点编码,将线段分为两部分,分别进行裁剪。
3. 实现Liang-Barsky算法(1)定义窗口边界首先,定义窗口边界,包括左边界、右边界、上边界和下边界。
计算机图形学中二维裁剪算法的研究随着计算机技术的发展,计算机图形学也日益成熟。
在我们的日常生活中,也成了随处可见的必需部分。
在医学、娱乐、图形艺术、商业、教育培训、科学工程等众多领域,计算机图形学的应用非常普遍。
计算机图形学主要研究的是在计算机中构造图形,将用数学模型描述的图形数据采用合适的算法转换为屏幕上图形的显示。
计算机图形学学科研究的对象为二维图形学和三维图形学及其显示和变化情况。
点、线、面为二维图形学范畴,几何体和场等数学构造方法则为三维图形学范畴。
现在,计算机图形学的一些基本算法已经形成了固化在硬件中的规范软件包,这个学科也日趋成熟和完善。
但是依然有很多算法还需要不断的改进才能应用到实际中,而裁剪算法就是其中之一。
本文主要对二维图形裁剪中的椭圆形窗口裁剪算法进行了研究,使其具有较高的效率和稳定性。
标签:计算机图形学裁剪算法椭圆形窗口线裁剪算法1 裁剪概述裁剪算法,简称裁剪,是计算机图形学中很多重要问题的基础,它就是从数据集合中识别指定区域内或指定区域外图形部分的过程。
裁剪用途很广泛,最典型的就是确定场景中位于指定区域内的景物部分。
其中,指定区域成为裁剪窗口,一般为矩形,由四条边组成,上、下、左、右,即:(Xl,Yb),(Xr,Yt)。
实质上来说,裁剪就是确定哪些多边形等几何体位于裁剪窗口内。
对于点(X,Y),只要判断两对不等式:Xl≤X≤Xr,Yb≤Y≤Yt即可。
如果四个点坐标的不等式都不成立,则这个点在矩形窗口外,否则,在窗口内。
有一种最简单的裁剪方法,就是将所有图形扫描转换成点,然后在进行判断。
但是这种方法时间消耗太大,非常不可取。
倘若将全部在窗口外的图形完全排除而不进行扫描转换,则时间上面可以高效很多,故一般采用先裁剪再扫描的方法。
按裁减对象来分,裁剪算法大概分为如下几种:点裁剪、直线段裁剪、区域多边形裁剪、曲线裁剪和文字裁剪。
裁剪有多方面应用,主要包括:使用实体造型创建对象、在三维视图中标示出可见面、对图形的一部分进行删除、复制或移动操作、防止图形边界混淆、从特定场景中抽取指定部分等。
基于六角网格的矩形窗口的圆裁剪法
韩丽
【期刊名称】《渤海大学学报(自然科学版)》
【年(卷),期】2003(024)004
【摘要】裁剪作为计算机图形学中的一个重要内容,目前研究的算法很多,尤其在矩形窗口的图形裁剪算法更是使用最广泛的一类算法,但其算法都是基于直角坐标系统提出和实现,而早在60年代初,一些数学家就已经提出了平面上点的最佳分面是按六角网格分布的,并于90年代末实现了六角网格的显示系统,基于六角网格显示系统的图形生成已成为了发展的必然,本算法基于六角网格系统的矩形窗口圆裁剪给出了具体算法和分析,此算法可以适用于在矩形窗口裁剪椭圆及其它对称的图形.【总页数】3页(P64-66)
【作者】韩丽
【作者单位】辽宁师范大学,计算机与信息技术学院,辽宁,大连,116029
【正文语种】中文
【中图分类】TP301.6
【相关文献】
1.基于AutoCAD下圆形窗口裁剪法 [J], 尉朝闻
2.一个基于六角网格的圆形窗口的裁剪算法 [J], 孙长嵩;李丽洁;宋阳
3.六角网格上的圆与椭圆生成算法 [J], 刘勇奎;邹善举;米守防;李春时
4.六角网格下圆的双步生成算法 [J], 唐棣;邹黎黎
5.改进的六角网格系统上矩形窗口裁剪算法 [J], 付文超;张传林
因版权原因,仅展示原文概要,查看原文内容请购买。
Sutherland-Hodgman裁剪算法是一种用于裁剪凸多边形的算法。
该算法的基本思想是在多边形的每一条边上进行裁剪,逐步得到裁剪后的多边形。
以下是详细的Sutherland-Hodgman裁剪算法的步骤:
步骤:
1.确定裁剪窗口:定义一个裁剪窗口(clipping window),它是一个矩形,
用来指定裁剪区域。
2.初始化:对于输入多边形的每一条边,按顺序执行以下步骤:
–记录当前边的起点和终点。
–将裁剪窗口的一个边作为“裁剪边”。
–初始化一个空的输出多边形。
3.迭代裁剪:遍历每一条输入多边形的边,依次进行以下操作:
–对于当前边,判断其与裁剪边的相对位置关系(在窗口内、窗口外或跨越窗口边界)。
–根据相对位置关系,更新输出多边形:
•如果边完全在窗口内,则将边的终点添加到输出多边形中。
•如果边跨越窗口边界,则计算边与裁剪边的交点,并将交点添
加到输出多边形中。
•如果边完全在窗口外,则不添加任何点。
4.更新裁剪边:对于每一轮迭代,更新裁剪边为下一条窗口的边。
依次遍历
裁剪窗口的四个边。
5.重复直到完成:重复步骤3和步骤4,直到遍历完所有输入多边形的边。
6.输出结果:输出多边形即为裁剪后的结果。
示例代码:
以下是一个简单的示例代码,用C语言实现Sutherland-Hodgman裁剪算法:
请注意,这只是一个简单的示例,实际应用中可能需要更多的边界条件和错误处理。
计算机图形学裁剪算法详解裁剪算法详解在使⽤计算机处理图形信息时,计算机内部存储的图形往往⽐较⼤,⽽屏幕显⽰的只是图的⼀部分。
因此需要确定图形中哪些部分落在显⽰区之内,哪些落在显⽰区之外,以便只显⽰落在显⽰区内的那部分图形。
这个选择过程称为裁剪。
最简单的裁剪⽅法是把各种图形扫描转换为点之后,再判断各点是否在窗内。
但那样太费时,⼀般不可取。
这是因为有些图形组成部分全部在窗⼝外,可以完全排除,不必进⾏扫描转换。
所以⼀般采⽤先裁剪再扫描转换的⽅法。
(a)裁剪前 (b) 裁剪后图1.1 多边形裁剪1直线段裁剪直线段裁剪算法⽐较简单,但⾮常重要,是复杂图元裁剪的基础。
因为复杂的曲线可以通过折线段来近似,从⽽裁剪问题也可以化为直线段的裁剪问题。
常⽤的线段裁剪⽅法有三种:Cohen-Sutherland,中点分割算法和梁友栋-barskey 算法。
1.1 Cohen-Sutherland裁剪该算法的思想是:对于每条线段P1P2分为三种情况处理。
(1)若P1P2完全在窗⼝内,则显⽰该线段P1P2简称“取”之。
(2)若P1P2明显在窗⼝外,则丢弃该线段,简称“弃”之。
(3)若线段既不满⾜“取”的条件,也不满⾜“弃”的条件,则在交点处把线段分为两段。
其中⼀段完全在窗⼝外,可弃之。
然后对另⼀段重复上述处理。
为使计算机能够快速判断⼀条直线段与窗⼝属何种关系,采⽤如下编码⽅法。
延长窗⼝的边,将⼆维平⾯分成九个区域。
每个区域赋予4位编码CtCbCrCl.其中各位编码的定义如下:图1.2 多边形裁剪区域编码图5.3线段裁剪裁剪⼀条线段时,先求出P1P2所在的区号code1,code2。
若code1=0,且code2=0,则线段P1P2在窗⼝内,应取之。
若按位与运算code1&code2≠0,则说明两个端点同在窗⼝的上⽅、下⽅、左⽅或右⽅。
可判断线段完全在窗⼝外,可弃之。
否则,按第三种情况处理。
求出线段与窗⼝某边的交点,在交点处把线段⼀分为⼆,其中必有⼀段在窗⼝外,可弃之。