专题七第1讲几何证明选讲

几何证明选讲第一讲相似三角形的判定及有关性质:1．平行线等分线段定理：如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等推论1：经过三角形一边中点且与另一边平行的直线必平分第三边。

推论2：经过梯形一腰的中点且与底边平行的直线必平分另一腰.2。

平行线分线段成比例定理:三条平行线截两条直线，所得的对应线段成比例。

推论：平行于三角形一边的直线截其他两边（或两边的延长线),所得的对应线段成比例。

3．相似三角形的判定及性质：相似三角形的定义：对应角相等，对应边成比例的两个三角形叫做相似三角形.相似三角形对应边的比值叫做相似比(或相似系数）。

预备定理:平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似。

相似三角形判定定理：1).两角对应相等，三角形相似.2）。

两边对应成比例且夹角相等，三角形相似.3）。

三边对应成比例，三角形相似。

直角三角形相似判定定理：1)如果两个直角三角形有一个锐角对应相等，则它们相似。

2）如果两个直角三角形的两条直角边对应成比例,则它们相似。

3）如果一个直角三角形的斜边和一条直角边与另一个三角形的斜边和直角边对应成比例,则它们相似。

4）直角三角形被斜边上的高线分成的两个直角三角形和原三角形相似。

相似三角形的性质：1)相似三角形的对应角相等。

2)相似三角形的对应边成比例。

3）相似三角形的对应高线的比，对应中线的比和对应角平分线的比都等于相似比.4）相似三角形的周长比等于相似比.5)相似三角形的面积比等于相似比的平方.6）相似三角形外接圆的的直径比、周长比等于相似比，外接圆的面积比等于相似比的平方。

4。

直角三角形的射影定理:在直角三角形中，斜边上的高是两条直角边在斜边上的射影的比例中项，每一条直角边是它在斜边上的射影和斜边的比例中项.Rt△ABC ，∠C=900，AD⊥CDBC2=AB·BD CD2=AD·BD CA2=AD·AB第二讲直线与圆的位置关系1圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半。

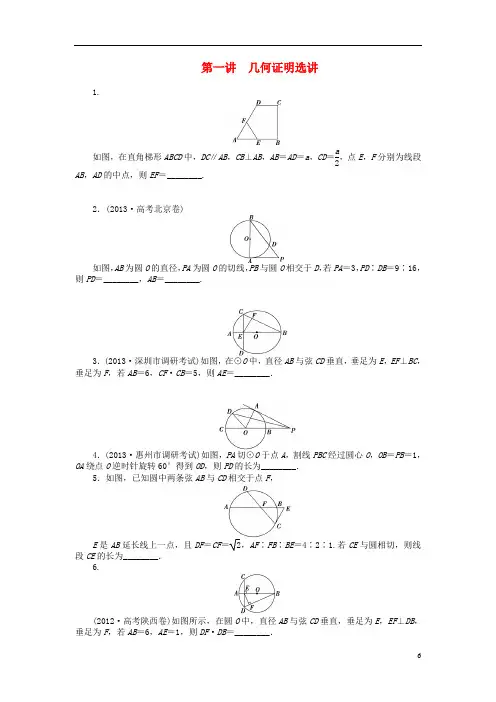
第一讲 几何证明选讲1.如图，在直角梯形ABCD 中，DC ∥AB ，CB ⊥AB ，AB ＝AD ＝a ，CD ＝a2，点E ，F 分别为线段AB ，AD 的中点，则EF ＝________.2．(2013·高考北京卷)如图，AB 为圆O 的直径，PA 为圆O 的切线，PB 与圆O 相交于D ，若PA ＝3，PD ∶DB ＝9∶16，则PD ＝________，AB ＝________.3．(2013·深圳市调研考试)如图，在⊙O 中，直径AB 与弦CD 垂直，垂足为E ，EF ⊥BC ，垂足为F ，若AB ＝6，CF ·CB ＝5，则AE ＝________．4．(2013·惠州市调研考试)如图，PA 切⊙O 于点A ，割线PBC 经过圆心O ，OB ＝PB ＝1，OA 绕点O 逆时针旋转60°得到OD ，则PD 的长为________．5．如图，已知圆中两条弦AB 与CD 相交于点F ，E 是AB 延长线上一点，且DF ＝CF ＝2，AF ∶FB ∶BE ＝4∶2∶1.若CE 与圆相切，则线段CE 的长为________．6.(2012·高考陕西卷)如图所示，在圆O 中，直径AB 与弦CD 垂直，垂足为E ，EF ⊥DB ，垂足为F ，若AB ＝6，AE ＝1，则DF ·DB ＝________．7．(2013·高考湖北卷)如图，圆O 上一点C 在直径AB 上的射影为D ，点D 在半径OC 上的射影为E ，若AB ＝3AD ，则CE EO的值为________．8.(2013·高考广东卷)如图，AB 是圆O 的直径，点C 在圆O 上．延长BC 到D 使BC ＝CD ，过C 作圆O 的切线交AD 于E .若AB ＝6，ED ＝2，则BC ＝________．9．如图，AB 为半圆的直径，DE 为半圆的一条切线，点C 为切点，AD ⊥DE 于D ，BE ⊥DE 于E 交半圆于F ，若AD ＝3，BE ＝7，那么线段DE 的长为________．10．如图，AB 、AC 是圆O 的两条弦，过点C 作圆O 的切线与BA 的延长线相交于D ，且CA 平分∠BCD ，DE 垂直于CA 的延长线于E ，则CE ∶BD ＝________．11．已知：如图，PT 切⊙O 于点T ，PA 交⊙O 于A 、B 两点且与直径CT 交于点D .CD ＝2，AD ＝3，BD ＝6，则PB ＝________．12．如图，△ABC 中，D 是AB 的一个三等分点，DE ∥BC ，EF ∥DC ，AF ＝2，则AB ＝________．13．如图，AD 、CE 分别是△ABC 的两条高，若AC ＝10，sin B ＝45，则DE ＝________．14．在△ABC 中，已知CM 是∠ACB 的平分线，△AMC 的外接圆交BC 于点N .若AC ＝12AB ，则BN AM＝________．答案：1．【解析】如图，连接BD ，DE ，由题意知DE ⊥AB ，DE ＝32a ，即BC ＝DE ＝32a ， ∴BD ＝（a 2）2＋（32a ）2＝a ， ∴EF ＝12BD ＝a2.【答案】a22．【解析】由于PD ∶DB ＝9∶16，设PD ＝9a ，则DB ＝16a .根据切割线定理有PA 2＝PD ·PB .又PA ＝3，PB ＝25a ，∴9＝9a ·25a ，∴a ＝15，∴PD ＝95，PB ＝5.在Rt △PAB 中，AB 2＝PB 2－AP 2＝25－9＝16， 故AB ＝4.【答案】9543．【解析】设AE ＝x ，则EB ＝6－x ，在Rt △CEB 中，EF ⊥BC ，∴CE 2＝CF ·CB ＝5.又易知CE ＝ED ，由相交弦定理得AE ·EB ＝CE ·ED ＝CE 2＝5，即x (6－x )＝5，得x ＝1.【答案】1 4．【解析】∵PA 切⊙O 于点A ，B 为PO 的中点，∴∠AOB ＝60°，∴∠POD ＝120°.在△POD 中，由余弦定理，得PD 2＝PO 2＋DO 2－2PO ·DO ·cos ∠POD ＝4＋1－4×(－12)＝7，故PD ＝7.【答案】7 5．【解析】设BE ＝a ， 则AF ＝4a ，FB ＝2a .∵AF ·FB ＝DF ·FC ，∴8a 2＝2，∴a ＝12，∴AF ＝2，FB ＝1，BE ＝12，∴AE ＝72.又∵CE 为圆的切线，∴CE 2＝EB ·EA ＝12×72＝74，∴CE ＝72. 【答案】726．【解析】由题意知，AB ＝6，AE ＝1，∴BE ＝5.∴CE ·DE ＝DE 2＝AE ·BE ＝5. 在Rt △DEB 中，∵EF ⊥DB ，∴由射影定理得DF ·DB ＝DE 2＝5. 【答案】57．【解析】设圆O 的直径AB ＝2R ，则AD ＝2R 3，DO ＝R 3，DB ＝4R 3.由相交弦定理，得CD2＝AD ·DB ，所以CD ＝223R .在Rt △CDO 中，CO ＝R ，由射影定理可得EO ＝DO 2CO ＝R 9，于是CE ＝R －R 9＝8R 9，故CEEO＝8.【答案】88．【解析】法一：因为AB 为圆O 的直径，所以AC ⊥BC .又BC ＝CD ，所以△ABD 是等腰三角形，所以AD ＝AB ＝6，∠DAC ＝∠BAC .因为CE 切圆O 于点C ，所以∠ECA ＝∠ABC .又因为∠BAC ＋∠ABC ＝90°，所以∠DAC ＋∠ECA ＝90°，故CE ⊥AD .故CD 2＝DE ·DA ＝2×6＝12，所以BC ＝CD ＝2 3.法二：如图，连接OC ，因为BO ＝OA ，BC ＝CD ，所以OC ∥AD .又因为CE 切圆O 于点C ，所以OC ⊥CE ，所以AD ⊥CE .因为AB 为圆O 的直径，所以AC ⊥BD .又BC ＝CD ，所以△ABD 是等腰三角形，故∠ADB ＝∠ABD ，所以△ABC ∽△CDE ，则AB BC ＝CD DE，所以BC ·CD ＝AB ·DE ，即BC 2＝AB ·DE ＝6×2＝12，BC ＝2 3.【答案】2 3 9.【解析】连接OC，则OC ⊥DE ，得OC 是梯形ABED 的中位线，所以OC ＝12(AD ＋BE )＝5，而AB ＝2OC ＝10，连接AF ，则∠AFB ＝90°，由四边形AFED 为矩形， 得EF ＝3，由BE ＝7，得BF ＝4，于是DE ＝AF ＝AB 2－BF 2＝102－42＝221. 【答案】221 10.【解析】如图，作△CDE 关于DE 的对称的△FDE 得∠FCD ＝∠CFD ， 又∠FCD ＝∠FCB ，得∠FCB ＝∠CFD ⇒CB ∥DF ，那么∠CBD ＝∠FDA ＝∠FCD ，又∠FCD ＝∠CBD ， 因此∠CFD ＝∠FDA ⇒AF ＝AD ，于是BD ＝BA ＋AD ＝CA ＋AF ＝CF ＝2CE ⇒CE ∶BD ＝1∶2. 【答案】1∶2 11．【解析】由于AD ·BD ＝CD ·TD ，得TD ＝9又由⎩⎪⎨⎪⎧PT 2＝PD 2－TD 2PT 2＝PB ·PA ⇒PB (PB ＋9)＝(PB ＋6)2－92⇒PB ＝15.【答案】1512．【解析】由⎭⎪⎬⎪⎫DE ∥BC ⇒AB AD ＝ACAEEF ∥DC ⇒AD AF ＝ACAE ⇒AB AD ＝ADAF ⇒AD 2＝AB ·AF ， 设BD ＝x ，则AD ＝2x ，AB ＝3x ，而AF ＝2，∴4x 2＝6x ，∴x ＝32，AB ＝92.【答案】9213．【解析】∵AD ⊥BC ，CE ⊥AB ，∴D 、E 都在以AC 为直径的圆上，即A 、E 、D 、C 四点共圆，∴∠BED ＝∠ACB ，又∠DBE ＝∠ABC ，∴△BDE ∽△BAC ，DE AC ＝BD AB ＝cos B ＝35(B 为锐角)，∴DE ＝35AC ＝6.【答案】6 14.【解析】如图，在△ABC 中，因为CM 是∠ACM 的平分线，所以AC BC ＝AM BM ，又已知AC ＝12AB ，所以AB BC＝2AMBM…①又因为BA 与BC 是圆O 过同一点B 的弦， 所以BM ·BA ＝BN ·BC ， 即BA BC ＝BNBM…②由①、②可知，2AM BM ＝BN BM ⇒BNAM＝2.【答案】2。

专题七 选修系列4第1讲 几何证明选讲(推荐时间：60分钟)一、填空题1. (2011·陕西)如图，∠B ＝∠D ，AE ⊥BC ，∠ACD ＝90°，且AB ＝6，AC ＝4，AD ＝12，则BE ＝________.2．(2011·湖南)如图，A ，E 是半圆周上的两个三等分点，直径BC ＝4，AD ⊥BC ，垂足为D ，BE 与AD 相交于点F ，则AF 的长为________．二、解答题3.如图所示，四边形ABCD 是平行四边形，点E 在边BA 的延长线上，CE 交AD 于点F ，∠ECA ＝∠D .求证：AC ·BE ＝CE ·AD .4．(2011·江苏)如图，圆O 1与圆O 2内切于点A ，其半径分别为r 1与r 2(r 1>r 2)．圆O 1的弦AB 交圆O 2于点C (O 1不在AB 上)．求证：AB ∶AC 为定值．5．如图，在直角梯形ABCD 中，DC ∥AB ，CB ⊥AB ，AB ＝AD ＝a ，CD ＝a 2，点E ，F 分别为线段AB ，AD 的中点，求EF 的长．6．如图所示，点P 是圆O 直径AB 延长线上的一点，PC 切圆O 于点C ，直线PQ 平分∠APC ，分别交AC 、BC 于点M 、N .求证：(1)CM ＝CN ；(2)MN 2＝2AM ·BN .7．如图，四边形ABCD 内接于⊙O ，AB ＝AD .过A 点的切线交CB 的延长线于E点．求证：AB 2＝BE ·CD .8．如图，PA 切⊙O 于点A ，割线PBC 经过圆心O ，OB ＝PB ＝1，OA 绕点O 逆时针旋转60°到OD ，求PD 的长．9. 如图，已知△ABC 的两条角平分线AD 和CE 相交于点H ，∠ABC ＝60°，F 在AC 上，且AE ＝AF . 求证：(1)B 、D 、H 、E 四点共圆；(2)CE 平分∠DEF .10．如图，已知AD 是△ABC 的外角∠EAC 的平分线，交BC 的延长线于点D ，延长DA 交△ABC 的外接圆于点F ，连结FB ，FC .(1)求证：FB ＝FC ；(2)求证：FB 2＝FA ·FD ；(3)若AB 是△ABC 外接圆的直径，∠EAC ＝120°，BC ＝6 cm ，求AD 的长．答 案1．4 2 2. 2333．证明 因为四边形ABCD 是平行四边形，所以AF ∥BC ，所以CE BE ＝EF EA .又因为AE ∥CD ，所以△AFE ∽△DFC ，所以EA CD ＝EFCF ，即CF CD ＝EF EA ＝CE BE. 又因为∠ECA ＝∠D ，∠CAF ＝∠DAC ， 所以△AFC ∽△ACD ，所以AC AD ＝CF DC ， 所以AC AD ＝CE BE ，所以AC ·BE ＝CE ·AD .4. 证明 如图，连结AO 1并延长，分别交两圆于点E 和点D .连结BD ，CE .因为圆O 1与圆O 2内切于点A ，所以点O 2在AD 上，故AD ，AE 分别为圆O 1，圆O 2的直径．从而∠ABD ＝∠ACE ＝π2. 所以BD ∥CE ，于是AB AC ＝AD AE ＝2r 12r 2＝r 1r 2. 所以AB ∶AC 为定值．5．解 连结DE ，由于E 是AB 的中点，故BE ＝a 2.又CD ＝a 2，AB ∥DC ，CB ⊥AB ， ∴四边形EBCD 是矩形．在Rt△AED 中，AD ＝a ，F 是AD 的中点，故EF ＝a 2. 6．证明 (1)∵PC 切圆O 于点C ，∴∠PCB ＝∠PAC ，又∵∠CPM ＝∠APM ，∴∠CNM ＝∠CPM ＋∠PCB ＝∠APM ＋∠PAM ＝∠CMN ，∴CM ＝CN .(2)∵∠CPN ＝∠APM ，∠PCN ＝∠PAM ， ∴△PCN ∽△PAM ，∴PC PA ＝CN AM，①同理△PNB ∽△PMC ，∴PB PC ＝BN CM .② 又∵PC 2＝PA ·PB ，③由①②③可知CM ·CN ＝AM ·BN ，∵CM ＝CN ，∴CM 2＝AM ·BN .∵AB 是圆O 的直径，∴∠ACB ＝90°.∴MN 2＝2CM 2，即MN 2＝2AM ·BN .7．证明 连结AC .∵EA 切⊙O 于A ，∴∠EAB ＝∠ACB ，∵AB ＝AD ，∴∠ACD ＝∠ACB ，AB ＝AD .∴∠EAB ＝∠ACD .又四边形ABCD 内接于⊙O ，所以∠ABE ＝∠D .∴△ABE ∽△CDA .∴AB CD ＝BE DA，即AB ·DA ＝BE ·CD . ∴AB 2＝BE ·CD .8．解 方法一 连结AB ，∵PA 切⊙O 于点A ，B 为PO 中点，∴AB ＝OB ＝OA ，∴∠AOB ＝60°，∴∠POD ＝120°.在△POD 中，由余弦定理得PD 2＝PO 2＋DO 2－2PO ·DO ·cos∠POD ＝4＋1－4×(－12)＝7.∴PD ＝7. 方法二 过D 作DE ⊥PC ，垂足为E ，∴∠POD ＝120°，∴∠DOE ＝60°，可得OE ＝12，DE ＝32， 在Rt△PED 中， PD ＝PE 2＋DE 2＝254＋34＝7. 9．证明 (1)在△ABC 中，∵∠ABC ＝60°，∴∠BAC ＋∠BCA ＝120°.∵AD ，CE 分别是△ABC 的角平分线，∴∠HAC ＋∠HCA ＝60°，∴∠AHC ＝120°.∴∠EHD ＝∠AHC ＝120°.∴∠EBD ＋∠EHD ＝180°.∴B ，D ，H ，E 四点共圆．(2)连结BH ，则BH 为∠ABC 的平分线，∴∠EBH ＝∠HBD ＝30°.由(1)知B ，D ，H ，E 四点共圆，∴∠CED ＝∠HBD ＝30°，∠HDE ＝∠EBH ＝30°.∴∠HED ＝∠HDE ＝30°.∵AE ＝AF ，AD 平分∠BAC ，∴EF ⊥AD .∴∠CEF ＝30°.∴CE 平分∠DEF .10．(1)证明 因为AD 平分∠EAC ，所以∠EAD ＝∠DAC .因为四边形AFBC 内接于圆，所以∠DAC ＝∠FBC .因为∠EAD ＝∠FAB ＝∠FCB ，所以∠FBC ＝∠FCB ，所以FB ＝FC .(2)证明 因为∠FAB ＝∠FCB ＝∠FBC ，∠AFB ＝∠BFD ，所以△FBA ∽△FDB .所以FB FD ＝FA FB，所以FB 2＝FA ·FD .(3)解 因为AB 是圆的直径，所以∠ACB ＝90°.又∠EAC ＝120°，所以∠ABC ＝30°，∠DAC ＝12∠EAC ＝60°.因为BC ＝6， 所以AC ＝BC tan∠ABC ＝23，所以AD ＝ACcos∠DAC＝43(cm)．。