2018年高三物理复习：等时圆模型--(共11张)

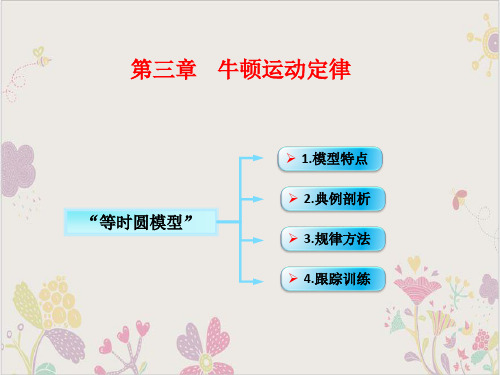
图1a bcdo图3例１题图一、模型界定物体沿光滑轨道运动，轨道的一端在圆周上，另一端在同一圆周的最高点或最低点。

二、 模型破解1.如图1所示，当质点从静止开始从圆周上不同的点沿光滑的弦运动到圆的最低点，所需的时间相同，都等于沿竖直直径自由下落的时间即gRt 4。

3.如图3所示，若轨道的顶端O 不在圆周的最高点也不在圆周的最低点时，从静止开始下滑的质点，沿不同轨道运动的时间不同，但随着轨道末端位置单调变化，如图4所示：（1）当各轨道上端相交于O 点时，物体沿各轨道由静止下滑的时间与各轨道在圆上对应于O 点下方的弧长成正相关关系，即对应弧长（而非弦长）越长，时间越长。

（2）当各轨道下端相交于O 点时，物体沿各轨道由静止下滑的时间与各轨道在圆上对应于O 点上方的弧长成正相关关系，即对应弧长越长，时间越长。

例 1.图甲是某景点的山坡滑道网片，为了探究滑行者在滑道直线部分AE 滑行的时间，技术人员通过测量绘制出如图乙所示的示意图。

AC 是滑道的竖直高度，D 点是AC 竖直线上的一点，且有AD=DE=10m ，滑道AE 可视为光滑，滑行者从坡顶A 点由静止开始沿滑道AE 向下做直线滑动，g 取l0m/s 2，则滑行者在滑道AE 上滑行的时间为D ．s 22A ．s 2B ．2sC ．s3【答案】B例2题图练1图例2. 如图所示，一质点自倾角为ɑ的斜面上方的定点A 沿光滑斜槽AP 从静止开始下滑，为使质点在最短的时间内从A 点到达斜面，则斜槽与竖直方向的夹角θ等于多少？最短时间为多少？（已知A 点离斜面的竖直高度为h ）【答案】当2αθ=时，时间最短为：)cos 1(cos 4min αα+=g h t∴当2αθ=时，时间最短为：)cos 1(cos 4min αα+=g h t例3.如图所示，在同一竖直线上有A 、B 两点，相距为h ，B 点离地高度为H ，现在要在地面上找寻找一点P ，使得从A 、B 两点分别向点P 安放的光滑木板，满足物体从静止开始分别由A 和B 沿木板下滑到P 点的时间相同，求OP 的长度。

微专题11 等时圆模型的两种情况【核心要点梳理】1．质点从竖直圆环上沿不同的光滑弦上端由静止开始滑到环的最低点所用时间相等，如图甲所示。

2．质点从竖直圆环上最高点沿不同的光滑弦由静止开始滑到下端所用时间相等，如图乙所示。

3．两个竖直圆环相切且两圆环的竖直直径均过切点，质点沿不同的光滑弦上端由静止开始滑到下端所用时间相等，如图丙所示。

【微专题训练】【经典例题选讲】【例题】如图所示，Oa、Ob和ad是竖直平面内三根固定的光滑细杆，O、a、b、c、d位于同一圆周上，c为圆周的最高点，a为最低点，O′为圆心。

每根杆上都套着一个小滑环(未画出)，两个滑环从O点无初速释放，一个滑环从d点无初速释放，用t1、t2、t3分别表示滑环沿Oa、Ob、da到达a、b所用的时间，则下列关系正确的是()A．t1＝t2B．t2>t3C．t1<t2D．t1＝t3[解析]设想还有一根光滑固定细杆ca，则ca、Oa、da三细杆交于圆的最低点a，三杆顶点均在圆周上，根据等时圆模型可知，由c、O、d无初速释放的小滑环到达a点的时间相等，即t ca＝t1＝t3；而由c→a和由O→b滑动的小滑环相比较，滑行位移大小相同，初速度均为零，但a ca>a Ob，由x＝12at2可知，t2>t ca，故选项A错误，B、C、D均正确。

[答案]BCD【变式1】(2018·江西省临川二中高三上学期第五次理综物理) 如图所示，有一半圆，其直径水平且与另一圆的底部相切于O点，O点恰好是下半圆的圆心，现在有三条光滑轨道AB、CD、EF，它们的上下端分别位于上下两圆的圆周上，三轨道都经过切点O，轨道与竖直线的夹角关系为α>β>θ，现在让一物块先后从三轨道顶端由静止下滑至底端，则物块在每一条倾斜轨道上滑动时所经历的时间关系为 ( )A ．t AB ＝t CD ＝t EF B ．t AB >t CD >t EFC ．t AB <t CD <t EFD ．t AB ＝t CD <t EF[解析] 设上面圆的半径为r ，下面圆的半径为R ，则轨道的长度s ＝2r cos α＋R ，下滑的加速度a ＝mg cos αm ＝g cos α，根据位移时间公式得，s ＝12at 2，则t ＝4r cos α＋2Rg cos α＝4r g ＋2R g cos α，因为α>β>θ，则t AB >t CD >t EF ，故B 正确，A 、C 、D 错误。