七年级立体图形三视图

1.4从三个方向看物体的形状知识精讲一．视图当我们从某一角度观察一个物体时，所看到的图像叫做物体的一个视图．视图也可以看做物体在某一角度的光线下的投影．二．常见立体图的三视图如图，我们用三个互相垂直的平面（例如墙角处的三面墙壁）作为投影面，其中正对着我们的叫做正面，正面下方的叫做水平面，右边的叫做侧面．一个物体在三个投影面内同时进行投影：在正面内得到的由前向后观察物体的视图，叫做主视图；在水平面内得到的由上向下观察物体的视图，叫做俯视图；在侧面内得到的由左向右观察物体的视图，叫做左视图．三．三视图的做法：1. 主视图与俯视图表示同一物体的长，主视图与左视图表示同一物体的高，左视图与俯视图表示同一物体的宽；主视图与俯视图的长对正，主视图与左视图的高平齐，左视图与俯视图的宽相等．2. 看得见部分的轮廓线画成实线；3. 看不见部分的轮廓线画成虚线.一个投射面水平放置，叫做水平投射面，投射到这个面内的图形叫做俯视图；一个投射面放置在正前方，叫直立投射面，投射到此平面内的图形叫做主视图；和水平投射面、直立投射面都垂直的投射面叫做侧立投射面，通常把这个平面放在直立投射面的右面，投射到这个平面内的图形叫做左视图；三点剖析一．考点：立体图形三视图二．重难点：立体图形三视图及由三视图求解立体图形三．易错点：1.画三视图时看不见的线应该用虚线；2.利用三视图确定小立方体的个数立体图形的三视图例题1、下列几何体的主视图、左视图、俯视图的图形完全相同的是（）A.三棱锥B.长方体C.三棱柱D.球体【答案】D【解析】主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图．例题2、如图，由5个完全相同的小正方体组合成一个立体图形，它的左视图是（）A.B.C.D.【答案】B【解析】解：从左面看易得第一层有2个正方形，第二层最左边有一个正方形．故选B．例题3、如图的几何体是由一些小正方形组合而成的，则这个几何体的俯视图是（）A.B.C.D.【答案】D【解析】从几何体的上面看共有3列小正方形，右边有2个，左边有2个，中间上面有1个，故选：D．例题4、如图是一个由若干个正方形搭建而成的几何体的主视图与左视图，那么下列图形中可以作为该几何体的俯视图的序号是：________________．【答案】①②③【解析】综合左视图跟主视图：从正面看，第一行第一列有3个正方形，第一行第二列有1个或第二行第2列有一个或都有一个.第二行第1列有2个正方体.随练1、如图①，这是一个正方体毛坯，将其沿一组对面的对角线切去一半，得到一个工件如图②，对于这个工件，左视图、俯视图正确的一组是（）①②a b c dA.a，bB.b，dC.a，cD.a，d 【答案】D【解析】左视图、俯视图是分别从物体的侧面和上面看所得到的图形．由三视图求解立体图形例题1、从三个不同方向看一个几何体，得到的平面图形如图所示，则这个几何体是（）A.圆柱B.圆锥C.棱锥D.球【答案】A【解析】∵主视图和左视图都是长方形，∴此几何体为柱体， ∵俯视图是一个圆， ∴此几何体为圆柱． 故选：A ．例题2、 如图是由一些相同的小正方体构成的立体图形的三种视图．那么构成这个立体图形的正方体有多少个小立方块（ ）A.4个B.5个C.6个D.7个 【答案】【解析】 根据图形可得：最底层有4个小立方块，第二层有1个小立方块，所以构成这个立体图形的小立方块有5个．例题3、 如图是某几何体的三视图，根据图中数据，求得该几何体的体积为（ ）A.60πB.70πC.90πD.160π 【答案】 B【解析】 观察三视图发现该几何体为空心圆柱，其内圆半径为3，外圆半径为4，高为10，所以其体积为22104370πππ⨯-=（），例题4、 由一些大小相同的小正方体组成的简单几何体的主视图和俯视图．（如图） （1）请你画出这个几何体的一种左视图；（2）若组成这个几何体的小正方体的块数为n ，请你写出n 的所有可能值．【答案】 （1）见解析；（2）8n =，9，10，11． 【解析】 （1）左视图有以下5种情形：（2）8n ，9，10，11．随练1、将如图绕AB边旋转一周，所得几何体的俯视图为（）A.B.C.D.【答案】B【解析】将该图形绕AB旋转一周后是由上面一个圆锥体、下面一个圆柱体的组合而成的几何体，从上往下看其俯视图是外面一个实线的大圆（包括圆心），里面一个虚线的小圆．随练2、如图所示的是某几何体的三视图，则该几何体的形状是（）A. 长方形B. 三棱柱C.圆柱D. 正方体【答案】C【解析】根据主视图和左视图为矩形判断出是柱体，根据俯视图是圆可判断出这个几何体应该是圆柱．随练3、如图是由一些相同的小正方体组成的几何体的三视图，则组成该几何体的小正方体的个数最少为（）A.7个B.8个C.9个D.10个【答案】C【解析】由俯视图可得底面有一排有6个小正方体；从主视图看，第二层最少有2个正方体，第3层最少有一个小正方体，组成该几何体的小正方体的个数为9个．随练4、如图是一个几何体的三视图，则这个几何体的侧面积是（）A.πB.9πC.18πD.27π【答案】C【解析】根据三视图可得：这个几何体为圆锥，∵直径为6，圆锥母线长为6，∴侧面积66218ππ=⨯⨯÷=；随练5、如右图，是一个由若干个小正方体搭建而成的几何体的主视图与左视图，那么下列图形中可以作为该几何体的俯视图的序号是___________．【答案】①②③【解析】根据几何的主视图和左视图即可判断．课后练习1、如图所示零件的左视图是（）A.B.C.D.【答案】D【解析】零件的左视图是两个竖叠的矩形．中间有2条横着的虚线2、在下面的四个几何体中，它们各自的左视图与主视图不全等的是（）A. B. C. D.【答案】D【解析】A、正方体的左视图与主视图都是正方形，不符合题意；B、球的左视图与主视图都是圆，不符合题意；C、有正方孔的正方体的左视图与主视图都是正方形里面有两条竖直的虚线，不符合题意；D、三棱锥的左视图与主视图都虽然都是三角形，但是形状不相同，符合题意．故选：D．3、下列几何体中，同一个几何体的主视图与俯视图不同的是（）A.圆柱B.正方体C.圆锥D.球【答案】C【解析】A、圆柱的主视图是矩形，俯视图是矩形，主视图与俯视图相同，故A选项错误；B、正方体的主视图是正方形，俯视图是正方形，主视图与俯视图相同，故B选项错误；C、圆锥的主视图是三角形，俯视图是圆及圆心，主视图与俯视图不相同，故C选项正确；D、球的主视图是圆，俯视图是圆，主视图与俯视图相同，故D选项错误．4、与如图所示的三视图对应的几何体是（）A.B.C.D.【答案】B【解析】根据主视图、左视图、俯视图判断即可得到.17、几个棱长为1的正方体组成的几何体的三视图如图所示，则这个几何体的体积是（）A.4B.5C.6D.7【答案】B【解析】综合三视图可知，这个几何体的底层应该有3＋1＝4个小正方体，第二层应该有1个小正方体，因此搭成这个几何体所用小正方体的个数是4＋1＝5个，所以这个几何体的体积是5．。

第四讲从三个方向看物体的形状一、从不同方向看简单立体图形在小学数学中，我们曾经辨认过从正面、左面（或右面）和上面三个不同方向观察同一物体时看到的物体的形状图.例如，图①是由小立方块搭成的几何体，从正面、左面、上面看到的几何体的形状图如图②所示.1.我们从三个不同方向观察同一物体时，一般可以看到不同的形状．从正面能够看到物体的和，从上面能够看到物体的和，从左面能够看到物体的和．2.易错警示：画从三个不同方向看一个立体图形所得的形状图时，要注意进行水平观察，且要分清物体的前后位置．例1如图，从不同方向看立体图形得到一些平面图形，根据这些平面图形说出立体图形的名称．例2观察图中的几何体，分别画出从正面、左面与上面看到的图形．练1 下列立体图形中，从上面看是正方形的是()练2 下列几何体中，从正面看和从左面看都是长方形的是()练3下面四个几何体中，从上面看得到的形状图是圆的几何体共有()A．1个B．2个C．3个D．4个练4 如图，是由一个圆柱体和一个长方体组成的几何体．其从正面看到的形状图是()练5 桌面上放着一个长方体和一个圆柱体，按如图所示的方式摆放在一起，从左面看得到的形状图是()二、根据从不同方向看到的形状图还原物体议一议一个几何体由几个大小相同的小立方块搭成，从上面和从左面看到的这个几何体的形状图如图所示，请搭出满足条件的几何体.你搭的几何体由几个小立方块构成？与同伴进行交流.画从正面和左面看到的形状图，有两种方法：方法一是先根据从上面看到的形状图摆出几何体，再画从正面和左面看到的形状图；方法二是先根据从上面看到的形状图确定从正面和左面看到的图形的列数，再确定每列正方形的个数．我们通常采用第二种方法．例3如图是从上面看到的由几个小立方块所搭成的几何体的形状图，小正方形中的数字表示在该位置的小立方块的个数，请画出从正面和左面看这个几何体的形状图．例4如图，是从正面、左面、上面看到的由一些大小相同的小立方块搭成的几何体的形状图，那么搭成这个几何体的小立方块的个数是()A．6B．7C．8D．9练1一个几何体从三个方向看得到的形状图如图所示，则这个几何体是()A．三棱锥B．三棱柱C．圆柱D．长方体三、课堂小结从不同的方向看立体图形的技巧：(1)从正面看立体图形时，可以想象为：将几何体从前向后压缩，使看到的面全部落在同一竖直的平面内．(2)从左面看立体图形时，可以想象为：将几何体从左向右压缩，使看到的面全部落在同一竖直的平面内．(3)从上面看立体图形时，可以想象为：将几何体从上向下压缩，使看到的面全部落在同一水平的平面内．四、课堂小测1．对于一些立体图形的问题，常把它们转化为________图形来研究和处理．从不同的方向看，将会得到不同形状的平面图形．通常我们是从________、________、三个方向看，从而得到相应的平面图形．2．下列立体图形中，从正面看是圆的是()3．如图所示的几何体，从上面看到的图形为()4．五个大小相同的正方体搭成的几何体如图所示，其从左面看到的图形是()5．如图，小明、小东、小刚和小华四人坐在桌子周围，桌子正中央有一把水壶，请选择他们分别看到的是水壶的哪个面：小明：______，小东：______，小刚：______，小华：______．第6题第7题6．如图是某几何体从上面看到的图形，该几何体可能是()A．圆柱B．圆锥C．球D．正方体7．一个几何体从三个方向看到的平面图形如图所示，这个几何体是()A．球B．圆柱C．圆锥D．立方体8．已知：如图，是由若干个大小相同的小正方体所搭成的几何体从三个方向看到的平面图形，则搭成这个几何体的小正方体的个数是()A．6 B．7 C．8 D．99．如图是由5块完全相同的小正方体所搭成的立体图形从上面看到的图形，小正方形中的数字表示在该位置小正方体的个数，其从正面看到的图形是()10．找出与图中几何体对应的从三个方向看到的图形，并在横线上填上对应的序号．11．5个棱长为1的正方体组成如图所示的几何体．(1)该几何体的体积是________(立方单位)，表面积是________(平方单位)；(2)画出该几何体从正面、左面、上面看到的图形．12．如图是一个几何体从正面和上面看到的图形，求这个几何体的体积(π取3.14)．13．学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子，碟子的个数与高度(单位：cm)的关系如下表：(1)当桌子上放有x个碟子时，请写出此时碟子的高度(用含x的式子表示)；(2)分别从三个方向看若干碟子，得到的图形如图所示，厨房师傅想把它们整齐地叠成一摞，求叠成一摞后的高度．碟子的个数碟子的高度1 22 2＋1.53 2＋34 2＋4.5… …。

七年级第一章三视图知识点在学习物理时，三视图是一种十分基础和重要的概念。

对于七年级的学生来说，掌握三视图的知识点是十分关键的。

下面将介绍三视图的概念、特点以及如何进行正确的绘制。

一、三视图的概念
三视图，顾名思义，就是指一件物体能够被分别画成正视图、左视图和俯视图三个不同方位的视图。

其中，正视图是指物体正对观察者的视图，左视图是指物体从左侧观察时的视图，俯视图是指物体从上方向下观察时的视图。

二、三视图的特点
1. 三视图互相独立：每个视图所表现的物体形状和大小都是独立的。

任何时候，三视图都应该互相独立，不应该重合或出现多余的线条。

2. 三视图共同构成一个立体图形：通过分析三个视图，我们可以更加全面地了解一个立体图形的形状和特征。

3. 三视图应该处于同一平面内：三视图应该在同一平面内展示，这样方便我们进行观察和比较。

三、正确绘制三视图的方法
1. 确定三视图的位置：首先要明确立体图形的位置和基准线，
然后确定正视图的位置，再绘制左视图和俯视图。

2. 绘制正视图：一般正视图是在左边，需要根据物品的形状和
大小合理绘制。

3. 绘制左视图和俯视图：左视图在正视图的右侧，需按照正视
图匹配线条精细绘制；俯视图在正视图的下方，需要做好比例和
对称。

4. 绘制通用线条：三视图中的通用线条指的是三个视图中都有
的线条，应该先绘制好，再逐一补充其他线条。

综上所述，三视图是学习物理中一个非常重要的知识点，对于七年级的学生来说，需要认真掌握。

正确绘制三视图不仅能够提高我们对于有关的物体形状和大小的理解，也有助于我们更好地进行模型设计和制作。

几何（二）立体图形的截面与三视图【知识要点】2．三视图法：（1）主视图：从看到的图形叫做主视图；（2）左视图：从看到的图形叫做左视图；（3）俯视图：从看到的图形叫做俯视图。

它们的关系：（1）主视图列数＝俯视图列数；主视图行数＝左视图行数；俯视图行数＝左视图列数（2）主视图中每列正方体的个数就是俯视图中每列数中最大的数值；主视图中每行正方体的个数就是左视图中相应的行中数字最大的数；3．多边形：在平面内，由一些线段首尾顺次相接组成的图形叫做多边形。

三角形、四边形、五边形、六边形等都是多边形。

【典型例题】例1 用一个平面去截一个正方体，可能出现哪些图形？请分别画出。

例2：如果用一个平面截一个正方体的一个角，剩下的几何体有几个顶点、几条棱、几个面？例3：用一个平面去截三棱柱最多可以截得五边形；用一个平面去截四棱柱最多可以截得六边形，用一个平面去截五棱柱最多可以截得七边形；如果用一个平面去截n 个棱柱，最多能截得几边形？例4:把两个长 3 厘米、宽2厘米、高1厘米的小长方体先粘合成一个大长方体，再把它分成两个大小相同的小长方体，末了一个小长方体的表面积最多可比起初一个小长方体的表面积大多少？例5:用小方块搭成的一个几何体，从不同的方向观察得到三视图如图2-1，试确定该几何体用了多少块小方块。

例6:如图2-2，是由几个小正方体所搭成的两个几何体的俯视图。

小正方形中的数字表示该位置小正方体的个数，请画出相应几何体的主视图和左视图。

例7：如图2-3：是由几个小立方体所搭的几何体的俯视图，小正方体中的数字表示该位置小正方体的个数，如果每个小正方体的棱长是1，求该几何 体的表面积。

例8：棱长为a 的正方体，摆放成如图2-4所示的形状.主视图 左视图 俯视图 图2-1（1（2图2-2 图2-3（1）如果这一物体摆放三层，试求该物体的表面积：（2）依图中摆放方法类推，如果该物体摆放了上下20层，求该物体的表面积；（3）第n 层，该物体的表面积是多少？思考：有一个正方体,它的6个面被分别涂上了不同的颜色,并且在每个面上至少贴有一张纸条.用不同的方法来摆放这个正方体,并从不同的角度拍下照片.(1)洗出照片后,把所拍摄的面的颜色种类不同的照片全部挑选出来,最多可以选出多少张照片?(2)观察(1)中选出的照片,发现各张照片里的纸条数各不相同.问:整个正方体最少贴有多少张纸条?【练习与拓展】一．选择题：1．一个平面去截一个正方体，截面的形状不可能是（ ）。

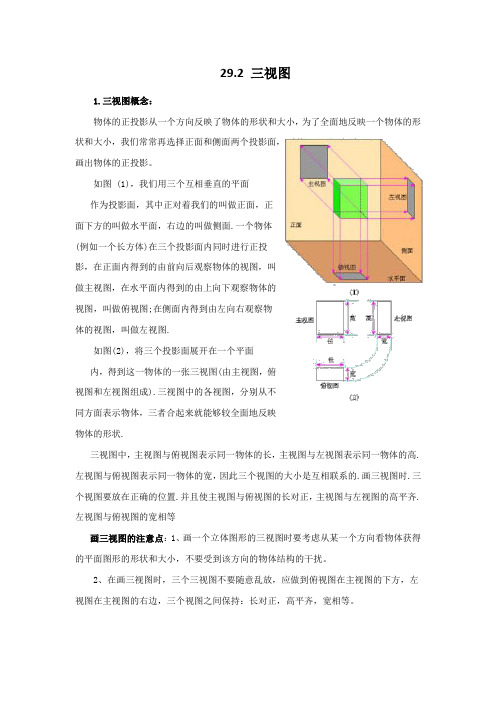
29.2 三视图1.三视图概念：物体的正投影从一个方向反映了物体的形状和大小，为了全面地反映一个物体的形状和大小，我们常常再选择正面和侧面两个投影面，画出物体的正投影。

如图 (1)，我们用三个互相垂直的平面作为投影面，其中正对着我们的叫做正面，正面下方的叫做水平面，右边的叫做侧面.一个物体(例如一个长方体)在三个投影面内同时进行正投影，在正面内得到的由前向后观察物体的视图，叫做主视图，在水平面内得到的由上向下观察物体的视图，叫做俯视图;在侧面内得到由左向右观察物体的视图，叫做左视图.如图(2)，将三个投影面展开在一个平面内，得到这一物体的一张三视图(由主视图，俯视图和左视图组成).三视图中的各视图，分别从不同方面表示物体，三者合起来就能够较全面地反映物体的形状.三视图中，主视图与俯视图表示同一物体的长，主视图与左视图表示同一物体的高.左视图与俯视图表示同一物体的宽，因此三个视图的大小是互相联系的.画三视图时.三个视图要放在正确的位置.并且使主视图与俯视图的长对正，主视图与左视图的高平齐.左视图与俯视图的宽相等画三视图的注意点：1、画一个立体图形的三视图时要考虑从某一个方向看物体获得的平面图形的形状和大小，不要受到该方向的物体结构的干扰。

2、在画三视图时，三个三视图不要随意乱放，应做到俯视图在主视图的下方，左视图在主视图的右边，三个视图之间保持：长对正，高平齐，宽相等。

典型例题例1.画出下图所示的一些基本几何体的三视图.分析:画这些基本几何体的三视图时，要注意从三个方面观察它们.具体画法为:1.确定主视图的位置，画出主视图;2.在主视图正下方画出俯视图，注意与主视图“长对正”。

3.在主视图正右方画出左视图.注意与主视图“高平齐”，与俯视图“宽相等”.解：例2.画出如图所示的支架(一种小零件)的三视图.分析:支架的形状，由两个大小不等的长方体构俯视图左视图主视图成的组合体.画三视四时要注意这两个长方体的上下、前后位置关系.解:如图29.2-7是支架的三视图例3.右图是一根钢管的直观图，画出它的三视图分析.钢管有内外壁，从一定角度看它时，看不见内壁.为全面地反映立体图形的形状，画图时规定;看得见部分的轮廓线画成实线.因被其他那分遮挡而看不见部分的轮廓线画成虚线.解:图如图29.2-7是钢管的三视图，其中的虚线表示钢管的内壁.例4．如图所示图形是一个多面体的三视图，请根据视图说出该多面体的具体名称。

七年级苏教版数学复习要点考点专题四：立体图形及三视图知识点一常见立体图形1．立体图形与平面图形①有些几何图形（如长方体、正方体、圆柱、圆锥、球等）的各部分不都在同一平面内，它们是立体图形．②有些几何图形（如线段、角、三角形、长方形、圆等）的各部分都在同一平面内，它们是平面图形．3．常见立体图形的分类曲面体圆柱、圆锥、球体按是否有顶点是棱柱、棱锥、圆锥否圆柱、球体总结：在对几何体分类时首先确定分类的标准，分类标准不同，结果也就不同，不论选择哪种分类标准，都要做到不重、不漏.4、点、线、面、体体：长方体、正方体、圆柱、圆锥、球、棱柱、棱锥都是几何体，几何体也称体．面：包围着体的是面．面有平面和曲面两种．线：面和面相交的地方形成线．点：线和线相交的地方是点．用运动的观点来看：点动成线、线动成面、面动成体．例1（中山区期末）三角形ABC绕BC旋转一周得到的几何体为()A．B．C．D．【解答】解：由图形的旋转性质，可知ABC旋转后的图形为C，故选：C．例2（邳州市期末）如图，在下列图形中，绕铅垂线旋转一周可得到如图所示几何体的是()A．B．C．D．【解答】解：A、是直角梯形绕高旋转形成的圆台，故A正确；B、是直角梯形绕底边的腰旋转形成的圆柱加圆锥，故B错误；C、绕直径旋转形成球，故C错误；D、绕直角边旋转形成圆锥，故D错误．故选：A．例3（皇姑区期末）下面是一个正方体，用一个平面去截这个正方体截面形状不可能为下图中的()A．B．C．D．【解答】解：无论如何去截，截面也不可能有弧度，因此截面不可能是圆．故选：D．知识点二几何体的表面展开图1．展开图：有些几何体的表面可以展开成平面图形，这个平面图形称为相应几何体的表面展开图.2．常见立体图形的平面展开图（1）圆柱的表面展开图是两个相同的圆面和一个长方形组成的；（2）圆锥的表面展开图是由一个圆面和一个扇形组成的；（3）棱柱的表面展开图是由两个相同的多边形和一个长方形组成的，侧面展开图是一个长方形。

第四章第2课立体图形的三视图(1)-七年级上册初一数学（人教版）一、引言本课主要介绍了立体图形的三视图。

在现实生活中，我们经常会遇到各种立体图形，比如立方体、长方体、圆柱体等等，而了解这些图形的三视图对我们理解和构造立体图形有重要的帮助。

本文将详细介绍立体图形的三视图的概念及其应用，帮助学生更好地理解和掌握立体图形的表达方式。

二、立体图形的三视图概念1. 什么是立体图形的三视图立体图形的三视图指的是一个立体图形在三个不同方向上的投影。

通常，我们可以将一个立体图形的三视图分别绘制在前视图、顶视图和侧视图上，以便更好地展示出其外观和尺寸。

2. 前视图、顶视图和侧视图的定义•前视图：立体图形在正对着它的方向上的投影视图，从正方向观察，是立体图形的正面视图。

•顶视图：立体图形在上方向的投影视图，从上方向观察，是立体图形的俯视图。

•侧视图：立体图形在侧面方向的投影视图，从一侧方向观察。

在绘制三视图时，我们一般按照一定的规则来绘制，以保证准确性和一致性。

三、绘制立体图形的三视图步骤绘制立体图形的三视图一般可以按照以下步骤进行：1. 确定各个视图的位置在绘制三视图之前，首先需要确定每个视图在纸上的位置。

一般来说，我们可以将前视图绘制在最上方，顶视图绘制在左侧，侧视图绘制在右侧，以保证三视图之间的关系清晰可见。

2. 绘制前视图在绘制前视图时，我们需要根据实际立体图形的形状和尺寸，在纸上垂直绘制图形的每个面。

可以用实线表示实际可见的支撑面，用虚线表示实际不可见的支撑面。

3. 绘制顶视图在绘制顶视图时，我们需要将立体图形向下投影至纸面上。

同样，可以用实线表示可见的支撑面，用虚线表示不可见的支撑面。

需要注意的是，顶视图在水平方向上的尺寸要与前视图保持一致。

4. 绘制侧视图在绘制侧视图时，我们将立体图形向左或向右投影至纸面上。

同样，用实线表示可见的支撑面，用虚线表示不可见的支撑面。

需要注意的是，侧视图在水平方向上的尺寸要与前视图和顶视图保持一致。

初中-数学-打印版
如何画简单组合体的三视图
如何画简单组合体的三视图
难易度：★★
关键词：画立体图形
答案：
（1）画简单组合体的三视图要循序渐进，通过仔细观察和想象，再画它的三视图。

（2）视图中每一个闭合的线框都表示物体上的一个平面，而相连的两个闭合线框常不在一个平面上。

（3）画物体的三视图的口诀为：主、俯：长对正；主、左：高平齐；俯、左：宽相等。

【举一反三】
典例：连线：将图中四个物体与（下面一排中）其相应的俯视图连接起来．
思路引导：本题考查学生对俯视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．俯视图是从物体上面所看到的图形，可根据各立体图形的特点进行判断．标准答案：如图所示：
初中-数学-打印版。