2010年中考数学复习同步练习(15)(四边形的证明)3 姓名

1、如图，四边形ABCD的对角线AC、BD交于点O，已知O是AC的中点，AE=CF，DF∥BE.(1)求证：△BOE≌△DOF；(2)若OD=1/2AC，则四边形ABCD是什么特殊四边形？请证明你的结论.2、已知：如图，在矩形ABCD中，点E，F分别在AB，CD边上，BE=DF，连接CE，AF.求证：AF=CE.3、如图，在平行四边形ABCD中，∠C=60°，M、N分别是AD、BC的中点，BC=2CD.(1)求证：四边形MNCD是平行四边形；(2)求证：BD=MN.4、如图，四边形ABCD是平行四边形，P是CD上一点，且AP和BP分别平分∠DAB和∠CBA.(1)求∠APB的度数；(2)如果AD=5 cm，AP=8 cm，求△APB的周长. 5、如图，在△ABC中，点D，E，F分别是AB，BC，CA的中点，AH是边BC上的高.(1)求证：四边形ADEF是平行四边形；(2)求证：∠DHF=∠DEF.6、已知：如图，在□ABCD中，点E、F在AC上，且AE=CF.求证：四边形BEDF是平行四边形.7、如图，四边形ABCD是平行四边形，AC是对角线，BE⊥AC，垂足为E，DF⊥AC，垂足为F.求证：BE=DF.8、如图3-34所示，E，F分别为平行四边形ABCD中AD，BC的中点，G，H在BD上，且BG＝DH，求证四边形EGFH是平行四边形．9、如图，在△ABC中，AB=AC，D为边BC上一点，以AB，BD为邻边作▱ABDE，连接AD，EC．（1）求证：△ADC≌△ECD；（2）若BD=CD，求证：四边形ADCE是矩形．10、如图，已知四边形ABDE是平行四边形，C为边B D 延长线上一点，连结AC、CE，使AB=AC.⑴求证：△BAD≌△AEC；⑵若∠B=30°，∠ADC=45°，BD=10，求平行四边形ABDE的面积.11、如图，在▱ABCD中，∠ABC的平分线BF分别与AC、AD交于点E、F.(1) 求证：AB＝AF；(2)当AB＝3，BC＝5时，求的值．12、已知，如图，在▱ABCD中，延长DA到点E，延长BC到点F，使得AE＝CF，连接EF，分别交AB，CD于点M，N，连接DM，BN.(1)求证：△AEM≌△CFN；(2)求证：四边形BMDN是平行四边形．13、如图所示，已知在平行四边形ABCD中，BE=DF，求证：AE=CF．14、已知：如图，在△ABC中，，D是BC 的中点，，CE∥AD．如果AC=2，CE=4．（1）求证：四边形ACED是平行四边形；（2）求四边形ACEB的周长；（3）直接写出CE和AD之间的距离．15、如图，已知：AB∥CD，BE⊥AD，垂足为点E，CF ⊥AD，垂足为点F，并且AE=DF．求证：四边形BECF是平行四边形．16、如图9，ABCD中，AE、CF分别平分∠DAC、∠BCA，则四边形AFCE是平行四边形吗？为什么？17、如图，在△ABC中，D是BC边上的一点，E是AD 的中点，过A点作BC的平行线交CE的延长线于F ，且AF=BD，连结BF（1）求证：D是BC的中点．（2）如果AB=AC ，试判断四边形AFBD的形状，并证明你的结论．18、如图，四边形ABCD是平行四边形，作AF∥CE，BE∥DF，AF交BE与G点，交DF与F点，CE交DF 于H点、交BE于E点．求证：△EBC≌△FDA．19、如图，在□ABCD中，为边上一点，且．（1）求证：;（2）若平分，，求的度数．20、如图，已知平行四边形ABCD中，AE⊥BC于E，AF⊥CD于F，（14分）（1）若AE=3cm，AF=4cm，AD=8cm，求：CD的长．（2）若平行四边形的周长为36cm，AE=4cm，AF=5cm，求平行四边形ABCD的面积．21、如图，平行四边形ABCD中，AE⊥BD, CF⊥BD，垂足分别为E、F．求证：四边形AECF是平行四边形．22、如图，在□ABCD中，点E、F分别是AD、BC的中点，分别连接BE、DF、BD．（1）求证：△AEB≌△CFD；（2）若四边形EBFD是菱形，求∠ABD的度数．23、已知,如图,在▱ABCD中,E是CD的中点,F是AE的中点,FC与BE交于点G.求证:GF=GC.24、已知,如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形.25、四边形ABCD的对角线AC、BD交于点O，BE⊥AC于E，DF⊥AC于F，点O既是AC的中点，又是EF的中点．(1)求证：△BOE≌△DOF；(2)若OA ＝BD ，则四边形ABCD 是什么特殊四边形？请说明理由．26、如图，四边形中，，点在的延长线上，联结，交于点，联结DB ，，且.(1) 求证：；（2）当平分时，求证：四边形是菱形.27、已知：如图，在□ABCD 中，E 是CA 延长线上的点，F 是AC 延长线上的点，且AE ＝CF ．求证：（1）△ABE ≌△CDF ；（2）BE ∥DF ．28、如图，在□ABCD 中，AC 、BD 交于点O ，EF 过点O ，分别交CB 、AD 的延长线于点E 、F .。

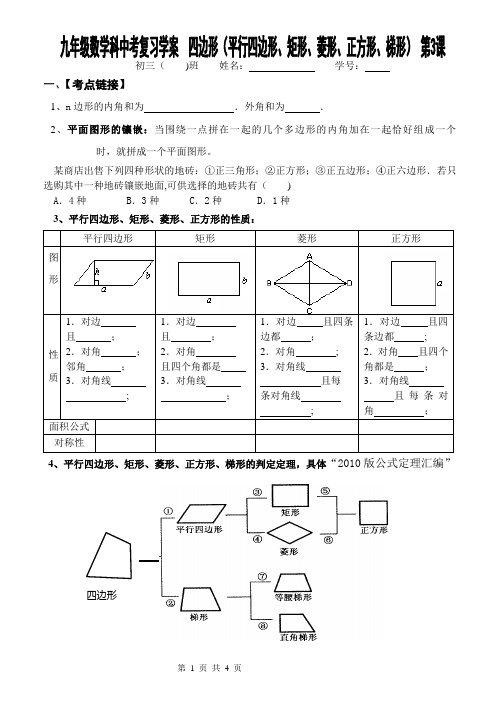
初三（)班姓名：学号：一、【考点链接】1、n边形的内角和为．外角和为．2、平面图形的镶嵌：当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个_________时，就拼成一个平面图形。

某商店出售下列四种形状的地砖：①正三角形；②正方形；③正五边形；④正六边形．若只选购其中一种地砖镶嵌地面,可供选择的地砖共有（)A．4种 B．3种 C．2种 D．1种3、平行四边形、矩形、菱形、正方形的性质：平行四边形矩形菱形正方形图形性质1．对边且；2．对角；邻角；3．对角线;1．对边且；2．对角且四个角都是3．对角线；1．对边且四条边都；2．对角;3．对角线且每条对角线;1．对边且四条边都;2．对角且四个角都是；3．对角线且每条对角；面积公式对称性4、平行四边形、矩形、菱形、正方形、梯形的判定定理，具体“2010版公式定理汇编”_四边形5、中点四边形如图:四边形ABCD 中，E 、F 、G 、H 分别为各边的中点，顺次连结E 、F 、G 、H ，得到： ⑴。

四边形一定是 形⑵。

当AC 与BD 满足_ ______时,四边形EFGH 为矩形； ⑶.当AC 与BD 满足___ ____时,四边形EFGH 为菱形；⑷。

当AC 与BD 满足__ _ ____时，四边形EFGH 为正方形。

二、【中考演练】6、在下列命题中,是真命题的个数有( )①两条对角线互相垂直的四边形是矩形 ②两条对角线相等的四边形是菱形 ③两条对角线相等的四边形是平行四边形 ④两条对角线互相平分的梯形是等腰梯形 ⑤两条对角线互相垂直且相等的四边形是正方形 A 0个 B.1个 C.2个 D 。

3个7、下列给出的条件中，能判断四边形ABCD 是平行四边形的是( )A 。

AB ∥CD ，AD=BC B 。

AB=AD ，CB=CD C.∠B=∠C ，∠A=∠D D 。

AB=CD ，AD=BC8、如图,已知四边形ABCD 是平行四边形，下列结论中不正确的是( ）A 、当AB=BC 时，它是菱形B 、当AC ⊥BD 时，它是菱形 C 、当∠ABC=900时，它是矩形 D 、当AC=BD 时,它是正方形9、若正方形的一条对角线长为cm 2,则这个正方形的面积是 10、如图，在等腰梯形ABCD 中，AD ∥BC ,对角线AC 、BD 相 交于点O ，以下四个结论：①DCB ABC ∠=∠ ，②OA =OD ， ③BDC BCD ∠=∠,④S AOB ∆=S DOC ∆，其中正确的是（ ) A 。

1九年级数学上四边形证明测试题一、精心选一选，相信自己的判断！（每小题3分，共30分） 1、四边形的四个内角中，最多时钝角有A 1 个B 2 个C 3 个D 4 个 2、四边形具有的性质是A 对边平行B 轴对称性C 稳定性D 不稳定性 3、一个多边形的每一个外角都等于720，则这个多边形的边数是A 四边B 五边C 六边D 七边 4、下列说法不正确的是A 平行四边形对边平行B 两组对边平行的四边形是平行四边形C 平行四边形对角相等D 一组对角相等的四边形是平行四边形 5、一个等腰梯形的两底之差为12，高为6，则等腰梯形的锐角为A ︒30B ︒45C ︒60D ︒756、平行四边形的两条对角线将此平行四边形分成全等三角形的对数是A 2 对B 3对C 4对D 5 对 7、 菱形具有而平行四边形不具有的性质是A .内角和是360°； B. 对角相等； C. 对边平行且相等； D. 对角线互相垂直. 8、 平行四边形各内角的平分线围成一个四边形，则这个四边形一定是 A. 矩形； B. 平行四边形； C. 菱形； D. 正方形9、 如图，在等腰梯形ABCD 中，AB ∥CD ，AD=BC= a cm ，∠A=60°，BD 平分∠ABC ，则这个梯形的周长是A. 4a cm ；B. 5a cm ；C.6a cm ；D. 7a cm ；10、等边三角形的一边上的高线长为cm 32A cm 3B cm5.2 Ccm 2D cm 4二、耐心填一填：（把答案填放相应的空格里。

每小题3分，共24分）。

11. 中，对角线相交于点O ，AC ⊥CD ，AO = 3，BO = 5，则CO =_____，CD=______，AD =________ 12. 中，AB 、BC 、CD 的长度分别为2x +1， 3x ，x +4的周长是_____________13. 在△ABC 中，D 、E 、F 分别是AB 、BC 、AC 的中点，若△ABC 的周长为30 cm ，则△DCE 的周长为__________ 1 4. 在等腰梯形ABCD 中，AD ∥BC ，AB=CD ，∠B=40，则∠A=_____，∠C=____，∠D=_____. 15. 菱形的对角线长分别为24和10，则此菱形的周长为___________，面积为____________. 16. 已知中，∠A -∠B = 30°，则∠C = __________，∠D = __________.BB217. 判定一个四边形是正方形主要有两种方法，一是先证明它是矩形，然后证明______________，二是先证明它是一个菱形，再证明_____________________.18. 如图，已知四边形ABCD 是一个平行四边形，则只须 补充条件__________________，就可以判定它是一个菱形 三、解答证明题：：（本大题共6小题，共66分）19．（11分）在平行四边形ABCD 中，BC = 2AB ，E 为BC 中点，求∠AED 的度数；20．（11分）如图，四边形ABCD 中，AD = BC ，AE ⊥BD ，CF ⊥BD ，垂足为E 、F ，BE = DF ，求证：四边形ABCD 是平行四边形；21．（11分）如图：在⊿ABC 中，∠BAC = 90，AD ⊥BC 于D ，CE 平分∠ACB ，交AD 于G ，交AB 于E ，EF ⊥BC 于F ，求证：四边形AEFG 是菱形；22．（11分）如图，以正方形ABCD 的对角线AC 为一边，延长AB 到E ，使AE = AC ，以AE 为一边作菱形AEFC ，若菱形的面积为29，求正方形边长；BDBDB CF323．（11分）如图AD 是⊿ABC 边BC 边上的高线，E 、F 、G 分别是AB 、BC 、AC 的中点，求证：四边形EDGF 是等腰梯形；24．（11分）如图，AC 、BD 是矩形ABCD 的对角线，AH ⊥BD 于H ，CG ⊥BD 于G ，AE 为∠BAD 的平分线，交GC 的延长线于E ，求证：BD = CE ；C4九年级数学上证明（三）测试参考答案解答证明题：：（本大题共6小题，共46分 证19：∵ E 为BC 中点，∴BE = EC =21BC ， ∵BC = 2AB∴AB = BE = EC = DC∴∠BAE =∠BEA ，∠CED =∠CDE ∵四边形ABCD 是平行四边形 ∴∠B +∠C =︒180∴∠BAE +∠BEA+∠CED +∠CDE +∠B +∠C =︒360 ∴2（∠BEA +∠CED ）+︒180=︒360 ∴∠BEA +∠CED =︒90∴∠AED =-︒180（∠BEA +∠CED ）=︒=︒-︒9090180 其他证法正确的也给分。

【考点分析】一、证明两线段相等1.两全等三角形中对应边相等。

2.同一三角形中等角对等边。

3.等腰三角形顶角的平分线或底边的高平分底边。

4.平行四边形的对边或对角线被交点分成的两段相等。

5.直角三角形斜边的中点到三顶点距离相等。

6.线段垂直平分线上任意一点到线段两段距离相等。

7.角平分线上任一点到角的两边距离相等。

8.过三角形一边的中点且平行于第三边的直线分第二边所成的线段相等。

9.同圆（或等圆）中等弧所对的弦或与圆心等距的两弦或等圆心角、圆周角所对的弦相等。

10.圆外一点引圆的两条切线的切线长相等或圆内垂直于直径的弦被直径分成的两段相等。

11.两前项（或两后项）相等的比例式中的两后项（或两前项）相等。

12.两圆的内（外）公切线的长相等。

二、证明两角相等1.两全等三角形的对应角相等。

2.同一三角形中等边对等角。

3.等腰三角形中，底边上的中线（或高）平分顶角。

4.两条平行线的同位角、内错角或平行四边形的对角相等。

5.同角（或等角）的余角（或补角）相等。

6.同圆（或圆）中，等弦（或弧）所对的圆心角相等，圆周角相等，弦切角等于它所夹的弧对的圆周角。

7.圆外一点引圆的两条切线，圆心和这一点的连线平分两条切线的夹角。

8.相似三角形的对应角相等。

9.圆的内接四边形的外角等于内对角。

10.等于同一角的两个角相等三、证明两直线平行1.垂直于同一直线的各直线平行。

2.同位角相等，内错角相等或同旁内角互补的两直线平行。

3.平行四边形的对边平行。

4.三角形的中位线平行于第三边。

5.梯形的中位线平行于两底。

6.平行于同一直线的两直线平行。

7.一条直线截三角形的两边（或延长线）所得的线段对应成比例，则这条直线平行于第三边。

四、证明两直线互相垂直1.等腰三角形的顶角平分线或底边的中线垂直于底边。

2.三角形中一边的中线若等于这边一半，则这一边所对的角是直角。

3.在一个三角形中，若有两个角互余，则第三个角是直角。

4.邻补角的平分线互相垂直。

沪科版九年级数学中考复习四边形相关证明与计算强化训练（含答案）1.如图，在矩形ABCD中，对角线AC的垂直平分线分别与边AB和边CD的延长线交于点M，N，与边AD交于点E，垂足为O.(1) 求证：△AOM≌△CON；(2) 若AB＝3，AD＝6，请直接写出AE的长为________．2.如图，在▱ABCD中，E为BC的中点，连接AE并延长交DC的延长线于点F，连接BF，AC.若AD＝AF，求证：四边形ABFC是矩形．3.如图，在△ABC中，AB＝AC，D，E分别是线段BC，AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF.求证：(1) △BDE≌△FAE；(2) 四边形ADCF为矩形．4.如图，在菱形ABCD中，E，F分别是边AD，AB的中点．(1) 求证：△ABE≌△ADF；(2) 若BE＝√3，∠C＝60°，求菱形ABCD的面积5.如图，菱形ABCD的对角线AC，BD相交于点O，E是AD的中点，点F，G在AB上，EF ⊥AB，OG∥EF.(1) 求证：四边形OEFG是矩形；(2) 若AD＝10，EF＝4，求OE和BG的长．6.如图，过▱ABCD对角线AC与BD的交点E作两条互相垂直的直线，分别交边AB，BC，CD，DA于点P，M，Q，N.(1) 求证：△PBE≌△QDE；(2) 顺次连接点P，M，Q，N，求证：四边形PMQN是菱形．7.如图，在菱形ABCD中，将对角线AC分别向两端延长到点E，F，使得AE＝CF.连接DE，DF，BE，BF.求证：四边形BEDF是菱形．8.如图，▱ABCD的对角线AC，BD相交于点O，过点O作EF⊥AC，分别交AB，DC于点E，，求EF的长；F，连接AF，CE. (1) 若OE＝32(2) 判断四边形AECF的形状，并说明理由．9.如图，四边形ABCD是菱形，H为对角线AC的中点，点E在AB的延长线上，CE⊥AB，垂足为E，点F在AD的延长线上，CF⊥AD，垂足为F.(1) 若∠BAD＝60°，求证：四边形CEHF是菱形；(2) 若CE＝4，△ACE的面积为16，求菱形ABCD的面积．点M，N.(1) 求证：四边形BNDM是菱形；(2) 若BD＝24，MN＝10，求菱形BNDM的周长．11.如图，在▱ABCD中，BC＝2AB，AB⊥AC，分别在边BC，AD上的点E与点F关于AC对称，连接EF，AE，CF，DE.(1) 试判定四边形AECF的形状，并说明理由；(2) 求证：AE⊥DE.12.如图，在矩形ABCD中，O为对角线AC的中点，过点O作直线分别与矩形的边AD，BC 交于M，N两点，连接CM，AN.(1) 求证：四边形ANCM为平行四边形；(2) 若AD＝4，AB＝2，且MN⊥AC，求DM的长．GC，以DC，CF为邻边作菱形DCFE，连接CE.(1) 判断四边形CEDG的形状，并证明你的结论；(2) 连接DF，若BC＝√3，求DF的长．14.如图，在▱ABCD中，对角线AC与BD相交于点O，点E，F分别在BD和DB的延长线上，且DE＝BF，连接AE，CF.(1) 求证：△ADE≌△CBF.(2) 连接AF，CE.当BD平分∠ABC时，四边形AFCE是什么特殊四边形？请说明理由．15.如图，在正方形ABCD中，对角线AC，BD相交于点O，E，F分别是边BC，CD上的点，且∠EOF＝90°.求证：CE＝DF.(1) 求证：△BAE≌△CDE；(2) 求∠AEB的度数．17.如图，在正方形ABCD中，点E，F在AC上，且AF＝CE.求证：四边形BEDF是菱形．18.如图，在正方形ABCD中，G是BC边上任意一点(不与点B，C重合)，DE⊥AG于点E，BF∥DE，且交AG于点F.(1) 求证：AF－BF＝EF.(2) 四边形BFDE是否可能是平行四边形？如果可能，请指出此时点G的位置；如果不可能，请说明理由．形ABCE关于直线AE的对称图形为四边形ANME，延长ME交AB于点P，记四边形PADE 的面积为S.，求S的值；(1) 若DE＝√33(2) 设DE＝x，求S关于x的函数解析式．20.如图，在边长为4的正方形ABCD中，E为对角线AC上一动点(不与点A，C重合)，连接DE，作EF⊥DE交射线BA于点F，过点E作MN∥BC分别交CD，AB于点M，N，作射线DF交射线CA于点G.(1) 求证：EF＝DE；(2) 当AF＝2时，求GE的长．答案1.如图，在矩形ABCD中，对角线AC的垂直平分线分别与边AB和边CD的延长线交于点M，N，与边AD交于点E，垂足为O.(1) 求证：△AOM≌△CON；(2) 若AB＝3，AD＝6，请直接写出AE的长为________．证明：(1) ∵MN是AC的垂直平分线，∴AO＝CO，∠AOM＝∠CON＝90°.∵四边形ABCD是矩形，∴AB∥CD.∴∠M＝∠N.在△AOM和△CON中，{∠M=∠N，∠AOM=∠CON，AO=CO，∴△AOM≌△CON(AAS)2.如图，在▱ABCD中，E为BC的中点，连接AE并延长交DC的延长线于点F，连接BF，AC.若AD＝AF，求证：四边形ABFC是矩形．证明：∵四边形ABCD是平行四边形，∴AB∥CD.∴∠BAE＝∠CFE，∠ABE＝∠FCE.∵E 为BC的中点，∴EB＝EC.∴△ABE≌△FCE(AAS)．∴AB＝FC.∵AB∥CF，∴四边形ABFC 是平行四边形．∵AD＝BC，AD＝AF，∴BC＝AF.∴四边形ABFC是矩形3.如图，在△ABC中，AB＝AC，D，E分别是线段BC，AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF.求证：(1) △BDE≌△FAE；(2) 四边形ADCF为矩形．证明：(1) ∵AF∥BC，∴∠DBE＝∠AFE.∵E是线段AD的中点，∴DE＝AE.∵∠DEB＝∠AEF，∴△BDE≌△FAE(AAS)(2) ∵△BDE≌△FAE，∴DB＝AF.∵D是线段BC的中点，∴BD＝CD.∴AF＝CD.∵AF∥CD，∴四边形ADCF是平行四边形．∵AB＝AC，∴AD⊥BC.∴∠ADC＝90°.∴四边形ADCF为矩形4.如图，在菱形ABCD中，E，F分别是边AD，AB的中点．(1) 求证：△ABE≌△ADF；(2) 若BE＝√3，∠C＝60°，求菱形ABCD的面积证明：(1) ∵四边形ABCD是菱形，∴AB＝AD.∵E，F分别是边AD，AB的中点，∴AF＝AE.在△ABE和△ADF中，{AB=AD，∠A=∠A，AE=AF，∴△ABE≌△ADF(SAS)(2) 连接BD.∵四边形ABCD是菱形，∴AB＝AD，∠A＝∠C＝60°.∴△ABD是等边三角形.∵E是边AD的中点，∴BE⊥AD.∴∠ABE＝30°.∴AB＝2AE.∵在Rt△AEB中，AE2＋BE2＝AB2，BE＝√3，∴AE2＋(√3)2＝(2AE)2.∴AE＝1(负值舍去)．∴AB ＝2AE＝2.∴AD＝AB＝2.∴S菱形ABCD＝AD·BE＝2×√3＝2√35.如图，菱形ABCD的对角线AC，BD相交于点O，E是AD的中点，点F，G在AB上，EF ⊥AB，OG∥EF.(1) 求证：四边形OEFG是矩形；(2) 若AD＝10，EF＝4，求OE和BG的长．证明：(1) ∵四边形ABCD是菱形，∴BD⊥AC，∠DAO＝∠BAO，OB＝OD.∵E是AD的中点，∴AE＝OE＝DE＝12AD.∴∠EAO＝∠AOE.∴∠BAO＝∠AOE.∴OE∥FG.∵OG∥EF，∴四边形OEFG是平行四边形．∵EF⊥AB，∴∠EFG＝90°.∴四边形OEFG是矩形(2) ∵四边形ABCD是菱形，∴BD⊥AC，AB＝AD＝10.∴∠AOD＝90°.∵E是AD的中点，∴OE＝AE＝12AD＝5.由(1)，知四边形OEFG是矩形，∴FG＝OE＝5.∵AE＝5，EF＝4，∴AF＝√AE2−EF2＝3.∴BG＝AB－AF－FG＝10－3－5＝26.如图，过▱ABCD对角线AC与BD的交点E作两条互相垂直的直线，分别交边AB，BC，CD，DA于点P，M，Q，N.(1) 求证：△PBE≌△QDE；(2) 顺次连接点P，M，Q，N，求证：四边形PMQN是菱形．证明：(1) ∵四边形ABCD是平行四边形，∴EB＝ED，AB∥CD.∴∠EBP＝∠EDQ.在△PBE和△QDE中，{∠EBP=∠EDQ，EB=ED，∠BEP=∠DEQ，∴△PBE≌△QDE(ASA)(2) ∵△PBE≌△QDE，∴EP＝EQ.同理，可证△BME≌△DNE(ASA)，∴EM＝EN.∴四边形PMQN是平行四边形．∵PQ⊥MN，∴四边形PMQN是菱形7.如图，在菱形ABCD中，将对角线AC分别向两端延长到点E，F，使得AE＝CF.连接DE，DF，BE，BF.求证：四边形BEDF是菱形．证明：∵四边形ABCD是菱形，∴AD∥BC，CD＝CB＝DA＝BA，∠DCA＝∠BCA.∴∠DCF ＝∠BCF.∵CF＝CF，∴△CDF≌△CBF(SAS)．∴DF＝BF.∵AD∥BC，∴∠DAC＝∠BCA.∴∠DAE＝∠BCF.∵AE＝CF，DA＝BC，∴△DAE≌△BCF(SAS)．∴DE＝BF.同理，可证△DCF≌△BAE(SAS)，∴DF＝BE.∴四边形BEDF是平行四边形．∵DF＝BF，∴▱BEDF是菱形8.如图，▱ABCD的对角线AC，BD相交于点O，过点O作EF⊥AC，分别交AB，DC于点E，F ，连接AF ，CE. (1) 若OE ＝32，求EF 的长；(2) 判断四边形AECF 的形状，并说明理由．证明：(1) ∵ 四边形ABCD 是平行四边形，∴ AB ∥CD ，AO ＝CO.∴ ∠EAO ＝∠FCO.又∵ ∠AOE ＝∠COF ，∴ △AOE ≌△COF(ASA)．∴ OE ＝OF ＝32.∴ EF ＝2OE ＝3(2) 四边形AECF 是菱形理由：∵ △AOE ≌△COF ，∴ AE ＝CF.又∵ 在▱ABCD 中，AE ∥CF ，∴ 四边形AECF 是平行四边形．又∵ EF ⊥AC ，∴ ▱AECF 是菱形．9.如图，四边形ABCD 是菱形，H 为对角线AC 的中点，点E 在AB 的延长线上，CE ⊥AB ，垂足为E ，点F 在AD 的延长线上，CF ⊥AD ，垂足为F. (1) 若∠BAD ＝60°，求证：四边形CEHF 是菱形；(2) 若CE ＝4，△ACE 的面积为16，求菱形ABCD 的面积．证明：(1) ∵ 四边形ABCD 是菱形，∠BAD ＝60°，∴ ∠EAC ＝∠FAC ＝30°.又∵ CE ⊥AB ，CF ⊥AD ，∴ CE ＝CF ＝12AC.∵ H 为对角线AC 的中点，∴ EH ＝FH ＝12AC.∴ CE ＝CF ＝EH ＝FH.∴ 四边形CEHF 是菱形(2) ∵ CE ⊥AB ，CE ＝4，△ACE 的面积为16，∴ 12AE ×4＝16.∴ AE ＝8.设AB ＝x ，则BE ＝8－x.∵ 四边形ABCD 是菱形，∴ AB ＝BC ＝x.在Rt △BEC 中，由勾股定理，得42＋(8－x)2＝x 2，解得x ＝5，即AB ＝5.∴ S 菱形ABCD ＝AB ·CE ＝5×4＝2010.如图，在四边形ABCD 中，AD ∥BC ，对角线BD 的垂直平分线与边AD ，BC 分别相交于点M ，N.(1) 求证：四边形BNDM 是菱形；(2) 若BD ＝24，MN ＝10，求菱形BNDM 的周长．证明：(1) ∵ AD ∥BC ，∴ ∠DMO ＝∠BNO.∵ MN 是对角线BD 的垂直平分线，∴ OB ＝OD ，MN ⊥BD.在△MOD 和△NOB 中，{∠DMO =∠BNO ，∠MOD =∠NOB ，OD =OB ，∴ △MOD ≌△NOB(AAS)．∴ OM ＝ON.∵ OB ＝OD ，∴ 四边形BNDM 是平行四边形．∵ MN ⊥BD ，∴ 四边形BNDM 是菱形 (2) ∵ 四边形BNDM 是菱形，BD ＝24，MN ＝10，∴ BM ＝BN ＝DM ＝DN ，OB ＝12BD ＝12，OM ＝12MN ＝5.在Rt △BOM 中，由勾股定理，得BM ＝√OM 2+OB 2＝√52+122＝13，∴ 菱形BNDM 的周长为4BM ＝4×13＝5211.如图，在▱ABCD 中，BC ＝2AB ，AB ⊥AC ，分别在边BC ，AD 上的点E 与点F 关于AC 对称，连接EF ，AE ，CF ，DE.(1) 试判定四边形AECF 的形状，并说明理由； (2) 求证：AE ⊥DE.证明：(1) 四边形AECF 是菱形理由：∵ 四边形ABCD 是平行四边形，∴ AD ∥BC.∴ ∠OAF ＝∠OCE.∵ 点E 与点F 关于AC 对称，∴ AE ＝AF ，CE ＝CF ，OE ＝OF.在△AOF 和△COE 中，{∠OAF =∠OCE ，∠AOF =∠COE ，OF =OE ，∴ △AOF≌△COE(AAS).∴ AF ＝CE.∴ AE ＝AF ＝CE ＝CF.∴ 四边形AECF 是菱形．(2) ∵ BC ＝2AB ，AB ⊥AC ，∴ ∠ACB ＝30°.∴ ∠B ＝60°.∵ AE ＝CE ，∴ ∠EAC ＝∠ACB ＝30°.∴ ∠BAE ＝90°－30°＝60°＝∠B.∴ △ABE 是等边三角形．∴ AE ＝AB ＝BE ，∠AEB ＝60°.∴ ∠AEC ＝120°.∵ 四边形ABCD 是平行四边形，∴ AB ∥CD ，AB ＝CD.∴ ∠DCE ＝180°－∠B ＝120°.又∵ CE ＝AE ，∴ CE ＝BE ＝12BC ＝AB ＝CD.∴ ∠CED ＝∠CDE ＝30°.∴ ∠AED ＝120°－30°＝90°.∴ AE ⊥DE12.如图，在矩形ABCD 中，O 为对角线AC 的中点，过点O 作直线分别与矩形的边AD ，BC交于M ，N 两点，连接CM ，AN.(1) 求证：四边形ANCM 为平行四边形；(2) 若AD ＝4，AB ＝2，且MN ⊥AC ，求DM 的长．证明：(1) ∵ 在矩形ABCD 中，O 为对角线AC 的中点，∴ AD ∥BC ，AO ＝CO.∴ ∠OAM ＝∠OCN ，∠OMA ＝∠ONC.在△AOM和△CON 中，{∠OAM =∠OCN ，∠OMA =∠ONC ，AO =CO ，∴ △AOM ≌△CON(AAS)．∴ AM ＝CN.∵ AM ∥CN ，∴ 四边形ANCM 为平行四边形(2) ∵ 在矩形ABCD 中，AD ＝BC ，由(1)，知AM ＝CN ，∴ DM ＝BN. ∵ 四边形ANCM 为平行四边形，MN ⊥AC ，∴ ▱ANCM 为菱形．∴ AM ＝AN ＝NC ＝AD －DM.∴ 在Rt △ABN 中，根据勾股定理，得AN 2＝AB 2 ＋BN 2.∴ (4－DM)2＝22＋DM 2.∴ DM ＝3213.如图，四边形ABCD 为矩形，G 是对角线BD 的中点，连接GC 并延长至点F ，使CF ＝GC ，以DC ，CF 为邻边作菱形DCFE ，连接CE.(1) 判断四边形CEDG 的形状，并证明你的结论； (2) 连接DF ，若BC ＝√3，求DF 的长．证明：(1) 四边形CEDG 是菱形∵ 四边形ABCD 为矩形，∴ ∠BCD ＝90°.∵ 在Rt △BCD 中，G 是BD 的中点，∴ GC ＝12BD＝GD ＝BG.∵ 四边形DCFE 是菱形，∴ CF ＝DE ，DE ∥CF ，即DE ∥GC.∵ CF ＝GC ，∴ DE ＝GC.∴ 四边形CEDG 是平行四边形．又∵ GC ＝GD ，∴ ▱CEDG 是菱形(2) 设DF 交CE 于点N.∵ 四边形DCFE 是菱形，∴ DF ⊥CE ，DF ＝2DN ，DC ＝CF ＝DE.∵ CF ＝GC ，∴ DC ＝BG ＝GD.∵ 在Rt △BCD 中，DC 2＋(√3)2＝(2DC)2.∴ DC ＝1.∵ 四边形CEDG 是菱形，∴ DE ＝CE.∴ DE ＝CE ＝DC.∴ △DCE 是等边三角形．∴ ∠DCE ＝60°.∴ 在Rt △DNC 中，∠CDN ＝30°.∴ CN ＝12DC ＝12.∴ DN ＝√DC 2−CN 2＝√32.∴ DF ＝2×√32＝√314.如图，在▱ABCD中，对角线AC与BD相交于点O，点E，F分别在BD和DB的延长线上，且DE＝BF，连接AE，CF.(1) 求证：△ADE≌△CBF.(2) 连接AF，CE.当BD平分∠ABC时，四边形AFCE是什么特殊四边形？请说明理由．证明：(1) ∵四边形ABCD是平行四边形，∴AD＝CB，AD∥BC.∴∠ADB＝∠CBD.∴∠ADE＝∠CBF.在△ADE和△CBF中，{AD=CB，∠ADE=∠CBF，DE=BF，∴△ADE≌△CBF(SAS)(2) 当BD平分∠ABC时，四边形AFCE是菱形理由：∵BD平分∠ABC，∴∠ABD＝∠CBD.∵四边形ABCD是平行四边形，∴OA＝OC，OB＝OD，AD∥BC.∴∠ADB＝∠CBD.∴∠ABD＝∠ADB.∴AB＝AD.∴▱ABCD是菱形．∴AC⊥BD，即AC⊥EF.∵DE＝BF，∴OD＋DE＝OB＋BF，即OE＝OF.又∵OA＝OC，∴四边形AFCE是平行四边形．∵AC⊥EF，∴四边形AFCE是菱形．15.如图，在正方形ABCD中，对角线AC，BD相交于点O，E，F分别是边BC，CD上的点，且∠EOF＝90°.求证：CE＝DF.证明：∵四边形ABCD为正方形，∴OC＝OD，∠OCE＝∠ODF＝45°，∠COD＝90°.∴∠DOF＋∠COF＝90°.∵∠EOF＝90°，即∠COE＋∠COF＝90°，∴∠COE＝∠DOF.∴△COE ≌△DOF(ASA)．∴CE＝DF16.如图，在正方形ABCD的外侧，作等边三角形ADE，连接BE，CE.(1) 求证：△BAE≌△CDE；(2) 求∠AEB的度数．证明：(1) ∵△ADE为等边三角形，∴AD＝AE＝DE，∠EAD＝∠EDA＝60°.∵四边形ABCD 为正方形，∴AB＝AD＝CD，∠BAD＝∠CDA＝90°.∴∠EAB＝∠EDC＝150°.在△BAE和△CDE中，{AB=DC，∠EAB=∠EDC，AE=DE，∴△BAE≌△CDE(SAS)(2) ∵AB＝AD，AD＝AE，∴AB＝AE.∴∠ABE＝∠AEB.∵∠EAB＝150°，∴∠AEB＝12×(180°－150°)＝15°17.如图，在正方形ABCD中，点E，F在AC上，且AF＝CE.求证：四边形BEDF是菱形．证明：∵四边形ABCD是正方形，∴AB＝AD＝CD＝BC，∠DAE＝∠BAE＝∠BCF＝∠DCF＝45°.在△ABE和△ADE中，{AB=AD，∠BAE=∠DAE，AE=AE，∴△ABE≌△ADE(SAS)．∴BE＝DE.同理，可证△BFC≌△DFC，∴BF＝DF.在△ABF和△CBE中，{AB=CB，∠BAF=∠BCE，AF=CE，∴△ABF≌△CBE(SAS)．∴BF＝BE.∴BE＝BF＝DE＝DF.∴四边形BEDF是菱形18.如图，在正方形ABCD中，G是BC边上任意一点(不与点B，C重合)，DE⊥AG于点E，BF∥DE，且交AG于点F.(1) 求证：AF－BF＝EF.(2) 四边形BFDE是否可能是平行四边形？如果可能，请指出此时点G的位置；如果不可能，请说明理由．证明：(1) ∵ 四边形ABCD 是正方形，∴ AB ＝DA ，∠BAF ＋∠DAE ＝90°.∵ DE ⊥AG ，∴ ∠AED ＝∠GED ＝90°.∴ ∠DAE ＋∠ADE ＝90°.∴ ∠BAF ＝∠ADE.∵ BF ∥DE ，∴ ∠BFA ＝∠GED ＝∠AED.∴ △ABF ≌△DAE(AAS).∴ BF ＝AE.∴ AF －BF ＝AF －AE ＝EF (2) 四边形BFDE 不可能是平行四边形 理由：如图，连接AC ，BE ，DF.∵ 四边形ABCD 是正方形，∴ ∠BAD ＝90°，AC 平分∠BAD.∴ ∠DAC ＝45°.假设四边形BFDE 是平行四边形，∴ BF ＝DE.由(1)，得∠AED ＝90°，AE ＝BF ，∴ AE ＝DE.∴ ∠EAD ＝∠EDA ＝45°.此时点G 与点C 重合，这与“G 是BC 边上任意一点(不与点B ，C 重合)”矛盾，∴ 假设不成立，即四边形BFDE 不可能是平行四边形．19.如图，在矩形ABCD 中，AB ＝2，AD ＝1，E 为边CD 上的一点(不与点C ，D 重合)，四边形 ABCE 关于直线AE 的对称图形为四边形ANME ，延长ME 交AB 于点P ，记四边形PADE 的面积为S.(1) 若DE ＝√33，求S 的值；(2) 设DE ＝x ，求S 关于x 的函数解析式．证明：(1) ∵ 四边形ABCD 是矩形，∴ ∠D ＝90°，AB ∥CD.∵ 在Rt △ADE 中，AD ＝1，DE ＝√33，∴ AE ＝√AD 2+DE 2＝2√33.∴ AE ＝2DE.∴ ∠EAD ＝30°.∴ ∠AED ＝90°－∠EAD ＝60°.∵ AB ∥CD ，∴ ∠BAE ＝∠AED ＝60°.∵ 四边形ABCE 关于直线AE 的对称图形为四边形ANME ，∴ ∠AEC ＝∠AEM.∵ ∠PEC ＝∠DEM ，∴ ∠AEP ＝∠AED ＝60°.∴ ∠AEP ＝∠BAE.∴ PE ＝PA.∴ △APE 为等边三角形．∴ PA ＝AE ＝2√33.∴ S ＝12 (DE ＋PA)×AD ＝12×(√33+2√33)×1＝√32(2) 过点E 作EF ⊥AB ，垂足为F.由(1)，可知∠AEP ＝∠AED ＝∠PAE ，∴ AP ＝PE.设AP ＝PE ＝a ，AF ＝DE ＝x ，则PF ＝|a －x|，EF ＝AD ＝1. ∴ 在Rt △PEF 中，|a －x|2＋1＝a 2，解得a ＝x 2+12x.∴ S ＝S △ADE ＋S △APE ＝12x ×1＋12×x 2+12x×1＝3x 2+14x20.如图，在边长为4的正方形ABCD 中，E 为对角线AC 上一动点(不与点A ，C 重合)，连接DE ，作EF ⊥DE 交射线BA 于点F ，过点E 作MN ∥BC 分别交CD ，AB 于点M ，N ，作射线DF 交射线CA 于点G. (1) 求证：EF ＝DE ；(2) 当AF ＝2时，求GE 的长．证明：(1) ∵ 四边形ABCD 是正方形，AC 是对角线，∴ AB ∥CD ，AB ＝DC ＝BC ，∠DCB ＝∠B ＝90°，∠ECM ＝12∠DCB ＝45°.∵ MN ∥BC ，∠BCM ＝90°，∴ ∠NMC ＋∠BCM ＝180°，∠MNB ＋∠B ＝180°.∴ ∠NMC ＝90°，∠MNB ＝90°.∴ ∠MEC ＝∠MCE ＝45°，∠DME ＝∠ENF ＝90°.∴ MC ＝ME.∵ AB ∥CD ，MN ∥BC ，∴ 四边形MNBC 为平行四边形．∴ MN ＝BC.∴ DC ＝MN.∴ DC －MC ＝MN －ME ，即DM ＝EN.∵ DE ⊥EF ，∴ ∠DEF ＝90°.∴ ∠DEM ＋∠FEN ＝90°.∵ ∠EDM ＋∠DEM ＝90°，∴ ∠EDM ＝∠FEN.在△DME 和△ENF 中，{∠EDM =∠FEN ，DM =EN ，∠DME =∠ENF ，∴ △DME ≌△ENF(ASA).∴ EF＝DE(2) 当点F 在线段AN 上时，由(1)，知△DME ≌△ENF ，∴ ME ＝NF.∵ 四边形MNBC 是平行四边形，∴ MC ＝BN.又∵ ME ＝MC ，AB ＝4，AF ＝2，∴ BN ＝MC ＝NF ＝1.∵ ∠EMC ＝90°，∴ CE ＝√2.∵ AF ∥CD ，∴ △DGC ∽△FGA.∴ CDAF ＝CGAG .∴ 42＝CGAG .∵ AB ＝BC ＝4，∠B ＝90°，∴ AC ＝4√2.∵ AC ＝AG ＋GC ，∴ AG ＝4√23，CG ＝8√23.∴ GE ＝CG －CE ＝8√23−√2＝5√23；当点F 在线段NA 的延长线上时，如图，同理，可得FN ＝BN.∵ AF ＝2，AB ＝4，∴ AN ＝1.∵ AB ＝BC ＝4，∠B ＝90°，∴ AC ＝4√2.∵ AF ∥CD ，∴ △GAF ∽△GCD.∴ AFCD ＝GAGC .∴ 24＝AG+4√2.∴ AG ＝4√2.∵ AN ＝NE ＝1，∠ENA ＝90°，∴ AE ＝√2.∴ GE ＝AG ＋AE ＝4√2+√2＝5√2.综上所述，GE 的长为5√23或5√2。

中考数学模拟题汇总《平行四边形的判定与证明》专项练习(附答案解析)一、综合题1．如图，在Rt△ABC中，∠ACB=90°，点D、E分别是AB、BC的中点，点F在AC的延长线上，∠FEC=∠B．（1）求证：DE=CF；（2）若AC=6cm，AB=10cm，求四边形DCFE的面积．2．已知△ABC内接于⊙O，AB是⊙O的直径，OD∥AC，AD＝OC.（1）求证：四边形OCAD是平行四边形；（2）若AD与⊙O相切，求∠B.3．已知：如图，点D在ΔABC的边AB上，CF//AB，DF交AC于E，EA=EC．（1）如图1，求证：CD=AF；（2）如图2，若AD=BD，请直接写出和ΔBDC面积相等的三角形．4．如图，在四边形ABCD中，点E和点F是对角线AC上的两点，AE=CF，DF=BE，且DF//BE，过点C作CG⊥AB交AB的延长线于点G．（1）求证：四边形ABCD是平行四边形；（2）若tan∠CAB=25，∠CBG=45°，BC=4√2，则▱ABCD的面积是．5．已知，如图，E、F是四边形ABCD的对角线AC上的两点，AF=CE，DF=BE，DF∥BE．（1）求证：△AFD≌△CEB；（2）四边形ABCD是平行四边形吗？请说明理由．6．如图，▱ABCD中，AC，BD相交于点O，E，F分别是OA，OC的中点.（1）求证：BE=DF；（2）设ACBD=k，当k为何值时，四边形DEBF是矩形？请说明理由.7．如图，在ΔABC中，点D、E、F分别在AB、AC、BC上，DE // BC，EF // AB．（1）求证：ΔADE∽ΔEFC；（2）如果AB=6，AD=4，求SΔADESΔEFC的值．8．如图，已知平行四边形ABCD，过A点作AM⊥BC于M，交BD于E，过C点作CN⊥AD于N，交BD于F，连接AF、CE．（1）求证：四边形AECF为平行四边形；（2）当AECF为菱形，M点为BC的中点时，求AB：AE的值．BC，9．如图，等边△ABC的边长是4,D、E分别为AB、AC的中点，延长BC至点F，使CF=12连接CD和EF .（1）求证：DE=CF；（2）求EF的长.10．如图，在四边形ABCD中，AB∥CD，且AB＝2CD，E，F分别是AB，BC的中点，EF与BD交于点H.（1）求证：四边形DEBC是平行四边形；（2）若BD＝9，求DH的长.11．已知锐角△ABC内接于⊙O，AD⊥BC于点D，连接AO．（1）如图1，求证：∠BAO＝∠CAD；（2）如图2，CE⊥AB于点E，交AD于点F，过点O作OH⊥BC于点H，求证：AF＝2OH；，BC＝2√15，求AC的长．（3）如图3，在（2）的条件下，若AF＝AO，tan∠BAO＝1312．如图，抛物线y=x2+bx+c与x轴交于点A(−1，0)，B(5，0)，与y轴交于点C.（1）求抛物线的解析式和顶点D的坐标.（2）连结AD，点E是对称轴与x轴的交点，过E作EF∥AD交抛物线于点F（F在E的右侧），过点F作FG∥x轴交ED于点H，交AD于点G，求HF的长.13．如图，CD是⊙O的直径，点A是⊙O外一点，AD与⊙O相切于点D，点B是⊙O上一点（点B不与点C，D重合），连接AO，AB，BC .（1）当BC与AO满足什么位置关系时，AB是⊙O的切线？请说明理由；（2）在（1）的条件下，当∠DAO=度时，四边形AOCB是平行四边形.（x＞0）的图象经过点A、B，点B的坐标为（2，2）．过点A作AC⊥x轴，垂足14．如图，已知函数y= kx为C，过点B作BD⊥y轴，垂足为D，AC与BD交于点F．一次函数y=ax+b的图象经过点A、D，与x轴的负半轴交于点EOD，求a、b的值；（1）若AC= 32（2）若BC∥AE，求BC的长．15．如图，在四边形ABCD中，AB=CD，BF=DE，AE⊥BD，CF⊥BD，垂足分别为E，F．（1）求证：△ABE≌△CDF；（2）若AC与BD交于点O，求证：AO=CO．16．如图.在一次数学研究性学习中，小华将两个全等的直角三角形纸片Rt△ABC和Rt△DEF拼在一起，使点A与点F重合，点C与点D重合（如图），其中∠ACB=∠DFE=90°，发现四边形ABDE是平行四边形.如图，小华继续将图中的纸片Rt△DEF沿AC方向平移，连结AE，BD，当点F与点C重合时停止平移.（1）请问：四边形ABDE是平行四边形吗？说明理由.cm时，请判断四边形ABDE的形（2）如图，若BC=EF=6cm，AC=DF=8cm，当AF=92状，并说明理由.参考答案与解析1．【答案】（1）证明：在△CDE 和△ECF 中，∵∠ACB=∠ECF=90°，点D 、E 是分别是AB 、BC 的中点．∴CD=BD=AD ，∴∠B=∠DCE ，∠CED=∠ECF=90°， 又∵∠FEC=∠B ．．∠FEC=∠DCE ，又∵CE=EC ．∴△CDE ≌△ECF （ASA ），∴DE=CF ；（2）解：在Rt △ABC 中，∵∠ACB=90°，∴BC=√AB 2−AC 2=√102−62=8cm ， ∵点D 、E 分别是AB 、BC 的中点，∴DE ∥CF ，又DE=CF ， ∴四边形DCFE 是平行四边形，∴DE=12AC=12×6=3cm ，CE=12BC=12×8=4cm ， ∴S 四边形DCFE =DE ×CE=3×4=12cm ． 2．【答案】（1）证明：∵OA ＝OC ＝AD ， ∴∠OCA ＝∠OAC ，∠AOD ＝∠ADO ， ∵OD ∥AC ， ∴∠OAC ＝∠AOD ，∴180°﹣∠OCA ﹣∠OAC ＝180°﹣∠AOD ﹣∠ADO ， 即∠AOC ＝∠OAD ， ∴OC ∥AD ， ∵OD ∥AC ，∴四边形OCAD 是平行四边形；（2）解：∵AD 与⊙O 相切，OA 是半径， ∴∠OAD ＝90°， ∵OA ＝OC ＝AD ， ∴∠AOD ＝∠ADO ＝45°，∵OD∥AC，∴∠OAC＝∠AOD＝45°，∵AB是⊙O的直径，∴∠ACB＝90°，∴∠B＝45°.3．【答案】（1）证明：∵CF//AB∴∠DFC=∠ADF，∠DAC=∠ACF又∵EA=EC∴ΔADE≌ΔCFE(AAS)∴CF=AD又∵CF//AD∴四边形ADCF为平行四边形∴DC=AF（有一组对边平行且相等的四边形为平行四边形）（2）解：ΔADC，ΔADF，ΔCFD，ΔCFA∵AD=BD，∴SΔADC=SΔBDC (等底等高面积相等)∵四边形ADCF是平行四边形，∴SΔADC=SΔCDF=SΔADF=SΔACFF (等底等高面积相等) ．故与ΔBDC面积相等的三角形为：ΔADC，ΔADF，ΔCFD，ΔCFA．4．【答案】（1）证明：∵AE=CF，∴AE+EF=CF+EF，即AF=CE，∵DF//BE，∴∠DFA=∠BEC，∵DF=BE，∴ΔADF≅ΔCBE(SAS)，∴AD=CB，∠DAF=∠BCE，∴AD//CB，四边形ABCD是平行四边形（2）245．【答案】（1）证明：∵DF∥BE，∴∠DFA=∠BEC，在△ADF和△CBE中{DF=BE∠DFA=∠BECAF=CE，∴△AFD≌△CEB（SAS).（2）解：四边形ABCD是平行四边形，理由如下：∵△AFD≌△CEB，∴AD=CB，∠DAF=∠BCE，∴AD∥BC，∴四边形ABCD是平行四边形．6．【答案】（1）证明：如图，连接DE，BF，∵四边形ABCD是平行四边形，∴OA=OC，OB=OD，∵E，F分别是OA，OC的中点，∴OE=12OA=12OC=OF，∴四边形DEBF是平行四边形，∴BE=DF .（2）解：由（1）已证：四边形DEBF是平行四边形，要使平行四边形DEBF是矩形，则BD=EF，∵OE=12OA=12OC=OF，∴EF=OE+OF=12OA+12OC=OA=12AC，即AC=2EF，∴k=ACBD =2EFEF=2，故当k=2时，四边形DEBF是矩形. 7．【答案】（1）证明：∵DE//BC，EF//AB，∴∠A＝∠CEF，∠AED＝∠C，∴△ADE∽△EFC．（2）解：∵AB＝6，AD＝4，∴DB＝6－4＝2，∵DE//BC，EF//AB，∴四边形DBFE是平行四边形，∴EF＝DB=2，∵△ADE∽△EFC，SΔADE SΔEFC =(ADEF)2=(42)2=4．8．【答案】（1）证明∵四边形ABCD是平行四边形（已知），∴BC∥AD（平行四边形的对边相互平行）。

A B E C D 1 年中考数学复习同步练习（15）（四边形）1一、选择题：1．（08山东）只用下列图形不能镶嵌的是 （ ）A 、三角形B 、四边形C 、正五边形D 、正六边形2．若n 边形每个内角都等于150°，那么这个n 边形是 （ ）A 、九边形B 、十边形C 、十一边形D 、十二边形3．（08青海）一个多边形内角和是1080°，则这个多边形是 （ ）A 、六边形B 、七边形C 、八边形D 、九边形4．（08北京）若一个多边形的内角和等于720°，则这个多边形的边数是 （ ）A 、5B 、6C 、7D 、85．（08哈尔滨）某商店出售下列四种形状的地砖：①正三角形；②正方形；③正五边形；④正六边形．若只选购其中一种地砖镶嵌地面，可供选择的地砖共有 （ ）A 、1种B 、2种C 、3种D 、4种6．（08白银）如图，把矩形ABCD 沿EF 对折后使两部分重合，若∠1=50°，则AEF ∠= （ ）A 、110°B 、115°C 、120°D 、130°7．（08厦门）在平行四边形ABCD 中，∠B = 50°，那么下列各式中，不能．．成立的是（ ） A 、∠A=60° B 、∠A=120° C 、∠C+∠D=180° D 、∠C+∠A=180°8．下列条件中，能判定四边形是平行四边形的是 （ ）A 、一组对边相等B 、对角线互相平分C 、一组对角相等D 、对角线互相垂直 9．（08贵阳）如图，在平行四边形ABCD 中，E 是AB 延长线上的一点，若60A ∠=o，则1∠的度数为 （ ） A 、120° B 、60° C 、45° D 、30°10．（08义乌）下列命题中，真命题是 （ ）A 、两条对角线垂直的四边形是菱形B 、对角线垂直且相等的四边形是正方形C 、两条对角线相等的四边形是矩形D 、两条对角线相等的平行四边形是矩形二、填空题：11．（07嘉兴）四边形的内角和等于__________；12．内角和为1440°的多边形是 ；13．一个正多边形的每一个外角都等于72°，则这个多边形的边数是_________；14．矩形的两条对角线的一个交角为60°，两条对角线的长度的和为8cm ，则这个矩形的一条较短边为 cm ；A B C EFG 15．（08肇庆）边长为5cm 的菱形，一条对角线长是6cm ，则另一条对角线的长是 ；16．若正方形的一条对角线的长为2cm ，则这个正方形的面积为 ；三、解答题：17．（08西宁）如图，已知：ABCD Y 中，BCD ∠的平分线CE 交边AD 于E ，ABC ∠ 的平分线BG 交CE 于F ，交AD 于G ．求证：AE DG =．18．（08乌鲁木齐）如图，在四边形ABCD 中，点E 是线段AD 上的任意一点（E 与A D ，不重合），G F H ，，分别是BE BC CE ，，的中点．（1）证明四边形EGFH 是平行四边形；（2）在（1）的条件下，若EF BC ⊥，且12EF BC =，证明平行四边形EGFH 是正方形．B G A E F H D C年中考数学复习同步练习（15）（四边形）1一、15．（1）∵E是AB中点，∴AB=2BE，AB=2CD，∴CD=EB，又AB∥CD，∴四边形CBED是平行四边形，∴CB∥DE，∴DEM BFMEDM FBM∠=∠⎧⎨∠=∠⎩，∴△EDM∽△FBM．（2）△EDM∽△FBM，∴DM DE BM BF=，•∴F是BC中点，DE=2FB，∴DM=2BM，∴BM=13DB=3。

2.4 证明（3）同步练习考标要求1 能有综合法证明与平行四边形的性质、判定以及三角形中位线有关的问题，体会严谨证明的必要性。

2 进一步培养表达能力。

一 填空题一 填空题（每小题5分，共25分）1 （2007乐山）如图（1），在平面四边形ABCD 中，CE AB ⊥，E 为垂足．如果125A =∠，则BCE =∠ （ ） Ａ．55Ｂ．35Ｃ．25Ｄ．302（2007嘉兴）如图，在菱形ABCD 中，不一定成立的是（ ）（A ）四边形ABCD 是平行四边形（B ）AC ⊥BD （C ）△ABD 是等边三角形 （D ）∠CAB ＝∠CAD 3（2007日照）如图，在周长为20cm 的□ABCD 中，AB ≠AD ，AC 、BD 相交于点O ，OE ⊥BD 交AD 于E ，则△ABE 的周长为(A)4c m (B)6cm(C)8cm (D)10cm4．（2007连云港）如图，在△ABC 中，点E ，D ，F 分别在边 AB ，BC 、CA 上，且DE ∥CA ，DF ∥BA 。

下列四个判断中， 不正确．．．的是（ ） A ．四边形AEDF 是平行四边形B ．如果∠BAC =90°，那么四边形AEDF 是矩形 C ．如果AD 平分∠BAC ，那么四边形AEDF 是菱形 D ．如果AD ⊥BC 且AB=AC ，那么四边形AEDF 是菱形5 在△ABC 中，DE 是中位线，∠B 的平分线交DE 于F,则△ABF 一定是（ ）A 锐角三角形B 直角三角形C 钝角三角形D 直角三角形 或钝角三角形A EB CD1题图C2题图FED CB A4题图二 填空题（每小题5分，共25分）6 △ABC 与平行四边形ABCD 如图放置，点D 、G 分别在边AB 、AC 上，点E 、F 在边BC 上，已知BE=DE ，CF=FG,则∠A 的度数是_____7如图，平行四边形ABCD 中，点E 在AD 上，以BE 为折痕，将△ABE 向上翻折，点A 正好落在CD 上的点F,若△FDE 的周长为10,△FCB 的周长为24，则FC 的长为_______8如图，在菱形A BCD 中，对角线AC 、BD 相交于点O,E 为BC 中， 则与OE 相等的线段有____________________9 如图，矩形ABCD 中，，将∠D 与∠C 分别沿着过A 和B 的直线AE 、AF 向内折叠，使点D 、C 重合于点G ，且∠EGF=∠AGB ，则AD=________.10 如图，有一块边长为4的正方形塑料模板ABCD ，A 点，两直角边分别与CD 交于点F ，与CB 的延长线交于点E ，则四边形___________三 解答题（12×3+14=50）11（2007年哈尔滨）已知：如图，点E 为正方形ABCD 的边AD 上一点，连接BE ，过点AH ⊥BE,垂足为H ，延长AH 交CD 于点F 。