大学物理静电场的高斯定理

第四章 电 场一、常见带电体的场强、电势分布2）均匀带电球面（球面半径 ）的电场：3）无限长均匀带电直线（电荷线密度为）: E = ，方向：垂直于带电直线。

2r( rR ) 4）无限长均匀带电圆柱面（电荷线密度为）:E =2r (rR )5）无限大均匀带电平面（电荷面密度为）的电场: E =/20 ，方向：垂直于平面。

二、静电场定理 1、高斯定理：e = ÑE v dS v = q 静电场是有源场。

Sq 指高斯面内所包含电量的代数和；E 指高斯面上各处的电场强度，由高斯面内外的全 部电荷产生； Ñ E vdS v 指通过高斯面的电通量，由高斯面内的电荷决定。

2、环路定理： Ñ E v dl v =0 静电场是保守场、电场力是保守力，可引入电势能三、求场强两种方法1、利用场强势叠加原理求场强 分离电荷系统： E v = E v i ；连续电荷系统： E v = dE v i =12、利用高斯定理求场强 四、求电势的两种方法n1、利用电势叠加原理求电势 分离电荷系统：U =U i ；连续电荷系统： U = dU i =1电势零点v v 2、利用电势的定义求电势 U =电势零点Edl五、应用vv b点电荷受力： F = qE电势差： U ab =U a -U b = b EdraE =1 qU =q4r 24r1）点电荷：E =0 (rR ) q2 (rR ) 4r 2U =q (r R ) 4r q (r R ) 4Ra 点电势能：W a = qU a由 a 到 b 电场力做功等于电势能增量的负值 A ab = -W = -（W b -W a ）六、导体周围的电场1、静电平衡的充要条件： 1）、导体内的合场强为 0，导体是一个等势体。

2）、导体表面的场强处处垂直于导体表面。

E v ⊥表面。

导体表面是等势面。

2、静电平衡时导体上电荷分布： 1）实心导体： 净电荷都分布在导体外表面上。

大学物理电磁学知识点总结篇一：大学物理电磁学知识点总结大学物理电磁学总结一、三大定律库仑定律：在真空中，两个静止的点电荷q1和q2之间的静电相互作用力与这两个点电荷所带电荷量的乘积成正比，与它们之间距离的平方成反比，作用力的方向沿着两个点电荷的连线，同号电荷相斥，异号电荷相吸。

uuurqqurF21=k122errurur高斯定理：a)静电场：Φe=EdS=∫s∑qiiε0（真空中）b)稳恒磁场：Φm=uurrBdS=0∫s环路定理：a)静电场的环路定理：b)安培环路定理：二、对比总结电与磁∫LurrLEdl=0∫urrBdl=0∑Ii（真空中）L电磁学静电场稳恒磁场稳恒磁场电场强度：E磁感应强度：B定义：B=ururF定义：E=(N/C)q0基本计算方法：1、点电荷电场强度：E=urrurdF（dF=Idl×B）(T)Idlsinθ方向：沿该点处静止小磁针的N极指向。

基本计算方法：urqurer4πε0r21ruruIdl×er0r1、毕奥-萨伐尔定律：dB=24πr2、连续分布的电流元的磁场强度：2、电场强度叠加原理：urnur1E=∑Ei=4πε0i=1rqiuueri∑r2i=1inrururur0Idl×erB=∫dB=∫4πr23、安培环路定理（后面介绍）4、通过磁通量解得（后面介绍） 3、连续分布电荷的电场强度：urρdVurE=∫ev4πεr2r0urdSururλdlurE=∫er,E=∫es4πεr2l4πεr2r004、高斯定理（后面介绍）5、通过电势解得（后面介绍）几种常见的带电体的电场强度公式：几种常见的磁感应强度公式：1、无限长直载流导线外：B=2、圆电流圆心处：电流轴线上：B=ur1、点电荷：E=qurer4πε0r210I2R0I2πr2、均匀带电圆环轴线上一点：urE=B=3、圆rqxi22324πε0(R+x)R2IN2(x2+R2)3210α23、均匀带电无限大平面：E=2ε0（N为线圈匝数）4、无限大均匀载流平面：B=4、均匀带电球壳：E=0(r<R)（α是流过单位宽度的电流）urE=qurer(r>R)4πε0r25、无限长密绕直螺线管内部：B=0nI（n是单位长度上的线圈匝数）6、一段载流圆弧线在圆心处：B=（是弧度角，以弧度为单位）7、圆盘圆心处：B=rurqr(rR)20I4πR0ωR2（是圆盘电荷面密度，ω圆盘转动的角速度）6、无限长直导线：E=λ2πε0xλ0(r>R)2πε0r7、无限长直圆柱体：E=E=λr(r<R)4πε0R2电场强度通量：N·m2·c-1）（磁通量：wb）（sΦe=∫dΦe=∫EcosθdS=∫ssururEdS通量uurrΦm=∫dΦm=∫BdS=∫BcosθdSsss若为闭合曲面：Φe=∫sururEdS若为闭合曲面：uurrΦm=BdS=BcosθdS∫∫ss均匀电场通过闭合曲面的通量为零。

第四章 电 场一、常见带电体的场强、电势分布 1）点电荷：2014q E r πε=04q U rπε=2）均匀带电球面（球面半径R ）的电场：200()()4r R E qr R r πε≤⎧⎪=⎨>⎪⎩00()4()4qr R r U q r R R πεπε⎧>⎪⎪=⎨⎪≤⎪⎩3）无限长均匀带电直线（电荷线密度为λ）:02E rλπε=，方向：垂直于带电直线。

4）无限长均匀带电圆柱面（电荷线密度为λ）: 00()()2r R E r R rλπε≤⎧⎪=⎨>⎪⎩5）无限大均匀带电平面（电荷面密度为σ）的电场:0/2E σε=，方向：垂直于平面。

二、静电场定理 1、高斯定理：0e Sq E dS φε=⋅=∑⎰静电场是有源场。

q ∑指高斯面内所包含电量的代数和；E指高斯面上各处的电场强度，由高斯面内外的全部电荷产生；SE dS ⋅⎰指通过高斯面的电通量，由高斯面内的电荷决定。

2、环路定理：0lE dl⋅=⎰ 静电场是保守场、电场力是保守力，可引入电势能三、求场强两种方法1、利用场强势叠加原理求场强 分离电荷系统：1ni i E E ==∑；连续电荷系统：E dE =⎰2、利用高斯定理求场强 四、求电势的两种方法1、利用电势叠加原理求电势 分离电荷系统：1nii U U==∑；连续电荷系统： U dU =⎰2、利用电势的定义求电势 rU E dl =⋅⎰电势零点五、应用点电荷受力：F qE = 电势差： bab a b aU U U E dr =-=⋅⎰a由a 到b六、导体周围的电场1、静电平衡的充要条件： 1）、导体内的合场强为0，导体是一个等势体。

2）、导体表面的场强处处垂直于导体表面。

E ⊥表表面。

导体表面是等势面。

2、静电平衡时导体上电荷分布： 1）实心导体： 净电荷都分布在导体外表面上。

2）导体腔内无电荷： 电荷都分布在导体外表面，空腔内表面无电荷。

3）导体腔内有电荷+q ，导体电量为Q ：静电平衡时，腔内表面有感应电荷-q ，外表面有电荷Q ＋q 。

第四章 电 场一、常见带电体的场强、电势分布 1)点电荷:2014q E r πε=04qU rπε=2)均匀带电球面(球面半径R)的电场:200()()4r R E qr R r πε≤⎧⎪=⎨>⎪⎩00()4()4qr R r U q r R R πεπε⎧>⎪⎪=⎨⎪≤⎪⎩3)无限长均匀带电直线(电荷线密度为λ):02E rλπε=,方向:垂直于带电直线。

4)无限长均匀带电圆柱面(电荷线密度为λ): 00()()2r R E r R rλπε≤⎧⎪=⎨>⎪⎩5)无限大均匀带电平面(电荷面密度为σ)的电场:0/2E σε=,方向:垂直于平面。

二、静电场定理 1、高斯定理:0e SqE dS φε=⋅=∑⎰v v Ñ 静电场就是有源场。

q ∑指高斯面内所包含电量的代数与;E ϖ指高斯面上各处的电场强度,由高斯面内外的全部电荷产生;S E dS ⋅⎰v v Ñ指通过高斯面的电通量,由高斯面内的电荷决定。

2、环路定理:0lE dl ⋅=⎰vv Ñ 静电场就是保守场、电场力就是保守力,可引入电势能三、求场强两种方法1、利用场强势叠加原理求场强 分离电荷系统:1n i i E E ==∑v v ;连续电荷系统:E dE =⎰v v2、利用高斯定理求场强 四、求电势的两种方法1、利用电势叠加原理求电势 分离电荷系统:1nii U U==∑;连续电荷系统: U dU =⎰2、利用电势的定义求电势 rU E dl =⋅⎰v v 电势零点五、应用点电荷受力:F qE =v v 电势差: bab a b aU U U E dr =-=⋅⎰a 点电势能由a 到b六、导体周围的电场1、静电平衡的充要条件: 1)、导体内的合场强为0,导体就是一个等势体。

2)、导体表面的场强处处垂直于导体表面。

E ⊥v表表面。

导体表面就是等势面。

2、静电平衡时导体上电荷分布: 1)实心导体: 净电荷都分布在导体外表面上。

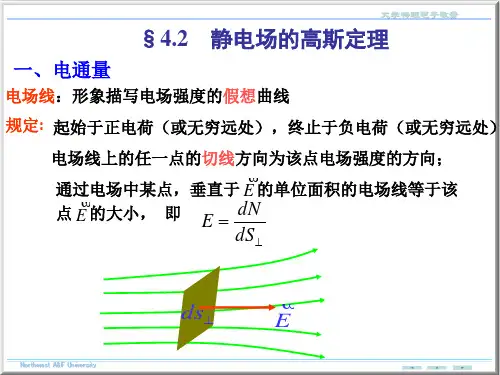
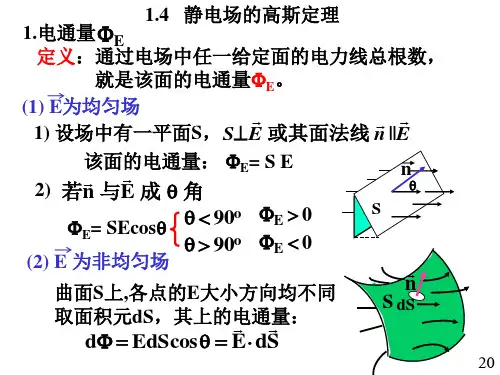
《大学物理》作业 No .2 静电场中的高斯定理班级 ___________ 学号 ___________ 姓名 ___________ 成绩 ________ 说明：字母为黑体者表示矢量内容提要1.电通量⎰⋅=Φs d S E 电场强度穿过任意曲面的电通量在数值上等于穿过该面的电场线条数；对于封闭曲面，电场线穿出规定电通量为正。

2.真空中高斯定理∑⎰=⋅内q d s 01εS E（1）.高斯定理表明穿过封闭曲面的电通量仅与面内电荷有关，面外电荷分布对该通量无贡献；(2).空间任意一点（包括高斯面上各点）的电场由高斯面内外所有场源电荷共同决定；（3）.高斯定理是静电学的一条重要基本定理，反映了静电场的有源性，同时该定理又是从库仑定律导出的，反映了库仑平方反比律的正确性；（4）.运用高斯定理可以方便地求解具有某些对称性分布的电场，根据电场的对称性分布特点，选取恰当的高斯面，从而简化积分，求出电场。

基本要求1.理解电通量概念，掌握电通量计算2.理解并掌握真空中高斯定理3.会用高斯定理计算几种典型对称电荷分布的电场一、 选择题1. 将一个点电荷（忽略重力）无初速地放入静电场中，关于电荷的运动情况，正确的是：[ ] （A ）电荷一定顺着电场线加速运动；（B ）电荷一定逆着电场线加速运动；（C ）到底是顺着还是逆着电场线运动，由电荷的正负决定；（D ）以上说法均不正确。

2.关于电场线，以下说法正确的是[ ] (A) 电场线上各点的电场强度大小相等；(B) 电场线是一条曲线，曲线上的每一点的切线方向都与该点的电场强度方向平行；(C) 电场线是电场空间实际存在的系列曲线；(D) 在无电荷的电场空间，电场线可以相交.3.如图2.1，一半球面的底面圆所在的平面与均强电场E 的夹角为30° ，球面的半径为R ，球面的法线向外，则通过此半球面的电通量为 [ ] (A) π R 2E/2 . (B) -π R 2E/2.(C) π R 2E .(D) -π R 2E .4.关于高斯定理的理解有下面几种说法,其中正确的是[ ] (A) 如高斯面上E 处处为零,则该面内必无电荷；(B) 如高斯面内无电荷,则高斯面上E 处处为零；(C) 如高斯面上E 处处不为零,则高斯面内必有电荷；(D) 如高斯面内有净电荷,则通过高斯面的电通量必不为零；(E) 高斯定理仅适用于具有高度对称的电场5. 两个同心均匀带电球面，半径分别为a R 和b R (b a R R <) , 所带电量分别为a Q 和b Q ，设某点与球心相距r , 当b a R r R <<时， 该点的电场强度的大小为：[ ] (A) 2b a 041r Q Q +⋅πε (B) 2b a 041r Q Q -⋅πε (C))(412bb 2a 0R Q r Q +⋅πε (D) 2a 041r Q ⋅πε 6. 如图2.2所示，两个“无限长”的、半径分别为R 1和R 2的共轴圆柱面均匀带电，轴线方向单位长度上的带电量分别为1λ 和2λ， 则在内圆柱面里面、距离轴线为r 处的P 点的电场强度大小 [ ] (A) r0212πελλ+ (B) 20210122R R πελπελ+ (C) 1014R πελ (D) 0 二、 填空题1.将一电量为q 的点电荷置于一正方体盒子的中心，则穿过盒子六个面的电通量是多少 ,如果将点电荷置于盒子的一个顶点处，穿过盒子各个面的电通量又是多少 .2.如图2.3所示,真空中两个正点电荷,带电量都为Q ,相距2R ,若以其中一点电荷所在处O 点为中心,以R 为半径作高斯球面S ,则通过该球面的电场强度通量Φ= ;若以r 0表示高斯面外法线方向的单位矢量,则高斯面上a 、b 两点的电场强度的矢量式分别为 ， .三、计算题 1. 一半径为R 的带电球体，其电荷体密度分布为⎩⎨⎧><=)(0)(R r R r Ar ρ , 其中A 为一常数，试求球体内、外的场强分布。