当前位置：文档之家 › 第四章 半导体的导电性

第四章 半导体的导电性

  • 格式：ppt
  • 大小：2.46 MB
  • 文档页数：45

下载文档原格式

  / 45

合集下载

华南理工半导体物理—第四章

华南理工半导体物理—第四章


E=0 2
1 6 3 随机热运动 4
5
当一个小电场E施加于半导体时，每一个电子会从电场上 受到一个-qE的作用力，且在各次碰撞之间，沿着电场的反向 被加速。因此，一个额外的速度成分将再加至热运动的电子上 ，此额外的速度成分称为漂移速度(drift velocity) 一个电子由于随机 的热运动及漂移成分两 者所造成的位移如图所 示。 值得注意的是，电 子的净位移与施加的电 场方向相反。
电离杂质散射 • 半导体中的电离杂质形成正、负电中心， 对载流子有吸引或排斥作用，从而引起载 流子散射。

电离杂质散射几率
Pi N iT
3
2
上式表明，随着温度的降低，散射几率 增大。因此，这种散射过程在低温下是 比较重要的。
Байду номын сангаас
晶格振动散射
半导体晶体中原子的振动是引起载流子 被散射的主要原因之一。
mn n 0.26 0.911030 kg 1000104 m2 / V s c q 1.6 1019 C
1.48 1013 s 0.148 ps.
又
1 3 3kT 2 mn vth kT vth 107 cm / s 2 2 mn
所以，平均自由程则为
漂移运动，迁移率与电导率
• 漂移运动：载流子在电场力作用下的定向运动， 定向运动的速度称为漂移速度
j E
vd n E
j nqvd
jn nqn E
n nqn
J jn j p (nqn nq p ) E
(nqn nq p )
载流子散射
j E
dI dV J E ds dl
半导体中电流的大小还可以从另一个角度 来理解。
第四章 半导体的导电性 布置作业解答

第四章 半导体的导电性 布置作业解答

第四章 半导体的导电性1、300K 时，Ge 的本征电阻率为47cm Ω⋅，如电子和空穴迁移率分别为39002cm /(V s)⋅和19002cm /(V s)⋅，试求本征Ge 的载流子浓度。

解：首先，已知Ge 的本征电阻率i ρ＝47cm Ω⋅，可得Ge 的本征电导率i σ＝1i ρ＝1/47S cm 又()i i n p n q σμμ=+本征Ge 的载流子浓度1331921 2.29010/()47/ 1.6010(39001900)/()ii n p n cm q S cm C cm V s σμμ-===⨯+⨯⨯⨯+⋅ 2、试计算本征Si 在室温时的电导率，设电子和空穴迁移率分别为14502cm /(V s)⋅和5002cm /(V s)⋅。

当掺入百万分之一的As 后，设杂质全部电离，试计算其电导率。

比本征Si 的电导率增大了多少倍？解：(1)本征Si 的电导率()i i n p n q σμμ=+已知室温下22103,1450/(),500/(1.51)0n p i u cm V s u c cm m n V s - =⋅ =⨯⋅= ，代入上式得：64.6810/i S cm σ-=⨯(2) 已知Si 的原子密度为223510/cm ⨯，掺入百万分之一的As 后，在Si 中As 的浓度为：22316361510/510/10D N cm cm =⨯⨯=⨯ 因为杂质全电离，所以电离出的电子浓度1630510/D n N cm ==⨯当电离杂质浓度163510/i N cm =⨯时，可查图4-14得电子迁移率为：2850/()n cm V s μ=⋅由于1030(1.510/)i n n cm ⨯ ，又在室温下，则产生载流子以杂质电离为主，可忽略本征激发，即忽略少子空穴对导电的贡献，故此时电导率为： 163192510/ 1.6010850/() 6.8/n nqu cm C cm V s S cm σ-==⨯⨯⨯⨯⋅= 故：666.8// 1.45104.6810/i S cm S cmσσ==⨯⨯ 即电导率增大了145万倍。

08-第四章-半导体的导电性

08-第四章-半导体的导电性

e e * 2me
en
vdx1 秒
平均自由时间
弛豫时间
系统从非平衡态恢复到平衡态 所需时间
* 的统计表示 t=0时，撤除电场，有N0个电子作定向运动 N(t)为t时刻还未遭到碰撞的电子数 P为单位时间内电子被碰撞的几率 在tt+dt时间内被碰撞的电子数可表示为：
N (t ) N (t dt) N (t ) Pdt dN (t ) PN (t )
n型半导体载流子浓度随温度的变化曲线ln(n)-1/T n型半导体载流子浓度随掺杂浓度ND的变化曲线 半导体费米能级随掺杂浓度ND - NA的变化曲线
N型半导体中的电子浓度随温度的变化关系
ln(n) 斜率：Eg/2k 斜率：ED/2k
1/T
n型半导体载流子浓度随掺杂浓度ND的变化曲线
p,n
n p
C N * 临界浓度 D 的估算
非简并 弱 简并
简并
强简并
-2kT
0
5kT
Ef-Ec
Ec

ND 3 EC ED KT N D dEf Ef ln 0 ln 2 2 2 N C dT 2NN D3
1 2 1 e t 2 r vd (0)t at * 2 m 2 e
在tt+dt时间内被碰撞的电子数为 PN (t )dt
这些电子定向位移之和为 rPN (t )dt
N0个电子定向位移之总和为 S 0 rPN (t )dt
S
0

1 e 2 e N 0 e 2 t PN exp( Pt ) dt N 0 0 * * * 2 me me P2 me
* 简并的温度范围 简并时的电中性方程：n N D
半导体的导电性

半导体的导电性

第四章半导体的导电性本章主要内容载流子在外加电场作用下的漂移运动半导体的迁移率、电导率和电阻率随温度和杂质浓度的变化规律迁移率的本质-----散射4.1 载流子的漂移运动迁移率1、欧姆定律对于金属，电流I = V(电压）/R（电阻）V-I关系是直线对于半导体，流过不同截面的电流强度不一定相同，“即电流分布不均匀，而欧姆定律不能说明材料内部各处电流的分布情况。

电流密度：通过垂直于电流方向的单位面积的电流J = ∆I/∆S单位：A/cm2或A/m2欧姆定律微分形式：上式把通过导体中某一点的电流密度和该处的电导率及电场强度直接联系了起来。

S故: 半导体导电= 电子导电J = Jn + Jp = (nqu平均自由程：载流子在连续两次散射间自由运动的平均路程平均自由时间：载流子通过平均自由程所需的平均时间τ电场：载流子加速---定向运动；散射：载流子运动方向改变---杂乱无章，各个方向；半导体的主要散射机构：离化杂质散射晶格散射中性杂质散射位错散射(P为散射几率)起因：常温下，浅施主带正电• 双曲线，电离杂质处于一个焦点 • 速度小，作用时间长，偏离角θ大，τ小 • 弹性散射，不改变入射电子能量，只改变运动方向 τ ∝ T3/2/NI 杂质浓度（2）、晶格散射 晶格原子在其平衡位置附近不断进行热振动，且各个 原子的振动不是孤立的。

分析表明：晶格中原子的振动都 是由若干不同的基本波动按波的叠加原理组合而成，这些 基本波动称为格波。

q代表格波波矢， q 的方向即波的传播方向晶格散射：载流子在运动过程中遭受振动的晶格原子的散射， 失去在电场中获得的能量，失去动量。

在能带具有单一极值的半导体中 起主要散射作用的是长波。

即波 长比原子间距大很多倍的格波。

电子热运动速度~105m/s 电子波波长约10-8m 根据动量守恒要求，声子波长 范围应在同一量级，即10-8m,而 晶体中原子间距为10-10m，因而 起主要散射作用的是长波。

半导体物理学刘恩科第七版第4章导电性

半导体物理学刘恩科第七版第4章导电性

声学波(频率低) 、光学波(频率高)。本质上，它们体现了 两种不同形式的运动。 无论声学波还是光学波，原子位移和波传播方向之间的关 系都是一个纵波两个横波
(4)格波的能量和动量
准动量：hq
能 量：有多个可能： （1/2 + n）h1
其中，ha为格波的能量量子，称作声子。当格波能量减 少一个ha，称放出一个声子，当格波能量增加一个ha，称
无外电场时，载流子总是做无规则热运动，宏观上不 能形成定向的运动，故不能形成电流。
外电场作用下，载流子一方面做无规则热运动，一方 面做定向运动(空穴与电场方向一致，电子相反)。 载流子获得漂移速度，宏观上形成定向运动，故形成 电流。
在外电场和散射双重作用下，载流子从电场中获得速 度，散射又不断地将载流子散射到各个方向，使漂移 不能无限地增大。
电子和晶格散射时，将吸收或放出一个声子。
q2 k 2 k' 2 2 k k' cos (k'k)2 2 k k' (1 cos )
若散射前后k=k’, 则
q 2k sin
2
设散射前后电子速度大小为, 声子速度为u， hk=mn* , 对
长声学波，ha =hqu, 散射前后电子能量变化为：
对锗、硅及III-V族化合物半导体，原胞中含有 2个原子，对应一个q有6个不同的格波。6个格 波的频率和振动方式完全不同。
声学波：频率最低的3个格波； 光学波：频率高的3个波。
由N个原胞构成的半导体晶体，有N个不 同波矢q构成的格波 (N为固体内含有的 原子数) 。
每个q有6个不同频率的格波，所以共有6N 个格波，分为6支，3支为声学波,3支为光学 波。
实际半导体中的载流子在外电场作用下，速度不会无限增 大，根本原因: 受散射（碰撞）的缘故。
半导体物理刘恩科4-3

半导体物理刘恩科4-3


RH
Ey Ex Bz
称为霍耳系数
• 一种载流子的霍耳效应 • 横向霍耳电场对载流子的作用与洛伦 兹力作用相抵消时，达到稳定状态。 稳定时，霍耳电场应满足：
qEy q x Bz
• x方向的电流：
n型半导体，附加电场Ey沿y轴负方向
J x nq x
RH
1 nq
p 型半导体，附加电场Ey沿y轴正向
− 散射作用：电子在运动过程中不断地遭到散射，波矢产 生突变使分布发生改变。单位时间体积元内因散射电子 数变化为：
Hale Waihona Puke dN2(k '
fk'
vfr'
fs'
)dkdr
体积元dkdr内电子数变化 －非平衡条件
下分布方程：
f t
• r
f
•
k•k
f
f t
s
稳定条件下，分布函数不随时间变化： f 0 t
霍耳效应
概念
把通有电流的半导体放在均匀磁场中， 设电场沿x方向，电场强度为Ex；磁 场方向和电场垂直，沿z方向，磁感 应强度为Bz，则在垂直于电场和磁 场的十y或一y方向将产生一个横向 电场Ey，这个现象称为霍耳效应。
霍耳电场Ey与电流密度Jx和磁感应强度 Ex成正比：
或：
Ey RH Ex Bz
f E
vi
v
j
d
k
对球形等能面
nq2 mn*
v2
v2
所以
n
nq
q mn*
v2
v2
§4.6 强电场下的效应 热载流子（自学）
Effect at Large Field, Hot Carrier
欧姆定律的偏离现象 :
11-第四章-半导体的导电性

11-第四章-半导体的导电性


2 2 e v RH p * H h 2 mh v
H
e
2v 2 v
2
v2
2
H
h
2v 2 v
2
v2
2
1 H RH en
e
H RH
2 2 x 1 2 2 H 0 BZ 1 H 2 2 2 2 x x ( BZ 1) H B 1 BZ Z vx J x envx 0 0 en
y方向开路
v y 0 代入(1)式 m* v vx x x
T2 +
+
T1
x
习题：第125页 4，6，11，16，18，19

F
x

f x e x ev y Bz f y e y evx Bz
m *v x

0 0
m *v y

B (0,0, Bz ) (1) ( x , y ,0) (2) v (vx , v y ,0)
y方向短路
vx e 2 v B x Z 从(2)式得 v y m* vx Bz vx Bz 代入(1)式 x
N型半导体
RH
2 2 v2 1 v 2 2 en v
P型半导体
RH
2 v e
2 2 v2 1 v 2 2 ep v
n nee ne
2 v e
m
* e
v
2

m
*
v
2
p pe h pe
2 v e * mh v2
半导体物理学[第四章半导体的导电性]课程复习

半导体物理学[第四章半导体的导电性]课程复习

第四章半导体的导电性
4．1 理论概要与重点分析
由于半导体的电阻率能用四探针法很方便地测量，所以常用它作为半导体的重要性能参量。

(3)由上可见，分析半导体的导电性，应从载流子浓度和迁移率两方面入手。

而载流子浓度问题在第3章中做了系统的讨论，在这里应用时，应全面考虑。

而迁移率的问题是本章的重点。

迁移率是载流子在晶体中运动时不断遭受到各种散射因素的作用决定的。

半导体中的主要散射机构是电离杂质散射和晶格振动散射。

而晶格振动散射又以长纵声学波和光学波的散射为主。

散射作用的强弱用散射概率p(或平均自由时间τ=1/p)来衡量，它表示单位时间内一个载流子遭受到散射的次数。

经分析，几
种主要的散射机构单独决定的散射概率与杂质浓度N
和温度T有如下的关系：
i
(5)半导体在外加电磁场的作用下，电子的分布函数要发生变化，稳态时分布函数的变化满足玻尔兹曼方程。

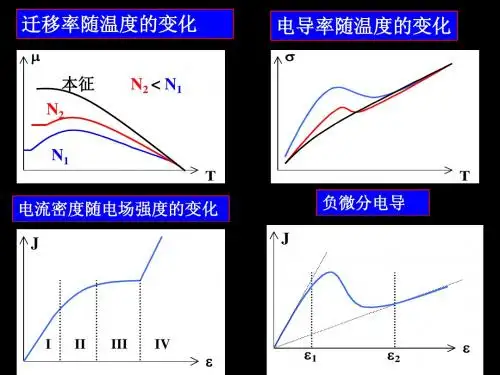
(6)在强电场作用下，载流子的平均漂移速度不再与电场强度成正比。

随着电场强度的增加，漂移速度的增加比线性变得缓慢，最后达到一个饱和值。

很显然，这时的迁移率变得与电场有关，这一物理现象可用热载流子与光学波的晶格散射概念予以解释。

(7)由于GaAs的导带具有多能谷结构，而最低能谷和次低能谷间的能量间隔较小，当电场强度达到一定程度时，最低能谷中电子从电场中获得能量后，使其与次低能谷的能量相当。

即会发生谷间散射，低能谷中的电子向高能谷中转移，且随电场强度的进一步增加，转移的电子越多，高能谷中电子的有效质量远大于
低能谷的有效质量，因而在这个区域内会出现微分负电导现象。

半导体物理刘恩科4-2

半导体物理刘恩科4-2


n
pq2 m*p
p
The Scattering of Carriers
对等能面为多极值半导体迁移率与有效质量 的关系要稍复杂 :
硅导电电子导带极值有六个，等能面为旋转椭球面，椭球
长轴方向沿<100>，有效质量分别为mt和ml。不同极值的能
谷中的电子，沿电场强度E方向x的迁移率不同。
迁移率:
c
q n
1
P 当几种散射机构同时存在时
总散射几率 : P Pi
i
The Scattering of Carriers
电导率( )和迁移率( )与平均自由时间的
关系:
外电场作用下电子的平均漂移速度
电子在两次散射期间作加速运动，第二次散射前的速度变：
vx
v0x
qE mn*
t
电子平均速度变化即是漂移速度：
相应地
对n型半导体
n
nqn
nq2 n
mn*
对p型半导体
p
pq p
pq2 p
mp*
对一般半导体
n
p
nqn
pq p
nq2 n
mn*
pq2 p
m
* p
Temperature Dependence of Carrier Concentration and Mobility
3迁移率与杂质和温度的关系
上述载流子输运理论的局限性：
根据载流子在电场中的加速以及它 们的散射概念，求出了在一定电场下载 流子的平均漂移速度，从而得出电导率、 迁移率与散射几率或平均自由时间的关 系。但是这种分析过于简单，原因有以 下两点：
① 计算中把平均自由时间τ看作—个常数，τ应是载 流子速度的函数，没有考虑载流子速度的统计分布和载 流子热运动速度的区别，需对具有不同热运动速度的载 流子的漂移速度求统计平均值，才能得出精确的结果。
半导体物理分章答案第四章

半导体物理分章答案第四章

可忽略
可忽略
占主导
非本征区
本征区
低温区
0 K
4.6 强电场下的效应 热载流子 Effect at Large Field, Hot Carrier
学习重点：
强电场下欧姆定律发生偏离的原因
1、欧姆定率的偏离与强电场效应
N型锗样品电流与电场强度的关系
光学波散射：
正负离子的振动位移会产生附加势场，因此化合物半导体中光学波散射较强。例如：GaAs 对于元素半导体，只是在高温条件下才考虑光学波散射的作用。例如：Ge、Si 离子晶体中光学波对载流子的散射几率
4.3 迁移率与杂质浓度和温度的关系
当几种散射机构同时存在时
2
平均自由时间τ和散射几率P的关系
晶格振动表现为格波
1
N个原胞组成的晶体→格波波矢有N个。格波的总数等于原子自由度总数
2
一个格波波矢q 对应3(n-1)支光学波+3支声学波。
3
光学波=N (n-1)个纵波+2 N (n-1)个横波
4
声学波=N个纵波+2N个横波
5
晶格振动散射可理解为载流子与声子的碰撞，遵循两大守恒法则
6
准动量守恒
7
1、迁移率( Mobility ) 2、散射机制(Scattering mechanisms) 3、迁移率、电阻率与温度的关系
第四章 半导体的导电性 Electrical conduction of Semiconductors
202X
重点：
漂移运动 迁移率 电导率
学习重点：
202X
§4.1 载流子的漂移运动 迁移率 The drift motion of carrier, mobility
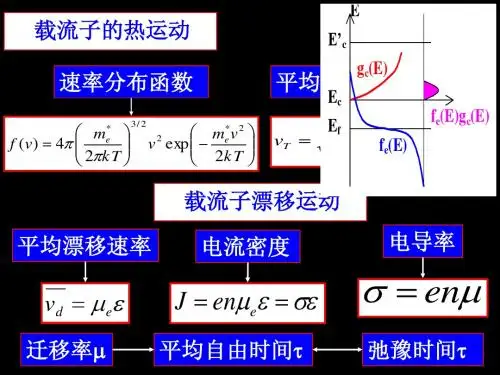
09-第四章-半导体的导电性

09-第四章-半导体的导电性


f f f t t d t C
稳态时 f 0
t
f f t d t C
撤除外场后，分布函数从非平 衡态过渡到平衡态所需时间
外场只有电场
f f0 f f t t C
平均热运动速率：vT

8k T 7 1 10 cm / s * me
平均漂移速率： vd e 1350 平均自由程： l vT 2 10 6 cm
半导体的电导率
e * me e * mh
J (nee pe h ) P型半导体 p>>n
Pl m
* 3/ 2 hh
* 3/ 2 lh
m
* 3/ 2 hh
m
P : Ph : Pl m
* 3/ 2 hd
:mБайду номын сангаас
:m
* 3/ 2 lh
J h ( Ph e h Pl el ) Pe hc
e h * mhh
e l * mlh
3/ 2
hc
e * mhc
载流子的热运动
E E’c gc(E)
速率分布函数
* me f (v ) 4 2k T 3/ 2 * 2 me v v exp 2k T 2
平均速率
Ec
平均动能
fe(E)gc(E) E fkT 3 8 vT E kT * fe(E) me 2
1 1 1 2 * * * mec 3 ml mt
ec
* m * 空穴电导有效质量 hc
空穴浓度 P ＝重空穴浓度 Ph ＋轻空穴浓度 Pl

第四章_半导体的导电性


设有N个电子以速度v沿某方向运动，N(t)表示在t时刻尚
未遭到散射的电子数。则 t 到 t＋△t 时间内被散射的电 子数为N(t) P△t，即：
N (t ) N (t t ) N (t ) Pt
当△t很小时，可以写为：
dN t N t＋t －N t lim ＝－ PN t t 0 dt t
30
4.2.2 载流子的散射
3）其他散射机构
a. 中性杂质散射：在温度很低时，未电离的杂质(中性杂质)的数目
比电离杂质的数目大得多，这种中性杂质也对周期性势场有一定 的微扰作用而引起散射．但它只在重掺杂半导体中，当温度很低，
晶格振动散射和电离杂质散射都很微弱的情况下，才起主要的散
射作用． b. 位错散射：位错线上的不饱和键具有受主中心作用，俘获电子后
h l 3 2 1 f h l P0 1 2 nq
k0T
k 0T
n q＝
exph a k0T 1
1
γl为声子频率， nq为平均声子数 ，f h γ k0T 为T的缓缓变函
l
பைடு நூலகம்

其值值0.6变化到1.0
散射几率随温度的变化主要取决于 平均声子数，其随温度按指数上升:
14
4.2.1 漂移运动
迁移率与电导率
总漂移电流密度为：
J nqn ＋pqp E
与欧姆定律微分形式比较得
到半导体电导率表示式为：
nq n ＋pq p
电子和空穴的漂移运动
15
4.2.1 漂移运动
迁移率与电导率
对于n型半导体（n>>p），电导率为
nqn
对于p型半导体（p>>n），电导率为：

半导体物理学——半导体的导电性

半导体物理学黄整载流子输运半导体中载流子的输运有三种形式：¾漂移¾扩散¾产生和复合2沿电场的反方向作定向运动（定向运动的速度称为漂移速度）dv 电流密度Ad I qnv =−dJ qnv =−4d v nq J =E μnq =Eσ=nq σμ=q 5半导体的电导率和迁移率半导体的导电作用为电子导电和空穴导电的总和==n p J J J +当电场强度不大时，满足J =σ E()n p nq pq μμ+En pnq pq σμμ=+N 型半导体n nq σμ=p n >>P 型半导体p pq σμ=n n ===n p >>6本征半导体i p ()i n p n q σμμ+散射概念的提出外加电场的作用下载流子应当作加速运动外加电场的作用下，载流子应当作加速运动−dJ qnv =不断增大但是J σ=E恒定7热运动在无电场作用下，载流子永无停息地做着无规则的、杂乱无章的运动，称为热运动。

晶体中的碰撞和散射引起净速度为零，净电流为零。

平均自由时间为τm~0.1ps8当有外电场作用时，载流子既受电场力的作用，同时不断发生散射。

载流子在外电场的作用下为热运动和漂移运动的叠加，因此电流密度恒定。

9散射的原因根本原因是周载流子在半导体内发生散射的期性势场遭到破坏附加势场ΔV使能带中的电子在不同k状态间跃迁，并使载流子的运动速度及方向发生改变。

10晶格振动对电子的散射格波¾形成原子振动的基本波动¾格波波矢q=2π/λ¾对应于某一q值的格波数目不定，一个晶体中格波的总数取决于原胞中所含的原子数¾Si、Ge半导体的原胞含有两个原子，对应于每一个q就有六个不同的格波，频率低的三个格波称为声学波，频率高的三个为光学波¾长声学波（声波）振动在散射前后电子能量基本不变，为弹性散射；光学波振动在散射前后电子能量有较大的改变，为非弹性散射12长光学波，能谷内部非弹性散射。

半导体物理习题答案第四章

半导体物理习题答案第四章第4章半导体的导电性2.试计算本征Si 在室温时的电导率，设电⼦和空⽳迁移率分别为1350cm 2/V?s 和500 cm 2/V?s 。

当掺⼊百万分之⼀的As 后，设杂质全部电离，试计算其电导率。

掺杂后的电导率⽐本征Si 的电导率增⼤了多少倍解：将室温下Si 的本征载流⼦密度?1010/cm 3及题设电⼦和空⽳的迁移率代⼊电导率公式()i i n p n q σµµ=+即得：101961.510 1.610(1350500) 4.4410 s/cm i σ--=+=?；已知室温硅的原⼦密度为5?1022/cm 3，掺⼊1ppm 的砷，则砷浓度22616351010510 cm D N --=??=?在此等掺杂情况下可忽略少⼦对材料电导率的贡献，只考虑多⼦的贡献。

这时，电⼦密度n 0因杂质全部电离⽽等于N D ；电⼦迁移率考虑到电离杂质的散射⽽有所下降，查表4-14知n-Si 中电⼦迁移率在施主浓度为5?1016/cm 3时已下降为800 cm 2/V?s 。

于是得1619510 1.610800 6.4 s cm n nq σµ-===/该掺杂硅与本征硅电导率之⽐866.4 1.44104.4410i σσ-==?? 即百万分之⼀的砷杂质使硅的电导率增⼤了亿倍5. 500g 的Si 单晶中掺有?10-5g 的B ，设杂质全部电离，求其电阻率。

（硅单晶的密度为2.33g/cm 3，B 原⼦量为）。

解：为求电阻率须先求杂质浓度。

设掺⼊Si 中的B 原⼦总数为Z ，则由1原⼦质量单位=?10-24g 算得618244.510 2.51010.8 1.6610Z --?==个 500克Si 单晶的体积为3500214.6 cm 2.33V ==，于是知B 的浓度∴1816-32.510 1.1610 cm 214.6A Z N V ?===? 室温下硅中此等浓度的B 杂质应已完全电离，查表4-14知相应的空⽳迁移率为400 cm 2/V?s 。

半导体物理答案

第一篇 半导体中的电子状态习题1-1、 什么叫本征激发？温度越高，本征激发的载流子越多，为什么？试定性说明之。

1-2、 试定性说明Ge 、Si 的禁带宽度具有负温度系数的原因。

1-3、试指出空穴的主要特征。

1-4、简述Ge 、Si 和GaAS 的能带结构的主要特征。

1-5、某一维晶体的电子能带为[])sin(3.0)cos(1.01)(0ka ka E k E --=其中E 0=3eV ，晶格常数a=5х10-11m 。

求：（1） 能带宽度；（2） 能带底和能带顶的有效质量。

题解：1-1、 解：在一定温度下，价带电子获得足够的能量（≥E g ）被激发到导带成为导电电子的过程就是本征激发。

其结果是在半导体中出现成对的电子-空穴对。

如果温度升高，则禁带宽度变窄，跃迁所需的能量变小，将会有更多的电子被激发到导带中。

1-2、 解：电子的共有化运动导致孤立原子的能级形成能带，即允带和禁带。

温度升高，则电子的共有化运动加剧，导致允带进一步分裂、变宽；允带变宽，则导致允带与允带之间的禁带相对变窄。

反之，温度降低，将导致禁带变宽。

因此，Ge 、Si 的禁带宽度具有负温度系数。

1-3、 解：空穴是未被电子占据的空量子态，被用来描述半满带中的大量电子的集体运动状态，是准粒子。

主要特征如下：A 、荷正电：+q ；B 、空穴浓度表示为p （电子浓度表示为n ）；C 、E P =-E nD 、m P *=-m n *。

1-4、 解：（1） Ge 、Si:a ）Eg (Si ：0K) = 1.17eV ；Eg (Ge ：0K) = 0.744eV ；b ）间接能隙结构c ）禁带宽度E g 随温度增加而减小；（2） GaAs ：a ）Eg (0K) = 1.52eV ；b ）直接能隙结构；c ）Eg 负温度系数特性： dE g /dT = -3.95×10-4eV/K ；1-5、 解：（1） 由题意得：[][])sin(3)cos(1.0)cos(3)sin(1.002220ka ka E a k d dE ka ka aE dk dE+=-=eVE E E E a kd dE a k E a kd dE a k a k a k ka tg dk dE ooo o 1384.1min max ,01028.2)4349.198sin 34349.198(cos 1.0,4349.198,01028.2)4349.18sin 34349.18(cos 1.0,4349.184349.198,4349.1831,04002222400222121=-=∆<⨯-=+==>⨯=+====∴==--则能带宽度对应能带极大值。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
a
dE 8m u ln dt s
n
2
2k0Te Te （ 1－ ） mn T
设电场强度为E时的迁移率为 ，平均漂移速度 为 d ，仍定义 d＝ E ，则在电场作用下，单位 时间内电子由电场中获得的能量为：
2 dE q E dt d
AB段 温度很低，本征激发可忽略，载流子主要由杂 质电离提供，它随温度升高而增加；散射主要由电离 杂质决定，迁移率也随温度升高而增大，所以，电阻 率随温度升高而下降．
BC段 杂质已全部电离，本征激发仍不显著，载流 子饱和，晶格振动散射为主，迁移率随温度升高而 降低，电阻率随温度升高而稍有增大． C段 温度继续升高，本征激发很快增加，本征载 流子的产生远超过迁移率的减小对电阻率的影响， 这时，本征激发成为矛盾的主要方面，杂质半导体 的电阻率经一个极大值之后将随温度的升高而急剧 地下降，表现出同本征半导体相似的特性．
1)电离杂质散射：
电离杂质散射
散射概率P：单位时间内载流子受到散射的次数。
Pi NiT
－3 2
散射概率和电离杂质浓度以及温 度之间的关系
2)晶格振动的散射
在一定温度下，晶格中原子都在各自的平衡位 置附近作微小振动。振动在晶格中传播形成格 波。格波有声学波和光学波。
声学波：原胞质心的整体运动产生的格波； 光学波：原胞中原子间的相对运动产生的格波。 角频率为ωa的格波，能量是量子化的，只能是
设电子浓度为n，每个能谷单位体积中有 n/6个电子，电流密度Jx为：
n n n J X＝ q1 Ex＋ q 2 Ex＋ q3 Ex 3 3 3 1 ＝ nq 1＋ 2＋3 Ex 3
J X＝nqc Ex
q n c＝ mc
1 c＝ 1＋ 2＋3 3
1 1 1 2 ＝ ＋ mc 3 ml mt
第四章 半导体的导电性
4.1 载流子的漂移运动和迁移率 1.欧姆定律
V E l
V I R
l R S

1

I J S
J E
2、漂移速度和迁移速度
dQ nq d dsdt
J dQ / dtds
d
平均漂移速度
J n nq d
d E


nq
μ为迁移率，单位电场下电子的 平均漂移速度。单位cm2/V.s 3、半导体中的电导率和迁移率
下面以掺杂Si、Ge半导体为例，定性分析迁移率随 杂质浓度和温度的变化情况．在这种半导体中，通 常起主要作用的散射机构是声学波散射和电离杂质 散射． 32 q T q 1 s i 32
m AT
m
BNi
q 1 m AT 3 2＋ BNi T3 2
对Ⅲ-Ⅴ 族化合物半导体，如GaAs，光学波散射 不可忽略，总的迁移率表示为：
原因：在强电场下载流子成为热载流子。即载流 子从电场中获得能量的速率大于其与晶格振动发射声 子失去能量的速率，载流子热运动速度增加。
根据τ＝ln/v，在不考虑平均自由程变化的情 况下，可使平均自由时间随电场增加而减小，而迁 移率则降低．
0
4qln 3 2 m n k0T

4qln 3 2m n k0Te
1 i n i q n＋ p
1、电阻与杂质浓度的关系
2、电阻率随温度的变化
对纯半导体材料，电阻率主要由本征载流子浓度ni决 定．随着温度上升ni急剧增加，而迁移率只稍有下降， 本征半导体电阻率随温度增加而单调下降。 对杂质半导体，有杂质电离和本征激发两个因素存 在，又有电离杂质散射和晶格振动散射两种散射机构 的存在，因而电阻率随温度的变化关系更为复杂。1来自1i＋
1
s
＋
1
0
1) 杂质浓度增加，在室温下，杂质全部电离，因此 杂质散射增强，迁移率减小. 2) 当杂质浓度较低时(小于1017cm3)，起主要散射机 构为声学波散射，电离杂质散射忽略，所以温度升 高，迁移率迅速减小。 3) 当杂质浓度较高时(大于1019cm3)，低温区，温度 升高 ，迁移率有所上升；高温区，迁移率随温度升 高而下降。 低温、高掺杂以电离杂质散射为主；高温、低掺杂 以晶格散射为主。
N（t）＝N0exp（－pt）
设N0为t＝0时未遭散射的电子数。所以在t到t ＋dt时间内被散射的电子数为：
dN＝N0 Pe
平均自由时间：
pt
dt
1 ＝ N0


0
1 N 0 Pte dt＝ P
- pt
2、电导率、迁移率与平均自由时间的关系 设沿x方向施加电场E，考虑到载流子具有各 向同性的有效质量 ，如在t＝0时，某个电子恰 好遭到散射，散射后沿x方向的速度为vx0，经 过时间t后又遭到散射，在t时间作加速运动， 再次散射前的速度为：
q x＝x0 Et mn
平均漂移速度
x＝
x 0 0
q EtP exp Pt dt mn
x0＝0
q 1 q x＝ E E n mn P mn
＝
x
E
q n n＝ mn
p＝
q p m
p
nq n ＝ ＋ mn mp
即：
T 2 dE q E 0 Te dt d
当电子与晶格散射达到稳定状态时，有
dE dE ＋ 0 dt s dt d
J nqn ＋pqp E
nq n ＋pq p
nqn pqp
i n i q n ＋ p
电子漂移电流和空 穴漂移电流
4.2 载流子的散射 1、载流子散射的概念
载流子在外场下的运动，能否无限加速？
欧姆定律：电流密度恒定。
电场存在时：载流子在电场力作用下运动，获 得速度；电子受到散射失去速度。 2、半导体的主要散射机构
（1）中性杂质散射：在温度很低时，未电离的杂质(中性杂质) 的数目比电离杂质的数目大得多，这种中性杂质也对周期性 势场有一定的微扰作用而引起散射．但它只在重掺杂半导体 中，当温度很低，晶格振动散射和电离杂质散射都很微弱的 情况下，才起主要的散射作用． （2）位错散射：位错线上的不饱和键具有受主中心作用，俘获 电子后成为一串负电中心,其周围将有电离施主杂质的积累，从 而形成一个局部电场，这个电场成为载流子散射的附加电场。 （3）等同能谷间散射：对于Ge、Si，导带结构是多能谷的， 即导带能量极小值有几个不同的波矢值．载流子在这些能谷中 分布相同，这些能谷称为等同能谷．对这种多能谷半导体，电 子的散射将不只局限在一个能谷内，而可以从一个能谷散射到 另一个能谷，这种散射称为谷间散射．
2
pq2 p
nq n n＝ mn
2
p＝
nq p
2
m p
n p i＝n i q ＋ m m p n
2
对等能面为旋转椭球面的多极值半导体，沿晶体的 不同方向有效质量不同，所以迁移率与有效质量的 关系较为复杂． 下面以硅为例说明迁移率计算。 [100]能谷中的电子，沿x方向的 迁移率：μ 1 =qτ n／ml 其余能谷中的电子，沿x方向的 迁移率：μ 2=μ 3=qτ n／mt
求室温本征硅的电阻率和掺杂百万分之一硼后电阻 率。
i
1 ni q( n p )
4.1105 ( cm )
1 0.25 pq p
4.6 强电场下的效应、热载流子 1、欧姆定律的偏离
半导体中载流子在弱电场作用下的输运满足欧姆定 律．然而，在强电场作用下，载流子的输运特性不 同于弱电场下的情况，欧姆定律不再成立。反映出 电导率(迁移率)随场强变化。 n型锗： 电场小于700V/cm,漂移速度与电场成正比，迁 移率与场强无关。 场强在700~5000V/cm之间，漂移速度增加缓慢， 迁移率随场强增加而降低。 场强大于5000V/cm，漂移速度达到饱和。
l
若几种散射同时起作用时，则总的散射概率应该是各 种散射概率的总和，即：
P PI I 1,2,3,
1


1
1
I


1
I
结论：多种散射机构同时存在时，与每种散射单独 存在时比起来，平均自由时间变得更短了，且趋向 于最短的那个平均自由时间；迁移率也更少了，且 趋向于最少的那个迁移率．在实际情况中，应找到 起主要作用的散射机构，迁移率主要由它决定。
4.3 迁移率与杂质浓度和温度的关系 1、平均自由时间和散射概率的关系 散射几率一般都是载流子速度的函数，而且 速度也是统计分布的，为简单起见，先不考虑 载流子速度的统计分布的影响，而采用简单的 模型来讨论迁移率、电导率和散射几率的关系， 进而讨论它们与杂质浓度和温度的关系． 自由时间：载流子在电场中作漂移运动时，会不 断地遭到散射，只有在连续两次散射之间的时间 内作加速运动，这段时间称为自由时间． 平均自由时间：自由时间长短不一，取若干次而 求得其平均值称为载流子的平均自由时间。
(n 1 )a 2
声子：晶格振动的能量量子。
根据统计计 算，格波的 平均能量为
1 1 a a a 2 exp( )-1 k0T
1 nq = ωa exp( )-1 koT
包含平均声子 数为 晶格振动对 载流子的散 射可以看成 载流子与声 子的碰撞。
k '-k q E '- E a
设有N个电子以速度v沿某方向运动，N（t）和N（t ＋△t）分别表示在t时刻和t＋△t时刻尚未遭到散射 的电子数。则t到t＋△t时间内被散射的电子数为N（t） P△t，即：
N (t ) N (t t ) N (t ) Pt
dN t N t＋t －N t lim ＝－ PN t t 0 dt t
3、迁移率与杂质和温度的关系 电离杂质散射： 声学波散射： 光学波散射： 电离杂质散射：