材料力学 第十一章分解
- 格式：ppt
- 大小：4.92 MB
- 文档页数：68
下载文档原格式
合集下载
材料力学第十一章
2F 2 ⋅ 3l 8
2F 2 ⋅ l
×2+
4=
7lF 2
2EAi π E(2d )2
π Ed 2 8π Ed 2
（c）取 d x 长的微段（如右图），在均布轴力 f 的作用下，它具有的应变能
dVε
=
1 2
FN (x)dΔ
式中
FN (x)
=
F l
x,
dΔ = FN (x)dx = Fx dx EA EAl
=
Vε
(F
)
+
Vε
(M
)
+
1 2
(Mθ
+
Fwmax
)
。
11-2 图示简支梁中点只承受集中力 F 时，梁的最大转角为θ max ，应变能为Vε (F ) ；中 点只承受集中力偶 M 时，最大挠度为 wmax ，梁的应变能为Vε (M ) 。当同时在中点施加 F
和 M 时，梁的应变能为多少？
解 对于线性结构简支梁，先加 F 时梁贮存的应变能
（顺）
（二）单位载荷法解(a)
(a3)
(a4)
(a5)
149
解 图（b）
FA
=
FB
=
Me 2a
AD 段
M (x1 ) =
Me 2a
x1 ， M 1(x1 ) =
x1 ， M
2 (x1 ) =
− x1 2a
DC 段
M (x2 ) = M e ， M 1(x2 ) = 2a − x2 ， M 2 (x2 ) = −1
11-5 超静定问题有哪几类？怎样确定超静定问题的次数？什么是相当系统？什么是静 定基？静定基是否唯一？
答 超静定问题有外约束超静定、内约束超静定及外约束超静定加内约束超静定混合。 全部未知力个数与全部独立平衡方程数的差就是超静定问题的次数。 拆去多余内、外约束，用相应的约束力代替其作用，使之成为静定形式的结构，它就 是原结构的相当系统（相当系统加上变形协调条件称为原超静定结构的等效系统）。 解除约束后的不包括外载荷的静定结构称为原结构的静定基。 静定基不唯一。
材料力学 第十一章分解
非圆对称
当压力超过一定数值时，圆环将 不能保持圆对称的平衡形式，而 突然变为非圆对称的平衡形式
失稳或屈曲
上述各种关于平衡形式的突然变化，统称为稳定失效
压杆 承受轴向压力的杆件。
工程中的压杆
工程中的压杆
柱、桁架的压杆、薄壳结构及薄壁容器等、在有 压力存在时，都可能发生失稳。
提升 油缸
3、稳定平衡、临界平衡（随遇平衡）、不稳定平衡
把物体在原来位置上和现在位置上所处的平衡状态 称为临界平衡
实际上不属稳定平衡。
4、压杆的失稳
压杆丧失其直线形状的平衡而过渡为曲线形状平衡 （弯曲平衡）
屈曲： 压杆从直线平衡到弯曲平衡的转变过程；
屈曲位移：由于屈曲，压杆产生的侧向位移；
通常，屈曲将使构件失效，并导致相关的结构发生坍塌。 由于这种失效具有突发性，常常带来灾难性后果。
2EI
Fcr l 2
两端铰支细长压杆临界压力的欧拉公式。
Fcr 与抗弯刚度（ EI ）成正比。
压杆失稳时，总是绕抗弯刚度最小的轴发生弯曲变形。 因此，对于各个方向约束相同的情形
I 应是截面最小的形心主惯性矩。
Fcr
2EI
l2
适用范围：
1、两端为铰支座的细长杆
2、线弹性，小变形
公式的推导中应用了弹性小挠度微分方程，因 此公式只适用于弹性稳定问题。
5临界压力 使中心受压的直杆由直线平衡形式转变为曲线
平衡形式时所受的轴向压力； Fcr
★当F=Fcr时有两种可能的平衡状态：
即：屈曲位移ω =0的直线状态； 屈曲位移为无穷小的无限接近于直线的弯曲状态;
故临界压力可以理解为：
压杆保持直线形态平衡的最大载荷；
第十一章材料力学课程课件PPT
2.18
BC
第11章
表达式为
变 型能法
11.3 卡 氏 定 理
δ1 =
证明如下: 设 FP1 , FP 2 , , FPn 作用于弹性体上(图11.6),这些力产生的相应位移 为 δ1 , δ 2 ,δ n ,在变形过程中,外力所做的功等于弹性体的变形能,于 是变形能 U 为 FP1 , FP 2 , , FPn 的函数.
M θB W = 0 ,而外力 2
偶所做的功为 M0
M 02 l U = ,由 2 EI
W =可得 U
M 0θ B M 02l = 2 2 EI
θB =
M 0l EI
2.17
第11章
变 型能法
11.3 卡 氏 定 理
其结果与梁的变形一章中计算结果一致.从上面的计算可以看出,由于 变形能为力的函数,若将变形能对力求偏导数,则
与集中力对应的是线位移,与集中力偶对应的是角位移.在线弹性体的 情况下,广义力和广义位移是线性关系,运用胡克定理,上式还可以写 成: FP2 l Cδ 2 U= = (11.11) 2C 2l 式中,C是杆的刚度,从上式可以看出,弹性变形能是广义力或广义位 移的二次函数.
2.13
第11章
变 型能法
(a) (b) 图11.1 轴向受拉杆外力的功 (a) 受拉直杆;(b) 与关系
2.4
P
第11章
W=
变 型能法
1 FP l 2
11.2 变形能的计算
(11.2)
根据式(11.1)可知,受拉杆的弹性变形能为
U =W = 1 FP l 2
因,上式可写成
l = FP l EA
(11.3)
2.5
第11章
材料力学刘鸿文第六版最新课件第十一章 交变应力
一个应力循环
按正弦规律变化的交变应力 如图所示。
σmax σm σmin σ a
在交变应力中，应力每重复变化一次称为一个“应力循环”。
应力重复变化的次数称为“应力循环次数”，用N表示。
应力的极大值称为最大应力，用σmax表示；
应力的极小值称为最小应力，用σmin表示。
循环特征 r——最小应力与最大应力的比值
第十一章 交变应力
§11.1 交变应力与疲劳失效 §11.2 交变应力的循环特征，应力幅和平均应力 §11.3 疲劳（持久）极限 §11.4 影响疲劳极限的因素 §11.5 对称循环下构件的疲劳强度计算 §11.6 疲劳极限曲线 §11.7 不对称循环下构件的疲劳强度计算 §11.8 弯扭组合交变应力的强度计算 §11.9 变幅交变应力 §11.10 提高构件疲劳强度的措施
15
外形突变影响的描述 有效应力集中系数 对称循环时的有效应力集中系数为：
k
( 1)d ( 1 )k
对扭转:
k
( 1)d ( 1)k
其中，(-1)d , (-1)d , 表示无应力集中的光滑试样的持久极限； (-1)k , (-1)k , 表示有应力集中的相同尺寸的试样的持久极限。
显然，有： k 1, k 1 值越大说明应力
坐标平面上确定A、B、C三点。折线ACB即为简化曲线。
a
A
1
O
r 1
r 0
G
G ( m, a )
C
(
0
,0
max
M W
860 12.3 106
70 MN
m2
min 70 MN m 2
r 1
28
2.确定 K
由图11-9，a 中曲线2查得端铣加工的键槽，当材料
按正弦规律变化的交变应力 如图所示。
σmax σm σmin σ a
在交变应力中，应力每重复变化一次称为一个“应力循环”。
应力重复变化的次数称为“应力循环次数”，用N表示。
应力的极大值称为最大应力，用σmax表示；
应力的极小值称为最小应力，用σmin表示。
循环特征 r——最小应力与最大应力的比值
第十一章 交变应力
§11.1 交变应力与疲劳失效 §11.2 交变应力的循环特征，应力幅和平均应力 §11.3 疲劳（持久）极限 §11.4 影响疲劳极限的因素 §11.5 对称循环下构件的疲劳强度计算 §11.6 疲劳极限曲线 §11.7 不对称循环下构件的疲劳强度计算 §11.8 弯扭组合交变应力的强度计算 §11.9 变幅交变应力 §11.10 提高构件疲劳强度的措施
15
外形突变影响的描述 有效应力集中系数 对称循环时的有效应力集中系数为：
k
( 1)d ( 1 )k
对扭转:
k
( 1)d ( 1)k
其中，(-1)d , (-1)d , 表示无应力集中的光滑试样的持久极限； (-1)k , (-1)k , 表示有应力集中的相同尺寸的试样的持久极限。
显然，有： k 1, k 1 值越大说明应力
坐标平面上确定A、B、C三点。折线ACB即为简化曲线。
a
A
1
O
r 1
r 0
G
G ( m, a )
C
(
0
,0
max
M W
860 12.3 106
70 MN
m2
min 70 MN m 2
r 1
28
2.确定 K
由图11-9，a 中曲线2查得端铣加工的键槽，当材料
工程力学材料力学答案-第十一章解析
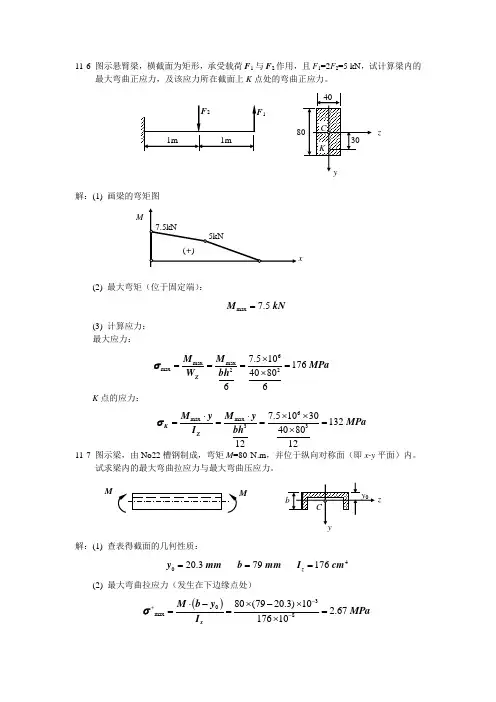
11-6 图示悬臂梁，横截面为矩形，承受载荷F 1与F 2作用，且F 1=2F 2=5 kN ，试计算梁内的最大弯曲正应力，及该应力所在截面上K 点处的弯曲正应力。
解：(1) 画梁的弯矩图(2) 最大弯矩（位于固定端）：max 7.5 M kN =(3) 计算应力： 最大应力：K 点的应力：11-7 图示梁，由No22槽钢制成，弯矩M =80 N.m ，并位于纵向对称面（即x-y 平面）内。
试求梁内的最大弯曲拉应力与最大弯曲压应力。
解：(1) 查表得截面的几何性质：4020.3 79 176 z y mm b mm I cm ===(2) 最大弯曲拉应力（发生在下边缘点处）()30max880(7920.3)10 2.67 17610x M b y MPa I σ-+-⋅-⨯-⨯===⨯6max max max227.510176 408066ZM M MPa bh W σ⨯====⨯6max max 337.51030132 ********K ZM y M y MPa bh I σ⋅⋅⨯⨯====⨯x M1zM M z(3) 最大弯曲压应力（发生在上边缘点处）30max88020.3100.92 17610x M y MPa I σ---⋅⨯⨯===⨯ 11-8 图示简支梁，由No28工字钢制成，在集度为q 的均布载荷作用下，测得横截面C 底边的纵向正应变ε=3.0×10-4，试计算梁内的最大弯曲正应力，已知钢的弹性模量E =200 Gpa ，a =1 m 。
解：(1) 求支反力31 44A B R qa R qa ==(2) 画内力图(3) 由胡克定律求得截面C 下边缘点的拉应力为：49max 3.010******* C E MPa σε+-=⋅=⨯⨯⨯=也可以表达为：2max4C C z zqa MW W σ+== (4) 梁内的最大弯曲正应力：2maxmax max 993267.5 8C zz qa M MPa W W σσ+====qxxF SM11-14 图示槽形截面悬臂梁，F =10 kN ，M e =70 kNm ，许用拉应力[σ+]=35 MPa ，许用压应力[σ-]=120 MPa ，试校核梁的强度。
材料力学(刘鸿文)第十一章 交变应力ppt课件
a 为常数 等幅交变应力
不稳定的交变应力
max min 不是常量 a 为变化的
不等幅交变应力；
（1）对称循环： 火车轮轴横截面边缘上点的弯曲正应力随时间作周期性变化
ω
A ωt
σ t
maxmin
m 0
a ma xmin
r 1
（2）非对称循环：
ωt
σ σm
t 静平衡位置
ma x min 0
具体过程如下：
（1）、原因
由于构件的形状变化、材料不均匀、表面加工质量等 原因，使得构件内某局部区域的应力偏高，形成高应 力区；
（2）、微观裂纹形成 构件长期在交变应力的作用下，在最不利或较弱的晶
体，沿最大切应力作用面形成滑移带，滑移带开裂形成 微观裂纹；
(3)、宏观裂纹 分散的微观裂纹经过集结沟
平均应力：
m
maxm
2
in
应力幅：
a
m
axm
2
in
循环特征：
r min , max
且 1r1
以上五个特征值中，只有二个是独立的。满足
max ma
minma
★具体描述一种交变应力，可用最大应力 max 和循环特性r， 或用平均应力 m 和应力幅值 a 。
2、几种典型的交变应力 稳定的交变应力： max min 均不变，
§11–1 概述 §11–2 交变应力的几个名词术语 §11–3 材料持久限及其测定
§11–4 构件持久限及其计算 §11–5 对称循环下构件的疲劳强度计算 §11–6 持久极限曲线 §11–7 非对称循环下的疲劳强度计算 §11–8 提高构件疲劳强度的措施
§11–１ 交变应力与疲劳失效
一、交变应力：构件内一点处的应力随时间作周期性变化。
不稳定的交变应力
max min 不是常量 a 为变化的
不等幅交变应力；
（1）对称循环： 火车轮轴横截面边缘上点的弯曲正应力随时间作周期性变化
ω
A ωt
σ t
maxmin
m 0
a ma xmin
r 1
（2）非对称循环：
ωt
σ σm
t 静平衡位置
ma x min 0
具体过程如下：
（1）、原因
由于构件的形状变化、材料不均匀、表面加工质量等 原因，使得构件内某局部区域的应力偏高，形成高应 力区；
（2）、微观裂纹形成 构件长期在交变应力的作用下，在最不利或较弱的晶
体，沿最大切应力作用面形成滑移带，滑移带开裂形成 微观裂纹；
(3)、宏观裂纹 分散的微观裂纹经过集结沟
平均应力：
m
maxm
2
in
应力幅：
a
m
axm
2
in
循环特征：
r min , max
且 1r1
以上五个特征值中，只有二个是独立的。满足
max ma
minma
★具体描述一种交变应力，可用最大应力 max 和循环特性r， 或用平均应力 m 和应力幅值 a 。
2、几种典型的交变应力 稳定的交变应力： max min 均不变，
§11–1 概述 §11–2 交变应力的几个名词术语 §11–3 材料持久限及其测定
§11–4 构件持久限及其计算 §11–5 对称循环下构件的疲劳强度计算 §11–6 持久极限曲线 §11–7 非对称循环下的疲劳强度计算 §11–8 提高构件疲劳强度的措施
§11–１ 交变应力与疲劳失效
一、交变应力：构件内一点处的应力随时间作周期性变化。
《材料力学》第11章典型习题解析
第11章典型习题解析1.用卡氏第二定理求图12.3所示刚架A 截面的位移和B 截面的转角。
略去剪力Q 和轴力N 的影响，E Ⅰ为已知.解：（1）A 截面的位移AB 段弯矩：M(x)=-Px （0≤x ≤l ） ∂M(x) /∂P=-x在A 处虚加一水平力向右的力Q,之后，再令其为0.那么,BC 段弯矩：M(y)=-2P l - Q l +(P+Q)y∂M(y) /∂P=-2l +y ∂M(y) /∂ Q=-l +yA 截面的竖直位移:Y A ==∂∂∑⎰EI P Mdx ML 0 ()()()()⎰⎰+-+-+--L LEIdy y L Py PL EI dx x Px 00222 =EIPL 223A 截面的水平位移: X A =EI Q M M L ∂∂∑⎰0dx=()()EI dy y L Qy Py QL PL L 200+-++--⎰ 积分，令Q=0得 ()()EIPL EI dy y L Py PL XA L 1252230=+-+-=⎰(2)B 截面的转角在B 处虚加一力偶M B,AB 段弯矩：M(x)=-Px （0≤x<l ）BC 段弯矩：M(y)=-2P l -B M +Py （0<y<l ）∂M(x) /∂MB=0 ∂M(y) /∂MB =-1 ∑⎰∂∂=L B B EI dx M M M 0θ =()()⎰-+--L B EI dxPy M PL 0212 EIPL 432= 2.用卡氏第二定理求图示的A 截面的位移和B 截面的转角。
略去剪力Q 和轴力N 的影响，E Ⅰ为已知。
解：（1）A 截面的位移在A 点虚加一向下的力F ，支反力2qL F P Y B ++= （L 为AB 和AD 的长度） P X qL P Y C C -=--=,2AB 段弯矩： M1=0∂ M1 /∂F=0AD 段弯矩：M2(x)=2qL P F qx 2++⋅1（）x-2∂M2(x) /∂F=xCD 段弯矩：M3(y)=PyaⅠⅠ2ⅠC DA 截面的竖直位移:∑⎰∂∂=L A EIdx F M M Y 0=⎰⋅⎥⎦⎤⎢⎣⎡-⋅⎪⎭⎫ ⎝⎛++L EI xdx qx x F qL P 02222 积分，令F=0得34A PL qL Y 6EI 24EI =+求A 截面的水平位移时， 在A 处虚加一水平力向右的力Q, 再令其为0.那么, 支反力B qL Y P Q 2=++ （L 为AB 和AD 的长度）C C qL Y P Q X P Q 2=-+=-+（）+，（） AB 段弯矩： M1=0∂ M1 /∂Q=0AD 段弯矩：M2(x)=(P+Q)x ⋅∂M2(x) /∂Q=xCD 段弯矩：M3(y)=（P+Q ）y∂M3(y) /∂Q=yA 截面的水平位移∑⎰∂∂=L A EI dx Q M M X 0=()⎰⋅+L EIdx x Q P 022=()⎰⋅+L EI ydy y Q P 0积分，令Q=0得 EIPL X A 23= (2) B 截面的转角在B 处虚加一顺时针的力偶M B, 积分，并令其为零。
材料力学课后习题答案11章
S z (η2 ) = 2.5 × 10 − 5 + (0.010η2 )(0.050 −
S z ,max (η 2 ) = 3.75 × 10 −5 m 3
η2
2
)
τ1 =
FSy S z , max (η1 ) 5 × 103 × 2.5 × 10 −5 N = = 3.75 × 106 Pa = 3.75MPa I zδ 3.333 × 10 − 6 × 0.010m 2 FSy S z , max (η2 ) I zδ 5 × 103 × 3.75 × 10 −5 N = = 5.63 × 106 Pa = 5.63MPa −6 2 3.333 × 10 × 0.010m
2 = 2.5 × 10 −5 + 2.5 × 10 −4 η 2 − 5 × 10 −3 η 2
τ 1, max =
FSy S z , max (η1 ) I zδ 1
=
5 × 103 × 1.25 × 10 −5 N = 3.00 ×106 Pa = 3.00MPa 2.08 × 10 − 6 × 0.010m 2
S z , A (ω ) =
δ
2 yA =
0.010 × 0.050 2 m 3 = 1.25 × 10 − 5 m 3 2
= 1.875 × 10 −4 m 3
据公式
τ (η ) =
得
FS S z (ω ) I zδ
40 × 10 3 × 1.25 × 10 −5 N τA = = 1.499 × 10 6 Pa = 1.499MPa −5 2 3.335 × 10 × 0.010m
[
]
11-6
试指出图示截面的剪心位置。
题 11-6 图 解： （a）双对称截面，剪心与形心重合； （b）角钢形截面，剪心在二边条中心线相交处； （c）T 形截面，剪心在翼缘中心线与腹板中心线相交处。
材料力学第十一章
解超静定梁的基本步骤如下。 （1）判断超静定次数，去掉多余约束，得到静定基。 （2）用未知的多余约束力代替去掉的多余约束加到静定基上（即得到相 当系统）。 （3）根据多余约束处的变形条件及其相应的物理条件建立补充方程，解 出多余未知约束力。 （4）由静定基的平衡条件求出其他约束力，画出内力图，并作强度或刚度 计算。
Fl2 M Al 0 16EI 3EI
所以
MA
3Fl 16
(
)
这里与按图 11-5（b）所示的静定基求得的结果相同（负号表明 MA 实际方 向与图上所设方向相反）。
多余约束力求出后，可对超静定梁进行强度或刚度计算。一般在静定基
上进行。如图
11-5（b）所示的悬臂梁，在
F
和
FB（
FB
5 16
图 11-5（a）所示的梁，也可选 MA 作为多余约束力，即去掉 A 处的 转角约束，使 A 处变成固定铰支座，其静定基将变成简支梁 AB ，如图 116（a）所示，上面作用有载荷 F 和多余约束力矩 MA 。
（a）
（b） （c）
图11-6
A 处的变形协调条件可由叠加法写出，可得
θAF θAM A 0 式中， θAF 和 θAM A 分别为 F 和 MA 单独作用时 A 处的转角，如图 11-6（b）、（c） 所示。再由物理条件，代入式（a），得补充方程为
材料力学
第十一章 超静定系统
一
超静定系统的概念
二 弯曲超静定问题
三
力法解超静定系统
四
对称及反对称性质的应用
五
连续梁及三弯矩方程
第一节 超静定系统的概念
在图 11-1（a）中，将被车削的工件简化成悬臂梁。当车削力 F 作用时， 固定端（卡盘）有三个未知约束力 FAx ， FAy 和 MA ，如图 11-1（b）所示。独 立的静力平衡方程式也有三个，即
材料力学
y max
Mmax y I
2.9Fp 1000 15
304
170
64
Fp 155.4 N 即Fp的容许值为155.4N
解题指导：
如果采用max=（M1*y/I)+(M2*y/I)计算， 是错误的。因为M1所引起的最大正应力在a 点， M2所引起的最大正应力在b点。显然不 能将两个不同点处的正应力相加作为该截面 上的最大正应力。
4
d3
4 32
d 3
32
MT Wp
m
d3
3 16
d 3
16
r3
2 4 2
4 32
d 3
2
4
3 16
d 3
2
160
d 3
100MPa
d 80mm
取 d 80mm
解题指导：
弯扭组合变形的最大特点是：其危险点属于二 向受力状态，危险点上的正应力并不在其横截面 上，因而必须应用强度理论进行强度计算。
11.3 直径为d的等截面折杆，位于水平面内，杆的
A端承受垂直向下的荷载Fp力作用，已知[]。试求： （1）指出危险截面的位置；
（2）求危险截面上的最大弯曲正应力max和 最大扭转剪应力τmax；
（3）用第三强度理论求许可荷载[Fp]
a
B
C
A
Fp
a
解： （1）固定端C截面为危险截面
（2）内力图
xy
r3
2 x
材料力学答案第十一章
材料力学答案第十一章第十一章能量方法第十一章答案11.1 图示桁架各杆的材料相同，截面面积相等。
试求在 F 力作用下，桁架的变形能。
FFN1FN 2F N2 ( x) V dx 2EA3F 2l 2.4EA2F, F N3F1 2 l2 2A 3 B222 F l22 F l 2 l l2 22EA 2EA11.2 计算图示各杆的应变能。
M eEI2A A F A CB ACB l / 2l /l l 3 3 x 2x1(a)e / l (b) M/ lMe(a)F 2l F 2l 3F 2l.V4EA 4EA2EAMe x12 Me x22l /3 2l /3l l(b) V dx1 dx22EI 0 2EIM e2x 12 l /3x 22 2 l /3M e 2 l2EIl 2.3 0 3 0 18EI11.3 传动轴受力情况如图所示。
轴的直径为 40mm ，材料为 45 钢，E = 210GPa ，G = 80GPa 。
试计算轴的应变能。
由扭转引起的应变能：V 20.2802dx 0.0322GI p由弯曲引起的应变能：V 120.2(531.4x)2dx 0.0292EIVV 1 V 2 0.061J .11.4 计算图示梁的应变能， 并说明是否满足叠加原理及其原因。
1k22Me=Fll(Fl Fx) 2F 2l3V2EI dx6EIEIF而V 1l( Fl )2F 2 l 3dx 2EI0 2EIV 2 l ( Fx)2F 2l 32EI dx6EI .xl不满足叠加原理，因为应变能与内力的关系不是线性的。
11.5 在外伸梁的自由端作用力偶矩 M e ，试用互等定理，并借助于附录 E ，求MACe跨度中点 C 的挠度 w c 。
BDl /2l /2a（见课本下册 p40 例 12-4）11.6 图示刚架的各杆的EI 皆相等，试求截面 A 、B 的位移和截面 C 的转角。
a b FqAx Cl Axxxhhl(aB(b(a) A 点：在 A 点加一个向下的单位力。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2EI
Fcr l 2
两端铰支细长压杆临界压力的欧拉公式。
Fcr 与抗弯刚度（ EI ）成正比。
压杆失稳时，总是绕抗弯刚度最小的轴发生弯曲变形。 因此，对于各个方向约束相同的情形
I 应是截面最小的形心主惯性矩。
Fcr
2EI
l2
适用范围：
1、两端为铰支座的细长杆
2、线弹性，小变形
公式的推导中应用了弹性小挠度微分方程，因 此公式只适用于弹性稳定问题。
杆端的约束愈强，则µ值愈小，压杆的临界力愈高； 杆端的约束愈弱，则值µ愈大，压杆的临界力愈低。
讨论：
（1）相当长度 l 的物理意义 压杆失稳时，挠曲线上两拐点间的长度就是压杆相当长度 l 。
l 是各种支承条件下，细长压杆失稳时，挠曲线中相当于
半波正弦曲线的一段长度。 长为L的一端固定一端自由的压杆的挠曲线与长为2L的 两端铰支的细长杆相当。
Fcr
2 EI
(2l )2
两端铰支
一端固定、一端铰支
Fcr
l
Fcr
2 EI
(1.0 l )2
C
Fcr
2 EI
(0.7l )2
两端铰支
Fcr
2 EI
(1.0 l )2
两端固定
Fcr
D
L
C
Fcr
2 EI
( )2
长度系数
一端固定、一端自由 两端铰支
一端固定、一端铰支
3、理想压杆
（轴线为直线，压力与轴线重合，材料均匀）
实际使用的压杆
轴线的初曲率、压力的偏心、材料的缺陷和不均匀 等因素总是存在的，为非理想受压直杆。
４、Euler解、精确解、实验结果的比较：
F
B
C 精确解
D
E
A F
Fcr
G
A’ Euler解 H 实验结果
δ
O
截面惯性矩 临界力
269103 N 269kN
长为L的一端固定、另端铰支的压杆，约与长为0.7L 的两端铰支压杆相当。
长为L的两端固定压杆与长为0.5L的两端铰支压杆相当;
讨论：
（2）横截面对某一形心主惯性轴的惯性矩 I
若杆端在各个方向的约束情况相同（球形铰等），则 I 应取最小的形心主惯性矩。
Fcr
(
2 EI
2.0 l )2
2 EI
Fcr ( 1.0 l )2
Fcr
(
2 EI
0.7 l )2
两端固定
Fcr
2 EI ( l )2
Fcr
2 EI
( 0.5 l )2
欧拉公式普遍形式
长度系数
l 相当长度
2
1
0.7
0.5
开始轴线为直线，接着必被压弯，发生较大的弯曲变形； 最后被折断；
两端承受压力的细长杆:
当压力超过一定的数值时，压杆会由原来的直线平衡形式, 突然变弯，致使结构丧失承载力；
狭长截面梁在横向力的作用下：
线弹性范围 铅锤面内的弯曲；
P Pcr
弯曲和扭转
受均匀压力的薄圆环：
p pcr
圆对称的平衡
§11-３其他支座条件下细长压杆的临界压力
类比法：
根据力学性质将某些点类比为支座点。 其它约束——折算成两端铰支。 对于其它约束情况的压杆，将挠曲线形状与两端铰支 压杆的挠曲线形状加以比较，用几何类比的方法，求 它们的临界力。
两端铰支
一端固定、一端自由
Fcr
L 2L
Fcr
2 EI
(1.0 l )2
§11-2 支细长压杆的临界压力 欧拉公式 =Fcr
M FN=Fcr
w(x)
弯矩
M ( x ) Fcrw( x )
挠曲线近似微分方程
w'' M ( x ) EI
令
k 2 Fcr
EI
w'' Fcr w EI
w'' k 2w 0
此方程的通解为 w Asin kx Bcos kx
稳定平衡 当球受到微小干扰，偏离其平 衡位置后，经过几次摆动，它 会重新回到原来的平衡位置。
不稳定平衡
处于凸面的球体，当球受到 微小干扰，它将偏离其平衡 位置，而不再恢复原位；
临界平衡
物体处于平衡状态，受到干扰后 离开原来的平衡位置;
干扰撤掉后:
既不回到原来的平衡位置，也 不进一步离开；
而是停留在一个新的位置上平衡；
.
§11-1 压杆稳定的概念 1、杆件在轴向拉力的作用下：
塑性材料：工作应力达到屈服极限时出现屈服失效； 脆性材料： 工作应力达到强度极限时断裂；
粗短杆在轴向压力的作用下
塑性材料的低碳钢短圆柱 被压扁； 铸铁短圆柱 脆断；
2、工程中的某些细长杆在轴向压力的作用下
表现出与强度完全不同的失效形式；
细长竹片受压时
利用杆的边界条件，
x0 w0
B0
可知压杆的微弯挠曲线为正弦函数：
w Asin Kx
利用边界条件
xl w0
Asin kl 0 A 0 即压杆没有弯曲变形；
kl n
n 1 ,2,3,.....
Fcr
n2 2 EI
l2
实际工程中有意义的是最小的临界力值，即 n 1
把物体在原来位置上和现在位置上所处的平衡状态 称为临界平衡
实际上不属稳定平衡。
4、压杆的失稳
压杆丧失其直线形状的平衡而过渡为曲线形状平衡 （弯曲平衡）
屈曲： 压杆从直线平衡到弯曲平衡的转变过程；
屈曲位移：由于屈曲，压杆产生的侧向位移；
通常，屈曲将使构件失效，并导致相关的结构发生坍塌。 由于这种失效具有突发性，常常带来灾难性后果。
5临界压力 使中心受压的直杆由直线平衡形式转变为曲线
平衡形式时所受的轴向压力； Fcr
★当F=Fcr时有两种可能的平衡状态：
即：屈曲位移ω =0的直线状态； 屈曲位移为无穷小的无限接近于直线的弯曲状态;
故临界压力可以理解为：
压杆保持直线形态平衡的最大载荷；
或压杆处于微弯状态（丧失稳定）的最小载荷。
非线性稳定理论已经证明：对于细长压杆，临界平衡是稳定的。
压杆的极限承载能力 压杆失稳后，压力的微小增量会引起屈服变形的显 著增大，杆件丧失了继续增大荷载的能力。
且由失稳造成的失效可以导致整个结构的坍塌。
为了保证压杆安全可靠的工作，必须使压杆处于 直线平衡形式，因而压杆是以临界力为其极限承 载能力。
非圆对称
当压力超过一定数值时，圆环将 不能保持圆对称的平衡形式，而 突然变为非圆对称的平衡形式
失稳或屈曲
上述各种关于平衡形式的突然变化，统称为稳定失效
压杆 承受轴向压力的杆件。
工程中的压杆
工程中的压杆
柱、桁架的压杆、薄壳结构及薄壁容器等、在有 压力存在时，都可能发生失稳。
提升 油缸
3、稳定平衡、临界平衡（随遇平衡）、不稳定平衡
Fcr l 2
两端铰支细长压杆临界压力的欧拉公式。
Fcr 与抗弯刚度（ EI ）成正比。
压杆失稳时，总是绕抗弯刚度最小的轴发生弯曲变形。 因此，对于各个方向约束相同的情形
I 应是截面最小的形心主惯性矩。
Fcr
2EI
l2
适用范围：
1、两端为铰支座的细长杆
2、线弹性，小变形
公式的推导中应用了弹性小挠度微分方程，因 此公式只适用于弹性稳定问题。
杆端的约束愈强，则µ值愈小，压杆的临界力愈高； 杆端的约束愈弱，则值µ愈大，压杆的临界力愈低。
讨论：
（1）相当长度 l 的物理意义 压杆失稳时，挠曲线上两拐点间的长度就是压杆相当长度 l 。
l 是各种支承条件下，细长压杆失稳时，挠曲线中相当于
半波正弦曲线的一段长度。 长为L的一端固定一端自由的压杆的挠曲线与长为2L的 两端铰支的细长杆相当。
Fcr
2 EI
(2l )2
两端铰支
一端固定、一端铰支
Fcr
l
Fcr
2 EI
(1.0 l )2
C
Fcr
2 EI
(0.7l )2
两端铰支
Fcr
2 EI
(1.0 l )2
两端固定
Fcr
D
L
C
Fcr
2 EI
( )2
长度系数
一端固定、一端自由 两端铰支
一端固定、一端铰支
3、理想压杆
（轴线为直线，压力与轴线重合，材料均匀）
实际使用的压杆
轴线的初曲率、压力的偏心、材料的缺陷和不均匀 等因素总是存在的，为非理想受压直杆。
４、Euler解、精确解、实验结果的比较：
F
B
C 精确解
D
E
A F
Fcr
G
A’ Euler解 H 实验结果
δ
O
截面惯性矩 临界力
269103 N 269kN
长为L的一端固定、另端铰支的压杆，约与长为0.7L 的两端铰支压杆相当。
长为L的两端固定压杆与长为0.5L的两端铰支压杆相当;
讨论：
（2）横截面对某一形心主惯性轴的惯性矩 I
若杆端在各个方向的约束情况相同（球形铰等），则 I 应取最小的形心主惯性矩。
Fcr
(
2 EI
2.0 l )2
2 EI
Fcr ( 1.0 l )2
Fcr
(
2 EI
0.7 l )2
两端固定
Fcr
2 EI ( l )2
Fcr
2 EI
( 0.5 l )2
欧拉公式普遍形式
长度系数
l 相当长度
2
1
0.7
0.5
开始轴线为直线，接着必被压弯，发生较大的弯曲变形； 最后被折断；
两端承受压力的细长杆:
当压力超过一定的数值时，压杆会由原来的直线平衡形式, 突然变弯，致使结构丧失承载力；
狭长截面梁在横向力的作用下：
线弹性范围 铅锤面内的弯曲；
P Pcr
弯曲和扭转
受均匀压力的薄圆环：
p pcr
圆对称的平衡
§11-３其他支座条件下细长压杆的临界压力
类比法：
根据力学性质将某些点类比为支座点。 其它约束——折算成两端铰支。 对于其它约束情况的压杆，将挠曲线形状与两端铰支 压杆的挠曲线形状加以比较，用几何类比的方法，求 它们的临界力。
两端铰支
一端固定、一端自由
Fcr
L 2L
Fcr
2 EI
(1.0 l )2
§11-2 支细长压杆的临界压力 欧拉公式 =Fcr
M FN=Fcr
w(x)
弯矩
M ( x ) Fcrw( x )
挠曲线近似微分方程
w'' M ( x ) EI
令
k 2 Fcr
EI
w'' Fcr w EI
w'' k 2w 0
此方程的通解为 w Asin kx Bcos kx
稳定平衡 当球受到微小干扰，偏离其平 衡位置后，经过几次摆动，它 会重新回到原来的平衡位置。
不稳定平衡
处于凸面的球体，当球受到 微小干扰，它将偏离其平衡 位置，而不再恢复原位；
临界平衡
物体处于平衡状态，受到干扰后 离开原来的平衡位置;
干扰撤掉后:
既不回到原来的平衡位置，也 不进一步离开；
而是停留在一个新的位置上平衡；
.
§11-1 压杆稳定的概念 1、杆件在轴向拉力的作用下：
塑性材料：工作应力达到屈服极限时出现屈服失效； 脆性材料： 工作应力达到强度极限时断裂；
粗短杆在轴向压力的作用下
塑性材料的低碳钢短圆柱 被压扁； 铸铁短圆柱 脆断；
2、工程中的某些细长杆在轴向压力的作用下
表现出与强度完全不同的失效形式；
细长竹片受压时
利用杆的边界条件，
x0 w0
B0
可知压杆的微弯挠曲线为正弦函数：
w Asin Kx
利用边界条件
xl w0
Asin kl 0 A 0 即压杆没有弯曲变形；
kl n
n 1 ,2,3,.....
Fcr
n2 2 EI
l2
实际工程中有意义的是最小的临界力值，即 n 1
把物体在原来位置上和现在位置上所处的平衡状态 称为临界平衡
实际上不属稳定平衡。
4、压杆的失稳
压杆丧失其直线形状的平衡而过渡为曲线形状平衡 （弯曲平衡）
屈曲： 压杆从直线平衡到弯曲平衡的转变过程；
屈曲位移：由于屈曲，压杆产生的侧向位移；
通常，屈曲将使构件失效，并导致相关的结构发生坍塌。 由于这种失效具有突发性，常常带来灾难性后果。
5临界压力 使中心受压的直杆由直线平衡形式转变为曲线
平衡形式时所受的轴向压力； Fcr
★当F=Fcr时有两种可能的平衡状态：
即：屈曲位移ω =0的直线状态； 屈曲位移为无穷小的无限接近于直线的弯曲状态;
故临界压力可以理解为：
压杆保持直线形态平衡的最大载荷；
或压杆处于微弯状态（丧失稳定）的最小载荷。
非线性稳定理论已经证明：对于细长压杆，临界平衡是稳定的。
压杆的极限承载能力 压杆失稳后，压力的微小增量会引起屈服变形的显 著增大，杆件丧失了继续增大荷载的能力。
且由失稳造成的失效可以导致整个结构的坍塌。
为了保证压杆安全可靠的工作，必须使压杆处于 直线平衡形式，因而压杆是以临界力为其极限承 载能力。
非圆对称
当压力超过一定数值时，圆环将 不能保持圆对称的平衡形式，而 突然变为非圆对称的平衡形式
失稳或屈曲
上述各种关于平衡形式的突然变化，统称为稳定失效
压杆 承受轴向压力的杆件。
工程中的压杆
工程中的压杆
柱、桁架的压杆、薄壳结构及薄壁容器等、在有 压力存在时，都可能发生失稳。
提升 油缸
3、稳定平衡、临界平衡（随遇平衡）、不稳定平衡