机械控制工程基础第二章2习题解答

习 题2.1 什么是线性系统?其最重要的特性是什么?下列用微分方程表示的系统中,x o 表示系统输出,x i 表示系统输入,哪些是线性系统? (1) x x x x x ioooo 222=++ (2) x tx x xiooo222=++ (3) x x x xio 222oo=++ (4) x tx x x xiooo222o=++ 解: 凡是能用线性微分方程描述的系统就是线性系统。

线性系统的一个最重要特性就是它满足叠加原理。

该题中（2）和（3）是线性系统。

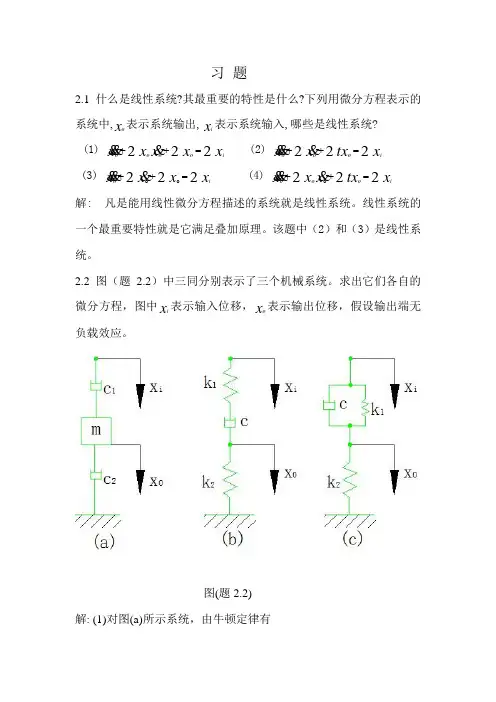
2.2 图（题2.2）中三同分别表示了三个机械系统。

求出它们各自的微分方程，图中x i 表示输入位移，x o 表示输出位移，假设输出端无负载效应。

图(题2.2) 解: (1)对图(a)所示系统，由牛顿定律有xm x c x x c ioo2o1)(=-- 即x c x c c xm i121oo )(=++ (2)对图(b)所示系统，引入一中间变量x,并由牛顿定律有)1()()(1x xc k x x oi-=-)2()(2x k x xc oo=-消除中间变量有x ck x k k xk k c io121o21)(=-- (3)对图(c)所示系统，由牛顿定律有 x k x x k x xc ooioi21)()(=-+-即x k x c x k k xc iioo121)(+=++ 2.3求出图(题2.3)所示电系统的微分方程。

图（题2.3）解:(1)对图(a)所示系统,设i 1为流过R 1的电流,i 为总电流,则有⎰+=idt Ci R u o122i R u u o i 11=-dti i Cu u oi)(111⎰-=-消除中间变量,并化简有u R C u CC R R uR C u R C u C C R R u R C iiiooo12211221222121211)()1(1+++=-+++(2)对图(b)所示系统，设i 为电流，则有⎰++=idtC i R u u oi111⎰+=i R idt Cu o221 消除中间变量,并化简有u Cu R u C C u R R iioo2221211)11()(+=+++2.4 求图(题2.4)所示机械系统的微分方程。

习 题2.1 什么是线性系统其最重要的特性是什么下列用微分方程表示的系统中,x o 表示系统输出,x i 表示系统输入,哪些是线性系统 (1) x x x x x ioooo 222=++&&& (2) x tx x xiooo222=++&&& (3) x x x x io222oo=++&&& (4) x tx x x xiooo222o=++&&& 解: 凡是能用线性微分方程描述的系统就是线性系统。

线性系统的一个最重要特性就是它满足叠加原理。

该题中（2）和（3）是线性系统。

2.2 图（题2.2）中三同分别表示了三个机械系统。

求出它们各自的微分方程，图中x i 表示输入位移，x o 表示输出位移，假设输出端无负载效应。

图(题2.2) 解: (1)对图(a)所示系统，由牛顿定律有 即xc x c c x m i&&&&121oo )(=++ (2)对图(b)所示系统，引入一中间变量x,并由牛顿定律有 消除中间变量有(3)对图(c)所示系统，由牛顿定律有 即x k x c x k k x c iioo121)(+=++&&2.3求出图(题2.3)所示电系统的微分方程。

图（题2.3）解:(1)对图(a)所示系统,设i 1为流过R 1的电流,i 为总电流,则有 消除中间变量,并化简有u R C u CC R R u R C u R C u C C R R u R C iiiooo12211221222121211)()1(1+++=-+++&&&&&&&(2)对图(b)所示系统，设i 为电流，则有 消除中间变量,并化简有2.4 求图(题2.4)所示机械系统的微分方程。

图中M 为输入转矩,C m 为圆周阻尼，J 为转动惯量。

习 题什么是线性系统其最重要的特性是什么下列用微分方程表示的系统中,x o 表示系统输出,x i 表示系统输入,哪些是线性系统 (1) x x x x x ioooo222=++&&& (2) x tx x xiooo222=++&&& (3)x x x x io222oo=++&&& (4) x tx x x xiooo222o=++&&& 解: 凡是能用线性微分方程描述的系统就是线性系统。

线性系统的一个最重要特性就是它满足叠加原理。

该题中（2）和（3）是线性系统。

图（题）中三同分别表示了三个机械系统。

求出它们各自的微分方程，图中x i 表示输入位移，x o 表示输出位移，假设输出端无负载效应。

图(题 解: (1)对图(a)所示系统，由牛顿定律有xm x c x x c i&&&&&oo2o1)(=--即xc x c c x m i&&&&121oo )(=++ (2)对图(b)所示系统，引入一中间变量x,并由牛顿定律有)1()()(1xx c k x x oi&&-=- )2()(2x k xx c oo=-&&消除中间变量有x ck x k k xk k c io&&121o21)(=-- (3)对图(c)所示系统，由牛顿定律有 x k x x k xx c ooioi21)()(=-+-&&即x k x c x k k x c iioo121)(+=++&&求出图(题所示电系统的微分方程。

图（题）解:(1)对图(a)所示系统,设i 1为流过R 1的电流,i 为总电流,则有⎰+=idtCi R u o122i R u u o i 11=-dti i Cu u oi)(111⎰-=-消除中间变量,并化简有u R C u CC R R u R C u R C uCC R R u R C iiiooo12211221222121211)()1(1+++=-+++&&&&&&&(2)对图(b)所示系统，设i 为电流，则有⎰++=idtC i R u u oi111⎰+=i R idt Cu o221 消除中间变量,并化简有uCu R u C C u R R iioo2221211)11()(+=+++&&求图(题所示机械系统的微分方程。

第2章系统的数学模型(习题答案)2.1什么是系统的数学模型？常用的数学模型有哪些？解：数学模型就是根据系统运动过程的物理、化学等规律，所写出的描述系统运动规律、特性、输出与输入关系的数学表达式。

常用的数学模型有微分方程、传递函数、状态空间模型等。

2.2 什么是线性系统？其最重要的特性是什么？解：凡是能用线性微分方程描述的系统就是线性系统。

线性系统的一个最重要的特性就是它满足叠加原理。

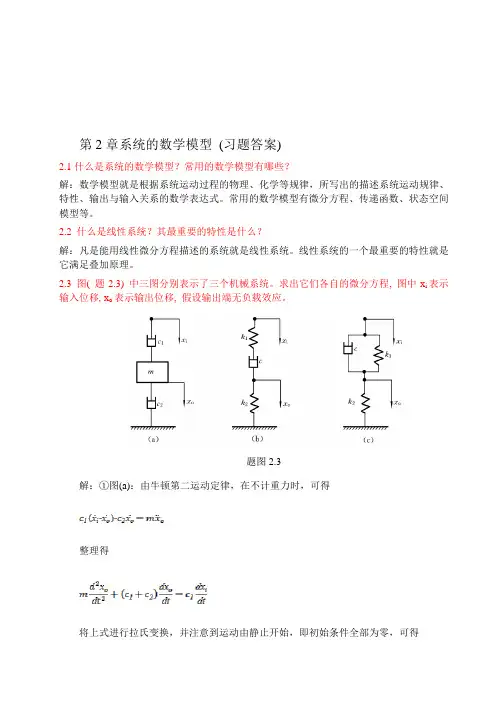
2.3 图( 题2.3) 中三图分别表示了三个机械系统。

求出它们各自的微分方程, 图中x i表示输入位移, x o表示输出位移, 假设输出端无负载效应。

题图2.3解：①图(a)：由牛顿第二运动定律，在不计重力时，可得整理得将上式进行拉氏变换，并注意到运动由静止开始，即初始条件全部为零，可得[]于是传递函数为②图(b)：其上半部弹簧与阻尼器之间，取辅助点A，并设A点位移为x，方向朝下；而在其下半部工。

引出点处取为辅助点B。

则由弹簧力与阻尼力平衡的原则，从A和B两点可以分别列出如下原始方程：消去中间变量x，可得系统微分方程对上式取拉氏变换，并记其初始条件为零，得系统传递函数为③图(c)：以的引出点作为辅助点，根据力的平衡原则，可列出如下原始方程：移项整理得系统微分方程对上式进行拉氏变换，并注意到运动由静止开始，即则系统传递函数为2.4试建立下图（题图2.4）所示各系统的微分方程并说明这些微分方程之间有什么特点，其中电压)(t u r 和位移)(t x r 为输入量；电压)(t u c 和位移)(t x c 为输出量；1,k k 和2k 为弹簧弹性系数；f 为阻尼系数。

+-+-C)(t u r )(t u c )(t r )(t x c f1k 2k CR)(t u r )(u c +-+-f)(t r )(t x c )(a )(b )(c )(d R 2R题图2.4【解】：)(a方法一：设回路电流为i ，根据克希霍夫定律，可写出下列方程组：⎪⎩⎪⎨⎧=+=⎰i R u u dt i C u cc r 1消去中间变量，整理得：dtdu RC u dt du RCrc c =+方法二：dtdu RC u dt du RCRCs RCs CsR R s U s U rc c r c =+⇒+=+=11)()( 由于无质量，各受力点任何时刻均满足∑=0F ，则有：cc r kx dt dxdt dx f =-)(dtdx k f x dt dx k f rc c =+⇒()r r c c r c u dtduC R u dt du C R R Cs R R Cs R Cs R R CsR s U s U +=++⇒+++=+++=221212212)(1111)()( 设阻尼器输入位移为a x ，根据牛顿运动定律，可写出该系统运动方程r rc c aa c a r c r x dtdx k f x dt dx f k k k k dt dx f x x k x x k x x k +=++⇒⎪⎩⎪⎨⎧=--=-22121221)()()( 结论：)(a 、)(b 互为相似系统，)(c 、)(d 互为相似系统。

习 题什么是线性系统其最重要的特性是什么下列用微分方程表示的系统中,x o 表示系统输出,x i 表示系统输入,哪些是线性系统 (1) x x x x x ioooo 222=++&&& (2) x tx x xiooo222=++&&& (3) x x x x io222oo=++&&& (4) x tx x x xiooo222o=++&&& 解: 凡是能用线性微分方程描述的系统就是线性系统。

线性系统的一个最重要特性就是它满足叠加原理。

该题中（2）和（3）是线性系统。

图（题）中三同分别表示了三个机械系统。

求出它们各自的微分方程，图中x i 表示输入位移，x o 表示输出位移，假设输出端无负载效应。

图(题 解: (1)对图(a)所示系统，由牛顿定律有 即xc x c c x m i&&&&121oo )(=++ (2)对图(b)所示系统，引入一中间变量x,并由牛顿定律有 消除中间变量有(3)对图(c)所示系统，由牛顿定律有 即x k x c x k k x c iioo121)(+=++&&求出图(题所示电系统的微分方程。

图（题）解:(1)对图(a)所示系统,设i 1为流过R 1的电流,i 为总电流,则有 消除中间变量,并化简有u R C u CC R R u R C u R C u C C R R u R C iiiooo12211221222121211)()1(1+++=-+++&&&&&&&(2)对图(b)所示系统，设i 为电流，则有 消除中间变量,并化简有求图(题所示机械系统的微分方程。

图中M 为输入转矩,C m 为圆周阻尼，J 为转动惯量。

解：设系统输入为M （即），输出θ(即)，分别对圆盘和质块进行动力学分析，列写动力学方程如下：消除中间变量x,即可得到系统动力学方程KM M c Mm C R c k KJ c C km R cJ mC mJ mmm++=++-++++&&&&&&&&&θθθθ）（22)()()4( 输出y(t)与输入x(t)的关系为y(t)= 2x(t)+x 3(t)。

《机械控制工程基础》习题及解答目录第１章绪论第２章控制系统的数学模型第３章控制系统的时域分析第４章控制系统的频域分析第５章控制系统的性能分析第６章控制系统的综合校正第７章模拟考试题型及分值分布第1章绪论一、选择填空题1。

开环控制系统在其控制器和被控对象间只有（正向作用）.P2A。

反馈作用 B.前馈作用 C。

正向作用 D。

反向作用2.闭环控制系统的主反馈取自（被控对象输出端）。

P3A.给定输入端B.干扰输入端 C。

控制器输出端 D。

系统输出端3。

闭环系统在其控制器和被控对象之间有（反向作用）。

P3A.反馈作用B.前馈作用 C。

正向作用 D.反向作用A。

输入量 B。

输出量 C。

反馈量 D。

干扰量4.自动控制系统的控制调节过程是以偏差消除(偏差的过程）。

P2-3A。

偏差的过程 B。

输入量的过程 C.干扰量的过程 D.稳态量的过程5.一般情况下开环控制系统是（稳定系统)。

P2A.不稳定系统B.稳定系统 C。

时域系统 D。

频域系统6.闭环控制系统除具有开环控制系统所有的环节外，还必须有（B)。

p5A.给定环节B.比较环节 C。

放大环节 D.执行环节7.闭环控制系统必须通过（C）。

p3A.输入量前馈参与控制 B。

干扰量前馈参与控制C。

输出量反馈到输入端参与控制 D。

输出量局部反馈参与控制8.随动系统要求系统的输出信号能跟随(C的变化)。

P6A。

反馈信号 B。

干扰信号 C。

输入信号 D。

模拟信号9。

若反馈信号与原系统输入信号的方向相反则为（负反馈）。

P3A。

局部反馈 B。

主反馈 C.正反馈 D.负反馈10．输出量对系统的控制作用没有影响的控制系统是（开环控制系统)。

P2A。

开环控制系统 B。

闭环控制系统 C.反馈控制系统 D.非线性控制系统11。

自动控制系统的反馈环节中一般具有（ B ）。

p5A。

.给定元件 B.检测元件 C．放大元件 D．执行元件12. 控制系统的稳态误差反映了系统的〔B 〕p8A. 快速性B.准确性C. 稳定性 D。

第二章习题答案2-1试求下列函数的拉氏变换，假设0<t 时，0)(=t f（1）)3cos 1(5)(t t f -= 答案：⎪⎭⎫⎝⎛+-=22315)(s s s s F （2）t et f t10cos )(5.0-= 答案：2210)5.0(5.0)(+++=s s s F （3）)35sin()(π+=t t f 答案：22225235521)(+⋅++⋅=s s s s F （4）atn e t t f =)( 答案：1)(!)(+-=n a s n s F 2-2求下列函数的拉氏变换（1）te t t tf 33232)(-++= 答案：32182)(42+++=s ss s F （2）)0(4sin 2cos )(333≥++=---t te t e e t tf t t t答案：222244)3(42)1(1)3(6)(++++++++=s s s s s F（3）te t t tf 22)1()2(15)(-+-⋅= 答案：)2(32)2(25)(----+=s s e s e s s F （4）⎩⎨⎧><≤≤=ππt t t tt f ,000sin )(答案：提示)sin(sin )(π-+=t t t f ，se s s s F π-+++=1111)(22 2-3已知)1(10)(+=s s s F（1）利用终值定理，求∞→t 时)(t f 值 答案：10)1(10lim )(lim )(lim 0=+==→→∞→s s ss sF t f s s t（2）通过取)(s F 的拉氏反变换，求∞→t 时)(t f 值答案：[]()101)(10lim 11110lim )(lim )(lim 11=-⋅=⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛+-==-∞→-∞→-∞→∞→tt t t t e t s s L s F L t f 2-4已知2)2(1)(+=s s F （1）利用初值定理，求)0(f 和)0(f '的值。

习 题2.1 什么是线性系统?其最重要的特性是什么?下列用微分方程表示的系统中,x o 表示系统输出,x i 表示系统输入,哪些是线性系统? (1) x x x x x ioooo 222=++ (2) x tx x xiooo222=++ (3) x x x xio 222oo=++ (4) x tx x x xiooo222o=++ 解: 凡是能用线性微分方程描述的系统就是线性系统。

线性系统的一个最重要特性就是它满足叠加原理。

该题中（2）和（3）是线性系统。

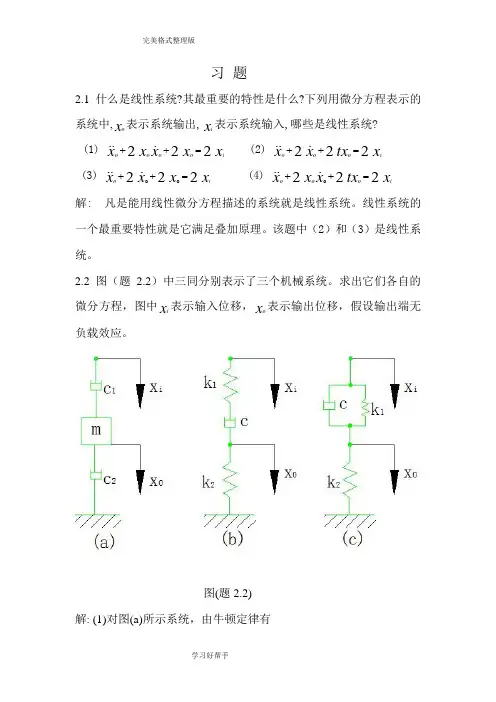
2.2 图（题2.2）中三同分别表示了三个机械系统。

求出它们各自的微分方程，图中x i 表示输入位移，x o 表示输出位移，假设输出端无负载效应。

图(题2.2) 解: (1)对图(a)所示系统，由牛顿定律有xm x c x x c ioo2o1)(=-- 即x c x c c xm i121oo )(=++ (2)对图(b)所示系统，引入一中间变量x,并由牛顿定律有)1()()(1x xc k x x oi-=- )2()(2x k x xc oo=-消除中间变量有x ck x k k xk k c io121o21)(=-- (3)对图(c)所示系统，由牛顿定律有 x k x x k x xc ooioi21)()(=-+-即x k x c x k k xc iioo121)(+=++ 2.3求出图(题2.3)所示电系统的微分方程。

图（题2.3）解:(1)对图(a)所示系统,设i 1为流过R 1的电流,i 为总电流,则有⎰+=idt Ci R u o122i R u u o i 11=-dti i Cu u oi)(111⎰-=-消除中间变量,并化简有u R C u CC R R uR C u R C u C C R R u R C iiiooo12211221222121211)()1(1+++=-+++(2)对图(b)所示系统，设i 为电流，则有⎰++=idtC i R u u oi111⎰+=i R idt Cu o221 消除中间变量,并化简有u Cu R u C C u R R iioo2221211)11()(+=+++2.4 求图(题2.4)所示机械系统的微分方程。

《机械控制工程基础》习题及解答目录第１章绪论第２章控制系统的数学模型第３章控制系统的时域分析第４章控制系统的频域分析第５章控制系统的性能分析第６章控制系统的综合校正第７章模拟考试题型及分值分布第1章绪论一、选择填空题1.开环控制系统在其控制器和被控对象间只有（正向作用）。

P2A.反馈作用B.前馈作用C.正向作用D.反向作用2.闭环控制系统的主反馈取自（被控对象输出端）。

P3A.给定输入端B.干扰输入端C.控制器输出端D.系统输出端3.闭环系统在其控制器和被控对象之间有（反向作用）。

P3A.反馈作用B.前馈作用C.正向作用D.反向作用A.输入量B.输出量C.反馈量D.干扰量4.自动控制系统的控制调节过程是以偏差消除（偏差的过程）。

P2-3A.偏差的过程B.输入量的过程C.干扰量的过程D.稳态量的过程5.一般情况下开环控制系统是（稳定系统）。

P2A.不稳定系统B.稳定系统C.时域系统D.频域系统6.闭环控制系统除具有开环控制系统所有的环节外，还必须有(B)。

p5A.给定环节B.比较环节C.放大环节D.执行环节7.闭环控制系统必须通过（C）。

p3A.输入量前馈参与控制B.干扰量前馈参与控制C.输出量反馈到输入端参与控制D.输出量局部反馈参与控制8.随动系统要求系统的输出信号能跟随（C的变化）。

P6A.反馈信号B.干扰信号C.输入信号D.模拟信号9.若反馈信号与原系统输入信号的方向相反则为（负反馈）。

P3A.局部反馈B.主反馈C.正反馈D.负反馈10．输出量对系统的控制作用没有影响的控制系统是（开环控制系统）。

P2A.开环控制系统B.闭环控制系统C.反馈控制系统D.非线性控制系统11.自动控制系统的反馈环节中一般具有（ B ）。

p5A..给定元件B.检测元件 C．放大元件 D．执行元件12. 控制系统的稳态误差反映了系统的〔 B 〕p8A. 快速性B.准确性C. 稳定性D.动态性13.输出量对系统的控制作用有直接影响的系统是（ B ）p3A.开环控制系统B.闭环控制系统C.线性控制系统D.非线性控制系统14.通过动态调节达到稳定后，被控量与期望值一致的控制系统为（无差系统）。

祝守新邢英杰韩连英《机械工程控制基础》习题解答机械控制工程基础答案提示第二章系统的数学模型2-1试求如图2-35所示机械系统的作用力F(t)与位移y(t)之间微分方程和传递函数。

F(t)图2-35题2-1图解：依题意：d2ytadytmFtfkytdt2bdtd2ytdytafkytFt故m2dtbdtY传递函数:G2Fmfk2-2对于如图2-36所示系统，试求出作用力F1(t)到位移某2(t)的传递函数。

其中，f为粘性阻尼系数。

F2(t)到位移某1(t)的传递函数又是什么？图2-36题2-2图解：依题意：d2某1td某1td某2t对m1：F1k1某1tfm12dtdtdt对两边拉氏变换：F1k1某1f某1某2m12某1①d2某2td某1td某2t对m2：F2tfk2某2tm2dt2dtdt对两边拉氏变换：F2f某1某2k2某2m22某2②m12fk1某1f某2F1故：2f某1m2fk2某2F2SF1m22fk2fF2某12m12fk1m22fk2f故得：2fF1F2m1fk2某2222mfkmfkf1122故求F1t到某2t的传递函数令：F20某2fG1F1m12fk1m22fk2f2fm1m24fm1m23m1k2m2k12fk1k2k1k2求F2t到某1t的传递函数令：F10某1fG1F2m12fk1m22fk2f22-3试求图2-37所示无源网络传递函数。

fm1m24fm1m23m1k2m2k12fk1k2k1k2o图2-37题2-3图解（a）系统微分方程为i1tdti2tR1Cuii2tR1itR2u0itR2iti1ti2t拉氏变换得I1R1I2CUiI2R1I1R2U0I1R2II1I2R2R1C1U0R2CR11R1R2消去中间变量I1,I2,I得：GR1R2UiR1R2CR11C1R1R2（b）设各支路电流如图所示。

系统微分方程为uitR1i3tu0tR1i3tL11234di2tdtu0ti4tdtC2di5tdtu0tR2i6tu0tL25i2ti3ti4ti5ti6t6由（1）得：UiR1I3Uo由（2）得：R1I3L1I2由（3）得：Uo i4C2由（4）得：UoL2I5由（5）得：UoR2I6由（6）得：I2I3I4I5I6故消去中间变量I1,I2,I3,I4,I5,I6得：L2L1UL1o1L2R1UiL1L2LC2L1L2R1R2L2112L1L2R1R22-4证明Lcot22证明：设ftcot由微分定理有Ld2ft2Ff0f(1)0dt2由于f0co01，f0in00，d2ftdt22cot将式（2）各项带入式（1）中得L2cot2F即2F2F整理得F222-5求f(t)122t的拉氏变换。

习 题2.1 什么是线性系统其最重要的特性是什么下列用微分方程表示的系统中,x o 表示系统输出,x i 表示系统输入,哪些是线性系统 (1) x x x x x ioooo 222=++ (2) x tx x xiooo222=++ (3) x x x xio 222oo=++ (4) x tx x x xiooo222o=++ 解: 凡是能用线性微分方程描述的系统就是线性系统。

线性系统的一个最重要特性就是它满足叠加原理。

该题中（2）和（3）是线性系统。

2.2 图（题2.2）中三同分别表示了三个机械系统。

求出它们各自的微分方程，图中x i 表示输入位移，x o 表示输出位移，假设输出端无负载效应。

图(题2.2) 解: (1)对图(a)所示系统，由牛顿定律有 即x c x c c xm i121oo )(=++ (2)对图(b)所示系统，引入一中间变量x,并由牛顿定律有 消除中间变量有(3)对图(c)所示系统，由牛顿定律有 即x k x c x k k xc iioo121)(+=++ 2.3求出图(题2.3)所示电系统的微分方程。

图（题2.3）解:(1)对图(a)所示系统,设i 1为流过R 1的电流,i 为总电流,则有 消除中间变量,并化简有u R C u CC R R u R C uR C u C C R R u R C iiiooo12211221222121211)()1(1+++=-+++(2)对图(b)所示系统，设i 为电流，则有 消除中间变量,并化简有2.4 求图(题2.4)所示机械系统的微分方程。

图中M 为输入转矩,C m 为圆周阻尼，J 为转动惯量。

解：设系统输入为M （即），输出θ(即)，分别对圆盘和质块进行动力学分析，列写动力学方程如下：消除中间变量x,即可得到系统动力学方程KM M c Mm C R c k KJ c C km R cJ mC mJ mmm++=++-++++ θθθθ）（22)()()4(2.5 输出y(t)与输入x(t)的关系为y(t)= 2x(t)+0.5x 3(t)。

控制工程基础习题解答第二章2-1．试求下列函数的拉氏变换，假定当t<0时，f(t)=0。

(1).()()t t f 3cos 15-= 解：()[]()[]9553cos 152+-=-=s ss t L t f L (2). ()t et f t10cos 5.0-=解：()[][]()1005.05.010cos 25.0+++==-s s t eL t f L t(3). ()⎪⎭⎫⎝⎛+=35sin πt t f 解：()[]()252355cos 235sin 2135sin 2++=⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+=s st t L t L t f L π 2-2．试求下列函数的拉氏反变换。

(1).()()11+=s s s F解：()[]()⎥⎦⎤⎢⎣⎡++=⎥⎦⎤⎢⎣⎡+=---11121111s k s k L s s L s F L()10111==⎥⎦⎤⎢⎣⎡+=s s s s k ()()111112-=-=+⎥⎦⎤⎢⎣⎡+=s s s s k()[]te s s L s F L ----=⎥⎦⎤⎢⎣⎡+-=111111 (2).()()()321+++=s s s s F解：()[]()()⎥⎦⎤⎢⎣⎡+++=⎥⎦⎤⎢⎣⎡+++=---3232121111s k s k L s s s L s F L()()()1223211-=-=+⎥⎦⎤⎢⎣⎡+++=s s s s s k ()()()2333212=-=+⎥⎦⎤⎢⎣⎡+++=s s s s s k ()[]tt e e s s L s F L 231123221-----=⎥⎦⎤⎢⎣⎡+++-=(3).()()()2222522+++++=s s s s s s F 解：()[]()()⎥⎦⎤⎢⎣⎡+++++=⎥⎦⎤⎢⎣⎡+++++=---22222225232112211s s k s k s k L s s s s s L s F L()()()22222225221-=-=+⎥⎦⎤⎢⎣⎡+++++=s s s s s s s k ()()()3331331222222513223222232==-=---=-+---=++⎥⎦⎤⎢⎣⎡+++++=--=+k k jjjjk k k j s s s s s s s s j s k s k ()[]()()t e e s s s L s s s s L s F Ltt cos 32111322223322221211-----+-=⎥⎦⎤⎢⎣⎡+++++-=⎥⎦⎤⎢⎣⎡+++++-=2-3．用拉氏变换法解下列微分方程（1）()()()()t t x dt t dx dt t x d 18622=++，其中()()00,10===t dt t dx x 解：对方程两边求拉氏变换，得：()()()()()()()()()()()()()()()()()[]()0,8747818747814242168616181618060042132132122222≥-+==-===++++=++++=++++==+-+-=+-+=-----t e e s X L t x k k k s k s k s k s s s s s s s s s s s X ss X s sX s s X s ss X x s sX t dt t dx sx s X s t t（2）()()210=+t x dtt dx ，其中()00=x 解：对方程两边求拉氏变换，得：()()()()()()()()()[]()0,515151511010221021001012121≥-==-==++=+==+=+---t e s X L t x k k s k s k s s s X s s X s sX ss X x s sX t（3）()()300100=+t x dtt dx ，其中()500=x 解：对方程两边求拉氏变换，得：()()()()()()()()()[]()0,4734731001003005030010050300100010012121≥+====++=++==+-=+---t e s X L t x k k s k s k s s s s X ss X s sX s s X x s sX t2-4．某系统微分方程为()()()()t x dtt dx t y dt t dy i i 322300+=+，已知()()0000==--i x y ，其极点和零点各是多少？解：对方程两边求拉氏变换，得：()()()()()()()()()()()233223323022030000-=-=++==+-=+-z p i i i i s s s s s X s Y s G s X x s sX s Y y s sY2-5．试求图2-25所示无源网络传递函数。