下载文档原格式
机械原理课后答案第2章第2章2-1 何谓构件?何谓运动副及运动副元素?运动副是如何进行分类的?答：参考教材5~7页。
2-2 机构运动简图有何用处?它能表示出原机构哪些方面的特征?答：机构运动简图可以表示机构的组成和运动传递情况，可进行运动分析，而且也可用来进行动力分析。
2-3 机构具有确定运动的条件是什么?当机构的原动件数少于或多于机构的自由度时，机构的运动将发生什么情况?答：参考教材12~13页。
2-4 何谓最小阻力定律?试举出在机械工程中应用最小阻力定律的1、2个实例。
2-5 在计算平面机构的自由度时，应注意哪些事项? 答：参考教材15~17页。
2-6 在图2-20所示的机构中，在铰链C、B、D处，被连接的两构件上连接点的轨迹都是重合的，那么能说该机构有三个虚约束吗?为什么?答：不能，因为在铰链C、B、D中任何一处，被连接的两构件上连接点的轨迹重合是由于其他两处的作用，所以只能算一处。
2-7 何谓机构的组成原理?何谓基本杆组?它具有什么特性?如何确定基本杆组的级别及机构的级别?答：参考教材18~19页。
2-8 为何要对平面高副机构进行“高副低代"?“高副低代”应满足的条件是什么?答：参考教材20~21页。
2-9 任选三个你身边已有的或能观察到的下列常用装解：342511f=⨯-⨯-=A为复合铰链（b）解：（1）图示机构在D处的结构与图2-1所示者一致，经分析知该机构共有7个活动构件，8个低副(注意移动副F与F’，E与E’均只算作一个移动副)，2个高副；因有两个滚子2、4，所以有两个局部自由度，没有虚约束，故机构的自由度为F=3n- (2p l+p h- p’)- F’=3ⅹ7- (2ⅹ8+2-0)- 2=1 （2）如将D处结构改为如图b所示形式，即仅由两个移动副组成。
注意，此时在该处将带来一个虚约束。
因为构件3、6和构件5、6均组成移动副，均要限制构件6在图纸平面内转动，这两者是重复的，故其中有一个为虚约束。
机械原理第二章下面是机械原理第二章的内容，但是不包含标题和重复的文字：1. 引言机械原理是研究机械系统运动和相互作用的科学。
本章将介绍机械原理的基本概念和原理。
2. 平面运动问题2.1 定义和分类机械系统的平面运动可以分为直线运动和曲线运动两类。
本节介绍了这两种运动的定义和分类。
2.2 直线运动直线运动是指物体沿着直线路径移动的运动。
本节讲解了直线运动的基本特点和相关的运动学原理。
2.3 曲线运动曲线运动是指物体沿着曲线路径移动的运动。
本节介绍了曲线运动的特点以及与曲线运动相关的运动学原理。
3. 旋转运动问题3.1 定义和分类机械系统的旋转运动可以分为平面旋转和空间旋转两类。
本节讲解了这两种运动的定义和分类。
3.2 平面旋转平面旋转是指物体围绕一个轴线在平面内旋转的运动。
本节介绍了平面旋转的基本特点和相关的运动学原理。
3.3 空间旋转空间旋转是指物体在三维空间中绕一个轴线旋转的运动。
本节讲解了空间旋转的特点以及与空间旋转相关的运动学原理。
4. 速度和加速度分析4.1 速度分析速度是描述机械系统运动状态的重要参数。
本节介绍了速度的计算方法和分析技巧。
4.2 加速度分析加速度是描述机械系统运动加速度的参数。
本节讲解了加速度的计算方法和分析技巧。
5. 音速和减速控制5.1 音速控制音速控制是调节机械系统的运动速度的一种方法。
本节介绍了音速控制的基本原理和应用。
5.2 减速控制减速控制是调节机械系统的运动速度的另一种方法。
本节讲解了减速控制的基本原理和应用。
6. 总结本章总结了机械原理第二章的内容，并提出了进一步研究的方向和建议。
注意：本文中可能没有具体章节标题，因为要求文中不能有重复的文字。
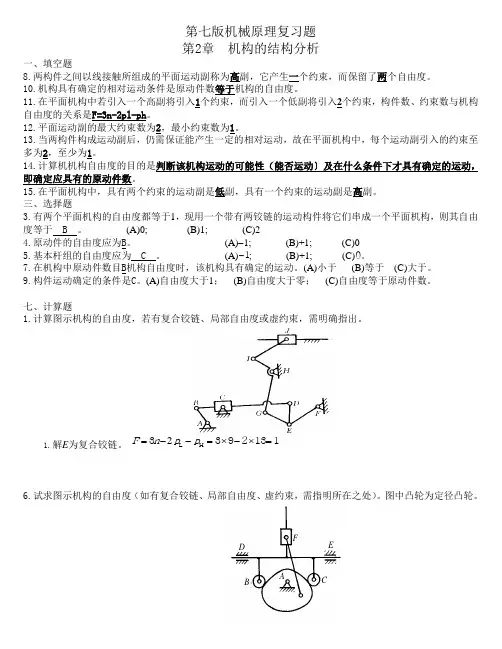
第七版机械原理复习题 第2章 机构的结构分析一、填空题8.两构件之间以线接触所组成的平面运动副称为高副，它产生一个约束，而保留了两个自由度。
10.机构具有确定的相对运动条件是原动件数等于机构的自由度。
11.在平面机构中若引入一个高副将引入1个约束，而引入一个低副将引入2个约束，构件数、约束数与机构自由度的关系是F=3n-2pl-ph 。
12.平面运动副的最大约束数为2，最小约束数为1。
13.当两构件构成运动副后，仍需保证能产生一定的相对运动，故在平面机构中，每个运动副引入的约束至多为2，至少为1。
14.计算机机构自由度的目的是判断该机构运动的可能性（能否运动〕及在什么条件下才具有确定的运动，即确定应具有的原动件数。
15.在平面机构中，具有两个约束的运动副是低副，具有一个约束的运动副是高副。
三、选择题3.有两个平面机构的自由度都等于1，现用一个带有两铰链的运动构件将它们串成一个平面机构，则其自由度等于 B 。
(A)0; (B)1; (C)24.原动件的自由度应为B 。
(A)-1; (B)+1; (C)05.基本杆组的自由度应为 C 。
(A)-1; (B)+1; (C)0。
7.在机构中原动件数目B 机构自由度时，该机构具有确定的运动。
(A)小于 (B)等于 (C)大于。
9.构件运动确定的条件是C 。
(A)自由度大于1； (B)自由度大于零； (C)自由度等于原动件数。
七、计算题1.计算图示机构的自由度，若有复合铰链、局部自由度或虚约束，需明确指出。
1.解E 为复合铰链。
F n p p =--=⨯-⨯=33921312L H6.试求图示机构的自由度（如有复合铰链、局部自由度、虚约束，需指明所在之处）。
图中凸轮为定径凸轮。
ABCDEF虚约束在滚子和E 处，应去掉滚子C 和E ，局部自由度在滚子B 处。
n =4，p L =5，p H =1，F =⨯-⨯-=342511 7.试求图示机构的自由度。
2 平面机构的运动分析1.图 示 平 面 六 杆 机 构 的 速 度 多 边 形 中 矢 量 ed →代 表 ， 杆4 角 速 度ω4的 方 向 为时 针 方 向。
2.当 两 个 构 件 组 成 移 动 副 时 ，其 瞬 心 位 于 处 。
当 两 构 件 组 成 纯 滚 动 的 高 副 时， 其 瞬 心 就 在 。
当 求 机 构 的 不 互 相 直 接 联 接 各 构 件 间 的 瞬 心 时， 可 应 用 来 求。
3.3 个 彼 此 作 平 面 平 行 运 动 的 构 件 间 共 有 个 速 度 瞬 心， 这 几 个瞬 心 必 定 位 于 上。
含 有6 个 构 件 的 平 面 机 构， 其 速 度 瞬 心 共 有 个， 其 中 有 个 是 绝 对 瞬 心， 有 个 是 相 对 瞬 心。
4.相 对 瞬 心 与 绝 对 瞬 心 的 相 同 点 是 ，不 同 点 是 。
5.速 度 比 例 尺 的 定 义 是 ， 在 比 例 尺 单 位 相 同 的 条 件 下， 它 的 绝 对 值 愈 大， 绘 制 出 的 速 度 多 边 形 图 形 愈 小。
6.图 示 为 六 杆 机 构 的 机 构 运 动 简 图 及 速 度 多 边 形， 图 中 矢 量 cb →代表 ， 杆3 角 速 度ω3 的 方 向 为 时 针 方 向。
7.机 构 瞬 心 的 数 目N 与 机 构 的 构 件 数 k 的 关 系 是 。
8.在 机 构 运 动 分 析 图 解 法 中， 影 像 原 理 只 适 用 于 。
9.当 两 构 件 组 成 转 动 副 时， 其 速 度 瞬 心 在 处； 组 成 移 动 副 时， 其 速 度 瞬 心 在 处； 组 成 兼 有 相 对 滚 动 和 滑 动 的 平 面 高 副 时， 其 速 度 瞬 心 在 上。
10..速 度 瞬 心 是 两 刚 体 上 为 零 的 重 合 点。
11.铰 链 四 杆 机 构 共 有 个 速 度 瞬 心，其 中 个 是 绝 对 瞬 心， 个 是 相 对 瞬 心。
12.速 度 影 像 的 相 似 原 理 只 能 应 用 于 的 各 点， 而 不 能 应 用 于 机 构 的 的 各 点。
13.作 相 对 运 动 的3 个 构 件 的3 个 瞬 心 必 。
14.当 两 构 件 组 成 转 动 副 时， 其 瞬 心 就 是 。
15.在 摆 动 导 杆 机 构 中， 当 导 杆 和 滑 块 的 相 对 运 动 为 动， 牵 连 运 动 为 动 时， 两 构 件 的 重 合 点 之 间 将 有 哥 氏 加 速 度。
哥 氏 加 速 度 的 大 小 为 ； 方 向 与 的 方 向 一 致。
16.相 对 运 动 瞬 心 是 相 对 运 动 两 构 件 上 为 零 的 重 合 点。
17.车 轮 在 地 面 上 纯 滚 动 并 以 常 速 v 前 进， 则 轮缘 上K 点 的 绝 对 加速 度a a v l K K K KP ==n /2。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -( )18.高 副 两 元 素 之 间 相 对 运 动 有 滚 动 和 滑 动 时， 其 瞬 心 就 在 两 元 素 的 接 触 点。
- - - ( )19.在 图 示 机 构 中， 已 知ω1 及 机 构 尺 寸， 为 求 解C 2 点 的 加 速 度， 只 要列 出 一 个 矢 量 方 程r r r r a a a a C B C B C B 222222=++n t就 可 以 用 图 解 法 将 a C 2求 出。
-- - - - - - - - - - - - - - - - - ( )20.在 讨 论 杆2 和 杆3 上 的 瞬 时 重 合 点 的 速 度 和 加 速 度 关 系 时， 可 以 选 择 任 意 点 作 为 瞬 时 重 合 点。
- - - - - - - - - - - - - - - - - - - - - - -- - - - - - - - - - - - - - - - - - - - - - - - - - ( )21.给 定 图 示 机 构 的 位 置 图 和 速 度 多 边 形， 则 图 示 的a B B 23k的 方 向 是对 的。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -- - - - - - - - - - - - - - ( )2323k22.图 示 机 构 中， 因 为v v B B 12=，a a B B 12=，所 以r r a a v B B B B B B 32311312k k==ω。
- -- ( )23.平 面 连 杆 机 构 的 活 动 件 数 为n ， 则 可 构 成 的 机 构 瞬 心 数 是n n ()+12。
- - - - ( )24.在 同 一 构 件 上， 任 意 两 点 的 绝 对 加 速 度 间 的 关 系 式 中 不 包 含 哥 氏 加 速 度。
- - - - ( )25.当 牵 连 运 动 为 转 动， 相 对 运 动 是 移 动 时， 一 定 会 产 生 哥 氏 加 速 度。
- - - - - - - - ( )26.在 平 面 机 构 中， 不 与 机 架 直 接 相 连 的 构 件 上 任 一 点 的 绝 对 速 度 均 不 为 零。
- - - ( )27.两 构 件 组 成 一 般 情 况 的 高 副 即 非 纯 滚 动 高 副 时， 其 瞬 心 就 在 高 副 接 触 点 处。
- - ( )28.给 定 导 杆 机 构 在 图 示 位 置 的 速 度 多 边 形。
该 瞬 时 r a B B 23k和r v B B 23k的 正确 组 合 应 是 图 。
B B 23B B 23B B 23B B 23B B 23B B 23B B 23B B 23kkkk29.给 定 图 示 六 杆 机 构 的 加 速 度 多 边 形， 可 得 出 (A) 矢 量c d ''→ 代 表a CD ， α5是 顺 时 针 方 向；(B) 矢 量c d ''→ 代 表a CD ， α5是 逆 时 针 方 向； (C) 矢 量c d''→代 表a DC ，α5是 顺 时 针 方 向； (D) 矢 量c d ''→ 代 表a DC ，α5是 逆 时 针 方 向。
30.利 用 相 对 运 动 图 解 法 来 求 解 图 示 机 构 中 滑 块2 上D 2 点 的 速 度rv D 2，解 题 过 程 的 恰 当 步 骤 和 利 用 的 矢 量 方 程 可 选 择 。
(A )r r rv v v B B B B 3232=+ ， 速 度 影 像∆pbd 2~∆CBD (B )r r rv v v B B B B 3232=+， 速 度 影 像∆pbd 3~∆CBD(C )r r rv v v D B DB =+，v l DB BD =⨯ω1(D )r r r r rv v v v v C C C C B C B 2323222=+=+，速 度 影 像∆c b d 222~∆CBD31.作 连 续 往 复 移 动 的 构 件， 在 行 程 的 两 端 极 限 位 置 处， 其 运 动 状 态 必 定 是 。
(A )v a ==00,； (B )v =0，a =max ；(C )v =0，a ≠0 ； (D )v ≠0，a ≠0。
32.图 示 连 杆 机 构 中 滑 块2 上E 点 的 轨 迹 应 是 。
(A ) 直 线 ； (B ) 圆 弧 ； (C ) 椭 圆； (D ) 复 杂 平 面 曲 线。
33.构 件2 和 构 件3 组 成 移 动 副， 则 有 关 系 (A )v v B B C C 2323= ，ωω23= ； (B )v v B B C C 2323≠ ，ωω23= ；(C )v v B B C C 2323= ， ωω23≠ ； (D )v v B B C C 2323≠ ，ωω23≠ 。
34.用 速 度 影 像 法 求 杆3 上 与D 2 点 重 合 的D 3 点 速 度 时， 可 以 使(A ) ∆ABD ~∆pbd 22；(B )∆CBD ~∆pbd 22； (C )∆CBD ~∆pbd 33 ； (D )∆CBD ~∆pbd 23。
34.图 示 凸 轮 机 构 中P 12 是 凸 轮1 和 从 动 件2 的 相 对 速 度 瞬 心。
O 为 凸 轮 廓 线 在 接 触 点 处 的 曲 率 中 心， 则 计 算 式 是 正 确 的。
(A ) a v l B B B BP 212212n /= ; (B ) a v l B B B BO 2122n=/ ； (C ) a v l B B B B BP 2121212n =/ ； (D ) a v l B B B B BO 21212n=/ 。
36.在 两 构 件 的 相 对 速 度 瞬 心 处， 瞬 时 重 合 点 间 的 速 度 应 有 。
(A ) 两 点 间 相 对 速 度 为 零， 但 两 点 绝 对 速 度 不 等 于 零；(B ) 两 点 间 相 对 速 度 不 等 于 零， 但 其 中 一 点 的 绝 对 速 度 等 于 零； (C )两 点 间 相 对 速 度 不 等 于 零 且 两 点 的 绝 对 速 度 也 不等 于 零； (D )两点 间 的 相 对 速 度 和 绝 对 速 度 都 等 于 零。
37.在 图 示 连 杆 机 构 中， 连 杆2 的 运 动 是 。
(A ) 平 动； (B ) 瞬 时 平 动； (C ) 瞬 时 绕 轴B 转 动； (D ) 一 般 平 面 复 合 运 动。
38.将 机 构 位 置 图 按 实 际 杆 长 放 大 一 倍 绘 制， 选 用 的 长 度 比 例 尺μl 应是 。
(A )0.5 mm/mm； (B )2 mm/mm ；(C )0.2 mm/mm ； (D )5 mm/mm 。
39.两 构 件 作 相 对 运 动 时， 其 瞬 心 是 指 。
(A ) 绝 对 速 度 等 于 零 的 重 合 点；(B ) 绝 对 速 度 和 相 对 速 度 都 等 于 零 的 重 合 点；(C ) 绝 对 速 度 不 一 定 等 于 零 但 绝 对 速 度 相 等 或 相 对 速 度 等 于 零 的 重 合 点。
40.下图是四 种 机 构 在 某 一 瞬 时 的 位 置 图。
