2012-2013高一数学期末复习题

2012学年高一数学期末复习（必修一）4一、选择题：本大题10小题，每小题5分，满分50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1、已知全集I ={0,1,2,3,4}，集合{1,2,3}M =，{0,3,4}N =，则()I M N 等于 ( ) A.｛0，4｝ B.｛3，4｝ C.｛1，2｝ D. ∅ 2、设集合2{650}M x x x =-+=，2{50}N x x x =-=，则MN 等于（ ） A.｛0｝ B.｛0，5｝ C.｛0，1，5｝ D.｛0，－1，－5｝3、计算：9823log log ⋅＝（ ）A 12B 10C 8D 64、函数2(01)x y a a a =+>≠且图象一定过点 ( )A （0,1）B （0,3）C （1,0）D （3,0）5、“龟兔赛跑”讲述了这样的故事：领先的兔子看着慢慢爬行的乌龟，骄傲起来，睡了一觉，当它醒来时，发现乌龟快到终点了，于是急忙追赶，但为时已晚，乌龟还是先到达了终点…用S 1、S 2分别表示乌龟和兔子所行的路程，t 为时间，则与故事情节相吻合是 （ ）6、函数12log y x =的定义域是（ ）A {x ｜x ＞0}B {x ｜x ≥1}C {x ｜x ≤1}D {x ｜0＜x ≤1}7、把函数x1y -=的图象向左平移1个单位，再向上平移2个单位后，所得函数的解析式应为 （ ）A 1x 3x 2y --=B 1x 1x 2y ---=C 1x 1x 2y ++=D 1x 3x 2y ++-= 8、设x x e 1e )x (g 1x 1x lg )x (f +=-+=，，则 ( ) A f(x)与g(x)都是奇函数 B f(x)是奇函数，g(x)是偶函数C f(x)与g(x)都是偶函数D f(x)是偶函数，g(x)是奇函数9、使得函数2x 21x ln )x (f -+=有零点的一个区间是 ( ) A (0，1) B (1，2) C (2，3) D (3，4)10、若0.52a =，πlog 3b =，2log 0.5c =，则（ ）A a b c >>B b a c >>C c a b >>D b c a >> 二、填空题：本大题共4小题，每小题5分，满分20分11、函数5()2log (3)f x x =++在区间[-2，2]上的值域是______12、计算：2391－　⎪⎭⎫ ⎝⎛＋3264＝______ 13、函数212log (45)y x x =--的递减区间为______14、函数122x )x (f x -+=的定义域是______ 三、解答题 ：共5小题，满分80分。

2012-2013学年度第一学期期末考试高一数学试题一.选择题（本大题共12个小题，每小题5分,共60分）1.已知集合x B A {},5,4,3,2,1{==│}3<x ，则=B A （ ）}2,1.{A }5,4,3.{B x C .{│}3<x x D .{│}3≥x2.已知,0sin >α且,0cos <α则角α所在的象限是（ ）.A 第一象限 .B 第二象限 .C 第三象限 .D 第四象限3.已知函数,25)(--=x x x f 则函数)(x f （ ） .A 在),2(+∞-上是减函数 .B 在),2(+∞-上是增函数 .C 在),2(+∞上是减函数 .D 在),2(+∞上是增函数4.设C 是线段AB 上一点,且O CA BC ,3=是平面内一点,若43=λ+则=λ（ ）31.A 32.B 41.C 43.D 5.下列函数中，既是奇函数又是最小正周期为1的周期函数的是（ ）)32sin(.ππ+=x y A )c o s ()s i n (.x x y B ππ= x y C π2c o s .= x y D π2t a n .=6.已知21,e e 都是单位向量，它们的夹角是,1200则│21e e +│=（ ）2.A3.B 2.C 1.D7.函数R x x x x f ∈-=,cos 4cos )(2的值域为（ ）]5,3.[-A ]5,4.[-B ]5,0.[C ),4.[+∞-D8.已知函数)(x f 是函数xa y log =的反函数，若,2)21(=f 则（ ）x x f A 2)(.= x x f B 4)(.= x x f C 2log )(.= xx f D 4log )(.=9.已知向量b 与)2,1(-=a 的夹角为,1800且│b │=52，则b =（ ）)4,2.(-A )4,2.(-B )2,4.(C )2,4.(--D10.设,log 213=a 321log =b ,3)21(=c 则（ ）c b a A >>. b c a B >>. b a c C >>. a b c D >>.11.将函数)62sin()(π+=x x f 的图象向左平行移动)0(>ϕϕ个单位长度后，得到函数)32cos(π+=x y 和图象，则ϕ的最小值为（ ）6.πA 65.πB 3.πC 32.πD12.关于x 的方程t x x =+sin 2sin 在]2,0[π上有且仅有2个解，则实数t 的取值范围是（ ）]1,0.[A )1,0.(B ]3,1.[C )3,1.(D二.填空题（本大题共4个小题，每小5分，共20分）13.已知函数)(x f 是定义在R 上的奇函数，当,0≥x 时)1(3log )(+=x x f ，则=-)2(f ；14.若函数R x x a x x f ∈+=,cos sin 2)(的最小值为,3-则实数=a ； 15.已知,2cos sin ),,2(ααππα=∈则=αsin ；16若函数122)(+=x xx f 则 +-+-++++)2()1()2013()2()1(f f f f f =-+)2013(f ； 三解答题：（本大题共6个小题，共70分，要求写出必要文字说明，证明过程或演算步骤） 17（10分）已知α是第三象限，,55sin -=α求ααtan ,cos 的值. 18(12分)已知.3tan =α （1）求)4tan(πα+的值；(2)求ααααcos sin cos sin -+的值.19(12分)已知)2,(),1,0(k B A AC =).3,2(（1）若三点C B A ,,共线，求│AB │；（2）若090=∠ACB ，求k 的值. 20(12分)已知函数R x x x x f ∈+-=,2sin )32sin()(π.(1) 求函数)(x f 的最小正周期； (2)求函数)(x f 的单调增区间. 21(12分)已知函数31313131)(,)(--+=-=x x x g xx x f ,0≠x .(1)写出函数)(x f 的单调区间；（2）分别计算)3()3()9(),2()2()4(g f f g f f --,由此概括出关于)(),(x g x f 的一般结论，并给出证明.22(12分)已知函数)(x f 是定义在R 上的奇函数,且)1(+=x f y 是偶函数.(1)求证:)(x f 是周期函数;(2)若)(x f 在]1,1[-上是增函数,求证:)(x f 在]3,1[上是减函数.2012-2013学年度第一学期期末考试高一数学答题卡座位号：；得分；二.填空题（本大题共4个小题，每小题5分，共20分）13 ; 14 ; 15 ; 16 .三.解答题（本大题6个小题，共70分，要求写出必要的证明、演算或推理过程）17(10分)18(12分)19(12分) 20(12分)21(12分)22（12分）2012-2013学年度第一学期期末考试高一数学参考答案一选择题：51- ABDCB 106- DABAC 1211- CD 二填空题： 1.13-， 5.14 21.15 2013.16 三解答题： 17解α是第三象限角，且55sin -=α …… 1分 ∴ 552)55(1sin 1cos 22-=---=--=αα …… 5分 ∴ 21)525(55c o s s i n t a n =-⨯-==ααα …… 9分 所以：21tan ,552cos =-=αα …… 10分 18解：（1）3tan =α∴ 2131134tantan 14tantan )4tan(-=⨯-+=-+=+παπαπα …… 6分（2）αααcos sin tan = 且 3t a n=α ∴ααcos 3sin = …… 8分 ∴2cos cos 3cos cos 3cos sin cos sin =-+=-+αααααααα …… 12分 19 解：(1) )2,(),1,0(k B A∴=)1,(k又 三点C B A ,,共线.∴∥ …… 3分又 =)3,2(∴0213=⨯-k∴32=k =)1,32( …… 5分所以：││3131)32(22=+=…… 6分（2）因为=-=)2,2()1,()3,2(k k -=- …… 8分由090=∠ACB 得BC ⊥AC∴BC •AC =0 …… 10分又 AC =)3,2(∴032)2(2=⨯+-⨯k所以：5=k …… 12分 20解：（1）因为x x x f 2sin )32sin()(+-=πx x x x f 2sin 3sin2cos 3cos2sin )(+-=∴ππx x 2cos 232sin 23-=)62sin(3π-=x …… 5分所以；函数)(x f 的最小正周期为.π …… 6分 （2）由z k k x k ∈+≤-≤+-,226222πππππ得 …… 8分z k k x k ∈+≤≤+-,36ππππ…… 11分所以：函数)(x f 的单调增区间为z k k k ∈++-],3,6[ππππ…… 12分21解：（1）函数)(x f 的单调增区间为)0,(-∞和),0(+∞；无单调减区间. …… 4分 (2)计算，得0)3()3()9(,0)2()2()4(=-=-g f f g f f …… 6分概括结论： 0)()()(2=-x g x f x f ,0≠x …… 8分证明：当 0≠x 时，))((])()[()()()(313131313123122x x x x x x x g x f x f +---=---)()(32323232-----=x x xx0=所以：命题成立. …… 12分22证明（1）因为函数)1(+=x f y 是偶函数)1()1(+=+-∴x f x f …… 3分用1+x 代替x 得 )()2(x f x f -=+ 又)(x f 是奇函数；∴ )()2(x f x f -=+)()]([)2()4(x f x f x f x f =--=+-=+∴ …… 5分所以：函数)(x f 是周期函数，4是它的周期. …… 6分 (2)任取]3,1[,21∈x x 且.21x x <由（1）得)2()42()2()(--=-+-=+-=x f x f x f x f …… 8分 则)2()2()()(1221---=-x f x f x f x f由]3,1[,21∈x x 且.21x x <得]1,1[2,212-∈--x x 且2212->-x x 又因为函数)(x f 在]1,1[-上是增函数)2()2(12->-∴x f x f0)()(21>-∴x f x f 即)()(21x f x f > …… 11分所以：函数)(x f 在]3,1[上是减函数. …… 12分。

2012-2013学年度石家庄市高一第二学期期末试卷数学答案一、选择题：共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1-5：ADDBC 6-10：DACBD11：B 12：【普通高中】D 【示范高中】A二、填空题：本大题共4小题，每小题5分，共20分.13.2014.215. 1 16. 【普通高中】1(1)2n -- 【示范高中】1()2n三、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．17. (本小题满分10分)解： （I ）设等差数列{}n a 的公差为d ，1(1)n a d n ∴=+- …………………………………1分又521,,a a a 成公比不为1的等比数列，2215a a a = …………………………………3分2(1)1(14)d d +=⨯+2d =或0d =（舍） …………………………………5分 （Ⅱ）111111()(21)(21)22121n n n b a a n n n n +===--+-+ ………………………………7分 1111111111(1)(1)233557212122121n nS n n n n =-+-+-+-=-=-+++ …………10分 18．（本小题满分12分） 解：第一步：在BEF ∆中，sin sin BE EFBFE FBE=∠∠, 所以sin sin()a BE γαβγ=++， …………………………………4分第二步：在AEF ∆中, sin sin AE EFAFE EAF=∠∠, 所以sin()sin()a AE γδβγδ+=++， …………………………………8分第三步：在ABE ∆中，AB =即AB =…………12分 19．（本小题满分12分）解：当0m =时，两直线方程为6x =-，0x =，满足题意； ……………………………2分 当0m ≠时，直线方程为2216y x m m =--与2233m y x m -=-， 由题意可知，2123mm m--= …………………………………4分 即3(2)m m =-2230m m --=，解得1m =-或3m =； …………………………………6分 当1m =-时，两直线方程为60x y ++=，203x y ++=，满足题意； …………………………………8分当3m =时，两直线方程为960x y ++=，960x y ++=，两直线重合，不合题意． ……………………10分 ∴0m =，1m =-． ……………………12分 20. （本小题满分12分） 解：（I ）∵2sin (2sin sin )(2sin sin )a A B C b C B c ＝－＋－，得22(2)(2)a b c b c b c ＝－＋－，即222bc b c a ＝＋－，………………………………2分∴2221cos =22b c a A bc +-=， …………………………………4分 ∴60A =. …………………………………6分(Ⅱ)∵A B C ＋＋＝180， ∴18060120B C＋＝－＝.由sin sin B C +=sin sin(120)B B +-=，……………………………8分∴sin sin120cos cos120sin B B B +-=∴3sin 2B B +=sin(30)1B += .…………………………………10分 又∵0120B＜＜，3030150B＜＋＜， ∴3090B＋＝，即60B＝. ∴60A B C ＝＝＝，∴ABC 为正三角形． …………………………………12分21．（本小题满分12分） 解：（I ）∵侧棱1AA ⊥底面ABCD ， ∴平面ABCD ⊥平面11CDD C ，∴点A 到面1MCC 的距离等于点A 到边CD 的距离，…………………………………2分在菱形ABCD 中，060B ∠=，2AB AD ==，所以h = …………………………………4分三棱锥1MCC A -的体积111142332MCC V S h ∆=⨯=⨯⨯⨯=. …………………………………6分 （II ）将矩形11DD C C 绕1DD 按逆时针旋转90 展开，与矩形11DD A A 共面,此时11A M MC AC +≥当且仅当点M 是棱1DD 的中点时，1A M MC +取得最小值． ………………………………8分在矩形11ADD A中MA =在矩形11ABB A中1AB =在11MB D ∆中1MB ==，所以在1MB A ∆中得：222111AB MA MB MA MB =+⇔⊥ …………………………………10分同理：11,MC MB MC MA M B M ⊥=⇒⊥ 面MAC .…………………………………12分 22. （本小题满分12分） 解: (Ⅰ) 210x bx b ++->(1)(1)0x x b ++->当11b -=-，即2b =时，解集为{|1}x x ≠-； …………………………………2分 当11b -<-，即2b <时，解集为{|1x x <-或1}x b >-；………………………………4分 当11b ->-，即2b >时，解集为{|1x x b <-或1}x >-．……………………………6分 (Ⅱ) 若对任意12,[1,1]x x ∈-，有12()()4f x f x -≤， 等价于对任意()f x 在[1,1]-上的最大值与最小值之差4M ≤, …………………………………8分据此分类讨论如下： ①当12b->，即2b <-时，(1)(1)24M f f b =--=->，与题设矛盾； ②当12b -<-，即2b >时，(1)(1)24M f f b =--=>，与题设矛盾； ③当102b -≤-<，即02b <≤时，2(1)()(1)422b b M f f =--=+≤恒成立； ④当012b ≤-≤，即20b -≤≤时，2(1)()(1)422b b M f f =---=-≤恒成立． …………………………10分综上可知，22b -≤≤． …………………………………12分附加题：(本小题满分10分)设圆心为(,1)C a a -，半径为r ，则点C 到直线2l 的距离1|43(1)14||711|55a a a d +-++==…………………………2分 点C 到直线3l 的距离是2|34(1)10||76|55a a a d +-++==…………………………4分 由题意，得222|711|,5|76|()3.5a r a r +⎧=⎪⎪⎨+⎪+=⎪⎩…………………………6分解得2,5a r ==， …………………………8分即所求圆的方程是22(2)(1)25x y -+-= . …………………………10分。

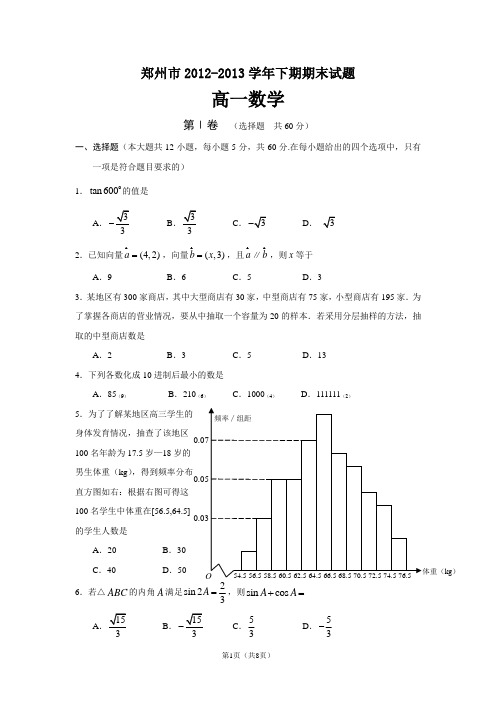
kg ）郑州市2012-2013学年下期期末试题高一数学第Ⅰ卷 （选择题共60分）一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的） 1．tan 600的值是A．3-B ．3C ．D ．2．已知向量(4,2)a = ，向量(,3)b x =，且a ∥b ，则x 等于A ．9B ．6C ．5D ．33．某地区有300家商店，其中大型商店有30家，中型商店有75家，小型商店有195家．为了掌握各商店的营业情况，要从中抽取一个容量为20的样本．若采用分层抽样的方法，抽取的中型商店数是A ．2B ．3C ．5D ．134．下列各数化成10进制后最小的数是A ．85（9）B ．210（6）C ．1000（4）D ．111111（2）5．为了了解某地区高三学生的 身体发育情况，抽查了该地区 100名年龄为17.5岁—18岁的 男生体重（kg ），得到频率分布直方图如右：根据右图可得这 100名学生中体重在[56.5,64.5]的学生人数是 A ．20 B ．30C ．40D ．506．若△ABC 的内角A 满足2sin 23A =，则sin cos A A += AB ．C ．53D ．53-7．已知(,)2παπ∈，3sin 5α=，则tan()4πα+等于A ．17B ．7C ．17- D ．7-8．将函数sin()(0,||2y x πωϕωϕ=+>≤的图象沿x 轴方向向左平移3π则ω，ϕ的值分别为A ．1，3π B ．1，3π- C ．2，3πD ．2，3π-9．已知向量a 与b的夹角为120，||3a = ，||a b += ||b 等于A ．5BC ．2D ．410．要得到函数cos(2)4y x π=-的图象，只需将函数cos(23y x π=+的图象 A ．向左平移24π个单位长度B ．向右平移24π个单位长度C ．向左平移724π个单位长度D ．向右平移724π个单位长度11．已知(2sin cos )(32sin 2cos )0x x x x -++=，则2sin 22cos 1tan x xx++的值为A ．85B ．58C ．43D ．3412．已知sin ,0()(1)1,0x x f x f x x π<⎧=⎨-->⎩，则1111(()66f f -+的值为A ．0B ．12C ．1-D ．2-第Ⅱ卷（非选择题 共90分）二、填空题（本大题共4小题，每小题5分，共20分．）13．若某程序框图如右图，则该程序运行后输出的k 的值为 ． 14．cos 43cos77sin 43cos167+的值为 ．15．已知向量(1,sin )a θ= ，(1,cos )b θ= ，则||a b - 的最大值为 ．16．对于下列命题：①函数sin()()y k x k Z π=-+∈为奇函数；。

2012-2013学年第二学期期末考试高一数学一、选择题（本题共12小题，每小题 5分，共60分）1.sin 480︒等于 （ ）A ．2-B ．12-C ．12D ．22.已知4sin 5α=，并且α是第二象限的角，那么tan α的值等于 （ ） A 43- B 34- C 43 D 343. 下列各式中，其值为23的是 （ ）A ．2sin15cos15B ．22sin 15cos 15+C ．22sin 151-D ．22cos 15sin 15- 4. 把－114π表示成θ＋2k π(k ∈Z)的形式，使|θ|最小的θ为 ( ) A ．34π B.π4 C.-34πD ．－π45.下列向量组中能作为表示它们所在平面内所有向量的基底的是 （ ） A.=a (0,0), =b (1,-2) B.=a (-1,2), =b (2,-4) C.=a (3,5), =b (6,10) D.=a (2,-3), =b (6, 9)6.设βα,为钝角，=+-==βαβα,10103cos ,55sin （ ） A ．π43 B ．π45 C ．π47 D ．π45或π477.将函数sin()3y x π=-的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再将所得的图象向左平移3π个单位，得到的图象对应的解析式是 （ ）A.1sin 2y x =B.1sin()26y x π=-C.1sin()22y x π=-D.sin(2)6y x π=-8.已知a = (0,1)，b = (33，x )，向量a 与b 的夹角为π3，则x 的值为 ( )A ．±3B ．± 3C ．±9D ．39.已知向量a ＝(2,sin θ），b ＝（１，θcos ）且a ⊥b ，其中),2(ππθ∈，则θθcos sin -等于 （ ）A ．55-B ．5C ． 5D ．510. 若AD 与BE 分别为△ABC 的边BC ，AC 上的中线，且AD a = ,BE b = ，则BC为( )A. 2433a b +B. 4233a b +C. 2233a b - D ．2233a b -+11. 已知函数()sin()(f x A x A ωϕωπϕπ=+>0,>0,-<<)的部分图象如图所示，则函数()f x 的解析式为 （ ）A ．1()2sin()24f x x π=+B ．13()2sin()24f x x π=+ C ．1()2sin()24f x x π=- D ．13()2sin()24f x x π=-12. 已知||2||,||0a b b =≠ ,且关于x 的方程2||0x a x a b ++⋅= 有实根,则a 与b 的夹角的取值范围是 ( ) A. [,]3ππ B. [,]6ππ C.2[,]33ππD. [0,6π] 二、填空题（每小题5分，共20分）13．已知扇形的圆心角为0120，半径为3，则扇形的面积是________．14. 设向量a 与b 的夹角为θ，且)3,3(=a，)1,1(2-=-a b ，则=θcos ________．15. 上的最小值为 ． 16. 给出下列六个命题，其中正确的命题是______．（填写正确命题前面的序号） ①存在α满足sin α＋cos α＝32. ②y ＝sin(32π－2x)是偶函数.③0,0,0a b a b ≠≠≠ 若则. ④22a b a b = 与是两个单位向量，则.⑤若α、β是第一象限角，且α＞β，则tan α＞tan β. ⑥若12sin(2)sin(2)44x x ππ-=-，则12x x k π-=，其中k Z ∈.三、解答题（本题共6小题，共70分） 17．(10分)已知角α的终边与单位圆交于点P （45，35）. （I ）求tan α值； （II ）求sin()2sin()22cos()ππααπα++--的值.18. (12分)已知函数()f x ＝3sin2x －2sin 2x .(1)求函数()f x )的最大值； (2)求函数()f x 的零点的集合．19.设21,e e 是两个不共线的向量，12122,3,AB e ke CB e e =+=+ 122CD e e =-，若A 、B 、D 三点共线，求k 的值. (12分)20. (12分)的最小正周期为π.（Ⅰ）求ω的值；（Ⅱ）求函数()f x 的单调递增区间21. (12分) 已知点O (0,0)，A (1,2)，B (4,5)及OP OA t AB =+,试问：(1)t 为何值时，P 在x 轴上，P 在y 轴上，P 在第二象限？(2)四边形OABP 能否成为平行四边形，若能，求出t 的值，若不能，请说明理由．22. (12分)已知)3),4((cos 2x -=，)).2214cos(,2(xk -+=π()1f x a b =⋅- 且函数，（,k Z x R ∈∈）.（1）求函数)(x f 在),0(π上的值域； （2）若=+)6(παf 554，)2,0(πα∈，求)42tan(πα+的值.。

2012—2013学年度第一学期高一数学期末练习一试题附答案班级_______________姓名________________学号___________得分_______________一、填空题(每题3分，共36分)1、集合|01x M x x ⎧⎫=≥⎨⎬-⎩⎭，12|N y y x ⎧⎫==⎨⎬⎩⎭，则M N = _____________。

{}()01,+∞2、函数()1f x =()g x =()()f x g x +=____________。

[]10,1x +∈3、函数()112-≤-=x x y 的反函数是_____________________。

0y x =≥4、若函数(31)xy a =-为指数函数，则a 的取值范围为 ；122,,333⎛⎫⎛⎫+∞ ⎪ ⎪⎝⎭⎝⎭5、命题“若b a >，则122->b a ”的否命题为________________.若a b ≤，则221a b ≤- 6、函数23x y a-=+，)10(≠>a a 且的图像必经过定点 。

()2,47、集合101x A xx ⎧-⎫=>⎨⎬+⎩⎭，{}a b x x B <-=，若“1a =”是“A B ≠∅ ”的充分条件， 则b 的取值范围是 。

22b -<<8、已知lg 2a =，103b=，则6log = 。

（用,a b 表示）12()b a b ++9、函数2()21f x x a x =-+有两个零点，且分别在(0,1)与(1,2)内，则实数a 的取值范围是______________。

514a <<10、不等式22(1)30ax a x a --++<的解集为∅，则实数a 的取值范围是 。

1,5⎡⎫+∞⎪⎢⎣⎭11、国内快递以内的包裹的邮资标准如下表：元。

712、直线5y =与曲线2||y x x a =-+有四个交点，则实数a 的取值范围是 。

2012—2013学年度（下期）期末考试试卷高一数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．共150分，考试时间120分钟．注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．答卷时，考生务必将答案涂写在答题卡规定的位置上，答在试卷上的无效。

3．考试结束后，将答题卡交回，试题卷由学校自己保存。

4．祝各位考生考试顺利。

参考公式：若11(,)x y ，22(,)x y ，…(,)n n x y 为样本点，y bx a =+为回归直线，则11n i i x x n ==∑， 11ni i y y n ==∑；1221ni ii nii x y nx yb xnx==-=-∑∑，a y bx =-．第Ⅰ卷（选择题， 共50分）一、选择题：本大题10个小题，每小题5分，共50分，在每小题给出的四个备选项中，只有一项是符合题目要求的．1．已知一组数据按从小到大的排列为：2-，0，3，a ，5，8，9，10，且这组数据的众数为3，则这组数据的中位数为（ ）A ．3B ．3.5C ．4D ．4.5 2．如果a b >，那么下列不等式一定成立的是（ ）A ．c b c a +>+B ．b c a c ->-C ．b a 22->-D ．22b a >3．一个容量为100的样本，其数据的分组与各组的频数如下表：则样本数据落在(10,40]的频率为（ ）A ．0.13B ．0.39C ．0.52D ．0.644．执行如图所示的程序框图．若输出15S =， 则框图中① 处可以填入（ ） A ．5k < B ．4k < C ．3k <D ．2k <乙甲3m 7464414555909875．ABC Δ中，若2sin cos sin A B C ⋅=，则ABC Δ的形状一定是（ ）A ．直角三角形B ．等腰直角三角形C ．等边三角形D ．等腰三角形 6．如图，矩形ABCD 中，点E 为边CD 的中点．若在矩形ABCD 内部随机取一个点Q ，则点Q 取自△ABE 内部的概率等于 ( ) A ．14 B ．13 C ．23 D ．127．有一长为m 10的斜坡，倾斜角为75，在不改变坡高和坡顶的前提下，通过你同意坡面的方法将它的倾斜角改为30，则坡底要延长 ( ) A ．m 310 B ．m 210 C ．m 10 D ．m 58．等差数列{}n a 的前m 项的和为30，前2m 项的和为100，则它的前3m 项的和为（ ）A ．130B ．170C ．210D ．2609．已知正项等比数列{}n a 满足: 7652a a a =+,若存在两项,m n a a 14a =，则14m n+的最小值为（ ）A ．23B ．35C ．625D ．不存在10．△ABC 的内角A 、B 、C 的对边分别是a ，b ，c ，若已知sin sin b B c A =．则c b的取值范围为（ ） A ． B ． C ． D ．)+∞ 第Ⅱ卷（非选择题，共100分）二、填空题：本大题5个小题，每小题5分，共25分，把答案填写在答题卡相应位置上． 11．由正数组成的等比数列{}n a 中，23=a ，87=a ，则=5a _________． 12．如图是某青年歌手大奖赛上七位评委为甲、乙两名选手打出的分数的茎叶图(其中m 为数字0～9中的一个)，去掉一个最高分和一个最低分后，甲、乙两名选手得分的平均数分别为12,a a ，则12,a a 的大小关系是_____________(填12a a >，12a a <，12a a =)．EDCBA 第6题图13． 某程序的框图如图所示，执行该程序，则输出T 的值为 ．14．某校计划招聘男教师x 名,女教师y 名, x 和y 须满足约束条件25,2,6,x y x y x -≥⎧⎪-≤⎨⎪<⎩则该校招聘的教师人数最多是 名．15．已知数列{}n a 中，11a = ，11(1)(1)(1)n nn n n a a n a +--=≥+-，n S 是数列1n a ⎧⎫⎨⎬⎩⎭的前n 项和．则2013S = ．三、解答题：本大题6个小题，共75分，解答应写出必要的文字说明、演算步骤或推理过程，并答在答题卡相应位置上．16．（本小题满分13分，（Ⅰ）小问8分，（Ⅱ）小问5分）已知等比数列{}n a 满足22a =，2532a a ⋅=，n S 为等差数列{}n b 的前n 项和，11b =，525S =．(Ⅰ) 求数列{}n a 和{}n b 的通项公式； (Ⅱ) 求数列{}n n a b +的前n 项和n T ．17．（本小题满分13分，（Ⅰ）小问7分，（Ⅱ）小问6分） 已知函数2()22f x x x =-+．（Ⅰ）若关于x 的不等式()f x mx <的解集为（1,2），求实数m 的值； （Ⅱ）设函数()()(0)f x g x x x=>，求函数()g x 的最小值．18．（本小题满分13分，（Ⅰ）小问6分，（Ⅱ）小问7分）某地为了调查培训需求，决定用分层抽样的方法从行政领导、教研员、教师三个群体的相关人员中，抽取若干人组成调查小组，有关数据见下表（Ⅰ）求调查小组的总人数；（Ⅱ）若从调查小组中的行政领导和教研员中随机选2人作深度访谈，求其中恰好有1人是行政领导的概率．19．（本小题满分12分，（Ⅰ）小问10分，（Ⅱ）小问2分）调查了某地若干户家庭的年收入x （单位：万元）和年饮食支出y （单位：万元），下表是部分调查数据：（Ⅰ）根据所给数据求回归直线方程；（Ⅱ）利用（Ⅰ）中所求的直线方程预测年收入为9万元家庭的年饮食支出． 20．（本小题满分12分，（Ⅰ）小问6分，（Ⅱ）小问6分）在△ABC 中，三个内角A ，B ，C 的对边分别为a ，b ，c ，且22224cos 2cos a B ac B a b c -=+-．（Ⅰ）求角B ；（Ⅱ）若b =ABC ∆面积的最大值．21．（本小题满分12分，（Ⅰ）小问6分，（Ⅱ）小问6分）已知数列{}n a 满足：0n a >，且对一切n N *∈,有33332123n n a a a a S ++++=，其中n S 为数列{}n a 的前n 项和．（Ⅰ）求数列{}n a 的通项公式； （Ⅱ）记数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和为n T ，是否存在正整数m ，n ，且1m n <<，使得1T、m T 、n T 成等比数列？若存在，求出所有符合条件的m ，n 的值；若不存在，请说明理由．。

信阳市2012-2013学年度上期期末调研考试高 一 数 学第Ⅰ卷 （选择题 共60分）一．选择题（本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的．）1．在①1{0,1,2}⊆；②{1}{0,1,2}∈；③{0,1,2}{0,1,2}⊆；④{0}∅⊆上述四个关系中，错误．．的个数是 A ．1个 B ．2个 C ．3个 D ．4个2．若lg 2a =，lg3b =，则lg0.18等于A ．22a b +-B ．31a b +-C ．32a b --D ．22a b +-3．下列四个函数：① 3y x =-；② 211y x =+；③2210y x x =+-；④(0)1(0)x x y x x-≤⎧⎪=⎨->⎪⎩，其中值域为R 的函数有A ．1个B ．2个C ．3个D ．4个4．函数22log (56)y x x =--的单调递减区间是A ．5(,)2-∞ B ．5(,)2+∞ C ．(,1)-∞- D ．(6,)+∞ 5．直线1l ：310ax y ++=，2l ：2(1)10x a y +++=，若12l l ，则a 等于A ．3-B ．2C ．3-或2D ．3或2-6．直线0(0)ax by c ab ++=≠在两坐标轴上的截距相等，则,,a b c 满足的条件是A ．a b =B ．||||a b =C ．a b =且0c =D ．0c =或0c ≠且a b = 7．圆22(1)(2)1x y ++-=上的动点P 到直线3490x y --=的最短距离为A ．3B ．4C ．5D ．68．一个长方体的长、宽、高分别为2、1、1，其顶点都在同一球面上，则该球的表面积为A ．3πB ．6πC ．12πD ．24π9．设,,l m n 是互不重合的直线，,αβ是不重合的平面，则下列结论正确的是A ．若,l l αβ⊥，则αβ⊥B ．若,l αβα⊥⊂，则l β⊥C ．若,l n m n ⊥⊥，则l mD ．若,,l n αβαβ⊥⊂⊂，则l n ⊥10．设()f x 是定义在R 上的奇函数，当0x >时，()2x f x e =-，则()f x 的零点个数A ．0个B ．1个C ．2个D ．3个11．设函数2()ax b f x x c +=+的图象如右图所示，则,,a b c 的大小关系是A ．a b c >>B ．a c b >>C ．b a c >>D ．c a b >>12．如图，在正方体1111ABCD A B C D -中，,,E F G 分别是棱11111,,A B BB B C 的中点，则下列结论中：①FG BD ⊥； ②1B D ⊥面EFG ；③面EFG 面11ACC A ； ④EF 面11CDD C ．正确结论的序号是A ．①和②B ．②和④C ．①和③D ．③和④第Ⅱ卷（非选择题 共90分）二．填空题（本大题共4小题，每小题5分，共20分．把答案填在题中横线上）13．如图，长方体''''OABC D A B C -中，||3OA =，||4OC =，|'|5OD =，点P 为''A C 与''B D 的交点，则||OP = ．14．一个几何体的三视图如图所示，则这个几何体的体积为 ．15．下列四个命题：① 奇函数()f x 在(,0)-∞上为增函数，则()f x 在(0,)+∞上也是增函数；② 若函数2()2f x ax bx =++与x 轴没有交点，则280b a -<，且0a >；。

2012～2013学年度第一学期期末考试高一数学试题一、填空题：（本大题共14小题，每小题5分，共70分．请将答案填入答题纸填空题的相应答题线上．） 1． 240sin 的值为 ▲ ． 2．函数11y x=-的定义域为 ▲ ． 3．已知幂函数．．．)(x f y =的图象过点)22,2(，则(2)f = ▲ ． 4．若函数4()(1)1f x x m x =+-+为偶函数，则实数m 的值为 ▲ ．5．已知扇形的中心角为120，半径为3，则此扇形的面积为 ▲ ．6．将函数3sin 2y x =的图象向右平移6π个单位后所得图象的函数解析式是y = ▲ ． 7．=++3285lg 24lg ▲ ．8．在平面直角坐标系xoy 中，已知以x 轴为始边的角α、β的终边分别经过点(4,3)-、(3,4)，则tan()αβ+= ▲ ．9．函数2()2f x x x =++的单调增区间是 ▲ ．10．如图，在44⨯的方格纸中，若起点和终点均在格点的向 量m,n,p 满足x +y =p m n （x ,y ∈R ），则y x +4的值为 ▲ ．11．若函数2()2(1)f x x ax b a =-+>的定义域与值域都是[1,]a ，则实数b = ▲ ． 12．已知直线(0)4x παα=<<与函数x x g x x f 2sin )(,cos )(==和x x h sin )(=的图象及x 轴依次交于点,,,P M N Q ，则22MQ PN +的最小值为 ▲ ．13．已知点G 、H 分别为ABC ∆的重心（三条中线的交点）、垂心（三条高所在直线的交点），若4,6AC AB == ，则HG BC ⋅的值为 ▲ ．14．已知函数1)(-=mx x f ，1)1()(2-+-=x m x x g ，若对任意的00>x ，)(0x f 与)(0x g 的值p nm第10题图不异号．．．，则实数m 的值为 ▲ ． 二、解答题（本大题共6小题，共90分．解答应写出文字说明、证明过程或演算步骤．）15．（本小题满分14分）已知集合{}26,A x x x R =≤≤∈，{}15,B x x x R =-<<∈，全集U R =． （1）求()U A C B ；（2）若集合{},C x x a x R =<∈，A C =∅ ，求实数a 的取值范围．16．（本小题满分14分）已知函数()sin()(0,0)6f x A x A πωω=+>>的部分图象如图所示．(1)求,A ω的值；(2)求()f x 的单调增区间； (3)求()f x 在区间[,]64ππ-上的最大值和最小值.17．（本小题满分14分）销售甲、乙两种商品所得利润分别是1y 、2y 万元，它们与投入资金x 万元的关系分别为11y m x a =++，2=y bx ，（其中,,m a b 都为常数），函数y 1，y 2对应的曲线1C 、2C 如图所示． (1)求函数1y 、2y 的解析式；(2) 若该商场一共投资4万元经销甲、乙两种商品，求该商场所获利润的最大值．y x2π3π6O 1-118．（本小题满分16分）已知向量a =()1,cos α，b =()1,sin β，(3,1)=c ，且()+a b ∥c . （1）若3πα=，求cos 2β的值；（2）证明：不存在角α，使得等式 +=-a c a c 成立； （3）求2⋅-b c a 的最小值． 19．（本小题满分16分）已知函数3)(,)(2+==ax x g x x f （a ∈R ）． （1）记函数()()()F x f x g x =-， (i)判断函数()F x 的零点个数；(ii)若函数()F x 在[0,1]上是减函数，求实数a 的取值范围．（2）设(),1()(),1f x x G x g x x <⎧=⎨≥⎩．若对于函数()y G x =图象上异于原点O 的任意一点P ，在函数()y G x =图象上总存在另一点Q ，使得0OP OQ ⋅<，且PQ 的中点在y 轴上，求a 的取值范yxO 8581C 2C围． 20．（本小题满分16分）已知函数()f x 是区间[0,)D ⊆+∞上的增函数，若()f x 可表示为12()()()f x f x f x =+，且满足下列条件：①1()f x 是D 上的增函数；②2()f x 是D 上的减函数；③函数2()f x 的值域[0,)A ⊆+∞，则称函数()f x 是区间D 上的“偏增函数”． (1) (i) 问函数sin cos y x x =+是否是区间(0,)4π上的“偏增函数”？并说明理由；(ii)证明函数x y sin =是区间(0,)4π上的“偏增函数”． (2) 证明：对任意的一次函数()(0)f x kx b k =+>， 必存在一个区间[0,)D ⊆+∞， 使()f x 为D 上的“偏增函数”．2012～2013学年度第一学期期末考试高一数学(类一)试题参考答案一、填空题 1． 23-； 2． (,1)-∞； 3． 8； 4． 1； 5． π； 6． 3sin(2)3y x π=-； 7． 6； 8．724； 9． 1(,)2-+∞（1[,)2-+∞也对）； 10．7； 11． 5； 12． 43； 13．320-； 14． 21．二、解答题15． 解：（1）{}15,B x x x R =-<<∈ ，{}15U C B x x x ∴=≤-≥或，…………………………………………………………4分 {}()=56U A C B x x ∴≤≤ ． ………………………………………………………8分（2）{}26,A x x x R =≤≤∈ ，{},C x x a x R =<∈，A C ≠∅ ，a ∴的取值范围是2a ≤． ……………………………………………………………14分(不写等号扣2分)16． 解：（1）由图象知1A =， …………………………………………………………2分 由图象得函数的最小正周期为22()36πππ-=， 则由2ππω=得2ω=．…………………………………………………………………4分（2）222262k x k πππππ-+≤+≤+ ，∴222233k x k ππππ-+≤≤+. 36k x k ππππ∴-+≤≤+.所以()f x 的单调递增区间为[,],36k k k Z ππππ-++∈. …………………………9分（3）,64x ππ-≤≤2,32x ππ-≤≤22663x πππ∴-≤+≤. 1sin(2)126x π∴-≤+≤ . ………………………………………………………12分当2,62x ππ+=即6x π=时，()f x 取得最大值1；当2,66x ππ+=-即6x π=-时，()f x 取得最小值12-. ………………………14分 17．解：（1）由题意0835m a m a +=⎧⎪⎨+=⎪⎩，解得54,54-==a m ，1441,(0)55y x x =+-≥ ……………………………………………………4分 又由题意588=b 得51=b215y x =(0)x ≥ ……………………………………………………………………7分（不写定义域扣一分）（2）设销售甲商品投入资金x 万元，则乙投入（x -4）万元 由（1）得4411(4)555y x x =+-+-，(04)x ≤≤……………………………10分 令1,(15)x t t +=≤≤，则有5154512++-=t t y =1)2(512+--t ，(15)t ≤≤，当2=t 即3=x 时,y 取最大值1.答：该商场所获利润的最大值为1万元．……………………………………………14分 （不答扣一分）18． 解： (2,cos sin ),a b αβ+=+(3,1)=c ，且()+a b ∥c .2c o s s i n ,3αβ∴+=…………………………………………………………3分（1）3πα=，11cos ,sin 26αβ∴=∴=，217cos 212sin .18ββ∴=-=………………………………………………………6分 （2）假设存在角α使得等式成立则有222222a a c c a a c c +⋅+=-⋅+ 0a c ∴⋅=3c o s -=∴α不成立∴不存在角α使得等式成立．………………………………………………………11分 （3）2cos sin ,3αβ+=2sin cos [1,1]3βα∴=-∈-， 15cos 33α∴-≤≤，又1cos 1α-≤≤，1cos 13α∴-≤≤， ………………………………………………………13分222282sin cos cos cos 3135(cos )212b c a βαβαα∴⋅-=+-=--+=-++∴当cos 1α=时，32min =y ． …………………………………………………16分 19． 解：（1）(i)3)(2--=ax x x F2120,a ∆=+>∴函数()F x 有2个零点 ． …………………………………………4分(ii) 2(),()0()2,(),()0F x F x F x x ax F x F x ≥⎧=--=⎨-<⎩由题意⎪⎩⎪⎨⎧≥-≤-0)1(02F a， 02≤≤-∴a ．…………………………………8分（2）2,1()3,1x x G x ax x ⎧≤=⎨+>⎩， 由题意易知P ,Q 两点在y 轴的两侧，不妨设P 点坐标在y 轴的左侧，设),(211x x P ，当011<<-x ，则),(211x x Q -，2211(1)0OP OQ x x ⋅=-< 恒成立，…………………12分当11-≤x ，则设点Q （3,11+--ax x ），22111(3)0OP OQ x x ax ⋅=-+-+<恒成立，12ax ∴>恒成立，,11-≤x12a x ∴<恒成立，只要 min 12()a x ∴< ， ………………………………14分 22,1min11-=⎪⎪⎭⎫ ⎝⎛∴-≤x x ,2a ∴<-． ………………………………16分20． 解：（1）(i) sin cos y x x =+是区间(0,)4π上的“偏增函数”．…………1分 记12()sin ,()cos f x x f x x ==，显然1()sin f x x =在(0,)4π上单调递增，2()cos f x x =在(0,)4π上单调递减，且22()cos (0,)2f x x =∈, 又()sin cos 2sin()4y f x x x x π==+=+在(0,)4π上单调递增， 故sin cos y x x =+是区间(0,)4π上的“偏增函数”．……………………………4分 (ii) sin (sin cos )cos 2sin()cos 4y x x x x x x π==-+=-+，记12()2sin(),()cos 4f x x f x x π=-=，显然1()2sin()4f x x π=-在(0,)4π上单调递增，2()cos f x x =在(0,)4π上单调递减，且22()cos (0,)2f x x =∈， 又12()()()sin y f x f x f x x ==+=在(0,)4π上单调递增，故sin y x =是区间(0,)4π上的“偏增函数”． …………………………………10分 (2) 证：当0b >时，令1()(1)f x k x =+，2()f x x b =-+，(0,)D b =，显然(0,)D b =[0,)⊆+∞，0k > ,()f x kx b ∴=+在(0,)b 上单调递增，1()(1)f x k x =+在(0,)b 上单调递增，2()f x x b =-+在(0,)b 上单调递减，且对任意的(0,)x b ∈，22()()0f x f b >=，因此0b >时，必存在一个区间(0,)b ，使()(0)f x kx b k =+>为D 上的“偏增函数”． …………………………………13分当0b ≤时，取0,c >且满足0c b +>，令1()(1)f x k x c =+-，2()f x x b c =-++，(0,)D b c =+[0,)⊆+∞，显然，()f x kx b =+在(0,)b c +上单调递增，1()(1)f x k x c =+-在(0,)b c +上单调递增，2()f x x b c =-++在(0,)b c +上单调递减，且对任意的(0,)b c +，22()()0f x f b c >+=，因此0b ≤时，必存在一个区间(0,)b c +，使()(0)f x kx b k =+>为D 上的“偏增函数”． 综上，对任意的一次函数()(0)f x kx b k =+>， 必存在一个区间[0,)D ⊆+∞， 使()f x 为D 上的“偏增函数”． ………………………………………………………16分 (其他构造方法相应给分)。