第三章 非稳态导热
- 格式:pdf
- 大小:1.77 MB
- 文档页数:42

第三章 非稳态导热(unsteady state conduction)物体的温度随时间而变化的导热过程称非稳态导热。
0≠τ∂∂t,任何非稳态导热过程必然伴随着加热或冷却过程。
根据物体内温度随时间而变化的特征不同,非稳态导热过程可分为两类:(1)周期性导热(periodic unsteady conduction ):物体的温度按照一定的周期发生变化; 如建筑物的外墙和屋顶温度的变化。
(2)瞬态导热(transient conduction):物体的温度随时间不断升高或降低,在经历相当长时间后,物体的温度逐渐趋于周围介质的温度,最终达到热平衡。
分析非稳态导热的任务:找出温度分布和热流密度随时间和空间的变化规律。
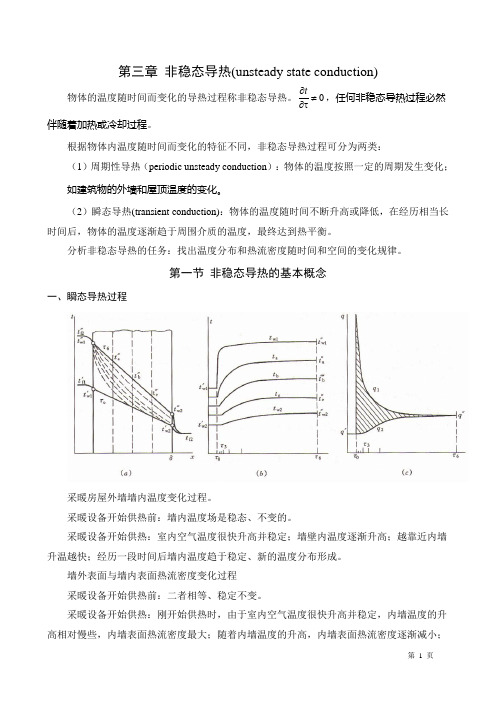
第一节 非稳态导热的基本概念一、瞬态导热过程采暖房屋外墙墙内温度变化过程。
采暖设备开始供热前:墙内温度场是稳态、不变的。
采暖设备开始供热:室内空气温度很快升高并稳定;墙壁内温度逐渐升高;越靠近内墙升温越快;经历一段时间后墙内温度趋于稳定、新的温度分布形成。
墙外表面与墙内表面热流密度变化过程 采暖设备开始供热前:二者相等、稳定不变。
采暖设备开始供热:刚开始供热时,由于室内空气温度很快升高并稳定,内墙温度的升高相对慢些,内墙表面热流密度最大;随着内墙温度的升高,内墙表面热流密度逐渐减小;随着外墙表面的缓慢升高,外墙表面热流密度逐渐增大;最终二者相等。
上述非稳态导热过程,存在着右侧面参与换热与不参与换热的两个不同阶段。
(1)第一阶段(右侧面不参与换热)是过程开始的一段时间,特点是:物体中的一部分温度已经发生变化,而另一部分仍维持初始状态时的温度分布(未受到界面温度变化的影响),温度分布显现出部分为非稳态导热规律控制区和部分为初始温度区的混合分布,物体内各处温度随时间的变化率是不一样的,即:在此阶段物体温度分布受t分布的影响较大,此阶段称非正规状况阶段或初始阶段(initialregime)。
(2)第二阶段(右侧面参与换热)当右侧面参与换热以后,物体中的温度分布不受t影响,主要取决于边界条件及物性。




第三章非稳态导热本章要点:z不稳定导热的概念z不稳定导热的分析解z非稳态导热的图线解z集总热容法z非稳态导热的数值解z二维及三维非稳态导热不稳定导热概念一、含义不稳定导热分为周期性和非周期性两种。
周期性不稳定导热的含义:各点的温度随时间作周期性变化。
例1:内燃机活塞中的温度每分钟内波动几百次,温度波动区域内离活塞表面1mm左右;例2:机加工中将高温零件突置于冷却液体中或置于加热炉;例3:换热设备因壁处于起动变负荷或停机过程。
实际物体,只要边界上的温度或热流发生变化,引起物体从表面逐步深入到内部的温度变化,造成每一个与热流方向相垂直的截面上通过的热流不相等。
这热流的差额便用来改变物体的内能。
二、简单的图例设有一块平壁,其温度为t0,突然使左侧表面温度升高至t1(如:将它同恒温度为的高温表面紧密接触),右侧仍与温度为的t0空气接触。
紧挨高温表面那部分温度很快上升。
(其余部分如CD,当Q1 = Q2时,进入稳态)。
Q1> Q2热储存使内部升温——不稳态导热——(举一例子,例2-1).三、实际物体的例子往往更复杂物体受热(或受冷)侧的壁温不一定保持为常数。
气轮机起动过程中,汽缸壁温度变化。
为便于分析,将缸壁作为平壁,设气轮机的冷态起动前汽缸壁与保温层保持为均匀的温度t(AN直线).z(1) 将温度较高的蒸汽送入气轮机,蒸汽遇到较冷的壁面即发生凝结,使缸壁表面温度很快上升到较近于相应的蒸汽压力下的饱和温度,但缸壁大部分地区的温度仍保持原来的数值(曲面CBN)。
z(2) 由于进入气轮机的蒸汽温度及压力在不断上升,所以汽缸内表面及其余部分的温度也持续地依次升高,直至起动过程结束,缸壁中的温度分布也随之稳定,如曲线CD。
(保温层中温度的变化情况与之类似)。
z四、数学方法(建立数学模型)求解传热问题z(1) 常对实际问题适当简化——建立数学模型——求解(a.精确解 b.近似解c.数值解)简化涉及三个方面:①边界条件的简化(导热问题归纳三类A 、B、C)②导热物体内部热阻的简化处理(集总热容法下一节讲)③导热物体的形状的简化(从实物各种形状中抽象简化出了无限大平板,无限长圆柱等概念).有厚度直径,一般遇到的物体不会是无限大,但长(l )、宽(w )远大于厚度( ),可近似即认为平板上下左右面四周换热,对板内各点的温度值影响极小,仅仅是厚度的函数简化为1-D 导热。
(2 )坐标系的选择——不同形状选用相应坐标系。
(3)建立数学方程,求得通解,与定解条件(初始,边界条件)——特解l 〈〈δl d 〈〈δδ非稳态导热分析解z 对于无限大平板常物性的非稳态导热,由分离变量法(乘积解法)。
求解得平板内的温度分布关系式(3-11)τθθ∂∂=∂∂22x a 0)0,(θθ=x 0),(0=∂∂=x x x τθθτθλh x x =∂∂−),(f W w T T −=θfT T −=θz分析解往往是一个无穷级数,计算很繁琐。
Heisler(海斯勒)将一些典型几何形状的非稳态导热。
由分析解形式制成各种图线。
正规状况阶段的实用计算方法为了获得F>0.2时非稳态导热物体的O温度场及所交换的热量,除了直接应用公式(3-25)、(3-27)、(3-28)等来计算外,可以采用近似拟合公式或诺模图,分述如下。
(1)采用近似拟合公式在文献[7]中对三种几何形体的第一特征值μ,表3-2中的系数A、B及零阶第一类贝塞尔函数J 0(x)提出了如下拟合公式:3201)(1)1()(dx cx bx a x J bB cB a B eb a A B b a i i cB ii +++=++=−+=+=−−1μ(3-29a)(3-29b)(3-29c)(3-29d)式(3-29a)~(3-29d)中的常数列于表3-3、3-4中非稳态导热图线解z 使用方便,图线最多只能表示三维问题。
z 必须将方程无因次化以达到减少变量之目的。
令:z 以前已推导过无因次化的过程——i θθθ=∗Lx x =∗w i hl B λ=20L a F τ=δ=L 022F x ∂∂=∂∂∗∗∗θθ——对流边界条件——初始条件一般关系式对称物体中心点(x *=0)温度比为通过计算参数,,查图线--→,--→×= =()01,1F B x i x ∗=∗∗−=∂∂∗θθ()10,=∗∗x θ()∗∗=x F B f i ,,0θ()0,F B f i c =∗θδλh 2δτa δx cθθi c θθc θθi c θθi θθ∗θ集总热容法z除了边界上温度或热流变化→引起物体由表及里温度变化不稳定过程,还与物体外表面与内部的传热热阻有关。
热阻小,热流很容易以小温差通过、高热阻热流通过困难,且需要较大的温差才能推动,与电工学电路中的电流电阻的关系道理相同。
z 因此,物体内部的瞬时温度分布与物体内的导热热阻与外表面的对流热阻相比较的情况有关。
z 若外表面对流热阻较大而内部导热热阻较小,则物体内的温度随时间变化比较均匀,各处的温度较近相同。
反之,如果外表面传热容易,内部传热困难,则物体内各处的温度相差较大。
z →, 的比较。
对不稳定导热过程还有十分重要的作用。
A L λs hA 1A L λs hA 1z内热阻外热阻z下面谈谈物体内导热热阻可忽略的加热(冷却)过程。
z例:金属淬火(通“淬”)——通称“蘸火”,金属内部温度变化取决于表面的对流换热和内部导热。
(液、气体对流换热系数相差大)如果内部导热热阻比表面的对流热阻小得多,则主要温度梯度便出现在表面的流体层内。
而金属内部任何点的温度,与同一瞬间整个物体的平均温度非常接近。
这时认为金属内部的温度分布是均匀的假设就是合理的。
z 集总热容系统与电工学中阻容电路相似z 对无限大平板,无限长圆柱或圆球它们在牛顿加热(冷却)过程中的温度变化过程如图。
z 在时瞬时热流z 集总热容特性电热类比z 将代入上式得集总热容系统的温度变化τρτd dT V c Q =()T e T T T F B f i i +−=−0()τρτρρcV hA s f i s e cV hA T T cV Q −⎟⎟⎠⎞⎜⎜⎝⎛−−=()0F B i f s i e T T hA Q −=−τz 自至时间内的加给物体的总热量z讨论:B i (准则)对导热物体内的温度分布起有十分重要的作用。
(1)其物理意义:物体内的导热热阻与表面对流热阻之比,与导热过程是否稳定并无关系。
(2)稳定导热的情况出发分析B i 对物体温度分布的影响一面保持T 1,另一面与温度为T f 的流体相接触,平壁稳态导热:0=τττ=()()010F B f i I e T T cV d Q Q −−−==∫ρτττ()()f T T hA T T L A −=−221λz →z 如图可见B i 对固体内导热温差与流体跟表面的对流温差之间提供了一个相对比较的尺度。
B i <<1体内导热热阻<<对流热阻.即:T 1-T 2<<T 2-T fz 相反:B i >>1,T 1-T 2>>T 2-T fi f B hL hAA L T T T T ===−−λλ1221o x tt 0o x t t 0o xt t 0t ∞t∞t∞t ∞t ∞t∞(a)Bi →∞()Bi →0()Bi 为有限大小图3-3 毕渥数Bi 对平板温度场变化的影响z③平壁初温T i浸没在T f流体中冷却,不同Bi对温度分布的影响:z B i<<1内部温度分布差不多是均匀,温度梯度小得可忽略,物体内的温度分布只是时间的函数,与空间位置无关可作为集总热容系统分析。
z B i>>1表面对流热阻小得可以忽略,在任何瞬时外壁面温度都几乎等于流体温度,而壁内部温度分布则是时间和位置的函数,显然不能作集总热容系统分析→实际处理不稳定导热问题是。
首先必须计算Bi的大小。
一般如果Bi <<0.1 ,用计算温度变化的误差不会超过5% 。
Bi 越小,作集总热容系统分析处理的精确度越高。
0 FB i ie−=θθz 例测量气流温度的热电偶,其结点可视为球体,结点与气流之间的换热系数,结点的热物性试求:z (1)换热时间常数为1秒的热电偶结点直径为多大?z (2)把结点从25℃环境温度放入的200 ℃气流中要多长时间才能达到199℃?()K m W h ⋅=2400()K m W ⋅=20λ()K kg J c ⋅=40038500mkg =ρz 解:首先算结点直径,并检查B i 数值球:,,的d →(m)2d A s π=63dV π=s t 1=τ16=⋅==d h c hA V c s t ρρτ4008500140066×××==ρc h d 41006.7−×=206/1006.7400640−××===⎟⎠⎞⎜⎝⎛=λλλd h A V h s r h B i 41035.2−×=<< 0.1z 说明热偶结点当成集总热容系统处理合适。
z 达199 ℃所需时间z 可见,结点直径d 和越小,而h 越大,则温度反应越快。
(sec)2.520019920025ln 40064001006.78500ln 4=−−××××=−−=−f f i s T T T T hA v c ρτc ρ非稳态导热数值解一.三种差分格式向前中心向后差分见书P 111二、差分方程:以一维非稳态导热为例(1)(2)22x T T ΔΔ=ΔΔατ)(11k i k i T T T −Δ=ΔΔ+ττ二阶差分方程三、稳定判别准则时间步长距离的相关性,要满足稳定性判别准则:)2(111222k i k i k i T T T x x T −+Δ=ΔΔ−+将(2)、(3)代入(1)得k i ki k i k i T x T T x T )21()(21121ΔΔ−++ΔΔ=−++τατατΔx Δ(3)1-D <=1/2 2-D <=1/43-D <=1/6用向后差分2xΔΔτα2x ΔΔτα2x ΔΔτα)2(1111121++−+++−+ΔΔ=−k i k i k i k i k i T T T x T T τα二维及三维非稳态导热z 用数学分析成数值解法直接求解较复杂,对一些典型的几何形状,将2—D 及3—D 用1—D 温度场叠加,可直接利用海斯勒图求多维问题。
z 一、短圆柱的导热方程及边界条件τθαθθ∂∂=∂∂+∂∂∂∂*2*2*1)(1r r r r r fi fT T TT −−=*θz 边界条件:z z r=0z z r=R 1*=θ0=τ0*=∂∂r θ**θθλh x=∂∂−δ±=x **θθλh x =∂∂−z 二、分组方程z 假设z 得出:第一组:第二组:z z z),(),(),,(21*τθτθτθx r r x =τθαθ∂∂=∂∂∂∂*1*11)(1r r rr τθαθ∂∂=∂∂*2*21x)0(1*1==τθ)0(1*2==τθ*1*1θθλh r=∂∂−)(R r =*2*2θθλh r=∂∂−)(R r =0*1=∂∂−rθλ)0(=r三、分别求解z 由无限长圆柱体的海斯勒图求得z 无限大平板求z 得出*1θ*2θ*2*1*θθθ=。