平行四边形的判定(1)

判定平行四边形的五种方法平行四边形的判定方法有：（1）证两组对边分别平行；（2）证两组对边分别相等；（3）证一组对边平行且相等；（4）证对角线互相平分；（5）证两组对角分别相等。

下面以近几年的中考题为例说明如何证明四边形是平行四边形。

一、两组对边分别平行如图1,已知△ ABC是等边三角形，D、E分别在边BC AC上，且CD=CE连结DE并延长至点F，使EF=AE连结AF、BE和CF（1）请在图中找出一对全等三角形，并加以证明；⑵ 判断四边形ABDF是怎样的四边形，并说明理由,解：（1）选证△ BDE^A FEC证明：•••△ ABC是等边三角形，••• BC=ACZ ACD=60v CD=CE二BD=AEA EDC是等边三角形••• DE二EC/ CDEH DEC=60•••/ BDE/ FEC=120又v EF=AE 二BD二FE 二△ BDE^A FEC（2）四边形ABDF是平行四边形理由：由（1）知，△ ABC △ EDC △ AEF都是等边三角形v/ CDE/ABC/ EFA=60 ••• AB// DE BD// AF v四边形ABDF是平行四边形点评：当四边形两组对边分别被第三边所截，易证截得的同位角相等，内错角相等或同旁内角相等时，可证四边形的两组对边分别平行，从而四边形是平行四边形。

二、一组对边平行且相等例2已知：如图2,在正方形ABCD中, G是CD上一点，延长BC到E，使CE=CG连结BG并延长交DE于F⑴求证：△ BCG^^DCE(2)将厶DCE绕点D顺时针旋转90°得到△ DAE，判断四边形E‘ BGD是什么特殊四边形并说明理由。

分析：(2)由于ABCD是正方形，所以有AB// DC又通过旋转CE=AE已知CE=CG所以E A=CG这样就有BE =GD可证E BGD是平行四边形。

解：( 1)v ABCD是正方形，•••/ BCDM DCE=90 又T CG=C，△ BCG^ DCE(2)v^ DCE绕D顺时针旋转90°得到△ DAE，••• CE=AE，T CE=CG 二CG=AE，•••四边形ABCD是正方形••• BE // DG AB=CD••• AB- AE 二CDCG,即卩BE =DG•••四边形DE BG是平行四边形点评：当四边形一组对边平行时，再证这组对边相等，即可得这个四边形是平行四边形三、两组对边分别相等例3如图3所示，在△ ABC中，分别以AB AC BC为边在BC的同侧作等边△ ABD等边△ ACE等边△ BCF求证：四边形DAEF是平行四边形；分析：利用证三角形全等可得四边形DAEF的两组对边分别相等，从而四边形DAEF是平行四边形。

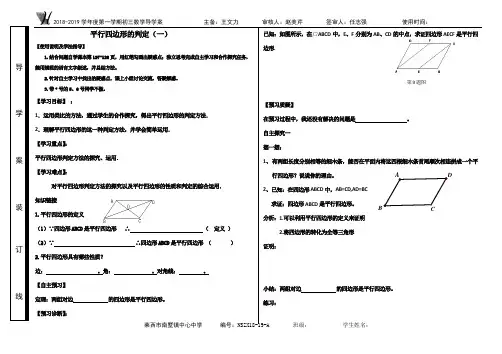
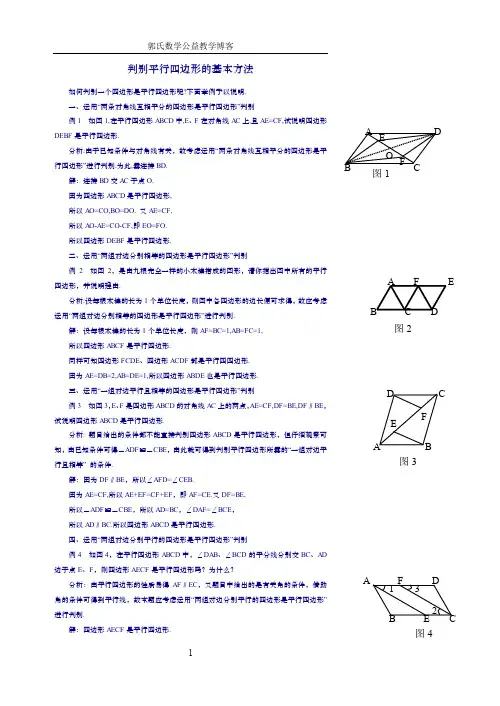
判别平行四边形的基本方法如何判别一个四边形是平行四边形呢?下面举例予以说明.一、运用“两条对角线互相平分的四边形是平行四边形”判别例1 如图1,在平行四边形ABCD中,E、F在对角线AC上,且AE=CF,试说明四边形DEBF是平行四边形.分析:由于已知条件与对角线有关，故考虑运用“两条对角线互相平分的四边形是平行四边形”进行判别.为此,需连接BD.解：连接BD交AC于点O.因为四边形ABCD是平行四边形,所以AO=CO,BO=DO. 又AE=CF,所以AO-AE=CO-CF,即EO=FO.所以四边形DEBF是平行四边形.二、运用“两组对边分别相等的四边形是平行四边形”判别例2 如图2，是由九根完全一样的小木棒搭成的图形，请你指出图中所有的平行四边形，并说明理由.分析:设每根木棒的长为1个单位长度，则图中各四边形的边长便可求得，故应考虑运用“两组对边分别相等的四边形是平行四边形”进行判别.解：设每根木棒的长为1个单位长度，则AF=BC=1,AB=FC=1,所以四边形ABCF是平行四边形.同样可知四边形FCDE、四边形ACDF都是平行四四边形.因为AE=DB=2,AB=DE=1,所以四边形ABDE也是平行四边形.三、运用“一组对边平行且相等的四边形是平行四边形”判别例3 如图3，E、F是四边形ABCD的对角线AC上的两点，AE=CF,DF=BE,DF∥BE，试说明四边形ABCD是平行四边形.分析: 题目给出的条件都不能直接判别四边形ABCD是平行四边形，但仔细观察可知，由已知条件可得△ADF≌△CBE，由此就可得到判别平行四边形所需的“一组对边平行且相等” 的条件.解：因为DF∥BE，所以∠AFD=∠CEB.因为AE=CF,所以AE+EF=CF+EF，即AF=CE.又DF=BE,所以△ADF≌△CBE，所以AD=BC，∠DAF=∠BCE，所以AD∥BC.所以四边形ABCD是平行四边形.四、运用“两组对边分别平行的四边形是平行四边形”判别例4 如图4，在平行四边形ABCD中，∠DAB、∠BCD的平分线分别交BC、AD 边于点E、F，则四边形AECF是平行四边形吗？为什么？分析：由平行四边形的性质易得AF∥EC，又题目中给出的是有关角的条件，借助角的条件可得到平行线，故本题应考虑运用“两组对边分别平行的四边形是平行四边形”进行判别.解：四边形AECF是平行四边形.图1图2AB C DEF图3AB CDEF图41 32理由：因为四边形ABCD 是平行四边形，所以AD ∥BC ，∠DAB =∠BCD ， 所以AF ∥EC .又因为∠1=21∠DAB ，∠2=21∠BCD ， 所以∠1=∠2.因为AD ∥BC ，所以∠2=∠3， 所以∠1=∠3，所以AE ∥CF . 所以四边形AECF 是平行四边形.判定平行四边形的五种方法平行四边形的判定方法有：（1）证两组对边分别平行；（2）证两组对边分别相等；（3）证一组对边平行且相等；（4）证对角线互相平分；（5）证两组对角分别相等。

平行四边形的判定定理平行四边形是一种特殊的四边形，具有以下特点：对边平行且对角线相等。

在数学中，判定一个四边形是否为平行四边形有多种方法。

方法一：利用对边平行的性质判定一个四边形ABCD是否为平行四边形时，可以先利用对边平行的性质进行判断。

步骤：1.检查边AB和边CD是否平行。

2.检查边BC和边AD是否平行。

如果边AB和边CD以及边BC和边AD都是平行的，则可以断定四边形ABCD是一个平行四边形。

方法二：利用对角线相等的性质判定一个四边形ABCD是否为平行四边形时，可以利用对角线相等的性质进行判断。

步骤：1.计算对角线AC的长度。

2.计算对角线BD的长度。

如果对角线AC的长度等于对角线BD的长度，则可以断定四边形ABCD是一个平行四边形。

方法三：利用对边比例相等的性质判定一个四边形ABCD是否为平行四边形时，还可以利用对边比例相等的性质进行判断。

步骤：1.计算边AB与边CD的长度比（AB/CD）。

2.计算边BC与边AD的长度比（BC/AD）。

如果边AB与边CD的长度比等于边BC与边AD的长度比，即AB/CD = BC/AD，那么四边形ABCD是一个平行四边形。

方法四：利用四个角的性质判定一个四边形ABCD是否为平行四边形时，也可以利用四个角的性质进行判断。

步骤：1.检查角A与角C是否相等。

2.检查角B与角D是否相等。

如果角A与角C相等，并且角B与角D相等，则可以断定四边形ABCD是一个平行四边形。

总结通过以上四种方法，我们可以判定一个四边形是否为平行四边形。

可以根据实际情况选择其中一种或多种方法来进行判定，以便快速准确地得出结论。

请注意，以上的判定定理仅适用于四边形，其他多边形无法用这些方法判定是否为平行四边形。

在实际应用中，合理选择合适的方法，结合几何定理，可以更好地解决相关问题。

希望本文能对你理解和应用平行四边形的判定定理有所帮助。

平行四边形的判定（一）一、教学目的和要求使学生掌握平行四边形的判定定理，并理解性质与判定的区别与联系。

二、教学重点和难点重点：平行四边形的判定定理；难点：掌握平行四边形的性质和判定的区别及熟练应用。

三、教学过程（一）复习、引入 提问：1. 什么叫平行四边形？平行四边形有什么性质？（学生口答，教师板书）⎪⎪⎪⎩⎪⎪⎪⎨⎧⇒对角线互相平分邻角互补两组对角分别相等两组对边分别相等两组对边分别平行平行四边形2. 将以上的性质定理，分别用命题形式叙述出来。

（如果……那么……）根据平行四边形的定义，我们研究了平行四边形的其它性质，那么如何来判定一个四边形是平行四边形呢？除了定义还有什么方法？平行四边形性质定理的逆命题是否成立？（二）新课（板书课题）定理1：两组对边分别相等的四边形是平行四边形。

已知：四边形ABCD 中，AB ＝CD ，AD ＝BC 求证：四边ABCD 是平行四边形。

分析：证明：连结BD 在中和CDB ABD ∆∆么？）是平行四边形。

（为什四边形ABCD CB//AD ,CD //AB ,,CDB ABD DB BD ,CB AD ,CD AB ∴∴∠=∠∴∠=∠∠=∠∠=∠∴∆≅∆∴===43214321定理2：一组对边平行且相等的四边形是平行四边形。

已知：四边形ABCD 中，CD AB 平行且等于求证：四边形ABCD 是平行四边形。

定定理1证明。

例1 已知：如图3连结BE 、DF求证：21∠=∠分析：ABCD 的性质可得DE//BF ，又AD ＝BC ，E 、F 为中点则有DE ＝BF ，根据“一组对边平行且相等的四边形是平行四边形”的判定定理，可得四边形EBFD 是平行四边形。

证明由学生完成。

提问：此题还有什么方法，证明四边形BEDF 是平行四边形。

学生会想到证明CDF ABE ∆≅∆，得到BE ＝DF ，利用两组对边相等证明四边形是平行四边形。

但应指出第二种方法较第一种方法繁，也就是说要找出较简捷的证法，准确地使用判定定理，就要先分析图形的性质，及所具备的条件；比如证四边形BFDE 是平行四边形，已知ED//BF 了，所以再考虑第二个条件就应该是：ED ＝BF ，或BE//DF ；显然证明ED ＝BF ，比证明BE//DF 要方便。

平行四边形的判定（1）学习单一、判定定理的探究探究1：如图，四边形ABCD中，AB=CD，试探究四边形ABCD是否为平行四边形？D归纳：平行四边形的判定定理（1）：符号语言：∵，∴探究2：如图，四边形ABCD中，对角线AC、BD交于点O，且AO=CO,BO=DO，试探究四边形ABCD是否为平行四边形？D归纳：平行四边形的判定定理（1）：符号语言：∵，∴探究3：如图，四边形ABCD中，∠A=∠C, ∠B=∠D, 试探究四边形ABCD是否为平行四边形？D归纳：平行四边形的判定定理（1）：符号语言：∵，∴二、判定定理的使用1、已知：如图，□ABCD的对角线AC、BD交于点O，E、F是AC上的两点，并且AE=CF 求证：四边形BFDE是平行四边形D2、如图，AB=DC=EF ，AD=BC ，DE=CF ，则图中有哪些互相平行的线段？为什么？F EDB三、 课堂练习1、 在四边形ABCD 中，对角线AC 、BD 相交于点O若AD=8cm ，AB=4cm ，那么当BC= CD= 时，四边形ABCD 为平行四边形 若AC=10cm ，BD=8cm ，那么当AO= DO= 时，四边形ABCD 为平行四边形2、如图所示，∠1=∠2，∠3=∠4，问四边形ABCD 是否为平行四边形？A3、已知：如图，O 为□ABCD 的对角线AC 的中点，EF 经过点O ，且与AB 交于E ，于CD 交于F 求证：四边形AECF 是平行四边形C4、 如图，已知E 、F 、G 、H 分别是□ABCD 的边AB 、BC 、CD 、DA 上的点，且AE=CG ,BF=DH 求证：四边形EFGH 是平行四边形D5、 如图，四边形ABCD 中，AD=12，OD=OB=5，AC=26，∠ADB=90°求BC 的长和四边形ABCD 的面积C。

“6.2平行四边形的判定（1）”教学设计设计者：海德学校王倩老师一、教材分析平行四边形判定是北师大版八年级下册教材的第六章第二节内容，这部分内容既对平行四边形的定义和性质加以回顾，又对前面学过的全等三角形进行延伸. 同时还为后续学习特殊平行四边形奠定基础，在教学上起着“承上启下”的作用，目的是培养学生简单的推理能力和图形迁移能力.本节内容是平行四边形判定的第一课时，主要探究与边有关的判定方法.二、学情分析对于平行四边形，学生小学阶段就接触过，对其有直观的感知和认识，进入初中阶段，八年级下半学期，学生已经学习了全等三角形、平行线等一些基本几何图形的定义，性质和判定，初步经历了猜想、证明等研究过程，获得了一定的探索图形性质和判定的活动经验，学生的抽象思维能力、逻辑推理能力已经慢慢形成，所以对于平行四边形的研究可以考虑采用类比的方式进行教学设计，同时，在学习过程中，激发学生的探究欲望和合作交流能力.三、教学目标1.经历平行四边形判别条件的探索过程,发展学生的合情推理意识；2.探索并证明平行四边形的判定定理，培养学生的逻辑思维能力和推理论证能力；3.掌握平行四边形的判定条件，体会归纳、类比、化归的数学思想.四、教学重点难点重点：探究平行四边形的判定定理的过程需要经过对逆命题的猜想、图形验证、逻辑证明三个过程，判定定理的探究过程是本节课的重点.难点：学习完平行四边形的判定后，根据题目给出的条件，如何灵活准确的选择性质定理和判定定理，是本节的难点.五、教学过程(一)复习回顾，引出课题1．平行四边形的定义是什么？2．平行四边形还有哪些性质？3．研究几何图形的一般思路？设计意图：学生已经学习过关于平行四边形的定义和性质，通过小问题引发学生思考，引出课题.（二）互逆入手，提出猜想问题1：怎样判定一个四边形是否是平行四边形呢？当然，我们可以根据平行四边形的原始定义：两组对边分别平行的四边形是平行四边形加以判定．那么是否存在其他的判定方法呢？由研究几何图形的一般思路，写出性质的逆命题，以上逆命题是否正确呢?给出猜想，并加以证明.设计意图：类比以前研究过的全等三角形、平行线、直角三角形等图形的判定方法，写出性质的逆命题，给出猜想，并加以证明，本环节注重让学生体会类比的数学思想，发展学生的合情推理能力，为下节课的学习作出铺垫.（三）互逆入手，提出猜想猜想1：两组对边分别相等的四边形是平行四边形.已知：如图，四边形ABCD中，AB=CD，AD=CB.求证：四边形ABCD是平行四边形.证明:如图，连结BD.在△ABD和△CDB中，∵ AB＝CD，AD＝CB，BD＝DB，∴ △ABD≌△CDB，∴ ∠1＝∠2，∠3＝∠4，∴ AB∥CD , AD∥CB，∴ 四边形ABCD是平行四边形.【总结】平行四边形定理1：两组对边分别相等的四边形是平行四边形.符号语言：∵AB＝DC,AD＝BC，∴四边形ABCD是平行四边形.问题2：从边的角度，如果弱化条件，只有一组对边满足什么条件，可以构成平行四边形呢？猜想2：两组对边分别相等的四边形是平行四边形.已知：如图，四边形ABCD中，AB=DC，AB∥CD.求证：四边形ABCD是平行四边形.证明：如图（2）,连接AC.∵AB∥CD,∴∠1＝∠2.又∵AB＝CD，AC＝CA，∴△ABC≌△CDA.∴BC＝DA.∴四边形ABCD是平行四边形（两组对边分别相等的四边形是平行四边形）.【总结】平行四边形定理2：一组对边平行且相等的四边形是平行四边形.符号语言：∵AB=DC，AB∥CD,∴四边形ABCD是平行四边形.问题3：从边的角度，我们现在学了多少种平行四边形的判定方法？判定方法1（定义法）：两组对边分别平行的四边形是平行四边形.判定方法2：两组对边分别相等的四边形是平行四边形.判定方法3：一组对边平行且相等的四边形是平行四边形.问题4：在研究平行四边形的时候，仍然采用了怎样的研究思路？问题5：在探究和证明过程中，体现了哪些数学思想？设计意图：让学生经历猜想证明的过程，发展学生演绎推理能力.本环节注重学生的自主合作交流能力，体会归纳、化归的数学思想. （四）运用判定，解决问题【例题1】如图，在平行四边形ABCD 中，点E ，F 分别在BC ，AD 的中点，求证：四边形AECF 是平行四边形．证明：∵四边形ABCD 是平行四边形， ∴AD =BC ，AB =DC ，∠B =∠D . ∵点E ，F 分别在BC ，AD 的中点,∴AF =DF =21AD ，CE =BE = 21BC .∴AF =CE , BE =DF .∴△ABE ≌△CDF （SAS ）∴AE =CF . 问题6：请同学们思考，还有其它方法吗？证明：∵四边形ABCD 是平行四边形， ∴AD =BC ，AD ∥BC .∴AF =21AD ，CE = 21BC .∴AF =CE ，AF ∥CE .∴四边形AECF 是平行四边形．变式：在上题中，如果将“点E ，F 分别在BC ，AD 的中点”改为“点E ，F 分别在BC ，AD 上，且BE =DF ”，结论是否仍然成立？请说明理由.【例题2】已知：如图，在四边形ABCD 中，AB ∥CD ，E ，F 为对角线AC 上两点，且AE =CF ，DF ∥BE ．求证：四边形ABCD 为平行四边形． 证明：∵AB ∥CD ，∴∠DCA =∠BAC∵DF ∥BE ，∴∠DFA =∠BEC . ∴∠AEB =∠DFC ∵ AE =CF ，∴△AEB ≌△CFD （ASA ）∴AB =CD ∵AB ∥CD ，∴四边形ABCD 为平行四边形．设计意图：在例题中，让学生学会分析条件，运用平行四边形判定定理，进行相关证明，体会一题多变，一题多解的数学学习方法.DBF E（五）巩固练习，拓展提升【练习1】如图，在平行四边形ABCD 中，已知AE 、CF 分别是∠DAB 、∠BCD 的角平分线，试证明四边形AFCE 是平行四边形．证明：∵在平行四边形ABCD 中，AE 、CF 分别是∠DAB 、 ∠BCD 的角平分线∴∠B =∠D ,AB =CD , AD ∥BC∠BAE =∠DCF=21∠DAB =21∠BCD .∴△ABE ≌△CDF (ASA ). ∴BE =DF . ∴AF =CE .∵AF ∥CE ,∴四边形AFCE 是平行四边形【练习2】如图，已知△ABC 是等边三角形，E 为AC 上一点，连接BE ．将△BEC 旋转，使点C 落在BC 上的点D 处，点B 落在BC 上方的点F 处，连接AF ．求证：四边形ABDF 是平行四边形．证明：∵△ABC 是等边三角形， ∴AB =BC ，∠ABC =∠ACB =60°. ∵△FCD 由△BEC 旋转得到, ∴CD =EC ,FD =BC∴FD =AB , △CDE 是等边三角形. ∴∠EDC =60°,∴∠EDC =∠ABC . ∴FD ∥AB ∴四边形ABDF 是平行四边形．设计意图：学生通过自主探索，获得新知，本环节加以应用，巩固新知，题目设计层层递进，发展学生的逻辑思维能力. （六）总结升华DFABCE设计意图：引导学生归纳本节课的知识要点和运用的数学思想方法，使学生慢慢养成总结知识的学习习惯.（七）自主作业完成《平行四边形判定（1）》配套练习.必做：基础题（1-7题）.选做：拓展题（8题）.设计意图：让学生课后对本节内容进行巩固练习，作业设计采用分层方法，满足各层次学生需求。

判别平行四边形的基本方法如何判别一个四边形是平行四边形呢?下面举例予以说明.一、运用“两条对角线互相平分的四边形是平行四边形”判别例1 如图1,在平行四边形ABCD中,E、F 在对角线AC上,且AE=CF,试说明四边形DEBF 是平行四边形.分析:由于已知条件与对角线有关，故考虑运用“两条对角线互相平分的四边形是平行四边形”进行判别.为此,需连接BD.解：连接BD交AC于点O.因为四边形ABCD是平行四边形,所以AO=CO,BO=DO. 又AE=CF,所以AO-AE=CO-CF,即EO=FO.所以四边形DEBF是平行四边形.二、运用“两组对边分别相等的四边形是平行四边形”判别例2 如图2，是由九根完全一样的小木棒搭成的图形，请你指出图中所有的平行四边形，图1AB C DEF并说明理由.分析:设每根木棒的长为1个单位长度，则图中各四边形的边长便可求得，故应考虑运用“两组对边分别相等的四边形是平行四边形”进行判别.解：设每根木棒的长为1个单位长度，则AF=BC=1,AB=FC=1,所以四边形ABCF是平行四边形.同样可知四边形FCDE、四边形ACDF都是平行四四边形.因为AE=DB=2,AB=DE=1,所以四边形ABDE也是平行四边形.三、运用“一组对边平行且相等的四边形是平行四边形”判别例3 如图3，E、F是四边形ABCD的对角线AC上的两点，AE=CF,DF=BE,DF∥BE，试说明四边形ABCD是平行四边形.分析: 题目给出的条件都不能直接判别四边形ABCD是平行四边形，但仔细观察可知，由已知条件可得△ADF≌△CBE，由此就可得到判图3别平行四边形所需的“一组对边平行且相等”的条件.解：因为DF∥BE，所以∠AFD=∠CEB.因为AE=CF,所以AE+EF=CF+EF，即AF=CE.又DF=BE,所以△ADF≌△CBE，所以AD=BC，∠DAF=∠BCE，所以AD∥BC.所以四边形ABCD是平行四边形.四、运用“两组对边分别平行的四边形是平行四边形”判别例 4 如图4，在平行四边形ABCD中，∠DAB、∠BCD的平分线分别交BC、AD边于点E、F，则四边形AECF是平行四边形吗？为什么？分析：由平行四边形的性质易得AF∥EC，又题目中给出的是有关角的条件，借助角的条件可得到平行线，故本题应考虑运用“两组对边分别平行的四边形是平行四边形”进行判别.解：四边形AECF是平行四边形.AB CDEF图41 32理由：因为四边形ABCD 是平行四边形，所以AD ∥BC ，∠DAB=∠BCD ，所以AF ∥EC.又因为∠1=21∠DAB ，∠2=21∠BCD ，所以∠1=∠2.因为AD ∥BC ，所以∠2=∠3， 所以∠1=∠3，所以AE ∥CF.所以四边形AECF 是平行四边形.判定平行四边形的五种方法平行四边形的判定方法有：（1）证两组对边分别平行；（2）证两组对边分别相等；（3）证一组对边平行且相等；（4）证对角线互相平分；（5）证两组对角分别相等。

判定平行四边形的五种方法平行四边形的判定方法有：（1）证两组对边分别平行；（2）证两组对边分别相等；（3）证一组对边平行且相等；（4）证对角线互相平分；（5）证两组对角分别相等。

下面以近几年的中考题为例说明如何证明四边形是平行四边形。

一、 两组对边分别平行如图1，已知△ABC 是等边三角形，D 、E 分别在边BC 、AC 上，且CD=CE ，连结DE 并延长至点F ，使EF=AE ，连结AF 、BE 和CF(1)请在图中找出一对全等三角形，并加以证明；(2)判断四边形ABDF 是怎样的四边形，并说明理由。

解：（1）选证△BDE≌△FEC证明：∵△ABC 是等边三角形，∴BC=AC，∠ACD=60°∵CD=CE，∴BD=AE，△EDC 是等边三角形∴DE=EC，∠CDE=∠DEC=60°∴∠BDE=∠FEC=120°又∵EF=AE，∴BD=FE，∴△BDE≌△FEC（2）四边形ABDF 是平行四边形理由：由（1）知，△ABC、△EDC、△AEF 都是等边三角形∵∠CDE=∠ABC=∠EFA=60°∴AB∥DF，BD∥AF∵四边形ABDF 是平行四边形。

点评：当四边形两组对边分别被第三边所截，易证截得的同位角相等，内错角相等或同旁内角相等时，可证四边形的两组对边分别平行，从而四边形是平行四边形。

二、 一组对边平行且相等例2 已知：如图2，在正方形ABCD 中，G 是CD 上一点，延长BC 到E ，使CE=CG ，连结BG 并延长交DE于F(1)求证：△BCG≌△DCE；(2)将△DCE 绕点D 顺时针旋转90°得到△DAE′，判断四边形E′BGD 是什么特殊四边形？并说明理由。

分析：（2）由于ABCD 是正方形，所以有AB∥DC，又通过旋转CE=AE′已知CE=CG ，所以E′A=CG，这样就有BE′=GD，可证E′BGD 是平行四边形。

A FB DC E 图1解：（1）∵ABCD是正方形，∴∠BCD=∠DCE=90°又∵CG=CE，△BCG≌△DCE（2）∵△DCE绕D顺时针旋转90°得到△DAE′，∴CE=AE′，∵CE=CG，∴CG=AE′，∵四边形ABCD是正方形∴BE′∥DG，AB=CD∴AB-AE′=CD-CG，即BE′=DG∴四边形DE′BG是平行四边形点评：当四边形一组对边平行时，再证这组对边相等，即可得这个四边形是平行四边形三、两组对边分别相等例3 如图3所示，在△ABC中，分别以AB、AC、BC为边在BC的同侧作等边△ABD，等边△ACE，等边△BCF。