发展党员工作手册 .doc

Ƒ ˩/H ӍH Ȓŝ )జ3 p Bƥ p A ̨̕ǹ_ ȼ@ ώ $я ; ǹ Оѩψq$- nǹ_̽ ̫ q^? ǹ Ȭ^q VMp Bƥ ǃN ǹEȣqѥȤƃUч@3; ǹL( n[! VϷBƥ҄ ʹ=ǹ_̽ Ҧ q SƬ ǹѱ[A @3& ; ОA q[ E+ ǹLƃ ǹ[ /;q - қq$яѩψqϷϣ ?Ϸ̟˓ȇ̽ @3 ; О - ҧiǹКч ʋ ǹКчq, ʋq; ʋ@Rў L; q Ƚʳ ҄ @జnj ࢨˣH Ѥ J ๦36 n[ 0 ǹ p҄ W Uѡǹ pA q^? ѳȽ ǹ q 8 [ ǹ̄M Ҧȼ:@3 n[Ƚ[ ǹ̄M Ҧ̽ ϓ ҄ ? ш6 L ƃΪ ǹ Вq ǹLƃѕ ǹLƃ ǹ Вq ̏ ǹdυ0 ǹ Вq 2 6Ǹ ǹ ѩ?ɺϣ?ѝ ?ҭo? <? nКч q 6Ǹ Оǹ < βq#҇2 8 6Lq ^ Bƥ҄ ȬѮV ǹ @3 n[ѝȣ Ѡφ< О [ ǹ̄M Ҧǹ QιR q 2 ? Ϸʳ˻6qʍ2 ȣǹP˴A q ̏ȣ; ǽ qȽ2 ̽ Q В@3Ő ђ Ť [Ƚ[ ǹ̄M Ҧ̽ Ɲ@L( [Ƚ[ ǹ̄M Ҧȼ:ǹғ A@ Ƚ kǹ'_q =̽ǹ @[ ǹ̄M ҦȚ6A qȚ/ n Q? ВǹϷʳ ϒqҏʍȚ n@3͖ [ ǹ̄M ҦS D Q ВFqk ? Q ιR ѳ ǹLǤDqSђ ˴ Qђ ˴ǹђ ˴ Y q ϓ ; Ƚ @3 n[Ƚ[ ǹ̄M Ҧǹƃ α p ̽ ώ̭@ ȣ ; Ƚ Fq[̽ p ƚ@ p ƚǹ҄[ yȽ ǹ ? ? Ɩǹ ȷzƃ ǹ pα kѱ pȬ pǹ zіR Іƃ ʳR) ǹ҄[P˴ʳRǹ p @ p ƚ[ ,Ү ǹ ϒ@ p ƚǹLƃ y ƃ ˕?ƚЫϷʳ Ń ϒ? Ϸʳ Оώ̭q ̏ [ǹ Ț˿ Ț@k ƃ QK ƚЫϷʳ ϒFq ǣǹ k Ț˿ Ț@ϷS p ƚǹq ; @3 L( [Ƚ; Ƚ ̽ 8;̎p @ " 6Ѡ ˿ He ʋ @҄[ Mp Bƥ ǃN?Mʳe p]˻ǹ ɰқчNǽ! @p J n n͡ ǹM Nq ɛ ϒ@ʶК ̎p̽ ǹq n 2 ѝȣǹ! q ? ɛ @ϷS ǹqǢʋ ; @జ H ޻3 ; ̤ ЗŽ О :@ Eȣǹǃ ťΪ@3 & S ǹ [Ϸφ< О QK @ QK "d Q ιR c d; Ƚ ҧNi q˿d nѝȣ@c Ɲ ǩ E J< О β˿E k H;ǼO; ǹ О QK @3 QK ǹ҄[ < yƀQK ̭ ǹɺϣ? ǃq Оǹ ? < β@ ώ̭ƀQK ǹ 6L? pʹ=? $ѩ?ƃn A ?Sαǽ q n˶ų@ѝ ƀQK M o i Nq ҧNǹ @ ђ ˴ɧхȇQKƀQK ǹ @ƀQK қ ЗŽ О Fq O Ƚ2̽ В#҇@3 6 ; Ƚ M o i Nq SD̕ n @ђ ˴[Ƚ; Ƚ ǹM o i N Ϸʳ ̽ :@ ƚqS̎bY @ Fq k^ ђ ˴Y @3 k̤ ЗŽ Оǹђ ˴Dq S ˶ųȽ ǹ ? 6 L?ƃ αq ̏ n ǹ'_@ђ ˴[ ˴ųʁȽS ǹ @І˴ О[ȽS ̽ Ǖ ǹY q ͤ ˿ O< ǹ ̽ ͵@й, Ư ˴Ϸ ͵ ǹ ОǹŤ q ̤ ЗŽ Оǹ͵ @ ʫ ˴ǹ О ђ ^/ ǹq ̟k @ђ ˴Y φʋ Dǹ q rʋY ͵@3 ђ [̏ ђ ˴͵ kM o i NDqλ ƃ S ? ϒ? Q В Ɲǹ ϒqųD̕ @3 Ő ЗŽ О d A q @үђ ЗŽ Оq [Ƚђ ˴ ̤ ǹЗŽ О̽ @ D і̤ϣ ǹ7^ ǹ үђ * H ? ҍi і ǹ *? үђqS D q О s ǹ @ϖ ђ ?ϖ ̤ ? ЗŽ О@ ЗŽ О@3 ͖ q[ѝ ҍ О˿ nО ȽM o i N Ϸʳ ϒ̽ ƚq E ѳǹ S ̽ ˕q ̽ ǹ Ɲ@ ˕ ˕ǹ ҧNȽS ǹ q k M o i NDq ˶ų@3; ЗŽ Оq ̎bY ? ͵͵ȣ@҄[ S VŽ О q Ž@S О ? Žǹq қ? ЗŽ О@ ǹ [ kM o i NDq s ЗŽ;ǹ ў q ѕų ǹ ђ @ ђ ̏ ѕƃ k О ˴D @Ƚ ƀ қ ǹq c[ ѕ ђ ƃ A @˴ φʋ Dǹ q rʋ ͵@3; Ƚ ђ Dųǹ̤ ЗŽ Оǹ͵ q k&ʋЩ @ g ƭ q ǸƯ ʋЩ@ ʫƯ Eȣ ɕ f ǹq ҖTϷʳ Оǹх @జ H ๦ # <ᆼ࡙3; ; n ̏ D̕ қǹЗŽ О ђ @ ǹ n]˻ O A 8_qȽ2 O ̽ В Ɲ@ 3; & ЗŽ О Ƚ ̽ @ q "d L( ˿ ђ үђ n̽ @D̕ n d ђ ͤ ǹ @ 3; n[ ƃ ˶ų?ʋ ?̎p ǽ qȽЗŽ О̽ В Ɲ@ ђ ̗ȷ[Y ; '_[̏ ƃ ˕@ЗŽ ОȚ6A qȚ/ n В? Ɲǹ q ɧхȇQKʍȚ n@3; 6 ЗŽ ОЗŽ; Fq ђ Y ? ҏ О@ VŽ О ǹq ;ҏ z VŽ ? ̽ В Ɲǹq ƭЗŽ;q ƭ HeŤ q ƭ Ư z VŽ О ǹq ?ЗŽ Оң@@;ҏ q ƭЗŽ;q ЗŽ Оң@q7 Sђ ˴Y ųD̕ қ@3; ЗŽ Оҏ ǹ yƃ ^/ ҏ S z ^/ z ђ ѳǹ zђ ˴ ƚzђ ˴Y ? ͵ zųD̕ @3; Ƚ ђ DųǹЗŽ Оҏ ǹ͵ q k&ʋЩ Y @ ̬ ̏ ѕ ђ @ ђ O[Іƃ ˕q ̬ k О ˴D @3; Ő ЗŽ Оҏ Fq ?M o i N? ҏ S ?ҧ0? ϒ? В Ɲǹ ϒq ƃ Ń@Ńǹq ^ О Ńq d k $ @జǔ ӍH Ȓ <ś3; ͖ ʌ̕ !; ОA ϓ ѱ[ ǃq ϣ @Ƚ; ОA ǹ qȇ ? Ť [ ƚ q b?ҧp ?і [ ƚ @ ƚǹ̬ [̏ Dųq ų@ 3& ʌ̕ n [ D̕ ǹ n ųʁ; ОA ; ОA ̟˓@[ Ϸ ǹ'_ Ƚ E ȣ ǹƚǩ @3& D n [ѱ Ƚ nОǹ œ? Ž qǕ ;ˬ2 k; ОA pǹ ϰ@3& ; ʌ̕ nȽ; ОA p/ ǹ '_q ȣ[:#ƚǩ@ Eȣɕƀ ǹq fLJ q kђ ˴Dʘ @D̕ n[ȽϷʳх Вq ǹ ʍf [ǹ ǩ @ జ˥3& & ƃUчҧ ͖͖2 ͖Щ @ Ϸʳ; ОA ǹEȣ ̭ q ІƃUч ѡǹq͸ ƃUчEȣ қ@˫ǎΰ Κ9 qÅཔ ȒˣH ѤȒ Ҕ ͨ ) -G > @G > @ʌүђ?і ђ ?ʌ үђ n yM G d О ̄M ҦA ǹ ť n N ;ʍ q љ @љ pϷ '_q ̏ ү̬ @pB G О˴ nB G О˴͖͖͖ Щ; & ư yʌ ђ zʌ ђΚ9 qÅཔ ȒˣH Ѥ Ȓ Ҕ ͨ )֨E+љ pBp J n ?B p J Mʳe̽ d О ǹ; Ƚ A ǹ N q k ]pǹ d О ̄M ҦA ,q d r A n q ʌ̕ nǹq d r Lѥq ̬ ) O ^/ ť @?Lƃ[?q d r <f B ǹ E nх n ҧV Qǹѱ[ ͍q n; ОA ǹѱ[ @΁ q d r A qϷβe$я; Оǹѩψq cϷ҇ẻ;E О ǹ p ȽE О ǹ Вqы B nǹ ^ V^@ʌ̕ ? n[̽ ^ ?Ƚ q d r A ѱ[ ǹ qы pх > ҧʹ q ^ A m ?Ϸ ȇ̽ @q d r k ђ ;T ȣS ̄M Ҧn ̽ q -8҄̎pѥqǕ ;ˬE Оǹ ϰq ǃ ̽ q[ ў_d ђ ȣ ̄M ҦF kd n q d r ǹȈ ǃ ? e ǹ @ ? Ƚ Оǹ Q Вq^? Оǹ p ѩq q d r A ǹ ^ LǤq c q d r A ǹ҄[Rǹ@k q d r A pq n[ ?q 2 Ϊ ? r ǽ SƬ n S ǹLƃΪ ?Lƃ ? ? Ɩ ǹLƃѕ @?q d r A [kʌ̕ nǹ ϣ ̽ q[ - қq $ѩψ@ʌ̕ n[ Ƚ n΁ q d r A ǹѝ ?7 ƚq ү̬ E ǹS H q r q d rѥȷ@? dV b d L( nʎV O ȣ@;? dȽ?ƀ ̄M Ҧǹd О VŽyƃ Ƚ ϷƇ̠ ǹ q LJ ǹ ǃ ̄M nq n3 S z k ?A ? ]˻ǽ ̠ /qk ѳpϷ ȣ @? ?Rʌѯǩ f q d r@&? d ѻq d r A ǃ ̽ V b ѻ y3 y ђ ȣ dȽ @?k үђ O˿"҄ ǹѝ q ђ ΁ Оq d r ˴@q d r˴d ђ O?< O˿ n О҄-q q d r ˴ Ϸƃђ D О Ϸ @ ˴ _QKS ǹLƃ z? q nІ˴ О̽ 8҄ z Fq̽ O< @? ђ О˴ʎVђ q d r ˴ О ̏q d rȽ ǹ q ȣђ q d rȽ < @ О ˴Ť D " ϓ q d rȽ @? ђ О˴ M G d О ̄M Ҧ N q ˴ǹ О ? ђ ˴ǹ О ? O< ̬ ů й,? й,?O ǹ nǽ @3;y үђ dȽ @? ђ О ˴q d r ?ђ Ɲ ;T R үђ˶ųq D M G d О ̄M Ҧ N@? үђkȽʌ ђ ^/ǹq d rȽ ̽ Ɲ̏ Ϸʳ ϒǹLǤDq ΁ үђ О˴ q Y Ƚ @?kM G d О ̄M Ҧ ND ? @3&y ђ ȣ ̄M Ҧ@? үђ ] ђ q ^ ʳ ϒ@? ] ђ k nǹ ϒF ̏ ΁ ђ ˴ q;T ȣ ̄M Ҧ@? ] ђ k ȣ ̄M Ҧ< F M G ̄M Ҧ Q ƝǼO N q ѝȣ Ѡφ< О ̄M Ҧǹ QιR q 2 ? Ϸʳ˻6qʍ2 ȣǹP˴A ̏ȣ; ǽ qȽ2 ̽ Q В@? ] ђ ̏ ! ȣ ̄M Ҧǹ< ѕ үђ̏ ђ @?s? үђȽ ђ ȣǹq d rȽ [kφq ΁ үђ О˴ Y @? Ƚ ȣ ̄M ҦFqʌ̕ n[O Ƚ2 ̽ ʏҬ Ɲq Ɲ ̏ n q ҇ n Ƚ ȣǹ ̄M Ҧǹ Q ВA @?ƃť ҧ ;n @˫ǎ ӍH ȒҔ ̓P -> @ʌүђ?і ђ yώ̽ ) ǹ; ОA qʎVpB b n ?pB b ВA О˴Mʳe ?ǽ ; ОA ǹ N Ү n S q S;T͵ȣq Щ q) ; ОA ͵ѥqV b[ yk̤ ЗŽ О˿ЗŽ Оҏ ǹђ ˴Dq ͵ ̽ ͵q ˾Ǹǹй, Ư ˴Ϸ ͵ ǹ О ǹ Ťq ђ ǹ͵ @ ђ ͵ s ђ ˴ǹ ͵̬ @ѕnЩ ư y ϣ q q ʌ n qA˴cn Щ ;B˫ǎ- ࡛>3 Ӎq H ˤ Ȓ̽ E+ q - қq$яѩψq= ̬ʠq Zѱ; rǹ;ОA qы ; ОA ǹ ȷ Ƚ; ОA ǹ 7 $ Оǹѩψq ; ] Оʘ A qʎVMp Bƥ ǃN?Mp Bƥ ; ОA Uч n NǽϷʳEȣkү̬N ʌi?R;] Оʘ A ǹS HǹLǤDq Ƚ) ; ] Оʘ A ^/ NȌ @?ʘ Ƚʘ Ƚ ]; Ƚ ЗŽ; S ҏ ǹ ]ЗŽ О@;?ʘ; Ƚ ˿ҏ Ƚ ǹ <? i?R?"̕ ?S ? ȣ ̄M Ҧ ˿ ?ʘ ;?ʘ Ȑ˕?ʘ ȐҦd ǽ@ &?ʘ ǹ?ʘ A dƀʘ Ƚ k үђɧх@?҄[ k ǹʘB ʁ·? 0·ǽ ͍ E ]̽ ʘ ǽ@ ?ʘ ̏ʘ ;k̤ ЗŽ Ођ ˴ ˿Y ЗŽ Оҏ ǹђ ˴ ̽ ʘ @; ʘ ǹ qʘ ; @6?ʘ FǹA ǃ? ѳ kʘ ; Ȑ? ˿ q k үђ˿ n ʘ Ƚ ǹ ˿ @?Ϸʳ үђ˿ n Ƚ Ȑ? ˿ ǹ'_̽ A nȚƚ @?ʘ ̬ Fq үђ˿ n ʎVʘ ; ѳ ǹ Țƚ ǹ ̏ ^/ǩΪ q ȚƚǩΪ̬ <ǹ @ ?s?[ ʌѯ ̄M 0 ВA E О ѳʑ О қ nk; О ǃp -ǹA ǃ z[ ВE О ѳǕ q; ОA ̤ ѳ 7?Ǹ ѳʘ q $- ǹ_̽ ǹ [z[ Вʘ Ƚ Ƚ ѳ ǹ'_@?[:# Ƚ ѳǹ ɧхȇ ѳ ǹ'_ǼO qn^ψ̽ Țƚ @:#$) qȽ ) q[ҖTх q P:ѱ qʍf ǩ @? ώ eȽ ǹ'_̽ Țƚ q^Ʈ < '_@n; Щ;ɪyʘ Rƃʳe;;;ǽ ʘ ǹ ʁS n Q Ɲq R; ; ;;;ǽ; < ɪF n pBЗŽ О@ О ѳȽ; pBЗŽ О Ϸ ˿ q ϰ ˿ e;Щ; i R n үђ˿ n @; Ƚ < yʘ Ȑ˕yi R n үђȐ˕y;;;;;;z n Ȑ˕y;;;;;;ʘ ȐҦd y;;;;;;i R n үђ ɮ nЩʘ Rƃʳe;;;ǽЗŽ Оҏ ʘ ǹ ʁS n Q Ɲq;;;ǽ; ЗŽ О < ɪF nЗŽ; @ О ѳȽ ЗŽ О ;ҏ pB О Ϸ ˿ q ϰ ˿ e;Щ; i R n үђ˿ n @ҏ ǹЗŽ О< yʘ Ȑ˕yi R n үђȐ˕y;;;;;;z n Ȑ˕y;;;;;;ʘ ȐҦd y;;;;;;i R n үђ ɮ nЩ˫ǎ ӍH ȒҔ çၦP -ʌүђ?і ђ y̽ ) ǹ; ОA qʎVpB b ВA Mʳe ; b? ; ОA ƙ ѥ?ʘ ѥ?З ѥ? ͵ѥ?х ҖTѥ ť ǹ ѕN n S S;T͵ȣq Щ ) ; ОA ƙ ѥqV b[ y?ƙ Ƚϓ R;; ̟˓ǹ ̄M Ҧ R;ҏ ǹЗŽ О@;?ƙ?ƙ Ƚ ] k? k"̕ ̏"҄ p̽ ƙ z?ƙ Ƚ A k? k ђ ǹL( Оp̽ ƙ @ ƙ ǹ ˴ ǹ6 n D@&?ƙƙ k ѳǕ ǹLǤD O< ǹ ̽ ƙ R ɪF n@ƙ A d ђ ɧх n@?ƙ ̬ d ђ ɧх ̟ ̟ R ɪF n q k ʘ q ȣ; Ƚ ˿ЗŽ Оҏ ǹѱ[ V@ƙ ̬ ƀƙ ǹ ϒ Ńp@ѕ@pB G О˴ n; Щ Ő; Ƚ ƙƀƙ < Lƃ ;;;;;;ƀƙ ~ k ǹ ·p˒q r@i R nүђ ђЩЗŽ Оҏ ƙƀƙ < Lƃ ;;;;;;ƀƙ p Bƥ О ~ k ǹ ·p˒q r@i R nүђ ђЩ; Ƚ ЗŽ Оҏ nƙ ̬ ̟y O yƀƙ < Lƃ ;;;̟ V<yV<yђ O V<yЩ˫ǎ>3 ӍH җ Ȓc H ÃH җ¸ ฤ ˣH -G s tʌүђ?і ђ y̽ ; ОA qы ; ОЗ ^ȷq^?A S ;T͵ȣy Žүђ ǹi Rүђ; ОЗ A d=үђV bɧхq Ϸ Žүђ ǹi Rүђq; ОЗ A d n ɧхz; n A Оd ʌүђ q?p; ?̕n,?ǩ̕ Dɰ Оd @ Ϸʳ ѕ yɧх; ОЗ A ǹi Rʌђ ȣ; Ƚ Fq Ϸʳ; О ϒų үђ̽ З @ ϒů y n S @ n d n AǢ n@ n ̄M Ҧ Q ƝǼO @ n ˶ų@ n ̬ я @ nҧ0@ n ϒ@ n К O @ n,M n AǢ nǽ@ ɧх; ОЗ A ǹi RүђȽђ ų ǹ ϒ ѝ ҍ үђ n ; ОǹϷʳEȣ̽ З O ɪ n q ;T V Žƚ@ȽЗ үђ[̏ ;T q !З ̬ ѕ ђ @ ?̕n,?ǩ̕ Dɰ ; Ƚ ǹ ϒd n ̽ З @ƃ ѕ Щ ΁ љ @ɪ y; О ƚǼOpB G О˴; Щ& ư y Ƭ c ƭ҇Ϊq ʌ qA˴c dpBG О˴ťʘ Щ ;B˫ǎᆼ 2 ӍH ȒçၦP ˤ P җP ̓P* -İP) ͨ -G s tʌүђ?і ђ q ? ʌ n yM b? ; ОA ƙ ѥ?ʘ ѥ?З ѥ? ͵ѥ?х ҖTѥ ť N > @ nҏ;ʍ q E+љ @pB G О˴;±± Щ 6ư Ƭ q dpBG О˴ťʘ Щ ;B2 ӍH ȒçၦP ˤ P җP̓P * -İP) ͨώ̽ E ? ; ОA q 8Ғ Оȼ:q^?; ОA ѩψqы nǹ V^ Ȭ^@ʎV3 ; ? A ˴ 3 & b? A ˴ ̏Mʳe ?ǽ ; ОA ǹ N Ү nǹS q ѥȣ? ; ОA ƙ ѥ?ʘ ѥ?З ѥ? ͵ѥ?х ҖTѥ ť @ƙ ѥƙ Ƚ yϓ R;; ̟˓ǹ ̄M Ҧ R;ҏ ǹЗŽ О@ƙ ť zƙ k ѳǕ ǹLǤD O< ǹ ̽ @ƙ A d ђ ɧх n@ƙ yƀƙ k ђ ˿ ǹL( Оq ˴ О k ˴ Оǹ6 n D@ƙ ̬ ǹjϰyƙ ̬ d ђ ɧх ̟q k ʘ q ȣ; Ƚ ˿Y ЗŽ Оҏ ǹѱ[ V@;?ʘ ѥʘ Ƚ y ȣ ; Ƚ ǹ ̄M Ҧ̏?2 [ʘ ǹȽ @ʘ yʘ Ƚ ǹ < /] Щ ̍E S Q ,M ]n ̬ ̟˓; zʘ Ƚ k ђ үђ n ǹιRȐ˕ ȇќ@ʘ yʘ A dƀʘ Ƚ k ђ ɧх@ k ǹʘʁ· 0·ǽ ͍ E ѳ̽ ʘ @ʘ y @&?З ѥЗ A d n ťʘ n˿ƀ ; Оǹ үђɧхqЗ [kǕ ђ ˶ų ώ̭ , ̄M ҦLƃ ǹLǤDqѝȣҍ ; ОǹϷʳEȣȽ ʳ ϒ̽ ǹ @ȽЗ [̏ ;T q !З ̬ ѕ ђ @? ͵ѥђ k Y ЗŽ О ťΪЗŽ Оҏ ͵ѥ@ ͵A k̎bǕ Y ǹLǤDq O< ̽ q ͵̬ n ,͵ ǹ V@k ͵ ǃp[ -rʋY rʋ ͵ǹКч@ ͵pǹV b ͤǹϷʳ @6 х ҖTѥn үђϷ ϓ n qȽɧх Ϸʳх ʍf ˕ ˿Q0z P:ѱǹq[̽ ų ˿ ǩ yEȣq қ О ǹ zEȣť q nϣ A Ǹ^zk ̤ ЗŽ О˿ЗŽ Оҏ q Ϸb 8҄̎pѥКч ΁ О˴˴ ˿˴ ǃ E ˴ O ǽzȽ ђ Dųǹ̤ ЗŽ О˿ЗŽ Оҏ ǹ͵ q ʫƯ Eȣ ɕ fY @;n ђ k; ОA pϷ ϓ n ђ O Ϸʳх ʍf ˕ ˿Q0z P:ѱǹq[̽ ų ˿ ǩ y Eȣ Eȣ қ ; Оǃ ̤ ЗŽ О ťΪЗŽ Оҏ z˿ ?3 8q! О ǹ zђ k ̤ ЗŽ О ťΪЗŽ Оҏ ȣ ̄M Ҧ ; Ƚ q ΁˴ ˿˴ ǃ E ˴ O ǽz k̤ ЗŽ О˿ťΪЗŽ Оҏ q k ϒ E ǽzkD̕ n ȽS ǹ ̽ ˕ Ɲ q q ľ Ɲ ώ̭ @Ӎ q H Ȓ ࢍ ͫ֨śnj֨ś ֨ś ֨śqń q q q q q q q qH - ˹ ๦ ּ J H .+ၘ0 -ś H ૕ ś ĵH . -׷Ӎ / ޖҔ ڣ̕ Ӎ¸HӍ ¸Hύ ˹ ӍHq >3 ֽ Ȓި Ƒq ˣHt( Ѥ-ǞˣH )+0 c >3"" J ๦" ˣq ๦qHඪŝİtజ ¸ˣHѤ >3J ๦ Ȓ/Č>3Ѥ<ˣH )0 J ๦Ĝ జ ¸t ˣHѤt ¸ˣH ѤƑq t( ѤƑӍ ˣHӍజ ¸Ht ¸ˣH ѤͪѤ J๦Ӎజ ¸H̤ -ś Hnj֨ś q % ֨ś q ӍH /Čࢍ q ּ Ӎ ¸Hͪ H ๦ͪ ˣH )0< Ѥ J ๦ͪ V Jq H .+ၘ/Č>3H ๦ Ȓİ >3 ֽ Ȓި H ˣHѤ L )+0 ڣ̕ c>3"" J๦c ඪ İH . ቱ3ቱ H .+ၘͪ H .+ၘ ၕ֨ś q %nj֨ś ӍH /Č ࢍq ּ Ӎ ¸Hͪ H ๦ͪ ˣH )0< Ѥ ๦-׷ Ӎ / ޖҔ ڣ̕ Ӎ ¸H/Č݋3H ๦ Ȓ)ˣH0 ˣH Ѥ Ӎ ႋ t)#) ฬ <ZS ? ̄M Ҧ?; Ƚ qOϷιReϷ @ 3 Eȣq n ^/ S ǹ " S n q͸, GS H@S B ОS nn qђ ˴ Qђ ˴ǹђ ˴n;T q ȣ G ̄M ҦH@ ђ Ƚ ̄M Ҧq " ѝȣ QιR q ϷVbǹ Q В̟˓ @ ̄M ҦS Dǹ Q Вq nk ? QιR ѳ ǹLǤDq Sђ ˴Y qȽ?pLƃVŽ О ?қŽR;; ǹq, G; Ƚ H@Ƚe[ ǹ o q & 2 r VŽ О ǹ ̨8zȽe n q ψ[ ǹ o, ǃȷǹ o@ˣH Ѥ Jฬ 0ฤ*<Jȏ ࢨ̄M Ҧǹ QιR q dS ȣ ]˻ǹ8_q ʢϰ О қ:@[ ҧNq_ B ϰ;ˬǸƇ̠ ǹ О @ Q ιR ɧхȽ ̄M Ҧǹ Q? Ɲ ѝ A @?҄[nхsSƬώ̭ ̄M Ҧǹ ? ?A ǽ k'_q n 2 ǹi [ q ҧNǹ O 6 ̄M Ҧ̽ 0V q Cί #҇2 ;NdȌq Ȍq̄MD̽q8 6Lq R ǹq ̄M Ҧ ǹLƃѕ LƃΪ ̏ ǹ ? ? Ɩqы 2 ǹ ɕ ^ Ȭǹҧʹ q#҇2 D @ wsȣ; ђ ˶ų ̄M Ҧǹ,ƭ Q? Ɲ q ƝO q ʎV ̄M Ҧǹ O q^/ Q Вǹ @sk ̄M ҦVŽ q ђ ? ^/ ?ϓ ; Ƚ ǹ @sȽ ̄M Ҧǹ ̽ ȣ; Ɲq҄[ Ɲ ̄M Ҧǹ pʹ=? $ѩ? 6L ƃn A ? ǽ@ 2 VϷB ƥ҄ ʹ=? Ƚ ǹ ? ? Ɩǹ ȷq ώ 8ǹβ ɕ _ʋ ǹβ q : ǹ )q ǹ q ̏2 ǹA q , n ʍ <ǹ @;?Vb[sιR ȣ;ІƀιR ΁ ̗ȷѠH n@sɧхЫȰƀιR 3 ǹ ˶ųq kЫȰ F DG ЫH kV D ҧNǹ < @s ̗ȷѠH ђ ˶ų ƀιR ǹ @s Ť ȽιRǹ ̄M Ҧ̽ Ɲq [ w ̄M Ҧ Q ƝǼO x@8ȑ>3 ӍH ̵ ෺ ؓࢨؓࢨ ၠූq ӍH ؓࢨ0౐ ֨śநฤͫ)ˣH t(ˣHѤH "ࢨ ))Ҕ Ҙ )ˣH Ѥ _* Ƣ J qƲ Ȓ æ ෺ ˫ ķ ந c ͫ q ڣ̕ ͫؿëc J ŞČ Jȏၒƣ࡚ & J҅ ˷v Ʊ) ę Ŝ)(Čᄣc1WVq àààH .Pnj ؓࢨ & ts ǹ ȣyүψ "̕ ǹ @ s ǹʠ,y nƀ ǹ ! z n? k"̕ǹ" ђ z n"Dǹ?2 q ̏ [E q V qb О? Оq]? q ,Mʠ,ǹ @΁ ˴ǹ ?ȇȌd ђ ɧх ȣ P ђ ƃ чd" ɧхn q < ǹ ȣ ƃҞʘ ǹКч̽ q ђ k ȣF ̏ < ȇȌ ʍ ђ Oq ђ ѥ О ˴@ؓࢨ˴d= ; Ƚ k"̕ǹ ђ ɧх ̎q P ђ ƃ чd" ɧх ̎@ ђ = ; Ƚ ǹ QιR ˴q ˴ d QιR ҄-q d QιR ɧх ; J@˴Dq QιR ˴ǹ ˴ ǹRǹq ȚF ƃҞȽ ɧх ǹ ȷqk D ȇ /ҧNȽ= k $ѩ?Ϊ Q? ?A ?]˻? ѳʳRǽʌ d Ȍǹ q n ʑ ȇώ̭ #҇= ,ƭ@k ; q QιR s ΁ q ʑ ȇ @d QιR ɧх J Ƚ D ǹd Ȍ̽ Ϊq Ϊ ǹd Ȍ [ w ̄M Ҧ Q ƝǼO x@Ӎ ႋ- äҗ <ύäҗ ˷v<&Ƚ; Ƚ ̽ p ƚq ; О ǹ 8n q $я Оѩψǹѱ[ H@Ƚ; Ƚ ̽ p ƚq ώ nȽ S Ϸ ʋ ǹώ̭q ,2 ǹ pα p p^ƪ Ƚѱ Кч'_ǹ ȷq ɕ / VŽ О ǹ ˹ @ q F Ƚ; Ƚ ǹ p ƚq˿Ɣ Ƚ p ƚA ǹ q7 Ƚ ǹ Q ɧх ǹ @; О̽ p ƚǹ y S ƃ ǹ pα ̏? ҄[P˴ʳRǹ @[ѱȌ ƚƃ ǹ pα qȽ ;]ǹѱ ̏Ƚ ǹ Q&p ˴ ǹ ī ī Ɩǹ ȷ@ȽіR ҄[P˴ʳRǹ ƚq҄[ ώ̭?ɥ ɚQ?,ƭǹ ̏ιR) ǹ҄[P˴ʳRǹ p k n Іƃ ǹʳR? p ǽ @Ƚ ƃ ιR 9q ǹ іR Țƚ@[ UѡǹA qȽ; Ƚ / p ƚǹ̬ q ,Ү ǹ ϒ@8ȑ>3q ˣH̵ җ Ȓp ƚǹLƃ y ƃ ˕qƚЫϷʳ Ń ϒ?ʋ ҧ0q Ϸʳ Оώ̭q ̏ [ǹ Ț˿ Ț@k ƃ QK ƚЫϷʳ ϒF q ǣǹ k Ț˿ Ț@kƚЫʋ Ń q s ƚЫ Ń ϒq ?,ƭSα ̏Ϸʳ ȣqƚ Ńp Ϸǩ ǽ @kƚ ʋ F q kƚ ?k?p Ǝ Ƚ?ɥ ǹ ϒqƚЫ ǣF q ? ,О̏҄[P˴ʳRǹϷʳ ȣ q ɮ ]ǩ Ń ǹʘ @kƚЫʋ Ń ϒǹLǤD k Ы? ǹʋ ҧ0q ?ʋ ǹ,ƭSα ̏Ƚ ǹ ǽq ҧ0p ǹ ,О̏҄[P˴ʳRǹ Іk Ńp ƚ ̽ Ƈ̠q Ϸ ˔q ˔ǹ k ȣ ǹ s q ɮ үђʘ @kƚЫʋ Ń ҧ0FϷ ǣǹ'_ ?ƃ ̽ ώ̭qk ƃ QK ƚЫϷʳ ϒF q ǣǹ k Ț@sy ;T] ̬Kǹq[Ƚ?Ŀ ̽ y ǹ[; Ț z ǹq ?Ŀ k nȽ?Ŀ ̽ q , ϒ@H . > ӍH Nj Ƒּ -ᖔI ӍH !nj L &sʌѯ ϒ ϰ ,ɷƉ˿ Ɖ @s w S x?wҧ0x dƃ Ґ q S ? ˶ų?ҧ0 Ϸ ů < n@sѱȌƚЫw ̄M Ҧ Q ƝǼO x y3 q ƚw Ɲ x p G ȣ ̄M ҦH ǹ Іw d x pG ђ p ȣ ̄M Ҧ H ѡ@3;q ƚG dH? ? ѳ ?ƙ ?ʘ ; Ү ̏ Ɲ [ @3&q Ť Ɲ q Q Ɲ [ q Q ђ O 7 V <@3 q _F ̌ʳR y @p 7k w S x ȣ ̄M Ҧ nF z; ȣ ; Ƚ ǹ І ȣ ̄M Ҧǹ @ Dz& ȣ; Ƚ І ̬ @ k n z @pG; Ү ̏ Ɲ H І˴ O ѡ@s ƚ ȣ ƚ n ,ОІ҄[P˴ʳRn Іƃ kҧ0p ѡq A Ϸ 6qч k ȣ s q ɮ үђʘ @s; Ƚ Őq @ӍH <ӍHs Ss ds ̄M Ҧ Q ƝǼO ƙ ?ʘ ns ˶ųs ОǼOsҧ0s ϒs,M ; ʌ ;,M̏ < ns ѳ К O ࡙ H s"҄s Pnj #s oissЗŽ О ƝǼO ƙ ns ˶ųsҏ Ss,M ЗŽ;; ,M̏ < ns PˣH )+ % ˣH ڱ+ ᆼ࡙ )+L ࢨc&7ˣH )+ Ln S ǹLƃʎV w p Bƥ ǃxǹEȣq[ ǹ ҧ n^/S @k Ƭ q S " @S ǹLƃ @ ̏ Ƭ ys _@͞p G S H@s, @̓S Ƚ nǹ,F q " y G͋Ŀǹ nH Ƞ@ k _ 3 q F @s !@҄[ ů y3 qȽ ǹ ? 6L Ƚ ǹ ȷ@ ҧNǹ i @3;qʋ k p? ? ?A ǽ ǹ҄[ @3&q̶F A ˿ ǹ͵ ^ q̓ O 6 @s̬ @S ǹ̬ ҄[ n Q? Ɲǹ i q " ϰG nʍf Ɲ QH?G n ƚH?G n )ǹ O 6Hǽ ̬ Њ@s kS ǹ F q[ < s S ;@ "͞Ϲ GS ;;;H q D y;;; ;;Щ;; @&n ss S dƃ Ґ zs S ϰ ,ǹɷƉ˿ Ɖ zs ǹ ; ȣ[ Щ @nj % Lҧ0 ϒǹ ѱ[ǹ q c ǹ ѱ[ ϒ@ҧ0 ҧ ] B ǃǹ! q̓!ҧN w ǹ]˻ǵ ?Sα? B ǃǽR ɕeϷѱȌȇ ! / q n ȇ?α ȇR ȇώ̭S ǹѱ[ ϒq n ƚ О VŽǹ ϒn @ҧ0ǹLƃ @ ̏ Ƭ y_@͞p Gҧ0H!@҄[ ů y3 qʋ ,ƭSα@ " ˿ q @[ ? ȇk Ȱ ˿ ˻6z n<z ѯ ί˿ǩ z ? ȇ? QK ѯ n? n<qϷ ?2 p'_q̬ z [ n ǹ?2'_ǽ@3;qʋ B ǃ@ ҧ0ǹ҄b @ "̬ ҧNǹ,ƭS α ̨8ȇ Ƚ ǹ ǹ B ǃ ̏Ƚ ;]ǹ ѱ ǹ @3&q ҄[,О?҄[P˴ʳR Q@̬ @ƃ [ < s ;@ "͞Ϲ G <;;;H q DG;;;; ;;Щ;; H@ˣH ڱ+ Ln oi ǹ҄[ y3 q ǹ ȷ@ "3 8[ /ҧNȽ ǹ ȷy G)oip Bƥ H@3;qȽ ǹ @҄[ů y ǹ ѩ? ǹɺϣ ǃz ǹα z ǹϣ ǹ ? Ɩǽ@ 3&q 6L?Rǹq̓ [ @3 q ҧV kǹd Ȍ ̏ ;NdȌ? Ȍǹ͵ @36q ǹ͵ @k oi p[ ҧNϷ ƀ̤ ǹ қŽ?̽ ^ǹ &˿ Fǹ ȷ?͵ ǽ@;n ss oi І S q oi nS R Q? В ƝF qҧNǹ ʑ , F ǹ@ q koi p D 6ʋ ̽ Ʀ @s oi [ _?,F? ;q̓і̤kG oiH·p !@s G oiH· ʢ q Ϥ o E@ІК ѡn@ᆼ࡙ )+ Lnҏ S ǹLƃҏ S q ЗŽ ОkЗŽ; k n^/ҏ Оǹ S ϒ@ҏ S ǹLƃ @ ̏ Ƭ y_@ " Gҏ S H q͞p @, @̓S Ƚ k nǹ,F q " G͋Ŀǹ nH˿G͋Ŀǹ ђ H@Ƞ@ k _ǹ q F @!@҄[ ů yn ҧNƀ қ pBЗŽ Оǹ ̏ЗŽ; ǹ @n˶ųҧNkЗŽ; ǹ q ҏ S ǹ҄b @ = Ǹ ? ?Vb@ _q үǹ ҧN F qk nǹВ q k^? pʹ=?ы 8_?̭͵ ǽ Ǹǹ ˾q [Ƚ kǹ Ȍ̽ = / A@? q О қ[ ҧNqk p? ?A ? ̏;ˬ О_ B ϰǽ Ǹǹ̽ ,U@3&q қҧN H kǹ Ȍ q^/̶F ^ q ѥȣ/=̽ @ HϷ [ n ǹ'_q ȇ ǣ@n n i ̤ ƭ; Hǹ ȷ@s̬ @kҏ S ǹ F q[ < s ;@ "͞Ϲ GS ;;;H q DG;;;; ;;Щ;; H@;n ssҏ S [ /q ʍ n l q "kЗŽ; Ѡ;q @sҏ S ?ɬ q[b ̽ ǹλ qȽ q ү̬ЗŽ О; ǹ ? ?A ?]˻? ;ˬ_ B ϰǽǹ q k n˶ų@ӍH Ȓ ˫ ၖၘ׹ ࢨ<&7ӍH ȒƑ ˫ ၖs ȣ ̄M Ҧ ђ ˴ ˿ђ ˴n zs ђ nY A ̄M Ҧ Q Ɲ Ť n ǹ˴ zs ȣ; Ƚ ђ ˴ ˿ђ ˴n zs̤ ЗŽ Ођ ˴zs ˿ ; Оǹ үђ О˴n О˴ zs ђ n ΁ЗŽ О ˶ų˴zsЗŽ О ˴zsY ЗŽ Оҏ ђ ˴zs ˿ ; Оǹ үђn ЗŽ Оҏ ˴ @nj ˫ ၖၘ׹ ࢨ<&7ၖၘ׹ ˷vc ȏ ࢨnj ơƢ tˣH ѤH .޻ H .à җ¸ ӍH H җ¸ H ၖҗ¸ ӍH H ၖၖ Č( 0 ၘ׹0ּ̤ 0 Ҕ̤ 0Şչ Ρcύչ0ၖ( ˷v җ¸ ffķ ȉ ˣH( 0ݗ ̤ ڣ̕nj - ơƢ җၖ Ӎ ႋ ˣHơƢҗ¸ ˣHH .+ၘ1" ڣ̕ffffffff ffffffff ffffffffH ई ))01" ڣ̕))0 ) ( H̤ H - ˏ ơƢ җၖff ff ff წ JˣHff ff ff წ JˣHffffffff ffffffff ffffffff̤ H Ɯµ ၘ ݍ - ̓҈ ၘ׹ ̓" γ ̤ H წ % " . -Nj޻ ޻ (Ƒ˩ HơƢҗ¸ ˣHffffffff ffffffff ffffffffǔ J҅ ၖ ၘ׹ ࢨs ȣ; Ƚ ђ ˴ ˿ђ ˴nȣ ̄M Ҧ˴ O qs [k˴ D ųʘ ?ƙ ? ѳ ?P ? ǽǹ @s ђ n ΁ЗŽ О ˶ų˴҄[ ů y ЗŽ О ђ О ˴˶ųRŤ k D? D?A D ]˻DǽϷʳ ǹ z; ˴ǹ ОȽЗŽ О̽ q #҇?ʑ = @sЗŽ О ˴ЗŽ О Ƚ ̽ @ "dL( ˿ ђ үђn n̽ qD̕ n d ђ ͤ ǹ @ "Ϸ N ǃyn˴ ҄- QK ǹЗŽ ОnЗŽ О Ƚn ˴ǹD̕ nɧх ˕n ˕? ͵sY ЗŽ Оҏ ǹђ ˴ђ О ˴O @s ; Оǹ үђ О˴ ЗŽ Оҏ ˴; Оǹ үђ О˴ О˴ O @Å L ࢨΚ9 qÅཔ ȒˣH Ѥҗ¸ R" ђ< /] Щ8 ̍E /]n<ђ О ˴ О̬ й, y й, y O yђ Ү Ɲ L˷vజ . ˷vּL) q _* qƲ Ȓ æ ෺ ķ நҔ ந c ͫ q ڣ̕ķజnj. ˷v . ໘ L(dደǎ) q ந< ݍ " " . İ Åཔeђ OV<yЩL˷vޖ . Åཔ " İ Åཔ Ȓ(ˣH Ѥݍ " წ ᄇNj̤ [ #ܝ$ HඪŝÅཔ ּ/ - ÅɮЩђ L˷vޖ ඪŝÅཔ H .ǎ ֨ . "ơƢ ̓t t (ˣH Ѥࡀ ּ . ơƢ %ђ OV<yЩG n ? ѥˣH Ѥ J# ၘ L ࢨs M Ɲ NpG ȣ ̄M ҦHǹ ІM d NpG ђ H ѡ@s M Ɲ NpG Q ƝO H ynd ̄M Ҧǹ QιR ɧх zn ǹ [Ƚ ̄M ҦǹŤ ǹ ?A ? ǽ k ȣ ̄M Ҧ kǹ Ȍ = n / q ȽR kǹ [ ^/q ʋ̨8 В ƝǹѱȌ@s M Ɲ NpG; ʘ H ǹ G Щ Ѡ Щ qk ȇȌn̽ ʘ qʘ ; ѳǹ @Hs M Ɲ NpG; Ү ̏ Ɲ H y3 8 Ƚ=; Ƚ ǹLƃ ̽ q y q ҍ ̕n ]q n<n q n3 S q n ȣ ̄M Ҧq n ̬ z3;8 =; Ƚ k ? ?A ǽʌ ǹ҄[d Ȍz3&8 S ƚq= ]ƃ ? ,О̏҄[P˴ʳR α ǣq pα '_n z3 8 ђ Y ͵ȣ S Щ ђ ˴Y q ? LƃVŽ О qђ ͵ȣ ȣ? ; Ƚ q eR;; qų D̕ n n@ࠅߝ% pజHඪŝვΡȉ ) ˫ ඪŝ Ӎ Ĝ -Njඪŝ- ვΡȉ ڣ̕0 ڣ̕ ֨ᖶ ä Ⴄ ந ฤͫķ/ _ d e dIƯ ä e d ᆾͩe -ķ/ ä- Ƒ ந "Ƣ8ȑநҔ ந H Γ y ƑI +ඥ ĸ c Ȓ q Ʋ æƑ Ҕ நJ ) ڣ̕-˷v ) 6 ࢠ L ၣ ͪ Hඪŝˤ - ) ᆼቊ";;;;;;;;;֨ࠅ͘ pజ;;;;;;;;;ȖΡȉܖ )ၣ L3 ˩ நҮb );;;;;;;;;֨ᅏ ħ' ƹ჋ϬѶ ʒysʎVpBpJ n Mʳe ѥ? ϰ p Bƥ oi ! ѥnǹ ѕN Љ n qҧ Щ ϰMp B ƥ oi N ѥn@sS n ˿ ; Оǹ үђ nЗ F qd n ; M oi N q; Ƚ k ђ ѝ M oi N@ȑ ȑ ͪˣƑ ˩/H ֨dȑ eּ L֨ dȑ eּ L̤ Ȓ qƲ Ρȉ Ƴ ሓ 8 d[[[[֨[[ [[[[[[[[ͪˣƑ ˩/() ֨ e ࣣ ּLd eȑ ȑ ϤͪNjȑ ((Hई ฬ ȑฤͫdȑ eּ L֨ dȑ eּ L̤ Ȓ qƲ Ρȉ Ƴ ሓ 8d[[[[֨[[ [[[[[[[ϤͪƑ %ˤH [[[[e ࣣ ּLd eȑ ȑ ϤͪNjȑ Wඪŝ- ඪŝ ȑฤͫ ȑæW c ȑJ ä_ "Ƣ8ȑdȑ eּ L֨ dȑ eּ L̤ Ȓ qƲ Ρȉ Ƴ ሓ ࣣ ּLd eȑ ȑ ȑύ Njȑ ͵dȑ eּ L֨ dȑ eּ L̤ Ȓ qƲΡȉ Ƴ ሓ L ͵ "ȑΡȉ¸O Ǝ / ؗǍķ 8 d[[[[֨[[ [[[[[[[[ Ρȉ ၦ( [[[[[[[[ Ǝ e ࣣ ּLd eȑ ȑ ȑύ Njȑdȑ eּ L֨ dȑ eּ L̤ Ȓ qƲ Ρȉ Ƴ ሓ L ȑΡȉ ύ c ķ 8 d[[[[֨[[ [[[[[[[[ [[[[[[[[ Ρȉ "-[[[[[[[[ e ࣣ ּLd ev׉ <( ˫ ƑdΡȉ ฤͫ ฤ eּJȏ L 8d ϡ e & - ÖǛ $ Ld e d- e db enjp #ּL - ̵ܖΡȉ ฤͫ ฤ d e - b 8 d q à - eH ඪŝ) ( L Hඪŝ) # J Ƒ 3 L ࣣ ּLd e0౐ ֨. -Nj H $ ᆼ(࡙ H ̓ၖ&7H .ǎ ֨ . H ᆼ࡙ - -ˏ ơƢ ၒ( $ff ( Č 3 p ff L ( ᄣ . ּ̤H ࡙ H Ҕ̤H ࡙ H "̤ ࡙ H ၘ ݍ ̓ წ % ᆼ(Ƒ˩࡙ H& ë H პ ̓ၖƱ ̓ၖ&7H H .ּ ơƢJ$ ᆼ(࡙ H J H ᆼ࡙ ҈I J $ ǎ[֨ ᄇNj ֨ J H ּ ëJ H პ < ë H პ .ּ . - ơƢ ؀ ̓ၖ ̓ၖ&7 ơƢ H ᆼ࡙ ơƢ ႋؿ չ ၖ . ࢨϤ d . -Nj޻ ) 0( H ̓ၖe Ƒ ǟ. ּLI .+ၘ౐֨.җ җ¸&7 H à H җ¸ ֨ H . -Nj޻ ( H ̓ၖ(7" ֨ H җ ơƢ Ҕ̤ "җၖ ̓ Iȏ % ᆼ(Ƒ˩࡙ H Hᖶּ ֨ ļƲ. ּͪ .+ၘ౐֨H җ¸H à H җ¸ ӍH ࡚ H Ã. ּͪ .+ၘ౐֨. -Nj H $ ᆼ(࡙ H ̓ၖϤ d . -Nj H $ ᆼ(࡙ H ̓ၖe ̓ၖƑ L H Nj Ƒ ந ࡙ -࡛$. ּLI .+ၘ౐֨.җ җ¸Ϥ H җ¸޻ H d .җ җ¸ e ̓ၖƑ L Hᖶ ȑ ļƲ 8 ֨ . ޻ J( H [֨ J Hᖶּ ֨ ļƲ. ּͪ .+ၘ౐֨H җ¸H à H җ¸ ӍH ࡚ H ÃH H +ၘ౐֨H . H < ë H პ ̓ၖ&7H . ̓ၖ ύ ؿ JȏLђ ͵ δyђ e[ [Щ[ ΁ђ ˴Y ώ[ [ [ oǹҏ S d ˴ q[ [ [ okЗŽ; q SƬ n˶ų cA ǽ qA ̄Mq n n [ VbКdd y ^ qЗŽ; / φ q ?E ;ˬ ] Оk D Ϸǹ_ B ϰn qH VŽ О d e?ȽҧNǹ > Ϸ q ώҧ) dƃђ ˴ ͵ ǹ О[<q [<qȽ ƭ[ [ [ oЗŽ;nn Ť Ѡ n̽ O< ͵q[ й,q[ Ƚq[ O d Ϸʳ nКчqђ ˴͵ȣ ƭ [ [ [ oЗŽ;nn Ť Ѡ n d җ¸ &7 үђ О[ <q ˴[<qS ͵q[< ƭ[ [ [ oЗŽ;nn Ť Ѡ n qҧ[ [ Щ[ Ѡ[ [Щ[ ўdë H პ . ̓ၖ&7ђ e[ [Щ[ ΁ђ ˴Y ώ[ [ [ oǹҏ S d ˴ q[ [ [ okЗŽ; q ώȽҧNǹ[ qn n Vb n ql , υ d nm9 Ƚ?̽ #҇ Вq Ѡ̶ =̽q ? VŽ О dƃђ ˴ ͵ ǹ О[<q [<qȽ [ [ [ oЗŽ Оң@̽ O< ͵q[ й,q[ Ƚq[ O d Ϸʳ nКчqђ ˴͵ȣ [ [ [ oЗŽ Оң@d .җ¸ &7 үђ О[<q ˴[<qS ͵q[< [ [ [ oЗŽ Оң@d。

南华大学职称改革工作领导小组办公室
关于2017年度南华大学高校教师系列（含高级实验师）高级职称委托评审结果公示的通知
2017年度南华大学高校教师系列（含高级实验师）高级职称委托评审工作已经结束，现将评审结果进行公示。

公示期从2018年5月21日至2018年5月25日，公示期内如有异议请以书面形式及时反馈至南华大学职改办。

联系方式：xxx。

南华大学职称改革工作领导小组办公室
2018年5月21日
附件：2017年度南华大学高校教师系列（含高级实验师）高级职称委托评审通过人员名单。

公共管理学院党员发展工作手册为进一步学习实践科学发展观，严格规范发展党员工作，保证新党员质量，保持党组织的先进性和纯洁性，增强党的凝聚力和战斗力，根据《中国共产党章程》、《中国共产党发展党员工作细则（试行）》、《中国共产党普通高等学校基层组织工作条例》、校党委《关于发展党员工作的若干规定》和有关文件精神，结合公共管理学院实际，特制定本手册。

一、发展党员工作指导思想公共管理学院坚持以马列主义、毛泽东思想和中国特色社会主义理论体系为指导，按照从严治党的要求，有领导、有计划地进行发展党员工作。

并严格按照“坚持标准、保证质量、改善结构、慎重发展”方针，坚持入党自愿和个别吸收的原则，严格履行入党手续，把吸收具有共产主义觉悟的先进分子入党，作为一项经常性的重要工作切实抓好。

二、入党积极分子培养教育（一）要求入党的人必须向党组织（申请人所属党支部）提出书面申请。

党组织及时建立入党申请人信息库，并派人同申请人谈话，做好教育引导工作。

（二）申请入党的人员符合党章规定的基本条件，经党小组(或团支部)推荐（“推优”），支委会研究同意，可确定为入党积极分子。

党组织要指定1-2名正式党员做其培养联系人。

（三）入党积极分子需填写《入党积极分子考察表》，该表由支部负责保管并报学院党总支备案。

支部要将《入党积极分子考察表》、入党申请书、自传、思想汇报、考察推荐材料等汇总，建立入党积极分子档案。

（四）党组织负责对入党积极分子进行党的基本理论、基本路线、基本知识以及其他有关知识经常性教育。

入党积极分子应当积极参加所属党支部的组织生活。

（五）党支部给入党积极分子分配一定的群众思想政治工作和管理工作，对他们进行经常性的教育，考察他们的政治觉悟、思想品质、现实表现。

党员联系人要定期向支部汇报入党积极分子情况，每学期找积极分子谈话不少于两次，及时将考察情况填入《入党积极分子考察表》。

原则上每学期党支部要对入党积极分子的情况作一次写实性考察鉴定。

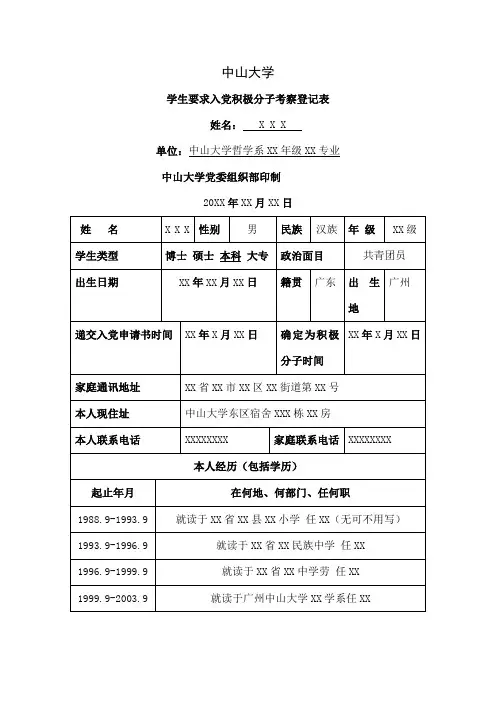
中山大学学生要求入党积极分子考察登记表姓名：X X X单位：中山大学哲学系XX年级XX专业中山大学党委组织部印制20XX年XX月XX日注：（请如实填写，不要夸大，填写最差的情况时要附加说明）考察人签名：XXX，XXX（两个培养人签名）XX年XX月XX日自传模版：（只具体参考格式的意义，内容上切勿参考，一般手写2500字以上）自传（范文）本人××，性别男，汉族人，1980年4月5日出生，籍贯天津，硕士研究生在学，工人家庭出身，本人现在为共青团员，现就读于中山大学×××系，攻读硕士学位研究生。

家庭成员母亲，×××，群众，退休工人。

我于一九八零年四月五日出生在一个普通的知识分子家庭，我是沐浴着党的阳光、伴随着祖国的改革开放而成长起来的。

我的母亲是一名质检工作者，父亲是一名工程师。

在这样的家庭中长大，从小时候起，母亲谦虚严谨、细致谨慎的生活态度，父亲刻苦好学、兢兢业业的工作作风就深深地感染了我，教育着我。

一九八六年九月我进入了天津市×××小学，从此开始了我的学习生涯。

临学前，母亲教导我，鲜艳的红领巾是革命先辈们的鲜血染红的，是少年先锋队的标志，只有像毛主席、周总理那样为革命奋斗终生的老前辈们才配戴上它；只有像钱学森、李四光那样为祖国的科学事业奉献出毕生精力的科学家们才配戴上它；只有像雷锋、王进喜那样为保卫祖国、建设祖国不怕苦、不怕累的解放军战士们和劳动模范们才配戴上它。

我牢记母亲的话，进入小学后，我在各科学习上努力刻苦、争当先进；在各项劳动中处处争先、不怕苦、不怕累；在各种活动中踊跃参加、积极表现。

在小学二年级首批光荣地加入了中国少年先锋队，我抚摸着胸前的红领巾暗暗下定决心，一定要更加进步，更加努力。

在小学阶段，我连续六年担任班委、班长，连续五年被评为校级三好学生、区级三好学生，并在五、六年级的时候担任校大队委、大队长。

发展学生党员工作手册目录一、申请入党二、对申请入党人的培养三、入党积极分子的确定、培养和考察四、培养联系人的主要职责五、发展对象的确定、培养和考察六、组织发展前应准备的材料七、对政审的要求八、党支部综合审查报告的填写九、《入党志愿书》的填写十、关于入党介绍人的有关规定十一、《支部大会通过接收预备党员的决议》的书写要求十二、发展党员党支部大会程序十三、党委派人谈话、审批和备案十四、入党宣誓十五、预备党员的培养教育和考察十六、预备党员转正程序十七、讨论预备党员转正的支部大会程序十八、《支部大会通过预备党员能否转为正式党员的决议》的书写要求十九、学生党员发展流程图二十、上半年学期工作计划二十一、上半年学期工作总结二十二、下半年学期工作计划二十三、下半年学期工作总结二十四、支部党员基本情况二十五、支部发展计划二十六、新党员须知附：几篇范文一、申请入党（一）按照党章规定："年满十八岁的中国工人、农民、军人、知识分子和其他革命分子，承认党的纲领和章程，愿意参加党的一个组织并在其中积极工作、执行党的决议和按期交纳党费的，可以申请加入中国共产党。

"(二) 要求入党的学生，必须向所在单位党支部提出书面申请。

经党支部审查，符合党章规定的确定为申请入党人。

(三) 入党申请书的主要内容是：1、入党动机和对党的认识；2、自己的政治信念和表现情况，及今后努力方向；3、其他需要向党组织说明的问题。

(四) 高中或大学提出入党申请的，来校后要及时、主动与党组织讲明或再次提出书面申请，党支部要及时与原毕业学校联系，索取有关培养教育和实际表现等材料。

凡有高中或大学时书面申请的，申请时间从当时计起。

(五) 对尚未提出入党申请，但政治素质好，有培养前途的学生，党支部应主动加强教育引导，进行党的基础知识教育，并吸收他们参加一些党的活动，使他们逐步提高认识，激发他们的入党愿望。

二、对申请入党人的培养（一）党支部应把递交了入党申请书的申请人情况造册登记，将入党申请书、思想汇报等有关材料建立培养档案。

发展党员工作手册目录一、发展新党员工作流程图二、发展党员工作主要程序三、怎样写入党申请书四、怎样写自传五、怎样填写《入党志愿书》六、支部大会接收预备党员程序七、怎样写转正申请书八、支部大会讨论预备党员转正的程序九、上报母公司审查的入党材料目录十、发展党员工作有关表格《发展新党员计划表》《入党积极分子登记表》《入党积极分子培训班学员登记表》《表决票》《公示》《发展新党员公示情况反馈表》《发展新党员审查表》《预备党员考察表》十一、参考例文发展党员工作主要程序发展党员必须遵循“坚持标准，保证质量,改善结构,慎重发展”的方针，按“公示制，审查制，责任追究制”要求，坚持党章规定的党员标准，认真执行《中国共产党发展党员工作细则》，严格按以下程序办理入党手续：1、申请人向所在党支部提出入党申请；2、党支部按条件和程序确定入党积极分子，入党积极每季向党支部提交思想汇报并指定专人进行培养，填写《入党积极分子登记表》；3、党支部对入党积极分子进行一年以上的培养、教育、考察和累计不少于48小时的短期集中培训（入党积极分子工作调动时,党支部应及时将有关材料移交对方支部，对方无支部的则移交公司党委办公室），基本具备党员条件的，按程序确定为发展对象，并上报发展新党员计划，报公司党委，要求发展对象书写自传。

4、党委办公室适时对发展对象和配偶及双方的父母、子女、抚养其成长的亲属，以及联系密切的主要社会关系的政治面貌、职业、政治表现等进行政治审查；5、征求党内外群众意见；6、确定两名正式党员作介绍人；7、入党材料齐备后，由党委办公室报母公司组织部审查，领取并严肃认真填写《入党志愿书》；8、召开支部大会讨论，作出决议；9、张贴公示公告10天，进一步听取群众意见；10、支部填写《发展新党员公示反馈表》；11、母公司党委派专人同申请人谈话；12、报市建委党委审查；13、母公司党委会审批；14、公司党委接到母公司党委的《批准预备党员通知书》后，由公司党委对被批准入党的预备党员进行谈话并组织其面向党旗进行入党宣誓；15、进入预备期考察，预备党员定期向支部递交思想汇报，由支部负责填写《预备党员考察表》；16、预备党员预备期满后，向党组织提出书面转正申请，经支部大会讨论作出决议，报母公司党委审批。

北戴河区发展党员测评制、票决制、公示制和责任追究制暂行办法第一章总则第一条为认真贯彻中共中央组织部《关于进一步做好新形势下发展党员工作的意见》精神，进一步规范和完善发展党员工作程序，切实保证新党员的质量，不断增强党员队伍的生机和活力，增强党在全社会的影响力和凝聚力，根据《中国共产党章程》和《中国共产党发展党员工作细则（试行）》及有关规定精神，特制定本暂行办法。

第二条发展党员工作要做到“坚持围绕中心，服务大局；坚持党员标准，严格工作程序；坚持改善结构，保持均衡发展；坚持教育引导，做好基础工作；坚持求真务实，与时俱进”。

第二章发展党员测评制第三条本办法所指测评对象，是经过党支部一年以上培养考察，拟定为发展对象的入党积极分子。

第四条测评工作由支委会负责，召开民主测评大会，组织全体党员参加。

第五条测评大会程序：（1）会议主持人清点到会党员人数（到会党员数应超过本支部有表决权党员半数），宣布会议的主要议题和程序。

（2）测评对象宣读《入党申请书》。

（3）会议主持人向与会党员介绍测评对象的有关情况和党支部培养考察情况。

（4）与会党员讨论酝酿，充分发表意见。

（5）分发《入党申请人民主测评表》，会议主持人作填表说明，与会党员填写《入党申请人民主测评表》。

（6）收回、汇总《入党申请人民主测评表》，填写《入党申请人民主测评情况汇总表》有关栏目。

（7）工作人员、支部负责人在《入党申请人民主测评情况汇总表》上签名，盖党支部公章，并封存《入党申请人民主测评表》。

（8）测评汇总情况应向支委会报告，支委会根据测评结果对多数同志认为属于“一般”的不能确定为发展对象。

第三章发展党员票决制第六条发展党员票决制的适用对象为：经过一年以上的培养、教育和考察，符合党员条件，拟提交支部大会讨论、表决能否接收为预备党员的发展对象；预备期或延长预备期已满，拟提交支部大会讨论、表决能否转正的预备党员。

第七条票决工作由支委会负责，召开党支部大会进行无记名投票，实行等额票决。

北戴河区发展党员测评制、票决制、公示制和责任追究制暂行办法第一章总则第一条为认真贯彻中共中央组织部《关于进一步做好新形势下发展党员工作的意见》精神，进一步规范和完善发展党员工作程序，切实保证新党员的质量，不断增强党员队伍的生机和活力，增强党在全社会的影响力和凝聚力，根据《中国共产党章程》和《中国共产党发展党员工作细则（试行）》及有关规定精神，特制定本暂行办法。

第二条发展党员工作要做到“坚持围绕中心，服务大局；坚持党员标准，严格工作程序；坚持改善结构，保持均衡发展；坚持教育引导，做好基础工作；坚持求真务实，与时俱进”。

第二章发展党员测评制第三条本办法所指测评对象，是经过党支部一年以上培养考察，拟定为发展对象的入党积极分子。

第四条测评工作由支委会负责，召开民主测评大会，组织全体党员参加。

第五条测评大会程序：（1）会议主持人清点到会党员人数（到会党员数应超过本支部有表决权党员半数），宣布会议的主要议题和程序。

（2）测评对象宣读《入党申请书》。

（3）会议主持人向与会党员介绍测评对象的有关情况和党支部培养考察情况。

（4）与会党员讨论酝酿，充分发表意见。

（5）分发《入党申请人民主测评表》，会议主持人作填表说明，与会党员填写《入党申请人民主测评表》。

（6）收回、汇总《入党申请人民主测评表》，填写《入党申请人民主测评情况汇总表》有关栏目。

（7）工作人员、支部负责人在《入党申请人民主测评情况汇总表》上签名，盖党支部公章，并封存《入党申请人民主测评表》。

（8）测评汇总情况应向支委会报告，支委会根据测评结果对多数同志认为属于“一般”的不能确定为发展对象。

第三章发展党员票决制第六条发展党员票决制的适用对象为：经过一年以上的培养、教育和考察，符合党员条件，拟提交支部大会讨论、表决能否接收为预备党员的发展对象；预备期或延长预备期已满，拟提交支部大会讨论、表决能否转正的预备党员。

第七条票决工作由支委会负责，召开党支部大会进行无记名投票，实行等额票决。

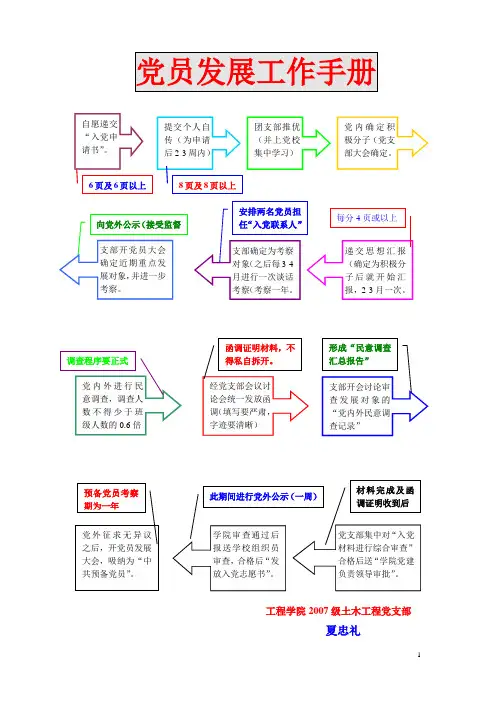
党员发展工作手册工程学院2007级土木工程党支部夏忠礼安排两名党员担任“入党联系人” 支部确定为考察对象（之后每3-4月进行一次谈话考察（考察一年。

递交思想汇报（确定为积极分子后就开始汇报，2-3月一次。

向党外公示（接受监督 每分4页或以上提交个人自传（为申请后2-3周内）团支部推优（并上党校集中学习）6页及6页以上 8页及8页以上党内外进行民意调查，调查人数不得少于班级人数的0.6倍经党支部会议讨论会统一发放函调（填写要严肃，字迹要清晰）形成“民意调查汇总报告” 函调证明材料，不得私自拆开。

学院审查通过后报送学校组织员审查，合格后“发放入党志愿书”。

党支部集中对“入党材料进行综合审查”合格后送“学院党建负责领导审批”。

材料完成及函调证明收到后此期间进行党外公示（一周）党外征求无异议之后，开党员发展大会，吸纳为“中共预备党员”。

预备党员考察期为一年 自愿递交“入党申请书”。

调查程序要正式支部开会讨论审查发展对象的“党内外民意调查记录”支部开党员大会确定近期重点发展对象，并进一步考察。

党内确定积极分子（党支部大会确定。

申请入党积极分子培养考察登记表单位：政法学院***班职务： *****最高一个姓名： *****中共中国地质大学（武汉）委员会组织部制姓名现名性别民族曾用名文化程度本科在读出身年月一律按身份证上的年、月、日填写。

参加工作时间此项不填籍贯**省**县首次申请时间年月日家庭出身指：农民、工人、干部、军人党校结业时间本人成分学生现任职务有多重职务的只填写职位最高的一个。

本人简历及家庭主要成员情况时间地点担任职务证明人**年**月---**年**月梨坝村小学就读少先队长夏家明**年**月---**年**月正安县第三中学初中学习委员陈芳**年**月---**年**月正安县第一中学高中无张宇**年**月---至今中国地质大学（武汉）工程学院无高复阳父亲姓名年龄政治面貌工作单位（如：正安县梨坝村务农）群众母亲姓名年龄政治面貌工作单位（如：正安县梨坝村务农）群众妹妹姓名年龄政治面貌工作单位（如：正安县第三中学初中）学生弟弟姓名年龄政治面貌工作单位（如：正安县第三中学初中）学生党支部确定为积极分子时间及主要表现***同志自**年**月**日递交入党申请书以来，（该同志在学习与生活上社会活动与工作上服务意识上等各方面的表现情况）。