高等数学II(电子)11-9 斯托克斯公式 环流量与旋度

第七节 斯托克斯公式与旋度格林公式揭示了平面上的二重积分与第二类曲线积分之间的关系，下面我们再介绍一个公式，它揭示了空间中第二类曲面积分与第二类曲线积分的关系，是格林公式的推广．一、 斯托克斯（S.G.G.Stokes ）公式设∑是具有边界曲线的定向曲面，我们规定其边界曲线∑∂的正向与定向曲面的∑法向量符合右手法则．记作+∂∑．比如，若∑是上半球面221y x z --=的上侧，则+∂∑是xOy 面上逆时针走向的单位圆周．定理1（斯托克斯公式） 设∑是一张光滑或分片光滑的定向曲面，∑的正向边界+∂∑为光滑或分段光滑的闭曲线．如果函数),,(z y x P 、),,(z y x Q 、),,(z y x R 在曲面∑上具有一阶连续偏导数，则有dxdy y P x Q dzdx x R z P dydz z Q yR ⎪⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎭⎫⎝⎛∂∂-∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂⎰⎰∑ ⎰+∂++=∑Rdz Qdy Pdx为便于记忆斯托克斯公式可以用如下形式表示⎰⎰⎰∂∂∂∂∂∂=++∑RQ P z y x dxdy dzdx dydz Rdz Qdy Pdx L 显然格林公式是斯托克斯公式的特殊情况．和平面上的曲线积分与路径无关的条件一样，有如下定理定理2 设G 是空间的一个一维单连通区域，z y x R z y x Q z y x P z y x ),,(),,(),,(),,(++=则),,(z y x F沿G 内定向曲线的积分与路径无关的充分且必要条件是yPx Q x R z P z Q y R ∂∂=∂∂∂∂=∂∂∂∂=∂∂,, 则曲线积分⎰++LRdz Qdy Pdx 与路径无关，只与起、终点有关．例1 计算⎰++++Lz y x ydzxdy zdx ，其中L 为平面1=++z y x 被坐标面所截下的三角形的整个边界，正向与三角形上侧的法向量之间符合右手规则．解 由曲面积分定义可知⎰⎰++=++++LL ydz xdy zdx z y x ydzxdy zdx利用斯托克斯公式2333===++=∂∂∂∂∂∂=++⎰⎰⎰⎰⎰⎰⎰⎰⎰xyD L dxdy dxdy dxdy dzdx dydz y x z z y x dxdy dzdx dydz ydz xdy zdx ∑∑∑例2 计算dz y x dy x z dx z y I )()()(222222-+-+-=⎰Γ其中Γ是用平面23=++z y x 截立方体]1,0[]1,0[]1,0[⨯⨯的表面所得的截痕，若从z 轴的正向看去，Γ取逆时针方向．解 取∑为平面23=++z y x 的上侧被Γ所围的部分，∑的单位向量)31,31,31(=n e ，由斯托克斯公式及第二类曲面积分的定义得dS y x x z z y z y x y x x z z y z y x dxdy dzdx dydz I ⎰⎰⎰⎰---∂∂∂∂∂∂=---∂∂∂∂∂∂=∑∑222222222222313131 29)(63322334)(34-=-=-=-=++-=⎰⎰⎰⎰⎰⎰∑∑的面积xy D D d dS dS z y x xyσ例3 求⎰-+-+-Ldz xy z dy zx y dx yz x )()()(222，L 为螺旋线)20( ,sin ,cos πθθθθ≤≤===b z a y a x ，θ增大的方向为正向．解 由于在3R 中，有x z Q y R -=∂∂=∂∂，y xRz P -=∂∂=∂∂，z y P x Q -=∂∂=∂∂ 该积分与路径无关，可取积分路径为直线AB ，其中)0,0,(a A ，)2,0,(b a B π，所以AB ：⎪⎩⎪⎨⎧===⇒==-tz y ax t z y a x 000 38)()()(33202222b dt t dz xy z dy zx y dx yz xb Lππ==-+-+-⎰⎰ 二、 旋度 对于)1(C向量场k z y x R j z y x Q i z y x P z y x F ),,(),,(),,(),,(++=称下述向量y P x Q x R z P z Q y R ⎪⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂Q y ∂∂= 为向量场F 的旋度（rotation ）记为rot ，即Q y rot ∂∂=有了旋度的概念，斯托克斯公式可以写为⎰⎰⎰⋅=⋅Ld d rot ∑当=rot 时，⎰⋅Ld 与路径无关．下面解释一下旋度的物理意义．第二类曲线积分⎰⋅=Ld Γ称为向量场)(M F 沿L 正向的环流量．为了说明环流量的意义，我们以河流中的旋涡这样一个特殊的流速场)(M F 为例，⎰⋅Ld M ∆)(表示沿曲线L ∆正向的速度的环流量．为形象起见，不妨设L ∆是一个圆，我们设想作一个与该圆同样大小的小圆叶轮，叶轮的轴的方向与小圆正向符合右手规则，若将此叶轮放至旋涡中某点M 处，叶轮开始转动，根据经验，转动的快慢与轴的方向和叶轮大小有关，即与转动的快慢取决于曲线积分⎰⎰⋅=⋅=LLds r d ∆τ∆∆Γ的大小，当轴垂直于旋涡表面（此时e 的方向与V 一致）时，转动较快，当轴与旋涡表面有倾角时，叶轮转动较慢，可见环流量⎰⋅=Ld ∆∆Γ表示叶轮沿周界L ∆正向转动趋势的大小．这个量表示了速度场)(M F 相对于有向闭曲线L ∆的一种总体形态，但是不能反映出场内某点处的转动趋势的大小．为此，作∆Γ与小圆叶轮面积S ∆（也表示叶轮面）之比，称为环流量平均面密度⎰⋅=Ld S S ∆∆∆∆Γ1当S ∆缩向点M 时，若极限⎰⋅=→→LM S M S d S S ∆∆∆∆∆∆Γ1lim lim存在，该极限值表示位于点M 处的小水滴沿叶轮轴的方向转动趋势的大小，这就是环流量面密度的概念根据积分中值定理，存在S M ∆∈*，使得nM n MS M S M S rot rot dS e rot S d rot S dS d =⋅=⋅=⋅=→→→⎰⎰⎰⎰*][lim 1lim 1lim ∆∆∑∆∆∑∆∆∆Γ． 一个旋度处处为零的向量场称为无旋场，无旋无源场称为调和场，调和场是物理学中一类重要的场，这种场和调和函数间有着密切的联系．本章的几个主要公式都是微积分学基本公式在二维和三维空间中的推广．微积分基本公式⎰-=ba a Fb F dx x F )()()('曲线积分基本公式))(())((a r f b r f d f -=⋅∇⎰Γ格林公式⎰⎰⎰+∂+=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂D DQdy Pdx dxdy y P x Q 斯托克斯公式⎰⎰⎰+∂⋅=⋅∑∑r d F S d F rot高斯公式S d F dV F div ⎰⎰⎰⎰⎰+∂⋅=ΩΩ三、 向量微分算子为方便记，在场论中经常运用一个运算符号，它称为∇（Nabla ）算子，其定义为k zj x i y ∂∂+∂∂+∂∂=∇ 这个算子可以作用到数量值函数上，也可以像通常的向量一样，与向量值函数作数量积和向量积，从而得出新的函数，其规定如下：1）设),,(z y x u u =，则u zux u y u u grad =∂∂+∂∂+∂∂=∇ 2）设k z y x R j z y x Q i z y x P z y x F ),,(),,(),,(),,(++=，则。

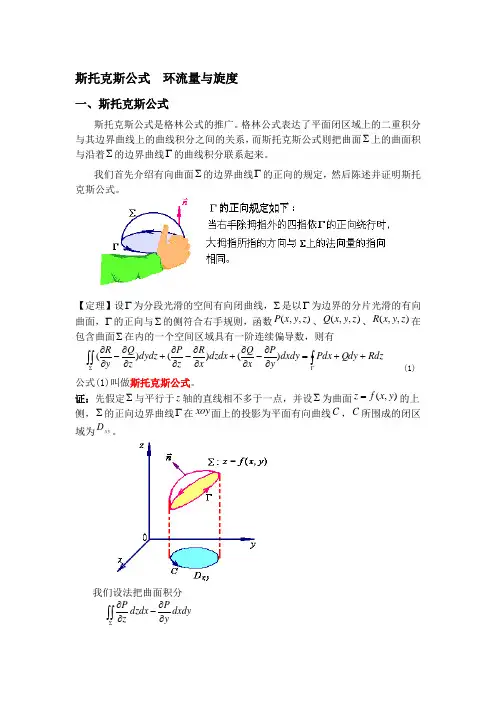
斯托克斯公式 环流量与旋度一、斯托克斯公式斯托克斯公式是格林公式的推广。

格林公式表达了平面闭区域上的二重积分与其边界曲线上的曲线积分之间的关系，而斯托克斯公式则把曲面∑上的曲面积与沿着∑的边界曲线Γ的曲线积分联系起来。

我们首先介绍有向曲面∑的边界曲线Γ的正向的规定，然后陈述并证明斯托克斯公式。

【定理】设Γ为分段光滑的空间有向闭曲线，∑是以Γ为边界的分片光滑的有向曲面，Γ的正向与∑的侧符合右手规则，函数),,(z y x P 、),,(z y x Q 、),,(z y x R 在包含曲面∑在内的一个空间区域具有一阶连续偏导数，则有⎰⎰⎰Γ∑++=∂∂-∂∂+∂∂-∂∂+∂∂-∂∂Rdz Qdy Pdx dxdy y P x Q dzdx x R z P dydz z Q y R )()()( (1) 公式(1)叫做斯托克斯公式。

证：先假定∑与平行于z 轴的直线相不多于一点，并设∑为曲面),(y x f z =的上侧，∑的正向边界曲线Γ在xoy 面上的投影为平面有向曲线C ，C 所围成的闭区域为xy D。

我们设法把曲面积分⎰⎰∑∂∂-∂∂dxdy y P dzdx z P化为闭区域xy D上的二重积分，然后通过格林公式使它与曲线积分联系。

根据对面积的和对坐标的曲面积分间的关系，有⎰⎰⎰⎰∑∑γ∂∂-β∂∂=∂∂-∂∂dS y P z P dxdy y P dzdx z P )cos cos ( (2)由第8.6节知道，有向曲面∑的法向量的方向余弦为221cos y x x f f f ++-=α，221cos y x y f f f ++-=β，2211cos y x f f ++=γ因此γβcos cos y f -=，把它代入(2)式得⎰⎰⎰⎰∑∑γ⎪⎪⎭⎫ ⎝⎛∂∂-⋅∂∂-=∂∂-∂∂dS y P f z P dxdy y P dzdx z P y cos 即⎰⎰⎰⎰∑∑γ⎪⎪⎭⎫ ⎝⎛∂∂+∂∂-=∂∂-∂∂dS y P f z P dxdy y P dzdx z P y cos (3)上式右端的曲面积分化为二重积分时，应把),,(z y x P 中的z 用),(y x f 来代替，因为由复合函数的微分法，有y f z P y P y x f y x P y ⋅∂∂+∂∂=∂∂)],(,,[所以，(3)式可写成⎰⎰⎰⎰∑∂∂-=∂∂-∂∂xy D dxdy y x f y x P y dxdy y P dzdx z P )],(,,[ 根据格林公式，上式右端的二重积分可化为沿闭区域xyD 的边界C 的曲线积分⎰⎰⎰=∂∂-xy D c dxy x f y x P dxdy y x f y x P y )],(,,[)],(,,[于是⎰⎰⎰∑=∂∂-∂∂c dx y x f y x P dxdy y P dzdx z P )],(,,[因为函数)],(,,[y x f y x P 在曲线C 上点),(y x 处的值与函数),,(z y x P 在曲线Γ上对应点),,(z y x 处的值是一样的，并且两曲线上的对应小弧段在x 轴上的投影也是一样，根据曲线积分的定义，上式右端的曲线积分等于曲线Γ上的曲线积分⎰Γdxz y x P ),,(,因此，我们证得 ⎰⎰⎰∑Γ=∂∂-∂∂dx z y x p dxdy y P dzdx z P ),,( (4)如果∑取下侧，Γ也相应地改成相反的方向，那末(4)式两端同时改变符号，因此(4)式仍成立。