872量子力学考试大纲

811《量子力学》中科院研究生院硕士研究生入学考试《量子力学》考试大纲本《量子力学》考试大纲适用于中国科学院研究生院物理学相关各专业（包括理论与实验类）硕士研究生的入学考试。

本科目考试的重点是要求熟练掌握波函数的物理解释，薛定谔方程的建立、基本性质和精确的以及一些重要的近似求解方法，理解这些解的物理意义，熟悉其实际的应用。

掌握量子力学中一些特殊的现象和问题的处理方法，包括力学量的算符表示、对易关系、不确定度关系、态和力学量的表象、电子的自旋、粒子的全同性、泡利原理、量子跃迁及光的发射与吸收的半经典处理方法等，并具有综合运用所学知识分析问题和解决问题的能力。

一．考试内容：（一）波函数和薛定谔方程波粒二象性，量子现象的实验证实。

波函数及其统计解释，薛定谔方程，连续性方程，波包的演化，薛定谔方程的定态解，态叠加原理。

（二）一维势场中的粒子一维势场中粒子能量本征态的一般性质，一维方势阱的束缚态，方势垒的穿透，方势阱中的反射、透射与共振，d--函数和d-势阱中的束缚态，一维简谐振子。

（三）力学量用算符表示坐标及坐标函数的平均值，动量算符及动量值的分布概率，算符的运算规则及其一般性质，厄米算符的本征值与本征函数，共同本征函数，不确定度关系，角动量算符。

连续本征函数的归一化，力学量的完全集。

力学量平均值随时间的演化，量子力学的守恒量。

（四）中心力场两体问题化为单体问题，球对称势和径向方程，自由粒子和球形方势阱，三维各向同性谐振子，氢原子及类氢离子。

（五）量子力学的矩阵表示与表象变换态和算符的矩阵表示，表象变换，狄拉克符号，谢振子的占有数表象。

（六）自旋电子自旋态与自旋算符，总角动量的本征态，碱金属原子光谱的双线结构与反常塞曼效应，电磁场中的薛定谔方程，自旋单态与三重态，光谱线的精细和超精细结构，自旋纠缠态。

（七）定态问题的近似方法定态非简并微扰轮，定态简并微扰轮，变分法。

（八）量子跃迁量子态随时间的演化，突发微扰与绝热微扰，周期微扰和有限时间内的常微扰，光的吸收与辐射的半经典理论。

专业代码及名称培养单位代码招生类专业代码及名称培养单位代码招生类别070121★数学物理001 硕，博3 623 数学分析《数学分析教程》常庚哲中国科大出版社数学分析：极限、连续、微分、积分的概念及性质4 802 线性代数与解析几何《线性代数》李炯生中国科大出版社《空间解析几何简明教程》吴光磊高等教育出版社线性代数：行列式，矩阵，线性空间线性映射与线性变换，二次型与内积；解析几何：向量代数，平面与直线，常见曲面070201理论物理004 硕、博3 624 普通物理A 中国科大、北大或其他高校物理系普通物理教材力学、电磁学、原子物理4 811 量子力学《量子力学》第一卷曾谨言科学出版社第三版量子力学的概念和基本原理、波函数和波动方程，一维定态问题、力学量算符与表象变换，对称性及守恒定律、中心力场、粒子在电磁场中的运动、定态微扰论、量子越迁070202粒子物理与原子核物理004 硕、博3 624 普通物理A 中国科大、北大或其他高校物理系普通物理教材力学、电磁学、原子物理4 811 量子力学《量子力学》第一卷曾谨言科学出版社第三版量子力学的概念和基本原理、波函数和波动方程，一维定态问题、力学量算符与表象变换，对称性及守恒定律、中心力场、粒子在电磁场中的运动、定态微扰论、量子越迁070203原子与分子物理004 硕、博234 硕、博3 624 普通物理A 中国科大、北大或其他高校物理系普通物理教材力学、电磁学、原子物理4 835 原子物理与量子力学《近代物理学》徐克尊高等教育出版社《原子物理学》杨福家高等教育出版社第三版《原子物理学》褚圣麟高等教育出版社《量子力学导论》曾谨言高等教育出版社原子结构和光谱、分子结构和光谱、量子力学概论070204等离子体物理004 硕、博4 808 电动力学A 《电动力学》郭硕鸿高等教育出版社第二版电磁现象的普遍规律，静电场和静磁场，电磁波的传播，电磁波的辐射（包括低速和高速运动带电粒子的辐射），狭义相对论4 872 等离子体物理导论《等离子体物理导论》F. F. Chen科学出版社1980《等离子体物理原理》马腾才胡希伟陈银华中国科大出版社1988 单粒子理论、等离子体平衡、等离子体波动、等离子体不稳定性070205凝聚态物理002 博203 硕3 624 普通物理A 中国科大、北大或其他高校物理系普通物理教材力学、电磁学、原子物理4 809 固体物理《固体物理》黄昆原著韩汝琦改编高等教育出版社晶体结构、晶体缺陷、晶体结合、晶体振动及热学性质、金属电子论、能带论、电导论4 811 量子力学《量子力学》第一卷曾谨言科学出版社第三版量子力学的概念和基本原理、波函数和波动方程，一维定态问题、力学量算符与表象变换，对称性及守恒定律、中心力场、粒子在电磁场中的运动、定态微扰论、量子越迁231 硕、博234 硕、博070207光学002 硕、博3 624 普通物理A 中国科大、北大或其他高校物理系普通物理教材力学、电磁学、原子物理4 811 量子力学《量子力学》第一卷曾谨言科学出版社第三版量子力学的概念和基本原理、波函数和波动方程，一维定态问题、力学量算符与表象变换，对称性及守恒定律、中心力场、粒子在电磁场中的运动、定态微扰论、量子越迁070221★量子信息物理学234 硕、博3 624 普通物理A 中国科大、北大或其他高校物理系普通物理教材力学、电磁学、原子物理4 811 量子力学《量子力学》第一卷曾谨言科学出版社第三版量子力学的概念和基本原理、波函数和波动方程，一维定态问题、力学量算符与表象变换，对称性及守恒定律、中心力场、粒子在电磁场中的运动、定态微扰论、量子越迁070301无机化学019 硕、博157 硕、博3 626 物理化学《物理化学》付献彩高等教育出版社第五版《物理化学-概念辨析·解题方法》范崇政中国科大出版社热力学、动力学、胶体表面、电化学、统计热力学4 818 无机化学《无机化学》（上、下册）武汉大学、吉林大学等校编高等教育出版社第三版无机化学基本原理、理论及元素无机化学234 硕、博070302分析化学019 硕、博3 626 物理化学《物理化学》付献彩高等教育出版社第五版《物理化学-概念辨析·解题方法》范崇政中国科大出版社热力学、动力学、胶体表面、电化学、统计热力学4 820 分析化学《分析化学》武汉大学主编高等教育出版社《定量分析化学》李龙泉等编著中国科大出版社误差与数据处理；酸碱滴定，配位滴定，氧化-还原滴定，沉淀滴定；重量分析；常用的分离方法与复杂物质分析070303有机化学019 硕、博3 626 物理化学《物理化学》付献彩高等教育出版社第五版《物理化学-概念辨析·解题方法》范崇政中国科大出版社热力学、动力学、胶体表面、电化学、统计热力学4 819 有机化学《有机化学》伍越环编著中国科大出版社《有机化学实验》兰州大学、复旦大学编高等教育出版社伍越环编著的《有机化学》全部内容070304物理化学（含化学物理）003 硕、博231 硕、博3 626 物理化学《物理化学》付献彩高等教育出版社第五版《物理化学-概念辨析·解题方法》范崇政中国科大出版社热力学、动力学、胶体表面、电化学、统计热力学4 815 结构化学《物质结构》潘道皑等人民教育出版社量子力学基础、原子分子电子结构、分子光谱、晶体结构4 818 无机化学《无机化学》（上、下册）武汉大学、吉林大学等校编高等教育出版社第三版无机化学基本原理、理论及元素无机化学以下为第2 组考试科目，共有 2 组考试科目，可任选一组3 624 普通物理A 中国科大、北大或其他高校物理系普通物理教材力学、电磁学、原子物理4 811 量子力学《量子力学》第一卷曾谨言科学出版社第三版量子力学的概念和基本原理、波函数和波动方程，一维定态问题、力学量算符与表象变换，对称性及守恒定律、中心力场、粒子在电磁场中的运动、定态微扰论、量子越迁234 硕、博070305高分子化学与物理020 硕、博3 626 物理化学《物理化学》付献彩高等教育出版社第五版《物理化学-概念辨析·解题方法》范崇政中国科大出版社热力学、动力学、胶体表面、电化学、统计热力学4 821 高分子化学与物理《高分子化学》潘才元中国科大出版社2001版；《高聚物的结构与性能》马德柱等科学出版社2003版考试范围包括指定参考书中所涉及的内容。

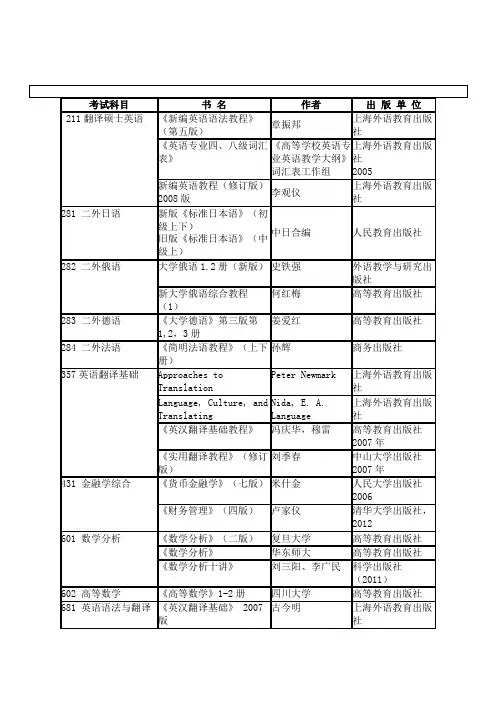
《量子力学》复习资料第一章 绪论1、经典物理学的困难：①黑体辐射；②光电效应；③氢原子线性光谱；④固体在低温下的比热。

2、★★★普朗克提出能量子假说：黑体只能以νh E =为能量单位不连续的发射和吸收辐射能量，⋯⋯==,3,2,1 n nh E n ν，能量的最小单元νh 称为能量子。

意义：解决了黑体辐射问题。

3、★★★（末考选择）爱因斯坦提出光量子假说：电磁辐射不仅在发射和吸收时以能量νh 的微粒形式出现，而且以这种形式在空间以光速c 传播，这种粒子叫做光量子，也叫光子。

意义：解释了光电效应。

【注】光电效应方程为0221W hv v m m e -= 4、★★★玻尔的三个基本假设：①定态假设：原子核外电子处在一些不连续的定常状态上，称为定态，而且这些定态相应的能量是分立的。

②跃迁假设：原子在与能级m E 和n E 相对应的两个定态之间跃迁时，将吸收或辐射频率为ν的光子，而且有m n E E hv -=.③角动量量子化假设：角动量必须是 的整数倍，即 ,3,2,1,==n n L意义：解决了氢原子光谱问题。

（末考选择）5、★★★玻尔理论后来也遇到了困难，为解决这些困难，德布罗意提出了微观粒子也具有波粒二象性的假说。

6、德布罗意公式：⇒⎪⎩⎪⎨⎧===k n h p h Eλν意义：将光的波动性和粒子性联系起来，两式的左端描述的是粒子性（能量和动量），右端描述的是波动性（频率和波长）。

7、（填空）德布罗意波长的计算：meUhmE h p h 22===λ 8、★★★康普顿散射实验的意义：证明了光具有粒子性。

（末考填空）同时也证实了普朗克和爱因斯坦理论的正确性。

9、★★★证实了电子具有波动性的典型实验：戴维孙-革末的电子衍射实验（也证实了德布罗意假说的正确性）、电子双缝衍射实验。

10、微观粒子的运动状态和经典粒子的运动状态的区别：（1）描述方式不同：微观粒子的运动状态用波函数描述，经典粒子的运动状态用坐标和动量描述；（2）遵循规律不同：微观粒子的运动遵循薛定谔方程，经典粒子的运动遵循牛顿第二定律。

)(Et r p i p Ae-⋅=ψ《量子力学》复习 提纲一、基本假设 1、（1）微观粒子状态的描述 （2）波函数具有什么样的特性 （3）波函数的统计解释2、态叠加原理（说明了经典和量子的区别）3、波函数随时间变化所满足的方程 薛定谔方程4、量子力学中力学量与算符之间的关系5、自旋的基本假设 二、三个实验1、康普顿散射（证明了光子具有粒子性） 第一章2、戴维逊-革末实验（证明了电子具有波动性） 第三章3、史特恩-盖拉赫实验（证明了电子自旋） 第七章 三、证明1、粒子处于定态时几率、几率流密度为什么不随时间变化；2、厄密算符的本征值为实数；3、力学量算符的本征函数在非简并情况下正交；4、力学量算符的本征函数组成完全系；5、量子力学测不准关系的证明；6、常见力学量算符之间对易的证明；7、泡利算符的形成。

四、表象算符在其自身的表象中的矩阵是对角矩阵。

五、计算1、力学量、平均值、几率；2、会解简单的薛定谔方程。

第一章 绪论1、德布洛意假设： 德布洛意关系：戴维孙-革末电子衍射实验的结果： 2、德布洛意平面波：3、光的波动性和粒子性的实验证据：4、光电效应：5、康普顿散射：∑=nnn c ψψ1d 2=⎰τψ（全）()ψψψψμ∇-∇2=** i j 0=⋅∇+∂∂j tρ⎥⎦⎤⎢⎣⎡+∇-=),(222t r V H μ)(,)(),(r er t r n tE i n n nψψψ-=n n n E H ψψ=附：（1）康普顿散射证明了光具有粒子性（2）戴维逊-革末实验证明了电子具有波动性 （3）史特恩-盖拉赫实验证明了电子自旋第二章 波函数和薛定谔方程1．量子力学中用波函数描写微观体系的状态。

2．波函数统计解释：若粒子的状态用()t r ,ψ描写，τψτψψd d 2*=表示在t 时刻，空间r处体积元τd 内找到粒子的几率（设ψ是归一化的）。

3．态叠加原理：设 n ψψψ,,21是体系的可能状态，那么，这些态的线性叠加∑=nnn c ψψ也是体系的一个可能状态。

2013年研究生入学考试大纲量子力学-江西师范大学物理与通信电子江西师范大学硕士研究生入学考试初试科目考试大纲科目代码、名称: 827量子力学适用专业: 070201理论物理、070205凝聚态物理、070207光学一、考试形式与试卷结构（一）试卷满分及考试时间本试卷满分为150分，考试时间为180分钟。

（二）答题方式答题方式为闭卷、笔试。

试卷由试题和答题纸组成；答案必须写在答题纸相应的位置上。

（三）试卷题型结构名词解释题（概念题）：2小题，每小题10分，共20分简答题（简述题）： 3小题，每小题10分，共30分分析论述题（综合题）：6-7小题，每小题10-20分，共100分二、考查目标（复习要求）全日制攻读硕士学位研究生入学考试《量子力学》科目考试的重点是要求了解量子力学诞生的实验基础和历史背景，了解物资具有波粒二象性的主要实验事实。

熟练掌握波函数的物理解释，薛定谔方程的建立及基本性质。

熟练掌握一些典第2页，共9页型模型下的定态薛定谔方程的精确解以及一些重要的近似求解方法（定态微扰论与变分法），理解这些解的物理意义，熟悉其实际的应用。

掌握量子力学中一些问题的处理方法，包括力学量的算符表示、对易关系、不确定度关系、态和力学量的表象、电子的自旋、粒子的全同性、泡利原理、量子跃迁等处理方法等，并具有综合运用所学知识分析问题和解决问题的能力。

三、考查范围或考试内容概要第一章波函数和薛定谔方程重点：波粒二象性，量子现象的实验主要证实。

波函数及其统计解释，薛定谔方程，连续性方程，薛定谔方程的定态解，态叠加原理。

1．了解波粒二象性假设的物理意义及其主要实验事实，2．熟练掌握波函数的标准化条件：有限性、连续性和单值性。

深入理解波函数的概率解释。

3．理解态叠加原理．4．熟练掌握薛定谔方程的建立过程。

深入了解定态薛定谔方程，了解定态与非定态波函数的意义及相互关系。

了解连续性方程的推导及其物理意义。

第二章一维势场中的粒子重点：一维势场中粒子能量本征态的一般性质，一维方势阱的束缚态，方势垒的穿透，方势阱中的反射、透射与共振，一维简谐振子。

中国地质大学研究生院硕士研究生入学考试《量子力学》考试大纲一、考试形式与试卷结构1、考试方式：闭卷，笔试2、题型：填空题与选择题约30%解答题（包括证明题）约70%二、其他（一）、量子力学产生的过程和新进展考试内容：经典物理学的困难，光和粒子的波拉二象性，德布罗意波。

考试要求：1．了解经典物理学的困难。

2．理解光和粒子的波粒二象性。

3．掌握德布罗意假设及其实验验证。

（二）、波函数和薛定谔方程考试内容：波函数的统计诠释，态迭加原理，薛定谔方程，概率流密度和概率守恒定律，定态薛定谔方程，一维束缚态；方势阱，线性谐振子；一维散射态：势垒贯穿。

考试要求：1．理解波函数的统计解释。

2．掌握态迭加原理，明确它和经典波叠加原理的区别。

3．理解Schrodinger方程的建立的原则，掌握自由粒子的Schrodinger方程；熟练掌握含时Schrodinger方程。

4．掌握几率流密度和粒子数守恒定律，并能熟练运用。

5．掌握定态的概念和性质，熟练运用定态Schrodinger方程求解能量本征值问题。

6．掌握一维束缚态：无限深势阱，线性谐振子的求解过程和结论。

7．掌握一维散射态的求解过程，明确反射系数、透射系数物理意义，掌握势垒贯穿的物理实质。

（三）、力学量和算符考试内容：力学量与算符的关系，动量算符和角动量算符，箱归一化；电子在库仑场中的运动，氢原子（类氢原子），算符的对易关系；厄密算符的本征值、本征函数及其性质，共同本征函数，不确定度关系，力学量完全集合，力学量随时间的演化，守恒定律．考试要求：1．掌握量子力学关于力学量算符假定，明确厄密算符的概念及其性质。

2．掌握动量算符和角动量算符的对易关系及其本征值问题的求解，理解自由粒子波函数箱归一化问题。

3．了解电子在库仑场中的运动的能量本征方程的过程，并掌握其结论。

4．理解氢原子（类氢原子）求解过程，掌握结论。

5．掌握算符的对易关系、两个力学量算符有共同本征函数的条件及力学量完全集的概。

考研是我一直都有的想法，从上大学第一天开始就更加坚定了我的这个决定。

我是从大三寒假学习开始备考的。

当时也在网上看了很多经验贴，可是也许是学习方法的问题，自己的学习效率一直不高，后来学姐告诉我要给自己制定完善的复习计划，并且按照计划复习。

于是回到学校以后，制定了第一轮复习计划，那个时候已经是5月了。

开始基础复习的时候，是在网上找了一下教程视频，然后跟着教材进行学习，先是对基础知识进行了了解，在5月-7月的时候在基础上加深了理解，对于第二轮的复习，自己还根据课本讲义画了知识构架图，是自己更能一目了然的掌握知识点。

8月一直到临近考试的时候，开始认真的刷真题，并且对那些自己不熟悉的知识点反复的加深印象，这也是一个自我提升的过程。

其实很庆幸自己坚持了下来，身边还是有一些朋友没有走到最后，做了自己的逃兵，所以希望每个人都坚持自己的梦想。

本文字数有点长，希望大家耐心看完。

文章结尾有我当时整理的详细资料，可自行下载，大家请看到最后。

宁波大学物理学的初试科目为：(101)思想政治理论和(201)英语一(672)普通物理（电磁学、光学）和(872)量子力学参考书目为：1.《光学教程》（第三版）姚启钧编，高等教育出版社，2002年2.《电磁学》（上、下册，第二版）赵凯华等编，高等教育出版社，1985年3.《量子力学》周世勋编著，高等教育出版社，1979年首先简单介绍一下我的英语复习经验。

⑴单词：英语的单词基础一定要打好，如果单词过不了关，那你其他可以看懂吗？？单词可以用木糖英语单词闪电版就够了。

也可以用app软件。

但是这样就会导致玩手机（如果你自制力超强），单词的话到考前也不能停止的。

我的单词并没有背好，导致英语后来只有60+，很难过…⑵阅读：阅读分数很高，所以一定要注重，可以听木糖英语的名师讲解，或者木糖英语的课程，阅读最重要的是自己有了自己的方法，有一个属于自己的做题方法可以节省很多时间，如果初次做题还没有什么思路，那就可以多看看真题里面的答案解析考研英语很难，和四六级是完全不同的！大家肯定都听说过，所以阅读暑假就可以开始做了，真题反复摸索，自己安排好时间。