电动力学第四章复习思考题
- 格式:pptx
- 大小:89.63 KB
- 文档页数:2

电动力学第四章习题答案电动力学第四章习题答案电动力学是物理学中的一个重要分支,研究电荷和电场、电流和磁场、电磁感应等现象。
在学习电动力学的过程中,习题是非常重要的一部分,通过解答习题可以加深对理论知识的理解和应用能力的培养。
本文将为大家提供电动力学第四章的一些习题答案,希望能对大家的学习有所帮助。
1. 问题:一个半径为R的均匀带电球壳,总电荷量为Q。
求球壳上任意一点的电场强度。
解答:由于球壳是均匀带电的,所以球壳上的电荷分布是均匀的。
根据库仑定律,球壳上任意一点的电场强度与该点到球心的距离r有关。
当r<R时,由于球壳内部没有电荷,所以电场强度为0;当r>R时,由于球壳外部的电荷均匀分布,可以将球壳看作一个点电荷,根据库仑定律,电场强度与点电荷的电荷量和距离成正比。
所以球壳上任意一点的电场强度为:E = k * Q / r^2其中,k为电场常量。
2. 问题:一个半径为R的均匀带电球壳,总电荷量为Q。
求球壳内部的电场强度。
解答:由于球壳内部没有电荷分布,所以球壳内部的电场强度为0。
3. 问题:一个半径为R的均匀带电球壳,总电荷量为Q。
求球壳外部的电场强度。
解答:根据问题2的解答可知,球壳内部的电场强度为0。
所以球壳外部的电场强度与球壳上的电荷量和距离成正比。
可以将球壳看作一个点电荷,根据库仑定律,球壳外部的电场强度为:E = k * Q / r^2其中,k为电场常量,r为球壳上任意一点到球心的距离。
4. 问题:一个半径为R的均匀带电球壳,总电荷量为Q。
求球壳内部和外部的电势。
解答:球壳内部的电势为0,因为电场强度为0。
球壳外部的电势可以通过积分求解。
根据电势的定义,电势差为从参考点到某一点的电场强度在该段距离上的积分。
所以球壳外部的电势为:V = ∫E·dr其中,E为球壳外部的电场强度,r为从参考点到某一点的距离。
5. 问题:一个半径为R的均匀带电球壳,总电荷量为Q。
求球壳上的电势。

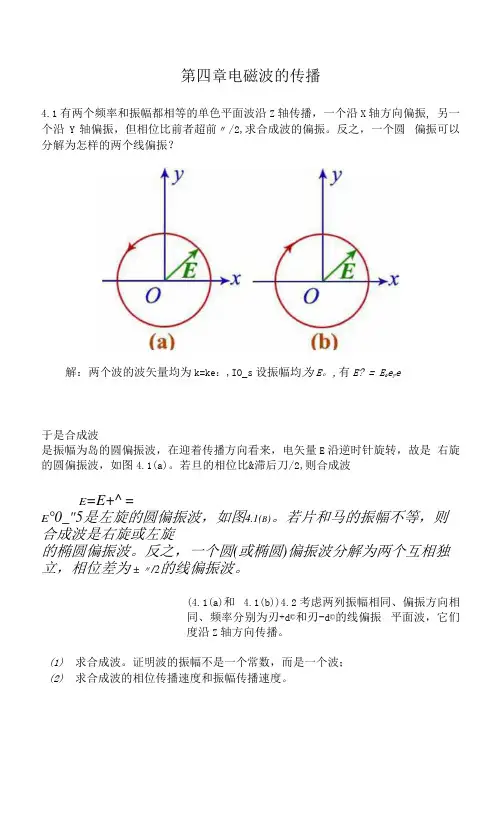
第四章电磁波的传播4.1有两个频率和振幅都相等的单色平面波沿Z轴传播,一个沿X轴方向偏振, 另一个沿Y轴偏振,但相位比前者超前〃/2,求合成波的偏振。
反之,一个圆偏振可以分解为怎样的两个线偏振?解:两个波的波矢量均为k=ke:,IO_s设振幅均为E。
,有E? = E o e y e于是合成波是振幅为岛的圆偏振波,在迎着传播方向看来,电矢量E沿逆时针旋转,故是右旋的圆偏振波,如图4.1(a)。
若旦的相位比&滞后刀/2,则合成波E=E+^=E°0_"5是左旋的圆偏振波,如图4.1(B)。
若片和马的振幅不等,则合成波是右旋或左旋的椭圆偏振波。
反之,一个圆(或椭圆)偏振波分解为两个互相独立,相位差为±〃/2的线偏振波。
(4.1(a)和 4.1(b))4.2考虑两列振幅相同、偏振方向相同、频率分别为刃+d©和刃-d©的线偏振平面波,它们度沿Z轴方向传播。
(1)求合成波。
证明波的振幅不是一个常数,而是一个波;(2)求合成波的相位传播速度和振幅传播速度。
E 、= A, sin 奴xcos«ysin k.zE : = A, sin k^xsin k v y cos k z z 再由条件(2),有x=a 处,将(7), (8), (9)三式代入上述条件,解得k v = 〃饥1 a,k 、. = n7r !b(m,n = 0,1,2,...)yk : = J.-k : _k : = yj(co/c)2 -(ni7r/a)2 -(n/r/b)2管内电场还应满足V.E = 0,将(7), (8), (9)三式代入这条件,得A {k ix + A 2k y + A 3k, = 0可见4勺&中只有两个是独立的,即(7), (8), (9)表示的解中,对每一组 m,n 的值,管内有两种独立的波模。
4.13写出矩形波导管内磁场H 满足的方程和边界条件。


2011级电动力学复习提纲数学准备理解散度、旋度、梯度的意义,熟悉矢量的梯度、散度、旋度在直角、球、圆柱坐标系中的运算,以及散度定理(高斯定理)、旋度定理(斯托克斯定理)。
章后练习1、2。
第1章理解全章内容,会推导本章全部公式。
重点推导麦克斯韦方程组,以及用积分形式的麦克斯韦方程组推出边值关系。
章后练习1、2、5、9、10、12第2章能推导能量转化与守恒定律,并且能说明各物理量及定律的物理意义。
能认识电磁场动量及动量转化和守恒定律,并且能说明各物理量及定律的物理意义。
了解电磁场的角动量,理解电磁场有角动量且角动量转化和守恒的意义。
P35例题,书后练习2、3第3章理解静电场和静磁场的势函数,为什么可以提出,在求解静电磁场时有什么意义。
势的方程和边值关系及推导。
深入理解唯一性定理,能应用其解释电磁现象,比如静电屏蔽现象。
熟悉电磁能量势函数表达式及意义。
会独立完成P48例题1,,P55例1、例2,P57例5,。
练习1、3、6、7第4章掌握静像法、简单情形下的分离变量法;理解多极矩法,掌握电偶极矩的势、场,以及能量、受力等;知道电四极矩的表示,计算。
了解磁偶极矩的表示、能量。
熟悉超导的基本电磁性质及经典电磁理论的解释。
会独立熟练计算P62例题1、P64例2及相关讨论;P69例1、P72例3;P74例1、例2。
练习3、4、5、7、10、12第5章1、理解如何由麦克斯韦方程推导自由空间的波动方程,理解其意义。
2、能推出电场和磁场的定态方程(亥姆霍兹方程),熟练掌握自由空间平面电磁波表达式,并且能应用其证明平面电磁波性质;3、能推导反射、折射定律、费涅尔公式,并且能应用其讨论布儒斯特定律、半波损失等常见现象;4、理解全反射现象,知道什么情形下发生全反射,折射波表示,透射深度;5、熟悉电磁波在导体空间表达式,理解其物理意义、理解良导体条件及物理意义;能推导导体中电荷密度;知道导体内电场和磁场的关系;理解趋肤效应,计算趋肤深度;理想导体的边值关系;6、理解波导管中电磁波的求解过程和结果,知道结构。

第4章 电磁波的传播平面电磁波4-1解:(1)由麦克斯韦方程组有 0=⋅∇D ,tDH ∂∂=×∇在均匀各向同性介质中有 E D ε=,H Bμ=E E E 2)()(∇−⋅∇∇=×∇×∇∴E2−∇=又 t B E ∂∂×−∇=×∇×∇ )(B t×∇∂∂−=22t E∂∂−=με 得波动方程 0222=∂∂−∇t E Eμε 同理可得 0222=∂∂−∇t B B με 由波动方程 012222=∂∂−∇t y v y 可得 με1=v (2)对时谐电磁波 B i t BEω=∂∂−=×∇,tD H ∂∂=×∇ D i ω−=B i E×∇=×∇×∇∴ω)(E μεω2=E k 2=其中 μεω=k又 E E E 2)()(∇−⋅∇∇=×∇×∇E 2−∇=得亥姆霍兹方程 022=+∇E k E同理可得 022=+∇B k B4-2证:(1)平面电磁波 )(0),(t x k i e E t x E ω−⋅=)(0t x k i e E E ω−⋅⋅∇=⋅∇ ∵)(0t x k i e E k i ω−⋅⋅=0=⋅=E k i 0=⋅∴E k ,同理 0=⋅B k ,即电磁波是横波。
(2)][)(0t x k i eE E ω−⋅×∇=×∇ ∵0)(E e t x k i ×∇=−⋅ω)(0t x k i e E k i ω−⋅×=E k i ×= 又 B i t BE ω=∂∂−=×∇B E k ω=×∴ 即k B E、、组成右手螺旋关系 (3)B E k∵ω=×,即ωE k B×=k E k k ×=ωE e k k ×=ωE e v k×=1 其中k ke k=为传播方向的单位矢量。

4-1 把一台三相感应电动机用原动机驱动,使其转速n 高于旋转磁场的转速s n ,定子接到三相交流电源,试分析转子导条中感应电动势和电流的方向。
这时电磁转矩的方向和性质是怎样的?若把原动机去掉,电机的转速有何变化?为什么? 【答】 感应电动机处于发电机状态,转子感应电动势、转子有功电流的方向如图所示,应用右手定则判断。
站在转子上观察时,电磁转矩e T 的方向与转子的转向相反,即电磁转矩e T 属于制动性质的转矩。
若把原动机去掉,即把与制动性质电磁转矩e T 平衡的原动机的驱动转矩去掉,电动机将在电磁转矩e T 的作用下减速,回到电动机状态。
4-2 有一台三相绕线型感应电动机,若将其定子三相短路,转子中通入频率为1f 的三相交流电流,问气隙旋转磁场相对于转子和相对于空间的转速及转子的转向。
【答】 假设转子中频率为1f 的交流电流建立逆时针方向旋转的气隙旋转磁场,相对于转子的转速为p f n s 160=;若转子不转,根据左手定则,定子将受到逆时针方向的电磁转矩e T ,由牛顿第三定律可知,定子不转时,转子为顺时针旋转,设其转速为n ,则气隙旋转磁场相对于定子的转速为n n s -。
4-3 三相感应电动机的转速变化时,转子所生磁动势在空间的转速是否改变?为什么? 【答】 不变。
因为转子所产生的磁动势2F 相对于转子的转速为n sn p f s p f n s ∆====1226060,而转子本身又以转速n 在旋转。
因此,从定子侧观看时,2F 在空间的转速应为()s s n n n n n n =+-=+∆,即无论转子的实际转速是多少,转子磁动势和定子磁动势在空间的转速总是等于同步转速s n ,在空间保持相对静止。
4-4 频率归算时,用等效的静止转子去代替实际旋转的转子,这样做是否影响定子边的电流、功率因数、输入功率和电机的电磁功率?为什么?【答】 频率归算前后,转子电流的幅值及其阻抗角都没有变化,转子磁动势幅值的相位也不变,即两种情况下转子反应相同,那么定子的所有物理量以及电磁功率亦都保持不变。

电动力学思考题第一章电磁现象的普遍规律1.麦克斯韦方程组的实验基础是什么?为什么说它们是有机的组合?2.电动力学的三大基本假设是什么?各说明了什么?3.麦克斯韦方程组的三种形式各是什么?***适用范围各是什么?麦克斯韦方程组的积分和微分形式如下:/baike/pic/item/5af4d7ea09f911c0d539c9ef.jpg除此之外,还有矢量形式:E=Qr’/4πε.r3 …………………………(1)其中E和r’为矢量,Q为电荷的电量。
、对(1)式的等号两边取散度,就可以得到上述微分形式中的第一式。
、A= u.Qv/4πr’……………………………(2)其中A、v、r’为矢量,Q为电荷的电量。
、对(2)式的等号两边先取旋度,再取散度,就可以得到上述微分形式中的第二式。
、E=B×v=B×ds/dt…………………………(3)其中E、B、v、s为矢量。
、对(3)式的等号两边取旋度,就可以得到上述微分形式中的第三式。
、H=D×v………………………………………(4.1)B= u. D×v……………………………………(4.2)B=ε. u. E×v=(E0×v)/C^2 …………………(4.3)、(4.1)、(4.1)、(4.3)三式是等价的,又因为位移电流和传导电流都可以写成“电通量的变化率”或“电位移量的变化率”。
对(4)式等号两边取旋度,就可以得到上述微分形式中的第四式。
4.E, H ,B, H四个物理量中,那两个是基本物理量?为什么?5.电磁场的能量密度、能流密度和动量密度的定义式和表达式是什么?单位时间内通过边界面单位面积流动的电磁能,即能流密度矢量S = E H系统的电磁场能量密度为6.传导电流,位移电流的定义式各是什么?两种电流的区别是什么?相同点是什么?位移电流是电位移矢量随时间的变化率对曲面的积分。
英国物理学家麦克斯韦首先提出这种变化将产生磁场的假设并称其为“位移电流”。


电动力学思考题第一章数学基础和基本理论序言1、电动力学为什么不叫作电磁动力学?2、当一名中学教师是否需要学习理论物理?3、从事实验物理研究或技术开发的人员是否有必要学好理论物理?4、爱因斯坦的生平给了我们什么启发?第一节电动力学的数学基础1、矢量叉乘的导数结果中的两项叉乘顺序为什么不能颠倒?2、张量与并矢的联系与区别是什么?3、某区域散度为零的场是无源场吗?4、唯一性定理的意义?第二节静态场基本方程1、为什么在多数情况下利用连续分布的电场强度计算公式不能得到电场强度?2、电荷守恒定律的意义是什么?3、两电流元之间的相互作用力为什么不满足牛顿第三定律?4、静态场方程的物理意义。
第三节麦克斯韦方程组1、描述电磁感应的物理机制。
2、为什么说麦克斯韦方程是电磁场的基本方程?3、分析介质中的麦克斯韦方程组与真空中的方程组的主要区别和联系。
4、为什么说洛伦兹力公式是一个假设?第四节电磁场的势函数1、规范不变性的意义和重要性。
2、通过达朗伯方程的求解方法体会物理学方程求解技巧。
3、为什么说电磁相互作用需要时间?4、电势参考点的选取对实际结果有影响吗?第五节边值关系和场方程的完备性1、微分方程在介质分界面上为什么不适用?2、法向分量连续其相应的切向分量也连续吗?3、导体表面上的边值关系与两个介质分界面上的边值关系的异同。
4、为什么完备性可以归结为电磁场的唯一性定理?第六节电磁场的能量和动量1、玻印停矢量与能量密度之间的联系是什么?2、深刻理解电磁场能量的传输。
3、相互作用能为什么又称为带电体系在外场中的能量?4、用语言描述电磁场动量守恒定律。
第二章狭义相对论第一节经典时空观及其局限性1、经典时空观主要体现在那几个方面。
2、怎样理解不能在一个参照系内部做实验来确定该参照系相对另一系的速度。
3、以太概念及其作用是什么?4、迈克尔孙实验的历史作用是什么?第二节相对论的时空理论1、光速不变为什么会导致同时的相对性?2、光锥的几何意义说明了什么?3、洛伦兹变换的物理意义。

习题四参考答案1.一个半径为R 的电介质球,极化强度为2/r r K P ,电容率为 .计算⑴ 束缚电荷的体密度和面密度; ⑵ 自由电荷体密度; ⑶ 球外和球内的电势;⑷该带电介质球产生的静电场的总能量.答案:⑴ 2rK p ,R K p ⑵ 20rKf⑶ r KR002R r001ln r K K R r⑷ 20012K R W 提示:⑴2rK P p , R KP e R r r p ˆ⑵ 因为f P10,所以 2r K f ⑶ 因为电荷分布具有球对称性,所以可以由高斯定理求电场强度E ,再求 ⑷ 两种方法都可以求解v dV W 21,V 是电荷分布的球区间。
或者,dV D E W21,这里V 是电场分布的全空间2.导体内有一半径为R 的球形空腔,腔内充满电容率为 的均匀电介质,现将电荷量为q 的点电荷放在腔内离球为)(R a a 处,如图所示,已知导体的电势为零,试求:①腔内任一点),( r p 的电势 ;②腔壁上感应电荷量的面密度;③介质极化电荷量的密度和面密度.解:用电像法求解①设导体不存在,整个空间都充满了电容率为 的均匀介质,像电荷q 使腔壁电势为0.041s q s q 解之得 aR b 2q aR q由此得介质内任一点),( r p 的电势为cos 2cos 2412222br b r q ar a r q . ②腔壁上感应电荷量的面密度为2/32222)cos 2(4)(ˆ)(ˆ aR a R R q a R r e E e D n Rr r ③介质内极化电荷量的密度为200)()( E P P)1())((00. q q p )1(0. 介质表面极化电荷面密度R r p rE ep n ))(()(ˆ002/322220)cos 2(4))(( aR a R R qa R . 3.接地的空心导体球内外半径为1R 和2R ,在球内离球心为 1R a a 处置一点电荷q ,求空间的电势分布.导体球上的感应电荷有多少?分布在内表面还是外表面?答案:cos /2//cos 2412122121220a R R a R R aqR Ra a R qq q ',分布在内表面.感应电荷不等于像电荷.提示:该题的解法与例题2完全类似,只是像电荷在球外空间。
(0134)《电动力学基础》复习思考题答案一.填空1..t BE ∂∂-=⨯∇ 2.0=∂∂+⋅∇t J ρ3.B E g ⨯=4.tA E ∂∂--∇=φ5.完全抗磁性 6.相同 7.衰减的. 8.c r t /=9.012=∂∂+⋅∇tc A ϕ10.2201c v m m -=11..000tEJ B ∂∂+=⨯∇εμμ 12.H E S ⨯= 13.A B⋅∇=14..00rr EH μμεε=15.越浅. 16.c r t /- 17.惯性系等价18.241re p r⋅=πεϕ 19.ερϕ/2-=∇20.垂直 21.缩短, 变慢22.成立 23.相对的 24.与导体表面垂直 25.辐射功率与4ω成正比, 与r 成反比26.0. 5米27.共振频率为101f .28.流过垂直于i 轴的单位投影面的动量的j 分量;29.A.光速在真空中总等于c ;B .一切物理规律对惯性系等价; C.电场E和磁场B对不同惯性系中的观察者看是不一样的;D.惯性质量对不同观察者也是不一样的. 30. 加速运动的带电粒子总是会辐射的.31.,'q q -= 距离上表面a ,在导体面下侧,与q 关于上表面对称;32. a 233.在相对论中, 频率不仅在源运动方向上改变,也在垂直于运动的方向上改变; 34.仍然为零35.电磁波存在截止频率. 36.023ω 二.证明题 1.证明: 设xy 平面为界面,上方充满介质ε,μ的均匀介质,下方介质的相应常数为ε'和μ'。
入、反、折射波为)(0t x ki e E E ω-⋅= )'(0''t x ki e E E ω-⋅= )"(0""t x ki e E E ω-⋅=设入射波在xz 平面内,由边界条件,E在切线方向连续,)'()'()("'t y k x k i ox t y k x k i ox t x k i ox y x yx eE eE e E ωωω'-'+''-''+-=+在任意时刻t ,对任意x 和y 成立则要求x x xk k k =''=' yy y k k k ''='=因为设入射波在xz 平面内,0=y k ,所以即折射波和反射波也在xz 平面内。
电动力学答案第一章 电磁现象的普遍规律1. 根据算符∇的微分性与向量性,推导下列公式:B A B A A B A B B A )()()()()(∇⋅+⨯∇⨯+∇⋅+⨯∇⨯=⋅∇AA A A )()(221∇⋅-∇=⨯∇⨯A 解:(1))()()(c c A B B A B A ⋅∇+⋅∇=⋅∇B A B A A B A B )()()()(∇⋅+⨯∇⨯+∇⋅+⨯∇⨯=c c c cB A B A A B A B )()()()(∇⋅+⨯∇⨯+∇⋅+⨯∇⨯=(2)在(1)中令B A =得:A A A A A A )(2)(2)(∇⋅+⨯∇⨯=⋅∇,所以 AA A A A A )()()(21∇⋅-⋅∇=⨯∇⨯ 即 AA A A )()(221∇⋅-∇=⨯∇⨯A 2. 设u 是空间坐标z y x ,,的函数,证明:u u f u f ∇=∇d d )( , u u u d d )(A A ⋅∇=⋅∇, uu u d d )(AA ⨯∇=⨯∇ 证明:(1)z y x z u f y u f x u f u f e e e ∂∂+∂∂+∂∂=∇)()()()(z y x z uu f y u u f x u u f e e e ∂∂+∂∂+∂∂=d d d d d d u uf z u y u x u u f z y x ∇=∂∂+∂∂+∂∂=d d )(d d e e e (2)z u A y u A x u A u z y x ∂∂+∂∂+∂∂=⋅∇)()()()(A zuu A y u u A x u u A z y x ∂∂+∂∂+∂∂=d d d d d d uu z u y u x u u A u A u A z y x z z y y x x d d )()d d d d d d (Ae e e e e e ⋅∇=∂∂+∂∂+∂∂⋅++= (3)uA u A u A z u y u x u uu z y x zy x d /d d /d d /d ///d d ∂∂∂∂∂∂=⨯∇e e e Azx y y z x x y z yu u A x u u A x u u A z u u A z uu A y u u A e e e )d d d d ()d d d d ()d d d d (∂∂-∂∂+∂∂-∂∂+∂∂-∂∂=z x y y z x x y z y u A x u A x u A z u A z u A y u A e e e ])()([])()([])()([∂∂-∂∂+∂∂-∂∂+∂∂-∂∂=)(u A ⨯∇= 3. 设222)'()'()'(z z y y x x r -+-+-=为源点'x 到场点x 的距离,r 的方向规定为从源点指向场点。
习题四参考答案1.一个半径为R 的电介质球,极化强度为2/r r K P =,电容率为ε.计算⑴ 束缚电荷的体密度和面密度; ⑵ 自由电荷体密度; ⑶ 球外和球内的电势;⑷该带电介质球产生的静电场的总能量.答案:⑴ 2rK p -=ρ,R K p =σ ⑵ ()20rKf εεερ-=⑶ ()r KR002εεεεϕ-=()R r >⎪⎪⎭⎫ ⎝⎛+-=001ln εεεεϕr K K ()R r <⑷ 2012⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛+=εεεεπεK R W 提示:⑴2rK P p -=⋅-∇= ρ,R KP e R r r p =⋅== ˆσ⑵因为f P ρεερ⎪⎭⎫⎝⎛-=10,所以()2r K f εεερ-= ⑶因为电荷分布具有球对称性,所以可以由高斯定理求电场强度E ,再求ϕ ⑷两种方法都可以求解⎰=vdV W ρϕ21,V 是电荷分布的球区间。
或者,⎰∞⋅=dV D E W21,这里V 是电场分布的全空间2.导体内有一半径为R 的球形空腔,腔内充满电容率为ε的均匀电介质,现将电荷量为q 的点电荷放在腔内离球为)(R a a <处,如图所示,已知导体的电势为零,试求:①腔内任一点),(θr p 的电势ϕ;②腔壁上感应电荷量的面密度;③介质极化电荷量的密度和面密度.解:用电像法求解①设导体不存在,整个空间都充满了电容率为ε的均匀介质,像电荷q ' 使腔壁电势为0.041=⎪⎭⎫⎝⎛''+=s q s q πεϕ 解之得aR b 2=q aR q -=' 由此得介质内任一点),(θr p 的电势为⎥⎦⎤⎢⎣⎡-+'+-+=θθπεϕcos 2cos 2412222br b r q ar a r q . ②腔壁上感应电荷量的面密度为2/32222)cos 2(4)(ˆ)(ˆθπϕεϕεεσaR a R R q a R r e E e D n Rr r -+--=⎪⎭⎫ ⎝⎛∂∂=∇⋅=⋅-=⋅= ③介质内极化电荷量的密度为ϕεεεερ200)()(∇-=-⋅-∇=⋅-∇=E P Pρεεερεε)1())((00--=--=. q q p )1(0εε--=. 介质表面极化电荷面密度R r p rE ep n ))(()(ˆ00∂∂--=-⋅=⋅=ϕεεεεσ2/322220)cos 2(4))((θπεεεaR a R R qa R -+--=. 3.接地的空心导体球内外半径为1R 和2R ,在球内离球心为()1R a a <处置一点电荷q ,求空间的电势分布.导体球上的感应电荷有多少?分布在内表面还是外表面?答案:()()⎥⎥⎦⎤⎢⎢⎣⎡-+-+-+=θθπεϕcos /2//cos 2412122121220a R R a R R aqR Ra a R qq q -=',分布在内表面.感应电荷不等于像电荷.提示:该题的解法与例题2完全类似,只是像电荷在球外空间。
《电动力学基础》复习思考题一、填空1、电荷守恒定律的微分形式 。
2、电偶极子的电势 。
3、静电场的泊松方程 。
4、圆电流圈的矢势 。
5、平面电磁波,其等相面t r k ω-⋅ = ,因此它描述的是一个平面波。
6、平面波波矢k 的方向和E 的方面及B 的方向 。
7、平面波电场和磁场波幅的关系 、8、狭义相对论的基本假设有 , 。
9、动系的尺子将 ,动系的时钟将 。
10、因果关系对一切惯性系 。
11、同时是 。
12、质能关系式 ,13、电磁势的推迟解τπμ'-'=⎰⎰⎰d Rc R t r j t r A v)/,(4),( ,它的物理意义是 。
14、电磁场的边值关系______________________, _________________________,___________________, _________________________.15、电磁场的能量密度____________________________16、磁场的矢势和B 的关系___________________;17、电磁场的E 和标势及矢势的关系____________________________二、证明题1、推导静磁场的方程式2、推导电磁作用下的能量守恒定理3、推导介质的界面上,电场的边值关系4、有两种绝缘介质,界面上没有面自由电荷,证明电力线的曲折满足5、推导真空中的静电场的方程式三、计算题1. 平行板电容器内有两层介质,厚度分别为l 1 ,l 2,介电系数为ε1,ε2,加在两板上的 电动势为ε,求出电容器两极上的自由电荷密度.2. 有中心为O,半径为R 的均匀带电球,电荷密度为ρ, 在O ’处挖一个半径为R/2的球形空洞,OO ’=R/2,试算出空洞内的电场强度.3. 平行板电容器内有两层介质,厚度分别为1 和2 ,介电系数为1ε,2ε,如介质漏电,电导率分别为1σ和2σ,试求在电流达到稳恒时,两极板上及介质界面上的自由电荷面密度,设两极间电动势为ε。