《连续体力学》习题及解答5分析

1．如图所示，有一块木板静止在光滑且足够长的水平面上，木板质量为M=4kg ，长为L=1.4m ；木板右端放着一小滑块，小滑块质量为m=1kg ，其尺寸小于L 。

小滑块与木板之间的动摩擦因数为μ==04102.(/)g m s（1）现用恒力F 作用在木板M 上，为了使得m 能从M 上面滑落下来，问：F 大小的范围是什么？（2）其它条件不变，若恒力F=22.8牛顿，且始终作用在M 上，最终使得m 能从M 上面滑落下来。

问：m 在M 上面滑动的时间是多大？2.如图所示，平板车B 的质量为3.0kg ，以4.0m/s 的速度在光滑水平面上向右运动．质量为1.0kg 的物体A 被轻放到车的右端，设物体与车上表面间的动摩擦因数为0.25．求：①如果平板车足够长，那么平板车最终速度多大？物体在车上滑动的时间是多少？ ②要使物体不从车上掉下，车至少要有多长？3、如图3-29所示，质量M=8Kg 的小车放在水平光滑的平面上，在小车右端加一水平恒力F ，F=8N ，当小车向右运动的速度达到1.5m/s 时，在小车前端轻轻放上一个大小不s 计，质量为m=2kg 的小物块，物块与小车间的动摩擦因数μ=0.2，小车足够长，求从小物块放上开始经过t=1.5s ，小物块通过的位移大上为多少？(取g=10m/s 2)4．如图所示，光滑水平面上的长L 为木板以恒定速度v 0向右运动，将一个质量为m 、长度也是L 金属板与木板左右对齐轻放于木板上，。

金属板与木板间动摩擦因数为μ。

求：⑴为保证金属板不能从木板上掉下，木板的速度v 0应满足什么条件？⑵保持木板匀速运动外力对木板所做功是多少？ 5.如图所示，质量为m=5kg 的长木板放在水平地面上，在木板的最右端放一质量也为m=5kg 的物块A 。

木板与地面间的动摩擦因数μ1=0.3，物块与木板间的动摩擦因数μ2=0.2。

现用一水平力F=60N 作用在木板上，使木板由静止开始匀加速运动，经过t=1s ，撤去拉力。

高三物理连接体试题答案及解析1.（13分）如图所示，在粗糙水平台阶上静止放置一质量m=1.0kg的小物块，它与水平台阶表面的动摩擦因数μ=0.25，且与台阶边缘O点的距离s=5m．在台阶右侧固定了一个1/4圆弧挡板，圆弧半径R=m，今以O点为原点建立平面直角坐标系。

现用F=5N的水平恒力拉动小物块，已知重力加速度．（1）为使小物块不能击中挡板，求拉力F作用的最长时间；（2）若小物块在水平台阶上运动时，水平恒力一直作用在小物块上，当小物块过O点时撤去拉力，求小物块击中挡板上的位置的坐标．【答案】（1）；（2）x=5m，y=5m【解析】（1）为使小物块不会击中挡板，拉力F作用最长时间t时，小物块刚好运动到O点．由牛顿第二定律得：（1分）解得：（1分）减速运动时的加速度大小为：（1分）由运动学公式得：（1分）而（1分）解得：（1分）（2）水平恒力一直作用在小物块上，由运动学公式有：（1分）解得小物块到达O点时的速度为：（1分）小物块过O点后做平抛运动．水平方向：（1分）竖直方向：（1分）又（2分）解得位置坐标为：x=5m，y=5m （1分）【考点】牛顿第二定律，平抛运动2.（16分）电磁感应现象是电磁学中最重大的发现之一，它揭示了电、磁现象之间的本质联系。

电路中感应电动势的大小，跟穿过这一电路的磁通量的变化率成正比，即，这就是法拉第电磁感应定律。

（1）如图所示，把矩形线框abcd放在磁感应强度为B的匀强磁场里，线框平面跟磁感线垂直。

设线框可动部分ab的长度为L，它以速度v向右匀速运动。

请根据法拉第电磁感应定律推导出闭合电路的感应电动势E=BLv。

（2）两根足够长的光滑直金属导轨平行放置在倾角为θ的绝缘斜面上，两导轨间距为L。

两导轨间接有阻值为R的电阻。

一根质量为m的均匀直金属杆MN放在两导轨上，并与导轨垂直。

整套装置处于磁感应强度为B匀强磁场中，磁场方向垂直于斜面向上。

导轨和金属杆的电阻可忽略。

让金属杆MN由静止沿导轨开始下滑。

2 二阶张量及其若干运算法则(一) 概念、理论和公式提要2-1 张量的乘法① 张量的外乘(并乘) 张量的外乘用⊗表示，其外积为张量，其阶数等于外乘诸张量阶数之和。

② 张量的内乘(点乘) 张量的点乘用“·”表示(有时也可省去“·”)，其内积为张量，其阶数为内乘诸张量阶数之和减去2倍内乘的次数。

③ 张量的双点乘记作“∶”(两次点乘)，例如B A∶；其积为张量，其阶数为诸张量阶数之和减2倍点乘次数。

设)(CT )(CT )(CT p n m 为，为，为C B A ，则)42(CT ⨯-++=p n m 为，∶∶D D C B A (2-1-1) 取)2(CT 244为，则，，D ===p n m ，其分量为rp mnrp ijmn ij C B A D = (2-1-2)其中A 分量的后两个指标与B 分量的前两个指标，B 分量的后两个指标与C 分量的前两个指标依次相同。

④ 二阶张量ij ij T T =T T T T ∶，定义为的范数记为为正方根，且有时才取等号只当，o T T =≥0 (2-1-3) 的绝对值为标量，ααααT T = (2-1-4) R T R T +≤+ (2-1-5) R T R T ⋅≤∶ (2-1-6) a T a T ≤⋅ (2-1-7)R a a 的模，为矢量亦为二阶张量。

⑤ 设C B A B A 次缩拼为张量外积的和，则和分是是和s t r )(CT )(CT ，记为C B A =⊗s C)2(s t r -+为C 阶张量，其分量关系为mn k k k k k k ij mn ij s s B A C 2121= (2-1-8)反之，如果已知C B 和为张量，其分量与带指标的量 ij A 满足上式，则 ij A 为张量A 的分量，称为商法则或张量识别定理。

A 的阶数等于s 2的阶数加C ，减去B 的阶数。

特别地当B ，t s =的分量的全部指标都是哑标时，则A 的阶数等于B 和C 的阶数之和。

五．液体的表面现象 1．液体的表面张力 液体的表面像一张绷紧的弹性薄膜， 液体的表面像一张绷紧的弹性薄膜， 有收缩的趋势， 有收缩的趋势，在液体的表面层上 存在着一种沿着液体表面的应力— 存在着一种沿着液体表面的应力 —表面张力。为研究液体表面张力 表面张力。 表面张力 的大小， 的大小，我们在液体表面上划一条 假想的线元∆l， 假想的线元 ，把液面分割为两部 分，表面张力就是这两部分液面相 互之间的拉力。 互之间的拉力。
已知水和油边界的表面张力系数为， 例 已知水和油边界的表面张力系数为，为使半径 的一个大油滴在水中散布成多个半径为r的小 为R的一个大油滴在水中散布成多个半径为 的小 的一个大油滴在水中散布成多个半径为 油滴，问外界要作多少功？ 油滴，问外界要作多少功？ 一个大油滴在水中散布成N个小油滴的过程中 个小油滴的过程中， 解：一个大油滴在水中散布成 个小油滴的过程中， 液体表面积增大
理论上还可推出杨氏模量Y、剪切模量 和泊松系数 理论上还可推出杨氏模量 、剪切模量N和泊松系数 μ之间的关系： 之间的关系： Y N= 2(1 + µ ) 3、剪切形变的势能 、 用类似的方法可得出发生剪切形变的弹性势能密度
1 E = Nϕ 2 2
0 P
三、弯曲和扭转形变
1、梁的弯曲 、 水平横梁都会在自身重力和两端 支持力作用下发生弯曲。 支持力作用下发生弯曲。可认为 梁的上半部受压缩而下半部受拉 越靠边缘形变越大。 伸，越靠边缘形变越大。 对一个高为h，宽为 的矩形梁， 对一个高为 ，宽为b 的矩形梁， 可求出中性层的曲率半径R为 可求出中性层的曲率半径 为：
bb′ ≈ϕ 定义剪切应变： 定义剪切应变：tgϕ = ab
φ角也称为切变角。 角也称为切变角。 角也称为切变角

2 2
[
]
[
]
在流入面： v1 = −v1 * n1 ，在流出面： v2 = v2 * n1
2、给定速度场 v1 = ax1 + bx2 ， v2 = ax2 + bx1 ， v3 =
x1 + x2 ， ρ 0 = ρ * e −2 at 。其中 a，
2 2
b，c，ρ为常数 求：是否满足质量守恒方程 解答： 质量守恒方程：
∫ [t − ρ * v(v • n )]dS
S1
C
=
S1 + S 2 + S 3 + S 4
∫ [t − ρ * v(v • n)]dS ∫ [− p n
2 S3
C
= =
∫ [t − ρ * v(v • n )]dS + ∫ [t − ρ * v(v • n )]dS + ∫ [t − ρ * v(v • n )]dS + ∫ [t − ρ * v(v • n )]dS
(
)
3、
Ω • r = w× r
w × r = eijk w j rk ei
•
Ω • r = Ωim rm ei
所以
• •
•
•
eijk w j rk = Ωim rm
eijk w j = Ωik
⎡ 0 Ω=⎢ ⎢ w3 ⎢ ⎣− w2
•
− w3 0 w1
w2 ⎤ − w1 ⎥ ⎥ 0 ⎥ ⎦
4、
L = ∫ ρ * r × vdv = ∫ ρ * r × (w × r )dv = ∫ ρ [w(r • r ) − r (r • w)]dv = ∫ ρ [(r • r ) − (r ⊗ r )]dv • w

d
d
高中物理奥林匹克竞赛专题连续体 力学
l0 l
2.应力（stress）
作用在物体内部单位 面积上的作用力称应 力，应力是内力。
fn
f
S f t
应力的数学表达：
f
S
lim f d f S0 S d S
高中物理奥林匹克竞赛专题连续体 力学
3.应力与应变的关系
应力伴随应变的增大而增大，它反映了发生形变的物 体内部的紧张程度。对于一般的固体材料，若形变不超过一 定的限度，应力与相关的应变成正比，此称胡克定律。
(R. Hooke)
拉伸应变 体应变 剪切应变
拉＝Y
l l0
体＝K
V V0
剪＝G
x d
高Y中物、理K奥林和匹G克竞称赛专弹题性连续模体 量
力学
弹性体的拉伸和压缩形变
正压力（拉伸压缩应力）
＝ Fn S
（1）
其中，F 沿作用力截面的法线方向。
例：如图示，0
高中物理奥林匹克竞赛专题连续体 力学
绝对伸长（或压缩）与原长之比称为相对伸长（或压缩）。公式：
刀剪断物体前即发生这类形变。
2、剪应力 shearing stress
t
Ft S
其中：S为假想截面ABCD的面积，力F t在该
面上均匀分布。
高中物理奥林匹克竞赛专题连续体 力学
表现为平行截面gt
l l
（10）
b b’ ψ
c c’
Ft
切应角 shearing angular
高中物理奥林匹克竞赛专题连续体 力学
弹性力学是固体力学的重要分支，它研究弹性物体 在外力和其它外界因素作用下产生的变形和内力，也称 为弹性理论。它是材料力学、结构力学、塑性力学和某 些交叉学科的基础，广泛应用于建筑、机械、化工、航 天等工程领域。

《连续介质力学》例题和习题第一章 矢量和张量分析第一节 矢量与张量代数一、矢量代数令112233A A A =++A e e e ,112233B B B =++B e e e ,则有112233A A A αααα=++A e e e111222333()()()A B A B A B +=+++++A B e e e112233112233112233()()A A A B B B A B A B A B •=++•++=++A B e e e e e e112233112233111112121313212122222323313132323333()() A A A B B B A B A B A B A B A B A B A B A B A B ⨯=++⨯++=⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯A B e e e e e e e e e e e e e e e e e e e e e e e e又因为: 11⨯=e e 0;123⨯=e e e ;132⨯=-e e e ;213⨯=-e e e ;22⨯=e e 0;231⨯=e e e ; 312⨯=e e e ;321⨯=-e e e ;33⨯=e e 0则: 233213113212213(_)()()A B A B A B A B A B A B ⨯=+-+-A B e e e 习题:1、证明下列恒等式：1）[]2()()()()⨯•⨯⨯⨯=•⨯A B B C C A A B C2) [][]()()()()⨯•⨯=•⨯-•⨯A B C D A C D B B C D A2、请判断下列矢量是否线性无关？1232=-+A e e e 23=--B e e 12=-+C e e .其中i e 为单位正交基矢量。

3、试判断[]816549782-⎡⎤⎢⎥=⎢⎥⎢⎥--⎣⎦A 是否有逆矩阵；如有，请求出其逆阵[]1-A 。

二、张量代数例1：令T 是一个张量，其使得矢量a ，b 经其变换后变为2=+Ta a b ，=-Tb a b ，假定一个矢量2=+c a b ，求Tc 。

四、 刚体的角动量原理
刚体→质点系(由无限多个质元构成的连续体)
质点系的角动量原理
M外
dL dt
即L ， tt1 2M 外 dt
同样适用于刚体
五. 刚体的角动量守恒定律
若 M 外 0， L 则 J 常矢量
注意: (1)定轴转动时，M外=0时，J=常量，即刚体保持静止或匀
角速转动。
解：设面密度为σ 取半径为r 宽为dr 的薄圆环,
R O r dr
d m d s 2 rdr
Jr2 d m R r2 2 r2 d r 1 R 4 1 m 2R
0
2
2
（适用圆柱对轴线的转动惯量。）
[例3] 求长为L、质量为m的均匀细棒对图中不同轴的转动惯量。
解：取如图坐标，dm=dx
1. 作用于刚体的力对空间某点A的力矩
M Ar AF
2. 作用于刚体的力对转轴的力矩
z
A
rAF z
(1)力在转动平面内。
M Zr F
o r
大 小 M Zr： F sin
M z有两个方向，Mz有正负
(2)力不在转动平面内。
M Zr F 面
Fz 平行于转轴，对转轴产生的的力矩为零。
F
Ft
(2) Fi 0 不等价 Mi 0
F面
Fn
3. 当有n 个力作用于刚体，则
M zM 1zM 2z M nz
即定轴转动的刚体所受到的对转轴的合力矩应等于各
力对转轴的力矩的代数和。
z
4. 刚体中内力对给定转轴的力矩的 矢量和等于零，只需考虑外力矩 的作用。
O
d rr21
1 f21
f121 2
2
总结

连续介质力学作业（第二章）参考答案1、初始构型和当前构型的转换关系：21122X X x +=，21222X X x +=，33X x = 其中()321,,X X X 为一个物质点在初始构型上的坐标，()321,,x x x 为同一个物质点在当前构型上的坐标。

参考基是~3~2~1,,e e e 标准正交基求：（1）变形梯度F（2）右Cauchy-Green 变形张量C （3）Green 变形张量E（4）初始构型上一向量~33~22~11~e X e X e X X ++=，变形后在当前构型上是~x ，证明~~~~X C X x x ••=•和()~~~~~~2X E X X X x x ••=•−•（5）左Cauchy-Green 变形张量b （6）Almansi 变形张量A解答：（1）⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛3213211001220221X X X x x x （2）⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=•=100232022310012202211001220221TTF F C（3）()⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=−=000041220224121I C E （4）~33~221~121~2222e X e X X e X X x +⎟⎟⎠⎞⎜⎜⎝⎛++⎟⎟⎠⎞⎜⎜⎝⎛+=[]~~3213212321222123221221~~100023202232223232222XC X X X X X X X X X X X X X X X X X x x ••=⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=+++=+⎟⎟⎠⎞⎜⎜⎝⎛++⎟⎟⎠⎞⎜⎜⎝⎛+=• []()~~321321212221~~~~210002120221222121XE X X X X X X X X X X X X X x x ••=⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=++=•−• （5）⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=1001220221F ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡•⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=•=1000232022310012202211001220221TTF F b（6）()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡−−=−=−10005.2220225.2211b I A2、一个连续体内的任意一点，初始时刻坐标为()Y X ,，经过t 时刻后，变为()y x ,，其中：atY X x +=，Y y = ，其中a 是常数。

第一章 连续体力学思考题1-1 在固体的形变中，弹性模量是一个重要的参数。

杨氏模量的物理意义是什么？答：对于一般的固体材料，若形变不超过一定的限度，应力与相关的应变成正比。

在拉伸应变中l l Y∆＝拉σ 其中，比例系数Y 称为杨氏模量。

弹性模量实际上反映了材料对形变的抵抗能力。

在拉伸应变中，杨氏模量反映了材料对拉伸形变的抵抗能力。

1-2 生物材料的应力～应变关系与一般固体的应力～应变关系有什么不同？答：晶体材料的原子排列很有规则，原子间的键合比较紧密，可以产生较大的应力，杨氏模量一般较高；而生物材料绝大多数是由非均匀材料组成的聚合物，这些聚合物的长链大分子互相纠缠在一起，彼此之间相互作用较弱。

当受到外力拉伸时，不仅生物材料的分子本身可以伸长，而且分子之间也容易发生滑动，杨氏模量相对较小。

1-3 液体的表面张力与橡胶弹性膜的收缩力有什么不同？答：前者来源于分子间的吸引力，后者来源于分子的形变；前者只存在于液体表面，后者存在于发生应变的弹性膜的整个横截面上。

1-4 图1-1中表示土壤中的悬着水，其上、下两液面都与大气接触。

已知 上、下液面的曲率半径分别为A R 和B R (B R >A R )，水的表面张力系数为γ，密度为ρ。

问悬着水高度h 为多大？解：在上液面下取A 点，设该点压强为A p ，在下液面内取B 点，设该点压强为B p 。

对上液面应用拉普拉斯公式，得AA R p p γ20=- 对下液面使用拉普拉斯公式，得 BB 02R p p γ=- 图1-1 土壤中的悬着水 又因为gh p p ρ+=A B 将三式联立求解可得⎪⎪⎭⎫ ⎝⎛-=B A 112R R g h ργ1-5 在自然界中经常会发现一种现象，在傍晚时地面是干燥的，而在清晨时地面却变得湿润了。

试解释这种现象的成因。

答：由于水的表面张力系数与温度有关，毛细水上升的高度会随着温度的变化而变化，温度越低，毛细水上升的高度越高。

力学试题及答案解析一、单项选择题（每题2分，共20分）1. 以下哪个选项是力的三要素？A. 大小、方向、作用点B. 大小、方向、速度C. 大小、速度、作用点D. 方向、速度、作用点答案：A解析：力的三要素包括力的大小、方向和作用点。

这三个要素共同决定了力的作用效果。

2. 牛顿第一定律描述的是：A. 物体在没有外力作用下的运动状态B. 物体在受到平衡力作用下的运动状态C. 物体在受到非平衡力作用下的运动状态D. 物体在受到任意力作用下的运动状态答案：A解析：牛顿第一定律，也称为惯性定律，描述了物体在没有外力作用时，将保持静止或匀速直线运动的状态。

3. 以下哪个选项是重力的方向？A. 垂直向上B. 垂直向下C. 水平方向D. 任意方向答案：B解析：重力是地球对物体的吸引力，其方向总是垂直向下。

4. 以下哪个选项是摩擦力产生的条件之一？A. 两物体间有相对运动B. 两物体间有相对运动趋势C. 两物体间有接触D. 两物体间有接触且有相对运动趋势答案：D解析：摩擦力产生的条件包括两物体间有接触、有相对运动趋势以及两物体间存在粗糙表面。

5. 以下哪个选项是动量守恒定律的表述？A. 系统内力远大于外力时，系统动量守恒B. 系统外力为零时，系统动量守恒C. 系统内力远小于外力时，系统动量守恒D. 系统外力不为零时，系统动量不守恒答案：B解析：动量守恒定律指出，当系统所受外力为零时，系统的总动量保持不变。

6. 以下哪个选项是动能的单位？A. 焦耳B. 牛顿C. 瓦特D. 帕斯卡答案：A解析：动能的单位是焦耳（J），它是能量的单位。

7. 以下哪个选项是机械能守恒的条件？A. 只有重力做功B. 只有弹力做功C. 只有重力和弹力做功D. 只有重力、弹力和摩擦力做功答案：C解析：机械能守恒的条件是系统内只有重力和弹力做功，没有其他形式的能量转换。

8. 以下哪个选项是胡克定律的表述？A. 弹簧的弹力与形变量成正比B. 弹簧的弹力与形变量成反比C. 弹簧的弹力与形变量的平方成正比D. 弹簧的弹力与形变量的平方成反比答案：A解析：胡克定律表明，在弹性限度内，弹簧的弹力与形变量成正比。

J z杆 = ∫
3l / 4
−l / 4
r 2 dm = ∫
3l / 4
−l / 4
3l / 4 −l / 4
=
7 ml 2 48
（3）由转动定理
M z = Jzβ ⇒ β =
M z 36 g = Jz 37l
1-3、有一质量为 m1、 m2（m1>m2）两物体分别悬挂在两个半径不同的组 合轮上，如图。求物体的加速度及绳的张力，大，小两轮间无相对运动， 且半径分别为 R、r，转动惯量分别为 J1、J2， 。轮和轴间无摩擦。 解：设垂直于纸面向里为力矩 的正方向，又大小轮之间无相对运动， 则它们具有共同的角加速度β，由转动定理得：
p A + ρv A + ρghA = p B + ρghB , 2 hA = hB , vB = 0, 1 2 ⇒ ρv A = pB − p A 2 2 ρ ′gh ∴ vA = = 56.4m / s ρ
（J 杆1 + 2 J 物1）ω 1 = （J 杆 2 + 2 J 物 2）ω 2 1 1 ⇒ ( m1l 2 + 2m 2 r12 )ω 1 = ( m1l 2 + 2m 2 r22 )ω 2 12 12 ⇒ ω 2 = 6rad / s
（2）两个小物体飞离棒的瞬间时，系统的角动量仍然守恒，但物体飞离，仅剩下杆的转 动惯量，所以
1 2 ρv2 = ρgh 2 2( H − h) ∴ x = v2 t = 2 gh ⋅ g
解：（1）
v2 = 2 gh
= 2 h( H − h)
5
（2）设在水面下 y 处再开一小孔，则有
2 y ( H − y ) = 2 h( H − h)

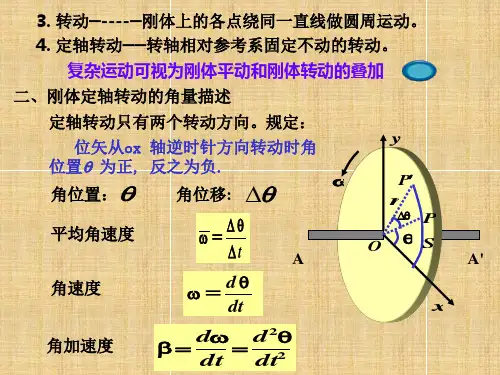
第一章 连续体力学一、本章重难点1、刚体定轴转动的特点及描述刚体定轴转动的各个物理量。

理解线量与角量的关系。

2、力矩、转动动能、转动惯量、刚体定轴转动定理。

3、角动量，刚体定轴转动的角动量定律、角动量守恒定律4、应力、应变的概念，应变的几种形式5、理解应力与应变的关系，弹性模量6、流体、理想流体、流线和流管、定常流动7、流体的连续性方程、伯努利方程8、泊肃叶定律9、层流、湍流、雷诺数10、粘性流体的伯努利方程、斯托克斯定律11、弯曲液面的附加压强（球形液面、柱形液面） 12、毛细现象、润湿和不润湿现象、气体栓塞二、课后习题解答1-1、一飞轮直径为0.2m ，质量为5.00kg ，t 边缘饶一轻绳，现用恒力拉绳子的一端，使其有静止均匀地加速，经0.50s 转速达10转/s 。

假定飞轮可看作实心圆柱体。

求； （1） 飞轮的角加速度及在这段时间转过的转数 （2） 拉力及拉力所做的功（3） 从拉动后t=10s 时飞轮的角速度及边缘上一点的速度和切向加速度及发向速度。

解： ,/1058.1,/6.12,/126,/1026.1)3(3.4921212125232202s m r a s m r a s m r v s t J J J J A t n t t z z z ⨯======⨯====-=ωβωβωωωωτN mr F mr J rF M F r M n t s rad t t z z z 4.31212190,25.2221/6.125)1(20==∴===⇒=⨯===⇒===⇒=βββθπθβθωββωϖϖϖ）（转1-2、有一根长为l 、质量为m 的匀质细杆，两端各牢固的连接一个质量为m 的小球，整个系统可绕一过O 点并垂直于杆的水平轴无摩察的转动，如图。

当系统转到水平位置时，求： （1） 系统所受的和力矩 （2） 系统的转动惯量 （3） 系统的角加速度解： （1）设垂直纸面向里为z 轴的正方向（即力矩的正方向），合力矩为两小球及杆的重力矩之和。

牛顿第二定律的应用――― 连接体问题【自主学习】一、连接体与隔离体两个或两个以上物体相连接组成的物体系统，称为 。

如果把其中某个物体隔离出来，该物体即为 。

二、外力和内力如果以物体系为研究对象，受到系统之外的作用力，这些力是系统受到的 力，而系统内各物体间的相互作用力为 。

应用牛顿第二定律列方程不考虑 力。

如果把物体隔离出来作为研究对象，则这些内力将转换为隔离体的 力。

三、连接体问题的分析方法1.整体法：连接体中的各物体如果 ，求加速度时可以把连接体作为一个整体。

运用 列方程求解。

2.隔离法：如果要求连接体间的相互作用力，必须隔离其中一个物体，对该物体应用 求解，此法称为隔离法。

3.整体法与隔离法是相对统一，相辅相成的。

本来单用隔离法就可以解决的连接体问题，但如果这两种方法交叉使用，则处理问题就更加方便。

如当系统中各物体有相同的加速度，求系统中某两物体间的相互作用力时，往往是先用 法求出 ，再用 法求 。

【典型例题】例1.两个物体A 和B ，质量分别为m 1和m 2，互相接触放在光滑水平面上，如图所示，对物体A 施以水平的推力F ，则物体A 对物体B 的作用力等于（ ） A.F m m m 211+ B.F m m m 212+ C.FD.F m21扩展：1.若m 1与m 2与水平面间有摩擦力且摩擦因数均为μ则对B 作用力等于。

2.如图所示，倾角为α的斜面上放两物体m 1和m 2，用与斜面平行的力F 推m 1，使两物加速上滑，不管斜面是否光滑，两物体 之间的作用力总为 。

例2.如图所示，质量为M 的木板可沿倾角为θ的光滑斜面下滑， 木板上站着一个质量为m 的人，问（1）为了保持木板与斜面相班级 姓名对静止，计算人运动的加速度？（2）为了保持人与斜面相对静止， 木板运动的加速度是多少？【针对训练】1.如图光滑水平面上物块A 和B 以轻弹簧相连接。

在水平拉力F 作用下以加速度a 作直线运动，设A 和B 的质量分别为m A 和m B ，当突然撤去外力F 时，A 和B 的加速度分别为（ ） A.0、0B.a 、0C.B A A m m a m +、B A A m m am +-D.a 、a m m BA-2.如图A 、B 、C 为三个完全相同的物体，当水平力F 作用 于B 上，三物体可一起匀速运动。

（3）金属液体(metallic liquid)：液体的导电性和导 热性都很好 。
（4）量子液体(quantum liquid) ：超流体(super liquid)， 超流体的黏滞性很小，是一种量子化效应。
水（H2O ）：水分子是极性分子 ，是溶剂。
怎么描写状态？
状态state 状态参量 状态方程 固体（刚体，如汽车）：位置坐标，速度或动量， 牛顿方程 液体，气体：温度（热学描述）、压力（力学描 述）、体积（几何描述）；液体状态方程，气体 状态方程 电子：微观粒子，态函数，不确定关系
p
dF ds
;
dF pds pady a gydy
F b a gydy 1 gab2
0
2
水闸
1.2.2液体的表面张力
液体自发收缩 成球的现象
莲叶的微观世界
由于表面张力水面像张开的网
它们为什么可以 漂在水面上 水黾shuǐ mǐn
1.2.2液体的表面张力
1、分子力
F r0~1010m
pApBgh
y pp x
z mg p
Fy 0
简单证明
B
yB yA A
Fy pxz ( p+p)xz mg
pxz ( p+p)xz xyz g 0
p y g; p g; dp g;dp gdy
y
dy
pB
yB
dp gdy; pB pA g(yB yA); pA pB gh
液体的结构特征是近程有序、远程无序。
液体的分类：
（1）极性液体(polar liquid)：由带极性的分子组成的液体。 这种液体分子的正负电部分不相重合而使分子具有极性。
（2） 非极性液体(non-polar liquid)又称范德瓦耳斯液体。 特征是液体的分子不带电荷或没有极性,分子之间主要依靠 微弱的分子力联系起来。

1 欧氏矢量空间 正交 变换 张量(一) 概念、理论和公式提要1-1 欧氏矢量空间 基和基矢 (1) 欧氏矢量空间满足下列条件的矢量集合称为实的矢量空间，记作R R ，中的每一个矢量，例如R w v u 称为、、的一个元素： (a) 的一个元素，且有为R v u + )()(w v u w v u ++=++(b) u R u o u o R 中的任何元素。

对于，使得中包含零矢量=+，存在一个反元素)(u -，使得o u u =-+)((c) 对于任意实数βα、，有为单位值，11)()()()(u u vu v u uu u uu =+=++=+=αααβαβααββα满足下列条件的实矢量空间称为欧氏矢量空间(Euclidean vector space)，记作E ：(a) 对v u v u E ⋅，可定义一个标量、是中的任意一对元素，它具有下列性质：u v v u ⋅=⋅ (1-1-1)0≥⋅u u (1-1-2)等号只当o u =时成立。

(b) 对任意实数w v u E ，，中的元素及、βα等，有w v w u w v u ⋅+⋅=⋅+βαβα)( (1-1-3)(c) u u 的大小或模记为，并定义为u u u ⋅=2（1-1-4）的正方根。

如果u u ，则称1=为单位矢量。

如果v u o v u v u 与，则称，，且≠≠=⋅00正交。

(2) 基 正交基(a) 空间E 内线性无关矢量的最大个数E E 维空间的维数，称为空间n n 记为n E 。

由于连续体占有三维物理空间，所以我们一般地是在三维物理空间内讨论问题。

(6) 在3E 内，定义θcos v u v u =⋅ (1-1-5) k v u v u θsin =⨯ (1-1-6)式中v u k v u ⨯≤≤为单位矢，它表示，的夹角和为)0(πθθ的方向；通常采用右手螺旋法则确定k v u k 、、，即按顺序符合右手法则，且v u k 和正交所在平面；所以v u v u 和是一个正交于⨯的矢量，其指向由右手法则确定。

& k0 2 0 0 0 0 & r , W = − k 0 0 2 0 0 & k0 2 0 0 0 0 0
2-12
& 0 k 0 r L = 0 0 0 0
0 0 0
0 & r k0 D= 2 0
r
=−
2 27 = 318 81
(3)ν , µ 两方向上直角的改变量 γ νµபைடு நூலகம்
r X 2 物质速度 V = 2 X 0
2-6
0 r 3 + X 3 t X 2 − X 3 −t e − e 空间速度 v = x 2 2 x 2 + X 3 t X 2 − X 3 −t e + e 2 2
2 0 − 2 0 0 0 r r ，小转动 Ω = 0 0 1 ，小转动张量的 e= 0 2 1 − 2 1 0 0 − 1 0
− 1 反偶矢量为 ω = 0 0
r
(2)ν 方向上的线应变 eνν
r r
2 1 + k 0 0 r r rT 0 , B = F ⋅ F = k 0 0 1
k0 1 0
0 0 1
2 2 C B C I 1C = I 1B = 3 + k 0 , I 2 = I 2 = 3 + k 0 , I 3 = I 3B = 1
2-4
(1)小应变
0 r 2 格朗日加速度场 A = 2 X 6 X 3 (1 + t ) r D= − 0 0 0 A 3 2 3 − 2 − A 0 r A , W = 0 − 3 A −A 2 3 A 2 9 0 − A 2 9 A 0 2 0