反射系数和透射系数
- 格式:ppt
- 大小:3.67 MB
- 文档页数:92


P 波入射Zoeppritz 方程的推导根据弹性力学的假设,介质是均匀各向同性的无限大介质,平面波是一种最简单的波动形式,其以波面为平面的形式在介质中传播,即平面波在垂直于波传播的任一平面上,各点的振动是同相的,实际上并不存在激发平面波的震源,所以它是一个数学抽象了的波动过程。
点震源激发的球面波向四面八方传播,当其距震源足够远时,在这个地方研究一个局部的等相位面,可以将其看成一个平面波。
在理论上,任何类型的波都可以用平面波的合成形式来表示,所以平面波是波动现象中最基本的形式,也是理论研究和实际应用的基础。
在地震勘探中,讨论在两种不同的介质分界面上的波的传播现象是十分重要的。
一般分为两种情况进行讨论,第一种,我们所研究的地球介质按其物性变化是分层的,具有层装结构。
因此,讨论两种弹性性质不同的介质分界面上波的传播情况。
第二种,地球表面是一个特殊的分界面,它将无限介质划分为两个半空间。
地面以上的空气介质,其密度与地面以下的岩石或海平面以下的海水层及岩石层的密度相比可以忽略。
因此,地球表面可以看成是一个弹性半空间表面,称为自由面,其上的应力作用为零。
根据本文所讨论的地质模型所涉及到的地质灾害,我们只讨论波在第一种介质分界面情况下波的传播,即平面波在弹性分界面上的反射与透射。
1.1波函数设有一平面谐纵波入射到两种半无限弹性介质的分界面上。
在这种情况下,波不仅会折回到入射介质中传播,而且会透射到另一种介质中传播;即同时存在反射波和透射射波。
反射波和透射波中都包含纵波和横波两种成份。
P 波在介质分界面上的反射和透射情况如图所示:关于位函数我们首先看:沿任意方向传播的平面波。
设N 是一个任意取定的单位方向矢量。
N li mj nk =++ (1) 下面来看沿N 方向的平面波,或称三维平面波的波函数形式。
三维平面波的波函数f 满足三维波动方程,即:2222222221f f f fx y z V t ∂∂∂∂++=∂∂∂∂ (2) 这里我们通过和一维平面波函数类比,可以得出三维平面波函数的形式。

电磁波的反射和透射电磁波的反射系数和透射系数反射系数(reflectioncoefficient)是指光(入射光)投向物体时,其表面反射光的强度与入射光的强度之比值。
受入射光的投射角度、强度、波长、物体表面材料的性质以及反射光的测量角度等因素影响。
1931年英国帝国化学工业公司(ICI)规定,在入射光的投射角度为45度的情况下,用入射光的强度与此时测得的垂直于客体表面的反射光的强度之比得到的系数值,称为扩散反射系数。
一般来讲,在颜色系列中,黑色的反射系数较小,为0.03;白色的反射系数较大,为0.8。
反射系数反射电压与入射电压之比(Z1-Z0)/(Z1+Z0)折射率T=1-R一、公式电压反射系数:电流反射系数:反射光振幅与入射光振幅的比值,其数值多以百分数表示。
反射系数的平方称为反射率。
在电磁波在介质界面的传播中,透射率为T=1R。
因为所以其中称为终端反射系数。
对均匀无耗传输线,任意点反射系数大小均相等,沿线只有相位按周期变化,其周期为λ/2,因此称反射系数具有λ/2重复性。
反射系数与透射系数(reflection/transmissioncoefficient)当电磁波由一个磁导率为μ1、介电常数为ε1的均匀介质,进入另一个具有磁导率为μ2、介电常数为ε2的均匀介质时,一部分电磁波在界面上被反射回来,另一分电磁波则透射过去。
反射波与透射波的振幅同入射波振幅之比,分别称之为反射系数与透射系数。
斜入射的情况下,利用光学的反射和折射公式极为方便。
但是,在平面波对平面边界垂直人射的情况下,例如在传输线、波导及某些自由波的情形,波阻抗和特性阻抗的概念是有用的。
对于玻璃,反射系数大约为0.3。
其他材料未知。



一、量子力学概述量子力学是描述微观粒子行为的理论物理学科,它是20世纪物理学的重要分支。
量子力学在物理学、化学领域有着广泛的应用,其研究成果对科技发展和人类生活产生了深远的影响。
在量子力学中,透射系数和反射系数是描述粒子在势垒中行为的重要物理量,它们能够量化地表征粒子在势垒中的运动规律。
二、透射系数和反射系数的定义1. 透射系数:透射系数是描述粒子穿过势垒的概率,通常用T来表示。
透射系数的数值范围在0到1之间,表示粒子从势垒的一侧穿过到另一侧的几率大小。
2. 反射系数:反射系数是描述粒子被势垒反射回的概率,通常用R来表示。
反射系数的数值范围也在0到1之间,表示粒子被势垒反射的几率大小。
三、量子力学求解透射系数和反射系数的方法量子力学求解透射系数和反射系数的方法主要有两种,一种是利用薛定谔方程进行求解,另一种是利用量子力学中的传播矩阵求解。
1. 利用薛定谔方程求解:通过求解薛定谔方程,可以得到粒子在势垒中的波函数。
从波函数中可以得到透射系数和反射系数的表达式,进而求解出它们的数值。
2. 利用传播矩阵求解:传播矩阵是量子力学中描述粒子传播和相互作用的重要工具,通过传播矩阵的性质和定义,可以建立起粒子在势垒中的传播过程,从而得到透射系数和反射系数的表达式和数值。
四、量子力学求解透射系数和反射系数的应用1. 材料物理:透射系数和反射系数的求解在材料物理中有着重要应用,可以帮助研究人员理解材料中粒子的行为规律,从而设计出具有特定功能和性能的材料。
2. 半导体器件:在半导体器件中,透射系数和反射系数的求解可以帮助工程师和设计者优化器件的结构和参数,提高器件的性能和稳定性。
3. 化学反应:化学反应中,透射系数和反射系数的求解可以帮助化学家研究反应物质在反应过程中的行为,为合成新的化合物提供理论参考。
五、结语量子力学求解透射系数和反射系数的问题是一个极具挑战性的课题,它涉及到量子力学的基本原理和数学方法,并且在科学研究和工程应用中具有重要的意义。

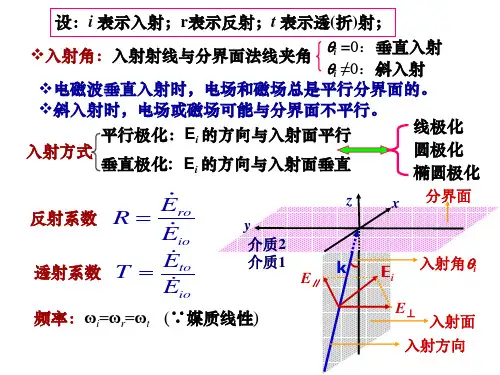

第6章 均匀平面波的反射与透射(一)思考题6.1 试述反射系数和透射系数的定义,它们之间存在什么关系?答:(1)反射波电场振幅E rm与入射波电场振幅E im的比值为分界上的反射系数;透射波电场振幅E tm与入射波电场振幅E im的比值为分界面上的透射系数。
(2)反射系数Γ和透射系数τ之间的关系为:6.2 什么是驻波?它与行波有何区别?答:频率和振幅均相同,振动方向一致,传播方向相反的两列波叠加后形成的波叫驻波。
行波在介质中传播时,其波等相面随时间前移,而驻波的波形不向前推进。
6.3 均匀平面波垂直入射到两种理想媒质分界面时,在什么情况下,反射系数大于0?在什么情况下,反射系数小于0?答:均匀平面波垂直入射到两种理想媒质分界时,当时,反射系数Γ>0;当时,反射系数Γ<0。
6.4 均匀平面波向理想导体表面垂直入射时,理想导体外面的合成波具有什么特点?答:均匀平面波向理想导体表面入射时,理想导体外面的合成波具有特点如下:合成波电场和磁场的驻波在时间上有的相移,在空间上也错开了且在导体边界上,电场为零。
驻波的坡印廷矢量的平均值为零,不发生电磁能量的传输过程,仅在两个波节之间进行电场能量和磁场能量的交换。
6.5 均匀平面波垂直入射到两种理想媒质分界面时,在什么情况下,分界面上的合成波电场为最大值?在什么情况下,分界面上的合成波电场为最小值?答:当均匀平面波垂直入射到两种理想媒质分界面时,的位置时,分界面上的合成波电场为最大值。
的位置时,分界面上的合成波电场为最小值。
6.6 一个右旋圆极化波垂直入射到两种媒质分界面上,其反射波是什么极化波?答:右旋圆极化。
6.7 试述驻波比的定义,它与反射系数之间有什么关系?答:驻波比的定义是合成波的电场强度的最大值与最小值之比,即6.8 什么是波阻抗?在什么情况下波阻抗等于媒质的本征阻抗?答:在空间任意点,均匀平面波的电场与磁场强度的模值之比称为自由空间的波阻抗,在均匀无耗各向同性的无界媒质中,均匀平面波的电场与磁场的模值之比称为媒质中的阻波抗。

当声波碰到室内某一界面后(如天花、墙),一部分声能被反射,一部分被吸收(主要是转化成热能),一部分穿透到另一空间。
透射系数:反射系数:吸声系数:声压和声强有密切的关系,在自由声场中,测得声压和已知测点到声源的距离,就可计算出该测点之声强和声源的声功率。
声压级Lp取参考声压为Po=2*10-5N/m2为基准声压,任一声压P的Lp为:听觉下限: p=2*10-5N/m2 为0dB能量提高100倍的 P=2*10-3N/m2 为20dB听觉上限: P=20N/m2 为120dB2、声功率级Lw取Wo为10-12W,基准声功率级任一声功率W的声功率级Lw为:3、声强级:3、声压级的叠加10dB+10dB=? 0dB+0dB=? 0dB+10dB=? 答案分别是:13dB,3dB,10dB.几个声源同时作用时,某点的声能是各个声源贡献的能量的代数和。
因此其声压是各声源贡献的声压平方和的开根号。
即:声压级为:声压级的叠加•两个数值相等的声压级叠加后,总声压级只比原来增加3dB,而不是增加一倍。
这个结论对于声强级和声功率级同样适用。
•此外,两个声压级分别为不同的值时,其总的声压级为两个声强级获声功率级的叠加公式与上式相同在建筑声学中,频带划分的方式通常不是在线性标度的频率轴上等距离的划分频带,而是以各频率的频程数n都相等来划分。
声波在室内的反射与几何声学3.2.1 反射界面的平均吸声系数(1)吸声系数:用以表征材料和结构吸声能力的基本参量通常采用吸声系数,以α表示,定义式:材料和结构的吸声特性和声波入射角度有关。
声波垂直入射到材料和结构表面的吸声系数,成为“垂直入射(正入射)吸声系数”。
这种入射条件可在驻波管中实现。
其吸声系数的大小可通过驻波管法来测定。
当声波斜向入射时,入射角度为θ,这是的吸声系数称为斜入射吸声系数,。
建筑声环境中,出现垂直入射和斜入射的情况较少,而普遍情况是声波从各个方向同时入射到材料和结构表面,如果入射声波在半空间中均匀分布,,则称这种入射情况为“无规则入射”或“扩散入射”。

量子力学是描述微观世界行为的理论框架,它是由著名的物理学家波恩和海森堡等人提出的。
量子力学理论对于解释微观粒子的行为有着重要的作用,其中求解透射系数和反射系数是量子力学中的一个重要问题。
在量子力学中,通过求解delta势的透射系数和反射系数可以帮助我们理解粒子在势场中的行为,也有利于我们了解粒子在势场中的传播规律。
下面我们将简要介绍一下求解透射系数和反射系数delta 势的过程。
1. 理论基础在量子力学中,我们知道波函数是描述微观粒子状态的函数。
对于在势场中运动的粒子,我们可以通过求解薛定谔方程来得到其波函数。
而delta势是一种理想化的势场模型,它在某一点上突变为一个无限大的数值。
对于delta势场中的粒子,我们可以通过求解薛定谔方程得到其波函数,并进而求解透射系数和反射系数。
2. 求解透射系数和反射系数的方法在求解透射系数和反射系数时,我们首先需要得到delta势场中的波函数。
通过求解薛定谔方程,我们可以得到波函数的形式。
我们可以利用波函数的连续性条件,得到不同区域中波函数的形式。
在定解问题后,我们可以利用波函数和其一阶导数的连续性条件,解出透射系数和反射系数的表达式。
根据透射系数和反射系数的定义,我们可以得到它们的具体表达式。
通过数值计算或者物理实验,我们可以验证我们得到的透射系数和反射系数的正确性。
3. 物理意义和应用求解透射系数和反射系数的结果对于研究粒子在势场中的行为有着重要的意义。
透射系数和反射系数可以帮助我们了解粒子在势场中的传播规律,可以帮助我们研究势场对于粒子运动的影响。
透射系数和反射系数的研究也对于材料科学和能源领域有着重要的应用。
通过研究材料的透射系数和反射系数,我们可以了解材料对于粒子的吸收和散射的特性,可以帮助我们设计新型的材料和能源材料。
4. 结论通过以上介绍,我们可以看出,求解透射系数和反射系数对于理解量子力学中的势场问题有着重要的意义。
通过求解薛定谔方程和利用波函数连续性条件,我们可以得到透射系数和反射系数的具体表达式。
P波入射Zoeppritz方程的推导根据弹性力学的假设,介质是均匀各向同性的无限大介质,平面波是一种最简单的波动形式,其以波面为平面的形式在介质中传播,即平面波在垂直于波传播的任一平面上,各点的振动是同相的,实际上并不存在激发平面波的震源,所以它是一个数学抽象了的波动过程。
点震源激发的球面波向四面八方传播,当其距震源足够远时,在这个地方研究一个局部的等相位面,可以将其看成一个平面波。
在理论上,任何类型的波都可以用平面波的合成形式来表示,所以平面波是波动现象中最基本的形式,也是理论研究和实际应用的基础。
在地震勘探中,讨论在两种不同的介质分界面上的波的传播现象是十分重要的。
一般分为两种情况进行讨论,第一种,我们所研究的地球介质按其物性变化是分层的,具有层装结构。
因此,讨论两种弹性性质不同的介质分界面上波的传播情况。
第二种,地球表面是一个特殊的分界面,它将无限介质划分为两个半空间。
地面以上的空气介质,其密度与地面以下的岩石或海平面以下的海水层及岩石层的密度相比可以忽略。
因此,地球表面可以看成是一个弹性半空间表面,称为自由面,其上的应力作用为零。
根据本文所讨论的地质模型所涉及到的地质灾害,我们只讨论波在第一种介质分界面情况下波的传播,即平面波在弹性分界面上的反射与透射。
1.1波函数设有一平面谐纵波入射到两种半无限弹性介质的分界面上。
在这种情况下,波不仅会折回到入射介质中传播,而且会透射到另一种介质中传播;即同时存在反射波和透射射波。
反射波和透射波中都包含纵波和横波两种成份。
P 波在介质分界面上的反射和透射情况如图所示:关于位函数我们首先看:沿任意方向传播的平面波。
设N r是一个任意取定的单位方向矢量。
N li mj nk =++r r r r(1)下面来看沿N r方向的平面波,或称三维平面波的波函数形式。
三维平面波的波函数f 满足三维波动方程,即:2222222221f f f fx y z V t∂∂∂∂++=∂∂∂∂(2)这里我们通过和一维平面波函数类比,可以得出三维平面波函数的形式。
第七章 平面电磁波的反射和透射 习题解答7-1.空气中的平面电磁波电场幅值为10V/m ,垂直入射到εr =25的无耗非磁性介质的表面,试确定:(1)反射系数和透射系数;(2)在空气中的驻波比;(3)入射波、反射波和透射波的平均功率流密度。
解 (1)由于空气和无耗非磁性介质的磁导率为120μμμ=≈所以,空气和无耗非磁性介质中的波阻抗分别为()()12120120245;πηπηπ==Ω====Ω 由此得到垂直入射情况下,两理想介质分界面的反射系数和透射系数为 2121241200.6724120r ηηππηηππ--==≈-++22122240.3324120t ηπηηππ⨯==≈++(2)驻波比定义为 11max minE r SE r由此得到空气中的驻波比为 1106750611067r .S.r .(3)假定电场矢量沿x e 方向,入射波沿+Z 方向传播,则可写出垂直入射情况下,入射波、反射波和透射波的电场和磁场复振幅矢量表达式为()()()1110110001111i i i i jk zi x jk z jk zi i z x y E e E e E e z z z e e e e E H k E ηηη---⨯⎧=⎪⎨=⨯=⎩=⎪ ()()()()1110000111111r r jk zr x jk z jk zr r r r z x y z z z E e E e E e e e e e E H k E ηηη-⎧=⎪⎨=⨯⨯=⎪-⎩= ()()()2220220002111t t tt jk z t x jk z jk zt t z x y E e E e E e z z z e e e e E H k E ηηη---⨯⎧=⎪⎨=⨯=⎩=⎪ 根据平均功率流密度的定义式*1Re 2av S E H ⎡⎤=⨯⎣⎦ 有11*2*10010111Re Re 2212jk z jk zi i i i av i i x y z E e E e E S E H e e e ηη--⎡⎤⎛⎫⎡⎤⎢⎥=⨯=⨯= ⎪⎣⎦⎢⎥⎝⎭⎣⎦()111*2*0010111Re Re 2221jk z jk zr r r r av r r x y z E e E e E S E H e e e ηη⎡⎤⎛⎫⎡⎤⎢⎥=⨯=⨯-=- ⎪⎣⎦⎢⎥⎝⎭⎣⎦ 22*2*20020111Re Re 2212jk z jk z t t t tav t t x y z E e E e E S E H e e e ηη--⎡⎤⎛⎫⎡⎤⎢⎥=⨯=⨯= ⎪⎣⎦⎢⎥⎝⎭⎣⎦而1200012024106733i r iti ;;EV /m ;E rE .V /m ;EtE.V /m数值代入得到()212011000.13/2iav zz W m S e e π=⨯≈⨯()221 6.70.06/2120rav z z W m S e e π=-⨯-≈-⨯()221 3.30.07/224tav z z W m S e e π=≈⨯7-4.一均匀平面电磁波沿+Z 方向传播,其电场强度矢量为()()()100sin 200cos V/m x y t kz t kz ωω=-+-E e e(1)应用麦克斯韦方程求相伴的磁场H ;(2)若在传播方向上z =0处放置一无限大的理想导体板,求z <0区域中的合成波的电场E 1和磁场H 1;(3)求理想导体板表面的电流密度。