2 7.1.2 复数的几何意义

【人教A版】高中数学必修第二册第七章7．1.2 复数的几何意义教学设计(教师独具内容)课程标准：理解复数的几何意义．教学重点：复数的几何意义、复数的模的概念及共轭复数的概念．教学难点：复数的几何意义的理解与应用．核心素养：1.通过复数、复平面内的点、复平面内的向量之间的对应关系培养直观想象素养.2.通过求复数的模及求一个复数的共轭复数培养数学运算素养.共轭复数的性质(1)两个共轭复数的对应点关于实轴对称．(2)实数的共轭复数是它本身，即z＝z－⇔z∈R.利用这个性质，可以证明一个复数是实数．(3)z z－＝|z|2＝|z－|2∈R.z与z－互为实数化因式．1．判一判(正确的打“√”，错误的打“×”)(1)在复平面内，对应于实数的点都在实轴上．( )(2)在复平面内，虚轴上的点所对应的复数都是纯虚数．( )(3)复数的模一定是正实数．( )(4)两个复数互为共轭复数是它们的模相等的必要条件．( )2．做一做(1)若OZ→＝(0，－3)，则OZ→对应的复数为____.(2)复数z＝1－4i位于复平面上的第____象限．(3)复数3i的模是____.(4)复数5＋6i的共轭复数是____.题型一复数与复平面内的点例1 在复平面内，若复数z＝(m2－m－2)＋(m2－3m＋2)i对应点(1)在虚轴上；(2)在第二象限；(3)在直线y＝x上，分别求实数m的取值范围． [跟踪训练1] 实数m取什么值时，复数z＝(m2＋5m＋6)＋(m2－2m－15)i.(1)对应的点在x轴上方；(2)对应的点在直线y＝－x上．题型二复数与复平面内的向量例2 已知平行四边形OABC的三个顶点O，A，C对应的复数分别为0,3＋2i，－2＋4i，试求：(1)AO→表示的复数；(2)CA→表示的复数；(3)点B对应的复数． [跟踪训练2] (1)复数4＋3i与－2－5i分别表示向量OA→与OB→，则向量AB→表示的复数是____.(2)在复平面内的长方形ABCD的四个顶点中，点A，B，C对应的复数分别是2＋3i,3＋2i，－2－3i，求点D对应的复数．题型三复数的模例3 设z∈C，则满足条件|z|＝|3＋4i|的复数z在复平面内对应的点Z的集合是什么图形？[跟踪训练3] 设z∈C，且满足下列条件，在复平面内，复数z对应的点Z 的集合是什么图形？(1)1<|z|<2；(2)|z－i|<1.1．已知a∈R，且0<a<1，i为虚数单位，则复数z＝a＋(a－1)i在复平面内所对应的点位于( )A．第一象限B．第二象限C．第三象限D．第四象限2．(多选)若复数z＝(a2－2a)＋(a2－a－2)i对应的点Z在虚轴上，则a的值可以是( )A．0 B．1C．2 D．33．若复数z1＝2＋b i与复数z2＝a－4i互为共轭复数，则a＝____，b＝____.4．已知复数z＝3＋a i，且|z|<5，则实数a的取值范围是____.5．如果复数z＝(m2＋m－1)＋(4m2－8m＋3)i(m∈R)对应的点在第一象限，求实数m的取值范围．一、选择题1．复数z1＝1＋3i和z2＝1－3i在复平面内的对应点关于( )A．实轴对称B．一、三象限的角平分线对称C．虚轴对称D．二、四象限的角平分线对称2．当23<m<1时，复数z＝(3m－2)＋(m－1)i的共轭复数在复平面内对应的点位于( )A．第一象限B．第二象限C．第三象限D．第四象限3．复数z1＝a＋2i，z2＝－2＋i，如果|z1|<|z2|，则实数a的取值范围是( ) A．－1<a<1 B．a>1C．a>0 D．a<－1或a>04．(多选)若|4＋25i|＋x＋(3－2x)i＝3＋(y＋5)i(i为虚数单位)，其中x，y是实数，则( )A．x＝3 B．y＝4C．x＋y i＝－3＋4i D．|x＋y i|＝55．已知复数z满足|z|2－2|z|－3＝0，则复数z对应点的轨迹是( )A．1个圆B．线段C．2个点D．2个圆二、填空题6．i为虚数单位，设复数z1，z2在复平面内对应的点关于原点对称，若z1＝2－3i，则z－2＝____.7．已知复数(2k2－3k－2)＋(k2－k)i在复平面内对应的点在第二象限，则实数k的取值范围是____.8．已知复数z1＝－1＋2i，z2＝1－i，z3＝3－2i，它们所对应的点分别是A，B，C，若OC→＝xOA→＋yOB→(x，y∈R)，则x＋y的值是____.三、解答题9．已知复数z＝(1＋2m)＋(3＋m)i(m∈R)．(1)若m＝1，且|z－|＝|x＋(x－1)i|，求实数x的值；(2)当m为何值时，|z－|最小？并求|z－|的最小值．1．在复平面上，复数i,1,4＋2i对应的点分别是A，B，C，求平行四边形的ABCD的点D对应的复数．2．已知x为实数，复数z＝x－2＋(x＋2)i.(1)当x为何值对，复数z的模最小？(2)当复数z的模最小时，复数z在复平面内对应的点Z位于函数y＝－mx＋n的图象上，其中mn>0，求1m＋1n的最小值及取得最小值时m，n的值．7．1.2 复数的几何意义(教师独具内容)课程标准：理解复数的几何意义．教学重点：复数的几何意义、复数的模的概念及共轭复数的概念．教学难点：复数的几何意义的理解与应用．核心素养：1.通过复数、复平面内的点、复平面内的向量之间的对应关系培养直观想象素养.2.通过求复数的模及求一个复数的共轭复数培养数学运算素养.共轭复数的性质(1)两个共轭复数的对应点关于实轴对称．(2)实数的共轭复数是它本身，即z＝z－⇔z∈R.利用这个性质，可以证明一个复数是实数．(3)z z－＝|z|2＝|z－|2∈R.z与z－互为实数化因式．1．判一判(正确的打“√”，错误的打“×”)(1)在复平面内，对应于实数的点都在实轴上．( )(2)在复平面内，虚轴上的点所对应的复数都是纯虚数．( )(3)复数的模一定是正实数．( )(4)两个复数互为共轭复数是它们的模相等的必要条件．( )答案(1)√(2)×(3)×(4)×2．做一做(1)若OZ→＝(0，－3)，则OZ→对应的复数为____.(2)复数z＝1－4i位于复平面上的第____象限．(3)复数3i的模是____.(4)复数5＋6i的共轭复数是____.答案(1)－3i (2)四(3) 3 (4)5－6i题型一复数与复平面内的点例1 在复平面内，若复数z＝(m2－m－2)＋(m2－3m＋2)i对应点(1)在虚轴上；(2)在第二象限；(3)在直线y ＝x 上，分别求实数m 的取值范围．[解] 复数z ＝(m 2－m －2)＋(m 2－3m ＋2)i 的实部为m 2－m －2，虚部为m 2－3m ＋2.(1)由题意得m 2－m －2＝0，解得m ＝2或m ＝－1. (2)由题意得⎩⎨⎧m 2－m －2<0，m 2－3m ＋2>0，∴⎩⎨⎧－1<m <2，m >2或m <1，∴－1<m <1.(3)由已知得m 2－m －2＝m 2－3m ＋2，∴m ＝2.复数集与复平面内所有的点组成的集合之间存在着一一对应关系．每一个复数都对应着一个有序实数对，复数的实部对应着有序实数对的横坐标，而虚部则对应着有序实数对的纵坐标，只要在复平面内找到这个有序实数对所表示的点，就可根据点的位置判断复数实部、虚部的取值．[跟踪训练1] 实数m 取什么值时，复数z ＝(m 2＋5m ＋6)＋(m 2－2m －15)i. (1)对应的点在x 轴上方； (2)对应的点在直线y ＝－x 上． 解 (1)由题意得m 2－2m －15>0， 解得m <－3或m >5，所以当m <－3或m >5时，复数z 对应的点在x 轴上方．(2)由题意，得m 2－2m －15＝－(m 2＋5m ＋6)，整理，得2m 2＋3m －9＝0，解得m ＝32或m ＝－3.所以当m ＝32或m ＝－3时，复数z 对应的点在直线y ＝－x 上.题型二 复数与复平面内的向量例2 已知平行四边形OABC 的三个顶点O ，A ，C 对应的复数分别为0,3＋2i ，－2＋4i ，试求：(1)AO →表示的复数；(2)CA →表示的复数；(3)点B 对应的复数．[解] 由题意得O 为原点，OA →＝(3,2)，OC →＝(－2,4)． (1)∵AO →＝－OA →＝－(3,2)＝(－3，－2)∴AO →表示的复数为－3－2i.(2)∵CA →＝OA →－OC →＝(3,2)－(－2,4)＝(5，－2)， ∴CA →表示的复数为5－2i.(3)∵OB →＝OA →＋OC →＝(3,2)＋(－2,4)＝(1,6)， ∴OB →表示的复数为1＋6i ，即点B 对应的复数为1＋6i.复数与平面向量一一对应是复数的另一种几何意义，利用这种几何意义，复数问题可以转化为平面向量来解决，平面向量问题也可以用复数方法来求解．[跟踪训练2] (1)复数4＋3i 与－2－5i 分别表示向量OA →与OB →，则向量AB →表示的复数是____.(2)在复平面内的长方形ABCD 的四个顶点中，点A ，B ，C 对应的复数分别是2＋3i,3＋2i ，－2－3i ，求点D 对应的复数．答案 (1)－6－8i (2)见解析解析 (1)因为复数4＋3i 与－2－5i 分别表示向量OA →与OB →，所以OA →＝(4,3)，OB →＝(－2，－5)，又AB →＝OB →－OA →＝(－2，－5)－(4,3)＝(－6，－8)，所以向量AB →表示的复数是－6－8i.(2)记O 为复平面的原点，由题意得OA →＝(2,3)，OB →＝(3,2)，OC →＝(－2，－3)． 设OD →＝(x ，y )，则AD →＝(x －2，y －3)，BC →＝(－5，－5)． 由题知，AD →＝BC →，所以⎩⎨⎧x －2＝－5，y －3＝－5，即⎩⎨⎧x ＝－3，y ＝－2，故点D 对应的复数为－3－2i. 题型三 复数的模例3 设z ∈C ，则满足条件|z |＝|3＋4i|的复数z 在复平面内对应的点Z 的集合是什么图形？[解] 由|z |＝|3＋4i|得|z |＝5.这表明向量OZ →的长度等于5，即点Z 到原点的距离等于5.因此满足条件的点Z的集合是以原点O为圆心，以5为半径的圆．巧用复数的模的几何意义解题(1)复平面内|z|的意义我们知道，在实数集中，实数a的绝对值，即|a|是表示实数a的点与原点O 间的距离．那么在复数集中，类似地，有|z|是表示复数z的点Z到坐标原点间的距离．也就是向量OZ→的模，|z|＝|OZ→|.(2)复平面内任意两点间的距离设复平面内任意两点P，Q所对应的复数分别为z1，z2，则|PQ|＝|z2－z1|.运用以上性质，可以通过数形结合的方法解决有关问题．[跟踪训练3] 设z∈C，且满足下列条件，在复平面内，复数z对应的点Z 的集合是什么图形？(1)1<|z|<2；(2)|z－i|<1.解(1)根据复数模的几何意义可知，复数z对应的点Z的集合是以原点O为圆心，1和2为半径的两圆所夹的圆环，不包括圆环的边界．(2)根据模的几何意义，|z－i|＝1表示复数z对应的点到复数i对应的点(0,1)的距离为1.∴满足|z－i|＜1的点Z的集合为以(0,1)为圆心，1为半径的圆内的部分(不含圆的边界)．1．已知a∈R，且0<a<1，i为虚数单位，则复数z＝a＋(a－1)i在复平面内所对应的点位于( )A．第一象限B．第二象限C．第三象限D．第四象限答案 D解析∵0<a<1，∴a>0且a－1<0，故复数z＝a＋(a－1)i在复平面内所对应的点(a ，a －1)位于第四象限．故选D.2．(多选)若复数z ＝(a 2－2a )＋(a 2－a －2)i 对应的点Z 在虚轴上，则a 的值可以是( )A ．0B ．1C ．2D ．3答案 AC解析 由点Z 在虚轴上可知，点Z 对应的复数是纯虚数和0，∴a 2－2a ＝0，解得a ＝2或a ＝0.故选AC.3．若复数z 1＝2＋b i 与复数z 2＝a －4i 互为共轭复数，则a ＝____，b ＝____. 答案 2 4解析 因为z 1与z 2互为共轭复数，所以a ＝2，b ＝4.4．已知复数z ＝3＋a i ，且|z |<5，则实数a 的取值范围是____. 答案 －4<a <4解析 |z |＝32＋a 2<5，解得－4<a <4.5．如果复数z ＝(m 2＋m －1)＋(4m 2－8m ＋3)i(m ∈R )对应的点在第一象限，求实数m 的取值范围．解 因为复数z 对应的点在第一象限， 所以⎩⎨⎧m 2＋m －1>0，4m 2－8m ＋3>0，解得m <－1－52或m >32.所以实数m 的取值范围为⎝ ⎛⎭⎪⎫－∞，－1－52∪⎝ ⎛⎭⎪⎫32，＋∞.一、选择题1．复数z 1＝1＋3i 和z 2＝1－3i 在复平面内的对应点关于( ) A ．实轴对称B ．一、三象限的角平分线对称C ．虚轴对称D ．二、四象限的角平分线对称 答案 A解析 复数z 1＝1＋3i 在复平面内的对应点为Z 1(1，3)，复数z 2＝1－3i 在复平面内的对应点为Z 2(1，－3)，点Z 1与Z 2关于实轴对称．2．当23<m <1时，复数z ＝(3m －2)＋(m －1)i 的共轭复数在复平面内对应的点位于( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限答案 A解析 ∵23<m <1，∴2<3m <3，∴0<3m －2<1且－13<m －1<0，∴复数z 在复平面内对应的点位于第四象限．∵一对共轭复数在复平面内对应的点关于实轴对称，∴复数z 的共轭复数在复平面内对应的点位于第一象限．故选A ．3．复数z 1＝a ＋2i ，z 2＝－2＋i ，如果|z 1|<|z 2|，则实数a 的取值范围是( ) A ．－1<a <1 B ．a >1 C ．a >0 D ．a <－1或a >0答案 A解析 依题意有a 2＋22<－22＋12，解得－1<a <1.4．(多选)若|4＋25i|＋x ＋(3－2x )i ＝3＋(y ＋5)i(i 为虚数单位)，其中x ，y 是实数，则( )A ．x ＝3B ．y ＝4C ．x ＋y i ＝－3＋4iD ．|x ＋y i|＝5答案 BCD解析 由已知，得6＋x ＋(3－2x )i ＝3＋(y ＋5)i ， 所以⎩⎨⎧x ＋6＝3，3－2x ＝y ＋5，解得⎩⎨⎧x ＝－3，y ＝4，所以|x ＋y i|＝|－3＋4i|＝5，故选BCD.5．已知复数z 满足|z |2－2|z |－3＝0，则复数z 对应点的轨迹是( ) A ．1个圆B ．线段C ．2个点D ．2个圆答案 A解析 由题意可知(|z |－3)(|z |＋1)＝0，即|z |＝3或|z |＝－1.∵|z |≥0，∴|z |＝3.∴复数z 对应的轨迹是1个圆．二、填空题6．i 为虚数单位，设复数z 1，z 2在复平面内对应的点关于原点对称，若z 1＝2－3i ，则z －2＝____.答案 －2－3i解析 复数z 1＝2－3i 对应的点为(2，－3)，则z 2对应的点为(－2，3)．所以z 2＝－2＋3i ，z －2＝－2－3i.7．已知复数(2k 2－3k －2)＋(k 2－k )i 在复平面内对应的点在第二象限，则实数k 的取值范围是____.答案 －12<k <0或1<k <2解析 根据题意，有⎩⎨⎧2k 2－3k －2<0，k 2－k >0，即⎩⎨⎧－12<k <2，k <0或k >1，所以实数k 的取值范围是－12<k <0或1<k <2.8．已知复数z 1＝－1＋2i ，z 2＝1－i ，z 3＝3－2i ，它们所对应的点分别是A ，B ，C ，若OC →＝xOA→＋yOB →(x ，y ∈R )，则x ＋y 的值是____.答案 5解析 由已知，得OA →＝(－1,2)，OB →＝(1，－1)，OC →＝(3，－2)，∴xOA →＋yOB →＝x (－1,2)＋y (1，－1)＝(－x ＋y,2x －y )．由OC →＝xOA→＋yOB →， 可得⎩⎨⎧－x ＋y ＝3，2x －y ＝－2，解得⎩⎨⎧x ＝1，y ＝4，∴x ＋y ＝5.三、解答题9．已知复数z ＝(1＋2m )＋(3＋m )i(m ∈R )．(1)若m ＝1，且|z －|＝|x ＋(x －1)i|，求实数x 的值；(2)当m 为何值时，|z －|最小？并求|z －|的最小值． 解 (1)由m ＝1，得z ＝3＋4i ，z －＝3－4i ， 则由|z －|＝|x ＋(x －1)i|， 得32＋－42＝x 2＋x －12，整理得x 2－x －12＝0，解得x ＝4或x ＝－3. (2)|z －|＝1＋2m2＋[－3＋m]2＝5m 2＋10m ＋10＝5m ＋12＋5≥ 5，当且仅当m ＝－1时，|z －|取得最小值，最小值为 5.1．在复平面上，复数i,1,4＋2i 对应的点分别是A ，B ，C ，求平行四边形的ABCD 的点D 对应的复数．解 解法一：由已知条件得点A (0,1)，B (1,0)，C (4,2)， 则AC 的中点E ⎝⎛⎭⎪⎫2，32，由平行四边形的性质知点E 也是边BD 的中点，设D (x ，y )，则⎩⎪⎨⎪⎧x ＋12＝2，y ＋02＝32，解得⎩⎨⎧x ＝3，y ＝3，即D (3,3)，∴点D 对应的复数为3＋3i.解法二：由已知得向量OA →＝(0,1)，OB →＝(1,0)，OC →＝(4,2)，其中O 为坐标原点．∴BA →＝(－1,1)，BC →＝(3,2)， ∴BD →＝BA →＋BC →＝(2,3)，∴OD →＝OB →＋BD →＝(3,3)，即点D 对应的复数为3＋3i. 2．已知x 为实数，复数z ＝x －2＋(x ＋2)i. (1)当x 为何值对，复数z 的模最小？(2)当复数z 的模最小时，复数z 在复平面内对应的点Z 位于函数y ＝－mx ＋n的图象上，其中mn>0，求1m＋1n的最小值及取得最小值时m，n的值．解(1)|z|＝x－22＋x＋22＝2x2＋8≥22，当且仅当x＝0时，复数z的模最小，为2 2.(2)当复数z的模最小时，Z(－2,2)．又点Z位于函数y＝－mx＋n的图象上，所以2m＋n＝2.又mn＞0，所以1m＋1n＝⎝⎛⎭⎪⎫1m＋1n⎝⎛⎭⎪⎫m＋n2＝32＋mn＋n2m≥32＋2，当且仅当n2＝2m2,2m＋n＝2时等号成立．所以m＝2－2，n＝22－2.所以1m＋1n的最小值为32＋2，此时m＝2－2，n＝22－2.。

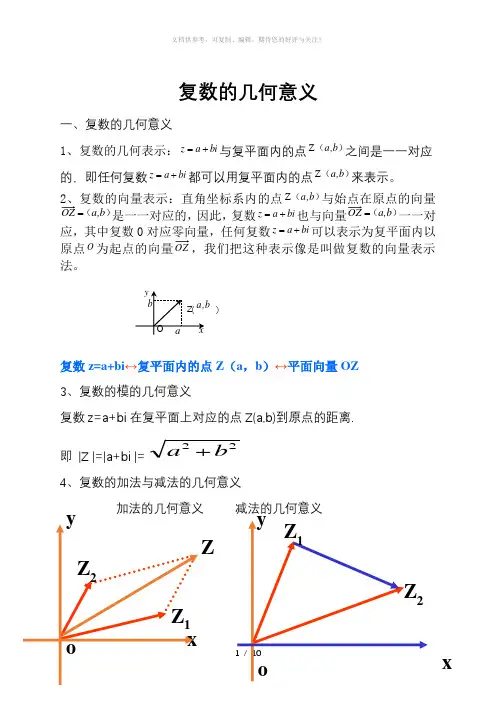
复数的几何意义一、复数的几何意义1、复数的几何表示：bi a z +=与复平面内的点）（b ,a Z 之间是一一对应的，即任何复数bi a z +=都可以用复平面内的点）（b ,a Z 来表示。

2、复数的向量表示：直角坐标系内的点）（b ,a Z 与始点在原点的向量）（b ,a OZ =是一一对应的，因此，复数bi a z +=也与向量）（b ,a OZ =一一对应，其中复数0对应零向量，任何复数bi a z +=可以表示为复平面内以原点O 为起点的向量OZ ，我们把这种表示像是叫做复数的向量表示法。

复数z=a+bi ↔复平面内的点Z （a ，b ）↔平面向量OZ 3、复数的模的几何意义复数z=a+bi 在复平面上对应的点Z(a,b)到原点的距离. 即 |Z |=|a+bi |=22b a +4、复数的加法与减法的几何意义加法的几何意义 减法的几何意义)ZZ 2Z1yz 1z 2≠0时， z 1+z 2对应的向量是以OZ 1、OZ 2、为邻边的平行四边形OZ 1ZZ 2的对角线OZ ， z 2-z 1对应的向量是Z 1Z 2 5、 复数乘法与除法的几何意义z 1=r 1（cos θ1+i sin θ1） z 2=r 2（cos θ2+i sin θ2）①乘法：z=z 1· z 2=r 1·r 2 [cos(θ1+θ2)+i sin(θ1+θ2)]如图：其对应的向量分别为oz oz oz 12→→→显然积对应的辐角是θ1+θ2 < 1 > 若θ2 > 0 则由oz 1→逆时针旋转θ2角模变为oz 1→的r 2倍所得向量便是积z 1·z 2=z 的向量oz →。

< 2 >若θ2< 0 则由向量oz 1→顺时针旋转θ2角模变为r 1·r 2所得向量便是积z 1·z 2=z 的向量oz →。

为此，若已知复数z 1的辐角为α，z 2的辐角为β求α+β时便可求出z 1·z 2=z a z 对应的辐角就是α+β这样便可将求“角”的问题转化为求“复数的积”的运算。

第七章 7.1 7.1.2A 级——基础过关练1．(2019年北京海淀区二模)已知复数z 在复平面上对应的点为(1，－1)，则( ) A ．z ＝－1＋i B ．z ＝1＋i C ．z ＋i 是实数D ．z ＋i 是纯虚数【答案】C 【解析】∵复数z 在复平面上对应的点为(1，－1)，∴z ＝1－i.∴z ＋i ＝1－i ＋i ＝1，即z ＋i 是实数．故选C ．2．已知0<a <2，复数z ＝a －i(i 是虚数单位)，则|z |的取值范围是( ) A ．(1，3) B ．(1，5) C ．(1,3)D ．(1,5)【答案】B 【解析】|z |2＝a 2＋1，∵0<a <2,0<a 2<4⇒1<a 2＋1<5，∴1<|z |< 5.故选B ． 3．(2019年陕西三模)在复平面内，表示复数z ＝5a ＋(6－a 2)i 的点在第二象限，则实数a 满足( )A ．－6<a <0B ．a <－6C ．0<a <6D ．－6<a <6【答案】A【解析】∵z ＝5a ＋(6－a 2)i对应的点在第二象限，∴⎩⎪⎨⎪⎧5a <0，6－a 2>0，解得－6<a <0.故选A ．4．复平面内，向量OA →表示的复数为1＋i ，将OA →向右平移一个单位后得到向量O ′A ′→，则向量O ′A ′→与点A ′对应的复数分别为( )A ．1＋i,1＋iB ．2＋i,2＋iC ．1＋i,2＋iD ．2＋i,1＋i【答案】C 【解析】向量OA →向右平移一个单位后起点O ′(1,0)，∵OA ′→＝OO ′→＋O ′A ′→＝OO ′→＋OA →＝(1,0)＋(1,1)＝(2,1)，∴点A ′对应复数2＋i.又O ′A ′→＝OA →，∴O ′A ′→对应复数为1＋i.故选C ．5．(2020年宜宾模拟)已知i 是虚数单位，复数m ＋1＋(2－m )i 在复平面内对应的点在第二象限，则实数m 的取值范围是( )A ．(－∞，－1)B ．(－1,2)C ．(2，＋∞)D ．(－∞，－1)∪(2，＋∞)【答案】A 【解析】∵复数m ＋1＋(2－m )i 在复平面内对应的点在第二象限，∴⎩⎪⎨⎪⎧m ＋1<0，2－m >0，解得m ＜－1.∴实数m 的取值范围是(－∞，－1)．故选A ． 6．(2020年重庆月考)已知实数m ，n 满足m －2i ＝n (2＋i)，则在复平面内，复数z ＝m ＋n i 所对应的点位于( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】C 【解析】∵m －2i ＝n (2＋i)，∴m －2i ＝2n ＋n i.∴⎩⎪⎨⎪⎧ m ＝2n ，n ＝－2，解得⎩⎪⎨⎪⎧m ＝－4，n ＝－2.∴复数z ＝m ＋n i ＝－4－2i.∴复数z ＝m ＋n i 所对应的点位于第三象限．故选C ．7．i 为虚数单位，设复数z 1，z 2在复平面内对应的点关于原点对称，若z 1＝2－3i ，则z 2的共轭复数为________．【答案】－2－3i 【解析】∵z 1＝2－3i ，∴z 1对应的点为(2，－3)，关于原点的对称点为(－2,3)．∴z 2＝－2＋3i.z 2的共轭复数为－2－3i.8．已知复数z ＝1－2m i(m ∈R )，且|z |≤2，则实数m 的取值范围是________． 【答案】⎣⎡⎦⎤－32，32 【解析】|z |＝1＋4m 2≤2，解得－32≤m ≤32. 9．实数m 分别取什么数值时，复数z ＝(m 2＋5m ＋6)＋(m 2－2m －15)i 满足下列条件？ (1)对应点在x 轴上方； (2)对应点在直线y ＝－x －5上．解：(1)由m 2－2m －15>0，得当m <－3或m >5时，z 的对应点在x 轴上方． (2)由(m 2＋5m ＋6)＋(m 2－2m －15)＋5＝0，得当m ＝－3－414或m ＝－3＋414，z 的对应点在直线y ＝－x －5＝0上．10．已知O 为坐标原点，OZ 1→对应的复数为－3＋4i ，OZ 2→对应的复数为2a ＋i(a ∈R )．若OZ 1→与OZ 2→共线，求a 的值．解：因为OZ 1→对应的复数为－3＋4i ，OZ 2→对应的复数为2a ＋i ，所以OZ 1→＝(－3,4)，OZ 2→＝(2a,1)．因为OZ 1→与OZ 2→共线，所以－3×1－4×2a ＝0，解得a ＝－38，即a 的值为－38.B 级——能力提升练11．(2020年合肥月考)设复数z 满足|z －1|＝|z －i|(i 为虚数单位)，z 在复平面内对应的点为(x ，y )，则( )A ．y ＝－xB ．y ＝xC ．(x －1)2＋(y －1)2＝1D ．(x ＋1)2＋(y ＋1)2＝1【答案】B 【解析】由z 在复平面内对应的点为(x ，y )，且|z －1|＝|z －i|，得|x －1＋y i|＝|x ＋(y －1)i|，∴(x －1)2＋y 2＝x 2＋(y －1)2，整理得y ＝x .故选B ．12．已知复数z 满足|z |＝2，则|z ＋3－4i|的最小值是( ) A ．5 B ．2 C ．7D ．3【答案】D 【解析】|z |＝2表示复数z 在以原点为圆心，以2为半径的圆上，而|z ＋3－4i|表示圆上的点到(－3,4)这一点的距离，故|z ＋3－4i|的最小值为(－3)2＋42－2＝3.13．(多选)下列命题中，正确的是( ) A ．复数的模是非负实数B ．复数等于零的充要条件是它的模等于零C ．两个复数模相等是这两个复数相等的必要条件D ．复数z 1>z 2的充要条件是|z 1|＞|z 2|【答案】ABC 【解析】①任意复数z ＝a ＋b i(a ，b ∈R )的模|z |＝a 2＋b 2≥0总成立，故A 正确；②由复数相等的条件z ＝0⇔⎩⎪⎨⎪⎧a ＝0，b ＝0⇔|z |＝0，故B 正确；③设z 1＝a 1＋b 1i ，z 2＝a 2＋b 2i(a 1，b 1，a 2，b 2∈R )，若z 1＝z 2，则有a 1＝a 2，b 1＝b 2，所以|z 1|＝|z 2|，故C 正确；④虚部不全为零的两个复数不能比较大小，但任意两个复数的模总能比较大小，故D 错．14．设A ，B 为锐角三角形的两个内角，则复数z ＝(cos B －tan A )＋itan B 对应的点位于复平面的( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】B 【解析】因为A ，B 为锐角三角形的两个内角，所以A ＋B >π2，即A >π2－B ，sin A >cos B ，cos B －tan A ＝cos B －sin Acos A <cos B －sin A <0.又tan B >0，所以点(cos B －tan A ，tan B )在第二象限．故选B ．15．已知复数z 1＝－1＋2i ，z 2＝1－i ，z 3＝3－2i ，它们所对应的点分别是A ，B ，C ，若OC →＝xOA →＋yOB →(x ，y ∈R )，则x ＋y 的值是________．【答案】5 【解析】由复数的几何意义可知，OC →＝xOA →＋yOB →，即3－2i ＝x (－1＋2i)＋y (1－i)，∴3－2i ＝(y －x )＋(2x －y )i.由复数相等可得⎩⎪⎨⎪⎧ y －x ＝3，2x －y ＝－2，解得⎩⎪⎨⎪⎧x ＝1，y ＝4.∴x ＋y＝5.16．已知两向量a ，b 对应的复数分别是z 1＝－3，z 2＝－12＋m i(m ∈R )，且a ，b 的夹角为60°，求m 的值．解：因为a ，b 对应的复数分别为z 1＝－3，z 2＝－12＋m i(m ∈R )，所以a ＝(－3,0)，b ＝⎝⎛⎭⎫－12，m .又a ，b 的夹角为60°， 所以cos 60°＝(－3，0)·⎝⎛⎭⎫－12，m (－3)2＋02·⎝⎛⎭⎫－122＋m 2，即12＝32314＋m 2，解得m ＝±32.17．已知复数z 对应的向量为OZ →(O 为坐标原点)，OZ →与实轴正方向的夹角为120°，且复数z 的模为2，求复数z .解：根据题意可画图形如图所示，设点Z 的坐标为(a ，b )，∵|OZ →|＝|z |＝2，∠xOZ ＝120°，∴a ＝－1，b ＝±3，即点Z 的坐标为(－1，3)或(－1，－3)．∴z ＝－1＋3i 或z ＝－1－3i.C 级——探索创新练18．已知t 为实数，复数z ＝(t 2＋t －2)＋(t 2＋3t ＋2)i. (1)当t 为何值时，复数z 为纯虚数？(2)当t ＝0时，复数z 在复平面内对应的点Z 落在直线y ＝－mx ＋n 上，其中mn ＞0，求1m ＋1n的最小值及取得最值时的m 和n 值． 解：(1)复数z 为纯虚数，∴⎩⎪⎨⎪⎧t 2＋t －2＝0，t 2＋3t ＋2≠0，解得t ＝1.(2)当t ＝0时，点Z (－2,2)，复数z 在复平面内对应的点Z 落在直线y ＝－mx ＋n 上，∴2m ＋n ＝2，∵mn ＞0，∴1m ＋1n ＝⎝⎛⎭⎫1m ＋1n ⎝⎛⎭⎫m ＋n 2＝32＋m n ＋n 2m ≥32＋2，当且仅当n 2＝2m 2等号成立． 又2m ＋n ＝2，∴m ＝2－2，n ＝22－2.。

7.1.2 复数的几何意义（练习）(60分钟120分)知识点1复数与复平面内点的关系1．(5分)复数z＝－1＋2i所对应的点在()A．第一象限B．第二象限C．第三象限D．第四象限B解析：由复数的几何意义知z＝－1＋2i对应复平面中的点为(－1,2)，而(－1,2)是第二象限中的点，故选B.2．(5分)复数z1＝1＋3i和z2＝1－3i在复平面内的对应点关于() A．实轴对称B．一、三象限的平分线对称C．虚轴对称D．二、四象限的平分线对称A解析：复数z1＝1＋3i在复平面内的对应点为Z1(1，3)，复数z2＝1－3i在复平面内的对应点为Z2(1，－3)，点Z1与Z2关于实轴对称，故选A.3．(5分)已知复数z＝(a2－2a)＋(a2－a－2)i(a∈R)对应的点在虚轴上，则()A．a≠2或a≠1B．a≠2且a≠1C．a＝0D．a＝2或a＝0D解析：由题意，得a2－2a＝0，解得a＝0或a＝2.故选D.4．(5分)已知复数z＝12i2，则复数z在复平面上对应的点在()A．直线y＝－12x上B．直线y＝12x上C ．直线x ＝－12上 D ．直线y ＝－12上C 解析：∵z ＝12i 2＝－12，∴z 对应的点在直线x ＝－12上，C 正确． 知识点2 复数与复平面内向量的关系5．(5分)在复平面内，O 为原点，向量OA →对应的复数为－1＋2i ，若点A 关于直线y ＝－x 的对称点为点B ，则向量OB →对应的复数为( )A ．－2－iB ．－2＋iC ．1＋2iD ．－1＋2iB 解析：因为复数－1＋2i 对应的点为A (－1,2)，点A 关于直线y ＝－x 的对称点为B (－2,1)，所以OB →对应的复数为－2＋i.6．(5分)与x 轴同方向的单位向量e 1，与y 轴同方向的单位向量e 2，它们对应的复数分别是( )A ．e 1对应实数1，e 2对应虚数iB ．e 1对应虚数i ，e 2对应虚数iC ．e 1对应实数1，e 2对应虚数－iD ．e 1对应实数1或－1，e 2对应虚数i 或－iA 解析：e 1＝(1,0)，e 2＝(0,1)．因此e 1对应实数1，e 2对应虚数i. 7.(5分)在△ABC 中，AB →，AC →对应的复数分别为－1＋2i ，－2－3i ，则BC →对应的复数为 ．－1－5i 解析：因为AB →，AC →对应的复数分别为－1＋2i ，－2－3i ，所以AB →＝(－1,2)，AC →＝(－2，－3)．又BC →＝AC →－AB →＝(－2，－3)－(－1,2)＝(－1，－5)，所以BC →对应的复数为－1－5i.知识点3 复数的模及应用8．(5分)下列四个式子中，正确的是( ) A ．z ＝|z | B ．|2＋3i|>|1－4i|C ．|2－i|>2i 2D ．i 2>|－i|C 解析：A 中z 是复数，|z |是实数，二者不一定相等，错误；B 中|2＋3i|＝13<|1－4i|＝17，错误；C 中|2－i|＝5>2i 2＝－2，正确；D 中i 2＝－1<|－i|＝1，错误．9．(5分)已知复数z 的实部为1，且|z |＝2，则复数z 的虚部是( ) A ．－ 3 B ．3i C ．±3iD ．±3D 解析：设复数z 的虚部为b (b ∈R ，b ≠0)，∵|z |＝2，实部为1，∴1＋b 2＝4，∴b ＝±3，选D.10.(5分)已知复数z ＝x －2＋y i(x ，y ∈R )的模是22，则点(x ，y )的轨迹方程是 ．(x －2)2＋y 2＝8 解析：由题意得(x －2)2＋y 2＝2 2，即(x －2)2＋y 2＝8. 11.(5分)复数z ＝－5－12i 在复平面内对应的点到原点的距离为 ． 13 解析：复数z ＝－5－12i 在复平面内对应点Z (－5，－12)．所以点Z 与原点O 的距离为|OZ →|＝(－5)2＋(－12)2＝13.12.(5分)已知复数z ＝x ＋1＋(y －1)i(x ，y ∈R )在复平面内的对应点位于第二象限，则点(x ，y )所构成的平面区域是( )A 解析：由题意，得⎩⎨⎧ x ＋1<0，y －1>0，即⎩⎨⎧x <－1，y >1，故点(x ，y )所构成的平面区域为A 项中的阴影部分．13．(5分)在复平面内，复数z ＝sin 2＋icos 2对应的点位于( ) A ．第一象限B ．第二象限提升篇C ．第三象限D ．第四象限D 解析：∵sin 2>0，cos 2<0，∴复数z 对应的点(sin 2，cos 2)在第四象限．故选D.14．(5分)如果复数z 满足条件z ＋|z |＝2＋i ，那么z ＝( ) A ．－34＋i B ．34－i C ．－34－iD ．34＋iD 解析：设z ＝a ＋b i(a ，b ∈R )．由复数相等的充要条件，得⎩⎨⎧a ＋a 2＋b 2＝2，b ＝1，解得⎩⎪⎨⎪⎧a ＝34，b ＝1，即z ＝34＋i.15．(5分)已知复数z 对应的向量为OZ →(O 为坐标原点)，OZ →与实轴正向的夹角为120°，且复数z 的模为2，则复数z 为( )A ．1＋3iB ．2C ．(－1，3)D ．－1＋3iD 解析：设复数z 对应的点为(x ，y )，则x ＝|z |·cos 120°＝2×⎝ ⎛⎭⎪⎫－12＝－1，y ＝|z |·sin 120°＝2×32＝3，∴复数z 对应的点为(－1，3)，∴z ＝－1＋3i.16.(5分)i 为虚数单位，设复数z 1，z 2在复平面内对应的点关于原点对称，若z 1＝2－3i ，则z 2＝ .－2＋3i 解析：复数z 1＝2－3i 对应的点为(2，－3)，则z 2对应的点为(－2,3)．所以z 2＝－2＋3i.17.(5分)复数4＋3i 与－2－5i 分别表示向量OA →与OB →，则向量AB →表示的复数是 ．－6－8i 解析：因为复数4＋3i 与－2－5i 分别表示向量OA →与OB →，所以OA →＝(4,3)，OB →＝(－2，－5)．又AB →＝OB →－OA →＝(－2，－5)－(4,3)＝(－6，－8)，所以向量AB →表示的复数是－6－8i.18.(5分)已知3－4i ＝x ＋y i(x ，y ∈R )，则|1－5i|，|x －y i|，|y ＋2i|的大小关系为 ．|y ＋2i|<|x －y i|<|1－5i| 解析：由3－4i ＝x ＋y i(x ，y ∈R )，得x ＝3，y ＝－4.而|1－5i|＝1＋52＝26，|x －y i|＝|3＋4i|＝32＋42＝5，|y ＋2i|＝|－4＋2i|＝(－4)2＋22＝20.∵20<5<26，∴|y ＋2i|<|x －y i|<|1－5i|. 19.(5分)若z 为纯虚数，且|z －1|＝|－1＋i|，则z ＝ .±i 解析：设z ＝a i(a ∈R 且a ≠0)，∴|z －1|＝|a i －1|＝a 2＋1.∵|－1＋i|＝2，∴a 2＋1＝2，∴a ＝±1，∴z ＝±i.20.(12分)实数x 分别取什么值时，复数z ＝x 2＋x －6＋(x 2－2x －15)i 对应的点Z 在：(1)第三象限？ (2)第四象限？(3)直线 x －y －3＝0上？解：(1)当实数x 满足⎩⎨⎧x 2＋x －6<0，x 2－2x －15<0，即－3<x <2时，点Z 在第三象限．(2)当实数x 满足⎩⎨⎧x 2＋x －6>0，x 2－2x －15<0，即2<x <5时，点Z 在第四象限．(3)当实数x 满足(x 2＋x －6)－(x 2－2x －15)－3＝0，即x ＝－2时，点Z 在直线x －y －3＝0上．21.(13分)已知O 为坐标原点，OZ 1→对应的复数为－3＋4i ，OZ 2→对应的复数为2a ＋i(a ∈R )．若OZ 1→与OZ 2→共线，求a 的值．解：因为OZ 1→对应的复数为－3＋4i ，OZ 2→对应的复数为2a ＋i ，所以OZ 1→＝(－3,4)，OZ 2→＝(2a,1)．因为OZ 1→与OZ 2→共线，所以存在实数k 使OZ 2→＝kOZ 1→，即(2a,1)＝k (－3，4)＝(－3k,4k )，所以⎩⎨⎧2a ＝－3k ，1＝4k ，所以⎩⎪⎨⎪⎧k ＝14，a ＝－38.即a 的值为－38.。