高考模拟测试题(一)

2024届湖北省高考模拟测试物理试题一、单项选择题：本题共8小题，每小题3分，共24分，在每小题给出的答案中，只有一个符合题目要求。

(共8题)第(1)题绽放激情和力量，升腾希望与梦想。

如图甲，“龙狮舞水城”表演中绸带宛如水波荡漾，展现水城特色，舞动的绸带可简化为沿x轴方向传播的简谐横波，图乙为时的波形图，此时质点P在平衡位置，质点Q在波谷位置，图丙为质点P的振动图像，则（ ）A．该波沿x轴负方向传播B．时，质点Q的振动方向沿y轴负方向C．时，质点P的加速度正在减小D．该波传播速度为3m/s第(2)题如图所示的变压器，输入电压为，可输出、、电压，匝数为的原线圈中电压随时间变化为．单匝线圈绕过铁芯连接交流电压表，电压表的示数为。

将阻值为的电阻R接在两端时，功率为。

下列说法正确的是（ ）A．n 1为1100匝，为B．间线圈匝数为120匝，流过R的电流为C．若将R接在两端，R两端的电压为，频率为D．若将R接在两端，流过R的电流为，周期为第(3)题半径为R的绝缘细圆环固定在图示位置，圆心位于O点，环上均匀分布着电量为Q的正电荷。

点A、B、C将圆环三等分，取走A、B处两段弧长均为的小圆弧上的电荷。

将一点电荷q置于延长线上距O点为的D点，O点的电场强度刚好为零。

圆环上剩余电荷分布不变，q为（ ）A．正电荷，B．正电荷，C．负电荷，D．负电荷，第(4)题小敏将一个排球以速度竖直向上抛出，经过一段时间后又返回原位置。

已知排球在运动过程中所受的空气阻力大小恒为其重力的，则上升和下降过程所用时间之比为（）A．B．C．D．第(5)题下图为游戏中小球转向器的横截面，转向器由两段光滑细圆弧形轨道Ⅰ、Ⅱ连接而成，半径分别为和，连接部分平滑，两轨道内径均远小于，且两轨道所在平面为水平面。

质量为的小球从点以速率射入，自点离开轨道。

已知小球直径略小于轨道内径，重力加速度为。

则小球在Ⅰ、Ⅱ轨道中运动时对轨道压力之比为（ ）A．B．C．D．第(6)题如图所示，一不可伸长轻绳两端各连接一质量为的小球，初始时整个系统静置于光滑水平桌面上，两球间的距离等于绳长。

2023年普通高等学校招生全国统一考试数学模拟测试（一）一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．i(1i)1i+=- （ ）A ．1B ．1-C ．i -D ．i 2．已知集合{0,1,2,3}A =，{|22,}x B y y x x A ==-∈，则A B =（ ）A ．{1,2}B ．{0,1,3}C ．{1,2,3}D ．{0,1,2} 3．已知向量(1,2)a =- ，(2,1)b = ，且(2)a a b ⋅-=（ ）A ．5B ．5-C ．11D ．11-4．关于椭圆2222:1(0)x y C a b a b+=>>，有以下四个命题．甲：长轴长为10．乙：短轴长为8．丙：离心率为45．丁：C 上的点到其左焦点的距离的最大值为8． 若只有一个假命题，则该命题是 （ ） A ．甲 B ．乙 C ．丙 D ．丁5．灯笼起源于中国的西汉时期，两千多年来，每逢春节人们便会挂起象征美好团圆意义的红灯笼，营造一种喜庆的氛围．如图1，某球形灯笼的轮廓由三部分组成，上下两部分是两个相同的圆柱的侧面，中间是球面的一部分(除去两个球冠)．如图2，球冠是由球面被一个平面截得的，垂直于截面的直径被截得的部分叫做球冠的高，若球冠所在球的半径为R ，球冠的高为h ，则球冠的面积2S Rh π=．已知该灯笼的高为40cm ，圆柱的高为4cm ，圆柱的底面圆直径为24cm ，则围成该灯笼所需布料的面积为（ ）A ．21536cm πB ．21472cm πC ．21824cm πD ．21760cm π6．泊松分布是统计学里常见的离散型概率分布，由法国数学家泊松首次提出．泊松分布的概率分布列为()e (0,1,2,)!kP X k k k λλ-=== ，其中e 为自然对数的底数，λ是泊松分布的均值．已知某线路每个公交车站台的乘客候车相互独立，且每个站台候车人数X 服从参数为(0)λλ>的泊松分布．若该线路某站台的候车人数为2和3的概率相等，则该线路公交车两个站台各有1个乘客候车的概率为（ ）A ．41e B ．44e C ．694e D ．69e 7．已知ln 33a =，22e b =，ln 77c =，则（ ）A ．b a c <<B ．a b c <<C ．b c a <<D ．c b a <<8．在正方体1111ABCD A B C D -中，N 是BC 上靠近点B 的一个四等分点，M 是棱1CC 上的动点，若平面1D MN 与平面ABCD 所成锐二面角的最小值为θ，则cos θ=（ ）A ．45B ．35CD二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，选对但不全的得2分，有选错的得0分．9．如图，四棱雉S ABCD -的底面为正方形，SD ⊥平面ABCD ，则下列结论正确的是 （ ） A ．AB SA ⊥B ．AC 与SB 所成的角为90︒C ．AD 与SB 所成的角等于CD 与SB 所成的角 D ．AB 与SC 所成的角等于DC 与SA 所成的角10．已知lg 2a =，lg 3b =，则（ ）A ．2107a b+=B ．2lg12a b +=C ．181log 102a b=+D ．361log 522aa b-=+11．已知抛物线2:4C y x =的准线与x 轴交于点K ，过焦点F 的直线l 与C 交于A ，B 两点，AB 的中点为M ，过点M 作AB 的垂线交x 轴于点Q ，点M 在C 的准线上的射影为点N ，则 （ ）A ．AF BF AF BF +=⋅B ．tan cos AKF MQF ∠=∠C ．//NF MQD ．32AB FQ =12．已知()f x 是R 上的奇函数，(1)1f =，且(2)(2)40f x f x x --++=恒成立，则 （ ）A ．(3)5f =B ．(4)8f =C ．(2023)4047f =D ．(2024)8096f =三、填空题：本题共4小题，每小题5分，共20分．13．在62x ⎛⎝的展开式中，第四项的系数为 ．14．写出满足圆心在直线2y x =，且被x 轴截得的弦长为2的圆的标准方程 ．15．已知函数()2sin (0)6f x x πωω⎛⎫=+> ⎪⎝⎭的部分图象如图所示，6855f f ππ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭，则ω= ．16．若函数3211()e 32xf x x ax ax =--有唯一一个极值点，则实数a 的取值范围是 ． 四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤． 17．(10分)已知数列{}n a 满足3333221232(1)n a a a a n n ++++=+ ． （1）求{}n a 的通项公式； （2）若12n n n b a a +=，求数列{}n b 的前n 项和n S ．在ABC △中，内角A ，B ，C 所对的边分别为a ，b ，c ，已知cos cos 2cos bc A ab C ac B +=． （1）证明：2a ，2b ，2c 成等差数列； （2）若sin 3sin A C =，求cos B ．如图，在直三棱柱111ABC A B C -中，AB BC ⊥，2AB BC ==，13CC =，点D ，E 分别在棱1AA ，1CC 上，且11AD C E ==，过点1A 的平面//α平面BDE ，平面11B C F α= ． （1）求1A F ；（2）求直线BF 与平面BDE 所成角的正弦值．二氧化碳会导致温室效应，是全球变暖的元凶之一．因为二氧化碳具有保温的作用，会逐渐使地球表面温度升高．某机构统计了当地近几年二氧化碳的排放量x (单位：百万吨)与该地平均气温升高值y (单位：℃)的一些数据，得到如下表格：x141721273239y 0.2 0.3 0.5 0.8 1.01.4（1）依据表中给出的数据，是否可用线性回归模型拟合y 与x 的关系?请计算相关系数r 并加以说明(计算结果精确到0.001)．(若0.75r ≥，则线性相关程度很高，可用线性回归模型拟合，否则不可用) （2）试用最小二乘法求出y 关于x 的回归方程．（3）某企业为降低二氧化碳的排放量，加大了研发投入，使得企业每天的二氧化碳排放量Z (单位：吨)近似服从正态分布(5,4)N ，则该企业每天的二氧化碳排放量Z 超过7吨的概率为多少?附：相关系数()()niix x y y r --=∑；回归方程ˆˆˆybx a =+中斜率和截距的最小二乘估计公式分别为121()()ˆ()niii nii x x y y b x x ==--=-∑∑，ˆˆay bx =-．若随机变量X 服从正态分布2(,)N μσ，则()0.6827P X μσμσ-<+= ． 参考数据：61126.6i ii x y==∑，62150)4(i i x x =-=∑，621.041(i i y y =-=∑ 3.61≈．已知函数()()ln 1(0)f x x a x a =-->．（1）若曲线()y f x =在x a =处的切线方程为(1)0a x y b --+=，求实数a ，b 的值； （2）若2a =，关于x 的方程()f x mx =有两个不同的实数解，求实数m 的取值范围．22．(12分)已知双曲线2222:1(0,0)x y C a b a b-=>>的右焦点为(2,0)F ，过点F 的直线l 与双曲线C 交于A ，B 两点．当l x ⊥轴时，AB =． （1）若A 点坐标为11(,)x y ，B 点坐标为22(,)x y ，证明：1221212()x y x y y y -=-． （2）在x 轴上是否存在定点M ，使得222AM BM AB +-为定值?若存在，求出定点M 的坐标及这个定值；若不存在，请说明理由．。

高考语文模拟试题（1）一、语言文字运用（共24分，其中选择题每小题3分）1．下列词语中加点的字，注音全都正确的一项是A．腼腆．(diǎn) 羸．(léi) 弱打擂．(lèi) 台饮鸩．（zhèn）止渴B．缄．（jiān）默强．（qiǎnɡ）迫小妮．(nī) 子情不自禁．（jīn）C．谄．(chǎn) 媚笑靥．(yè) 处．(chǔ) 女作奴颜婢．(bēi)膝D．叱咤．(zhà) 闷．（mēn）热跷．(qiāo) 跷板掎．（jī）角之势2．下列各句中，没有错别字的一项是A．房价下跌20%后会不会诱发恐慌性抛售，抛售现象出现后有关方面能否采取措施控制其联锁反应，是银行和企业最为关心的问题。

B．我们不相信正义的银行已经破产，我们不相信，在这个国家巨大的机会之库里已没有足够的储备，因此今天我们要求将支票对现。

C．中国留学生对美国大学的吸引力是显而易见的，他们有良好的教育，游历甚广，既丰富了大学的生源，也给了大学更广阔的视野。

D．皇帝之中“最佳歌词创作者”的贵冠恐怕非李煜莫属了，现今传下来的为数不多的数十篇歌词，可以称得上篇篇佳作，字字珠玑。

3．下列各句中，加点的词语运用错误的一项是A．一些商家先以模糊的广告词来请君入瓮．．．．，然后再用霸王条款限制消费者，让消费者哑巴吃黄连，有苦说不出。

B．铁道部曾经信誓旦旦．．．．地表示，要在11月20日之前把工程款清偿完毕，但时至当前，清欠工作还未落实到位。

C．作客．．他乡这么多年，我才算真正地明白，为什么各种异国的旅游景区都不能像故乡一样使我感到亲切和激动。

D．基于多数人的意见，鉴于．．该会计师事务所糟糕的业务情况和混乱的财务状况，我们同意注销该会计师事务所。

4．下列各句中，没有语病的一项是A．记者日前从相关会议上获悉，明年我国食品安全工作将进一步加大治理整顿力度，严打食品安全违法犯罪活动，坚决防止重大食品安全事件。

新高考全国I 卷语文模拟试题（附答案）一、现代文阅读（35 分）（一）现代文阅读I（本题共 5 小题，17 分）阅读下面的文字，完成1～5 题。

材料一：中国古典诗歌中的意象，是诗人情感与客观物象的融合，是诗人心灵的映照。

意象的运用，使诗歌具有了丰富的内涵和独特的艺术魅力。

诗歌中的意象往往具有特定的象征意义。

比如，梅花常被赋予高洁、坚贞的品质；菊花象征着淡泊、隐逸；杨柳则代表着离别、思念。

诗人通过这些意象，传达出自己的情感和思想。

意象的组合也能创造出丰富的意境。

不同的意象组合在一起，可以形成不同的意境。

如“明月松间照，清泉石上流”，明月、青松、清泉、山石等意象的组合，营造出一种清幽、宁静的意境。

此外，意象还可以通过比喻、拟人、夸张等修辞手法来增强表现力。

例如，“忽如一夜春风来，千树万树梨花开”，将雪花比作梨花，生动地描绘出了雪景的美丽。

材料二：在现代诗歌中，意象的运用也非常广泛。

现代诗人常常通过独特的意象来表达自己对生活、对世界的感悟。

与古典诗歌相比，现代诗歌中的意象更加多样化和个性化。

现代诗人可以从日常生活中的各种事物中选取意象，如汽车、高楼、电脑等。

同时，现代诗歌中的意象也更加注重对内心世界的挖掘和表达。

现代诗歌中的意象组合也更加自由和灵活。

诗人可以根据自己的创作意图，随意组合各种意象，创造出独特的意境。

然而，无论是古典诗歌还是现代诗歌，意象都是诗歌的灵魂。

它能够激发读者的联想和想象，使读者更好地理解诗歌的内涵。

1. 下列关于材料中“意象” 的表述，不正确的一项是（3 分）A. 意象是诗人情感与客观物象的融合，能使诗歌具有丰富内涵和独特艺术魅力。

B. 古典诗歌中的意象往往有特定象征意义，如梅花代表高洁坚贞，菊花象征淡泊隐逸。

C. 现代诗歌中的意象更加多样化和个性化，可从日常生活事物中选取，也更注重内心世界表达。

D. 古典诗歌和现代诗歌中的意象组合都很自由灵活，能创造出独特意境，激发读者联想想象。

深圳市育才中学2024年高三高考数学试题系列模拟卷（1）注意事项1．考试结束后，请将本试卷和答题卡一并交回．2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置． 3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．4．作答选择题，必须用2B 铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效． 5．如需作图，须用2B 铅笔绘、写清楚，线条、符号等须加黑、加粗．一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．若5(1)(1)ax x ++的展开式中23,x x 的系数之和为10-，则实数a 的值为（ ）A ．3-B ．2-C ．1-D ．12．若复数z 满足(1)34i z i +=+，则z 的虚部为（ ）A ．5B ．52C ．52-D ．-53．中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是A ．B ．C ．D ．4．已知函数，其中04?,?04b c ≤≤≤≤，记函数满足条件：(2)12{(2)4f f ≤-≤为事件A ，则事件A发生的概率为 A ．14B ．58C ．38D ．125．已知向量(1,4)a =，(2,)b m =-，若||||a b a b +=-，则m =（ ）A ．12-B ．12C ．-8D ．86．设抛物线2:2(0)C y px p =>的焦点为F ,抛物线C 与圆22:(3)3C x y +-='交于M ,N 两点,若||6MN =,则MNF 的面积为( )A ．28B ．38C ．328D ．3247．已知变量x ，y 间存在线性相关关系，其数据如下表，回归直线方程为 2.10.5ˆ8y x =+，则表中数据m 的值为（ ）变量x 01 2 3 变量y m35.57A ．0.9B ．0.85C ．0.75D ．0.58．已知函数21,0()2ln(1),0x x x f x x x ⎧-+<⎪=⎨⎪+≥⎩，若函数()()g x f x kx =-有三个零点，则实数k 的取值范围是（ ） A ．112⎡⎤⎢⎥⎣⎦， B ．112⎛⎫ ⎪⎝⎭， C ．(0,1)D ．12⎛⎫+∞ ⎪⎝⎭， 9．已知1111143579π≈-+-+-，如图是求π的近似值的一个程序框图，则图中空白框中应填入A ．121i n =-- B ．12i i =-+ C ．(1)21ni n -=+D ．(1)2ni i -=+10．某工厂一年中各月份的收入、支出情况的统计如图所示，下列说法中错误的是（ ）．A ．收入最高值与收入最低值的比是3:1B ．结余最高的月份是7月份C ．1与2月份的收入的变化率与4至5月份的收入的变化率相同D ．前6个月的平均收入为40万元11．对某两名高三学生在连续9次数学测试中的成绩（单位：分）进行统计得到折线图，下面是关于这两位同学的数学成绩分析．①甲同学的成绩折线图具有较好的对称性，故平均成绩为130分； ②根据甲同学成绩折线图提供的数据进行统计，估计该同学平均成绩在区间内；③乙同学的数学成绩与测试次号具有比较明显的线性相关性，且为正相关； ④乙同学连续九次测验成绩每一次均有明显进步． 其中正确的个数为（ ） A ．B ．C ．D ．12．已知双曲线2222:1x y C a b-=（0a >，0b >），以点P （,0b ）为圆心，a 为半径作圆P ，圆P 与双曲线C 的一条渐近线交于M ，N 两点，若90MPN ∠=︒，则C 的离心率为（ ）ABCD二、填空题：本题共4小题，每小题5分，共20分。

2023年普通高等学校招生全国统一考试新高考仿真模拟卷数学（一）一、单选题1．已知集合{}24xA x =<，{}1B =≤，则A B =（ ）A ．()0,2B ．[)1,2C ．[]1,2D ．()0,12．已知复数z 满足()()()1i 12i 1z z +=+-，则复数z 的实部与虚部的和为（ ） A ．1B ．1-C ．15D ．15-3．()()51223x x -+的展开式中，x 的系数为（ ） A ．154B ．162C ．176D ．1804．已知1tan 5α=，则2cos 2sin sin 2ααα=-（ ） A ．83-B ．83C ．38-D ．385．何尊是我国西周早期的青铜礼器，其造形浑厚，工艺精美，尊内底铸铭文中的“宅兹中国”为“中国”一词的最早文字记载．何尊的形状可以近似地看作是圆台与圆柱的组合体，高约为40cm ，上口直径约为28cm ，下端圆柱的直径约为18cm ．经测量知圆柱的高约为24cm ，则估计该何尊可以装酒（不计何尊的厚度，403π1266≈，1944π6107≈）（ ）A ．312750cmB ．312800cmC ．312850cmD ．312900cm6．已知()f x 是定义域为R 的奇函数，满足()()2f x f x =-，则()2022f =（ ） A ．2B ．1C ．1-D ．07．在四棱锥P ABCD -中，ABCD 是边长为2的正方形，AP PD ==PAD ⊥平面ABCD ，则四棱锥P ABCD -外接球的表面积为（ ）A ．4πB ．8πC ．136π9D ．68π38．已知抛物线C ：24y x =，O 为坐标原点，A ，B 是抛物线C 上两点，记直线OA ，OB 的斜率分别为1k ，2k ，且1212k k =-，直线AB 与x 轴的交点为P ，直线OA 、OB 与抛物线C 的准线分别交于点M ，N ，则△PMN 的面积的最小值为（ ）A B C D二、多选题9．已知函数()()1cos 02f x x x ωωω=>的图像关于直线6x π=对称，则ω的取值可以为（ ） A ．2B ．4C ．6D ．810．在菱形ABCD 中，2AB =，60DAB ∠=，点E 为线段CD 的中点，AC 和BD 交于点O ，则（ ） A ．0AC BD ⋅= B ．2AB AD ⋅= C ．14OE BA ⋅=-D ．52OE AE ⋅=11．一袋中有3个红球，4个白球，这些球除颜色外，其他完全相同，现从袋中任取3个球，事件A “这3个球都是红球”，事件B “这3个球中至少有1个红球”，事件C “这3个球中至多有1个红球”，则下列判断错误的是（ ）A ．事件A 发生的概率为15B ．事件B 发生的概率为310C ．事件C 发生的概率为335D ．1(|)31P A B =12．对于函数()()32,f x x x cx d c d =+++∈R ，下列说法正确的是（ ）A ．若0d =，则函数()f x 为奇函数B ．函数()f x 有极值的充要条件是13c <C ．若函数f （x ）有两个极值点1x ，2x ，则4412281x x +>D ．若2c d ==-，则过点()20，作曲线()y f x =的切线有且仅有3条三、填空题13．已知样本数据1-，1-，2，2，3，若该样本的方差为2s ，极差为t ，则2s t=______． 14．已知圆O ：221x y +=与直线l ：=1x -，写出一个半径为1，且与圆O 及直线都相切的圆的方程：______．15．已知椭圆()222210x y a b a b+=>>的左顶点为A ，左焦点为F ，过F 作x 轴的垂线在x轴上方交椭圆于点B ，若直线AB 的斜率为32，则该椭圆的离心率为______．16．已知f （x ）是偶函数，当0x ≥时，()()2log 1f x x =+，则满足()2f x x >的实数x 的取值范围是______．四、解答题17．已知数列{}n a 是等差数列，1324,,a a a a +成等比数列，56a =． (1)求数列{}n a 的通项公式；(2)设数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和为n S ，求证：()221n n S n +<+．18．在ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ，cos sin cos c B a A b C =-． (1)判断ABC 的形状； (2)若3ab ，D 在BC 边上，2BD CD =，求cos ADB ∠的值．19．如图，在直三棱柱111ABC A B C 中，D 、E 分别是AB 、1BB 的中点，12AA AC CB ==，AB =．(1)求证：1//BC 平面1A CD ；(2)若1BC =，求四棱锥1C A DBE -的体积； (3)求直线1BC 与平面1ACE 所成角的正弦值．20．新高考模式下，数学试卷不分文理卷，学生想得高分比较困难．为了调动学生学习数学的积极性，提高学生的学习成绩，张老师对自己的教学方法进行改革，经过一学期的教学实验，张老师所教的80名学生，参加一次测试，数学学科成绩都在[]50,100内，按区间分组为[)50,60，[)60,70，[)70,80，[)80,90，[]90,100，绘制成如下频率分布直方图，规定不低于80分（百分制）为优秀．(1)求这80名学生的平均成绩（同一区间的数据用该区间中点值作代表）；(2)按优秀与非优秀用分层抽样方法随机抽取10名学生座谈，再在这10名学生中，选3名学生发言，记优秀学生发言的人数为随机变量X ，求X 的分布列和期望．21．已知12,F F 分别为双曲线()222210,0x ya b a b-=>>左、右焦点，(P 在双曲线上，且124PF PF ⋅=． (1)求此双曲线的方程；(2)若双曲线的虚轴端点分别为12,B B （2B 在y 轴正半轴上），点,A B 在双曲线上，且()22B A B B μμ=∈R ，11B A B B ⊥，试求直线AB 的方程．22．已知函数()()211e 12x f x a x a x ax a =---+++，()R a ∈．(1)当1a =时，求f （x ）的单调区间；(2)当310,e a ⎛⎫∈ ⎪⎝⎭时，求证：函数f （x ）有3个零点．参考答案：1．B【分析】化简集合A 和B ，即可得出A B ⋂的取值范围. 【详解】解：由题意在{}24xA x =<，{}1B =≤中，{}2A x x =<，{}12B x x =≤≤ ∴{}12A B x x ⋂=≤< 故选：B. 2．D【分析】根据复数的运算法则求出复数43i 55z -+=，则得到答案.【详解】(1i)(2i 1)(2i 1)z z +=-+-(2i)2i 1z -=-，2i 1(2i 1)(2i)43i 43i 2i 5555z --+-+====-+-， 故实部与虚部的和为431555-+=-，故选：D. 3．C【分析】根据二项式定理可求得()523x +展开式通项，由此可确定12,T T ，结合多项式乘法运算进行整理即可确定x 的系数. 【详解】()523x +展开式的通项公式为：()55155C 2323C rr r r r r rr T x x --+=⋅⋅=⋅； 当1r =时，412523C 240T x x =⨯=；当0r =时，51232T ==；x ∴的系数为24023224064176-⨯=-=.故选：C. 4．A【分析】利用二倍角公式化简为正、余弦的齐次分式，分式上下同除2cos α，代入1tan 5α=可得答案.【详解】2222cos 2cos sin sin sin 2sin 2sin cos αααααααα-=--22111tan 825123tan 2tan 255ααα--===---, 故选：A. 5．C【分析】根据圆柱和圆台的体积公式计算可得结果. 【详解】下端圆柱的体积为：224π91944π⋅=6107≈3cm ，上端圆台的体积为：()22116π1414993⨯+⨯+16π4033=⨯1612663≈⨯6752=3cm ， 所以该何尊的体积估计为61076752+=128593cm . 因为12850最接近12859，所以估计该何尊可以装酒128503cm . 故选：C 6．D【分析】根据函数()f x 是定义域为R 的奇函数，且()()2f x f x =-得出函数()f x 是周期为4的周期函数，进而求解.【详解】因为函数()f x 是定义域为R 的奇函数，且()()2f x f x =-， 所以(2)()()f x f x f x +=-=-，所以(4)()f x f x +=， 即函数()f x 是周期为4的周期函数，因为函数()f x 是定义域为R 的奇函数，所以(0)0f =， 因为()()2f x f x =-，所以(2)(0)0f f ==， 又因为202245052=⨯+，所以(2022)(2)0f f ==， 故选：D . 7．C【分析】将该四棱锥的外接球放在一个长方体内，画出图形，利用已知条件找出球心，建立相应的关系式，求出外接球的半径，利用球体表面积公式计算即可. 【详解】由题意将该四棱锥放在一个长方体的中， 如图∴所示：取AD 的中点H ，连接PH ，连接,AC BD 交于1O ，由AP PD =则在等腰PAD 中有：PH AD ⊥，又平面PAD ⊥平面ABCD ，且平面PAD ⋂平面ABCD=AD ， 则PH ⊥平面ABCD ， 又112AH AD ==， 所以在Rt PAH △中，3PH ===，由底面为正方形ABCD ，所以它的外接圆的圆心为对角线的交点1O ， 连接1O H ，则1PH O H ⊥，PAD 外接圆的圆心为2O ，且在PH 上，过点1O ，2O 分别作平面ABCD 与平面PAD 的垂线，则两垂线必交于点O ，点O 即为四棱锥P ABCD -外接球的球心， 且1OO ⊥平面ABCD ，又PH ⊥平面ABCD ，即2O H ⊥平面ABCD ， 所以1OO ∥PH ，所以四边形12OO HO 为矩形. 如图∴连接2AO ，则22AO PO =，在2Rt AO H 中，22223O H PH PO PH AO AO =-=-=-，所以()2222222213AO AH HO AO =+=+-，解得253AO =，所以254333O H =-=，所以1243OO O H ==， 在图∴中连接OB ，由112O B BD =所以在1Rt OO B 中，OB ==即四棱锥P ABCD -外接球的半径为R OB ==， 所以四棱锥P ABCD -外接球的表面积为： 221364πR 4ππ9S ==⨯=⎝⎭，故选：C. 8．D【分析】设出A 、B 的坐标，由1212k k =-解得12y y 的值，再分别求出点M 、点N 的坐标，求得||MN 的式子，研究AB l 恒过x 轴上的定点可得点P 的坐标，进而用方法1基本不等式或方法2函数思想求得三角形面积的最小值.【详解】设211(,)4y A y ，222(,)4y B y ，则114k y =，224k y =， ∴12121612k k y y ==- ∴1232y y =-， ∴设OA l ：14y x y =，令=1x -得：14y y =-，∴14(1,)M y --，同理：24(1,)N y -- ∴12121212||44||||4||8y y y y MN y y y y --=-+==， 设AB l ：x my t =+，221044x my t y my t y x=+⎧⇒--=⎨=⎩ 20m t ∆=+>，124y y m +=，124y y t ，又∴1232y y =-，∴432t -=-，解得：8t =， ∴AB l ：8x my =+恒过点(8,0)，∴AB l 与x 轴交点P 的坐标为(8,0)，即：(8,0)P ， ∴点P 到准线=1x -的距离为8+1=9. 方法1：1211||1321||||888y y MN y y -==+≥⨯=1||y =.∴19||9||22PMN S MN MN =⨯=≥△， ∴∴PMN的面积的最小值为2. 方法2：12||||8y y MN -==∴20m ≥∴||MN ≥m =0时取得最小值.∴19||9||22PMN S MN MN =⨯=≥△， ∴∴PMN故选：D. 9．AD【分析】首先将函数()f x 化成一个三角函数，然后根据对称轴公式求得ω的表达式，对整数k 赋值求得结果.【详解】()()1cos sin 26f x x x x ωωωπ=+=+，因为函数()f x 的图象关于直线6x π=对称，所以662k ωπππ+=+π，k ∈Z ，解得26k ω=+，因为0ω>，所以当0k =时，2ω=；所以当1k =时，8ω=. 故选：AD. 10．ABD【分析】以O 为坐标原点可建立平面直角坐标系，利用平面向量数量积的坐标运算依次验证各个选项即可.【详解】四边形ABCD 为菱形，AC BD ∴⊥，则以O 为坐标原点，,OC OD 正方向为,x y 轴，可建立如图所示平面直角坐标系，2AB AD ==，60DAB ∠=，2BD ∴=，OA OC ===()0,0O ∴，()A ，()0,1B -，()0,1D ，12E ⎫⎪⎪⎝⎭，对于A ，ACBD ，0AC BD ∴⋅=，A 正确；对于B ，()3,1AB =-，()3,1AD =，312AB AD ∴⋅=-=，B 正确；对于C ，3122OE ⎛⎫= ⎪ ⎪⎝⎭，()BA =-，31122OE BA ∴⋅=-+=-，C 错误； 对于D ，3122OE ⎛⎫= ⎪ ⎪⎝⎭，3122AE ⎛⎫= ⎪ ⎪⎝⎭，915442OE AE ∴⋅=+=，D 正确. 故选：ABD. 11．ABC【分析】根据题意求出基本事件总数、满足条件的基本事件数，利用古典概型概率公式及条件概率公式求解即可.【详解】由题意7个球中任取3个球的基本事件总数为：37C 35=这3个球都是红球的基本事件数为：33C 1=，所以事件A 发生的概率为：1()35P A =，故A 错误， 这3个球中至少有1个红球的基本事件数为：1221334343C C C C +C 1812131⋅+⋅=++=，所以事件B 发生的概率为：31()35P B =，故B 错误， 这3个球中至多有1个红球的基本事件数为：123344C C C 18422⋅+=+=，事件C 发生的概率为22()35P C =,故C 错误， 因为1()()35P AB P A ==， 所以由条件概率公式得：1()135(|)31()3135P AB P A B P B ===， 故D 正确， 故选：ABC. 12．BCD【分析】对于A ：利用奇偶性的定义直接判断；对于B ：利用极值的计算方法直接求解；对于C ：先求出13c <，表示出244122161692781c x x c +=-+，即可求出；对于D ：设切点()00,x y ，由导数的几何意义得到3200025460x x x --+=.设()322546g x x x x =--+，利用导数判断出函数()g x 有三个零点，即可求解.【详解】对于A ：当0d =时，()32f x x x cx =++定义域为R .因为()()()()()3232f x x x c x x x cx f x -=-+-+-=-+-≠-， 所以函数()f x 不是奇函数.故A 错误；对于B ：函数()f x 有极值⇔ ()f x 在R 上不单调.由()32f x x x cx d =+++求导得：()232f x x x c =++'.()f x 在R 上不单调⇔()f x '在R 上有正有负⇔4430c ∆=-⨯>⇔13c <.故B 正确.对于C ：若函数f （x ）有两个极值点1x ，2x ，必满足0∆>，即13c <.此时1x ，2x 为2320x x c ++=的两根，所以1212233x x c x x ⎧+=-⎪⎪⎨⎪=⎪⎩. 所以()22212121242293c x x x x x x +=+-=-.所以()()222244222212121242216162293992781cc c x x x xx x c +=+-=--=-+ 对称轴164272329c -=-=⨯，所以当13c <时，()224412216162116116292781932738181c x x c +=-+>⨯-⨯+=. 即4412281x x +>.故C 正确；对于D ：若2c d ==-时，()3222f x x x x =+--.所以()2322f x x x '=+-.设切点()00,x y ，则有：()3200002000002203222y x x x y f x x x x ⎧=+--⎪-⎨=+-=⎪-⎩'， 消去0y ，整理得：3200025460x x x --+=不妨设()322546g x x x x =--+，则()26104g x x x '=--.令()0g x '>，解得：2x >或13x <-；令()0g x '<，解得： 123x -<<.所以()g x 在1,3⎛⎫-∞- ⎪⎝⎭，()2,+∞上单调递增，在1,23⎛⎫- ⎪⎝⎭上单调递减.所以()()()()()32111119254660333327g x g =-=-----+=>极大值， ()()322225242660g x g ==⨯-⨯-⨯+=-<极小值.所以作出的图像如图所示：因为函数()g x 有三个零点，所以方程3200025460x x x --+=有三个根，所以过点()20，作曲线()y f x =的切线有且仅有3条.故D 正确. 故选：BCD. 13．710##0.7 【分析】根据极差的定义可得()314t =--=，先求出平均数，再从方差，从而可求2s t.【详解】极差()314t =--=，平均数为()()1122315-+-+++=，故方差()()()()()222222114111*********s ⎡⎤=--+--+-+-+-=⎣⎦. 所以21475410s t ==.故答案为:710. 14．()2221x y +-=(答案不唯一)【分析】根据圆的圆心和半径,结合直线和圆的位置关系及两个圆的位置关系计算即可. 【详解】设圆心C 为()00,x y ,由已知圆C 与直线l ：=1x -相切, 圆C 与圆O ：221x y +=相切,可得0112x ⎧--=,即得0002x y =⎧⎨=⎩或0002x y =⎧⎨=-⎩或0020x y =-⎧⎨=⎩, 且已知半径为1,所以圆的方程可以为: ()2221x y +-=或()2221x y ++=或2221x y故答案为: ()2221x y +-=(答案不唯一) 15．12##0.5【分析】由题意设(),0A a -，2,b B c a ⎛⎫- ⎪⎝⎭，再由232AB b a k c a -==-+结合222a b c =+，即可得出答案.【详解】由题意可得，(),0A a -，(),0F c -，令椭圆()222210x y a b a b +=>>中x c =-，解得：2b y a=±，所以2,b B c a ⎛⎫- ⎪⎝⎭，而2032AB b a k c a -==-+，则2232a c a c a c a a -+==-+， 解得：12e =. 故答案为：12. 16．()(),01,-∞⋃+∞【分析】利用奇偶性和函数的单调性解不等式.【详解】当0x ≥时，()()2log 1f x x +，函数在[)0,∞+上单调递增，∴()(0)0f x f ≥=，又()f x 是偶函数，所以()f x 的值域为[)0,∞+.当0x ≥时，()()2log 1f x x +，不等式()2f x x >()22log 1x x +>，即()22log 10x x+->，设()22()log 1g x x x =+-，由函数y =()2log 1y x =+，2y x=-在()0,∞+上都是增函数， 得()g x 在()0,∞+上是增函数，由(1)0g =，则()0(1)g x g >=解得1x >； 当0x <时，由函数值域可知()0f x >，此时20x<，所以()2f x x >恒成立；综上可知，满足()2f x x>的实数x 的取值范围是()(),01,-∞⋃+∞.故答案为：()(),01,-∞⋃+∞ 17．(1)1n a n =+ (2)证明见解析【分析】（1）根据等比数列定义和等差数列通项公式可构造方程组求得1,a d ，进而确定n a ； （2）利用裂项相消法可求得n S ，整理即可证得结论. 【详解】（1）设等差数列{}n a 的公差为d ，1324,,a a a a +成等比数列，()23124a a a a ∴=+，即()()2111224a d a a d +=+，又5146a a d =+=，则由()()2111122446a d a a d a d ⎧+=+⎪⎨+=⎪⎩得：121a d =⎧⎨=⎩或163a d =-⎧⎨=⎩， 当16a =-，3d =时，30a =，不满足1324,,a a a a +成等比数列，舍去； 12a ∴=，1d =，()211n a n n ∴=+-=+.（2）由（1）得：()()111111212n n a a n n n n +==-++++， 1111111111233445112n S n n n n ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫∴=-+-+-+⋅⋅⋅+-+- ⎪ ⎪ ⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭()112222n n n =-=++， ()221n n S n n ∴+=<+.18．(1)直角三角形 (2)0【分析】（1）根据正弦定理的边角互化，即可得到结果；（2）由（1）中结论即可得到cos B ∠，从而得到AD 的值，然后在ABD △中结合余弦定理即可得到结果.【详解】（1）因为cos sin cos c B a A b C =-，由正弦定理可得， 2sin cos sin cos sin C B B C A +=即()2sin sin B C A +=所以()2sin sin ,0,πsin 1A A A A =∈⇒=且()0,πA ∈，所以π2A =即ABC 是直角三角形.（2）在直角ABC 中，有22223b c a b +==，即222c b =，所以c =， 又因为2BD CD =，所以23BD BC ==且cos c B a === 在ABD △中，由余弦定理可得，22222242cos 2b b AD AB BD AD B AB BD +-+-∠===⋅解得AD =， 在ABD △中由余弦定理可得，222222242cos 02b b b AD BD AB ADB AD BD +-+-∠===⋅19．(1)证明见解析 (2)23【分析】（1）连接1AC 交1A C 于点F ，连接EF ，则F 为1AC 的中点，利用中位线的性质可得出1DF //BC ，再利用线面平行的判定定理可证得结论成立；（2）过点C 在平面ABC 内作CM AB ⊥，垂足为点M ，证明出CM ⊥平面11AA B B ，计算出CM 的长以及四边形1A DBE 的面积，利用锥体的体积公式可求得四棱锥1C A DBE -的体积； （3）设1BC =，以点C 为坐标原点，CA 、CB 、1CC 所在直线分别为x 、y 、z 轴建立空间直角坐标系，利用空间向量法可求得直线1BC 与平面1A CE 所成角的正弦值. 【详解】（1）证明：连接1AC 交1A C 于点F ，连接EF ，则F 为1AC 的中点， 因为D 、F 分别为AB 、1AC 的中点，则1DF //BC ，因为DF ⊂平面1A CD ，1BC ⊄平面1A CD ，1//BC ∴平面1A CD . （2）解：因为1BC =，则122AA AC CB ===，AB == 222AC BC AB ∴+=，即AC BC ⊥，过点C 在平面ABC 内作CM AB ⊥，垂足为点M ， 因为1AA ⊥平面ABC ，CM ⊂平面ABC ，1CM AA ∴⊥，又因为CM AB ⊥，1AB AA A ⋂=，AB 、1AA ⊂平面11AA B B ，CM ∴⊥平面11AA B B ，由等面积法可得AC BC CM AB ⋅==因为1AA ⊥平面ABC ，AB ⊂平面ABC ，1AA AB ∴⊥，又因为11//AA BB 且11AA BB =，故四边形11AA B B 为矩形，所以，1111111212AA D A B E AA B B A DBE S S S S ⎫=--==⎪⎪⎝⎭△△矩形四边形11112333C A DBE A DBE V S CM -∴=⋅==四边形.（3）解：不妨设1BC =，因为AC BC ⊥，1CC ⊥平面ABC ，以点C 为坐标原点，CA 、CB 、1CC 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系，则()0,1,0B 、()0,0,0C 、()10,0,2C 、()12,0,2A 、()0,1,1E ， 设平面1A CE 的法向量为(),,n x y z =，()12,0,2CA =，()0,1,1CE =， 则1220n CA x z n CE y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩，取1x =，可得()1,1,1n =-， 因为()10,1,2BC =-，则111cos ,BC n BC n BC n⋅<>==-=⋅因此，直线1BC 与平面1A CE20．(1)73.5(2)分布列见解析；期望()910E X =【分析】（1）根据频率分布直方图估计平均数的方法直接计算即可；（2）根据频率分布直方图可确定优秀与非优秀学生对应的频率，根据分层抽样原则可确定10名学生中优秀学员的人数，由此可得X 所有可能的取值，根据超几何分布概率公式可求得X 每个取值对应的概率，由此可得分布列；由数学期望计算公式可求得期望. 【详解】（1）80名学生的平均成绩为()550.01650.03750.03850.025950.00510⨯+⨯+⨯+⨯+⨯⨯=73.5.（2）根据频率分布直方图知：优秀学员对应的频率为()0.0250.005100.3+⨯=，则非优秀学员对应的频率为10.30.7-=，∴抽取的10名学生中，有优秀学生100.33⨯=人，非优秀学生100.77⨯=人；则X 所有可能的取值为0,1,2,3，()37310C 3570C 12024P X ====；()1237310C C 63211C 12040P X ====；()2137310C C 2172C 12040P X ====；()33310C 13C 120P X ===；X ∴的分布列为：∴数学期望()721719012324404012010E X =⨯+⨯+⨯+⨯=. 21．(1)22145x y -=(2)y x =+y =【分析】（1）根据平面向量数量积坐标运算和点在双曲线上，可构造方程组求得22,a b 的值，由此可得双曲线方程；（2）由2,,A B B 三点共线可设:AB y kx =+用向量垂直的坐标表示，代入韦达定理结论可解方程求得k 的值，由此可得直线AB 方程. 【详解】（1）设()1,0F c -，()()2,00F c c >，则(1PF c =--，(2PF c =-，212854PF PF c ∴⋅=-+=，解得：3c =，229a b ∴+=；又P 在双曲线上，则22851a b-=，24a ∴=，25b =， ∴双曲线的方程为：22145x y -=.（2）由（1）得：(10,B，(2B ，()22B A B B μμ=∈R ，2,,A B B ∴三点共线，直线AB斜率显然存在，可设:AB y kx =+()11,A x y ，()22,B x y ，由22145y kx x y ⎧=⎪⎨-=⎪⎩得：()2254400k x ---=，()22540Δ801040k k ⎧-≠⎪∴⎨=->⎪⎩，即252k <且254k ≠，12x x ∴+=1224054x x k =--， 11B A B B ⊥，110B A B B ∴⋅=，又(111,B A x y =，(122,B B x y =，()1112121212125B A B B x x y y x x y y y y ∴⋅=+=+++(()1212125x x kx kx k x x =++++()()()222121222401801202005454k k kx xx x k k+=++++=-++=--，解得：k =252k <且254k ≠，∴直线AB方程为：y x =y = 【点睛】关键点点睛：本题考查直线与椭圆的综合应用问题，解题关键是能够利用平面向量垂直关系的坐标表示来构造等量关系，结合韦达定理的结论得到关于所求变量的方程的形式，从而解方程求得变量的值.22．(1)函数()f x 的单调递增区间为(,0)-∞和(1,)+∞，单调递减区间为(0,1). (2)证明过程见详解【分析】(1) 因为1a =，所以函数()()212e 22x f x x x x =--++，对函数求导，利用导函数的正负来判断函数的单调性即可求解；(2)对函数进行求导，求出导函数的零点，根据条件可得：函数()f x 在(,)a -∞和(ln ,)a -+∞上单调递增，在(,ln )a a -上单调递减，然后利用零点存在性定理即可证明.【详解】（1）因为1a =，所以函数()()212e 22x f x x x x =--++，所以()e (2)e 1(1)(e 1)x x x f x x x x '=+--+=--，当1x >或0x <时，()0f x '>，此时函数()f x 单调递增； 当01x <<时，()0f x '<，此时函数()f x 单调递减； 综上：函数()f x 的单调递增区间为(,0)-∞和(1,)+∞， 单调递减区间为(0,1).（2）因为函数()()211e 12x f x a x a x ax a =---+++，所以()e (1)e ()e ()()(e 1)x x x x f x a a x a x a a x a x a x a a '=+---+=---=--，令()0f x '=可得：x a =或ln x a =-，因为310,e a ⎛⎫∈ ⎪⎝⎭，所以ln 3a ->，当x a <或ln x a >-时，()0f x '>，此时函数()f x 单调递增； 当ln a x a <<-时，()0f x '<，此时函数()f x 单调递减；所以函数()f x 在(,)a -∞和(ln ,)a -+∞上单调递增，在(,ln )a a -上单调递减，故当x a =时，函数取极大值()()22e 10102aaf a a a f a =-+++>=->，因为当2x =-时，221(2)(3)10ef a a a -=-+--<；所以0(2,)x a ∃∈-，使得0()0f x =； 当ln x a =-时，函数取极小值，ln 2211(ln )(ln 1)e (ln )ln 1ln ln (ln )22a f a a a a a a a a a a a a --=-----++=---1ln (1ln )02a a a =-++<，（因为ln 3a ->，所以13ln 22a <-，因为3110e 2a <<<，所以312a +<，也即11ln 02a a ++<）所以0(,ln )x a a '∃∈-，使得0()0f x '=；又当x →+∞时，()f x →+∞，所以0(ln ,)x a ''∃∈-+∞，使得0()0f x ''=；故当310,e a ⎛⎫∈ ⎪⎝⎭时，函数()f x 有3个零点.【点睛】函数零点的求解与判断方法：答案第17页，共17页 (1)直接求零点：令()0f x =，如果能求出解，则有几个解就有几个零点．(2)零点存在性定理：利用定理不仅要函数在区间[,]a b 上是连续不断的曲线，且()()0f a f b <，还必须结合函数的图象与性质(如单调性、奇偶性)才能确定函数有多少个零点．(3)利用导数求出函数的极值点,再利用零点存在性定理进行判断零点的个数．。

江门市2023年高考模拟考试数 学本试卷共6页，22小题，满分150分，考试时间120分钟。

注意事项：1．答题前，务必将自己的姓名、准考证号填写在答题卡规定的位置上。

2． 做选择题时，必须用2B 铅笔将答题卷上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

3． 答非选择题时，必须用黑色字迹钢笔或签字笔，将答案写在答题卡规定的位置上。

4． 所有题目必须在答题卡上作答，在试题卷上作答无效。

5． 考试结束后，将答题卡交回。

一、选择题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合A -=1,0,1{}，21,1∉-∈-=A m A m m B }{，则集合B 中所有元素之和为A ．0B ．1C ．－1D ．22．已知i 为虚数单位，复数z 满足11+=+i i z ()，则z =A ．+2222i B ．-2222i C ．+-2222i D ．--2222i 3．命题“∀∈-≠x Q x ,502”的否定为 A ．∃∉-=x Q x ,502B ．∀∈-=x Q x ,502C ．∀∉-=x Q x ,502D.∃∈-=x Q x ,5024．已知多项式 x a x a a x x a +++++++=-)1()1()1()1(1010221010，则a 7=A ．－960B ．960C ．－480D ．4805．设非零向量m ，n 满足=m 2，=n 3，+=m n 32，则m 在n 方向上的投影向量为 A ．-n 185B ．n 185C ．-m85D ．m 85内部资料·注意保存试卷类型：A6．衣柜里有灰色，白色，黑色，蓝色四双不同颜色的袜子，从中随机选4只，已知取出两只是同一双，则取出另外两只不是同一双的概率为 A ．25 B ．45 C ．815 D ．897．已知等差数列a n }{∈+n N )(的前n 项和为S n ，公差d <0,a a <-1091，则使得S n >0的最大整数n 为A ．9B ．10C ．17D ．188．我们知道按照一定顺序排列的数字可以构成数列，那么按照一定顺序排列的函数可以构成函数列.设无穷函数列∈+f x n N n )(}{)(的通项公式为++=+++n x n f x n nx x n 12122)()()(，∈x 0,1)(,记E n 为f x n )(的值域，==+∞E E n n 1为所有E n 的并集，则E 为二、选择题：本题共4小题，每小题5分，共20分。

海南省2022-2023学年高考全真模拟卷（一）语文试题一、现代文阅读（35分）（一）现代文阅读Ⅰ（本题共5小题，19分）阅读下面的文字，完成1~5题。

材料一：近年来，现实题材电视剧创作数量、播出热度、社会关注度居高不下，开拓了大众化、生活化的荧屏世界，展现出影视剧制作的新风貌。

《人世间》《山海情》《大江大河》《父母爱情》等电视剧，通过普通人、家常事展现新中国成立以来的时代洪流，剧中有血有肉的平凡人物，让故事更接地气。

最是真实动人心。

金滩村，马得福在西北的风沙中建设家园，带领村民们种蘑菇脱贫致富；松山岛，江德福一家在东部的海风中守护着祖国的海疆……现实题材电视剧呈现着真实的生活场景、真实的喜怒哀乐、真实的命运变迁，以鲜活生动的影像记录下时代阔步前行的足迹。

现实题材电视剧的走红说明，一切创作技巧和手段都是为内容服务的，优秀的文艺作品需要做到思想内容和艺术表达有机统一、社会现实与艺术想象有机统一。

人民是文艺之母。

源于人民、为了人民、属于人民，是社会主义文艺的根本立场，也是现实题材电视剧经久不衰的关键。

现实题材电视剧从社会热点、民生关切中获取创作灵感，将人们关注的教育、医疗、住房、生育、养老等话题作为创作主题，并从微观个体的视角进行电视艺术演绎，因而能够让观众有置身剧中的代入感，在不知不觉中引发情感共鸣。

这说明，只有深入人民群众、了解人民的辛勤劳动、感知人民的喜怒哀乐，才能洞悉生活本质，才能把握时代脉动，才能领悟人民心声，才能使文艺创作具有深沉的力量和隽永的魅力。

从更大的视角来看，现实题材电视剧展现着微观个体与伟大时代的“双向奔赴”。

《人世间》作为一部以当代中国历史为背景的时代剧，以周秉昆一家几十年的经历为主要内容，通过讲述普通人物的命运变迁展现改革开放的时代洪流。

以小见大、以点带面，做到普遍性与特殊性相统一，不仅让宏大叙事通过具体细节变得可知可感，也通过艺术的方式揭示出时代进步的奥秘，即每个人的拼搏奋斗，汇聚成了推动时代前行的强大合力。

2024年全国1卷高考语文模拟试题及答案2024年全国1卷高考语文模拟试题及答案一、选择题1、下列词语中，字形和读音全部正确的一项是：（）A. 订正、汲取教训、锲而不舍、撒手锏B. 修茸、一筹莫展、越俎代庖、狙击手C. 针砭、明察秋毫、咎由自取、口头禅D. 矍铄、言简意赅、气冲霄汉、洗脚婢2、下列句子中，没有语病的一项是：（）A. 我们既要传承传统文化，又要与时俱进，以适应新的时代环境。

B. 大量的事实告诉我们，环境恶化导致生物灭绝，人类要善待大自然。

C. 有关部门高度重视人民的意见，以确保“禁烟令”的顺利实施。

D. 即使生活再艰辛，我也要坚持不懈地努力，因为我的梦想就是成为一个科学家。

3、下列作品中，属于鲁迅小说集《呐喊》的是：（）A. 《孔乙己》B. 《背影》C. 《荷塘月色》D. 《葫芦僧判断葫芦案》二、阅读理解阅读下面的文言文，完成4-6题。

未几，夫恬上前，问所欲言。

王曰：“吾欲言南尚可斗太守恶其无状。

”恬曰：“前日恬罪甚重，郎中令劳赐如令，是恬与并得罪。

”夫恬曰：“死未晚也。

”恬闻天下之至苦也莫苦于狱吏而吏道也莫患于无文而止在促捕之众也幸而道不携犹破折锐首而折左股而话之犹无所羞而夫恬为上相与为朝廷之法而以贾竖受货为资而挛拘牵张于辞语者恶独安？窃见郡县之吏徒以阿坐为毕能郡之大者也吏安得不悉虎狼还以道为尚父且父之不德而咎若曹罪乃大矣陷乃公独痴牧羊而道苦索则何？”恬不为理，引首以塞其气。

相与营当引太守舍，驾不能过半涂，良市卒正言于从者曰：“可与杀牛茵茵也。

”而恬得兵甚备，因恬请曰：“窃闻恬为人臣，佞而无骨，畏强怀弱，以货自免。

骄君甚则贵而求逆，暴君甚则利而求逆。

恬不知为死计，而尚与贾竖受货。

”恬得死诚节矣！4、下列句子中，断句正确的一项是：（）A. 前日/恬罪甚重B. 贾竖/受货为资/而挛拘牵张于辞语者/恶独安C. 引首以塞/其气D. 可与杀牛茵茵也5、下列关于文章内容的理解，正确的一项是：（）A. 夫恬认为自己的罪行很重，所以觉得自己应该被处死。

2023年普通高等学校招生全国统一考试模拟测试（新高考）数学试题及答案一、单选题（20分）请从每题的选项中选择一个最符合题意的答案，并在答题卡上将相应的字母涂黑。

1.若函数f(x)在区间[-1,3]上连续，则其必定是 A. 递减函数 B. 倒U型函数 C. 奇函数 D. 偶函数2.已知三角形ABC，AB=AC，角A=40°，则角B的度数等于 A. 40° B. 70° C. 80° D. 100°3.设a,b都是正数，且logₐ1/3=log₃b/2，则a/b的值等于 A. 1/4 B. 1/3 C. 1/2 D. 24.若a,b>0，且a+b=1，则a²+b²的最小值是 A. 1/2 B.1/√2 C. 1/4 D. 15.若直线y=mx+2与曲线y=4x²-3x-1有两个公共点，则m的取值范围是 A. (-∞,1/8) B. (-∞,0)∪(0,1/8) C. (-∞,1/8]∪[0,+∞) D. (-∞,0)二、多选题（20分）请从每题的选项中选择一个或多个最符合题意的答案，并在答题卡上将相应的字母涂黑。

6.设实数x满足条件|x-3| < 2，下列等式成立的是 A.x > 5 B. x < 1 C. x ≠ 3 D. x > 17.在直角坐标系中，下列函数中具有对称中心为(2,-1)的是 A. y=x-1 B. y=-(x-2)²-1 C. y=√(x²-4x+4) D. y=1/x-38.设集合A={a, a², a³}，则以下命题成立的是 A. 若a>1，则a>1/a² B. 若a<0，则a³<0 C. 若a=1, 则A={1} D. 若a=0，则A={0}9.已知函数f(x)=x³+ax²+bx+c，若它与y=x+3有恰有一个交点，并且这个交点横纵坐标都是正数，则以下命题成立的是 A. a+b = -1 B. a+c = -3 C. a+c > 0 D. a+b+c > 010.设集合A={x | x=x²-2x-3, x∈R}，B={x | x²+x-6=0,x∈R}，则以下命题成立的是A. A⊂B B. A∩B=∅ C. B⊆A D.B∪A=∅三、填空题（20分）请根据题目要求填写空缺，并在答题卡上写出完整的答案。

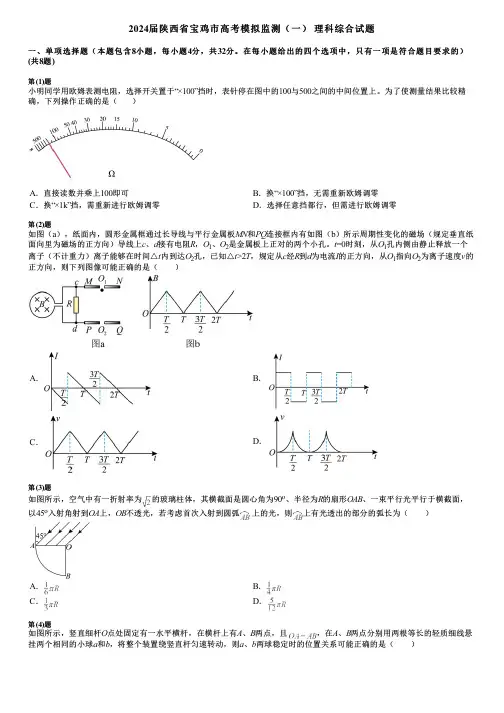
2024届陕西省宝鸡市高考模拟监测（一）理科综合试题一、单项选择题（本题包含8小题，每小题4分，共32分。

在每小题给出的四个选项中，只有一项是符合题目要求的）(共8题)第(1)题小明同学用欧姆表测电阻，选择开关置于“×100”挡时，表针停在图中的100与500之间的中间位置上。

为了使测量结果比较精确，下列操作正确的是（）A．直接读数并乘上100即可B．换“×100”挡，无需重新欧姆调零C．换“×1k”挡，需重新进行欧姆调零D．选择任意挡都行，但需进行欧姆调零第(2)题如图（a），纸面内，圆形金属框通过长导线与平行金属板MN和PQ连接框内有如图（b）所示周期性变化的磁场（规定垂直纸面向里为磁场的正方向）导线上c、d接有电阻R，O1、O2是金属板上正对的两个小孔。

t=0时刻，从O1孔内侧由静止释放一个离子（不计重力）离子能够在时间△t内到达O2孔，已知△t>2T，规定从c经R到d为电流I的正方向，从O1指向O2为离子速度v的正方向，则下列图像可能正确的是（ ）A．B．C．D．第(3)题如图所示，空气中有一折射率为的玻璃柱体，其横截面是圆心角为90o、半径为R的扇形OAB、一束平行光平行于横截面，以45o入射角射到OA上，OB不透光，若考虑首次入射到圆弧上的光，则上有光透出的部分的弧长为（ ）A．B．C．D．第(4)题如图所示，竖直细杆O点处固定有一水平横杆，在横杆上有A、B两点，且，在A、B两点分别用两根等长的轻质细线悬挂两个相同的小球a和b，将整个装置绕竖直杆匀速转动，则a、b两球稳定时的位置关系可能正确的是（ ）A ．B ．C ．D ．第(5)题霍尔推进器将来可能安装在飞船上用于星际旅行，其简化的工作原理如图所示，放电通道两端电极间存在加速电场，该区域内有与电场近似垂直的约束磁场（未画出）用于提高工作物质被电离的比例，工作时，工作物质氙气进入放电通道后被电离为氙离子，再经电场加速喷出，形成推力，某次测试中，氙气被电离的比例为，氙离子喷射速度为，推进器产生的推力为，推进器质量，已知氙离子的比荷为；计算时，取氙离子的初速度为零，忽略磁场对离子的作用力及粒子之间的相互作用，则（ ）A ．将该推进器用于宇宙航行时，飞船获得的加速度B ．氙离子的加速电压约为C．氙离子向外喷射形成的电流约为D．每秒进入放电通道的氙气质量约为第(6)题在地面上以初速度竖直上抛一物体A 后，又以初速度v0在同一地点竖直上抛另一物体B ，若要使两物体能在空中相遇，则两物体抛出的时间间隔必须满足什么条件（已知，不计空气阻力）（ ）A ．B ．C ．D ．第(7)题如图所示，手握绳端在竖直方向做简谐运动，形成的一列简谐横波以速度沿轴正向传播，时刻，在轴上、间的简谐横波如图所示，从此时刻开始，点处质点经过时间刚好第3次到达波峰，则下列说法正确的是（ ）A ．时刻，绳端正在向下振动B ．绳端的振动频率为C ．若将波的振动频率增大一倍，则波的传播速度也增大一倍D ．若将波的振动频率增大为原来的2倍，则简谐波的波长也会增大为原来的2倍第(8)题如图所示，平行板电容器充电后断开电源，上极板接地，在板间点处固定一个试探电荷q，现将下极板向下平移一小段距离，用表示试探电荷在点所受的电场力，用E表示极板间的电场强度，用表示点的电势，用表示试探电荷在点的电势能，则下列物理量随与下极板的距离的变化关系图线中，可能正确的是（ ）A．B．C．D．二、多项选择题（本题包含4小题，每小题4分，共16分。

2024年浙江省高考模拟卷学考测试物理试题(一）（基础必刷）一、单项选择题（本题包含8小题，每小题4分，共32分。

在每小题给出的四个选项中，只有一项是符合题目要求的）(共8题)第(1)题水平桌面上，一质量为的物体在水平恒力拉动下从静止开始运动。

物体通过的路程等于时，速度的大小为，此时撤去，物体继续滑行的路程后停止运动。

重力加速度大小为。

则（ ）A．的大小等于物体所受滑动摩擦力大小的倍B．的大小等于物体所受滑动摩擦力大小的倍C．在此过程中的冲量大小等于D．在此过程中所做的功为第(2)题如图甲所示为一台小型发电机构造示意图。

磁极、间的磁场看成匀强磁场，磁感应强度大小为，线圈共10匝，矩形线圈的面积为。

该发电机产生的感应电动势图象如图乙所示，该交流电通过自耦变压器对一定值电阻供电，不计发电机内阻，则下列说法正确的是（ ）A．矩形线圈面积为B．电阻中电流方向每秒钟改变100次C．线圈从开始后转过的过程中，电压表的读数先增大后减小D．当变压器滑片P向上滑动时、电阻消耗的功率减小第(3)题将有效值为220V，频率为50Hz的正弦交流电通过一信号发生设备后，其电压随时间变化的规律如图所示，其有效值与原交流电有效值的比值为（ ）A．1∶2B．1 ∶3C．1 ∶4D．1∶5第(4)题已知氘（）核的质量为，质子（）的质量为，中子（）的质量为，光速为c，则氘核的比结合能为（）A．B．C．D．第(5)题图示平面内固定两个等量异种点电荷，M、N两点关于两电荷的连线对称，M、P两点关于两电荷连线的中垂线对称。

下列说法正确的是（ ）A．M、P两点的电场强度相同B．N、P两点的电场强度相同C．N、P两点的电势相等D．电子在M点的电势能比在N点的大第(6)题如图，竖直虚线右侧区域有垂直纸面向里、磁感应强度大小为B的匀强磁场，磁场边缘有一质量为m的矩形匀质导线框，顶点a固定在虚线上，线框可绕a点在竖直平面内自由无摩擦转动，从图示位置由静止释放线框，线框顺时针摆动到左侧最高点时边与之间的夹角为45°。

【备考2023】高考生物精品模拟卷(一)(时间：90分钟满分：100分)一、单项选择题(本题共14小题，每题2分，共28分。

每题只有一个选项是正确的。

)1.下列关于生物体中化合物的叙述，正确的是()A.纤维素由葡萄糖聚合而成，是植物细胞的能源物质B.胆固醇参与构成动物细胞膜和血液中脂质运输C.蛋白质是生物体内重要的储能物质D.细胞中的无机盐主要以化合物的形式存在2.一片沼泽地中含有多种微生物，下列有关叙述正确的是()A.蓝细菌能进行光合作用，属于自养生物B.酵母菌有细胞壁和拟核，属于单细胞原核生物C.病毒的遗传物质是RNA，在活细胞内增殖D.硝化细菌含染色质，是该生态系统中的消费者3.糖类和脂质都是人体生命活动中必不可少的物质，但摄入过多会导致肥胖、血管堵塞等。

下列叙述正确的是()A.组成淀粉、糖原的葡萄糖之间的连接方式和排列方式相同B.磷脂、胆固醇和脂肪都是人体细胞细胞膜的重要组成成分C.维生素D属于脂质，限制维生素D的摄入可预防血管堵塞D.适当多运动和增大食物中富含纤维素的食物的比例可达到减肥效果4.mRNA的部分区域可以调控自身的翻译过程。

下图1、图2是mRNA调控翻译的两种机制，已知AUG为起始密码子，编码甲硫氨酸，其上游的一段序列为核糖体结合位点。

下列相关分析错误的是()图1图2A.核糖体结合到mRNA上时，携带甲硫氨酸的tRNA立即与mRNA进行碱基配对B.翻译速率过快时，机体可以通过合成翻译阻抑蛋白来对基因的表达进行调节C.图2表明温度升高会使碱基对之间的氢键断裂，从而促进核糖体与mRNA的结合D.图1、图2中调控翻译的两种机制均是通过调节核糖体与mRNA的结合来实现的5.在2022年北京冬奥会自由式滑雪女子大跳台决赛中，我国运动员谷爱凌以超高难度动作获得高分，夺得冠军。

下列对该名运动员机体生理功能调节的叙述，错误的是()A.比赛前，垂体活动加强导致肾上腺素和甲状腺激素分泌增加B.比赛中，细胞产生大量CO2以刺激脑干呼吸中枢使呼吸加快C.比赛中，大量出汗导致抗利尿激素分泌量增多以调节水盐平衡D.比赛中，肝糖原分解和非糖物质转化为葡萄糖以维持血糖平衡6.GPNMB(非转移性黑色素瘤糖蛋白B)是一种跨膜蛋白，在衰老细胞表面富集。

2023届河北省唐山市第十一中学高考模拟测试地理试题（一）学校:___________姓名：___________班级：___________考号：___________一、选择题组陶瓷可以大致分为传统陶瓷和先进陶瓷两类。

先进陶瓷以人工精制合成原料为主，广泛应用于生物医用材料（人工关节、血管支架等）等高精尖领域，国内生物医用材料的70%~80%依赖进口。

山东省淄博市博山区地处泰沂山脉北侧，距今已有6000年陶瓷生产历史，是我国五大陶瓷产地之一。

目前淄博市作为国内先进陶瓷主要集聚区，生物医用材料已成为淄博市陶瓷产业开发的重点。

近年来，淄博市持续推动产业技术创新联盟建设，以产业联盟带动产业发展。

下图为淄博市位置示意图。

据此完成下面小题。

1．影响淄博市成为国内先进陶瓷主要集聚区的主要因素是（）A．市场B．技术C．原料D．能源2．生物医用材料成为淄博市先进陶瓷产业开发的重点的主要原因是我国（）A．城镇化进程加快B．人口老龄化加重C．先进陶瓷技术水平高D．人口数量增长快3．淄博市持续推动先进陶瓷产业技术创新联盟建设的主要目的是（）A．提升创新能力B．降低生产成本C．获得规模效应D．共享基础设施江西流坑村历史悠久，四面环山，村落建设了多条东西向街巷，且该街巷直达河岸；村落西侧挖掘了高低串联的池塘（村民称之为“龙湖”），并与乌江相连；街巷均留有明沟或暗渠，并与“龙湖”相通。

下图为流坑村功能区分布示意图。

据此完成下面小题。

4．威胁流坑村生存的首要因素是（）A．滑坡B．干旱C．地震D．洪涝5．该村东西向街巷的主要作用有（）①防盗②防火③运输④通风A．①②B．①④C．②③D．③④6．该村挖掘高低串联的池塘的目的是（）A．减少工程量B．净化水质C．方便水运D．利于取水下图为新西兰人口金字塔模型图（含预测）。

据此完成下面小题。

7．依据图示信息可知，新西兰人口最可能（）A．1967年停止增长B．2020年增长迅速C．2048年呈负增长D．2048年老龄化初现8．该国应对未来人口问题，最有效的人口政策是（）A．鼓励生育B．放宽移民政策C．提倡优生D．加强人口教育巴斯海峡海水流动受风力影响，具有明显的季节变化。

2023届高考地理模拟试题（一）（全国卷）一、单项选择题：本题共11小题，每小题4分，共44分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

（新疆喀什地区疏附县2022届高三下学期3月一模考试地理试卷）终年积雪区与夏季最大融化区之间的界线即为融雪末期雪线，直接反映着冰川的进退。

高亚洲（又称中央亚洲）是位于亚洲中部地势较高的大山脉地区（范围下图），区域内积雪、冰川分布广泛。

在全球变暖大背景下，近几十年，高亚洲融雪末期雪线高度总体上表现为升高趋势，但兴都库什、西喜马拉雅地区融雪末期雪线高度反而呈微弱的下降趋势。

据此完成下面小题。

1.山地冰雪融化带对应的山地自然带是（）A.冰川带B.山地荒漠带C.山地苔原带D.山地针叶林带2.受地形地势影响，高亚洲融雪末期雪线高度变化的空间分布规律大致是（）A.沿“希萨尔→阿莱山→东昆仑→祁连山”一线降低B.沿“喜马拉雅→青藏高原内部→昆仑山→天山→阿尔泰山”一线降低C.沿“横断山→青藏高原内部→兴都库什山”一线降低D.自青藏高原内部及喜马拉雅高海拔地区向外围呈环状逐渐降低3.兴都库什、西喜马拉雅地区融雪末期雪线高度呈微弱下降趋势的原因最可能是（）A.降水集中在冬季且增加B.夏季风影响逐渐增强C.地壳相对其他区域下沉D.退耕（牧）节水政策推行得力（河南省百所名校2022届高三下学期第二次学业质量联合检测（乙卷））内陆港是设在内陆经济中心城市铁路、公路交会处，代表海港行使报关、报验等功能的物流中心。

近年来，深圳市改变传统的公路集疏运体系，形成“内陆港—专用铁路—沿海港口”三位一体的新型内陆港集疏运体系。

下图示意新旧集疏运体系对比。

据此完成下面小题。

4.新型内陆港集疏运体系主要有利于深圳市（）①缓解城市交通拥堵②提高对外开放水平③促进城市用地扩张④缓解城市大气污染A.①②B.②③C.③④D.①④5.与传统的公路集疏运体系相比，新型内陆港集疏运体系使深圳港（）A.降低通关效率B.减少用地成本C.用地变得紧张D.提高设备水平6.与传统货运铁路相比，新型内陆港集疏运体系中内陆港至深圳港之间的铁路专用线（）A.发车频次低B.运行速度慢C.停靠站点少D.连续性较差（陕西省咸阳市2023届高三下学期一模考试地理试卷）2022年8月23日，欧洲干旱观测站(EDO)的研究显示，欧洲正面临至少500年来最严重的干旱，该洲大陆近三分之二的地区处于预警和警戒状态，内河运输、粮食生产和能源供应整体堪忧。

2023-2024学年河北省部分学校高三下学期高考演练数学模拟试题（一模）一、单选题1．已知集合{}220|A x x x =-<，集合{}210|2x B x -=-≤，则A B ⋃=（）A ．{}|02x x <<B ．{}2|0x x <≤C ．{}|2x x <D ．{}2|x x ≤【正确答案】D【分析】根据一元二次不等式以及指数不等式化简集合,A B ,由集合的并运算即可求解.【详解】由于22021022202x x x x ---≤⇒≤⇒-≤⇒≤所以{}|02A x x =<<，{}|2B x x =≤，所以{}|2A B x x ⋃=≤.故选：D.2．已知复数1z ，2z ，“21z z >”是“211z z >”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【正确答案】D【分析】根据充分条件和必要条件的定义求解.【详解】若21z z >，可得复数1z ，2z 都为实数，当120z z <<时，211z z <，充分性不成立；反之，若211z z >取复数11i z =+，222i z =+，满足2121z z =>，但此时复数1z ，2z 均为虚数，不能比较大小，必要性不成立，所以“21z z >”是“211z z >”的既不充分也不必要条件；故选：D.3．若函数923log ,14()1,123x x f x x x x ⎧->⎪⎪=⎨⎪≤⎪++⎩，则523f f ⎡⎤=⎪⎢⎥⎢⎣⎛ ⎝⎦⎭⎥⎫（）A ．517B ．175C ．417D ．174【正确答案】C【分析】根据自变量的取值，即可代入到分段函数中，计算即可.【详解】由于5231>，所以5522935313log 34442f ⎛⎫=-=-= ⎪⎝⎭，故5211431217134f f f ⎡⎤⎛⎫==⎢⎥ ⎪⎝⎭⎢⎥⎣⎦+⎪⎭+⎛⎫ ⎝=，故选C.4．2021年5月22日上午10点40分，祝融号火星车安全驶离着陆平台，到达火星表面，开始巡视探测.为了帮助同学们深入了解祝融号的相关知识，某学校进行了一次航天知识讲座，讲座结束之后，学校进行了一次相关知识测试（满分100分），学生得分都在[]50,100内，其频率分布直方图如下，若各组分数用该组的中间值代替，估计这些学生得分的平均数为（）A ．70.2B ．72.6C ．75.4D ．82.2【正确答案】C【分析】根据题意，由频率之和为1，可得m 的值，然后结合平均数的计算公式，代入计算，即可得到结果.【详解】由条件可得()0.0040.0540.0120.010101m ++++⨯=，则0.020m =，故得分的平均数为.()0.004550.020650.054750.012850.010951075.4⨯+⨯+⨯+⨯+⨯⨯=故选：C5．中国国家大剧院的外观被设计成了半椭球面的形状.如图，若以椭球的中心为原点建立空间直角坐标系，半椭球面的方程为2222221x y z a b c++=（0,z ≥，,,0a b c >，且a ，b ，c 不全相等）.若该建筑的室内地面是面积为2(0)m m π>的圆，给出下列结论：①a b =；②c m =；③2ac m =；④若ac m >，则1c >，其中正确命题的个数为（）A ．1B ．2C ．3D ．4【正确答案】B【分析】根据已知得a b m ==，结合题设判断各项正误即可.【详解】在2222221x y z a b c ++=中，令0z =可得该建筑室内地面对应的曲线方程为22221x y a b+=，由室内地面是面积为2πm (0)m >的圆，故a b =，①对；且22ππa m =，则a b m ==，又,,a b c 不全相等，故c m ≠，②错；若2ac m =，则2mc m =，可得c m =，与,,a b c 不全相等矛盾，③错；若ac m >，则0mc m >>，故1c >，④对.故选：B.6．已知α是第三象限角，3cos 2sin 2αα+=，则tan α=（）A ．24B 33C 3D ．22【正确答案】A【分析】根据α是第三象限角，3cos 2sin 2αα+=，利用二倍角公式整理得26sin sin 10αα--=，求得sin α，再利用基本关系求解.【详解】∵α是第三象限角，3cos 2sin 2αα+=，∴()2312sin sin 2αα-+=，∴26sin sin 10αα--=，解得1sin 3α=-或1sin 2α=(舍去)，∴22cos 1sin 3αα=--=-，∴2tan 4α=，故选：A.7．直线:40l ax by +-=与圆22:4O x y +=相切，则22(3)(4)a b -+-的最大值为（）A ．16B ．25C ．49D ．81【正确答案】C【分析】利用圆与直线的位置关系得出,a b 的方程，根据方程分析利用22(3)(4)a b -+-表示的几何意义求解即可.【详解】由直线l 与圆O 相切可得：圆心()0,0O 到直线l 的距离等于圆的半径，2=，故224a b +=，即点(,)a b 在圆O 上，22(3)(4)a b -+-的几何意义为圆上的点(,)a b 与点(3,4)之间距离的平方，由224a b +=圆心为()0,0，因为22344+>，所以点(3,4)在圆224a b +=外，所以点(,)a b 到点(3,4)的距离的最大值为圆心到(3,4)的距离与圆半径之和，即27d r +=，所以22(3)(4)a b -+-的最大值为2749=.故选：C.8．为了提高同学们对数学的学习兴趣，某高中数学老师把《周髀算经》、《九章算术》、《孙子算经》、《海岛算经》这4本数学著作推荐给学生进行课外阅读，若该班A ，B ，C 三名同学有2名同学阅读其中的2本，另外一名同学阅读其中的1本，若4本图书都有同学阅读（不同的同学可以阅读相同的图书），则这三名同学选取图书的不同情况有（）A ．144种B ．162种C ．216种D ．288种【正确答案】A【分析】利用排列组合公式进行合理分类讨论即可.【详解】分两种情况：第一种情况，先从4本里选其中2本，作为一组，有24C 种，第二组从第一组所选书籍中选1本，再从另外2本中选取1本作为一组，剩余一本作为一组，再分给3名同学，共有211342231C C C A 2方法；第二种情况：从4本里任选2本作为一组，剩余的两本作为一组，有224222C C A 种分法，分给3名同学中的2名同学，有23A 种分法，剩余1名同学，从这4本中任选一本阅读，有14C 种分法，共有2221423422C C A C A ⋅种方法.故这三名同学选取图书的不同情况有222113214242233422C C 1C C C A A C 1442A +⋅=种.故选：A.二、多选题9．已知函数()sin cos (0)f x x x ωωω=+>的最小正周期为π2，若12()()2f x f x =-，则（）A ．()f x 关于直线1x x =对称B ．()f x 关于点2(,0)x 对称C ．12x x +的最大值为π2D ．12x x +的最小值为π8【正确答案】AD【分析】根据辅助角公式化简()f x ，利用周期的公式求解4ω=，进而根据12()()2f x f x =-可判断12,x x x x ==为()f x 的对称轴，即可判断AB,利用对称中心可求解DC.【详解】由π()sin cos cos )4f x x x x ω=+=+的最小正周期为π2可得2ππ2ω=，即4ω=，故π())4f x x =+，由12()()2f x f x =-可得1()f x ，2()f x 分别为()f x 的最大值和最小值，故()f x 关于直线1x x =对称，不关于点2(,0)x 对称，故A 正确，B 错误；由()π4πZ 4x k k +=∈可得()1πZ 416x kx k =-∈，故()f x 的对称中心()1ππ,0Z 416k k ⎛⎫-∈ ⎪⎝⎭，则121π1π2ππ,Z 41628x x n n n +=-=-∈，当0n =时，12x x +取得最小值π8，没有最大值，故C 错误，D 正确.故选：AD10．已知双曲线2222:1(0,0)x y C a b a b-=>>的虚轴长为2，过C 上点P 的直线l 与C 的渐近线分别交于点A ，B ，且点P 为AB 的中点，则下列正确的是（）A ．若(,)P m n 且直线l 的斜率存在，直线l 的方程为21mynx a -=B ．若(2,1)P ，直线l 的斜率为1C．若离心率e =2OAB S=△D ．若直线l 的斜率不存在，2AB =【正确答案】BCD【分析】根据点差法可得直线的斜率，进而可判断A ，利用A 选项的求解可判断B ，利用离心率可得渐近线方程，进而联立直线AB 与渐近线方程得交点坐标，利用三角形面积公式以及双曲线方程可判断C ，根据顶点和渐近线方程可求解D.【详解】由题意1b =，双曲线222:1x C y a-=.对于A ，若(,)P m n ，则2221m n a-=，即2222m a n a -=.设11(,)A x y ，22(,)B x y ，则221120x y a -=，222220x y a -=，利用点差法可得121222212122()2ABy y x x m m k x x a y y a n a n-+===-+=，所以直线l 的方程为y n -=2()mx m a n-，即2222a ny a n mx m -=-，所以22222mx a ny m a n a -=-=，即21mxny a -=，故A 错误；对于B ，若(2,1)P ，可得222211a -=,则a =l 的斜率为22121m a n ==⨯，即B 正确；对于C，若离心率222,2c e c a b a==+，可得2a =.则双曲线22:14x C y -=，其渐近线方程为2xy =±，设11(,)2x A x ，22(,2xB x -，直线()()121112:22x x x AB y x x x x +=-+-，令121220,x xy x x x ==+，则121221122212221OAB x x x x x x S x x +=+=△，由A 知AB 方程为14mxny -=，联立方程142mxny x y ⎧-=⎪⎪⎨⎪=⎪⎩可得142x m n =-，同理可得242x m n =+，所以1211442222OAB S x x m n m n ==⨯-+△2288244m n ===-，故C 正确；对于D ，若直线l 的斜率不存在，则直线l 过双曲线的顶点，所以(,0)P a ±，双曲线的渐近线方程为1y x a=±，当x a =±时，代入渐近线方程易得A ，B 两点的纵坐标为1±，所以2AB =，故D 正确；故选：BCD.11．如图，在直四棱柱1111ABCD A B C D -中，底面ABCD 是菱形，点P ，Q ，M 分别为11A D ，11C D ，BC 的中点，下列结论正确的有（）A ．//AC 平面PQMB ．该四棱柱有外接球，则四边形ABCD 为正方形C ．BC 与平面PQM 不可能垂直D ．BD QM⊥【正确答案】ABC【分析】根据线线平行即可判断A ，利用外接圆的对角互补，则可判断B ，利用反证法，结合线面垂直的性质定理可判断C,D.【详解】对A ，连接11AC ，由点P ，Q ，分别为11A D ，11C D 可得11//ACPQ ，11111////.AA BB CC AA BB CC == ，所以四边形11A ACC 为平行四边形，则11//AC AC ，故//AC PQ ，AC ⊄平面PQM ,PQ ⊂平面PQM ,则//AC 平面PQM ，即A 正确；对B ，若四棱柱有外接球，则四边形ABCD 有外接圆，则ABCD 对角互补，则ABCD 为正方形，即B 正确；对C ，若BC ⊥平面PQM ，PQ ⊂平面PQM ,则BC PQ ⊥，由//PQ AC 可得BC AC ⊥，与条件矛盾，故BC 与平面PQM 不可能垂直，即C 正确；对D ，取CD 的中点N ，连接MN ，QN ，则//MN BD ，1//QN CC ,1CC ⊥ 平面ABCD ，QN ∴⊥平面ABCD ，MN ⊂ 平面ABCD ，QN MN ∴⊥，90QNM ∴∠=︒，则90QMN ∠<︒，故BD 与QM 不垂直，即D 错误.故选：ABC.12．设()f x 是定义在R 上的偶函数，其图象关于直线2x =对称，当[0,2]x ∈时，2()f x x =，若方程()4log (5)(0,1)a f x x a a >=+≠在[]4,6-上恰有5个实数解，则（）A ．()f x 的周期为4B ．()f x 在[]8,10上单调递减C ．()f x 的值域为[]0,2D ．711a <<【正确答案】AD【分析】由对称性与奇偶性得到函数的周期性，即可判断A 、B ，结合所给函数解析式求出函数的值域，即可判断C ，画出函数()y f x =与4log (5)(1)a y x a =+>的图象，数形结合，即可判断D.【详解】由()f x 的图象关于2x =对称可得(4)()f x f x +=-，再由()f x 为偶函数可得()()f x f x -=，故()(4)f x f x =+，即()f x 的周期为4，即A 正确；当[0,2]x ∈时，由2()f x x =，可得()f x 在[0,2]上单调递增，故()f x 在[]8,10上单调递增，即B 错误；又(0)0f =，(2)4f =，故()f x 的值域为[]0,4，即C 错误；在同一坐标系下画出函数()y f x =与4log (5)(1)a y x a =+>的图象如图所示.由图可知，要使()y f x =与()4log (5)b g x x =+在[]4,6-上恰有5个不同交点，只需()()24641g g a ⎧<⎪>⎨⎪>⎩，即log 71log 1111a a a <⎧⎪<⎨⎪>⎩，解得711a <<，即a 的取值范围为()7,11，故D 正确.故选：AD三、填空题13．已知O 为ABC 的外心，若2OA =，且75BAC ∠=︒，则OB OC ⋅=__________.【正确答案】23-【分析】由平面向量数量积公式进行求解.【详解】由圆的性质可得2150BOC BAC ∠=∠=︒，2OA OB OC ===，故cos 22cos15023OB OC OB OC BAC ⋅=⋅∠=⨯⨯︒= 故23-14．若函数4()ln 42mxf x x-=-的图象关于原点对称，则实数m 的值为__________.【正确答案】2-【分析】根据奇函数的性质根据()()f x f x -=-，即可求解.【详解】依题意，()()f x f x -=-，即44ln ln 4242mx mxx x-+=-+,所以442424mx x x mx +-=+-，解得2m =±，当2m =时，42()ln42xf x x-=-，定义域{}2x x ≠不关于原点对称，故舍去，当2m =-时，42()ln 42xf x x+=-，定义域为{}22x x -<<，符合要求，故2m =-，故2-15．函数33()sincos sin cos 2222x x x xf x =-的最小值为__________.【正确答案】14-/0.25-【分析】根据二倍角公式化简()1sin 24f x x =-，即可求解最值.【详解】因为33()sin cos sin cos 2222x x x x f x =-22sin cos sin cos 2222x x x x ⎛⎫=-= ⎪⎝⎭1sin cos 2x x -1sin 24x =-，所以当π22π,Z 2x k k =+∈时，sin 21x =，此时()f x 的最小值为14-.故14-四、双空题16．如图，在三棱锥A BCD -中，AB CD ⊥，AD BC ⊥，且3BD AC =，点E ，F 分别为AD ，BC 的中点，则异面直线AC 与BD 所成角的大小为__________，AC 与EF 所成角的余弦值为__________.【正确答案】90︒10【分析】根据异面直线夹角的定义作辅助线，构造三角形.【详解】取AB 的中点G ，连接EG ，FG ，则//FG AC ，//EG BD ，故EFG ∠或其补角为异面直线AC 与EF 所成的角，过A 作AO ⊥平面BCD 于点O ，连接BO ，CO ，DO ，则AO CD ⊥，又AB CD ⊥，且AB AO A = ，故CD ⊥平面AOB ，故BO CD ⊥，同理可得DO BC ⊥，即O 为BCD △的垂心，故BD CO ⊥，又AO BD ⊥，AO CO O = ，AO ⊂平面AOC ，CO ⊂平面AOC ，故BD ⊥平面AOC ，故AC BD ⊥，即AC 与BD 所成角为90︒；所以90EGF ∠=︒，由3BD AC =可得3EG FG =，故cos FG EFG EF ∠==即异面直线AC 与EF故①90︒，②10.五、解答题17．已知n S 是公差不为0的等差数列{}n a 的前n 项和，2a 是1a ，4a 的等比中项，1278S =.(1)求数列{}n a 的通项公式；(2)已知1213n a n n b a --=⋅，求数列{}n b 的前n 项和n T .【正确答案】(1)n a n=(2)(1)31nn T n =-⨯+【分析】（1）根据题意列式求解1,a d ，即可得结果；（2）由（1）可得：1(21)3n n b n -=-⨯，利用错位相减法求和.【详解】（1）设数列{}n a 的公差为d ，因为2a 是1a ，4a 的等比中项，则2214a a a =，即2111()(3)a d a a d +=+，且0d ≠，整理得1d a =①，又因为121121211782dS a =+⨯⨯=，整理得163339a d +=②由①②解得，11a =，1d =，所以()11n a n n =+-=.（2）由（1）知，()11213213n n n n b a n ---=⨯=-⨯，则021133353(21)3n n T n -=⨯+⨯+⨯+⋅⋅⋅+-⨯，可得12313133353(23)3(21)3n nn T n n -=⨯+⨯+⨯+⋅⋅⋅+-⨯+-⨯，两式相减得0123121323232323(21)3n nn T n --=⨯+⨯+⨯+⨯+⋅⋅⋅+⨯--⨯16(13)1(21)313n n n --=+--⨯-(22)32n n =-⨯-，所以(1)31nn T n =-⨯+.18．为了了解大家对养宠物的看法，某单位对本单位450名员工（其中女职工有150人）进行了调查，发现女职工中支持养宠物的职工占13，若从男职工与女职工中各随机选取一名，至少有1名职工支持养宠物的概率为12.(1)求该单位男职工支持养宠物的人数，并填写下列22⨯列联表；支持养宠物不支持养宠物合计男职工女职工合计450(2)依据小概率值0.05α=的独立性检验，能否认为该单位职工是否支持养宠物与性别有关？附：()()()()()22n ad bc a b c d a c b d χ-=++++，n a b c d =+++.α0.100.050.0100.001x α2.7063.8416.63510.828【正确答案】(1)表格见解析(2)不能认为该单位职工是否支持养宠物与性别有关【分析】（1）运用对立事件列方程求出男职工支持养宠物的概率p ，再求出男职工中支持养宠物的人数；（2）根据卡方公式求解.【详解】（1）从男职工中随机选取1人，设支持养宠物的概率为p ，则2人中至少有一名支持养宠物是都不支持养宠物的对立事件，∴111(1)(1)32p ---=，解得14p =，则男职工中支持养宠物的人数为1300745⨯=，22⨯列联表如下：支持养宠物不支持养宠物合计男职工75225300女职工50100150合计125325450（2）零假设为：0H ：性别与态度无关联；由于22450(7510022550) 3.462 3.841125325300150χ<⨯-⨯=≈⨯⨯⨯，∴不能认为该单位职工是否支持养宠物与性别有关；综上，男职工中支持养宠物的人数为75；不能认为该单位职工是否支持养宠物与性别有关.19．在ABC 中，4AB =，AC =点D 为BC 的中点，连接AD 并延长到点E ，使3AE DE =.(1)若1DE =，求BAC ∠的余弦值；(2)若π4ABC ∠=，求线段BE 的长.【正确答案】(1)4-2【分析】（1）设BD DC x ==，由cos cos 0ADB ADC ∠+∠=结合余弦定理求解即可求出x =ABC 中，由余弦定理即可求出答案.（2）在ABC 中，由余弦定理求出BC =ABD △中，由余弦定理求出AD =，连接BE ，在ABE 中，由余弦定理即可求出线段BE 的长.【详解】（1）因为1DE =，3AE DE =，所以2AD =，因为πADB ADC ∠+∠=，所以cos cos 0ADB ADC ∠+∠=，设BD DC x ==，则222222022BD AD AB CD AD AC BD AD CD AD+-+-+=⋅⋅，即224164802222x x x x +-+-+=⋅⋅⋅⋅，解得x =2BC BD ==在ABC 中，由余弦定理知，222cos2AB AC BC BAC AB AC +-∠==-⋅（2）在ABC 中，由余弦定理知，2222cos AC AB BC AB BC ABC =+-⋅⋅∠，所以2816242BC BC =+-⋅⋅⋅，化简得280BC -+=，解得BC =因为D 是BC 的中点，所以12BD BC ==在ABD △中，由余弦定理知，2222cos AD AB BD AB BD ABC =+-⋅⋅∠16224102=+-⨯=，所以AD =，因为3AE DE =，所以32AE AD ==在ABD △中，由余弦定理知，222cos2AB AD BD BAE AB AD +-∠=⋅连接BE ，在ABE 中，由余弦定理知，2222cos BE AB AE AB AE BAE =+-⋅⋅∠=351624222⎛⎫+-⨯⨯= ⎪ ⎪⎝⎭，所以BE =20．如图，在三棱锥-P ABC 中，平面PAC ⊥平面ABC ，若PAC △为等边三角形，ABC 为等腰直角三角形，且AC BC =，点E 为AC 的中点，点D 在线段AB 上，且4AB AD =.(1)证明：AB ⊥平面PDE ；(2)求平面PDE 与平面PBC 所成锐二面角的余弦值.【正确答案】(1)证明见解析4【分析】（1）作出辅助线，得到DE AB ⊥，由三线合一得到PE AC ⊥，从而得到线面垂直，面面垂直，从而证明出结论；（2）建立空间直角坐标线，利用空间向量求解二面角的余弦值.【详解】（1）如图，取AB 的中点G ，由AC BC =可得CG AB ⊥，由4AB AD =可得D 为AG 的中点，由E 为AC 的中点可得DE 为ACG 的中位线，∴DE CG ∥，∴DE AB ⊥，∵E 为AC 的中点，PA PC =，∴PE AC ⊥，∵平面PAC ⊥平面ABC ，且平面PAC 平面ABC AC =，PE 在面PAC 内，∴PE ⊥平面ABC ，而AB ⊂平面ABC ，∴PE AB ⊥，又PE DE E = ，且PE DE ⊂，平面PDE ，∴AB ⊥平面PDE .（2）以C 为原点，CA 、CB 为x 、y 轴，过C 垂直于面ABC 的直线为z 轴，设4PA =.则(4,0,0)A ，(0,4,0)B ，(0,0,0)C，P ，则(2,0,PA =- ，()4,4,0AB =-，∴1(1,1,4PD PA AD PA AB =+=+=-，(2,4,PB =--，(2,0,PC =--，设平面PBC 的一个法向量为(,,)n x y z =，由24020n PB x y z n PC x ⎧⋅=-+-=⎪⎨⋅=--=⎪⎩，解得0y =，令x =1z =-，故1)n =-，由（1）可知(4,4,0)AB =-为平面PDE 的一个法向量，∴cos,4ABAB nA nBn=⋅=-⋅，又平面PDE与平面PBC21．已知抛物线2:2(0)C x py p=>的焦点为F，直线:(1)2(0)l y k x k=>--与C交于A，B 两点，当3k=时，28AF BF+=.(1)求抛物线C的方程；(2)若直线:(1)2m y k x=---与抛物线C交于M，N两点，证明：由直线AM，直线BN及y 轴围成的三角形为等腰三角形.【正确答案】(1)24x y=(2)证明见解析【分析】（1）根据直线抛物线方程的联立以及抛物线的定义即可求解；（2）根据直线与抛物线方程的联立以及坐标关系即可求解.【详解】（1）当3k=时，直线:3(1)235l y x x=--=-，与22x py=联立消去y，整理可得26100x px p-+=，由0∆>得236400p p->，即109p>.设11(,)A x y，22(,)B x y，可得126x x p+=，所以()12123101810y y x x p +=+-=-，由题意可得0,2p F ⎛⎫ ⎪⎝⎭，准线方程为2py =-，根据抛物线的定义可得12p AF y =+，22p BF y =+，所以121810191028AF BF y y p p p p +=++=-+=-=，解得2p =，满足0∆>，所以抛物线C 的方程为24x y =.（2）直线():12(0)l y k x k =-->与24x y =联立可得24480x kx k -++=，由0∆>得21616320k k -->，即2k >或1k <-（舍）设11(,)A x y ，22(,)B x y ，则124x x k +=；直线:(1)2m y k x =---与24x y =联立消去y ，整理可得24480x kx k +-+=，由0∆>得21616320k k +->，即1k >或2k <-（舍），故2k >，设33(,)M x y ，44(,)N x y ，则344x x k +=-；因为2231313131314()4AMy y x x x xk x x x x --+===--，同理424BN x x k +=，所以123404AMBN x x x xk k ++++==，所以由直线AM ，直线BN 及y 轴围成的三角形为等腰三角形.22．已知函数()()2ln 2R f x ax x x x a =--∈.(1)若4a =，求()f x '的极值；(2)若函数()2y f x x =+有两个零点1x ，2x ，且21x ex >，求证.12ln ln 3a x x +>【正确答案】(1)极大值为4ln 22-，无极小值(2)证明见解析【分析】（1）对()f x 求导，判断()f x '的单调性，即可求出()f x '的极值；（2）根据极值点的概念整理原不等式可得12211221ln ln ln ln x x x x x x x x +-=+-即112122111ln()ln 1x x xx x x x x +=-，构建新函数1()ln (e)1t t t t t ϕ+=>-，求导，利用导数证明()2t ϕ>即可.【详解】（1）2()ln 2f x ax x x x =--的定义域为(0,)+∞，当4a =时，()4ln 22f x x x '=-+，设()4ln 22g x x x =-+，则442()2xg x x x-'=-=，由()0g x =可得2x =，当02x <<时，()0g x '>，当2x >时，()0g x '<，∴()f x '在(0,2)上单调递增，在(2,)+∞上单调递减，∴()f x '的极大值为(2)4ln 22f '=-，无极小值；（2）由()20f x x +=可得2 ln 0ax x x -=，即1ln xa x=.设ln ()(0)xh x x x=>，则21ln ()x h x x -'=.由()0h x '=可得e x =，当(0,e)x ∈时，()0h x '>，函数()h x 单调递增，当(e,)x ∈+∞时，()0h x '<，函数()h x 单调递减.∴()h x 有极大值1(e)eh =，当01x <<时，()0h x <，当1x >时，()0h x >.要使()2y f x x =+有两个零点1x ，2x ，需有110ea <<，即e a >.∵1212ln ln 1x x a x x ==，由比例的性质可得12211221ln ln ln ln x x x x x x x x +-=+-，即()21211221ln ln x x x x x x x x =+-，故121212122211111ln()ln ln 1x x x x x x x x x x x x x x ++==--，设21x t x =，由21e 0x x >>可得t e >，设函数1()ln (e)1t t t t t ϕ+=>-，则212ln ()(1)t t t t t ϕ--'=-，设1()2ln s t t t t =--，则22211()110s t t t t ⎛⎫'=-+=-> ⎪⎝⎭，∴()s t 在(e,)+∞上单调递增，故1()(e)e 20es t s >=-->，故()0t ϕ'>，∴()t ϕ在(e,)+∞上单调递增，故e 12()(e)12e 1e 1t ϕϕ+>==+>--，∴212e x x >，故312e ax x >，故312ln()ln e ax x >，即12ln ln 3a x x +>.关键点点睛：本题（2）的关键点在于由题意得出1212ln ln 1x x a x x ==，建立关系112122111ln()ln 1x x xx x x x x +=-，再结合题意化简整理，再利用导数证明不等式.。