动态规划典型例题

动态规划练习题[题1] 多米诺骨牌（DOMINO）问题描述：有一种多米诺骨牌是平面的，其正面被分成上下两部分，每一部分的表面或者为空，或者被标上1至6个点。

现有一行排列在桌面上：顶行骨牌的点数之和为6+1+1+1=9；底行骨牌点数之和为1+5+3+2=11。

顶行和底行的差值是2。

这个差值是两行点数之和的差的绝对值。

每个多米诺骨牌都可以上下倒置转换，即上部变为下部，下部变为上部。

现在的任务是，以最少的翻转次数，使得顶行和底行之间的差值最小。

对于上面这个例子，我们只需翻转最后一个骨牌，就可以使得顶行和底行的差值为0，所以例子的答案为1。

输入格式：文件的第一行是一个整数n（1〈=n〈=1000〉，表示有n个多米诺骨牌在桌面上排成一行。

接下来共有n行，每行包含两个整数a、b（0〈=a、b〈=6，中间用空格分开〉。

第I+1行的a、b分别表示第I个多米诺骨牌的上部与下部的点数（0表示空）。

输出格式：只有一个整数在文件的第一行。

这个整数表示翻动骨牌的最少次数，从而使得顶行和底行的差值最小。

[题2] Perform巡回演出题目描述:Flute市的Phlharmoniker乐团2000年准备到Harp市做一次大型演出,本着普及古典音乐的目的,乐团指挥L.Y.M准备在到达Harp市之前先在周围一些小城市作一段时间的巡回演出,此后的几天里,音乐家们将每天搭乘一个航班从一个城市飞到另一个城市,最后才到达目的地Harp市(乐团可多次在同一城市演出).由于航线的费用和班次每天都在变,城市和城市之间都有一份循环的航班表,每一时间,每一方向,航班表循环的周期都可能不同.现要求寻找一张花费费用最小的演出表.输入: 输入文件包括若干个场景.每个场景的描述由一对整数n(2<=n<=10)和k(1<=k<=1000)开始,音乐家们要在这n个城市作巡回演出,城市用1..n标号,其中1是起点Flute市,n是终点Harp市,接下来有n*(n-1)份航班表,一份航班表一行,描述每对城市之间的航线和价格,第一组n-1份航班表对应从城市1到其他城市(2,3,...n)的航班,接下的n-1行是从城市2到其他城市(1,3,4...n)的航班,如此下去.每份航班又一个整数d(1<=d<=30)开始,表示航班表循环的周期,接下来的d个非负整数表示1,2...d天对应的两个城市的航班的价格,价格为零表示那天两个城市之间没有航班.例如"3 75 0 80"表示第一天机票价格是75KOI,第二天没有航班,第三天的机票是80KOI,然后循环:第四天又是75KOI,第五天没有航班,如此循环.输入文件由n=k=0的场景结束.输出:对每个场景如果乐团可能从城市1出发,每天都要飞往另一个城市,最后(经过k天)抵达城市n,则输出这k个航班价格之和的最小值.如果不可能存在这样的巡回演出路线,输出0.样例输入: 样例输出：3 6 4602 130 150 03 75 0 807 120 110 0 100 110 120 04 60 70 60 503 0 135 1402 70 802 32 0 701 800 0[题3] 复制书稿（BOOKS）问题描述：假设有M本书（编号为1，2，…M），想将每本复制一份，M本书的页数可能不同（分别是P1，P2，…PM）。

动态规划的具体应用例题3.1 最长不降子序列（1）问题描述设有由n个不相同的整数组成的数列，记为:a(1)、a(2)、……、a(n)且a(i)<>a(j) (i<>j)例如3，18，7，14，10，12，23，41，16，24。

若存在i1<i2<i3< … < ie 且有a(i1)<a(i2)< … <a(ie)则称为长度为e的不下降序列。

如上例中3，18，23，24就是一个长度为4的不下降序列，同时也有3，7，10，12，16，24长度为6的不下降序列。

程序要求，当原数列给出之后，求出最长的不下降序列。

（2）算法分析根据动态规划的原理，由后往前进行搜索。

1· 对a(n)来说，由于它是最后一个数，所以当从a(n)开始查找时，只存在长度为1的不下降序列；2· 若从a(n-1)开始查找，则存在下面的两种可能性：①若a(n-1)<a(n)则存在长度为2的不下降序列a(n-1)，a(n)。

②若a(n-1)>a(n)则存在长度为1的不下降序列a(n-1)或a(n)。

3· 一般若从a(i)开始，此时最长不下降序列应该按下列方法求出: 在a(i+1),a(i+2),…,a(n)中，找出一个比a(i)大的且最长的不下降序列，作为它的后继。

4.用数组b(i),c(i)分别记录点i到n的最长的不降子序列的长度和点i后继接点的编号(3) 程序如下:（逆推法）program li1;const maxn=100;var a,b,c:array[1..maxn] of integer;fname:string;f:text;n,i,j,max,p:integer;beginreadln(fname);assign(f,fname);reset(f);readln(f,n);+for i:=1 to n dobeginread(f,a[i]);b[n]:=1;c[n]:=0;end;for i:= n-1 downto 1 dobeginmax:=0;p:=0;for j:=i+1 to n doif (a[i]<a[j]) and (b[j]>max) then begin max:=b[j];p:=j end;if p<>0 then begin b[i]:=b[p]+1;c[i]:=p endend;max:=0;p:=0;for i:=1 to n doif b[i]>max then begin max:=b[i];p:=i end;writeln('maxlong=',max);write('result is:');while p<>0 dobegin write(a[p]:5);p:=c[p] end;end.3.2 背包问题背包问题有三种1.部分背包问题一个旅行者有一个最多能用m公斤的背包，现在有n种物品，它们的总重量分别是W1，W2，...,Wn,它们的总价值分别为C1,C2,...,Cn.求旅行者能获得最大总价值。

动态规划运筹学例题动态规划是运筹学中常用的一种优化技术，它利用规划、三角函数和其他数学技术来解决日常生活中的各种问题，比如最优路线问题、最优资源分配问题、最优出行路线问题等。

本文将通过一个例题，来介绍动态规划的基本思想，以及如何利用动态规划来解决问题。

例题一：已知一条路线，由A点到B点，有N个途经的节点，每个节点之间的距离已知。

求从A到B的最短路线。

按照动态规划的思想，首先将该问题分解为若干个子问题，并根据子问题的解来解决原问题，这种分解和解决问题的方式称为动态规划。

对于上面的问题，可以将其分解为N个子问题，分别是从A到第1个节点、从第1个节点到第2个节点、从第2个节点到第3个节点，以此类推，最后一个子问题是从第N-1个节点到B点的最短路程。

将上面的N个子问题中，从第i个节点到B点的最短路程记为d[i]，由于从第i个节点到B点可能经过i+1、i+2、……、N-1节点，因此要找到d[i]，只需要找到经过i+1、i+2、……、N-1节点的最短路程即可，即求d[i]=Min{d[i+1]+length[i][i+1],d[i+2]+length[i][i+2],…,d[N-1]+length[i][N-1]}，其中length[i][j]是第i个节点到第j个节点的距离。

以上就是动态规划的解题步骤，它能将原问题分解成若干个子问题，并找到最优解。

对于本例来说，通过上述步骤，就可以得到从A 到B的最短路程。

这种分解和求解问题的方法是动态规划，可以用来解决许多类似的问题，如：1）最优路线问题；2）旅行推销员问题；3）硬币找零问题。

动态规划的一大特点是，他能很好地将问题分解为多个子问题，并能从子问题的解中求解出最优解。

总之，动态规划是一种很有用的优化技术，它可以有效解决各种运筹学问题。

它不仅可以帮助我们解决许多具体问题，而且还能使我们更好地理解问题及其解法。

动态规划例题动态规划是一种以最优化原理为基础的问题求解方法，通过拆分问题为若干阶段，每个阶段求解一个子问题，再逐步推导出整个问题的最优解。

例如，有一个背包能够承受一定的重量，现有一些物品，每个物品都有自己的重量和价值。

我们希望将物品放入背包中，使得背包的总价值最大。

这个问题可以用动态规划来解决。

首先，我们定义一个二维数组dp，其中dp[i][j]表示在前i个物品中，容量为j的背包中所能放入的物品的最大价值。

那么，对于每一个物品，可以选择放入背包或者不放入背包。

如果选择放入背包，最大价值为dp[i-1][j-w[i]] + v[i]，其中w[i]表示第i个物品的重量，v[i]表示第i个物品的价值。

如果选择不放入背包，最大价值为dp[i-1][j]。

因此，dp[i][j]的状态转移方程为：dp[i][j] = max(dp[i-1][j-w[i]] + v[i], dp[i-1][j])。

基于这个状态转移方程，可以逐步求解从第1个物品到第n个物品的最大价值。

最终，dp[n][W]即为问题的最优解，其中W 表示背包的容量。

举个简单的例子，假设背包的容量为10，有3个物品，它们的重量分别为3、4、5，价值分别为4、5、6。

此时，可以得到如下的dp矩阵：0 0 0 0 0 0 0 0 0 0 00 0 0 4 4 4 4 4 4 4 40 0 0 4 5 5 9 9 9 9 90 0 0 4 5 5 9 10 10 14 14我们可以看到，dp[3][10]的最大价值为14，表示在前3个物品中，容量为10的背包中所能放入的物品的最大价值为14。

通过动态规划，我们可以有效地求解背包问题，得到物品放入背包的最优解。

这个例子只是动态规划的一个简单应用，实际上，动态规划可以解决各种复杂的问题，如最长公共子序列、最大子数组和、最大字段和等。

因此，学习动态规划是非常有意义的。

例1：机器负荷分配问题某公司新购进1000台机床，每台机床都可在高、低两种不同的负荷下进行生产，设在高负荷下生产的产量函数为g(x )=10x （单位：百件），其中x 为投入生产的机床数量，年完好率为a =0.7；在低负荷下生产的产量函数为h(y)=6y （单位：百件），其中y 为投人生产的机床数量，年完好率为b=0.9。

计划连续使用5年，试问每年如何安排机床在高、低负荷下的生产计划，使在五年内生产的产品总产量达到最高。

例2：某企业通过市场调查，估计今后四个时期市场对某种产品的需要量如下表：时期(k) 12 3 4 需要量(d k )2（单位）324假定不论在任何时期，生产每批产品的固定成本费为3(千元)，若不生产，则为零；生产单位产品成本费为1(千元)；每个时期生产能力所允许的最大生产批量为不超过6个单位，则任何时期生产x 个单位产品的成本费用为：若 0＜x ≤6 ， 则生产总成本＝3十1·x 若 x ＝0 ， 则生产总成本＝0又设每个时期末未销售出去的产品，在一个时期内单位产品的库存费用为0.5(千元)，同时还假定第1时期开始之初和在第4个时期之末，均无产品库存。

现在我们的问题是；在满足上述给定的条件下，该厂如何安排各个时期的生产与库存，使所花的总成本费用最低？例3：设某企业在第一年初购买一台新设备，该设备在五年内的年运行收益、年运行费用及更换新设备的净费用如下表：（单位：万元）年份(k) 役龄(t) 运行收益()k g t 运行费用()k r t 更新费用()k c t 第一年 0 22 6 18 第二年0 123 216 819 22第三年0122321185710192328第四年01232422191657101520243038第五年01234252320171446914202024303848试为该企业制定一个五年中的设备更新策略，使得企业在五年内总收益达到最大？例4：设有一辆栽重为10吨的卡车，用以装载三种货物，每种货物的单位重量及单件价值如表所示，问各种货物应装多少件，才能既不超过总重量又使总价值最大？货物 1 2 3单位重量 3 4 5单件价值 4 5 6。

动态规划典型案例解析及计算过程梳理动态规划（Dynamic Programming）是一种通过将问题分解为子问题来解决复杂问题的算法策略。

它通常用于优化问题，通过将问题的解决方案划分为相互重叠的子问题来降低计算复杂度。

下面将通过几个典型案例，详细解析动态规划的应用及其计算过程。

1. 斐波那契数列斐波那契数列是一种经典的动态规划问题。

它的定义是：F(n) =F(n-1) + F(n-2)，其中F(0) = 0，F(1) = 1。

我们需要计算第n个斐波那契数。

通过动态规划的思想，可以将该问题划分为子问题，即计算第n-1和第n-2个斐波那契数。

可以使用一个数组来保存已经计算过的斐波那契数，避免重复计算。

具体的计算过程如下：1. 初始化一个长度为n+1的数组fib，将fib[0]设置为0，fib[1]设置为1。

2. 从i=2开始遍历到n，对于每个i，计算fib[i] = fib[i-1] + fib[i-2]。

3. 返回fib[n]作为结果。

通过上述过程，我们可以快速地得到第n个斐波那契数。

这个案例展示了动态规划的重要特性，即将问题分解为子问题进行求解，并利用已经计算过的结果来避免重复计算。

2. 背包问题背包问题是另一个常见的动态规划问题。

问题的定义是：有一组物品，每个物品有自己的重量和价值，在限定的背包容量下，如何选择物品使得背包中的总价值最大化。

通过动态规划的思想，背包问题可以被划分为子问题。

我们可以定义一个二维数组dp，其中dp[i][j]表示在前i个物品中，背包容量为j时的最大价值。

具体的计算过程如下：1. 初始化一个大小为n+1行，m+1列的二维数组dp，其中n为物品数量，m为背包容量。

将所有元素初始化为0。

2. 从i=1开始遍历到n，对于每个i，从j=1开始遍历到m，对于每个j，进行如下判断：- 若当前物品的重量大于背包容量j，则dp[i][j] = dp[i-1][j]，即不选择当前物品；- 若当前物品的重量小于等于背包容量j，则dp[i][j] = max(dp[i-1][j], dp[i-1][j-wi] + vi)，即选择当前物品或不选择当前物品所能获得的最大价值。

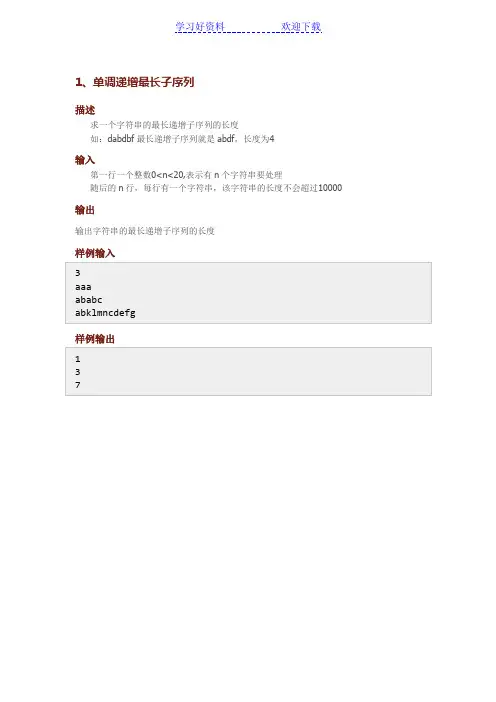
1、单调递增最长子序列描述求一个字符串的最长递增子序列的长度如：dabdbf最长递增子序列就是abdf，长度为4输入第一行一个整数0<n<20,表示有n个字符串要处理随后的n行，每行有一个字符串，该字符串的长度不会超过10000 输出输出字符串的最长递增子序列的长度样例输入3aaaababcabklmncdefg样例输出1372、最长公共子序列描述如题，需要写一个程序，得出最长公共子序列。

tip：最长公共子序列也称作最长公共子串(不要求连续)，英文缩写为LCS（Longest Common Subsequence）。

其定义是，一个序列S ，如果分别是两个或多个已知序列的子序列，且是所有符合此条件序列中最长的，则S 称为已知序列的最长公共子序列。

输入第一行给出一个整数N(0<N<100)表示待测数据组数接下来每组数据两行，分别为待测的两组字符串。

每个字符串长度不大于1000.输出每组测试数据输出一个整数，表示最长公共子序列长度。

每组结果占一行。

样例输入2asdfadfsd123abcabc123abc样例输出363、括号匹配时间限制：1000 ms | 内存限制：65535 KB描述给你一个字符串，里面只包含"(",")","[","]"四种符号，请问你需要至少添加多少个括号才能使这些括号匹配起来。

如：[]是匹配的([])[]是匹配的((]是不匹配的([)]是不匹配的输入第一行输入一个正整数N，表示测试数据组数(N<=10)每组测试数据都只有一行，是一个字符串S，S中只包含以上所说的四种字符，S的长度不超过100输出对于每组测试数据都输出一个正整数，表示最少需要添加的括号的数量。

每组测试输出占一行样例输入4[]([])[]((]([)]样例输出324、完全背包描述直接说题意，完全背包定义有N种物品和一个容量为V的背包，每种物品都有无限件可用。

动态规划常见类型题⽬⼀：01背包问题⼀个背包总容量为V，现在有N个物品，第i个物品体积为weight[i]，价值为value[i]，现在往背包⾥⾯装东西，怎么装能使背包的内物品价值最⼤？例题：给定⼀个数m，将m拆成不同的⾃然数的和的形式有多少种⽅案，这就是典型的01背包问题，背包容量为m，物品件数为k，这⾥⾯的k是隐含条件，可以求出来，因为m最多由1+2+…+k得到，由此可以根据m求得物品件数的上限。

题⽬⼆：完全背包问题⼀个背包总容量为V，现在有N个物品，第i个物品体积为weight[i]，价值为value[i]，每个物品都有⽆限多件，现在往背包⾥⾯装东西，怎么装能使背包的内物品价值最⼤？例题：假设现在有1元、2元、5元的纸币很多张，现在需要20块钱，你能给多少种找钱⽅案，这就可以认为是完全背包问题，即背包容量为20，物品体积分别为1、2、5。

题⽬三：最少硬币找零问题给予不同⾯值的硬币若⼲种种（每种硬币个数⽆限多），如何⽤若⼲种硬币组合为某种⾯额的钱，使硬币的的个数最少？在现实⽣活中，我们往往使⽤的是贪⼼算法，⽐如找零时需要13元，我们先找10元，再找2元，再找1元。

如果我们的零钱可⽤的有1、2、5、9、10。

我们找零18元时，贪⼼算法的策略是：10+5+2+1，四种，但是明明可以⽤两个9元的啊。

这种问题⼀般使⽤动态规划来解决。

⼀、⾸先来看01背包问题⽤⼀个数组f[i][j]表⽰，在只有i个物品，容量为j的情况下背包问题的最优解。

第i个物品可以选择放进背包或者不放进背包（这也就是0和1），假设放进背包（前提是放得下），那么f[i][j]=f[i－1][j-weight[i]+value[i]；如果不放进背包，那么f[i][j]=f[i－1][j]。

这就得出了状态转移⽅程： f[i][j]=max(f[i－1][j],f[i-1][j-weight[i]+value[i])⼆、完全背包问题和硬币找零问题其实这个两个问题⾮常相似，都是物品数⽬⽆限多，⼀个是不超过某个重量值W求最⼤value，⼀个是要获得某个value，求最⼩重量(每个硬币可以看成是重量为1的物品)。

[最短路问题]1．逆序法S5 = E（1）k = 4时，有3个状态D1、D2、D3，则f4 (D1) = d (D1, E) = 7，取x4 = E得S5 = E，为D1→E；f4 (D2) = d (D2, E) = 8，取x4 = E得S5 = E，为D2→E；f4 (D3) = d (D3, E) = 6，取x4 = E得S5 = E，为D3→E。

（2）k = 3时，有3个状态C1、C2、C3，则d (C1, D1) + f4 (D1) 取x3 = D2得S4 = D2，f3 (C1) = min d (C1, D2) + f4 (D2) = min = 10，为C1→D2→E；d (C1, D3) + f4 (D3)f3 (C2) = min d (C2, D2) + f4 (D2) = min = 13，取x3 = D2得S4 = D2或d (C2, D3) + f4 (D3) 取x3 = D3得S4 = D3，为C2→D2→E或C2→D3→E；f3 (C3) = min d (C3, D2) + f4 (D2) = min 10+8 = 15，取x3 = D3得S4 = D3，d (C3, D3) + f4 (D3) 9+6 为C3→D3→E。

（3）k = 2时，有3个状态B1、B2、B3，则f2 (B1) = min d (B1, C1) + f3 (C1) = min = 16，取x2 = C1得S3 = C1，d (B1, C2) + f3 (C2) 4+13 为B1→C1→D2→E；d (B2, C1) + f3 (C1) 取x2 = C1得S3 = C1，f2 (B2) = min d (B2, C2) + f3 (C2) = min = 13，为B2→C1→D2→E；d(B2, C3) + f3 (C3)f2 (B3) = min d (B3, C2) + f3 (C2) = min= 19，取x2 = C3得S3 = C3，d (B3, C3) + f3 (C3) 为B3→C3→D3→E。

动态规划应用案例动态规划是一种解决复杂问题的优化算法。

它通过将问题拆分成多个子问题，并记录每个子问题的解，以避免重复计算，从而提高算法的效率。

在实际应用中，动态规划被广泛用于解决各种问题，包括最优化问题、路径搜索问题、序列问题等。

本文将介绍几个动态规划的应用案例，以展示其在实际问题中的强大能力。

案例一：背包问题背包问题是动态规划中经典的一个例子。

假设有一个背包，容量为V，现有n个物品，每个物品的重量为wi，价值为vi。

要求在不超过背包容量的前提下，选取一些物品放入背包，使得背包中的物品总价值最大。

这个问题可以用动态规划来解决。

首先定义一个二维数组dp，其中dp[i][j]表示在前i个物品中选择一些物品，使得它们的总重量不超过j时的最大总价值。

然后，可以得到如下的状态转移方程：dp[i][j] = max(dp[i-1][j], dp[i-1][j-wi] + vi)最后，根据状态转移方程，可以循环计算出dp[n][V]的值，即背包中物品总价值的最大值，从而解决了背包问题。

案例二：最长递增子序列最长递增子序列是指在一个序列中，选取一些数字，使得这些数字按照顺序排列，且长度最长。

动态规划也可以应用于解决最长递增子序列问题。

假设有一个序列nums，长度为n。

定义一个一维数组dp，其中dp[i]表示以nums[i]为结尾的最长递增子序列的长度。

然后，可以得到如下的状态转移方程：dp[i] = max(dp[j] + 1)，其中j < i且nums[j] < nums[i]最后，循环计算出dp数组中的最大值，即为最长递增子序列的长度。

案例三：最大子数组和最大子数组和问题是指在一个数组中，选取一段连续的子数组，使得子数组的和最大。

动态规划也可以用于解决最大子数组和问题。

假设有一个数组nums，长度为n。

定义一个一维数组dp，其中dp[i]表示以nums[i]为结尾的连续子数组的最大和。

然后，可以得到如下的状态转移方程：dp[i] = max(dp[i-1] + nums[i], nums[i])最后，循环计算出dp数组中的最大值，即为最大子数组的和。

动态规划经典例题动态规划关键在于填表以及输出过程(个⼈理解)算法思想把原问题分解成若⼲个简单的⼦问题，保存已解决的⼦问题答案，避免重复计算。

动态规划常应⽤于有重叠⼦问题和最优⼦结构性质的问题。

⼦问题最优从⽽达到全局最优。

算法基本步骤找出最优解的性质递归的定义最优值以⾃底向上的⽅式计算最优值根据计算最优值的信息构造最优解经典案例⼀ 0/1背包问题import java.util.Scanner;import static sun.misc.Version.println;public class Dp{int n,v;//物品数量和容积int value[];int weight[];int dp[][];//dp[i][j]表⽰i个物品，容积为j时得到的最⼤价值public void Maxvalue(){for(int i=1;i<=n;i++){for(int j=0;j<=v;j++){//注意下标还有别的写法if(j>=weight[i]){dp[i][j]=Math.max(value[i]+dp[i-1][j-weight[i]], //拿了第i个dp[i-1][j]);//没拿}else{dp[i][j]=dp[i-1][j];}}}for(int i=0;i<=n;i++){for(int j=0;j<=v;j++){System.out.print(dp[i][j] + " ");}System.out.println();}}public void BestResult(int n,int v){boolean isAdd[]=new boolean[n+1];//记录物品是否拿了for(int i=n;i>=1;i--){ // 倒序if(dp[i][v]==dp[i-1][v]){isAdd[i]=false;}else{isAdd[i]=true;}v-=weight[i];}for(int i=1;i<=n;i++){//把结果正序输出System.out.println(i+"是"+isAdd[i]);}}public void Init(){Scanner sc =new Scanner (System.in);n=sc.nextInt();v=sc.nextInt();weight=new int [n+1];value=new int [n+1];dp=new int[n][v];for(int i=1;i<=n;i++){weight[i]=sc.nextInt();}for(int i=1;i<=n;i++){value[i]=sc.nextInt();}}public static void main(String[] args){Dp bag=new Dp();bag.Init();bag.Maxvalue();bag.BestResult(bag.n,bag.v);}}经典例题⼆矩阵连乘问题public class dp_matrix {int j=6;int p[];int s[][];//记录断点kint dp[][];//最⼩代价public dp_matrix() {p=new int[]{10,15,25,35,20,10,40};s=new int[j][j];dp=new int[j][j];}public void dp_matrix(){for(int i=0;i<j;i++){dp[i][i]=0;}for(int r=2;r<=j;r++){for(int i=0;i<=j-r;i++){int n=i+r-1;dp[i][n]=dp[i+1][n]+p[i]*p[i+1]*p[n+1];//i<js[i][n]=i;//在i+1分的for(int k=i+1;k<n;k++){int key=dp[i][k]+dp[k+1][n]+p[i]*p[k+1]*p[n];//注意下标if(key<dp[i][n]){dp[i][n]=key;//更新s[i][n]=k;// 更新}}}}}public void traceBack(int i ,int j){if(i==j){System.out.print(i);}else{System.out.print("(");traceBack(i,s[i][j]);traceBack(s[i][j]+1,j);System.out.print(")");}}public static void main(String[] args){dp_matrix matrix=new dp_matrix();matrix.dp_matrix();matrix.traceBack(0,5);}}经典例题三最长公共⼦序列public class Dp_Lcs {public void Maxlength(){String []m={"a","b","c","d"};String []n={"b","c","d"};int x=m.length;int y=n.length;int [][] dp=new int[m.length+1][n.length+1];//dp[i][j]表⽰xi与yi两个序列最长公共⼦序列的长度 int[][] s=new int[m.length][n.length];//s[i][j]⽤来储存m[i]与n[j]之间的关系for(int i=0;i<=x;i++){//初始化dp[i][0]=0;}for(int i=0;i<=y;i++){dp[0][i]=0;}for(int i=1;i<=x;i++){for(int j=1;j<=y;j++){if(m[i-1]==(n[j-1])){ //相等时dp[i][j]=dp[i-1][j-1]+1;//参照图s[i-1][j-1]=1;}else {dp[i][j]=Math.max(dp[i-1][j], dp[i][j-1]);if(dp[i][j]==dp[i-1][j]){s[i-1][j-1]=-1;}else s[i-1][j-1]=0;}}}for(int i=0;i<x;i++){for(int j=0;j<y;j++){System.out.print(s[i][j]);}System.out.println();}for(int i=0;i<x+1;i++){for(int j=0;j<y+1;j++){System.out.print(dp[i][j]);}System.out.println();}System.out.println("最长为"+" ");LCS(s,m,x,y);}public void LCS(int[][] s, String[] m, int i, int j){//{递归遍历s[i][j]if(i == 0 || j == 0){ return;}switch (s[i-1][j-1]) {case 1:LCS(s,m,i - 1, j - 1);System.out.println(m[i-1]+ " ");break;case 0:LCS(s,m,i - 2, j);break;default:LCS(s,m,i, j-2);break;}}public static void main(String[] args) { Dp_Lcs a=new Dp_Lcs();a.Maxlength();}}。

例1 求解下列整数规划得最优解:()123123max 45634510..01,2,3,j j Z x x x x x x s t x j x =++++⎧⎪⎨=⎪⎩≤≥为整数.解 （1）建立动态规划模型:阶段变量: 将给每一个变量 赋值瞧成一个阶段, 划分为3个阶段, 且阶段变量k=1,2,3. 设状态变量 表示从第 阶段到第3阶段约束右端最大值, 则 设决策变量k x 表示第k 阶段赋给变量k x 得值(1,2,3)k =、 状态转移方程: 阶段指标: 基本方程；()(){}()3113,2,1044()max ,()0.s k k k k k k k k k k x a f s u s x f s f s ++⎡⎤=⎢⎥⎢⎥⎣⎦⎧=+⎪⎨⎪=⎩≤≤ 其中1233,4, 5.a a a === 用逆序法求解: 当3k =时，()(){}{}33333443330055max 6max 6,ssx x f s x f s x ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦=+=≤≤≤而 表示不超过 得最大整数。

因此, 当 时, ；当 时, 可取0或1；当 时, 可取0, 1, 2,由此确定 现将有关数据列入表4.1中当 时, 有()(){}(){}22222332322220044max 5max 54,ssx x f s xf s xf s x ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦=+=+-≤≤≤≤而 。

所以当 时, ；当 时, ；当 时 。

由此确定 。

现将有关数据列入表4.2中、当时,有()(){}(){}11111221211110033max 4max 43,ssx x f s x f s x f s x ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦=+=+-≤≤≤≤例5 用动态规划方法解下列非线性规划问题⎩⎨⎧=≥≤++⋅⋅=3,2,1 0 max 3213221i x c x x x x x x z i 解: 解决这一类静态规划问题, 需要人为地赋予时间概念, 从而将该问题转化为多阶段决策过程。

动态规划经典问题1、三角数塔问题设有一个三角形的数塔，顶点为根结点，每个结点有一个整数值。

从顶点出发，可以向左走或向右走，如图所示：要求从根结点开始，请找出一条路径，使路径之和最大，只要输出路径的和。

【代码】//// 例题1 三角数字塔问题////#include <stdio.h>#include <stdlib.h>#define MAXN 101intn,d[MAXN][MAXN];int a[MAXN][MAXN];voidfnRecursive(int,int);//递推方法函数声明intfnMemorySearch(int,int);//记忆化搜索函数声明int main(){inti,j;printf("输入三角形的行数n(n=1-100):\n");scanf("%d",&n);printf("按行输入数字三角形上的数(1-100):\n");for(i=1; i<=n; i++)for(j=1; j<=i; j++)scanf("%d",&a[i][j]);for(i=1; i<=n; i++)for(j=1; j<=i; j++)d[i][j]=-1;//初始化指标数组printf("递推方法：1\n记忆化搜索方法：2\n");int select;scanf("%d",&select);if(select==1){fnRecursive(i,j);//调用递推方法printf("\n%d\n",d[1][1]);}if(select==2){printf("\n%d\n",fnMemorySearch(1,1));//调用记忆化搜索方法}elseprintf("输入错误！");return 0;}voidfnRecursive(inti,int j)//递推方法实现过程{for(j=1; j<=n; j++)d[n][j]=a[n][j];for(i=n-1; i>=1; i--)for(j=1; j<=i; j++)d[i][j]=a[i][j]+(d[i+1][j]>d[i+1][j+1]?d[i+1][j]:d[i+1][j+1]); }intfnMemorySearch(inti,int j)//记忆化搜索实现过程{if(d[i][j]>=0) return d[i][j];if(i==n) return(d[i][j]=a[i][j]);if(fnMemorySearch(i+1,j)>fnMemorySearch(i+1,j+1))return(d[i][j]=(a[i][j]+fnMemorySearch(i+1,j)));elsereturn(d[i][j]=(a[i][j]+fnMemorySearch(i+1,j+1)));}2、硬币问题问题描述：有n种硬币，面值分别为V1,V2,…,Vn, 每种有无限多。

动态规划题目【引例１、上楼梯】一个含有n阶的楼梯，一次可以走1阶或2阶，从底走到顶一共有几种走法？n<=90。

【引例2、数字三角形】a1有一个数字三角形，编程求从最顶层到最底层的一条路所经过位置上数字之和的最大值。

每一步只能向左下或右下方向走。

下图数据的路应为7->3->8->7->5，和为30。

输入：文件输入(从键盘读入文件名)，文件格式：第一行：R(1<=R<=10000),数字三角形共有R行；以下R行：依次表示数字三角形中每行中的数字。

每个数都是非负的，且<=100.输出：一个正整数，路径上数字之和的最大值。

输入样例：573 88 1 02 7 4 44 5 2 6 5输出样例：30【引例3、求最大连续子序列的和。

】a2输入：第一行：n（N<500）第二行：n个整数（-3000，3000）。

输出：最大连续子序列的和。

样例：输入：7-6 4 -1 3 2 -3 2输出：81、最长递增序列b1设有整数序列b1,b2,b3,…,bm，若存在i1<i2<i3<…<in，且bi1<bi2<bi3<…<bin，则称b1,b2,b3,…,bm 中有长度为n的递增序列bi1,bi2,bi3,…,bin。

求序列b1,b2,b3,…,bm中最大递增序列长度(n)。

输入：m（<1000）,整数序列输出：最大长度n样例：输入：7-6 4 -1 3 8 -3 2输出：42、背包问题b2设有ｎ种物品，每种物品有一个重量及一个价值。

同时有一个背包，最大载重量为W，今从ｎ种物品中选取若干件，使其重量的和小于等于W，而价值的和为最大。

输入数据：第一行两个数：物品总数Ｎ（<100），背包载重量W(<100)；两个数用空格分隔；第二行N个数,为Ｎ种物品重量Wi；两个数用空格分隔；第三行N个数,为N种物品价值Vi; 两个数用空格分隔；输出数据：第一行总价值；输入样例：4 103 4 5 77 15 20 25输出样例：353、迷宫寻宝b3一个n行m列的迷宫（1<=n,m<=50），入口在左上角，规定只能向下或向右走。

动态规划运筹学例题动态规划（DynamicProgramming）是运筹学中一种基于分析多阶段决策过程的重要算法。

它主要指用于多步决策的最优化方法，是在一定时期内，为了达到目标，从多种可能的决策中选择最优方案的过程。

它的最大特点就是将一个较大的复杂的问题分解成若干个小的子问题，将解决这些子问题的过程和结果组合起来，从而解决原问题。

下面以最常见的“背包问题”为例，来深入讲解动态规划的基本原理。

假设有一个背包，背包容量为5KG，要放入这个背包中的有：物品A（重量3kg，价值2），物品B（重量2kg，价值3），物品C（重量1kg，价值4）。

问：最多能放入背包中的最大价值是多少？动态规划会将这个问题分解成两个子问题，即：当第一个物品放入背包时，最多能放入背包中的最大价值是多少？当第二个物品放入背包时，最多能放入背包中的最大价值是多少？通过上面划分出来的2个子问题，我们就可以用动态规划来解决这个问题。

首先，定义f（i，w）表示前i个物品放入背包中，总重量不超过w的最大价值，即：f（i，w）=max{f（i-1，w），f（i-1，w-wi）+vi}其中，f（i-1，w）表示前i-1个物品放入背包中，总重量不超过w的最大价值，f（i-1，w-wi）+vi表示前i-1个物品放入背包中，总重量不超过w-wi的最大价值，再加上第i个物品的价值vi。

下面我们来解决上面所说的背包问题：对于第一个物品A，有两种情况，第一种情况：不放入背包，则背包中的最大价值f（1，5）=0；第二种情况：将物品A放入背包，则背包中最大价值f（1，2）=2。

由于5>2，所以f（1，5）=2。

第二个物品B，有两种情况，第一种情况：不放入背包，f（2，5）=2；第二种情况：将物品B放入背包，则背包中最大价值f（2，3）=2+3=5。

由于5>3，所以f（2，5）=5。

同理，有第三个物品C，有两种情况，第一种情况：不放入背包，f（3，5）=5；第二种情况：将物品C放入背包，则背包中最大价值f（3，4）=5+4=9。