管道的膨胀

管道膨胀量及推力计算1.管道膨胀量计算：管道在温度变化过程中会发生热胀冷缩，从而引起管道的膨胀或收缩。

通常使用以下公式计算管道的膨胀量：ΔL=α*L*ΔT其中，ΔL为管道的膨胀量，α为管道材质的线膨胀系数，L为管道的原始长度，ΔT为温度变化量。

线膨胀系数α是一个物质特性，反映了材料在单位温度变化下的长度变化。

具体的数值可以从材料手册或相关标准中查得。

2.管道推力计算：当流体在管道中流动时，流体的动量变化会产生推力。

推力的大小与流体流速、密度以及管道弯曲半径有关。

可以使用以下公式计算管道推力：F=ρ*A*V^2/2其中，F为管道的推力，ρ为流体的密度，A为管道的横截面积，V为流体的流速。

需要注意的是，这个公式是针对弯曲管道的推力计算。

若是直线管道，则推力为零。

3.管道膨胀量和推力的综合计算：在实际工程中，通常需要考虑管道的膨胀量和推力同时存在的情况。

对于这种情况，可以使用以下公式计算管道的有效膨胀量和推力：ΔL_eff = ΔL - ΔL_sup其中，ΔL_eff为管道的有效膨胀量，ΔL为管道的总膨胀量，ΔL_sup为管道支架的补偿量。

补偿量是为了减小管道在温度变化时的应力，并防止超过管道材质的可承受范围。

F_eff = F - F_sup其中，F_eff为管道的有效推力，F为管道的总推力，F_sup为管道支架的支持力。

支持力的作用是为了抵消由推力引起的管道变形，并保持管道在正常运行中的位置和形态。

管道的支架及材质的选择应根据实际工程情况来决定，以保证管道的安全运行和稳定性。

综上所述，管道膨胀量及推力计算是工程设计中不可或缺的一项内容。

通过合理计算和选择管道的支、吊设备，可以确保管道在温度变化或介质流动引起的膨胀力和推力下保持正常运行和稳定性。

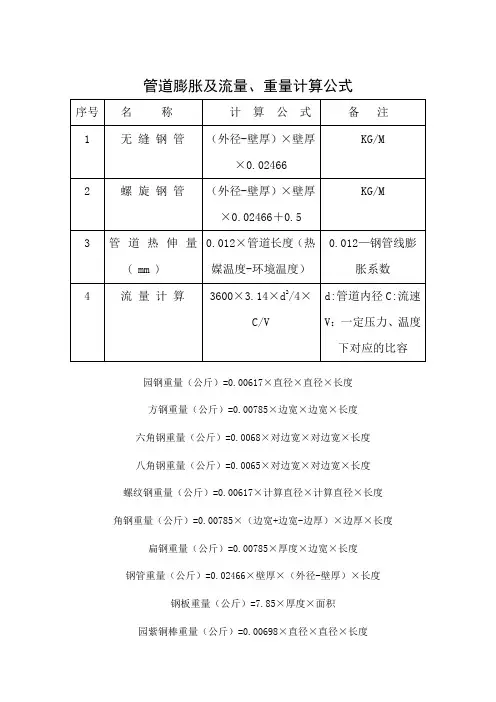
管道膨胀及流量、重量计算公式园钢重量（公斤）=0.00617×直径×直径×长度方钢重量（公斤）=0.00785×边宽×边宽×长度六角钢重量（公斤）=0.0068×对边宽×对边宽×长度八角钢重量（公斤）=0.0065×对边宽×对边宽×长度螺纹钢重量（公斤）=0.00617×计算直径×计算直径×长度角钢重量（公斤）=0.00785×（边宽+边宽-边厚）×边厚×长度扁钢重量（公斤）=0.00785×厚度×边宽×长度钢管重量（公斤）=0.02466×壁厚×（外径-壁厚）×长度钢板重量（公斤）=7.85×厚度×面积园紫铜棒重量（公斤）=0.00698×直径×直径×长度园黄铜棒重量（公斤）=0.00668×直径×直径×长度园铝棒重量（公斤）=0.0022×直径×直径×长度方紫铜棒重量（公斤）=0.0089×边宽×边宽×长度方黄铜棒重量（公斤）=0.0085×边宽×边宽×长度方铝棒重量（公斤）=0.0028×边宽×边宽×长度六角紫铜棒重量（公斤）=0.0077×对边宽×对边宽×长度六角黄铜棒重量（公斤）=0.00736×边宽×对边宽×长度六角铝棒重量（公斤）=0.00242×对边宽×对边宽×长度紫铜板重量（公斤）=0.0089×厚×宽×长度黄铜板重量（公斤）=0.0085×厚×宽×长度铝板重量（公斤）=0.00171×厚×宽×长度园紫铜管重量（公斤）=0.028×壁厚×（外径-壁厚）×长度园黄铜管重量（公斤）=0.0267×壁厚×（外径-壁厚）×长度园铝管重量（公斤）=0.00879×壁厚×（外径-壁厚）×长度注：公式中长度单位为米，面积单位为平方米，其余单位均为毫米。

消除管道热膨胀的形式1.引言1.1 概述管道热膨胀是指管道在受到热量加热时，由于其材料的热胀冷缩特性，导致管道长度变长或变短的现象。

这种现象在很多工程领域中都存在，特别是在管道输送液体或气体时更加明显。

管道热膨胀的主要原因是热量的传递。

当管道输送液体或气体时，由于液体或气体的温度变化，传导给管道内的金属材料，导致管道发生热胀冷缩。

这种膨胀和收缩的过程会导致管道产生应力和位移，并且可能对管道系统产生不利影响，如管道的破裂、泄露等。

为了解决管道热膨胀问题，需要采取相应的措施来消除或减小其对管道系统的影响。

常用的方法是通过合理的管道设计和安装方式，采取补偿措施来减小管道热膨胀造成的影响。

例如，在管道的设计中可以考虑设置膨胀节或伸缩节，通过这些装置来吸收管道的热胀冷缩变形；在管道的安装过程中，可以采用弯曲管道、Z型弯管以及导热跳距等方法来消除或减小管道热膨胀的影响。

总而言之，消除管道热膨胀的形式是一个复杂而重要的问题。

只有通过合理的管道设计和采取适当的安装措施，才能有效地减小管道热膨胀所带来的风险和不利影响。

在未来的研究中，我们可以进一步探索新的解决方案和技术，以适应不同工程环境中管道热膨胀问题的需求。

文章结构部分的内容可以从以下几个方面进行阐述：1.2 文章结构为了使读者更好地理解文章内容，本文将按照以下结构进行阐述：a) 引言部分：首先对本文的主题进行概述，介绍管道热膨胀的问题，并对文章的目的进行说明。

b) 正文部分：本部分将分为两个小节进行阐述。

首先，我们将介绍管道热膨胀的原因，包括温度变化引起的膨胀问题以及这种膨胀可能带来的危害。

随后，我们将重点介绍消除管道热膨胀的形式上的方法，包括预留伸缩节、采用弯头和弯管、采用支吊架等技术手段。

通过这些方法的应用，可以有效减少或消除管道热膨胀带来的不利影响。

c) 结论部分：最后将对全文进行总结，并对消除管道热膨胀的形式提出展望，提出一些可能的改进和发展方向。

管道专业施工相关热力计算
第一部分管道热推力的计算
一、管道热伸长计算
管道的热伸长量的大小与管材的种类、管段的长度及温差数值有关。

ΔL=αLΔt=αL(t2-t1) 公式一
式中ΔL——管段的热伸长量（m）；
α——管材的线膨胀系数[m/(m•)]；在附表1中查询
L——管段长度（m）；
t1 ——安装时环境温度（℃）；
t2 ——管内介质最高温度（℃）；
二、管道的热应力计算
管道受热时所产生的热应力大小与管材的性质、管段长度及热伸长量有关。

δ=E(ΔL/L) 公式二
式中δ——管道受热产生的热应力（MPa）；
E——管道的弹性模量（MPa）；在附表2中查询
ΔL——管段的热伸长量（m）；（由公式一得出）
L——管段长度（m）；
当管道受热时的应力知道后，乘以管道截面积，就是整个截面积所产生的总的热推力，即：
P=106δF 公式三
式中P——管道的热推力（N）
F——管道截面积（㎡）
δ——管道热应力（MPa）
附表1：常用钢材的线膨胀系数(×10-6m/m·℃)
附表2：不同温度下不同材料的弹性模量
第二部分相关补偿器的计算
一、管道的自然补偿
1、L形直角弯自然补偿；L形自然补偿管段如图。

管道膨胀系数
摘要：
1.管道膨胀系数的定义和计算公式
2.管道膨胀系数的影响因素
3.不同材质的管道膨胀系数
4.管道膨胀系数在工程实践中的应用
5.总结
正文：
管道膨胀系数是指管道在温度变化时，其长度或体积发生变化的程度。

它是一个重要的物理参数，对于管道的设计、施工和运行都有重要的意义。

管道膨胀系数的计算公式为：ΔL = aLΔT，其中，ΔL是管道长度的变化，a是管道的线性膨胀系数，L是管道的原始长度，ΔT是温度的变化。

管道膨胀系数的影响因素主要有以下几点：
- 管道的材料：不同的材料具有不同的膨胀系数，例如，钢的膨胀系数约为12×10^-6/℃，而铝的膨胀系数约为23×10^-6/℃。

- 管道的直径：管道的直径越大，其膨胀系数越小。

- 温度变化：温度变化越大，管道的膨胀系数越大。

在工程实践中，管道膨胀系数在以下几个方面得到了应用：
- 管道设计和施工：根据管道膨胀系数，可以确定管道的布局和尺寸，以防止管道因温度变化而产生过大的应力。

- 管道连接和支架：在管道连接和支架的设计中，需要考虑管道膨胀系
数，以保证管道在温度变化时能够自由膨胀，避免因约束而产生的应力。

- 温度控制系统：通过控制管道的温度，可以调节管道的膨胀系数，从而实现对管道长度的控制。

总结起来，管道膨胀系数是一个重要的参数，对于管道的设计、施工和运行都有重要的意义。

管道膨胀系数【原创版】目录一、管道膨胀系数的概念和影响因素二、管道膨胀系数的计算方法三、油品在管道内的膨胀率计算四、管道热膨胀伸长量计算五、实例：热力管道 dn1200 线膨胀系数六、结论：管道膨胀系数的应用和意义正文一、管道膨胀系数的概念和影响因素管道膨胀系数是指管道在温度变化时，管道长度的改变量与温度变化量之比。

它是一个反映材料膨胀或收缩程度的物理量，通常用线膨胀系数或平均线膨胀系数表示。

管道膨胀系数受材料、温度变化范围、管道长度等因素影响。

二、管道膨胀系数的计算方法管道膨胀系数的计算公式为：α = (ΔL/L) / (ΔT/T)，其中α为管道膨胀系数，ΔL 为管道长度的变化量，L 为管道的原始长度，ΔT 为温度的变化量，T 为原始温度。

三、油品在管道内的膨胀率计算油品在管道内的膨胀率是指油品在温度变化时，体积的改变量与原始体积之比。

油品的膨胀率受油品的种类、温度变化范围等因素影响。

计算油品在管道内的膨胀率时，需要知道油品的膨胀系数，可以通过实验或查阅资料获得。

四、管道热膨胀伸长量计算管道热膨胀伸长量是指管道在温度变化时，管道长度的改变量。

管道热膨胀伸长量的计算公式为：ΔL = α * L * ΔT，其中α为管道膨胀系数，L 为管道长度，ΔT 为温度变化量。

五、实例：热力管道 dn1200 线膨胀系数热力管道 dn1200 的线膨胀系数为 12×10^-6/℃。

假设管道安装时的温度为 20℃，管道工作时的温度为 80℃，管道长度为 100 米，则管道热膨胀伸长量为：ΔL = 12×10^-6/℃ * 100m * (80℃ - 20℃) = 960mm。

六、结论：管道膨胀系数的应用和意义管道膨胀系数是管道设计、施工和运行中一个重要的参数。

了解管道膨胀系数可以帮助我们预测管道在温度变化时的长度变化，从而确保管道的安全运行。

不锈钢管的膨胀系数不锈钢管是一种常见的管材，其具有高强度、耐腐蚀、易加工等优点，因此在工业、建筑、化工等领域得到广泛应用。

然而，在不同的温度下，不锈钢管的长度会发生变化，这就需要了解不锈钢管的膨胀系数，以便在设计和使用过程中进行合理的考虑。

不锈钢管的膨胀系数是指在温度变化时，单位长度的管材长度变化量与原长度之比。

通常用α表示，单位为1/℃。

由于不锈钢管的膨胀系数受到多种因素的影响，如温度、成分、加工方式等，因此不同类型的不锈钢管其膨胀系数也会有所不同。

一般来说，不锈钢管的膨胀系数随着温度的升高而增大。

在常温下，不锈钢管的膨胀系数较小，大约为1.2×10^-5/℃。

当温度升高到100℃左右时，膨胀系数会增加到1.4×10^-5/℃左右；当温度升高到500℃时，膨胀系数会进一步增加到2.0×10^-5/℃左右。

因此，在高温环境下使用不锈钢管时，需要考虑其膨胀系数对管道系统的影响。

除了温度之外，不锈钢管的膨胀系数还受到材料成分和加工方式的影响。

一般来说，镍含量越高的不锈钢管，其膨胀系数越大。

此外，冷拔和冷轧加工的不锈钢管比热轧加工的不锈钢管具有更小的膨胀系数。

在实际应用中，需要根据具体情况选择合适的不锈钢管，并考虑其膨胀系数对系统的影响。

例如，在设计高温管道系统时，需要预留一定的伸长量，以免因不锈钢管的伸长而导致系统失效。

此外，在安装过程中也需要注意控制不锈钢管的伸长量，避免出现过大的变形和应力集中。

总之，了解不锈钢管的膨胀系数是进行合理设计和使用的前提之一。

在实际应用中，需要根据具体情况选择合适的不锈钢管，并考虑其膨胀系数对系统的影响，以确保系统的安全运行和长期稳定性。

管道专业施工相关热力计算
第一部分管道热推力的计算
一、管道热伸长计算
管道的热伸长量的大小与管材的种类、管段的长度及温差数值有关。

ΔL=αLΔt=αL(t2-t1) 公式一
式中ΔL——管段的热伸长量（m）；
α——管材的线膨胀系数[m/(m•)]；在附表1中查询
L——管段长度（m）；
t1 ——安装时环境温度（℃）；
t2 ——管内介质最高温度（℃）；
二、管道的热应力计算
管道受热时所产生的热应力大小与管材的性质、管段长度及热伸长量有关。

δ=E(ΔL/L) 公式二
式中δ——管道受热产生的热应力（MPa）；
E——管道的弹性模量（MPa）；在附表2中查询
ΔL——管段的热伸长量（m）；（由公式一得出）
L——管段长度（m）；
当管道受热时的应力知道后，乘以管道截面积，就是整个截面积所产生的总的热推力，即：
P=106δF 公式三
式中P——管道的热推力（N）
F——管道截面积（㎡）
δ——管道热应力（MPa）
附表1：常用钢材的线膨胀系数(×10-6m/m·℃)
附表2：不同温度下不同材料的弹性模量
第二部分相关补偿器的计算
一、管道的自然补偿
1、L形直角弯自然补偿；L形自然补偿管段如图。

管道热胀冷缩
管道热胀冷缩是指管道在不同温度下会出现长度变化，即热胀冷缩现象。

当管道受热膨胀时，长度会增加，反之则会缩短。

这种现象在工业、建筑、暖通等领域都非常常见。

管道的热胀冷缩对管道的安装、使用和维护都会带来影响。

如果不注意管道的热胀冷缩问题，会导致管道变形、裂缝、泄漏等问题。

因此，对于管道的热胀冷缩问题，需要采取一些措施来解决。

一种解决方法是安装伸缩节。

伸缩节可以在管道受热膨胀或冷缩时，根据管道的长度变化来自行伸缩，吸收热胀冷缩产生的应力，保证管道的稳定性和安全性。

另外，还可以采用支吊架的方法。

支吊架可以使管道位置固定，不受到热胀冷缩的影响。

同时，支吊架还可以减小管道的振动，保证管道的正常运行。

在管道设计和安装中，应根据管道的长度、材料、温度等因素，合理设定伸缩节和支吊架的位置和数量。

这样才能有效解决管道热胀冷缩问题，确保管道的安全运行。

- 1 -。

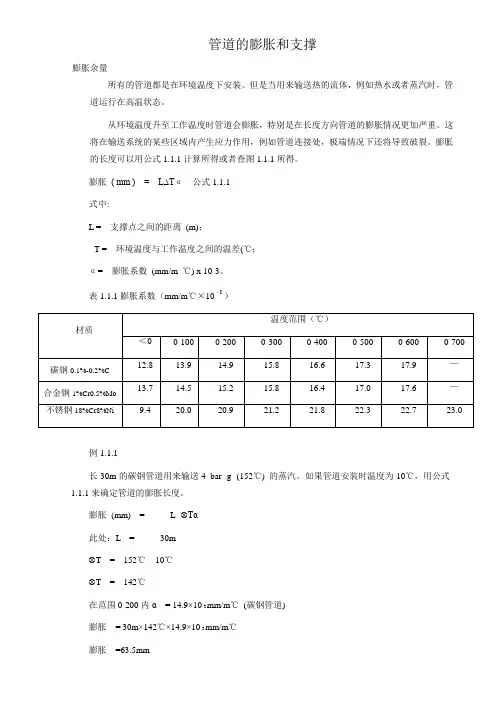
第一节 管材的线膨胀及伸缩量的计算一、热膨胀量的计算管道安装完毕投入运行时，常因管内介质的温度与安装时环境温度的差异而产生伸缩。

另外，由于管道本身工作温度的高低，也会引起管道的伸缩。

实验证明，温度变化而引起管道长度成比例的变化。

管道温度升高，由于膨胀，长度增加；温度下降，则由于收缩，长度缩短。

温度变化1度相应的长度成比例变化量称为管材的线膨胀系数。

不同材质的材料线膨胀系数也不同。

碳素钢的线膨胀系数为12×10—6／℃，而硬质聚氯乙烯管的线膨胀系数为80X10—6／℃，约为碳素钢的七倍。

管材受热后的线膨胀量，按下式进行计算：()L t t L 21-=∆α式中△L ——管道热膨胀伸长量(m)；α——管材的线膨胀系数(1／K)或(1／℃)； t 2——管道运行时的介质温度(℃)；t l ——管道安装时的温度(℃)，安装在地下室或室内时取t 1=—5℃；当室外架空敷设时，t 1应取冬季采暖室外计算温度；L ——计算管段的长度(m)。

不同材质管材的。

值见表2—1。

表2—1不同材质管材的线膨胀系数在管道工程中，碳素钢管应用最广，其伸长量的计算公式为()L t t L 2161012-⨯=∆-式中12×10—6——常用钢管的线膨胀系数(1／)。

根据式(2—2)制成管道的热伸长量△L 表(见表2—2)，由表中可直接查出不同温度下相应管长的热伸长量。

例有一段室内热水采暖碳素钢管道，管长70m ，输送热水温度为95℃，试计算此段管道的热伸长量。

解根据钢管的热膨胀伸长量计算式(2—2)△L=12×10—6(t 1—t 2)L=12×10—6（95+5）×70=0.084m由已知管长及送水温度，直接查表2—2，也可得管道的热伸长量△L 。

如果管道中通过介质的温度低于环境温度，则计算出来的是缩短量。

二、热应力计算如果管道两端不固定，允许它自由伸缩，则热伸缩量对管予的强度没有什么影响。

管道膨胀系数计算
管道膨胀系数是指管道在温度变化时，由于热胀冷缩导致的长度变化与温度变化的比值。

计算管道膨胀系数是非常重要的，因为它可以帮助工程师确定在不同温度下管道的设计和安装要求。

计算方法
管道膨胀系数可以通过以下公式来计算：
膨胀系数= (α × L × ΔT) / 1000
其中，α 是管道材料的线膨胀系数（单位：1/℃），L 是管道的长度（单位：mm），ΔT 是温度变化（单位：℃）。

示例
假设我们有一根长度为5000mm的钢管，钢管的线膨胀系数为0.0121/℃。

如果温度变化为50℃，我们可以使用上述公式来计算膨胀系数：
膨胀系数 = (0.0121 × 5000 × 50) / 1000 = 30.25
因此，钢管在50℃温度变化下的膨胀系数为30.25。

应用
计算得到的膨胀系数可以用于确定管道在不同温度下的变化情况，从而帮助工程师选择合适的管道设计和安装方法。

特别是在长距离的管道系统中，膨胀系数的计算对于管道的稳定性和安全性至关重要。

注意：以上计算结果仅供参考，请根据具体情况进行验证和调整。

参考资料。

蒸汽管道膨胀量计算公式在蒸汽管道工程中，膨胀量的计算方法和压力计算方法是一致的。

但压力计算方法是按工作压力计算的。

工作压力按蒸汽管道总的膨胀比确定。

工作压力在工作时不得超过工作管径的1/3或1/2以上；与工作温度和工作压力有关的设备中用的蒸汽量与工作压力成正比。

另外，蒸汽管道系统还应按设计的压力来考虑蒸汽管道的弹性元件的压力膨胀系数，但不应超过设备使用允许的值。

一、膨胀量管道在运行中，会发生变形，产生压力损失，造成损失较大时，必须加以补偿。

补偿装置的设计应符合下列规定：(1)弹性元件允许膨胀量：当管内介质中温度变化较大时，允许膨胀量为：式给出了在系统承受正常工作压力和温度变化时管内介质弹性元件的温度应变值。

计算公式如下：(2)伸长率：根据膨胀率计算公式可计算的伸长率。

二、蒸汽管道与流体之间流动性能蒸汽管道与流体之间的流动性能是由压力膨胀量和温度膨胀量两个方面的综合因素决定的。

不同的性质和压力值对膨胀量和温度的大小也有影响。

根据不同性质和压力值对膨胀量和温度的影响，可采用压力膨胀量和温度的相关系数关系来表示。

压力膨胀量与管道的膨胀系数呈正相关，温度的相关系数 r值为0时，膨胀量也可认为是无膨胀率的；而温度之间关系为正相关，膨胀率越大，温度越低，膨胀量也越大。

温度越高，膨胀量也越大；温度越低，膨胀量也越大；温度越高，膨胀量也越大。

因此确定膨胀率对蒸汽输出量和温度均有重要的意义。

三、膨胀系数对于蒸汽管道，膨胀系数是其弹性元件系统的最重要的性能指标。

它反映的是介质的温度、压力、体积分数和内压等变化对弹性元件的影响及其程度。

在设计蒸汽管道时应考虑在相同工况下，弹性元件的压力膨胀系数与温度和压力成正比，因此应采用相应的系数。

如果锅炉压力允许波动范围大，就不宜采用膨胀系数高的系数。

对于非蒸汽介质管道或不能用膨胀系数高的膨胀系数的管道中，当温度升高时，它在一定范围内的膨胀比随之增大，故可采用膨胀系数高的系数。

对于含气和含灰渣管道，如内管系统膨胀系数过大，可采用膨胀系数低的系数，如补偿器、换热器等。

管道膨胀及流量、重量计算公式园钢重量（公斤）=0.00617×直径×直径×长度方钢重量（公斤）=0.00785×边宽×边宽×长度六角钢重量（公斤）=0.0068×对边宽×对边宽×长度八角钢重量（公斤）=0.0065×对边宽×对边宽×长度螺纹钢重量（公斤）=0.00617×计算直径×计算直径×长度角钢重量（公斤）=0.00785×（边宽+边宽-边厚）×边厚×长度扁钢重量（公斤）=0.00785×厚度×边宽×长度钢管重量（公斤）=0.02466×壁厚×（外径-壁厚）×长度钢板重量（公斤）=7.85×厚度×面积园紫铜棒重量（公斤）=0.00698×直径×直径×长度园黄铜棒重量（公斤）=0.00668×直径×直径×长度园铝棒重量（公斤）=0.0022×直径×直径×长度方紫铜棒重量（公斤）=0.0089×边宽×边宽×长度方黄铜棒重量（公斤）=0.0085×边宽×边宽×长度方铝棒重量（公斤）=0.0028×边宽×边宽×长度六角紫铜棒重量（公斤）=0.0077×对边宽×对边宽×长度六角黄铜棒重量（公斤）=0.00736×边宽×对边宽×长度六角铝棒重量（公斤）=0.00242×对边宽×对边宽×长度紫铜板重量（公斤）=0.0089×厚×宽×长度黄铜板重量（公斤）=0.0085×厚×宽×长度铝板重量（公斤）=0.00171×厚×宽×长度园紫铜管重量（公斤）=0.028×壁厚×（外径-壁厚）×长度园黄铜管重量（公斤）=0.0267×壁厚×（外径-壁厚）×长度园铝管重量（公斤）=0.00879×壁厚×（外径-壁厚）×长度注：公式中长度单位为米，面积单位为平方米，其余单位均为毫米。