高中数学必修四1.4.3正切函数的性质和图象导学案

§1.4.3正切函数的图像与性质的导学案霍林郭勒市第三中学 展月娥◆一、【学习目标】1、知识目标会用单位圆内的正切线画正切曲线，并根据正切函数图象掌握正切函数的性质，用数形结合的思想理解和处理问题。

2、能力目标首先学生自主绘图，，然后再让学生观察，类比正弦，探索知识。

在得到正切函数图像的过程中，学会一类周期性函数的研究方式。

3、情感、态度与价值观通过自己动手得到图像让学生亲身经历数学研究的过程，体验探索的乐趣，增强学习数学的兴趣。

◆二、【重点难点】重点：正切函数的图象及其主要性质。

难点: 利用正切线画出函数y =tan x 的图象，对直线x =2ππ+k ，Z k ∈是y =tan x 的渐近线的理解，对单调性这个性质的理解。

三、【模块一: 自主学习】◆学法指导：认真思考课本P42上的探究，然后想想如何根据以往画正弦函数的经验来画出正切函数的图象及研究正切函数的性质。

从正切三角函数线及正切函数图象两个方面研究正切函数的性质.问题1画出下列各角的正切线：模块二：合作释疑问题2：.类比正弦函数我们用几何法做出正切函数x y tan =图象：思路点拨：第一步：作直角坐标系，并在直角坐标系y 轴左侧作单位圆。

第二步：找横坐标（把x 轴上 2π- 到 2π到这一段分成8等份）第三步：把单位圆右半圆中作出正切线。

第四步：找交叉点。

第五步：连线。

问题3：把上述图象向左、右扩展，得到正切函数R x xy ∈=tan ，且()z k k x ∈+≠ππ2的图象，称“正切曲线”问题4：观察正切曲线，回答正切函数的性质：定义域： 值域： 周期性： 单调性： 奇偶性: 渐近线:模块三：巩固训练，整理提高例题讲解:例1.讨论函数⎪⎭⎫⎝⎛+=4tan πx y 的定义域。

变式训练1. 求函数y ＝tan2x 的定义域。

例2.求函数y ＝)32tan(ππ+x 的定义域 ，周期和单调区间。

变式训练2.求函数)42tan(3π+=x y 的定义域 ，周期和单调区间。

1.4.3正切函数的图象与性质导学案主备人：张 民 曹县一中学习目标：1．了解画出正切函数图象的方法；2．掌握正切函数的性质，并能解决简单的有关问题； 3．体验数形结合、换元等基本数学思想方法.重难点： 正切函数的图象与性质及其应用. 教学过程：一．复习旧知：1.正切函数的定义是什么？2. 在单位圆中如何画出角α 的正切线？3.正切函数是否为周期函数，如果是，周期为多少？二．探究新知 如何作出正切函数的图象呢？1．利用正切线画出函数tan y x =，x ∈⎪⎭⎫⎝⎛-2,2ππ的图象.2.图象向左、右拓展到整个定义域内，得到正切函数：R x x y ∈=tan ，且()z k k x ∈+≠ππ2的图象，称“正切曲线”.（1）定义域：_____________； （2）值域：_____________； （3）周期性：_____________；（4）奇偶性：正切函数图象关于_________对称，是________函数；（5）单调性：在开区间z k k k ∈⎪⎭⎫ ⎝⎛++-ππππ2,2内，都是____________函数；(6)对称中心：________________________.思考：正切函数在整个定义域内是单调增函数吗？有单调减区间吗？三．典例分析：例1. 比较下列每组数的大小.o o(1)tan167与tan17313tan()5ππ-11（2）tan(-）与4练习：比较大小：思考：例2.求函数⎪⎭⎫ ⎝⎛+=323tan ππx y 的定义域、周期与单调区间.练习： 1.函数 xy 3tan =的定义域为 ,单调递增区间为 ,2. 函数 ）—（32tanπ+=x y 单调区间为︒︒143tan 138tan )1(与⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛-ππ517tan 413tan )2(与tan x ≥解不等式：四．课堂小结：五．课堂达标：六.作业布置：教材 46 页 6 题 , 7 题..tan43tan ,2tan ,1tan .1的大小与比较.)42tan(3..2区间的定义域、周期与单调求函数π+=x y。

1.4.3正切函数的图像与性质【学习目标】1、能正确作出正切函数图像；2、借助图像理解正切函数的性质；3、进一步研究正切函数的综合运用.【重点难点】正切函数的图像与性质【学习过程】一、复习旧知1.画出下列各角的正切线：2.正、余弦函数的图象是通过什么方法作出的？3.正、余弦函数的基本性质包括哪些内容？二、自主学习预习教材P42~ P45思考以下问题：知识探究（一）：正切函数的图象思考1：类比正弦函数图象的作法,利用正切线在下图中作正切函数tan ((,))22y x x ππ=∈-图象，具体应如何操作？思考2：上图中,直线2π-=x 和2π=x 与正切函数的图象的位置关系如何？图象的凸向有什么特点？思考3：结合正切函数的周期性, 如何画出正切函数在整个定义域内的图象？A 思考4：正切函数Z k k x x y ∈+≠=,2,tan ππ的图象叫做正切曲线.它是由被相互平行的直线Z k k x ∈+=,2ππ所隔开的无穷多支完成相同的曲线组成的。

因为正切函数是奇函数，所以正切曲线关于原点对称，此外，正切曲线是否还关于其它的点和直线对称？ 知识探究（二）：正切函数的性质观察正切函数Z k k x x y ∈+≠=,2,tan ππ的图象，完成下列思考：思考1：正切函数的定义域是 , 用区间表示为 思考2：根据诱导公式与周期函数的定义结合正切函数Z k k x x y ∈+≠=,2,tan ππ的图象，你能判断正切函数是周期函数吗？其最小正周期是什么？思考3：根据图像你能判断正切函数具有奇偶性吗？思考4：观察右图中的正切线,当角x 在⎪⎭⎫ ⎝⎛-2,2ππ内增加时, 正切函数值发生什么变化?由此反映出一个什么性质?思考5：结合正切函数的周期性，正切函数的单调性如何？思考6：正切函数在整个定义域内是增函数吗？正切函数会不会在某一区间内是减函数？思考7：正切函数的值域是什么?三、典型例题例1:比较下列两个三角函数值的大小．（1）710tan 72tan)1(ππ与（2）⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-517tan 413tan )2(ππ与变式练习1：比较下列两个三角函数值的大小．（1）815tanπ 914tan π （2）ο240tan ο260tan例2：根据正切函数图象，分别写出满足下列条件的x 的集合：（1）0tan >x （2）tan x >（3）0tan 1≥+x变式练习2：（1）函数1tan 2-=x y 的定义域是（2）函数)tan 1lg(x y -=的定义域是 例3：研究函数⎪⎭⎫ ⎝⎛+=4tan πx y 的基本性质变式训练3：（1）求函数⎪⎭⎫ ⎝⎛+=42tan πx y 的基本性质 （2）求函数)32tan(ππ+=x y 的定义域、周期和单调区间.课后思考：研究函数x y tan =的相关性质课后练习与提高1. 下列函数不等式中正确的是（ ）.A ．43tan tan 77ππ>B ．23tan tan 55ππ<{}C.|22,|2,2x k x k k x x k k Z ππππππ⎧⎫≤<+∈⋃=+∈⎨⎬⎩⎭ C ． 1315tan()tan()78ππ-<- D ．1312tan()tan()45ππ-<-2. 若,则（ ）.A ．B ．C ．D ．3.函数y = ）.A ．|22,2x k x k k ππππ⎧⎫≤<+∈⎨⎬⎩⎭B ．|22,2x k x k k ππππ⎧⎫<≤+∈⎨⎬⎩⎭D ．|222x k x k πππ⎧≤<+⎨⎩且}2,x k k Z ππ≠+∈4. 函数)43tan(2π+=x y 的周期是( )A ．32πB ．2πC ．3πD ．6π5. 函数x y π3tan =的最小正周期是（ ）A ．31B ．32C ．π6D ．π36. 函数tan()(0)6y ax a π=+≠的周期为（ ）.A ．2a πB ．2a πC ．a πD ．a πtan 0x ≤22,2k x k k Z πππ-<<∈2(21),2k x k k Z πππ+≤<+∈,2k x k k Z πππ-<≤∈,2k x k k Z πππ-≤≤∈7. 直线y a =(a 为常数)与正切曲线tan (y x ωω=为常数，且0)ω>相交的两相邻点间的距离为（ ）.A ．πB ．2πω C ．πω D ．与a 值有关8. 函数)4tan(x y -=π的定义域是（ ）A. {R x x ∈|且4π-≠x } B. {R x x ∈|且43π≠x }C. {R x x ∈|且z k k x ∈-≠,4ππ}D. {R x x ∈|且z k k x ∈+≠,43ππ}9. 在下列函数中，同时满足：①在0,2π⎛⎫⎪⎝⎭上递增；②以2π为周期；③是奇函数的是（）.A ．tan y x =B ．cos y x =C ．tan 2xy = D ．tan y x =-10. 3tan ,2tan ,1tan 的大小关系是 .11. 函数)42tan(1π-=x y 的定义域为 .12. 函数sin y x =与tan y x =的图像在[]1,1-上有 个交点。

课题：1.4.3正切函数的性质与图象编制：钱丽娟
【学习目标】
1.理解正切函数的定义域、值域、周期性、奇偶性、单调性，并掌握其应用。

2.能借助单位圆中的正切线画出正切函数的图象。

【教学重难点】
教学重点：用单位圆中的正切线画出正切函数图象。

教学难点：正切函数的性质。

【授课类型】新授课
【复习、预习思考】
2、思考：回忆正弦函数与余弦函数的图象与性质的学习过程，想一想如何研究正切函数的图象与性质？
【探究性质、图象】
1、 探究正切函数tan y x =的性质、图象
问题1、定义域
1、利用正切函数的定义，给出正切函数的定义域。

问题2、周期性
2、正切函数 tan y x = 是否是周期函数？
3、探究正切函数tan y x =的图象
问题3、奇偶性
问题4、单调性
3、能否利用正切线帮助理解正切函数 tan y x 的单调性？
问题5、值域
【例题讲解】
例1． 求函数 的定义域、周期、单调区间．
方法归纳：___________________________________________________________ 【本节小结】
1、正切曲线是先利用平移正切线得tan ()22
y x x =∈-ππ
，，的图象，再利用周期性
把该段图象向左、右拓展得到。

2、正切函数的性质。

【思考：周期公式推导】
1、正切型函数 y ＝A tan(ωx ＋φ)(ω≠0)的周期
一般结论：_____________________________
【作业】
1、课本P46 A 组第6、7题
2、练习册P29-30。

1.4.3.正切函数的性质与图象学习目标.1.会求正切函数y ＝tan(ωx ＋φ)的周期.2.掌握正切函数y ＝tan x 的奇偶性，并会判断简单三角函数的奇偶性.3.掌握正切函数的单调性，并掌握其图象的画法.知识点一.正切函数的性质 思考1.正切函数的定义域是什么？ 答案.{x |x ∈R 且x ≠π2＋k π，k ∈Z }.思考2.诱导公式tan(π＋x )＝tan x ，x ∈R 且x ≠π2＋k π，k ∈Z 说明了正切函数的什么性质？答案. 周期性.思考3.诱导公式tan(－x )＝－tan x ，x ∈R 且x ≠π2＋k π，k ∈Z 说明了正切函数的什么性质？答案. 奇偶性.思考4.从正切线上看，在⎝⎛⎭⎪⎫0，π2上正切函数值是增大的吗？答案.是.梳理.函数y ＝tan x ⎝ ⎛⎭⎪⎫x ∈R 且x ≠k π＋π2，k ∈Z 的图象与性质见下表：知识点二.正切函数的图象思考1.利用正切线作正切函数图象的步骤是什么？答案.根据正切函数的定义域和周期，首先作出区间(－π2，π2)上的图象.作法如下：(1)作直角坐标系，并在直角坐标系y 轴的左侧作单位圆. (2)把单位圆的右半圆分成8等份，分别在单位圆中作出正切线. (3)描点(横坐标是一个周期的8等分点，纵坐标是相应的正切线的长度). (4)连线，得到如图①所示的图象.(5)根据正切函数的周期性，把上述图象向左、右扩展，就可以得到正切函数y ＝tan x ，x ∈R 且x ≠π2＋k π(k ∈Z )的图象，把它称为正切曲线(如图②所示).可以看出，正切曲线是被相互平行的直线x ＝π2＋k π，k ∈Z 所隔开的无穷多支曲线组成的.思考 2.我们能用“五点法”简便地画出正弦函数、余弦函数的简图，你能类似地画出正切函数y ＝tan x ，x ∈⎝ ⎛⎭⎪⎫－π2，π2的简图吗？怎样画？ 答案.能，三个关键点：⎝ ⎛⎭⎪⎫π4，1，(0，0)，⎝ ⎛⎭⎪⎫－π4，－1，两条平行线：x ＝π2，x ＝－π2. 梳理.(1)正切函数的图象(2)正切函数的图象特征正切曲线是被相互平行的直线x ＝π2＋k π，k ∈Z 所隔开的无穷多支曲线组成的.类型一.正切函数的定义域 例1.求下列函数的定义域. (1)y ＝11＋tan x ；(2)y ＝lg(3－tan x ).解.(1)要使函数y ＝11＋tan x 有意义，必须且只需⎩⎪⎨⎪⎧1＋tan x ≠0，x ≠k π＋π2(k ∈Z )，所以函数的定义域为{x |x ∈R 且x ≠k π－π4，x ≠k π＋π2，k ∈Z }.(2)因为3－tan x >0，所以tan x < 3. 又因为当tan x ＝3时，x ＝π3＋k π(k ∈Z )，根据正切函数图象，得k π－π2＜x ＜k π＋π3 (k ∈Z )，所以函数的定义域是{x |k π－π2＜x ＜k π＋π3，k ∈Z }.反思与感悟.求定义域时，要注意正切函数自身的限制条件，另外解不等式时，要充分利用三角函数的图象或三角函数线.跟踪训练1.求函数y ＝tan x ＋1＋lg(1－tan x )的定义域.解.由题意得⎩⎪⎨⎪⎧tan x ＋1≥0，1－tan x >0，即－1≤tan x <1.在⎝ ⎛⎭⎪⎫－π2，π2内，满足上述不等式的x 的取值范围是⎣⎢⎡⎭⎪⎫－π4，π4，又y ＝tan x 的周期为π，所以函数的定义域是⎣⎢⎡⎭⎪⎫k π－π4，k π＋π4(k ∈Z ).类型二.正切函数的单调性及其应用 命题角度1.求正切函数的单调区间例2.求函数y ＝tan ⎝ ⎛⎭⎪⎫－12x ＋π4的单调区间及最小正周期.解.y ＝tan ⎝ ⎛⎭⎪⎫－12x ＋π4＝－tan ⎝ ⎛⎭⎪⎫12x －π4，由k π－π2<12x －π4<k π＋π2(k ∈Z )，得2k π－π2<x <2k π＋32π(k ∈Z )，所以函数y ＝tan ⎝ ⎛⎭⎪⎫－12x ＋π4的单调递减区间是⎝ ⎛⎭⎪⎫2k π－π2，2k π＋32π，k ∈Z ，周期T ＝π⎪⎪⎪⎪⎪⎪－12＝2π.反思与感悟.y ＝tan(ωx ＋φ) (ω>0)的单调区间的求法是把ωx ＋φ看成一个整体，解－π2＋k π<ωx ＋φ<π2＋k π，k ∈Z 即可.当ω<0时，先用诱导公式把ω化为正值再求单调区间.跟踪训练2.求函数y ＝tan ⎝⎛⎭⎪⎫2x －π3的单调区间. 解.∵y ＝tan x 在x ∈⎝ ⎛⎭⎪⎫－π2＋k π，π2＋k π (k ∈Z )上是增函数，∴－π2＋k π<2x －π3<π2＋k π，k ∈Z ，即－π12＋k π2<x <5π12＋k π2，k ∈Z .∴函数y ＝tan ⎝ ⎛⎭⎪⎫2x －π3的单调递增区间是⎝ ⎛⎭⎪⎫－π12＋k π2，5π12＋k π2 (k ∈Z ). 命题角度2.利用正切函数的单调性比较大小 例3.(1)比较大小：①tan 32°________tan 215°； ②tan 18π5________tan(－28π9).(2)将tan 1，tan 2，tan 3按大小排列为________.(用“<”连接) 答案.(1)①<.②<.(2)tan 2<tan 3<tan 1解析.(1)①tan 215°＝tan(180°＋35°)＝tan 35°， ∵y ＝tan x 在(0°，90°)上单调递增，32°<35°， ∴tan 32°<tan 35°＝tan 215°. ②tan 18π5＝tan(4π－2π5)＝tan(－2π5)，tan(－28π9)＝tan(－3π－π9)＝tan(－π9)，∵y ＝tan x 在(－π2，π2)上单调递增，且－2π5<－π9，∴tan(－2π5)<tan(－π9)，即tan 18π5<tan(－28π9).(2)tan 2＝tan(2－π)，tan 3＝tan(3－π)， ∵－π2<2－π<3－π<1<π2，且y ＝tan x 在(－π2，π2)上单调递增，∴tan(2－π)<tan(3－π)<tan 1， 即tan 2<tan 3<tan 1.反思与感悟.运用正切函数的单调性比较大小的步骤： (1)运用函数的周期性或诱导公式将角化到同一单调区间内； (2)运用单调性比较大小关系.跟踪训练3.比较大小：tan ⎝ ⎛⎭⎪⎫－7π4________tan ⎝ ⎛⎭⎪⎫－9π5.答案.>解析.∵tan ⎝ ⎛⎭⎪⎫－7π4＝－tan ⎝ ⎛⎭⎪⎫2π－π4＝tan π4，tan ⎝ ⎛⎭⎪⎫－9π5＝－tan ⎝⎛⎭⎪⎫2π－π5＝tan π5.又0＜π5＜π4＜π2，y ＝tan x 在⎝ ⎛⎭⎪⎫0，π2内单调递增，∴tan π5＜tan π4，∴tan ⎝ ⎛⎭⎪⎫－7π4＞tan ⎝ ⎛⎭⎪⎫－9π5. 类型三.正切函数的图象及应用例4.画出函数y ＝|tan x |的图象，并根据图象判断其单调区间、奇偶性、周期性. 解.由y ＝|tan x |，得y ＝⎩⎪⎨⎪⎧tan x ，k π≤x <k π＋π2(k ∈Z )，－tan x ，－π2＋k π<x <k π(k ∈Z )，其图象如图所示.由图象可知，函数y ＝|tan x |是偶函数， 单调递增区间为⎣⎢⎡⎭⎪⎫k π，k π＋π2(k ∈Z )， 单调递减区间为⎝ ⎛⎦⎥⎤－π2＋k π，k π(k ∈Z )，周期为π.反思与感悟.(1)作出函数y ＝|f (x )|的图象一般利用图象变换方法，具体步骤是： ①保留函数y ＝f (x )图象在x 轴上方的部分；②将函数y ＝f (x )图象在x 轴下方的部分沿x 轴向上翻折.(2)若函数为周期函数，可先研究其一个周期上的图象，再利用周期性，延拓到定义域上即可.跟踪训练4.设函数f (x )＝tan ⎝ ⎛⎭⎪⎫x 2－π3.(1)求函数f (x )的周期，对称中心； (2)作出函数f (x )在一个周期内的简图. 解.(1)∵ω＝12，∴周期T ＝πω＝π12＝2π.令x 2－π3＝k π2(k ∈Z )，得x ＝k π＋2π3(k ∈Z )， ∴f (x )的对称中心是⎝ ⎛⎭⎪⎫k π＋2π3，0(k ∈Z ).(2)令x 2－π3＝0，则x ＝2π3；令x 2－π3＝π2，则x ＝5π3；令x 2－π3＝－π2，则x ＝－π3.∴函数y ＝tan ⎝ ⎛⎭⎪⎫x 2－π3的图象与x 轴的一个交点坐标是⎝ ⎛⎭⎪⎫2π3，0，在这个交点左，右两侧相邻的两条渐近线方程分别是x ＝－π3，x ＝5π3，从而得到函数y ＝f (x )在一个周期⎝⎛⎭⎪⎫－π3，5π3内的简图(如图).1.函数y ＝tan(2x ＋π6)的最小正周期是(..)A.πB.2πC.π2D.π6答案.C解析.最小正周期为T ＝π|ω|＝π2. 2.函数f (x )＝tan(x ＋π4)的单调递增区间为(..)A.(k π－π2，k π＋π2)，k ∈ZB.(k π，(k ＋1)π)，k ∈ZC.(k π－3π4，k π＋π4)，k ∈ZD.(k π－π4，k π＋3π4)，k ∈Z答案.C3.在下列函数中同时满足：①在⎝⎛⎭⎪⎫0，π2上递增；②以2π为周期；③是奇函数的是(..)A.y ＝tan xB.y ＝cos xC.y ＝tan x2D.y ＝－tan x答案.C4.方程tan ⎝ ⎛⎭⎪⎫2x ＋π3＝3在区间[0，2π)上的解的个数是(..) A.5 B.4 C.3 D.2 答案.B解析.由tan ⎝ ⎛⎭⎪⎫2x ＋π3＝3，解得2x ＋π3＝π3＋k π(k ∈Z )，∴x ＝k π2(k ∈Z )，又∵x ∈[0，2π)，∴x ＝0，π2，π，3π2.故选B.5.比较大小：tan 1________tan 4.解析.由正切函数的图象易知tan 1＞0， tan 4＝tan(4－π)，而0＜4－π＜1＜π2，函数y ＝tan x 在⎝ ⎛⎭⎪⎫－π2，π2上为增函数， 所以tan 1＞tan(4－π)＝tan 4.1.正切函数的图象正切函数有无数多条渐近线，渐近线方程为x ＝k π＋π2，k ∈Z ，相邻两条渐近线之间都有一支正切曲线，且单调递增. 2.正切函数的性质(1)正切函数y ＝tan x 的定义域是⎩⎨⎧⎭⎬⎫x |x ≠k π＋π2，k ∈Z ，值域是R . (2)正切函数y ＝tan x 的最小正周期是π，函数y ＝A tan(ωx ＋φ) (A ω≠0)的周期为T ＝π|ω|. (3)正切函数在⎝ ⎛⎭⎪⎫－π2＋k π，π2＋k π(k ∈Z )上单调递增，不能写成闭区间，正切函数无单调减区间.课时作业一、选择题1.函数y ＝tan ⎝ ⎛⎭⎪⎫x ＋π5，x ∈R 且x ≠310π＋k π，k ∈Z 的一个对称中心是(..)A.(0，0)B.⎝ ⎛⎭⎪⎫π5，0C.⎝ ⎛⎭⎪⎫45π，0D.(π，0)答案.C2.函数f (x )＝lg(tan x ＋1＋tan 2x )为(..) A.奇函数B.既是奇函数又是偶函数C.偶函数D.既不是奇函数又不是偶函数解析.∵1＋tan 2x >|tan x |≥－tan x ，∴其定义域为{x |x ≠k π＋π2，k ∈Z }，关于原点对称.又f (－x )＋f (x )＝lg(－tan x ＋1＋tan 2x )＋lg(tan x ＋1＋tan 2x )＝lg 1＝0， ∴f (x )为奇函数，故选A.3.满足tan A >－1的三角形的内角A 的取值范围是(..) A.(0，34π)B.(0，π2)∪(π2，34π)C.(34π，π) D.(0，π2)∪(34π，π)答案.D解析.因为A 为三角形的内角，所以0<A <π.又tan A >－1，结合正切曲线得A ∈(0，π2)∪(3π4，π).4.下列各点中，不是函数y ＝tan(π4－2x )的图象的对称中心的是(..)A.(π8，0)B.(－π8，0)C.(π4，0)D.(－38π，0)答案.C解析.令π4－2x ＝k π2，k ∈Z ，得x ＝π8－k π4.令k ＝0，得x ＝π8；令k ＝1，得x ＝－π8；令k ＝2，得x ＝－3π8.故选C.5.函数f (x )＝tan ωx (ω>0)的图象的相邻两支截直线y ＝π4所得的线段长为π4，则f ⎝ ⎛⎭⎪⎫π4的值是(..)A.0B.1C.－1D.π4答案.A解析.由题意，得T ＝πω＝π4，∴ω＝4.∴f (x )＝tan 4x ，f ⎝ ⎛⎭⎪⎫π4＝tan π＝0. 6.函数y ＝tan x ＋sin x －|tan x －sin x |在区间⎝ ⎛⎭⎪⎫π2，3π2内的图象是(..)答案.D解析.当π2<x <π时，tan x <sin x ，y ＝2tan x <0；当x ＝π时，y ＝0；当π<x <3π2时，tan x >sin x ，y ＝2sin x <0.故选D.7.下列关于函数y ＝tan ⎝ ⎛⎭⎪⎫x ＋π3的说法正确的是(..)A.在区间⎝ ⎛⎭⎪⎫－π6，5π6上单调递增B.最小正周期是πC.图象关于点⎝ ⎛⎭⎪⎫π4，0成中心对称 D.图象关于直线x ＝π6成轴对称答案.B解析.令k π－π2<x ＋π3<k π＋π2，解得k π－5π6<x <k π＋π6，k ∈Z ，显然⎝ ⎛⎭⎪⎫－π6，5π6不满足上述关系式，故A 错误；易知该函数的最小正周期为π，故B 正确；令x ＋π3＝k π2，解得x ＝k π2－π3，k ∈Z ，任取k 值不能得到x ＝π4，故C 错误；正切函数曲线没有对称轴，因此函数y ＝tan ⎝⎛⎭⎪⎫x ＋π3的图象也没有对称轴，故D 错误.故选B.二、填空题8.函数y ＝3tan(3x ＋π4)的对称中心的坐标是________. 答案.⎝ ⎛⎭⎪⎫k π6－π12，0(k ∈Z ) 解析.由3x ＋π4＝k π2(k ∈Z )，得x ＝k π6－π12(k ∈Z )， 所以对称中心的坐标为⎝ ⎛⎭⎪⎫k π6－π12，0(k ∈Z ). 9.函数y ＝－tan 2x ＋4tan x ＋1，x ∈⎣⎢⎡⎦⎥⎤－π4，π4的值域为____________. 答案.[－4，4]解析.∵－π4≤x ≤π4， ∴－1≤tan x ≤1.令tan x ＝t ，则t ∈[－1，1]，∴y ＝－t 2＋4t ＋1＝－(t －2)2＋5.∴当t ＝－1，即x ＝－π4时，y min ＝－4， 当t ＝1，即x ＝π4时，y max ＝4. 故所求函数的值域为[－4，4].10.函数y ＝3tan ⎝⎛⎭⎪⎫ωx ＋π6的最小正周期是π2，则ω＝________. 答案.±2解析.T ＝π|ω|＝π2， ∴ω＝±2.11.函数y ＝1－tan x 的定义域是________.答案.(k π－π2，k π＋π4](k ∈Z ) 三、解答题12.判断函数f (x )＝lg tan x ＋1tan x －1的奇偶性. 解.由tan x ＋1tan x －1>0，得tan x >1或tan x <－1. ∴函数定义域为(k π－π2，k π－π4)∪(k π＋π4，k π＋π2)(k ∈Z )，关于原点对称.f (－x )＋f (x )＝lg tan (－x )＋1tan (－x )－1＋lg tan x ＋1tan x －1＝lg(－tan x ＋1－tan x －1·tan x ＋1tan x －1)＝lg 1＝0. ∴f (－x )＝－f (x )，∴f (x )是奇函数.13.求函数y ＝tan(x 2－π3)的定义域、周期、单调区间和对称中心. 解.①由x 2－π3≠k π＋π2，k ∈Z ， 得x ≠2k π＋53π，k ∈Z . ∴函数的定义域为{x |x ∈R 且x ≠2k π＋53π，k ∈Z }. ②∵T ＝π12＝2π.∴函数的周期为2π. ③由k π－π2<x 2－π3<k π＋π2，k ∈Z ， 解得2k π－π3<x <2k π＋53π，k ∈Z . ∴函数的单调增区间为(2k π－π3，2k π＋53π)，k ∈Z . ④由x 2－π3＝k π2，k ∈Z ， 得x ＝k π＋23π，k ∈Z . ∴函数的对称中心是(k π＋23π，0)，k ∈Z . 四、探究与拓展14.若tan x >tan π5且x 在第三象限，则x 的取值范围是________. 答案.(k π＋6π5，k π＋3π2)(k ∈Z ) 15.设函数f (x )＝tan(ωx ＋φ)(ω>0，0<φ<π2)，已知函数y ＝f (x )的图象与x 轴相邻两个交点的距离为π2，且图象关于点M (－π8，0)对称. (1)求f (x )的解析式；(2)求f (x )的单调区间；(3)求不等式－1≤f (x )≤3的解集.解.(1)由题意知，函数f (x )的最小正周期为T ＝π2， 即π|ω|＝π2. 因为ω>0，所以ω＝2，从而f (x )＝tan(2x ＋φ).因为函数y ＝f (x )的图象关于点M (－π8，0)对称， 所以2×(－π8)＋φ＝k π2，k ∈Z ， 即φ＝k π2＋π4，k ∈Z . 因为0<φ<π2，所以φ＝π4， 故f (x )＝tan(2x ＋π4). (2)令－π2＋k π<2x ＋π4<π2＋k π，k ∈Z ， 得－3π4＋k π<2x <k π＋π4，k ∈Z ， 即－3π8＋k π2<x <π8＋k π2，k ∈Z . 所以函数的单调递增区间为(－3π8＋k π2，π8＋k π2)，k ∈Z ，无单调递减区间. (3)由(1)知，f (x )＝tan(2x ＋π4). 由－1≤tan(2x ＋π4)≤3， 得－π4＋k π≤2x ＋π4≤π3＋k π，k ∈Z ， 即－π4＋k π2≤x ≤π24＋k π2，k ∈Z . 所以不等式－1≤f (x )≤3的解集为{x |－π4＋k π2≤x ≤π24＋k π2，k ∈Z }.。

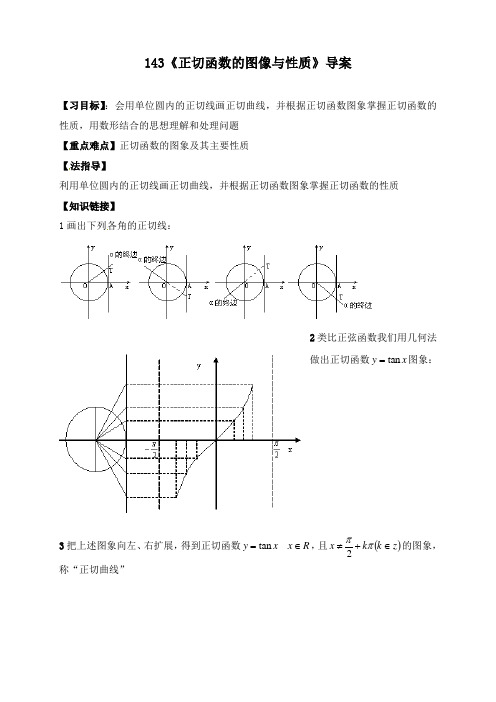
143《正切函数的图像与性质》导案【习目标】：会用单位圆内的正切线画正切曲线，并根据正切函数图象掌握正切函数的性质，用数形结合的思想理解和处理问题 【重点难点】正切函数的图象及其主要性质 【法指导】利用单位圆内的正切线画正切曲线，并根据正切函数图象掌握正切函数的性质 【知识链接】1画出下列各角的正切线：2类比正弦函数我们用几何法做出正切函数x y tan =图象：3把上述图象向左、右扩展，得到正切函数R x x y ∈=tan ，且()z k k x ∈+≠ππ2的图象，称“正切曲线”4观察正切曲线，回答正切函数的性质： 定义域： 值域： 最值： 渐近线： 周期性： 奇偶性 单调性： 图像特征： 三、提出疑惑同们，通过你的自主习，你还有哪些疑惑，请把它填在下面的表格中【习过程】例1讨论函数⎪⎭⎫ ⎝⎛+=4tan πx y 的性质变式训练1 求函数y ＝tan2的定义域、值域和周期例2求函数y ＝2tan x 1－的定义域变式训练2 y例3 比较tan 27π与tan 107π的大小变式训练3 tan 65π与tan (－135π)【习反思】 1、数知识： 2、数思想方法： 【基础达标】 一、选择题 1 函数)43tan(2π+=x y 的周期是 ( )(A)32π (B) 2π ()3π (D)6π2函数)4tan(x y -=π的定义域为 ( )(A)},4|{R x x x ∈≠π(B)},4|{R x x x ∈-≠π() },,4|{Z k R x k x x ∈∈+≠ππ (D)},,43|{Z k R x k x x ∈∈+≠ππ 3下列函数中同时满足(1)在(0 2π)上递增(2)以2π为周期(3)是奇函数的是 ( )(A)x y tan = (B)x y cos = ()x y 21tan = (D)x y tan -= 二、填空题4tan1tan2tan3的大小关系是_______________________ 5给出下列命题（1）函数y =sin||不是周期函数; (2)函数y =|cs2+1/2|的周期是π/2; (3)函数y =tan 在定义域内是增函数; (4)函数y =sin(5π/2+)是偶函数; (5)函数y =tan(2+π/6)图象的一个对称中心为(π/60)其中正确命题的序号是_______________(注把你认为正确命题的序号全填上) 三、解答题6求函数y=lg(1-tan)的定义域 [] [||]【拓展提升】 一、选择题 1、tan (,)2y x x k k Z ππ=≠+∈在定义域上的单调性为（ ）A ．在整个定义域上为增函数B ．在整个定义域上为减函数 ．在每一个开区间(,)()22k k k Z ππππ-++∈上为增函数D ．在每一个开区间(2,2)()22k k k Z ππππ-++∈上为增函数2、下列各式正确的是（ ）A ．1317tan()tan()45ππ-<- B ．1317tan()tan()45ππ->- ．1317tan()tan()45ππ-=- D ．大小关系不确定3、若tan 0x ≤则（ ） A ．22,2k x k k Z πππ-<<∈ B ．2(21),2k x k k Z πππ+≤<+∈．,2k x k k Z πππ-<≤∈ D ．,2k x k k Zπππ-≤≤∈二、填空题 4、函数tan 2()tan xf x x=的定义域为5、函数y 的定义域为 三、解答题[_____][+++++]6、 函数tan()4y x π=-的定义域是（ ）。

§1.4.3 正、余弦函数的值域、奇偶性、单调性1.掌握正、余弦函数的有关性质并会运用.2.熟记正、余弦函数的单调区间,并利用单调性解题.3740，找出疑惑之处）在已学过的内容中，我们要研究一个函数，往往从哪些方面入手？二、新课导学※ 探索新知问题1. 在同一直角坐标系中作y=sinx,y=cosx (x ∈R)的图象，观察它们的图象，你能得到一些什么性质？分别列出y=sinx, y=cosx x ∈R 的图象与性质问题2.观察y=sinx, y=cosx x ∈R 图象，探求y=sinx, y=cosx 的对称中心 及对称轴.※ 典型例题例1:求下列函数的最大值及取得最大值时x 的集合(1)3cosx y = (2)x y 2sin 2-=变式训练：（1）若)3cos(x y -=呢？变式训练：（2）若|2sin |2x y -=呢？例2:判断下列函数奇偶性（1）f(x)=1-cosx （2）g(x)=x-sinx变式训练：3、判断下列函数的奇偶性：⑴x x x f cos |sin |)(⋅=： ；⑵x x x f +=3tan )(：⑶x x x f cos )(+=： . 例3 .求)32sin(π+=x y 的单调增区间变式训练：（1）求)32cos(π+=x y 的单调增区间（2）求)32sin(π+-=x y 的单调增区间（3）求)62cos()32sin(ππ-++=x x y 的单调增区间例4.求下列函数的值域（1）x y 2sin 23-=（2）x x y sin |sin |+=（3）2sin 2cos 2-+=x x y （4）xx x y sin 1cos sin 22+= （5）⎥⎦⎤⎢⎣⎡-∈+=6,6),32sin(2πππx x y变式训练：已知b x a x f +-=)32sin(2)(π的定义域为[0，2π]，函数的最大值为1，最小值为-5，求a,b 的值.※ 动手试试1、函数x y sin =,21≥y 时自变量x 的集合 是___________.2、将54sin π=a ,45cos π-=b ,532sin π=c , 125cosπ=d ,从小到大排列起来为：__________. 3、函数x 2sin 2y =的奇偶数性为（ ）.A. 奇函数B. 偶函数C ．既奇又偶函数 D. 非奇非偶函数4、函数[]π2,0x cosx,32y ∈-=，其单调性是（ ）. A. 在[]　π,0上是增函数，在[],2ππ上是减函数B. 在⎥⎦⎤⎢⎣⎡23,2ππ上是增函数，在⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡πππ2,23,2,0 上分别是减函数 C. 在[]ππ2，上是增函数，在[]π,0上是减函数D. 在⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡πππ2,23,2,0上分别是增函数，在⎥⎦⎤⎢⎣⎡23,2ππ上是减函数三、小结反思⑴正、余弦函数的定义域、值域、有界性、单调性、奇偶性、周期性等都可以在图象上被充分地反映出来，所以正、余弦函数的图象十分重要.⑵结合图象解题是数学中常用的方法.※ 当堂检测（时量：5分钟 满分：10分）计分：1、设z k ∈，则三角函数x y 2sin =的定义域是（ ）A 、πππ+≤≤k x k 22B 、2πππ+≤≤k x k C 、222πππ+≤≤k x k D 、πππ+≤≤k x k2、在],[ππ-上是增函数，又是奇函数的是（ ）A 、2sinx y = B 、x y 21cos = C 、4sin x y -= D 、x y 2sin =3、已知函数3sin x y -=，其定义域是 . 4、已知函数x y cos 1-=，则其单调增区间是 ；单调减区间是 。

1.4.3正切函数的性质与图象学习目标：1、理解并掌握正切函数的周期性、奇偶性、单调性、值域等相关性质.2、会利用正切线及正切函数的性质作正切函数的图象.3、经历根据正切函数的性质描绘函数图象的过程，进一步体会函数线的作用.自学导引1．正切函数tan y x =的定义域是 ；2．回顾跟正切函数有关的诱导公式，想一想：正切函数是周期函数吗？如果是，那么最小正周期是 ；3. 回顾跟正切函数有关的诱导公式，想一想：正切函数是 (奇、偶)函数；4．正切函数在每个开区间_____________________________内均为增函数；典例精析例1求函数)ln(tan )(x x f =的定义域；变式 求函数)3(tan tan 1-=x x y 的定义域；例2若]4,3[ππ-∈x ，求函数1tan 2cos 12++=x xy 的最值及相应的x 的值；变式 函数]4,4[,tan sin ππ-∈+=x x x y 的值域为例3作出函数)321tan(π-=x y 在一个周期内的图象；变式 作出函数|sin tan |sin tan x x x x y --+=在区间)23,2(ππ内的大致图象；例4（1）求函数)46tan(3)(x x f -=π的周期和单调递减区间；（2）试比较)(πf 与)23(πf 的大小；变式 是否存在实数a ，且Z a ∈，使得函数)4cot(ax y +=π在)85,8(ππ∈x 上是单调递增的？若存在，求出a 的一个值；若不存在说明理由；例5（1）求函数x x y tan sin +=的定义域；（2）画出函数|tan |x y =的简图，并根据图象写出其最小正周期和单调区间；自主反馈1、与函数tan 24y x π⎛⎫=+⎪⎝⎭的图象不相交的一条直线是（ ） ()2A x π= ()2B x π=- ()4C x π= ()8D x π=2、函数1tan y x =-的定义域是 ．3、函数2tan 2tan 22++=x x y 的最大值是 ． 4、已知函数x y ωtan =在)2,2(ππ-内是减函数，则ω的取值范围是____________； 5、函数|)4tan(|π+=x y 的单调递增区间是__________________；1.4.3正切函数的性质与图象自学导引1．},2|{Z k k x x ∈+≠ππ2．π3．奇4．Z k k k ∈++-),2,2(ππππ 典例精析例1Z k k k ∈+),2,(πππ 变式 Z k k k k k k k ∈++++-),2,3()3,(),2(ππππππππππ例2当4π-=x 时，1min =y ；当4π=x 时，5min =y变式 ]122,122[+--例3图略 变式 图略例4（1）π4=T 减区间：Z k k k ∈+-],384,344[ππππ （2）)(πf >)23(πf 变式 存在，2-=a例5（1）},2|{},222|{Z k k x x Z k k x k x ∈+≠∈+<≤πππππ（2）图略 π=T 增区间：Z k k k ∈+),2,[πππ 减区间：Z k k k ∈-],,2(πππ 变式 Z k k k ∈++),2,6[ππππ 自主反馈1、D2、Z k k k ∈+-],4,2(ππππ3、24、01<≤-ω5、Z k k k ∈+-),4,4[ππππ。

正切函数的图象与性质撰稿：游斌 修订：高一备课组 学生姓名：__________第___小组一、学习目标，心中有数：1、了解用单位圆中的正切线作正切函数图象的方法；2、掌握正切函数的有关性质；3、能用正切函数图象和性质解决有关问题。

二．自主学习，体验成功：（一）、知识梳理 形成体系问题1、正切函数x y tan =的定义域是什么？是不是周期函数？若是，探索它的最小正周期是多少？问题2、如何利用正弦线画正弦曲线的？请用这种方法画出正切函数在)2,2(ππ-的图像。

1、根据正切函数的周期性，把上述图象向左、右扩展，得到正切函数 x y tan =， )(,2Z k k x ∉+≠ππ的图象，称“正切曲线”。

由图象可以看出，正切曲线是由被相互平行的直线)(,2Z k k x ∈+=ππ所隔开的无穷多支曲线组成的。

2、观察正切函数的图像，可以得到x y tan =有以下性质：（1）定义域： ；（2）值域：观察：当x 从小于()z k k ∈+2ππ，2π+π−→−k x 时，tan x −−→+∞ 当x 从大于()z k k ∈+ππ2，ππk x +−→−2时，-∞−→−x tan 。

（3）周期性：=T ；（4）奇偶性：由()x x tan tan -=-知，正切函数是 函数；（5）单调性：在开区间 内，函数单调递增。

问题4、正切函数是整个定义域上的增函数吗？为什么？π-32π-（二）、课前热身 自我检测1、比较大小（1）0138tan 0143tan （2）)43tan(π- )52tan π 2、观察正切曲线，满足0tan >x 的x 的取值的集合是 。

三、合作探究，共同进步例1、求函数)4tan(π+=x y 的定义域、值域、单调区间及对称中心。

例2、求x y 3tan =的周期小结：函数)tan(ϕω+=x y 的最小正周期ωπ=T 。

例3、解不等式3tan ≥x 。

四、过手训练，步步为营1、函数)0)(6tan(≠+=a ax y π的周期为（ ） A 、a π2 B 、a π2 C 、aπ D 、a π 2、若0tan ≤x ，则x 的取值范围是（ ）A 、πππk x k 222<<-，Z k ∈ B 、πππ)12(22+<≤+k x k ，Z k ∈ C 、πππk x k ≤<-2 ，Z k ∈ D 、πππk x k <≤-2，Z k ∈3、若)4tan()(π+=x x f ，则（ ）A 、)1()1()0(f f f >->B 、)1()1()0(->>f f fC 、)1()0()1(->>f f fD 、)1()0()1(f f f >>-4、函数)4tan(ππ+=x y 的最小正周期是 。

§1.4.3正切函数的图像与性质【教材分析】正切函数的图象和性质》 它前承正、余弦函数，后启必修五中的直线斜率问题。

研究正切函数的图象与性质过程不仅是对正、余弦曲线研讨方法的一种再现，更是一种提升，同时又为后续的学习奠定了基石。

教材单刀直入，直接进入画图工作，没有给出任何提示。

正切函数与正弦函数在研究方法上类似，我采用以类比的方式，让学生回忆正弦曲线的作图过程与方法，进而启发、引导学生发现作正切曲线的一种方法。

教材上直接圈定了区间（2,2ππ-），这样限制了学生的思维，我把空间留给学生，采用让学生自己选择周期，设计一个得到正切曲线的方法。

这样，不仅发挥了学生的能动性，增强动脑、动手绘图的能力，而且，在此过程中，学生会注意到画正切曲线的细节。

在得到图象后，单调性是一个难点，我设计了几个判断题帮助学生理解该性质，并用比大小的题型启发学生从代数和几何两种角度看问题。

【教学目标】正切函数是继正、余弦之后的又一个三角函数，三者在研究方法与研究内容上类似，但某些性质有所不同，这就养成学生在画图时必须全面考虑问题。

本着课改理念，养成学生对知识的勇于探索精神，学生亲自体会正切曲线的获得过程，这样学生的动手实践能力有了提高，又体会到学习数学的乐趣，根据教学要求及学生现有的认知水平，现制定以下教学目标： 1.会用单位圆内的正切线画正切曲线，并根据正切函数图象掌握正切函数的性质，用数形结合的思想理解和处理问题。

2.首先学生自主绘图，通过投影仪纠正图像，投影完整的正确图象，然后再让学生观察，类比正弦，探索知识。

3.在得到正切函数图像的过程中，学会一类周期性函数的研究方式，通过自己动手得到图像让学生亲身经历数学研究的过程，体验探索的乐趣，增强学习数学的兴趣。

【教学重点难点】教学重点：正切函数的图象及其主要性质。

教学难点：利用正切线画出函数y =tan x 的图象，对直线x =2ππ+k ，Z k ∈是y =tan x的渐近线的理解，对单调性这个性质的理解。