高三文科数学临考练兵测试题3

高考临考大练兵（文3）第Ⅰ卷（选择题，共60分）一、本题共12小题，每小题5分，共60分，在每小题给出的四个选项中只有一个选项是符合题目要求的、 1．设集合A ，B 是全集U 的两个子集，则A ⊂≠B 是C U B ⊂≠C U A 的 （ ） A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件2．若复数z 满足,21i iz=+ 则z 对应的点位于（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限3．已知函数)(x f y =的图像关于点（一1，0）对称，且当∈x （0，＋∞）时，xx f 1)(=，则当∈x （一∞，一2）时)(x f 的解析式为（ ）A ．x1-B ．21+x C ．21+-x D ．x-21 4．设a ，b ，c 是空间三条直线，α，β是空间两个平面，则下列命题中，逆命题不成立的是（ ）A ．当c ⊥α时，若c ⊥β，则α∥βB ．当α⊂b 时，若b ⊥β，则βα⊥C ．当α⊂b ，且c 是a 在α内的射影时，若b ⊥c ，则a ⊥bD ．当α⊂b ，且α⊄c 时，若c ∥α，则b ∥c 5．已知θ是第三象限角，m =|cos |θ，且02cos2sin>+θθ，则2cos θ等于 （ ）A ．21m+ B ．21m +-C ．21m- D ．21m-- 6．执行如图所示的算法程序,输出的结果是（ ）A ．24,4B ．24,3C ．96,4D ．96,37．已知关于的方程的两根分别为、，且，则的取值范围是 （ ）A ．]21,2[-- B ． C ．]2,21[ D ．)2,21( 8．已知数列}{n a 的前n 项和为)15(21-=n n S n ，+∈N n ，现从前m 项：1a ，2a ，…，m a 中抽出一项（不是1a ，也不是m a ），余下各项的算术平均数为37，则抽出的是（ ） A ．第6项 B ．第8项 C ．第12项 D ．第15项9．已知在平面直角坐标系满足条件则的最大值为 （ ）A ．4B ．8C ．12D ．1510．在正三棱锥A 一BCD 中，E ，F 分别是AB ，BC 的中点，EF ⊥DE ，且BC ＝1，则正三棱锥A 一BCD 的体积等于 （ ） A ．1212 B ．242 C．123 D ．24311．已知集合，集合， x 2(1)10(,)x a x a b a b R +++++=∈1x 2x 1201x x <<<ba12,2⎛⎫--⎪⎝⎭),(),1,2(),1,1(),2,1(),0,0(,y x M C B A O xOy 动点中--⎪⎩⎪⎨⎧≤⋅≤≤⋅≤-,21,22⋅{}(,)2||2A x y x y x y =∈Z ||≤，≤，，{}22()(2)(2)4B x y x y x y =-+-∈Z ，≤，，（第6题图）在集合A 中任取一个元素p ，则p ∈B 的概率是 （ ）A ．52B ．53C ．D ．254 12．已知双曲线12222=-by a x （a ＞0，b ＞0）的两个焦点为1F 、2F ，点A 在双曲线第一象限的图象上，若△21F AF 的面积为1，且21tan 21=∠F AF ，2tan 12-=∠F AF ，则双曲线方程为（ ）A ．1351222=-y x B ．1312522=-y xC ．1512322=-y x D ．1125322=-y x第Ⅱ卷（非选择题，共90分）二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上。

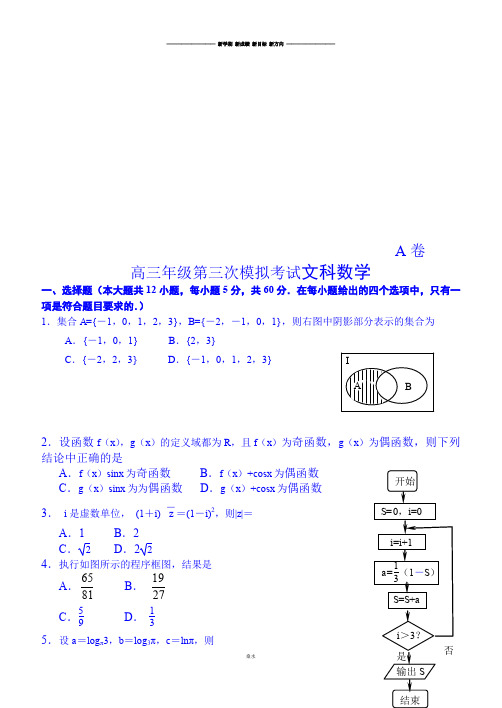
A 卷高三年级第三次模拟考试文科数学一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．集合A ={－1，0，1，2，3}，B ={－2，－1，0，1}，则右图中阴影部分表示的集合为A ．{－1，0，1}B ．{2，3}C ．{－2，2，3}D ．{－1，0，1，2，3}2．设函数f （x ），g （x ）的定义域都为R ，且f （x ）为奇函数，g （x ）为偶函数，则下列结论中正确的是A ．f （x ）sin x 为奇函数B ．f （x ）+cos x 为偶函数C ．g （x ）sin x 为为偶函数D ．g （x ）+cos x 为偶函数 3． i 是虚数单位， (1＋i) z －＝(1－i)2，则|z |＝ A ．1 B ．2 C ．2 D ．224．执行如图所示的程序框图，结果是A ．8165B ． 2719C ．59D ． 135．设a ＝log π3，b ＝log 3π，c ＝lnπ，则ABI 开始S=0，i =0 S =S +ai ＞3？ i =i +1 a=13（1－S ）A ．c ＞a ＞bB ．b ＞c ＞aC ．c ＞b ＞aD ．b ＞a ＞c6．在等差数列{a n }中，a 3＝5，a 4＋a 8＝22，则{11+⋅n n a a }的前20项和为A ．4140 B ．4120 C ．4342 D ．43217．已知函数f (x )＝cos(2x －π3)，g (x )＝sin2x ，将函数f (x )的图像经过下列哪种可以与g (x ) 的图象重合A ．向左平移π12个单位B ．向左平移π6个单位C ．向右平移π12个单位D ．向右平移π6个单位8．一个几何体的三视图如图所示，则其体积为A ．43（π+1）B ．23（π+1）C ．43（π+12）D ．23（π+12）9．向量a 、b 满足：|a |=|a +b |=|2a +b |=1，则|b |=A ．1B ．2C ．3D ．2（9题变式）．向量a 、b 满足：|a |=|a +b |=|2a +b |=1，则a 与b 的夹角为 A ．150° B ．60°C ．30°D ．45° 答案：A10．实数x ，y 满足⎪⎩⎪⎨⎧≤-+≥-+≥+-09303301y x y x y x ，则z ＝ax ＋y 的最大值为2a +3，则a 的取值范围是A ．[－3，1]B ．[－1，3]C ．[3，+∞）D ．（－∞，－1]11．异面直线l 与m 成60°，异面直线l 与n 成45°，则异面直线m 与n 成角范围是A ．[15°，90°]B ．[60°，90°]C ．[15°，105°]D ．[30°，105°]12．函数f (x )＝e －x +a ， g (x )=|ln x |，若x 1，x 2都满足f (x )＝g (x )，则 A ．x 1·x 2＞e B ．1＜x 1·x 2＜e C ．0＜x 1·x 2＜e －1 D ．e －1＜x 1·x 2＜1二、填空题（本大题共4小题，每小题5分，共20分．）13．设S n 是等比数列{a n }的前n 项和，公比q =2，S 5=93，则a 4= ．14．已知F 是抛物线y 2=8x 的焦点，M 是抛物线上的点且｜MF ｜＝3，N （－2，0），则直线MN 的斜率为 ．15．已知a ＞1，则12a a 的最小值为 ．16．等边三角形ABC 的顶点A ，B 在圆O ：x 2+y 2=1上，则|OC |的最大值为 ． 三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．） 17．（本小题满分12分）在△ABC 中，A ，B ，C 所对边分别为a ，b ，c ．2c 2－2a 2=b 2． （Ⅰ）证明：2c cos A －2a cos C =b ；（Ⅱ）若tan A =13，求角C 的大小．18．（本小题满分12分）谋市教育部门对甲校四年级学生进行体育学科测试，随机抽取15名学生的测试成绩，绘制茎叶图如下：（Ⅰ）依据上述数据，估计甲校此次的体育平均成绩－x ；（Ⅱ）从得分在70~80之间的学生中随机抽取两名学生，记这两名学生的平均成绩为－y ，求|－x －－y |≤1的概率．19．（本小题满分12分）如图，三棱柱ABC －A 1B 1C 1中，侧面BC C 1B 1是矩形，截面A 1BC 是等边三角形．甲校5 57 4 6 65 7 3 8 9 71 5 7 6 82 0 9（Ⅰ）求证：AB =AC ；（Ⅱ）若AB ⊥AC ，三棱柱的高为1，求C 1点到截面A 1BC 的距离． 20．（本小题满分12分）已知椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)，直线l 与椭圆C 有唯一公共点M ，当点M 的坐标为（3，12）时，l 的方程为3x +2y －4=0． （Ⅰ）求椭圆C 的方程；（Ⅱ）设直线l 的斜率为k ，M 在椭圆C 上移动时，作OH ⊥l 于H ，（O 为坐标原点），当|OH |＝ 45|OM |时，求k 的值． 21．（本小题满分12分）已知f (x )＝e x (x －a －1)－12x 2＋ax ，a ＞0．（Ⅰ）讨论f (x )的单调性；（Ⅱ）若x ∈(0，1)时，f (x )＜－a －1，求a 的取值范围．请考生在第(22)，(23)，(24)三题中任选一题作答，如果多做，则按所做的第一题记分．作答时用2B 铅笔在答题卡上把所选题目对应的题号涂黑． 22．（本小题满分10分）如图，C 是⊙O 的直径AB 上一点，CD ⊥AB ，与⊙O 相交于点D ，与弦AF 交于点E ，与BF 的延长线交于点G ，GT 与⊙O 相切于点T ．（Ⅰ）证明：CE ·CG ＝CD 2；（Ⅱ）若AC =CO =1，CD =3CE ，求GT ．ABCA 1B 1C 1C A E GD T23．（本小题满分10分）已知半圆C ：（x －2）2+y 2=4（y ≥0），直线l ：x －2y －2=0，以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系．（Ⅰ）写出C 与l 的极坐标方程；（Ⅱ）记A 为C 直径的右端点，C 与l 交于点M ，且M 为圆弧AB 的中点，求|OB |． 24．（本小题满分10分）设函数f (x )＝|ax －1|＋|x +2|，a ＞0． (1)若a =1，解不等式f (x )≤5； (2)若f (x )≥2，求a 的最小值．唐山市2014—2015学年度高三年级第三次模拟考试文科数学参考答案一、选择题：A 卷：BDCAC BCBCB AD B 卷：ADCBC BCACB BD 二、填空题：（13）24； （14）±223； （15）4； （16）2．三、解答题：（17）（Ⅰ）证明：因为2c 2－2a 2＝b 2，所以2c cos A －2a cos C ＝2c ·b 2＋c 2－a 22bc －2a ·a 2＋b 2－c 22ab＝b 2＋c 2－a 2b －a 2＋b 2－c 2b ＝2c 2－2a 2b＝b ． …5分（Ⅱ）解：由（Ⅰ）和正弦定理以及sin B ＝sin(A ＋C )得2sin C cos A －2sin A cos C ＝sin A cos C ＋cos A sin C ， 即sin C cos A ＝3sin A cos C ，又cos A cos C ≠0，所以tan C ＝3tan A ＝1，故C ＝45°． …12分（18）解：（Ⅰ）－x ＝55＋67＋64＋66＋75＋73＋78＋79＋81＋85＋87＋88＋92＋9015＝77．…5分（Ⅱ）从得分在70~80之间的学生中随机抽取两名学生的基本事件：{75，77}，{75，73}， {75，78}，{75，79}，{77，73}，{77，78}，{77，79}，{73，78}，{73，79}，{78，79}共10个；其中满足|－x －－y |≤1的事件：{75，77}，{75，78}，{75，79}，{77，78}，{77，79}，{73，79}共6个．所以满足|－x －－y |≤1的概率P ＝610＝ 3 5.…12分（19）解：（Ⅰ）证明：取BC 中点O ，连OA ，OA 1．因为侧面BCC 1B 1是矩形，所以BC ⊥BB 1，BC ⊥AA 1， 因为截面A 1BC 是等边三角形，所以BC ⊥OA 1， 所以BC ⊥平面A 1OA ，BC ⊥OA ，因此，AB ＝AC ． …5分（Ⅱ）设点A 到截面A 1BC 的距离为d ，由V A －A 1BC ＝V A 1－ABC 得S △A 1BC ×d ＝S △ABC ×1，得BC ×OA 1×d ＝BC ×OA ×1，得d ＝OA OA 1．由AB ⊥AC ，AB ＝AC 得OA ＝ 12BC ，又OA 1＝32BC ，故d ＝33． 因为点A 与点C 1到截面A 1BC 的距离相等，所以点C 1到截面A 1BC 的距离为33．…12分（20）解：（Ⅰ）由题意可得：3a 2＋14b 2＝1， …1分将3x ＋2y －4＝0代入椭圆C ： (3a 2＋4b 2)x 2－83a 2x ＋16a 2－4a 2b 2＝0由Δ＝0得3a 2＋4b 2＝16， …3分 联立解得：a 2＝4，b 2＝1．于是椭圆C 的方程为：x 24＋y 2＝1．…5分（II ）设直线l ：y ＝kx ＋m ，M (x 0，y 0)．将直线l 的方程代入椭圆C 得(1＋4k 2)x 2＋8kmx ＋4m 2－4＝0， …6分 令Δ＝0，得m 2＝4k 2＋1，且x 20＝4m 2－41＋4k 2．所以|OM |2＝1＋16k 21＋4k 2． ①C 1B 1A 1O B A C又|OH |2＝m 21＋k 2＝1＋4k 21＋k 2，② …10分① ②与|OH |＝ 45|OM |联立整理得：16k 4－8k 2＋1＝0，解得：k ＝± 12．…12分（21）解：（Ⅰ）f '(x )＝e x (x －a )－x ＋a ＝(x －a )(e x －1)， 当x ∈(－∞，0)时，f '(x )＞0, f (x )单增； 当x ∈(0，a )时，f '(x )＜0，f (x )单减； 当x ∈(a ，＋∞)时，f '(x )＞0，f (x )单增．所以，f (x )在(－∞，0)和(a ，＋∞)分别单调递增；在(0，a )单调递减． …6分 （Ⅱ）由（Ⅰ）可知：当a ≥1时，f (x )在(0，1)单调递减，f (x )＜f (0)＝－a －1． …8分 当0＜a ＜1时，f (x )在(0，a )单调递减；在(a ，1)单调递增，则f (x )＜－a －1当且仅当f (1)＝－a e ＋a － 12≤－a －1，解得：12(e －2)≤a ＜1．综上：a 的取值范围是[12(e －2)，＋∞)． …12分（22）解：（Ⅰ）证明：延长DC 与圆O 交于点M ，因为CD ⊥AB ，所以CD 2＝CD ·CM ＝AC ·BC ， 因为Rt △ACE ∽Rt △GBC ，所以AC CE ＝CGBC，即AC ·BC ＝CE ·CG ，故CD 2＝CE ·CG ．…5分（Ⅱ）因为AC ＝CO ＝1，所以CD 2＝AC ·BC ＝3， 又CD ＝3CE ，由（Ⅰ）得CG ＝3CD ，GT 2＝GM ·GD ＝(CG ＋CM )·(CG －CD )＝(CG ＋CD )·(CG －CD ) ＝CG 2－CD 2＝8CD 2＝24，故GT ＝26． …10分（23）解：（Ⅰ）将x ＝ρcos θ，y ＝ρsin θ代入已知，分别得C 和l 的极坐标方程为C ：ρ＝4cos θ（0≤θ≤ π2)，l ：ρcos θ－2ρsin θ－2＝0． …4分（Ⅱ）依题意，l 经过半圆C 的圆心C (2，0)．设点B 的极角为α，则tan α＝ 1 2，进而求得cos α＝255…6分OC A B FE GD T M由C 的极坐标方程得|OB |＝4cos α＝855． …10分（24）解：（Ⅰ）若a ＝1，f (x )＝⎩⎪⎨⎪⎧－2x －1，x ＜－2，3，－2≤x ≤1，2x ＋1，x ＞1．由f (x )的单调性及f (－3)＝f (2)＝5，得f (x )≤5的解集为{x |－3≤x ≤2}．…5分（Ⅱ）f (x )＝⎩⎪⎨⎪⎧－(a ＋1)x －1，x ≤－2，(1－a )x ＋3，－2＜x ＜ 1a ，(a ＋1)x ＋1，x ≥ 1a．当x ∈(－∞，－2]时，f (x )单调递减；当x ∈[ 1a，＋∞)时，f (x )单调递增，又f (x )的图象连续不断，所以f (x )≥2当且仅当f (－1)＝2a ＋1≥2，且f ( 1 a )＝ 1a＋2≥2，得a ≥ 1 2， 故a 的最小值为 12． …10分。

2024年高考第三次模拟考试
高三数学（文科）
（考试时间：120分钟试卷满分：150分）
注意事项：
1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上．
2．回答第Ⅰ卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．写在本试卷上无效．
3．回答第Ⅱ卷时，将答案写在答题卡上．写在本试卷上无效．
4．测试范围：高考全部内容
5．考试结束后，将本试卷和答题卡一并交回．
B．13π
C ．222+C ．70a 、b 、c ；且sin B C ．
12
π有三个零点，则实数m 的取值范围是（B ．[﹣4，4]
D ．
（﹣∞，﹣4）∪（为常数），若()f x 在ππ,62⎛ ⎝C ．
π3
上运动，则
y
x
的最大值是（C ．
23
的右焦点为,F O 为坐标原点，过，则双曲线的渐近线为（
）
估计此次满意度调查所得的平均分值x（同一组中的数据用该组区间的中点值为代表）位学生中，男女生人数相同，规定分值在（1）中的
的正方形，若三棱锥1E AB C -的体积为()2
1ln 1R 2
x x ax a -
++∈处的切线方程；上单调递减，求实数a 的取值范围．
()2210a b =>>的离心率为上任意一点，过P 作圆Γ的切线与椭圆.
23题中任选一题作答。

如果多做，则按所做的第一题计分。

江西省2024届高三下学期5月高考适应性大练兵数学仿真模拟试题（三模）注意事项：1．答卷前，考生务必将自己的姓名、准考证号等填写在答题卡指定位置上.2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本试卷上无效.3．考生必须保持答题卡的整洁.考试结束后，请将答题卡交回.一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．在复平面内，复数对应的点的坐标为，则（ ）z ()1,1-212i z =-A ．B ．C ．D ．42i 55-24i 55-42i 55+24i 55+2．椭圆的长轴长与焦距之差等于（ ）22:18035x y C +=A B ．C ．D ．3．函数的一个单调递减区间为（ ）()223x xf x -=A ．B ．C ．D ．(),0∞-()1,0-()0,1()1,+∞4．已知平面向量，，其中，若，则实数的取值范围是()221,a λλ=+(),1b μ=0λ>//a b r rμ（ ）A ．B ．C ．D ．)⎡+∞⎣[)2,+∞)+∞[)1,+∞5．设是两个不同的平面，是两条共面直线，，，则“”是“”的,αβ,a b a α⊂b β⊂a b αβ∥（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件6．为积极落实“双减”政策，丰富学生的课外活动，某校成立了手工艺社团，并开设了陶艺、剪纸等6门课程．该校甲、乙2名同学报名参加手工艺社团，每人仅报2门课程，其中甲不报陶艺、乙不报剪纸，且甲、乙两人所报课程均不相同，则甲、乙报名课程的方案种数为（ ）A ．18B ．24C ．36D ．427．已知函数的图象关于点中心对称，则（ ）()24sin cos 3cos 1f x x x x ωωω=+-11,2⎛⎫ ⎪⎝⎭tan ω=A ．3或B ．2或C ．或D ．或13-12-2-123-138．如图，将边长为1的正以边为轴逆时针翻转弧度得到，其中ABC AB θABC '△，构成一个三棱锥的取值范π0,2θ⎛⎫∈ ⎪⎝⎭C ABC '-θ围为（ ）A ．B ．C ．D ．π0,6⎛⎤ ⎥⎝⎦π0,4⎛⎤ ⎥⎝⎦π0,3⎛⎤ ⎥⎝⎦ππ,32⎡⎫⎪⎢⎣⎭二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．9．已知是等比数列的前5项中的其中3项，且，则的前7项和可能为1,2,8-{}n a 20a >{}n a （ ）A ．B ．C ．D ．43-434-43643210．已知集合，，则下列结论正确的是(){},20A x y x ay a =++=(){},10B x y ax ay =+-=（ ）A ．，B ．当时，a ∀∈R A ≠∅1a =-13,22A B ⎧⎫⎛⎫⋂=-⎨⎬⎪⎝⎭⎩⎭C ．当时，D ．，使得A B ⋂=∅1a =a ∃∈R A B=11．已知定义在上的函数满足，的导函数为R ()f x ()()()()21f xy xf y yf x x y =+++-()f x，则（ ）()f x 'A ．B ．是单调函数()12f -=-()f x C ．D ．为偶函数()()20180i f i f i =⎡⎤-+=-⎣⎦∑()f x '三、填空题：本题共3小题，每小题5分，共15分．12．某新能源汽车店五月份的前8天汽车销量（单位：辆）分别为：，4S 3,7,11,5,8,15,21,9则这组数据的分位数为．75%13．在中，内角所对的边分别为，是的中点，，则ABC ,,A B C ,,a b c D BC 22BC AD c ⋅=．sin sin B C =14．已知抛物线的焦点为，直线经过点交于两点，两()2:20C y px p =>F l F C ,M N ,M N 点在的准线上的射影分别为，且的面积是的面积的4倍，若轴被以C ,A B MAF △NBF y的值为．MN p 四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．15．已知函数，且曲线在点处的切线方程为()()2ln 1f x a x x x=--+()y f x =()()22f ,．220x by +-=(1)求的值；,a b (2)求的单调区间与最大值．()f x 16．如图，在正三棱柱中，为的中点．111ABC A B C -P 1BC(1)证明：；1BC PA ⊥(2)若，与平面所成角的正弦值．12AA =AB =1AB 11PA C17．已知双曲线的离心率为2()2222:10,0x y C a b a b -=>>(1)求的方程；C (2)若直线交于两点，为坐标原点，且的面积为的值．:2l y kx =+C ,A B O AOB k 18．已知袋中装有除颜色外均相同的4个黑球、1个白球，现从袋中随机抽取1个小球，观察颜色，若取出的是黑球，则放回后再往袋中加进1个黑球；若取出的是白球，则放回后再往袋中加进2个白球；第二次取球重复以上操作，记第次操作后袋中黑球与白球()1,2,3i i =的个数之差为．i X (1)求的分布列与数学期望；2X (2)求在第2次操作中取出黑球的条件下，的概率．33X =19．我国元代数学家朱世杰在他的《四元玉鉴》一书中对高阶等差数列求和有精深的研究，即“垛积术”．对于数列，①，从第二项起，每一项与它前邻一项的差构成数列12,,,,n a a a ⋅⋅⋅⋅⋅⋅，②，称该数列②为数列①的一阶差分数列，其中()111211,,,,n a a a -⋅⋅⋅⋅⋅⋅；对于数列②，从第二项起，每一项与它前邻一项的差构成数()111,2,,1,i i i a a a i n +=-=⋅⋅⋅-⋅⋅⋅列，③，称该数列③为数列①的二阶差分数列，其中()212222,,,,n a a a -⋅⋅⋅⋅⋅⋅按照上述办法，第次得到数列，()()21111,2,,2,i i i a a a i n +=-=⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅r ()12,,,,r r r n r a a a -⋅⋅⋅⋅⋅⋅④，则称数列④为数列①的阶差分数列，其中，若r ()()()()1111,2,,,ri r i r i a a a i n r -+-=-=⋅⋅⋅-⋅⋅⋅数列的阶差分数列是非零常数列，则称数列为阶等差数列（或高阶等差数{}n a ()2r r ≥{}n a r 列）．(1)若高阶等差数列为，求数列的通项公式；{}n a 3,4,9,18,31,48,⋅⋅⋅{}n a (2)若阶等差数列的通项公式．r {}n b ()421n b n =-（ⅰ）求的值；r （ⅱ）求数列的前项和．{}n b n n S 附：．()()222121126n n n n ++++⋅⋅⋅+=1．A【分析】根据复数的几何意义，由复平面内复数对应的点的坐标可以得出对应复数的代数z 形式，再结合复数的四则运算法则，即可得解.【详解】因为复数对应的点的坐标为，所以，z ()1,1-1i z =-所以，所以．()221i 2iz =-=-()()()22i 12i 2i 42i 12i 12i 12i 12i 55z +=-=-=----+故选：A ．2．B【分析】根据椭圆的标准方程求出，再求长轴长与焦距之差.,,a b c 2a 2c【详解】由题得，，所以，，280a =235b =a =c ==所以长轴长2a =2c =所以长轴长与焦距之差等于．22a c -=故选：B 3．C【分析】利用指数型复合函数的单调性即可得出答案.【详解】令，则，22t x x=-3ty =由复合函数的单调性可知：的单调递减区间为函数的单调递减区间，()f x 22t x x=-又函数，2()()2()t x x x t x -=---=即函数为偶函数，()t x 结合图象，如图所示，可知函数的单调递减区间为和，22t x x=-(),1∞--()0,1即的单调递减区间为和．()f x (),1∞--()0,1故选：C ．4．A【分析】根据向量平行，得到，结合基本不等式即可求.221λμλ+=【详解】由题意，因为，所以，又，//a b r r 221λμλ=+0λ>所以即时等号成立．22112λμλλλ+==+≥=12λλ=λ=故选：A 5．B【分析】举出反例说明“”不是“”的充分条件；再证明出以“”是“”的必a b αβ∥a b αβ∥要条件，即可.【详解】如图，，，，此时无法推出，a α⊂b β⊂l αβ= a b l ∥∥αβ∥所以“”不是“”的充分条件；a b αβ∥由共面，设，则，，,a b ,a b γ⊂a αγ⋂=b βγ= 又因为，所以，所以“”是“”的必要条件，αβ∥a b a b αβ∥综上，“”是“”的必要不充分条件.a b αβ∥故选：B.6．D【分析】分类讨论甲是否报剪纸，先安排甲，再安排乙，结合组合数分析求解.【详解】按甲报的课程分为两类：①若甲报剪纸，则从除了陶艺的其他4门课程中再选1门，有种结果，14C 乙再从剩余4门课程中选2门，有种结果，有种；24C 1244C C 24=②若甲不报剪纸，则从除了陶艺、剪纸的其他4门课程中选2门，有种结果，24C 乙再从剩余除剪纸外的3门课程中选2门，有种结果，有种；23C 2243C C 18=综上所述：共有种方案．241842+=故选：D ．7．A【分析】根据题意整理可得，其中，，结合正弦()()51sin 222f x x ωϕ=++4cos 5ϕ=3sin 5ϕ=函数对称性可得，，分类讨论的奇偶性，结合诱导公式分析求解.1π22k ϕω=-+k ∈Z k 【详解】由题意可知：，()()()3512sin2cos211sin 2222f x x x x ωωωϕ=++-=++其中，．4cos 5ϕ=3sin 5ϕ=因为的图象关于点中心对称，则，()f x 11,2⎛⎫ ⎪⎝⎭()()5111sin 2222f ωϕ=++=整理可得，则，()sin 20ωϕ+=2π,k k ωϕ+=∈Z 解得，，则，1π22k ϕω=-+k ∈Z 1tan tan π22k ϕω⎛⎫=-+ ⎪⎝⎭当时，；2,k m m =∈Z cos 11tan tan tan 22sin 3ϕϕϕωϕ-⎛⎫=-=-==-⎪⎝⎭当时，；21,k m m =+∈Z cosπsin 2tan tan 3221cos sin 2ϕϕϕωϕϕ⎛⎫=-=== ⎪-⎝⎭综上所述：或．tan 3ω=1tan 3ω=-故选：A ．8．C【分析】作辅助线，则即为三棱锥的外接球球心，翻折的角即为的大小，设O θCDC ∠'，结合题意分析可知，结合题意分析求解即可.OC R =2211412cos 2R θ=+【详解】取线段的中点，线段上靠近点的三等分点，的中点，AB D CD D G CC 'E 连接，则为正的外心，，可知为线段的中垂线，,,CD C D DE 'G ABC CD C D ¢=DE CC '在平面内过作的垂线交于，连接，CCD 'G CD ED O OC则即为三棱锥的外接球球心，翻折的角即为的大小．O θCDC ∠'设，则，OC R =DC DC '==2DEθ=DG=CG =，2EC EC θ='=可得2cos 2DG DE DO OEθθ==+==化简得，2211412cos 2R θ=+又因为，解得，R ≤22111343612cos 2R θ=+≤23cos 24θ≥结合，可得，所以．π0,2θ⎛⎫∈ ⎪⎝⎭cos2θ≥π026θ<≤π03θ<≤故选：C ．方法点睛：多面体与球切、接问题的求解方法1.涉及球与棱柱、棱锥的切、接问题时，一般过球心及多面体的特殊点（一般为接、切点）或线作截面，把空间问题转化为平面问题求解；2.利用平面几何知识寻找几何体中元素间的关系，或只画内切、外接的几何体的直观图，确定球心的位置，弄清球的半径(直径)与该几何体已知量的关系，列方程（组）求解．9．AB【分析】根据等比数列分析可知：且或8，分或，结合等边数列通0q <22a =2428a a =⎧⎨=⎩2482a a =⎧⎨=⎩项公式分析求解，再结合等边数列求和公式分析求解.【详解】设等比数列的公比为，{}n a q 因为等比数列中所有奇数项同号，所有偶数项同号，结合已知可知，其中2，8这两项的奇偶性相同，0q <又因为，可知或8，则有：20a >22a =若，，则，解得，符合题意，22a =48a =2134128a a q a a q ==⎧⎨==⎩112a q =-⎧⎨=-⎩所以的前7项和为；{}n a ()()71124312⎡⎤-⨯--⎣⎦=---若，，则，解得，此时，符合题意，28a =42a =2134182a a q a a q ==⎧⎨==⎩11612a q =-⎧⎪⎨=-⎪⎩51a =-所以的前7项和为；{}n a 711612431412⎡⎤⎛⎫-⨯--⎢⎥⎪⎝⎭⎢⎥⎣⎦=-⎛⎫-- ⎪⎝⎭综上所述：的前7项和为或．{}n a 43-434-故选：AB ．10．AB【分析】对于A ：根据直线方程分析判断；对于B ：根据题意求直线交点即可；对于C ：根据空集的定义结合直线平行运算求解；对于D ：根据直线重合分析求解.【详解】对于选项A ：因为表示过定点，且斜率不为0的直线，20x ay a ++=()0,2-可知表示直线上所有的点，(){},20A x y x ay a =++=20x ay a ++=所以，故A 正确；,a A ∀∈≠∅R对于选项B ：当时，则，，1a =-(){},20A x y x y =--=(){},10B x y x y =++=联立方程，解得，所以，B 正确；2010x y x y --=⎧⎨++=⎩1232x y ⎧=⎪⎪⎨⎪=-⎪⎩13,22A B ⎧⎫⎛⎫⋂=-⎨⎬⎪⎝⎭⎩⎭对于选项C ：当时，则有：A B ⋂=∅若，则；B =∅0a =若，可知直线与直线平行，且，B ≠∅20x ay a ++=10ax ay +-=0a ≠可得，解得；121a a a a =≠-1a =综上所述：或，故C 错误；0a =1a =对于选项D ：若，由选项C 可知，且，无解，故D 错误．A B =0a ≠121a aa a ==-故选：AB ．11．ACD【分析】对于A ：利用赋值法分析可得，；对于B ：根据()12f =-()12f -=-结合单调性的定义分析判断；对于C ：分析可得，即可()()112f f =-=-()()4f x f x -+=-得结果；对于D ：对求导，结合偶函数的定义分析判断.()()4f x f x -+=-【详解】因为，且的定义域为，()()()()21f xy xf y yf x x y =+++-()f x R 对于选项A ：令，则，可得；1x y ==()()1212f f =+()12f =-令，则，可得，故A 正确；1x y ==-()()12162f f =---=-()12f -=-对于选项B ：由选项A 可知，所以不是单调函数，故B 错误；()()112f f =-=-()f x 对于选项C ：令，可得1y =-，()()()()()()()1222224f x xf f x x x f x x f x -=--+-=--+-=--即，所以，故C 正确；()()4f x f x -+=-()()20180i f i f i =⎡⎤-+=-⎣⎦∑对于选项D ：由选项C 可知，()()4f x f x -+=-对两边求导得，即，()()0f x f x --+'='()()f x f x ''=-所以为偶函数，故D 正确．()f x '故选：ACD ．方法点睛：函数的性质主要是函数的奇偶性、单调性和周期性以及函数图象的对称性，在解题中根据问题的条件通过变换函数的解析式或者已知的函数关系，推证函数的性质，根据函数的性质解决问题．12．13【分析】将数据从小到大排列，然后算出分位数的位置，由百分位数的定义，即可得到75%答案.【详解】将这8个数据从小到大排列得，3,5,7,8,9,11,15,21因为，所以这组数据的分位数为．875%6⨯=75%1115132+=故1313【分析】根据给定条件，利用数量积的运算律，结合正弦定理边化角即可得解.【详解】在中，是的中点，，ABC D BC 2(()12)2BC AD AC AB AC AB c ⋅=-⋅+=则，即，因此，2224AC AB c -= 2224b c c -=225b c=所以.sin sin B bC c ==14【分析】先研究点在第一象限时，由的面积是的面积的4倍，求出直线的M MAF △NBF l 斜率，联立直线与抛物线方程求出的值；再根据对称性研究在第三象限时的值即可.p M p 【详解】如图，当点在第一象限时，由抛物线的定义，可得，，M MA MF=NB NF=所以，所以，221sin 241sin 2MAF NBFMA MF AMF MF S S NF NB NF BNF ∠===∠ 2MF NF =所以．如图，过点作于点，则，2MA NB=N 1NN MA ⊥1N 1N A NB=所以，所以，11123N M AM MN ==111cos 3N M N MN MN ∠==所以的斜率，1sin N MN∠=l 111sin tan cos N MN k N MN N MN ∠=∠==∠则直线，直线与联立，得，:2p l y x ⎫=-⎪⎭l 22y px =22450x px p -+=设与的横坐标分别为，，则，M N M x N x 54M N px x +=所以，94M N MN x x p p=++=所以以为直径的圆的半径，MN 928MNr p ==圆心到轴的距离，y 528M N x x d p+==所以弦长为，解得；==p=当点在第三象限时，由对称性可得Mp =综上，.p=故答案为15．(1)，1a =1b =(2)单调递增区间为，单调递减区间为，最大值为．31,2⎛⎫ ⎪⎝⎭3,2⎛⎫+∞ ⎪⎝⎭33ln224f ⎛⎫=-- ⎪⎝⎭【分析】（1）先根据切点在曲线上确定切点的坐标；再根据切点在切线上和导数的几何意义列出方程组求解即可.（2）根据导函数的符号与原函数单调性的关系即可得出单调区间；再根据单调性可求出最大值..【详解】（1）因为，()()2ln 1f x a x x x=--+所以，，()()22ln 21222f a =--+=-()211af x x x =-+-'则切点坐标为.()2,2-因为曲线在点处的切线方程为，()y f x =()()22f ,220x by +-=所以，解得．()222202222121b a f b ⨯-⨯-=⎧⎪⎨=-⨯+=-⎪-⎩'11b a =⎧⎨=⎩（2）由（1）可得：函数的定义域为：，.()f x ()1,+∞()()2312111x x f x x x x --=-+='--令，得；令，得.()0f x ¢>312x <<()0f x '<32x >所以的单调递增区间为，单调递减区间为，()f x 31,2⎛⎫ ⎪⎝⎭3,2⎛⎫+∞ ⎪⎝⎭所以的最大值为．()f x 33ln224f ⎛⎫=-- ⎪⎝⎭16．(1)证明见解析【分析】（1）取的中点，根据题意可得，，可证平面，BC D 1AA BC ⊥AD BC ⊥BC ⊥1AA PD 即可得结果；（2）建系标点，求平面的法向量，利用空间向量求线面夹角.11PA C 【详解】（1）取的中点，连接，BC D ,AD PD 且为的中点，则，P 1BC 1PD CC ∥因为，则，所以四点过面，11AA CC ∥1PD AA ∥1,,,P D A A 因为平面，平面，则，1AA ⊥ABC BC ⊂ABC 1AA BC ⊥又因为，且为的中点，则，AB AC =D BC AD BC ⊥且，平面，可得平面，1AA AD A ⋂=1,AA AD ⊂1AA PD BC ⊥1AA PD且平面，所以．1PA ⊂1AA PD 1BC PA ⊥（2）由（1）可得平面，平面，平面，PD ⊥ABC AD ⊂ABC BD ⊂ABC 所以，，PD AD ⊥PD BD ⊥以为原点，的方向分别为轴的正方向，建立空间直角坐标系，D ,,DB AD DP ,,x yz 则，，，，，()0,3,0A -()10,3,2A -()0,0,1P )12B ()12C 可得，，，)12AB =()11A C =()10,3,1A P =-设平面的法向量为，则，11PA C (),,m x y z =1113030m A C y m A P y z ⎧⋅=+=⎪⎨⋅=-=⎪⎩ 令，，可得，x =1y=3z =)m =设直线与平面所成的角为，1AB 11PA C θ则，111sin cos ,m AB AB m m AB θ⋅====所以直线与平面1AB 11PA C 17．(1)22126x y -=(2)或1k =±2k =±【分析】（1）由离心率及顶点到渐近线的距离列方程即可求；（2）联立直线与双曲线方程，利用韦达定理及弦长公式，点到直线距离公式求解面积即可.【详解】（1）记的半焦距为，由题得的离心率，①C c C 2ce a ==由对称性不妨设的顶点为，渐近线方程为，则②C (),0a 0bx ay -=ab c =又，③222+=a bc 联立①②③解得，a b =c =所以的方程为．C 22126x y -=（2）设，()()1122,,,A x y B x y 由得，222126y kx x y =+⎧⎪⎨-=⎪⎩()2234100k x kx ---=所以，()222230Δ16403120240k k k k ⎧-≠⎪⎨=+-=->⎪⎩解得，且，k <<)*k ≠所以，，12243k x x k +=-122103x xk -=-所以．AB ===又点到直线的距离，O l d =所以的面积，AOB1122S AB d =⋅===解得或，符合式，1k =±2k =±()*所以或．1k =±2k =±18．(1)分布列见解析，13135(2)．35164【分析】（1）先确定的取值，分别求解概率，写出分布列，利用期望公式可求期望；2X （2）先利用全概率公式求，再利用条件概率可求答案.()2P A【详解】（1）两次操作取出的球均为黑球，则第2次操作后袋中有6个黑球、1个白球，此时，25X =所以；()24525563P X ==⨯=两次操作取出的球均为白球，则第2次操作后袋中有4个黑球、5个白球，此时，21X =-所以；()213315735P X =-=⨯=两次操作取出的球中黑、白球各一次，则第2次操作后袋中有5个黑球、3个白球，此时，22X =所以，()()()222232621511335105P X P X P X ==-=-=-=--=所以的分布列为2X 2X 1-25P3352610523所以．()2326213112535105335E X =-⨯+⨯+⨯=（2）记事件为“在第次操作中取出黑球”，事件为“第3次操作后袋中黑球与白i A i ()1,2i =B 球的个数之差为3”．则，()()()()()21211214514825657105P A P A P A A P A P A A =+=⨯+⨯=若第1次操作取到的是白球，且第2次操作取到的是黑球，则第2次操作后袋中有5个黑球、3个白球，①若第3次取到的是白球，则第3次操作后袋中有5个黑球、5个白球，此时；30X =②若第3次取到的是黑球，则第3次操作后袋中有6个黑球、3个白球，此时；33X =若第1次操作取到的是黑球，且第2次操作取到的是黑球，则第2次操作后袋中有6个黑球、1个白球，①若第3次取到的是白球，则第3次操作后袋中有6个黑球、3个白球，此时；33X =②若第3次取到的是黑球，则第3次操作后袋中有7个黑球、1个白球，此时，36X =所以表示第1次操作取到的是白球，且第2次和第3次操作取到的是黑球或第1次和第2A B 2次操作取到的是黑球，且第3次操作取到的是白球，所以，()214545115785676P A B =⨯⨯+⨯⨯=所以．()()()222135682164105P A B P B A P A ===19．(1)2256n a n n =-+(2)（ⅰ）；（ⅱ）4r =n S 5316875315n n n =-+【分析】（1）根据阶等差数列的定义，分别求出一阶差分数列和二阶差分数列，发现二阶r 差分数列为常熟列，即可得出，即，得到为等差数列，求得24n a =()1114n n a a +-={}1n a ，即，然后用累加法即可求解；143n a n =-143n n a a n +-=-（2）（ⅰ）根据阶等差数列的定义，从一阶差分数列、二阶差分数列、三阶差分数列…依次r 往下求，当出现常数列时为止，即可确定为r 的值；（ⅰⅰ）结合二项式定理将转化为()421n -了，然后利用裂项相消求和与分组求和的方法即可得解.()552161118855n n n n ⎡⎤---+-⎣⎦【详解】（1）数列的一阶差分数列为，{}n a 1,5,9,13,17,⋅⋅⋅二阶差分数列为，为非零常数列，4,4,4,4,4,⋅⋅⋅所以，即，且，24n a =()1114n n a a +-=111a =所以数列是首项为1、公差为4的等差数列，{}1n a 所以，即，且，()111443n a n n =+-⨯=-143n n a a n +-=-13a =所以当时，2n ≥()()()112211n n n n n a a a a a a a a ---=-+-+⋅⋅⋅+-+，()][()()4134234133n n ⎡⎤=--+--+⋅⋅⋅+⨯-+⎣⎦()()2143132562n n n n n -=⨯--+=-+当时，，也满足上式，1n =13a =综上，数列的通项公式为．{}n a 2256n a n n =-+（2）（ⅰ），所以，()421n b n =-()()4431121216416n n n b b b n n n n+=-=+--=+，()()()()3322111641161641619219280n n n b b b n n n n n n +=-=+++-+=++所以，()()()()223221192119218019219280384384n n n b b b n n n n n +=-=++++-++=+所以，()()()43313841384384384384n n n b b b n n +=-=++-+=所以数列是4阶等差数列，即．{}n b 4r =（ⅱ）()()55505142332455555551C C C C C C n n n n n n n n --=--+-+-，()5543243251010515101051n n n n n n n n n n =--+-+-=-+-+所以，()545321112255n n n n n n ⎡⎤=--+-+-⎣⎦又()()()()4432012344324444421C 2C 2C 2C 2C 16322481n n n n n n n n n -=-+-+=-+-+，()552161118855n n n n ⎡⎤=---+-⎣⎦所以()()()1111455216112118855k k k k n n n n n S k k k k k n=====∑-=∑---∑+∑-()()()512111611885625n n n n n n n +++=-⨯+⨯-．5316875315n n n =-+关键点点睛：本题第2问的第ⅱ小问，求和关键是把平时熟悉的裂项相消求和与分组求和的方法应用到该题，结合二项式定理巧妙而关键的将转化为了()421n -，然后第一组可以用裂项相消求和的思想来求()552161118855n n n n ⎡⎤---+-⎣⎦()551615n n ⎡⎤--⎣⎦和，第二组用题干中给出的公式求和，第三组用等差数列公式求和即可.28n 1185n -。

第Ⅰ卷（选择题，共60分）一、本题共12小题，每小题5分，共60分，在每小题给出的四个选项中只有一个选项是符合题目要求的、1．设集合A ，B 是全集U 的两个子集，则A ⊂≠B 是C U B ⊂≠C U A 的 （ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件2．若复数z 满足,21i iz=+ 则z 对应的点位于（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限3．已知函数)(x f y =的图像关于点（一1，0）对称，且当∈x （0，＋∞）时，xx f 1)(=，则当∈x （一∞，一2）时)(x f 的解析式为（ ） A ．x1-B ．21+x C ．21+-x D ．x-21 4．设a ，b ，c 是空间三条直线，α，β是空间两个平面，则下列命题中，逆命题不成立的是（ ）A ．当c ⊥α时，若c ⊥β，则α∥βB ．当α⊂b 时，若b ⊥β，则βα⊥C ．当α⊂b ，且c 是a 在α内的射影时，若b ⊥c ，则a ⊥bD ．当α⊂b ，且α⊄c 时，若c ∥α，则b ∥c5．已知θ是第三象限角，m =|cos |θ，且02cos 2sin >+θθ，则2cos θ等于（ ）A ．21m+ B．21m+-C ．21m - D ．21m-- 6．执行如图所示的算法程序,输出的结果是（ ）A ．24,4B ．24,3C ．96,4D ．96,37．已知关于x 的方程2(1)10(,)x a x a b a b R +++++=∈的两根分别为1x 、2x ，且1201x x <<<，则ba的取值范围是（第6题图）（ ）A ．]21,2[-- B．12,2⎛⎫-- ⎪⎝⎭ C ．]2,21[D ．)2,21( 8．已知数列}{n a 的前n 项和为)15(21-=n n S n ，+∈N n ，现从前m 项：1a ，2a ，…，m a 中抽出一项（不是1a ，也不是m a ），余下各项的算术平均数为37，则抽出的是（ ）A ．第6项B ．第8项C ．第12项D ．第15项9．已知在平面直角坐标系),(),1,2(),1,1(),2,1(),0,0(,y x M C B A O xOy 动点中--满足条件 ⎪⎩⎪⎨⎧≤⋅≤≤⋅≤-,21,22 则OC OM ⋅的最大值为（ ）A ．4B ．8 C．12D ．1510．在正三棱锥A 一BCD 中，E ，F 分别是AB ，BC 的中点，EF ⊥DE ，且BC ＝1，则正三棱锥A 一BCD 的体积等于（ ）A ．1212B ．242C ．123D ．243 11．已知集合{}(,)2||2A x y x y x y =∈Z||≤，≤，，，集合{}22()(2)(2)4B x y x y x y =-+-∈Z，≤，，，在集合A 中任取一个元素p ，则p ∈B 的概率是（ ）A ．52 B ．53 C ．625D ．254 12．已知双曲线12222=-by a x （a ＞0，b ＞0）的两个焦点为1F 、2F ，点A在双曲线第一象限的图象上，若△21F AF 的面积为1，且21t an 21=∠F AF ，2tan 12-=∠F AF ，则双曲线方程为（ ）A ．1351222=-y x B ．1312522=-y xC ．1512322=-y x D ．1125322=-y x第Ⅱ卷（非选择题，共90分）二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上。

高考数学（文科）模拟试卷及答案3套模拟试卷一考试时间：120分钟 考试分数：150分第I 卷（选择题 共60分）一．选择题： （本大题共12小题，每小题5分，共60分）1、若集合2{06},{20}A x x B x x x =<<=+->，则A B =U （ ） A. {16}x x << B.{2,0}x x x <->或 C.{26}x x << D.{2,1}x x x <->或2、设1i2i 1iz -=++，则z =（ ） A ．0 B ．12C ．1D ．23、函数部分图象可以为（ ）A.B.C. D.4、A 地的天气预报显示，A 地在今后的三天中，每一天有强浓雾的概率为，现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率，先利用计算器产生之间整数值的随机数，并用0，1，2，3，4，5，6表示没有强浓雾，用7，8，9表示有强浓雾，再以每3个随机数作为一组，代表三天的天气情况，产生了如下20组随机数：402 978 191 925 273 842 812 479 569 683 231 357 394 027 506 588 730 113 537 779 则这三天中至少有两天有强浓雾的概率近似为（ ） A ． B ． C ．D ．5、设,m n 是两条不同的直线，,αβ是两个不同的平面，有下列四个命题： ①若,m ααβ⊂⊥，则m β⊥； ②若//,,m αββ⊂则//m α； ③若,//,//m m n ααβ⊥，则n β⊥； ④若//,//,//m n m n αβ，则//αβ. 其中正确命题的序号是( )A.①②B.①③C.②③D.③④6、朱载堉（1536—1611），明太祖九世孙，音乐家、数学家、天文历算家，在他多达百万字的著述中以《乐律全书》最为著名，在西方人眼中他是大百科全书式的学者王子。

他对文艺的最大贡献是他创建了“十二平均律”，此理论被广泛应用在世界各国的键盘乐器上，包括钢琴，故朱载堉被誉为“钢琴理论的鼻祖”。

高三第三次模拟考试数学（文）试题本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，其中第Ⅱ卷第22－24题为选考题，其它题为必考题．考生作答时，将答案答在答题卡上．在本试卷上答题无效．考试结束后，将本试卷和答题卡一并交回． 注意事项：1．答题前，考生务必先将自己的姓名、准考证号填写在答题卡上;2．选择题答案使用2B 铅笔填涂，如需改动，用橡皮擦干净后，再选涂其它答案标号；非选择题答案使用0.5毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚;3．请按照题号在各题的答题区域（黑色线框）内作答，超出答题区域书写的答案无效; 4．保持卡面清洁，不折叠，不破损．5．做选考题时，考生按照题目要求作答，并用2B 铅笔在答题卡上把所选题目对应的题号涂黑． 参考公式：样本数据n x x x ,,21的标准差 锥体体积公式222121[()()()]n s x x x x x x nL 13V Sh 其中x 为样本平均数 其中S 为底面面积，h 为高 柱体体积公式 球的表面积，体积公式V Sh 24S R 343V R其中S 为底面面积，h 为高 其中R 为球的半径第I 卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．设集合}0103|{2 x x R x M ，}2|||{ x Z x N ，则M N I 为A.)2,2(B.)2,1(C.{-1，0，1}D.}2,1,0,1,2{2．若复数)(13R x iix z 是实数，则x 的值为A. 3B. 3C. 0D.33．曲线C ：y = x 2 + x 在 x = 1 处的切线与直线 ax －y + 1 = 0 互相垂直，则实数 a 的值为 A. 3 B. －3 C.31 D. －314．已知变量x ，y 满足125,31x y x y z x y x则的最大值为A ．5B ．6C ．7D ．85．如图是一个几何体的三视图，则此三视图所描述几何体的表面积为 A ． )3412(B ．20C ． )3420(D ．28 6. 下列命题中：①若p ，q 为两个命题，则“p 且q 为真”是“p 或q 为真”的必要不充分条件.②若p 为：02,2 x x R ，则p 为：02,2 x x R . ③命题“032,2 x x x ”的否命题是“032,2 x x x ”. ④命题“若,p 则q”的逆否命题是“若p ，则q ”. 其中正确结论的个数是A ．1 B. 2 C.3 D.47．双曲线12222 by a x 的离心率为3,则它的渐近线方程是A ．x y 2B ．x y 22C ．x y 2D ．x y 21 8．将函数）（3cosx y 的图象上各点的横坐标伸长到原来的2倍（纵坐标不变），再向左平移6个单位，所得函数的最小正周期为 A ．π B ．2π C ．4πD ．8π9． 有以下程序：INPUT xIF 1x THEN()2f x xELSE IF 11x THEN2()f x xELSE ()2f x x END IFPRINT ()f x根据左边程序，若函数()()g x f x m 在R 上有且只有两个零点，则实数m 的取值范围是 A ．1m B ．01m C ．01m m 或 D ．0m 10．ABC 中,三边之比4:3:2:: c b a ，则最大角的余弦值等于A.41 B.87 C .21D.4111. 数列{}n a 中，352,1,a a 如果数列1{}1n a 是等差数列，则11aA. 0(B)111 (C)113 (D)1712．已知 0,230,2)(2x x x x x f ,若ax x f |)(|在]1,1[ x 上恒成立,则实数a 的取值范围是A.),0[]1(B.]0,1[C.]1,0[D.)0,1[第Ⅱ卷本卷包括必考题和选考题两部分。

2021年高考数学模拟考场仿真演练卷（全国Ⅲ卷）03文科数学（考试时间：120分钟 试卷满分：150分）注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答第Ⅰ卷时，选出每小题答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在本试卷上无效。

3．回答第Ⅱ卷时，将答案写在答题卡上。

写在本试卷上无效。

4．考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷一、选择题（本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．已知集合})ln(|{N x x e y x A ∈-==，，}11{，-=B ，则B A 的子集个数为（ ）。

A 、4 B 、8 C 、16 D 、322．在复平面内，复数2111ii i z -+-+=对应的点位于（ ）。

A 、第一象限 B 、第二象限 C 、第三象限 D 、第四象限3．如图所示，在ABC Rt ∆中， 90=∠C ， 30=∠B ，在BAC ∠内过点A 任作一射线与BC 相交于点D ，使得 30<∠DAC 的概率为（ ）。

A 、51B 、41C 、31 D 、21 4．函数|2|sin )()(x e e x f x x ⋅-=-的图像可能是（ ）。

A 、B 、C 、D 、5．如图所示，图中小正方形的边长为1，粗线画出的是某空间几何体的三视图，则该几何体的表面积为（ ）。

A 、2416+πB 、2417+πC 、2418+πD 、2420+π6．已知函数)(x f y =对任意实数x 都满足)()(x f x f -=π+，当)2(ππ∈，x 时，x x f tan )(=，若)1(f a =，)2(f b =，)3(f c =，则a 、b 、c 的大小关系为（ ）。

A 、c b a << B 、c a b << C 、b a c << D 、a b c <<7．过双曲线14222=--ty x 的右焦点2F 作垂直于x 轴的直线交双曲线于M 、N 两点，1F 为左焦点，当1MNF ∆的面积为58时，双曲线的离心率为（ ）。

新课标版版高考临考大练兵（文30）一、选择题（本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中， 只有一项是符合题目要求的）1．下列各式中正确的是（ ）(A) 0=Ф (B)}0{⊆Φ (C)}0{=Φ (D).Φ∈02．若复数(1+bi)(2+i)是纯虚数(i 是虚数单位，b 是实数)，则b=（ ）(A) -2 （B ）⋅-21 (C)21 (D)2 3．“21=m ”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=O 相互垂直”的（ ） (A)充分不必要条件 (B)必要不充分条件(C)充要条件 (D)既不充分也不必要条件4．函数||log 22x y =的图像大致是( )5．曲线y=2x 2在点P(1，2)处的切线方程是（ ）(A) 4x-y-2=0 (B) 4x+y-2=O(C) 4x+y+2=O (D) 4x-y+2=06．命题：“对任意的x ∈R ，0322≤--x x ”的否定是（ ）(A) 不存在032.,2≤--∈x x R x （B ）存在032,2≤--∈x x R x(C) 存在x ∈R ，x 2-2x-3>0 (D) 对任意的x ∈R ，x 2-2x-3>0 7. 椭圆12222=+by a x 的右焦点与抛物线y 2=8x 的焦点相同，离心率为21，则此椭圆 的方程为（ ）（A ）116..1222=+y x （B ）1121622=+y x （C ）1644822=+y x （D ）1486422=+y x 8．已知圆)0.(4)2()(:22>=-+-a y a x C 及直线l ：x-y+3=O ，当直线l 被圆C 截得的 弦长为32时，则a=（ ）（A ）2 （B ）22- （C ）12- （D ）12+9．在△ABC 中，b AC c AB ==,，若点D 满足BD DC 2=，则AD =（ ) （A ）c b 3231+（B ）c b 3235- （C ）c b 3132- （D ）c b 3132+ 10. 右图给出的是计算201614121++++ 的值的一 个算法流程图，其中判断框内应填入的条件是( )（A ）i>10 (B)i ≥10 (C) i<10 (D)i ≤10二、填空题（本大题共4小题，每小题5分，共20分）1l. 如图，一个简单空间几何体的三视图，其主视图与侧视图都是边长为2的正三角形，俯视图轮廓为正方形，则此几何体的表面积是 。