数学建模统计预测方法及预测模型

数学建模的主要建模方法数学建模是指运用数学方法和技巧对复杂的实际问题进行抽象、建模、分析和求解的过程。

它是解决实际问题的一个重要工具，在科学研究、工程技术和决策管理等领域都有广泛的应用。

数学建模的主要建模方法包括数理统计法、最优化方法、方程模型法、概率论方法、图论方法等。

下面将分别介绍这些主要建模方法。

1.数理统计法：数理统计法是基于现有的数据进行概率分布的估计和参数的推断，以及对未知数据的预测。

它适用于对大量数据进行分析和归纳，提取有用的信息。

数理统计法可以通过描述统计和推断统计两种方式实现。

描述统计主要是对数据进行可视化和总结，如通过绘制直方图、散点图等图形来展示数据的分布特征；推断统计则采用统计模型对数据进行拟合，进行参数估计和假设检验等。

2.最优化方法：最优化方法是研究如何在给定的约束条件下找到一个最优解或近似最优解的方法。

它可以用来寻找最大值、最小值、使一些目标函数最优等问题。

最优化方法包括线性规划、非线性规划、整数规划、动态规划等方法。

这些方法可以通过建立数学模型来描述问题，并通过优化算法进行求解。

3.方程模型法：方程模型法是通过建立数学方程或函数来描述问题，并利用方程求解的方法进行求解。

这种方法适用于可以用一些基本的方程来描述的问题。

方程模型法可以采用微分方程、代数方程、差分方程等不同类型的方程进行建模。

通过求解这些方程，可以得到问题的解析解或数值解。

4.概率论方法：概率论方法是通过概率模型来描述和分析不确定性问题。

它可以用来处理随机变量、随机过程和随机事件等问题。

概率论方法主要包括概率分布、随机变量、概率计算、条件概率和贝叶斯推理等内容。

利用概率论的方法，可以对问题进行建模和分析，从而得到相应的结论和决策。

5.图论方法：图论方法是研究图结构的数学理论和应用方法。

它通过把问题抽象成图，利用图的性质和算法来分析和求解问题。

图论方法主要包括图的遍历、最短路径、最小生成树、网络流等内容。

全国大学生数学建模比赛论文人口预测模型 The manuscript was revised on the evening of 2021中国人口预测模型摘要：人口数量的变化，关系到一个国家的未来。

认识人口数量的变化规律，建立人口模型，能够较准确的预报，是有效控制人口增长的前提。

本文对人口预测的数学模型进行了研究。

首先，建立人口指数模型、Logistic模型及灰度预测模型。

对我国2005年以后45年的人口增长进行了预测，根据1982年人口基本数据运用模型对1982年～2005年进行了预测，并用实际数据对预测结果进行了检验。

我们将预测区间分为2006～2030年、2030～2050年两个区间，以量化未来我国短中期与长期的人口变化。

关键词：人口数量的变化人口指数模型 Logistic模型灰度预测模型MATLAB Excel目录第一部分问题重述 (3)第二部分问题分析 (3)第三部分模型的假设 (3)第四部分定义与符号说明 (3)第五部分模型的建立与求解 (3)模型一 (3)模型二 (8)模型三 (12)第六部分对模型的评价 (14)第七部分参考文献 (15)第八部分附表 (15)一、问题重述人口问题始终是制约我国发展的关键因素之一。

本题要求根据已知数据，运用数学建模的思想对我国人口做出分析和预测。

具体问题如下：从中国的实际情况和人口增长的特点，例如我国老龄化进程加快、出生人口性别比持续升高、乡村人口城镇化等，利用参考附录中所提供的数据，建立中国人口增长的数学模型，由此对中国人口增长的中短期和长期趋势做出预测，并指出模型的优缺点。

二、 模型假设1、假设题目所给的数据真实可靠；2、假设不考虑我国人口大规模的朝国外迁移，也不考虑外国人大量涌入我国；3、假设不考虑战争、自然灾害、疾病对人口数目和性别比的影响；4、假设在本世纪中叶前，我国计划生育政策稳定。

5、假设中短期内生育率和死亡率保持相对稳定6、假设相同年龄段人口性别比基本稳定。

数学建模各类方法归纳总结数学建模是一门应用数学领域的重要学科，它旨在通过数学模型对现实世界中的问题进行分析和解决。

随着科技的不断发展和应用需求的增加，数学建模的方法也日趋多样化和丰富化。

本文将对数学建模的各类方法进行归纳总结，以期帮助读者更好地了解和应用数学建模。

一、经典方法1. 贝叶斯统计模型贝叶斯统计模型是一种基于概率和统计的建模方法。

它通过利用先验知识和已知数据来确定未知数据的后验概率分布，从而进行推理和预测。

贝叶斯统计模型在金融、医药、环境等领域具有广泛应用。

2. 数理统计模型数理统计模型是基于概率统计理论和方法的建模方法。

它通过收集和分析样本数据，构建统计模型，并通过参数估计和假设检验等方法对数据进行推断和预测。

数理统计模型在市场预测、风险评估等领域有着重要的应用。

3. 线性规划模型线性规划模型是一种优化建模方法，它通过线性目标函数和线性约束条件来描述和解决问题。

线性规划模型在供应链管理、运输优化等领域被广泛应用，能够有效地提高资源利用效率和降低成本。

4. 非线性规划模型非线性规划模型是一种对目标函数或约束条件存在非线性关系的问题进行建模和求解的方法。

非线性规划模型在经济学、物理学等领域有着广泛的应用，它能够刻画更为复杂的现实问题。

二、进阶方法1. 神经网络模型神经网络模型是一种模拟人脑神经元系统进行信息处理的模型。

它通过构建多层神经元之间的连接关系，利用反向传播算法进行训练和学习，实现对复杂数据的建模和预测。

神经网络模型在图像识别、自然语言处理等领域取得了显著的成果。

2. 遗传算法模型遗传算法模型是一种模拟自然界生物进化过程的优化方法。

它通过模拟遗传、交叉和突变等过程，逐步搜索和优化问题的最优解。

遗传算法模型在组合优化、机器学习等领域具有广泛的应用。

3. 蒙特卡洛模拟模型蒙特卡洛模拟模型是一种基于随机模拟和概率统计的建模方法。

它通过生成大量的随机样本，通过对样本进行抽样和分析，模拟系统的运行和行为，从而对问题进行求解和评估。

财务预测和建模方法财务预测和建模是企业管理和决策过程中至关重要的一环。

它们通过运用统计学和数学建模技术，帮助企业预测未来的财务情况，并为决策提供依据。

本文将介绍几种常用的财务预测和建模方法。

一、时间序列分析法时间序列分析法是一种根据历史财务数据进行预测的方法。

它基于假设，即过去的数据模式将在未来重复出现。

时间序列分析法主要包括以下步骤：（1）观察和识别数据模式：通过查看历史财务数据，分析数据的趋势、季节性、周期性等模式。

（2）选择适当的模型：根据观察到的数据模式，选择合适的时间序列模型，如移动平均模型、指数平滑模型、ARIMA模型等。

（3）模型参数估计：利用历史数据对选定的模型进行参数估计，以得到一个较为准确的模型。

（4）预测未来数据：使用参数估计的模型，对未来的财务数据进行预测。

二、回归分析法回归分析法是一种通过建立依赖于相关变量的数学模型来进行预测的方法。

在财务预测中，通常选择线性回归模型。

回归分析法主要包括以下步骤：（1）确定相关变量：通过分析历史数据，确定可能与财务指标相关的变量。

例如，可以选择销售额、市场规模、利率等作为解释变量。

（2）建立回归模型：根据选定的相关变量，建立一个线性回归模型，将解释变量与财务指标建立起关系。

（3）模型参数估计：利用历史数据对回归模型进行参数估计，以确定模型中的系数。

（4）预测未来数据：使用参数估计的回归模型，对未来的财务数据进行预测。

三、财务比率分析法财务比率分析法是一种通过分析企业财务比率的变化趋势来进行预测的方法。

财务比率是衡量企业财务状况和经营绩效的重要指标，包括偿债能力、盈利能力、运营能力等方面的比率。

财务比率分析法主要包括以下步骤：（1）选择关键比率：挑选出与企业关键财务指标相关的财务比率，如资产负债率、净利润率、存货周转率等。

（2）分析比率变化趋势：通过比较历史数据，观察并分析财务比率的变化趋势，判断企业财务状况的发展方向。

（3）预测未来比率：根据财务比率的变化趋势，预测未来的财务比率，并据此进行财务预测。

数学建模竞赛论文题目：地震预测数学建模姓名：张志鹏学号：12291233 学院：电气工程学院姓名：赵鑫学号：10291033 学院：电气工程学院姓名：张书铭学号：12291232 学院：电气工程学院目录摘要 (3)一、问题重述 (4)二、问题的分析 (4)三、建模过程 (5)问题1：地震时间预测 (5)1、问题假设 (5)2、参数定义 (6)3、求解 (6)问题2：地震地点预测 (7)1、问题假设： (7)2、参数定义 (8)3、求解过程： (8)四、模型的评价与改进 (12)参考文献 (13)摘要大地振动是地震最直观、最普遍的表现。

在海底或滨海地区发生的强烈地震，能引起巨大的波浪，称为海啸。

在大陆地区发生的强烈地震，会引发滑坡、崩塌、地裂缝等次生灾害。

对人们的生产生活成巨大影响，严重威胁人们的生命和财产安全，所以，对地震的预测是十分必要的。

本文根据从1900年以来中国发生的八级以上地震的时间和地点分析，利用合理的数学建模方法，对下一次中国可能发生的八级以上地震的和时间和地点进行合理的预测。

建模方法分为对于时间的预测和地点的预测两个方面。

问题1：对于时间的预测采用的方法为指数平滑法，它是通过计算指数平滑值，配合一定的时间序列预测模型对现象的未来进行预测。

其原理是任一期的指数平滑值都是本期实际观察值与前一期指数平滑值的加权平均。

问题2：对于地点的预测根据长久的数据表明，八级以上地震主要发生在东经70°——110°，北纬20°——50°这个范围内，据此将整个地震带划分为100个区域，按顺序进行编号。

建立时间与地震区域编号的数学模型，利用线性回归的方法对下次地震地点预测。

关键词：地震，预测，数学建模，指数平滑法，线性回归一、问题重述地震预报问题，大地震的破坏性是众所周知的，为了减少大地震带来的灾难，人们提出了各种预报地震的方法，以求减少大地震产生的破坏。

本赛题请大家用数学建模的方式预报下一次大地震发生的时间和地点。

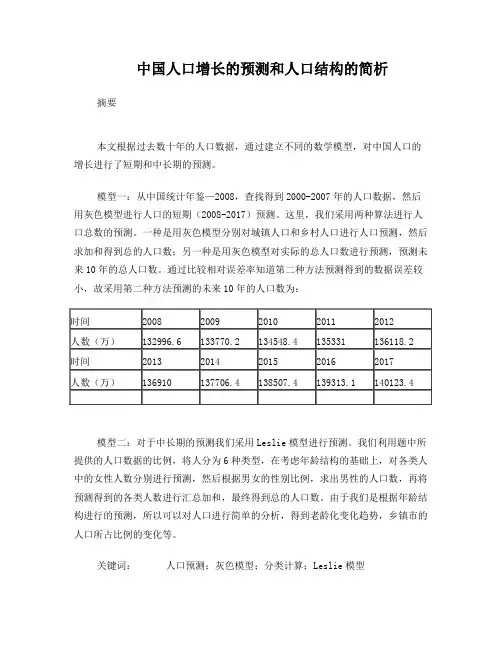
中国人口增长的预测和人口结构的简析摘要本文根据过去数十年的人口数据，通过建立不同的数学模型，对中国人口的增长进行了短期和中长期的预测。

模型一：从中国统计年鉴—2008，查找得到2000-2007年的人口数据，然后用灰色模型进行人口的短期（2008-2017）预测。

这里，我们采用两种算法进行人口总数的预测。

一种是用灰色模型分别对城镇人口和乡村人口进行人口预测，然后求加和得到总的人口数；另一种是用灰色模型对实际的总人口数进行预测，预测未来10年的总人口数。

通过比较相对误差率知道第二种方法预测得到的数据误差较小，故采用第二种方法预测的未来10年的人口数为：模型二：对于中长期的预测我们采用Leslie模型进行预测。

我们利用题中所提供的人口数据的比例，将人分为6种类型，在考虑年龄结构的基础上，对各类人中的女性人数分别进行预测，然后根据男女的性别比例，求出男性的人口数，再将预测得到的各类人数进行汇总加和，最终得到总的人口数。

由于我们是根据年龄结构进行的预测，所以可以对人口进行简单的分析，得到老龄化变化趋势，乡镇市的人口所占比例的变化等。

关键词：人口预测；灰色模型；分类计算；Leslie模型一、模型假设模型一的假设：1、不考虑国际迁移，认为国家内部迁移不改变人口总量；2、不考虑自然灾害、疾病等因素对人口数量的影响；3、文中短期预测到2017年4、大面积自然灾害、疾病的发生以及人们的生育观念等因素会对当年的生育率和人口数量产生影响，认为这些因素在预测误差允许的范围内．模型二的假设：1、每一年龄组的女性在每一个时间段内有相同的生育率和死亡率；2、在预测的时间段内男女的性别比例保持现状不变；3、不考虑人口的迁入和迁出；4、不考虑空间等自然因素的影响，不考虑自然灾害对人口数量的影响。

二、问题分析中国是一个人口大国，随着经济的不断发展，生产力达到较高的水平，现在的问题已不是仅仅满足个人的需要，而是要考虑社会的需要。

中国未富先老，对经济的发展产生很大的影响。

成绩统计预测高中数学建模一、问题背景与意义在当今的教育环境下，学习成绩的预测和评估对于学生、教师和家长都具有重要意义。

通过对学习数据的分析和建模，我们不仅可以更准确地了解学生的学习状况，还能为教学方法的改进和教学资源的优化配置提供科学依据。

特别是在高中数学这一关键学科中，建模预测的成绩数据能够为教师提供更有针对性的教学策略，帮助学生更好地掌握知识，进而提升整体教学质量。

二、数据收集与分析要进行有效的数学建模，首先需要收集相关的数据。

这些数据可能来源于多个方面，如学生的考试成绩、课堂参与度、家庭背景、学习习惯等。

在收集数据后，我们需要进行深入的分析，以理解数据之间的关系和潜在的模式。

例如，我们可以使用描述性统计来理解数据的分布，使用相关性分析来识别影响学习成绩的关键因素。

三、模型建立与选择在确定了数据后，我们需要选择合适的数学模型来进行预测。

这可能包括线性回归模型、决策树、支持向量机、神经网络等。

在选择模型时，我们需要考虑模型的预测能力、解释性以及计算的复杂性。

选择一个合适的模型可以帮助我们更好地理解数据中的模式，并准确地预测未来的结果。

四、模型实施与求解一旦选择了模型，我们就可以开始进行模型的实施和求解。

这通常包括数据的预处理、特征的选择和转换、模型的训练和优化等步骤。

在模型的实施过程中，我们需要不断地调整和优化模型的参数，以确保模型的预测效果。

同时，我们还需要考虑模型的泛化能力，以确保模型能够适应未来的数据。

五、结果分析与应用在得到模型的预测结果后，我们需要对其进行深入的分析。

这可能包括评估模型的准确性、比较不同模型的预测效果、解释模型的预测结果等。

最后，我们将根据分析的结果制定具体的行动计划，例如为特定的学生群体提供定制的教学方案，或者为教师提供教学策略的建议。

此外，这些预测结果还可以用于教育资源的分配、教师评估和学生升学指导等方面。

六、结论与建议通过本次研究，我们得出以下结论：首先，利用数学建模方法可以较为准确地预测学生的学习成绩；其次，不同的建模方法可能在预测精度和应用方面存在差异；最后，数据的质量和完整性对预测结果的准确性具有重要影响。

统计学的预测模型统计学的预测模型是统计学中一个重要的概念，它通过对历史数据的分析和建模，来预测未来事件的发生趋势或结果。

在现代社会，预测模型被广泛运用于各个领域，如金融、医疗、市场营销等，为决策提供重要参考。

本文将介绍统计学的预测模型的基本原理、常见方法和应用场景。

### 基本原理统计学的预测模型基于对数据的分析和统计推断，通过建立数学模型来描述数据之间的关系，并利用这些关系进行未来事件的预测。

其基本原理可以概括为以下几点：1. 数据收集：首先需要收集相关的历史数据，包括变量的取值和事件的结果。

数据的质量和数量对预测模型的准确性至关重要。

2. 数据分析：对收集到的数据进行探索性分析，包括描述统计、相关性分析等，以了解数据的特征和规律。

3. 模型建立：根据数据的特征和问题的需求，选择合适的预测模型，如线性回归、时间序列分析、决策树等，并进行模型的建立和参数估计。

4. 模型评估：通过模型的评估和验证，检验模型的拟合度和预测能力，选择最优的模型进行预测。

5. 预测应用：利用建立好的预测模型对未来事件进行预测，提供决策支持和参考建议。

### 常见方法在统计学的预测模型中，常见的方法包括但不限于以下几种：1. 线性回归：线性回归是一种用于建立自变量和因变量之间线性关系的模型，通过最小二乘法估计回归系数，进行预测和推断。

2. 时间序列分析：时间序列分析是一种用于处理时间序列数据的方法，包括趋势分析、季节性分析、周期性分析等，用于预测未来的时间序列数据。

3. 决策树：决策树是一种基于树形结构的分类和回归方法，通过构建决策树模型，进行数据的分类和预测。

4. 人工神经网络：人工神经网络是一种模拟人脑神经元网络的计算模型，通过多层神经元的连接和学习，进行复杂数据的预测和分类。

5. 支持向量机：支持向量机是一种用于分类和回归分析的机器学习方法，通过构建最优超平面，实现数据的分类和预测。

### 应用场景统计学的预测模型在各个领域都有着广泛的应用，以下是一些常见的应用场景：1. 金融领域：预测股票价格、汇率变动、信用风险等，为投资决策提供参考。

数学建模建立统计模型进行预测
一、建立统计模型进行预测的一般流程
二、建立统计模型进行预测的过程分析
(一)问题背景分析
需要考虑以下三个方面的问题:
(1)统计描述,即直观描述成对样本数据的统计相关性.
(2)统计建模与推断,即建立回归模型,检验并估计模型参数.
(3)统计应用,即利用模型进行统计预测或控制.
(二)建立统计模型
1.绘制散点图
绘制散点图是进行回归分析的第一步,可以直观地考察两个变量间的关系,为我们分析两个变量之间的关系类型提供帮助.
2.建立线性回归方程
一元线性回归模型为根据样本数据,利用最小二乘法对模型参数a,b进行估计,得到经验回归模型=x+.
3.回归结果分析
(三)模型的应用
回归模型的重要应用之一是预测,在给定x值时,根据回归方程,计算Y的预测值.
(四)数学建模活动的选题
(五)数学建模活动的要求
1.组建合作团队
数学建模实践活动需要团队协作.
2.开展研究活动
根据开题报告所规划的研究流程,通过背景分析、数据收集、数据分析、数学建模、获得结论等过程,完成课题研究.
3.撰写研究报告
以小组为单位,撰写一份研究报告.
4.交流展示
(六)数学建模活动研究报告的参考形式
年级班完成时间:
1.课题名称
2.课题组成员及分工
3.选题的意义
4.研究计划(包括对选题的分析、解决问题的思路等)
5.研究过程(包括收集数据、分析数据、建立模型、求解模型的过程,以及过程中出现的难点、解决方案等)
6.研究结果
7.收获与体会
8.对此研究的评价(由评价小组或老师填写)。

基于数学建模的经济增长预测模型经济增长预测模型是一种基于数学建模的方法，通过分析历史数据和经济指标，预测未来的经济增长趋势。

对于政府和企业来说，了解经济发展的趋势对于制定政策和商业决策至关重要。

基于数学建模的经济增长预测模型可以帮助我们更好地理解经济变动，并为未来做出准确的预测。

在构建经济增长预测模型时，我们首先需要选择适当的经济指标。

常见的经济指标包括国内生产总值（GDP）、就业率、通货膨胀率、投资水平等。

这些指标反映了一个国家或地区的经济活动和整体经济状况。

根据需要，我们可以选择多个指标来构建模型。

一种常见的经济增长预测模型是时间序列分析模型，其中最常用的是ARIMA模型（自回归滑动平均模型）。

ARIMA模型基于时间序列数据，通过对历史数据的分析来预测未来的经济增长趋势。

ARIMA模型的核心思想是将时间序列数据中的趋势、季节性和噪音等因素分离出来，从而更好地预测未来的发展趋势。

另一种常见的经济增长预测模型是计量经济学模型，其中最常用的是线性回归模型。

线性回归模型通过分析不同经济因素之间的关系，建立数学方程，从而预测未来的经济增长趋势。

线性回归模型可以帮助我们确定经济增长的驱动因素，并提供有关这些因素对经济发展的影响程度的信息。

为了构建准确的经济增长预测模型，我们需要进行数据的收集和处理。

首先，我们需要收集一段时间内的历史数据，包括经济指标和相应的时间标记。

然后，我们需要对数据进行清洗和预处理，包括去除异常值、填补缺失值、平滑数据等。

接下来，我们可以使用统计软件或编程语言来分析数据并构建预测模型。

在构建模型时，我们需要根据特定的问题和数据的性质选择合适的模型和算法。

对于ARIMA模型，可以使用自动模型选择算法来确定最佳的ARIMA参数。

对于线性回归模型，可以使用最小二乘法来估计回归系数，并进行模型诊断和验证。

一旦构建了经济增长预测模型，我们可以使用该模型来预测未来的经济增长趋势。

然而，需要注意的是，经济是一个复杂的系统，受到许多因素的影响，因此模型的预测结果可能存在误差。

数学建模模型常用的四大模型及对应算法原理总结四大模型对应算法原理及案例使用教程：一、优化模型线性规划线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，在线性回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。

如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。

案例实操非线性规划如果目标函数或者约束条件中至少有一个是非线性函数时的最优化问题叫非线性规划问题，是求解目标函数或约束条件中有一个或几个非线性函数的最优化问题的方法。

建立非线性规划模型首先要选定适当的目标变量和决策变量，并建立起目标变量与决策变量之间的函数关系，即目标函数。

然后将各种限制条件加以抽象，得出决策变量应满足的一些等式或不等式，即约束条件。

整数规划整数规划分为两类：一类为纯整数规划，记为PIP，它要求问题中的全部变量都取整数；另一类是混合整数规划，记之为MIP，它的某些变量只能取整数，而其他变量则为连续变量。

整数规划的特殊情况是0-1规划，其变量只取0或者1。

多目标规划求解多目标规划的方法大体上有以下几种：一种是化多为少的方法，即把多目标化为比较容易求解的单目标，如主要目标法、线性加权法、理想点法等；另一种叫分层序列法，即把目标按其重要性给出一个序列，每次都在前一目标最优解集内求下一个目标最优解，直到求出共同的最优解。

目标规划目标规划是一种用来进行含有单目标和多目标的决策分析的数学规划方法，是线性规划的特殊类型。

目标规划的一般模型如下：设xj是目标规划的决策变量，共有m个约束条件是刚性约束，可能是等式约束，也可能是不等式约束。

设有l个柔性目标约束条件，其目标规划约束的偏差为d+, d-。

设有q个优先级别，分别为P1, P2, …, Pq。

在同一个优先级Pk中，有不同的权重，分别记为[插图], [插图]（j=1,2, …, l）。