电力系统分析潮流计算例题

电力系统潮流计算结果教师：邱晓燕一、项目试计算下面2个算例计及负荷静态特性和不计负荷静态特性的潮流分布，并画出潮流分布图。

1．算例1图1所示的简单电力系统中，网络各元件参数的标幺值如下：01413.040.008.001920.050.012.01.1,3.001528.040.010.042024024410140141321012012j y y j z j y y j z k j z j y y j z ==+===+=====+=系统中节点1、2为PQ 节点，节点3为PV 节点，节点4为平衡节点，已给定05.1,10.1,5.013.055.018.030.04332211∠===--=+--=+s s s ss s s V V P j jQP j jQ P容许误差510-=ε。

2.算例2网络各元件参数的标幺值如图2所示，容许误差510-=ε。

图1P 4=5 V 4=1.05j0.0151.05:1 V 5=1.05 θ5=01.6+j0.82+j1④ 1:1.05 ②③① ⑤ j0.033.7+j1.30.08+j0.3j0.25j0.25j0.25 j0.250.04+j0.250.1+j0.35二、仿真结果利用psasp7.0 软件进行仿真，得出以下结果例1：潮流分布图如图1示（1）不计负荷静态特性，将节点4设置为slack节点(平衡节点) 仿真结果如下：（2）计及负荷静态特性，将节点4设置为PV-PQ节点仿真结果如下：例2：潮流分布图如图2所示（1）不计负荷静态特性，将节点5设置为slack节点(平衡节点) 仿真结果如下：（2）计及负荷静态特性，将节点5设置为PV-PQ节点仿真结果如下：。

第三章 电力系统的潮流计算3-1 电力系统潮流计算就是对给定的系统运行条件确定系统的运行状态。

系统运行条件是指发电机组发出的有功功率和无功功率（或极端电压），负荷的有 功功率和无功功率等。

运行状态是指系统中所有母线（或称节点）电压的幅值和 相位，所有线路的功率分布和功率损耗等。

3-2 电压降落是指元件首末端两点电压的相量差。

电压损耗是两点间电压绝对值之差。

当两点电压之间的相角差不大时， 可以近似地认为电压损耗等于电压降落的纵分量。

电压偏移是指网络中某点的实际电压同网络该处的额定电压之差。

电压 偏移可以用kV 表示，也可以用额定电压的百分数表示。

电压偏移=%100⨯-NNV V V 功率损耗包括电流通过元件的电阻和等值电抗时产生的功率损耗和电压 施加于元件的对地等值导纳时产生的损耗。

输电效率是是线路末端输出的有功功率2P 与线路首端输入的有功功率1P 之比。

输电效率=%10012⨯P P 3-3 网络元件的电压降落可以表示为()∙∙∙∙∙+=+=-2221V V I jX R V V δ∆式中，∙2V ∆和∙2V δ分别称为电压降落的纵分量和横分量。

从电压降落的公式可见，不论从元件的哪一端计算，电压降落的纵、横分量计算公式的结构都是一样的，元件两端的电压幅值差主要有电压降落的纵分量决定，电压的相角差则由横分量决定。

在高压输电线路中，电抗要远远大于电阻，即R X 〉〉，作为极端的情况，令0=R ，便得V QX V /=∆，V PX V /=δ上式说明，在纯电抗元件中，电压降落的纵分量是因传送无功功率而产生的，而电压降落的横分量则是因为传送有功功率产生的。

换句话说，元件两端存在电压幅值差是传送无功功率的条件，存在电压相角差则是传送有功功率的条件。

3-4 求解已知首端电压和末端功率潮流计算问题的思路是，将该问题转化成已知同侧电压和功率的潮流计算问题。

首先假设所有未知点的节点电压均为额定电压，从线路末端开始，按照已知末端电压和末端潮流计算的方法，逐段向前计算功率损耗和功率分布，直至线路首端。

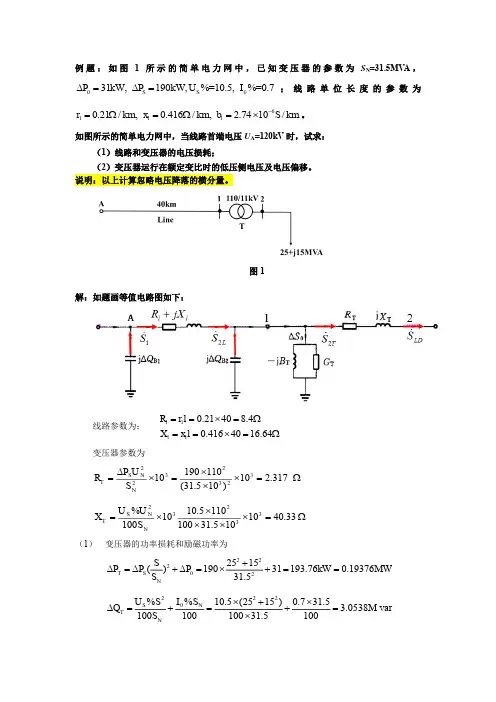
例题：如图1所示的简单电力网中，已知变压器的参数为S N =31.5MV A ，0S S 031kW,190kW,%=10.5,%=0.7P P U I ∆=∆=；线路单位长度的参数为61110.21/km,0.416/km, 2.7410S/km r x b -=Ω=Ω=⨯。

如图所示的简单电力网中，当线路首端电压U A =120kV 时，试求：（1）线路和变压器的电压损耗；（2）变压器运行在额定变比时的低压侧电压及电压偏移。

说明：以上计算忽略电压降落的横分量。

图1解：如题画等值电路图如下：线路参数为：0.21408.40.4164016.64l l l l R rl X x l ==⨯=Ω==⨯=Ω变压器参数为Ω=⨯⨯⨯=⨯∆=317.210)105.31(110190103232322N N S T S U P R Ω=⨯⨯⨯⨯⨯=33.4010105.311001105.1010100%33232N N S T S U U X （1） 变压器的功率损耗和励磁功率为222T S 02N 2515()19031193.760.1937631.5S P P P kW MW S +∆=∆+∆=⨯+==222S 0N T N %%10.5(2515)0.731.5 3.0538var 10010010031.5100U S I S Q M S ⨯+⨯∆=+=+=⨯1点处线路的充电功率var 66308.01104074.22121222M lU b Q N l B =⨯⨯⨯==计算L S 2 为：MVAj j Q Q Q j P P S B T LD T LD L 39.1719.25)66308.00538.315(19376.025)(22+=-+++=-∆++∆+=线路阻抗中的功率损耗为：MW R U Q P P l L L l 65044.0104021.011017390251901032223222222=⨯⨯⨯+=⨯+=∆-- v a r 2885.11040416.011017390251901032223222222M X U Q P Q l L L l =⨯⨯⨯+=⨯+=∆-- 计算功率1S 为 M V Aj j Q Q j P P S l L l I 68.1884.25)2885.139.17(65044.019.25)(221+=+++=∆++∆+=线路电压损耗（忽略电压降落的横分量） 1125.848.418.6816.64 4.40120=l l l A PR Q X U kV U +⨯+⨯∆== 1点电压为：1120 4.40115.60-A l U U U kV =∆=-=计算功率TS 2 为 M V Aj j Q Q j P P S T LD T LD T 833.17163.25)833.215(163.025)(2+=+++='∆++'∆+= 变压器电压损耗 22125.163 2.3217.83340.33 6.73115.60=T T T T T P R Q X U kV U +⨯+⨯∆== （2） 变压器低压侧折算到高压侧的电压为21115.60 6.73108.87=-T U U U kV '∆=-= 变压器低压侧的实际电压 22108.8710.8910=U U kV k '== 电压偏移为2210.8910%100%8.9%10N N U U m U --=⨯==。

复杂潮流计算例题
潮流计算是电力系统分析中的一项重要任务，用于计算电力系统中各个节点的电压和相角。

复杂潮流计算是潮流计算的一种，其中考虑了节点电压的复数形式（包括幅值和相角）。

以下是一些复杂潮流计算的例题：
1. 简单节点电压计算：
•给定一个电力系统的节点和支路参数，计算每个节点的复数电压。

使用节点电流法或其他适当的方法。

2. 无功补偿计算：
•在一个包含无功功率不平衡的电力系统中，计算各节点的无功功率，并确定需要连接多大容量的无功补偿装置以使系统中的无功功率平衡。

3. 线路功率损耗计算：
•给定一个电力系统的节点电压和支路参数，计算每条支路上的有功功率和无功功率，然后计算系统中的总有功损耗和总无功损耗。

4. 负荷流计算：
•考虑系统中的负荷，计算每个节点的复数电压以及每个节点的有功和无功功率。

确保负荷得到满足，即节点电压在合理范围内。

5. 电压稳定性评估：
•对一个电力系统进行电压稳定性评估，计算各节点的电压幅值，并确定系统中是否存在电压稳定性问题。

可能需要考虑调整发电机的励磁系统来提高电压稳定性。

这些例题涉及了复杂潮流计算中的一些常见方面，包括节点电压计算、功率损耗计算、无功补偿和电压稳定性评估等。

在解答这些例题时，通常需要使用潮流计算的基本方程和方法，例如功率方程、节点电流法、雅可比矩阵等。

这些例题可以帮助理解电力系统的潮流行为，同时提高解决实际问题的能力。

目录摘要 (2)1任务及题目要求 (2)2原理介绍 (3)2.1节点导纳矩阵 (3)2.2牛顿-拉夫逊法 (4)2.2.1牛顿-拉夫逊法基本原理 (4)2.2.2牛顿--拉夫逊法潮流求解过程介绍 (6)3分析计算 (11)4结果分析 (15)5总结 (16)参考资料 (17)节点导纳矩阵及潮流计算摘要电力网的运行状态可用节点方程或回路方程来描述。

节点导纳矩阵是以系统元件的等值导纳为基础所建立的、描述电力网络各节点电压和注入电流之间关系的线性方程。

潮流计算是电力系统分析中的一种最基本的计算，它的任务是对给定的运行条件确定系统的运行状态，如各母线上的电压（幅值及相角）、网络中的功率分布及功率损耗等。

本文就节点导纳矩阵和潮流进行分析和计算。

1任务及题目要求题目初始条件：如图所示电网。

1∠002阵Y；2+j13）给出潮流方程或功率方程的表达式；4）当用牛顿-拉夫逊法计算潮流时，给出修正方程和迭代收敛条件。

2原理介绍2.1节点导纳矩阵节点导纳矩阵既可根据自导纳和互导纳的定义直接求取，也可根据电路知识中找出改网络的关联矩阵，在节点电压方程的矩阵形式进行求解。

本章节我们主要讨论的是直接求解导纳矩阵。

根据节点电压方程章节我们知道，在利用电子数字计算机计算电力系统运行情况时，多采用IYV 形式的节点方程式。

其中阶数等于电力网络的节点数。

从而可以得到n 个节点时的节点导纳矩阵方程组：nn Y n +V （2-1） 由此可以得到n 个节点导纳矩阵：nn Y ⎫⎪⎪⎪⎪⎭它反映了网络的参数及接线情况，因此导纳矩阵可以看成是对电力网络电气特性的一种数学抽象。

由导纳短阵所了解的节点方程式是电力网络广泛应用的一种数学模型。

通过上面的讨论，可以看出节点导纳矩阵的有以下特点：（1）导纳矩阵的元素很容易根据网络接线图和支路参数直观地求得，形成节点导纳矩阵的程序比较简单。

（3）导纳矩阵是稀疏矩阵。

它的对角线元素一般不为零，但在非对角线元素中则存在不少零元素。

3 简单电力系统潮流计算3．1 思考题、习题1）电力线路阻抗中的功率损耗表达式是什么？电力线路始、末端的电容功率表达式是什么？2）电力线路阻抗中电压降落的纵分量和横分量的表达式是什么？3）什么叫电压降落、电压损耗、电压偏移、电压调整及输电效率？5）对简单开式网络、变电所较多的开式网络和环形网络潮流计算的内容及步骤是什么？6）变压器在额定状况下，其功率损耗的简单表达式是什么？9）为什么要对电力网络的潮流进行调整控制？调整控制潮流的手段主要有哪些？10）欲改变电力网络的有功功率和无功功率分布，分别需要调整网络的什么参数？16）110kV 双回架空线路，长度为150kM ，导线型号为LGJ-120，导线计算外径为15.2mm ，三相导线几何平均距离为5m 。

已知电力线路末端负荷为30+j15MVA ，末端电压为106kV ，求始端电压、功率，并作出电压向量图。

17）220kV 单回架空线路，长度为200kM ，导线型号为LGJ-300，导线计算外径为24.2mm ，三相导线几何平均距离为7.5m 。

已知电力线路始端输入功率为120+j50MVA ，始端电压为240kV ，求末端电压、功率，并作出电压向量图。

18）110kV 单回架空线路，长度为80kM ，导线型号为LGJ-95，导线计算外径为13.7mm ，三相导线几何平均距离为5m 。

已知电力线路末端负荷为15+j10MVA ，始端电压为116kV ，求末端电压和始端功率。

19）220kV 单回架空线路，长度为220kM ，电力线路每公里的参数分别为：kM S b kM x kM r /1066.2,/42.0,/108.06111-⨯=Ω=Ω=、线路空载运行，当线路末端电压为205kV ，求线路始端的电压。

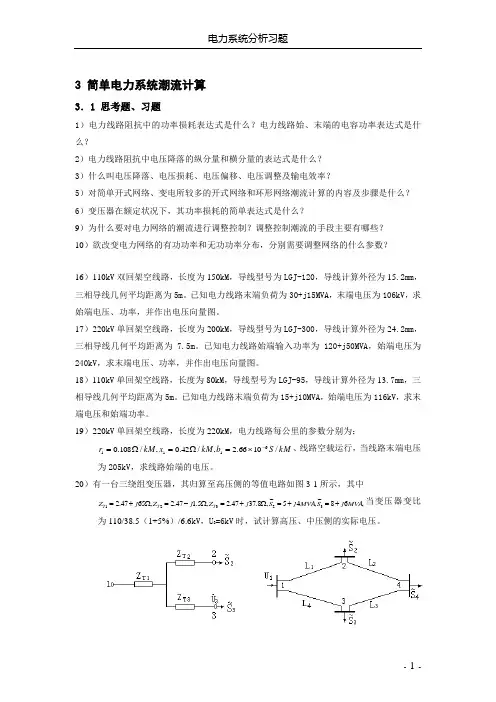
20）有一台三绕组变压器，其归算至高压侧的等值电路如图3-1所示，其中,68~,45~,8.3747.2,5.147.2,6547.232321MVA j S MVA j S j Z j Z j Z T T T +=+=Ω+=Ω-=Ω+=当变压器变比为110/38.5（1+5%）/6.6kV ，U 3=6kV 时，试计算高压、中压侧的实际电压。

牛拉法潮流计算例题首先，牛拉法潮流计算是一种用于电力系统稳态分析的方法，它可以用来计算电力系统中各个节点的电压幅值和相角，以及各个支路的电流大小和相角。

下面是一个牛拉法潮流计算的例题。

假设有一条简单的电力系统，由三个节点和两条支路组成。

节点1和节点2之间连接一条1欧姆的电阻，节点2和节点3之间连接一条0.5欧姆的电阻。

节点1的电压幅值为1.05千伏，相角为0度，节点3的电压幅值为1千伏，相角为-120度。

现在需要计算节点2的电压幅值和相角，以及两条支路的电流大小和相角，假设电力系统中各个元件均为纯电阻。

首先，我们可以列出节点间的导纳矩阵，其中导纳元素为各个支路的导纳值，节点1和节点2之间的导纳为1欧姆的导纳，节点2和节点3之间的导纳为0.5欧姆的导纳，对角线元素为各自节点所连支路的导纳之和。

接下来，我们需要选择一个节点作为参考节点，假设我们选择节点1作为参考节点。

然后，我们可以将节点电压表示为复数形式，即V1=1.05∠0度，V3=1∠-120度。

由于节点1的电压已知，我们可以将其表示为参考电压，即V1=1∠0度=1+j0。

然后，我们可以利用导纳矩阵和节点电压，求解未知节点的电压和支路电流。

具体地，我们可以列出节点2的电压方程式：I12=(V1-V2)/1I23=(V2-V3)/0.5I12=-I23其中，I12和I23分别是支路12和支路23的电流。

将节点电压表示为复数形式，并带入上式，得到：(V1-V2)/1=(1+j0-V2)/1(V2-V3)/0.5=(V2-1∠-120度)/0.5I12=I23化简上式，可得：V2=1.045-j0.2558I12=0.0045-j0.2558I23=0.0045+j0.1279因此，节点2的电压幅值为1.056千伏，相角为-14.34度，支路12的电流大小为0.2558安，相角为-83.66度，支路23的电流大小为0.1279安，相角为29.74度，计算完成。

潮流计算例题解析一、潮流计算例题解析嗨，宝子们！今天咱们来唠唠潮流计算的例题解析哈。

潮流计算呢，就像是在电网这个大江湖里摸清电流、电压这些大侠们的走向和状态。

咱先看一个简单的例题哈。

比如说有这么一个小电网系统，有几个节点，每个节点都有自己的特性。

咱就从最基础的节点开始分析。

节点分好几种类型呢，像PQ节点，这个节点的有功功率P和无功功率Q是给定的，就像一个被安排好任务的小卒子，只能按照规定的功率输出。

然后还有PV节点，这个节点的有功功率P和电压幅值V是给定的，它就有点像个小头目，在功率和电压方面有自己的固定指标。

还有平衡节点，这个可就厉害了，它是整个电网的基准，电压幅值和相角都是已知的，就像电网这个江湖里的武林盟主，给大家定标准呢。

咱就拿一个具体的数字例题来说。

假设有一个简单的三节点系统，节点1是平衡节点，给定电压幅值为1.05，相角为0度。

节点2是PQ节点，有功功率是0.5，无功功率是0.3。

节点3是PV节点，有功功率是0.8，电压幅值为1.0。

那咱咋计算潮流呢？首先要根据节点的类型列出相应的方程。

对于PQ节点，有功率平衡方程，也就是注入节点的有功功率和无功功率等于从节点流出的有功功率和无功功率。

对于PV节点呢，除了有功功率平衡方程，还有电压幅值的约束方程。

然后就开始各种计算啦。

要用到复数运算，把电压、电流这些都用复数表示。

比如说节点电压U = V∠θ，其中V是电压幅值，θ是相角。

电流I = Y U，这里的Y是导纳矩阵。

通过这些关系，就可以建立起方程组来求解各个节点的电压和相角啦。

在计算过程中，可能会遇到各种小麻烦。

比如说计算出来的结果不符合物理意义，那可能就是计算过程中某个参数设错了，或者方程列错了。

这时候就需要咱们回头检查，像个小侦探一样，从节点类型的设定，到方程的每一项，仔仔细细地排查。

反正就是说呢，潮流计算例题虽然看起来有点复杂，但是只要咱们把基础的概念搞清楚，节点类型分明白，方程列对，计算仔细，就一定能搞定哒。

电力系统的潮流计算西安交通大学自动化学院 2012。

103．1 电网结构如图3-11所示，其额定电压为10KV 。

已知各节点的负荷功率及参数： MVAj S )2.03.0(2+=，MVAj S )3.05.0(3+=，MVA j S )15.02.0(4+=Ω+=)4.22.1(12j Z ,Ω+=)0.20.1(23j Z ,Ω+=)0.35.1(24j Z试求电压和功率分布.解：（1）先假设各节点电压均为额定电压，求线路始端功率。

0068.00034.0)21(103.05.0)(22223232232323j j jX R V Q P S N +=++=++=∆0019.00009.0)35.1(1015.02.0)(22224242242424j j jX R V Q P S N +=++=++=∆则: 3068.05034.023323j S S S +=∆+=1519.02009.024424j S S S +=∆+=6587.00043.122423'12j S S S S +=++=又0346.00173.0)4.22.1(106587.00043.1)(22212122'12'1212j j jX R V Q P S N +=++=++=∆故： 6933.00216.112'1212j S S S +=∆+=（2） 再用已知的线路始端电压kVV 5.101=及上述求得的线路始端功率12S ，求出线路各点电压.kVV X Q R P V 2752.05.104.26933.02.10216.1)(11212121212=⨯+⨯=+=∆ kV V V V 2248.101212=∆-≈kVV V V kV V X Q R P V 1508.100740.0)(242422424242424=∆-≈⇒=+=∆kVV V V kV V X Q R P V 1156.101092.0)(232322323232323=∆-≈⇒=+=∆（3）根据上述求得的线路各点电压，重新计算各线路的功率损耗和线路始端功率.0066.00033.0)21(12.103.05.022223j j S +=++=∆ 0018.00009.0)35.1(15.1015.02.022224j j S +=++=∆ 故 3066.05033.023323j S S S +=∆+=1518.02009.024424j S S S +=∆+=则 6584.00042.122423'12j S S S S +=++=又0331.00166.0)4.22.1(22.106584.00042.122212j j S +=++=∆ 从而可得线路始端功率 6915.00208.112j S +=这个结果与第（1）步所得计算结果之差小于0。

第4章复杂电力系统的潮流计算一、填空题1.用计算机进行潮流计算时，按照给定量的不同，可将电力系统节点分为节点、节点、节点三大类，其中, 节点数目最多，节点数目很少、可有可无，节点至少要有一个.二、选择题1。

若在两个节点i、j之间增加一条支路，则下列关于节点导纳矩阵的说法正确的是（）A。

阶数增加1B.节点i的自导纳不变C。

节点i、j间的互导纳发生变化D。

节点j的自导纳不变2.若从节点i引出一条对地支路，则下列关于节点导纳矩阵的说法正确的是（)A.阶数增加1B.节点i的自导纳发生变化C。

节点i和其余节点间的互导纳均发生变化D。

节点导纳矩阵的所有元素均不变3。

若从两个节点i、j之间切除掉一条支路，则下列关于节点导纳矩阵的说法正确的是（)A.阶数减少1B.节点i、j间的互导纳一定变为0C。

节点i、j间的互导纳发生变化，但不一定变为0D.节点i、j的自导纳均不变4.若网络中增加一个节点k，且增加一条节点i与之相连的支路，则下列关于节点导纳矩阵的说法正确的是（）（1）阶数增加1(2)节点k的自导纳等于题干中所述支路的导纳(3)节点i的自导纳等于题干中所述支路的导纳（4）节点i、k间的互导纳等于题干中所述支路的导纳A.（1）（2）B。

(2)(3） C.（1）（4）D。

（2）（4）三、简答题1.什么是潮流计算?潮流计算的主要作用有哪些？潮流计算,电力学名词，指在给定电力系统网络拓扑、元件参数和发电、负荷参量条件下,计算有功功率、无功功率及电压在电力网中的分布。

潮流计算是电力系统非常重要的分析计算，用以研究系统规划和运行中提出的各种问题.对规划中的电力系统，通过潮流计算可以检验所提出的电力系统规划方案能否满足各种运行方式的要求;对运行中的电力系统,通过潮流计算可以预知各种负荷变化和网络结构的改变会不会危及系统的安全，系统中所有母线的电压是否在允许的范围以内，系统中各种元件(线路、变压器等)是否会出现过负荷,以及可能出现过负荷时应事先采取哪些预防措施等。

第3章简单电力系统的潮流分析一、填空题1.对于负荷，若电压滞后于电流，则其吸收的有功为正，吸收的感性无功为负；对于发电机，若电压滞后于电流，则其发出的有功为正，发出的感性无功为负，实则发出容性无功。

2.电力网的功率损耗由两部分组成：大部分产生在输电线路和变压器的串联阻抗上，随传输功率的增大而增大；少部分产生在输电线路和变压器的并联导纳上，可近似认为只与电压有关。

3.输电线路的对地支路上损耗的是容性无功，又称为充电功率。

4.变压器的功率损耗包括阻抗支路的变动损耗和对地导纳中的固定损耗两部分，其中前者与传输功率有关（填“有关”或“无关”），后者可近似认为只与电压有关。

5.若网络中某节点接有多个电源和多个负载，可将这些电源和负载的功率按复数求和，简化为一个功率，称该功率为该节点的运算功率。

6.任何一个负荷点都只能由一个方向取得电能的网络称为开式网络；若网络中任何一个负荷点均能从两个或两个以上方向取得电能，则称该网络为闭式网络。

7.两端供电网络中，电源点发出的功率包含两部分：一部分与负荷功率和线路阻抗大小有关，称为供载功率；另一部分与两端电源的电压差和线路阻抗有关，而与负荷功率无关，称为循环功率。

8.若闭式网络的供载功率与线路长度成反比分布，称之为均一网络。

9.闭式网络的电压最低点是无功分点。

二、选择题1.根据国际电工委员会（IEC）的约定，复功率的表达式为（A）A.*~IUS= B.I US=~C.IUS *~= D.**~IUS=2.超高压输电线路空载时，末端电压比始端电压（A）。

A.高B.低C.相同D.不一定3.“网络中某点的电压比网络额定电压低5%”，这句话描述的是（B）A.电压降落B.电压偏移C.电压损耗D.电压调整4.在计算环形网络的初步功率分布前，应先将网络从哪一点处拆开（A）A.电源点B.有功分点C.无功分点D.视在功率最大的负荷点5.在计算出环形网络的初步功率分布之后，要进行更为精确的潮流计算，须先将网络从哪一点处拆开（C）A.电源点B.有功分点C.无功分点D.视在功率最大的负荷点三、简答题1.潮流计算包括哪些内容？其目的是什么？2.电压降落、电压损耗和电压偏移的概念分别是什么？3.对于没有分支的简单开式网络，如果已知末端的功率和首端的电压，如何计算其潮流分布？4.对于35kV及以下电压等级的地方电力网，在潮流计算时可作哪些简化？5.什么是闭式网络的功率分点？有功、无功分点一定是同一点吗？四、计算题1.如下图所示，单回220kV 架空输电线长200km ，线路每千米参数为：r 1=0.108Ω/km ，x 1=0.426Ω/km ，b 1=2.66×10-6S/km ，线路空载运行，末端电压U 2为205kV ，求线路送端电压U 1。

电力系统分析大作业一、设计题目本次设计题目选自课本第五章例5—8,美国西部联合电网WSCC系统的简化三机九节点系统，例题中已经给出了潮流结果，计算结果可以与之对照.取ε=0。

00001 .二、计算步骤第一步，为了方便编程，修改节点的序号，将平衡节点放在最后。

如下图:9第二步，这样得出的系统参数如下表所示：第三步，形成节点导纳矩阵。

第四步，设定初值:；,。

第五步,计算失配功率=0，=—1。

25,=—0.9，=0,=—1,=0,=1。

63，=0。

85;=0。

8614,=—0。

2590，=—0。

0420,=0。

6275，=—0.1710，=0。

7101。

显然，.第六步，形成雅克比矩阵（阶数为14×14）第七步,解修正方程,得到:-0.0371,—0.0668，—0.0628,0。

0732,0。

0191，0。

0422，0。

1726,0。

0908；0.0334，0。

0084,0。

0223，0.0372，0。

0266，0。

0400。

从而—0.0371，-0。

0668，-0。

0628，0。

0732，0。

0191，0。

0422,0.1726，0。

0908；1。

0334,1.0084，1。

0223,1。

0372，1.0266，1。

0400。

然后转入下一次迭代。

经三次迭代后。

迭代过程中节点电压变化情况如下表：迭代收敛后各节点的电压和功率：最后得出迭代收敛后各支路的功率和功率损耗:三、源程序及注释由于计算流程比较简单，所以编写程序过程中没有采用模块化的形式,直接按顺序一步步进行。

disp(’【节点数:】’）;［n1］=xlsread（’input。

xls’，'A3:A3'）％节点数disp（'【支路数：】'）;[n]=xlsread（'input。

xls’,’B3:B3')%支路数disp('【精度：】’);Accuracy=xlsread('input。