下载文档原格式
四年级奥数方阵问题方阵问题我们在日常生活中经常遇到编排正方形体操队列，在方形台上或操场上摆鲜花、插彩旗，在正方形棋盘上摆棋子等问题，你可别小瞧了这些问题，这里面包含了许多数学奥秘呢，快来看看吧！1、运动会上，同学们东站了一个存有6行，每行6人的正方形队伍。
这个正方形队伍中一共存有()名同学。
2、49名同学可以站成一个（）行（）列的正方形队伍，64名同学可以站成一个（）行（）列的正方形队伍。
3、在一行队伍中，小明的左边存有4个同学，右边存有5个同学，这一行队伍共计10人，对吗？讲一讲：基准1：同学们排好一行，小明从左数站在第9个，从右数站在第6个。
你晓得这一行存有多少个同学吗？练一练：1、操场挂着一排颜色相同的彩旗，从左数，红旗就是第7面；从右数，红旗就是第4面，你晓得这一排彩旗存有多少面吗？2、同学们排成一队做操，调皮的小强东张西望，结果发现自己无论从前数，还是从后数都是第5个。
你知道总共有多少个同学在做操吗？试试看：有20只兔子排成一行在做操。
小白兔左边有7个小兔，小灰兔右边有3只小兔，问，小白兔与小灰兔中间还有几只小兔？基准2：运动会上，同学们准备工作在正方形操场四周挂上彩旗，四个角上都必须存有一面彩旗，并使每边存有8面彩旗，那么一共必须准备工作多少面彩旗呢?练一练：1、它的说法对吗？为什么？老师让我在正方形舞台四周摆上鲜花，每边摆6盆，6×4=24（盆），我想最少要用24盆花。
2、解放军叔叔们在一个哨所警戒，哨所的四个角上都存有一名哨兵，敌人无论从哨所的哪一方面看，都会看到有10人站岗，请你算一算这个哨所有多少解放军哨兵？试试看：16只兔子灌装在8个笼子里（例如右图），这样看看每边存有6只兔子，现在要使每边变为5只，该怎么调整笼中的兔子？例3：请问，原定每个年级有多少人参加比赛呢？通告由于服装不够，各班参加广播操比赛的同学必须增加23人，恳请各年级的也已方形队伍横竖各减少一排。
校体育组练一练：1、一个正方形方阵横竖增加一排后增加了11人，那原来每边存有多少人？2、军训学生进行队列表演，排成一个正方形队列，如果这个队列横竖再增加一排，就还需要补充19人，原来参加队列表演的学生有多少人？试试看：出席演出的正方形队伍，如果横竖都换成2行，则增加36人，原来的队伍存有多少人？例4：国庆游行队伍中，手持鲜花的少先队员在一辆彩车四周围成了每边2层的方阵。
四年级方阵问题知识点总结一、矩阵的基本概念1. 矩阵的定义矩阵是一个由若干数构成的矩形数表，它是数学中的一种重要工具，用来表示多个数的集合。
矩阵通常用大写字母表示。
2. 矩阵的元素矩阵的每个数称为矩阵的元素。
矩阵中的元素按照行列的顺序排列，可以用下标表示。
3. 矩阵的行和列矩阵中的横向排列的数字构成矩阵的一行，纵向排列的数字构成矩阵的一列。
二、加减乘除运算1. 加法两个相同阶数（即行数和列数相同）的矩阵相加时，只需对应位置上的元素相加即可。
2. 减法两个相同阶数的矩阵相减时，也是对应位置上的元素相减。
3. 数与矩阵相乘一个数与矩阵相乘时，只需把这个数与矩阵中的每一个元素相乘。
4. 矩阵相乘两个矩阵相乘时，首先要保证第一个矩阵的列数和第二个矩阵的行数相等，然后按照矩阵乘法的定义进行计算。
5. 矩阵的转置将原矩阵的行变为列，列变为行。
6. 矩阵的逆如果一个方阵乘以它的逆矩阵等于单位矩阵，则该方阵有逆矩阵。
三、矩阵的性质1. 矩阵的相等当且仅当两个矩阵的相同位置上的元素都相等时，这两个矩阵相等。
2. 矩阵的零元素矩阵中所有元素都为零的矩阵称为零元素矩阵，一般用O表示。
3. 矩阵的单位元素主对角线上元素全为1，其它元素全为0的矩阵称为单位元素矩阵，一般用E表示。
4. 矩阵的相加和相乘的结合律矩阵的相加和相乘满足结合律。
四、特殊矩阵1. 对称矩阵矩阵A的转置矩阵与原矩阵相等，即A的转置矩阵等于A，称为对称矩阵。
2. 上三角矩阵主对角线以下的元素全为0的矩阵称为上三角矩阵。
3. 下三角矩阵主对角线以上的元素全为0的矩阵称为下三角矩阵。
以上就是四年级方阵问题的知识点总结。
通过掌握这些知识点，学生可以更好地解决方阵问题，提高数学问题的解决能力和逻辑思维能力。
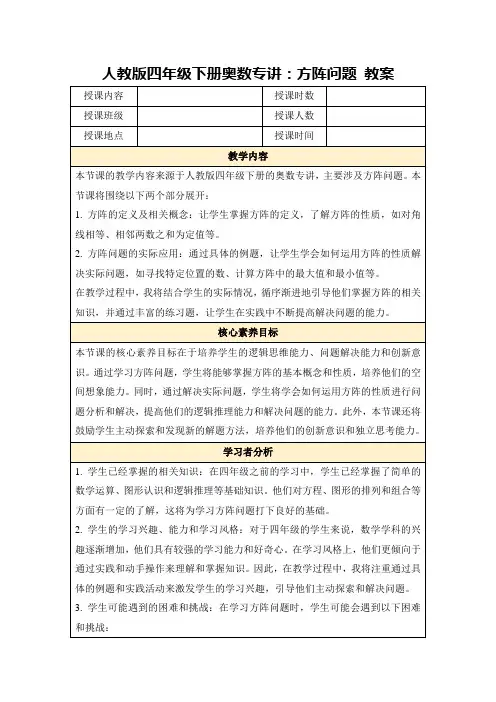
✧士兵排队，横着排叫行，竖着排叫列，若行数与列数相等，正好排成一个正方形，这就是一个方阵.方阵是由人和物排成的正方形，一般有实心方阵和空心方阵两种形式（如下图所示）.实心方阵2层空心方阵✧方阵的基本特点：1．方阵不论哪一层，每边上的人数都相同，每向里一层，每边上的人数就少2，每一层就少8（除“”外，此时内层比外层少7）.2．每边人数和每层人数的关系：每层人数＝每边人数×4－4＝(每边人数－1)×4每边人数＝每层人数÷4＋13．实心方阵的总人数＝每边人数×每边人数。
4．空心方阵的总人数＝(最外层每边人数－空心方阵的层数)×空心方阵的层数×4 最外层每边人数＝空心方阵的总人数÷空心方阵的层数÷4＋空心方阵的层数正方形舞台四周均匀地装彩灯，如果四个角都装一盏，且每边28盏，那么这个舞台四周共装彩灯多少盏？分析：由于角上的四盏灯各属于两行，所以让每边的灯数乘以4再减去多加的四盏灯即为所求。
解：角上的四盏灯各属于两行，所以彩灯总数为：1084428=-⨯ (盏)。
答：这个舞台四周共装彩灯108盏。
【答案】108【知识点】方阵问题 【难度】★★ 【出处】13年底稿学校开运动会，要在正方形操场四周插彩旗，4个角都插1面，每边插12面，一共要准备多少面彩旗？解：444412=-⨯ (面)答：一共要准备44面彩旗。
【答案】44【知识点】方阵问题 【难度】★★ 【出处】13年底稿某校四年级的同学排成一个方阵，最外一层的人数为100人，问最外一层每边上有多少人？这个方阵共有四年级学生多少人？ 解：方阵最外层每边的人数：2612514100=+=+÷(人)整个方阵的总人数：6762626=⨯ (人)答：最外一层每边上有26人；这个方阵共有四年级学生676人。
【答案】26；676【知识点】方阵问题 【难度】★★ 【出处】13年底稿有一个正方形池塘，四个角上都栽1棵树，一共栽了48棵树，那么每边栽多少棵树？解：每边栽树 131448=+÷（棵）答：每边栽13课树。
《方阵问题》详案教学目标:知识与技能：通过引导学生对方阵中最外层“每边数量、边数、总数量”的探究，探索出最外层每边数量、边数、总数量之间存在的数量关系。
过程与方法：通过学生动手操作、讨论交流等，引导学生经历探索过程，发现空心方阵排列的规律，体会数形结合、推理、归纳、模型等数学思想，积累数学思维的活动经验，体验解决问题策略的多样性。
情感态度价值观：让学生感受数学在日常生活中的广泛应用，培养学生的应用意识和解决实际问题的能力；学会倾听他人发言，能正确表达自己的意见。
教学重难点:教学重点：能利用画图的策略，寻找解决方阵问题的有效方法。
教学难点：通过对图形的研究，探索出正多变形最外层每边数量、边数、总数量之间的关系。
教学方法:教法：直观演示、引导归纳学法：观察、画图、推理、归纳上课准备：学生：探究纸；每人一支大头水彩笔老师：磁铁、课件一、情境引入。
师：（师点击课件）这是501班一部分同学练习广播操的队形。
请仔细观察，你能提一个数学问题吗？生看图提问。
师：接下来我们可以试着去解决这些问题。
想一想：一共有多少人呢？师：7列7行，说明这些同学站成了一个什么形状？我们把这种行数和列数相等的正方形队列就叫做方阵。
这节课我们就来研究方阵中的数学问题。
（师板书课题）二、新知探究。
（一）引导学生认识实心方阵和空心方阵。
这个方阵每行每列都站满了人，这样的方阵又叫做实心方阵。
我们刚刚用7×7=49算出了实心方阵的总人数，解决了第一个问题。
接下来，把站在最外层的男生不看，只看女生，女生站成了什么队形？有多少人呢？学生观察、答问。
师：如果不看里面的女生，只看最外层的男生，这个队形有什么特点呢？师：还能叫实心方阵吗？不能再叫实心方阵，我们把这样的方阵叫做空心方阵。
（师点击课件）这个方阵有多少人呢？咱们要研究这类问题，就得先研究这幅图。
（二）学生画图、研究、汇报师：要对这幅图进行研究，需要把这幅图从屏幕上挪到我们的纸上去。
第三讲方阵问题知识导航学生排队，士兵列队，横着排叫做行，竖着排叫做列。
如果行数与列数都相等，则正好排成一个正方形，这种图形就叫方队，也叫做方阵（亦叫乘方问题）。
核心公式：1．方阵总人数=最外层每边人数的平方（方阵问题的核心）2．方阵最外层每边人数=（方阵最外层总人数÷4）＋13．方阵外一层总人数比内一层总人数多24．去掉一行、一列的总人数＝去掉的每边人数×2－1例1:学校学生排成一个方阵，最外层的人数是60人，问这个方阵共有学生多少人?解析：方阵问题的核心是求最外层每边人数。
根据四周人数和每边人数的关系可以知：每边人数=四周人数÷4+1，可以求出方阵最外层每边人数，那么整个方阵队列的总人数就可以求了。
方阵最外层每边人数：60÷4+1=16（人）整个方阵共有学生人数：16×16=256（人）。
【巩固1】某校五年级学生排成一个方阵，最外一层的人数为60人.问方阵外层每边有多少人？这个方阵共有五年级学生多少人？解析：根据四周人数和每边人数的关系可以知：每边人数=四周人数÷4+1，可以求出方阵最外层每边人数，那么整个方阵队列的总人数就可以求了。
解：方阵最外层每边人数：60÷4＋1=16（人）整个方阵共有学生人数：16×16=256（人）答：方阵最外层每边有16人，此方阵中共有256人。
【巩固2】晶晶用围棋子摆成一个三层空心方阵，最外一层每边有围棋子14个.晶晶摆这个方阵共用围棋子多少个？解析：方阵每向里面一层，每边的个数就减少2个.知道最外面一层每边放14个，就可以求第二层及第三层每边个数.知道各层每边的个数，就可以求出各层总数。
解法1：最外边一层棋子个数：（14-1）×4=52（个）第二层棋子个数：（14-2-1）×4=44（个）第三层棋子个数：（14-2×2-1）×4=36（个）.摆这个方阵共用棋子：52+44＋36＝132（个）解法2：还可以这样想：中空方阵总个数=（每边个数一层数）×层数×4进行计算。
第三讲方阵问题（2）教学课题：方阵问题教学课时：两课时教学目标：1．认识数学中的方阵问题，能解决生活中一些简单的方阵问题。
2.通过猜想、实践、验证发现方阵排列的规律。
3.培养学生分析问题、解决问题的能力。
教学重难点：了解实心方阵和空心方阵的组成和特点，会计算组成实心方阵、空心方阵的物体的个数。
教具准备：3×3格、4×4格、5×5格方纸、围棋子若干粒、4×4格条形吹塑纸贴在地下。
本周通知：知识要点：学生排队，士兵列操，横着排叫做行，竖着排叫做列。
如果行数与列数都相等，则正好排成一个正方形，这种图形就叫方队，也叫做方阵。
方阵可分为实心方阵和空心方阵两种。
如果一个方阵中间都是排满了，就叫实心方阵；反之，就叫空心方阵。
教学过程：一、情境导入（课件出示）出示几组方队照片：（1）阅兵方队，仔细观察你能有什么发现？（队伍很整齐，每行和每列的人数相同，是一个方队，也叫方阵。
）（每位士兵前后的距离都相等，也就是前后士兵之间有一个间隔，间隔数等于一列队伍的人数减1。
）（每位士兵左右之间的距离相等，也就是说左右士兵之间有一个间隔，间隔数加1等于一行队伍的人数。
）（每位士兵之间都有间隔，而且士兵之间的距离是相等的。
）[设计意图：用阅兵式和实景图片引出本节课题，从学生的已有经验出发，激发学生的学习兴趣。
培养学生良好的兴趣爱好。
]过渡：其实在我们的学习中有些知识间有着密切的联系，我们今天这节课就来研究有关封闭图形中的植树问题和方阵问题之间的联系。
在课堂上我们可以借住一些学具能很好的进行探索和研究。
下面我们就先从棋子的简单摆放开始研究，好吗？看哪些同学观察的仔细，善于思考和发现。
让学生观察围棋的格子，动手完成3×3格、4×4格、5×5格的方阵分布。
二、教学过程如果班上同学都已经在春季学过方阵问题，可以直接把公式复习一遍。
●方阵总人数=最外层每边人数的平方（方阵问题的核心）●去掉一行，一列的总人数=去掉的每边人数×2－1●方阵最外层每边人数=（方阵最外层人数÷4）+1●方阵外一层每边人数比内一层每边人数多2●方阵外一层比内一层人数多8例1、（1）军训的学生进行队列表演，排成了一个每边7人的实心方阵，参加队列表演的一共有多少人？解析：画示意图帮助学生理解，去掉人数为7×7=49（人）（2）学校运动会上，准备在正方形的操场周围插上彩旗，如果四个角上都要插上一面彩旗，要使每边有7面彩旗，那么一共要准备多少面彩旗？解析：7×4-4=24（面）（3）100人排成了一个实心方阵，这个方阵每边多少人？解析：100=10×10（人）（4）有52个保安站在正方形体育馆的四周，四个角上都站有1人，如果每边站的人数相等，那么每边站了多少个保安？解析：52÷4+1=14（人）例2、（1）一个实心方阵，最外层有48颗棋子，这个方阵一共有多少颗棋子？解析：最外层共48颗棋子，可以算出每一边的棋子数为（48÷4）+1=13（颗），再算出这个实心方阵棋子总数为13×13＝169（颗）（2）一个三层的空心方阵，最外层每边有9颗棋子，这个方阵一共用了多少颗棋子？解析：已知最外层每边9颗，那么最外一层共有9×4－4＝32（颗），于是另外两层分别有32－8=24（颗），24－8=16（颗），这个空心方阵三层一共有32+24+16=72（颗）例3、一些学生如果排成三层空心方阵则多10人，如果在中间空心部分接着增排一层则又少6人，问共有多少学生？解析：在这个空心方阵中间增加第四层，需要学生10+6＝16（人），那么可以依次求出原方阵三层人数分别为24人，32人，40人。
方阵问题姓名：(1)方阵不论哪一层,每边上的人(或物)数量都相同,每向里一层,每边上的人数就少2。
(2)每边人(或物)数和四周人(或物)的关系;四周人(或物)数=[每边人(或物)数-1]×4每边人(或物)数=四周人(或物)数÷4+1(3)中实方阵的总人数(或物)=每边人(或物)数×每边人(或物)数(4)空心方阵的总人(或物)数=（最外层每边人(或物)数－空心方阵的层数）×空心方阵的层数×4例1、一个正方形池塘四周栽满了树，四个角上都有1棵，已知每边栽了8棵。
这个池塘四周一共栽了多少棵树？练习一：1、参加小学生运动会团体操表演的运动员组成了一个正方形队列，共排了20行，每行20人。
从这个正方形队列中去掉一行一列，去掉了多少人？还剩下多少人？2、小明用棋子摆成了一个实心方阵，后来他又加上11个棋子，使横竖各增加了一排，成为一个大的实心方阵。
原来的实心方阵有多少个棋子？3、同学们把学校的盆花摆成一个实心方阵还剩下4盆，如果横竖各增加一排成为大一点的实心方阵，又少15盆。
学校一共养了多少盆花？例2、用棋子摆成一个二层空心方阵，外层每边有10个棋子，求这个中空方阵一共用了多少个棋子？练习二：1、成都嘉祥外国语学校252名学生参加团体操表演，排成一个三层空心方阵，这个空心方阵外层每边应该排多少人？2、用盆花摆成一个12层的方阵花坛，最内层每边摆了10盆花。
摆这个花坛一共用了多少盆花？3、设计一个团体操表演队形，想排成一个中空方阵，最内层要24人，最外层要48人，这个表演队形一共需要多少人？4、一队战士排成三层空心方阵多出16人，如果在空心部分再增加一层又差28人。
这队战士共有多少人？如果排成一个实心方阵，每边多少人？例3、四年级同学参加体操表演，先排成每边16人的实心方阵队形，后来又变成一个四层空心方阵，这个中空方阵最外层有多少人？练习三：1、某学校四年级学生排成一个四层空心方阵还多15人，如果在方阵的空心部分再增加一层又少12人。
第三讲方阵问题知识导航学生排队，士兵列队，横着排叫做行，竖着排叫做列。
如果行数与列数都相等，则正好排成一个正方形，这种图形就叫方队，也叫做方阵（亦叫乘方问题）。
核心公式：1．方阵总人数=最外层每边人数的平方（方阵问题的核心）2．方阵最外层每边人数=（方阵最外层总人数÷4）＋13．方阵外一层总人数比内一层总人数多24．去掉一行、一列的总人数＝去掉的每边人数×2－1例1:学校学生排成一个方阵，最外层的人数是60人，问这个方阵共有学生多少人?解析：方阵问题的核心是求最外层每边人数。
根据四周人数和每边人数的关系可以知：每边人数=四周人数÷4+1，可以求出方阵最外层每边人数，那么整个方阵队列的总人数就可以求了。
方阵最外层每边人数：60÷4+1=16（人）整个方阵共有学生人数：16×16=256（人）。
【巩固1】某校五年级学生排成一个方阵，最外一层的人数为60人.问方阵外层每边有多少人？这个方阵共有五年级学生多少人？解析：根据四周人数和每边人数的关系可以知：每边人数=四周人数÷4+1，可以求出方阵最外层每边人数，那么整个方阵队列的总人数就可以求了。
解：方阵最外层每边人数：60÷4＋1=16（人）整个方阵共有学生人数：16×16=256（人）答：方阵最外层每边有16人，此方阵中共有256人。
【巩固2】晶晶用围棋子摆成一个三层空心方阵，最外一层每边有围棋子14个.晶晶摆这个方阵共用围棋子多少个？解析：方阵每向里面一层，每边的个数就减少2个.知道最外面一层每边放14个，就可以求第二层及第三层每边个数.知道各层每边的个数，就可以求出各层总数。
解法1：最外边一层棋子个数：（14-1）×4=52（个）第二层棋子个数：（14-2-1）×4=44（个）第三层棋子个数：（14-2×2-1）×4=36（个）.摆这个方阵共用棋子：52+44＋36＝132（个）解法2：还可以这样想：中空方阵总个数=（每边个数一层数）×层数×4进行计算。
（14-3）×3×4=132（个）答：摆这个方阵共需132个围棋子。
【巩固3】一个正方形的队列横竖各减少一排共27人，求这个正方形队列原来有多 少人？解析：依据：去掉一行、一列的总人数＝去掉的每边人数×2－1可知每边的人数是：142)127(=÷+（人）原人数是：1961414=⨯（人）答：略。
【巩固4】小红用棋子摆成一个正方形实心方阵用棋子100枚，最外边的一层共多 少枚棋子？解析：这要用到方阵的公式逆运算，100必然是一个数的平方数因为1001010=⨯（人），并且是实心的方阵，所以最外层有10人。
例2：参加中学生运动会团体操比赛的运动员排成了一个正方形队列。
如果要使这 个正方形队列减少一行和一列，则要减少33人。
问参加团体操表演的运动员 有多少人？解析：如下图表示的是一个五行五列的正方形队列。
从图中可以看出正方形的每 行、每列人数相等；最外层每边人数是5，去一行、一列则一共要去9人，因而我们可以得到如下公式：去掉一行、一列的总人数＝去掉的每边人数×2－1解 ：方阵问题的核心是求最外层每边人数。
原题中去掉一行、一列的人数是33，则去掉的一行（或一列）人数＝172)133(=÷+ 人方阵的总人数为最外层每边人数的平方，所以总人数为2891717=⨯（人）【巩固】 参加军训的学生进行队列表演，他们排成了一个七行七列的正方形队列， 如果去掉一行一列，请问：要去掉多少名学生？还剩下多少名学生？ · · · · · · · · · · · · · · · · · · · · · · · · ·解析：如上图表示的是一个4行4列的实心正方形队列，从图中可以看出正方形队列的特点：（1）正方形队列每行、每列的人数相等，因此总人数＝每行人数×每列人数。
（2）去掉横竖各一排时，有且只有1人是同时属于被减去的一行和一列的，如图中点A所示。
因此去掉的总人数＝原每行人数×2－1，或去掉的总人数＝减少后每行人数×2＋1。
本题中所求，即去掉的人数＝7×2－1＝13（人）或去掉的人数＝（7－1）×2＋1＝13（人）还剩的人数＝（7－1）×（7－1）＝36（人）或还剩的人数＝7×7－13＝49－13＝36（人）答：如果去掉一行一列，要去掉13名学生，还剩下36名学生。
例3：解放军战士排成一个每边12人的中空方阵，共四层，求总人数？解法1：这样想：把中空方阵的总人数，看作中实方阵总人数减去空心方阵人数。
（1）中实方阵总人数：12×12=144（人）（2）第四层每边人数：12-2×（4-1）=6（人）（3）空心方阵人数：（6-2）×（6-2）=16（人）（4）中空方阵人数：144-16=128（人）答：总人数是128人。
小结：中空方阵总人数=外边人数×外边人数-（内边人数-2）×（内边人数-2）解法2：这样想：把中空方阵分成四个相等的长方形。
（1）每个长方形的长=外边人数-层数12-4=8（人）（2）每个长方形的宽是层数：4人（3）总人数：8×4×4=128（人）答：总人数是128人。
小结：中空方阵总人数=（每边人数-层数）×层数×4【巩固】学校开展联欢会，要在正方形操场四周插彩旗。
四个角上都插一面，每边插7面。
一共要准备多少面旗子？解析：依据求外层个数的公式：（边数-1）×4⨯-（面）7(=)1424答：略。
例4：一个街心花园如右图所示.它由四个大小相等的等边三角形组成.已知 从每个小三角形的顶点开始，到下一个顶点均匀栽有9棵花.问大三角形边上栽有多少棵花？整个花园中共栽多少棵花？解析：①从已知条件中可以知道大三角形的边长是小三角形边长的2倍.又知道每个小三角形的边上均匀栽9株，则大三角形边上栽的棵数为：17129=-⨯（棵）。
②又知道这个大三角形三个顶点上栽的一棵花是相邻的两条边公有的，所以大三角形三条边上共栽花：483)117(=⨯-（棵）。
③.再看图中画斜线的小三角形三个顶点正好在大三角形的边上.再计算大三角形栽花棵数时已经计算过一次，所以小三角形每条边上栽花棵数为：729=-（棵）解：大三角形三条边上共栽花：483)1129(=⨯--⨯（棵）中间画斜线小三角形三条边上栽花：213)29(=⨯-（棵）整个花坛共栽花：692148=+（棵）答：大三角形边上共栽花48棵，整个花坛共栽花69棵。
【巩固】同学们做早操，排成一个正方形的方阵，从前、后、左、右数，小明都是第5个，这个方阵共有多少人？解析：如图，实心圆表示小明的位置，可以知道，这个队列每行都是9人。
解：每行每列数：9125=-⨯（人）共有：8199=⨯（人）例5：小明用围棋子摆了一个五层中空方阵，一共用了200枚棋子，请问：最外边一层每边有多少枚棋子？解析1：利用“相邻两层之间，每层的总数相差8”的特点，可知最外层共有棋子数：（200+8+8×2+8×3+8×4）÷5＝56（个）最外层每边的棋子数：56÷4+1＝15（个）解析2：如练习中的图，把棋子分成相等的四部分。
每一部分的棋子数：200÷4＝50（个）每一部分每排的棋子数：50÷5＝10（个）最外层每边的棋子数：10＋5＝15（个）综合列式为：200÷4÷5＋5＝15（个）答：最外边一层每边有15枚棋子。
【巩固】游行队伍中，手持鲜花的少先队员在一辆彩车的四周围成每边三层的方 阵，最外边一层每边12人，请问：彩车周围的少先队员共有多少人？解析1：请同学们自己画一个图，下图是一个三层中空方阵的示意图，不难发现， 有如下特点：（1）外层每边点的个数都比相邻内层的每边点的个数多2；（2）每相邻两层之间，点的总数相差8个。
最外层队员的总数：444412=-⨯（人）三层共有队员的总数：)2844()844(44⨯-+-+=283644++=108（人）解析2：如下图可分成相等的四部分，每一部分的人数：（12－3）×3＝9×3＝27（人）三层共有队员数：27×4＝108（人）答：彩车周围的少先队员共有108人。
这个问题还有别的解法，请同学们自己试着做一下。
课后作业1、若干名同学排成中实方阵则多12人，若要将这个方阵改摆成纵横两个方向各增加1人的方阵则还差9人排满，请问：原有学生多少人？解析：由于纵横两个方向各增加1人，因此不但将剩余12人摆上，而且还差9人，说明一横行与一竖行的人数总和是12＋9＝21人。
又由于纵横两个方向各增加1人，因此只有1人同属于横行与纵行，在数每边上的人数时，总被多数一次，因此可以用21人先加上被重复数过的1人，再除以2，也就得到每边人数。
列式为（21＋1）÷2＝11人。
求出每边人数，就可求出假设排满后的人数，列式为11×11＝121人，用121人减去差的9人就是原来人数，列式为121－9＝112人。
也可以根据原来的方阵再加上12，请你试一试。
答：原有学生112人。
2、有一队士兵排成一个中实方阵，最外一层有100人，请问：方阵中一共有士兵多少人？解析：要想求出方阵中一共有多少士兵，就应先求出方阵的最外层每边有多少人。
已知方阵最外一层有100人，用100÷4＝25人，每边是不是25人呢？不是的，因为平均分成4份后，还需要再加上1，才正好是每边上的人数，列式应该为100÷4＋1＝26人。
因此方阵中一共有26×26＝676人。
答：一共有676人。
说明：这道题关键是求出每边人数。
在求每边人数时，不要认为和“知道了正方形周长，求边长”一样，还必须要加上1。
3、小刚用若干枚棋子摆成一个中实方阵，最外层每边摆6枚，请问：要摆成这样一个中实方阵至少需要多少枚棋子？最外一层的棋子总数是多少？解析：如图，最外一层每边摆6枚，根据方阵每行每列个数相等特点，因此一共有6×6＝36枚棋子。
最外一层每边有6枚，如果用6×4＝24枚，就认为是最外一层棋子数的答案的话，那就错了。
因为正方形每个顶点上的棋子分属于一行一列，这样棋子在计算总数时就被多数了一次，这样的顶点一共有4个，需要把多数的减去，才能得到正确的结果。
