对带有季节变动的时间序列数据的预测分析题

时间序列分析王燕习题答案时间序列分析王燕习题答案时间序列分析是一门研究时间序列数据的统计学方法，它可以帮助我们理解和预测时间序列数据的趋势和模式。

王燕是这一领域的专家，在她的教材中提供了一系列的习题供学习者练习。

本文将给出一些关于时间序列分析中王燕习题的答案，希望能帮助读者更好地理解和应用这一方法。

第一题：给出一个时间序列数据，如何确定其季节性？季节性是时间序列数据中重复出现的周期性变化。

我们可以通过观察数据的图表来确定其季节性。

如果数据呈现出明显的周期性变化，且每个周期的长度相似，那么可以认为该时间序列具有季节性。

第二题：如何进行时间序列数据的平滑处理？时间序列数据的平滑处理是为了去除数据中的随机波动，使其更易于观察和分析。

常用的平滑方法有移动平均法和指数平滑法。

移动平均法是将一段时间内的数据求平均值，以此来代表整个时间段的数据。

指数平滑法则是通过对历史数据进行加权平均，赋予较近期数据更高的权重，以反映出时间序列数据的趋势。

第三题：如何进行时间序列数据的分解？时间序列数据的分解是为了将其拆解成趋势、季节性和随机成分三个部分，以便更好地理解和预测数据。

常用的分解方法有经典分解法和X-11分解法。

经典分解法是将时间序列数据拆解成趋势、季节性和随机成分，其中趋势是数据的长期变化，季节性是周期性的变化，随机成分则是无法解释的随机波动。

X-11分解法则是在经典分解法的基础上加入了一些调整和修正，使得分解结果更准确。

第四题：如何进行时间序列数据的预测？时间序列数据的预测是利用历史数据来预测未来的趋势和模式。

常用的预测方法有移动平均法和指数平滑法。

移动平均法是将时间序列数据的平均值作为未来的预测值。

指数平滑法则是通过对历史数据进行加权平均，赋予较近期数据更高的权重，以反映出时间序列数据的趋势。

此外，还可以使用ARIMA模型进行时间序列数据的预测，ARIMA模型是一种常用的时间序列预测模型，它结合了自回归、滑动平均和差分运算。

第10章时间序列预测教材习题答案下表是1981年一1999年国家财政用于农业的支出额数据（1）绘制时间序列图描述其形态。

（2）计算年平均增长率。

（3）根据年平均增长率预测2000年的支出额。

详细答案：（1）时间序列图如下：从时间序列图可以看出，国家财政用于农业的支出额大体上呈指数上升趋势（2）年平均增长率为：G = - 1 = 035 76 -1 = 113.55% -1 = 13.55%Y 打y110.21。

（3）。

下表是1981年一2000年我国油彩油菜籽单位面积产量数据（单位：kg / hm2 ）19901260 2000 1519(1)绘制时间序列图描述其形态。

(2)用5期移动平均法预测2001年的单位面积产量。

(3)采用指数平滑法，分别用平滑系数a二和a=预测2001年的单位面积产量说明用哪一个平滑系数预测更合适？详细答案：(1)时间序列图如下:（2）2001年的预测值为：冲1367 + 1479 + 1272 + 1469+W1? 7106 一小①^ooi = -------------- 7 -------------- 二 F 二14笨2- 」I (3)由Excel输出的指数平滑预测值如下表:年份单位面积产量指数平滑预测a= 误差平方指数平滑预测a=误差平方11981 14511982 1372，分析预测误差，年谕2001年a=时的预测值为：耳观=购 + (1-⑵耳=0.3x1519 + (1-03)x1380 2 = 1^21 8 =时的预测值为:耳DM=叱+ &讯=0.5x1519 + (1-0.5)x14074 = 1463 1比较误差平方可知，a二更合适月份营业额（万元）月份营业额（万元）1 295 10 4732 283 11 4703 322 12 4814 355 13 4495 286 14 5446 379 15 6017 1381 16 5878 431 17 6449 424 18 660（1）用3期移动平均法预测第19个月的营业额（2）采用指数平滑法，分别用平滑系数a二、a=和a二预测各月的营业额，分析预测误差，用哪一个平说明滑系数预测更合适？（3）建立一个趋势方程预测各月的营业额，计算出估计标准误差详细答案：(1)第19个月的3期移动平均预测值为:587 + 644 + 6601891630.33(2)F19= 0 3x660+(1 -0.3)x567.9 = 595.5 误差均方=。

3.2 具有季节性特点的时间序列的预测这里提到的季节，可以是自然季节，也可以是某种产品的销售季节等。

显然，在现实的经济活动中，表现为季节性的时间序列是非常多的。

比如，空调、取暖设备、季节性服装的生产与销售所产生的数据等。

对于季节性时间序列的预测，要从数学上完全拟合其变化曲线是非常困难的。

但预测的目的是为了找到时间序列的变化趋势，尽可能地做到精确。

从这个意义上来讲，可以有多种方法，下面介绍其中一种，即所谓季节系数法。

季节系数法的具体计算步骤如下：1．收集m 年的每年各季度或者各月份（每年n 个季度）的时间序列样本数据ij x 。

2．计算每年所有的季度或所有月份的算术平均值x ，即：mn k x k x m i nj ij ==∑∑==,1113．计算同季度或同月份数据的算术平均值n j xx mi ijj ,,2,1,1. ==∑=4．计算季节系数或月份系数x x j j /.=β。

其中n j ,,2,1 =为季度或者月份的序号。

5．预测计算。

当时间序列是按季度列出时，先求出预测年份（下一年）的年加权平均：mmm m w w w y w y w y w y ++++=+2122111式中，∑==nj iji xy 1为i 年份的年合计数：i w 为i 年份权数，按自然数列取值。

再计算预测年份的季度平均值4:111+++=m m m y y y 。

最后，预测年份第i 季度的预测值为：i m i m y y β⋅=++1,1季节系数法的Matlab 程序如下。

funjie.m%简单季节系数法，文件名funjie.mfunction JiJie=funjie(x) %输入m 年，每年n 个季节的历史数据 [m,n]=size(x);BarX=mean(mean(x)) %计算所有数据的算术平均值 BarXj=mean(x) %计算同季节的算术平均值 Betaj=BarXj./BarX %计算季节系数 y1=[1:m];y=y1*sum(x,2)/sum(y1) %计算预测下一年的年加权平均值 y2=y/n %计算预测年份的季节平均值 y3=y2*Betaj %预测年份的季节预测值 end【例3-11】某商店某类商品1999-2003年各季度的销售额如表3-6所示。

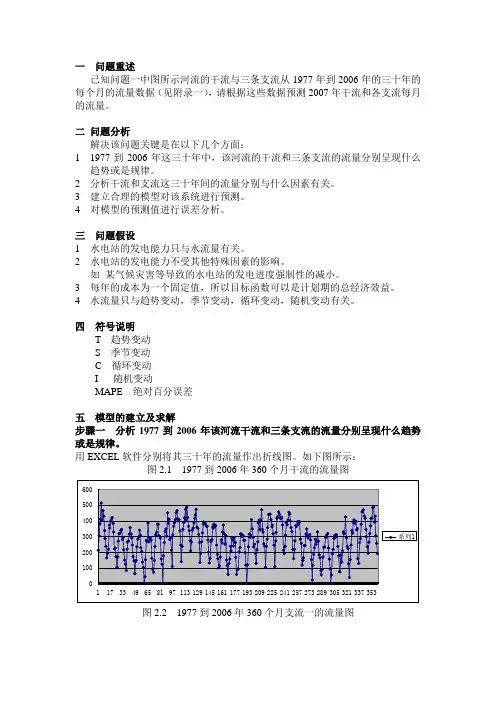
一问题重述已知问题一中图所示河流的干流与三条支流从1977年到2006年的三十年的每个月的流量数据（见附录一），请根据这些数据预测2007年干流和各支流每月的流量。

二问题分析解决该问题关键是在以下几个方面：11977到2006年这三十年中，该河流的干流和三条支流的流量分别呈现什么趋势或是规律。

2分析干流和支流这三十年间的流量分别与什么因素有关。

3建立合理的模型对该系统进行预测。

4对模型的预测值进行误差分析。

三问题假设1 水电站的发电能力只与水流量有关。

2 水电站的发电能力不受其他特殊因素的影响。

如某气候灾害等导致的水电站的发电进度强制性的减小。

3 每年的成本为一个固定值，所以目标函数可以是计划期的总经济效益。

4 水流量只与趋势变动，季节变动，循环变动，随机变动有关。

四符号说明T 趋势变动S 季节变动C 循环变动I 随机变动MAPE 绝对百分误差五模型的建立及求解步骤一分析1977到2006年该河流干流和三条支流的流量分别呈现什么趋势或是规律。

用EXCEL软件分别将其三十年的流量作出折线图。

如下图所示：图2.1 1977到2006年360个月干流的流量图图2.2 1977到2006年360个月支流一的流量图图2.3 1977到2006年360个月支流二的流量图图2.4 1977到2006年360个月支流三的流量图分析：由上述四个图我们可以看出：1干流和三个支流的每年的流量均随月份呈现周期性的变化。

2干流（图2.1）大概每十年为一次循环，每一次循环期内同期（同月份）水量呈现先平滑下降再平滑上升的趋势。

3 支流一（图2.2）三十年内同期水量大致呈上升趋势。

4 支流二（图2.3）三十年内同期水量大致呈下降趋势。

5 支流三（图2.4）三十年内同期水量无明显的长期趋势。

步骤二 分析影响干流和三条支流的流量的因素。

由步骤一我们可以将此系统看成一时间序列。

下面，我们对该时间序列进行分解分析。

注： 时间序列的构成因素可以分为四类，即趋势变动（T ）季节变动（S ）循环变动（C ）随机变动（I ）。

季节趋势的时间序列预测季节趋势的时间序列预测是指对时间序列数据中呈现出明显季节性变化趋势的情况进行预测和分析。

季节趋势可以是每年、每季度、每月或每周重复出现的波动情况，对于一些具有季节性特征的数据，如销售额、股票价格、天气数据等，进行季节趋势的预测可以帮助我们了解和预测未来的趋势。

在季节趋势的时间序列预测中，常用的方法有季节分解法、移动平均法、指数平滑法等。

一种常见的方法是季节分解法。

季节分解法首先将时间序列数据分解为三个部分：长期趋势分量、季节分量和随机波动分量。

长期趋势分量反映了时间序列数据的总体变化趋势，季节分量描述了季节性变化的规律，而随机波动分量反映了不可预测的随机波动。

季节分解法的步骤如下：1. 对时间序列数据进行平滑处理，例如可以使用移动平均法。

2. 对平滑处理后的数据进行季节性分量的估计，可以使用季节指数法或回归方法。

3. 得到季节性分量后，通过拟合趋势分量和随机波动分量来估计长期趋势分量和随机波动分量。

4. 根据长期趋势分量和季节性分量，得到未来的季节趋势预测结果。

另一种常见的方法是移动平均法。

移动平均法通过计算一定时间窗口内数据的平均值来平滑时间序列数据，以减少随机波动的影响。

常用的移动平均法有简单移动平均法、加权移动平均法等。

移动平均法的步骤如下：1. 确定时间窗口的大小，即要计算的数据个数。

2. 根据时间窗口的大小，计算每个时间点的平均值。

3. 根据计算的平均值，进行未来季节趋势的预测。

指数平滑法是另一种常见的方法，它通过对时间序列数据进行指数加权来平滑数据，较好地反映了时间序列的趋势和季节性变化。

指数平滑法的步骤如下：1. 初始化权重，通常为0.1到0.3之间的值。

2. 对时间序列数据进行指数平滑计算，得到平滑后的数据。

3. 根据平滑后的数据，进行未来季节趋势的预测。

在季节趋势的时间序列预测中，选择合适的方法需要根据数据的特点和需求来进行判断。

需要考虑的因素包括数据的周期性、趋势性以及随机波动的程度等。

文章编号:1002-1566(2000)06-0060-05季节性波动时间序列预测的分解季节指数法Ξ郭秀英1　尹兴国2　张艳云1(1.西南石油学院,南充　63700;2.川中钻井工程公司)摘　要:本文在分析研究已有季节性波动时间序列的预测方法基础上,提出了一种简单、易懂的实用预测方法,并通过实例验证了该方法是可行的。

关健词:季节性波动;时间序列;季节指数;趋势值一、引 言一般而言,季节性波动时间序明显地既具长期趋势性,又具季节性。

长期趋势是由于受到某些因素持续地同性质地影响,而表现为持续上升或下降或平衡的总变化趋势,其间变动幅度可能不等。

因而,其可能为线性的,也可能为非线性的。

而季节性则是受气候、社会、风俗习惯等的影响,而表现出以一年为周期随着自然季节的推移而呈现出在各年的一定季节出现高峰值,另一定季节出现低谷值,但各高峰值与低谷值不一定相等。

季节性波动时间序列变动的复杂性,决定了其预测存在一定困难,因此,人们不断探索,提出了各种各样的解决这一问题的方法。

但到目前为止,没有一种完善地普遍为人们接受的方法。

这些方法中无论哪一种方法都未全面考虑而或多或少地存在一定缺限。

如季节性因子分解预测法、Parsons连环比例法、定基比例法、Winters线性与季节性指数平滑法、时间序列分解法等都未考虑季节指数的趋势性变化。

而季节分解预测法、分解———组合预测法,虽然考虑了季节指数的趋势性变动,但未充分利用已知的数据信息。

著名的Box-Jenkins季节模型预测法,虽然理论上较完善,但方法较繁琐、复杂、理论上较难理解,而且预测费用也较高。

因此,仍不被人们接受。

为此,本文提出了一种既考虑季节性指数的趋势性变化,又充分利用其已知数据信息的简单、易懂的实用方法———分解季节指数法。

二、　分解季节指数法1.总体思想既考虑季节指数的趋势性变化,又充分利用已知数据信息。

即:首先,将季性波动时间序列的季节性“剔除”,预测出其长期趋势值,再预测出其季节指数;最后以季节指数预测值调整长期趋势预测值,而得出季节性波动时间序列的预测值。

季节预测法是一种基于时间序列数据的预测方法，它利用时间序列中的季节性规律来预测未来的趋势。

下面是一个使用季节预测法的简单例题：
假设你是一位餐厅老板，想要预测未来一个月的销售额。

你收集了过去几个月的销售额数据，发现销售额呈现出季节性波动，每个月的销售额都会出现一次高峰和一次低谷。

基于这些数据，你可以使用季节预测法来预测未来一个月的销售额。

具体步骤如下：1.将时间序列数据划分为若干个季节，每个季节包含若干个时间点。

在这个例子
中，你可以将每个月划分为一个季节，然后计算每个月的平均销售额。

2.计算季节性指数，即将每个季节的平均销售额除以所有季节的平均销售额。

例
如，如果某个月的平均销售额为1000元，而所有月份的平均销售额为800元，则该月份的季节性指数为1.25。

3.使用季节性指数来预测未来一个月的销售额。

假设过去几个月的季节性指数分
别为1.1、1.2、1.3和1.4，则未来一个月的销售额预测值为800 * 1.3 = 1040元。

需要注意的是，季节预测法只适用于具有明显季节性规律的时间序列数据。

如果数据中没有明显的季节性规律，或者季节性规律不稳定，则该方法可能不适用。

此外，还需要注意数据的异常值和缺失值对预测结果的影响。

一、单选题1、根据季度数据测定季节比率时，各季节比率之和为（）。

A.100%B.0C.400%D.1200%正确答案：C2、增长1%水平值的表达式是（）。

A.报告期增长量/增长速度B.报告期发展水平/100C.基期发展水平/100D.基期发展水平/1%正确答案：C3、若报告期水平是基期水平的8倍，则我们称之为（）。

A.翻了 3番B.翻了 8番C.发展速度为700%D.增长速度为800%正确答案：A4、若时间数列呈现出长时间围绕水平线的周期变化，这种现象属于（）。

A.无长期趋势、有循环变动B.有长期趋势、有循环变动C.无长期趋势、无循环变动D.有长期趋势、无循环变动正确答案：B5、银行年末存款余额时间数列属于（）。

A.平均指标数列B.时点数列C.时期数列D.相对指标数列正确答案：B6、某一时间数列，当时间变量t=1，2，3，...，n时，得到趋势方程为y=38+72t，那么，取t=0，2，4，6，8，...时，方程中的b将为（）。

A.36B.34C.110D.144正确答案：A7、某企业2018年的产值比2014年增长了 200%，则年平均增长速度为（）。

A.50%B.13.89%C.29.73%D.31.61%正确答案：D8、2010年某市年末人口为120万人，2020年年末达到153万人，则年平均增长量为（）万人。

A. 3B.33C. 3.3D.30正确答案：C9、在测定长期趋势时，如果时间数列逐期增长量大体相等，则宜拟合（）。

A.抛物线模型B.直线模型C.曲线模型D.指数曲线模型正确答案：B10、在测定长期趋势时，当时间数列的逐期增长速度基本不变时，宜拟合（）。

A.逻辑曲线模型B.二次曲线模型C.直线模型D.指数曲线模型正确答案：D二、多选题1、编制时间数列的原则有（）。

A.经济内容的一致性B.计算方法的一致性C.时间的一致性D.总体范围的一致性正确答案：A、B、C、D2、以下表述正确的有（）。

时间序列练习题时间序列分析是一种用于研究以时间为顺序的数据变动规律的方法。

它可以帮助我们理解和预测未来的趋势，对于决策和规划具有重要的意义。

本文将通过一些时间序列练习题，帮助读者更好地理解和应用时间序列分析。

练习题一：季度销售数据分析某公司的销售数据按照季度记录如下：季度销售额Q1 100Q2 200Q3 300Q4 400请你根据这些数据，进行以下的分析和预测：1. 绘制季度销售额的时间序列图。

2. 计算季度销售额的平均值。

3. 判断季度销售额是否存在趋势性，并进行趋势线的拟合。

4. 判断季度销售额是否存在季节性，如果存在，请进行季节性分解。

5. 使用你认为最适合的模型进行未来一年季度销售额的预测，并给出预测结果。

练习题二：月度股票收益率分析某股票连续12个月的收益率数据如下：月份收益率1 0.032 0.053 -0.024 0.025 -0.016 0.047 -0.038 0.019 0.0210 -0.0511 0.0112 0.03请你根据这些数据，进行以下的分析和预测：1. 绘制月度股票收益率的时间序列图。

2. 计算月度收益率的平均值和标准差。

3. 判断股票收益率是否存在趋势性，并进行趋势线的拟合。

4. 判断股票收益率是否存在季节性，如果存在，请进行季节性分解。

5. 使用你认为最适合的模型进行未来三个月股票收益率的预测，并给出预测结果。

练习题三：年度气温分析某城市过去10年（2011年至2020年）的年度平均气温数据如下：年份平均气温（摄氏度）2011 192012 212013 202014 182015 172016 182017 202018 222019 232020 21请你根据这些数据，进行以下的分析和预测：1. 绘制年度平均气温的时间序列图。

2. 计算年度平均气温的平均值、中位数和极差。

3. 判断气温是否存在趋势性，并进行趋势线的拟合。

4. 判断气温是否存在季节性，如果存在，请进行季节性分解。

时间序列分析期末题库试题及答案（以下是一个范例，您可以根据需要进行修改和调整）时间序列分析期末题库试题及答案时间序列分析是一门研究随时间变化的数据模式和规律的统计学方法，广泛应用于物理学、经济学、环境科学等领域。

在进行时间序列分析时，掌握相关的试题及其答案是提高分析能力和应对考试的重要途径。

本文将为您提供一份时间序列分析期末题库试题及答案，希望能帮助您更好地掌握这门学科。

一、简答题1. 请解释什么是时间序列分析。

答：时间序列分析是一种统计学方法，用于研究随时间变化的数据。

它可以揭示出数据内在的趋势、季节性和周期性等模式，帮助我们进行预测和决策。

2. 时间序列分析的主要步骤有哪些？答：时间序列分析的主要步骤包括：数据收集和整理、数据可视化、确定模型、模型识别和拟合、模型检验和评估、模型预测和应用。

3. 请解释平稳时间序列的概念。

答：平稳时间序列是指其数学期望、方差和自协方差不随时间的变化而发生显著变化的时间序列。

平稳时间序列的均值和方差不依赖于时间，具有稳定的趋势和季节性。

4. 如何进行时间序列的平稳性检验？答：常见的平稳性检验方法包括ADF检验、KPSS检验和单位根检验。

这些方法可以通过检验时间序列数据的单位根是否存在来判断其是否平稳。

5. 时间序列分析中的自相关和偏自相关函数有什么作用？答：自相关函数（ACF）和偏自相关函数（PACF）用于分析时间序列数据的相关性。

ACF可以帮助确定数据的季节性和周期性，而PACF可以帮助确定数据的自回归阶数。

二、计算题请根据以下时间序列数据，回答下面的问题：年份 | 销售额（万元）-----------------------2015 | 2002016 | 2302017 | 2502018 | 2802019 | 3002020 | 3201. 请绘制销售额的时间序列图。

答：（在此插入相应的时间序列图）2. 根据观察的时间序列图，总结该时间序列的趋势和季节性。

运⽤时间序列预测⽅法进⾏案例分析运⽤时间序列预测⽅法进⾏案例分析考虑季节因素许多年来，ccw⼀直有⼀个传统的观点；⼀年中前3个季度的呼叫量（销售量）⼗分稳定，在第四个季度会⼀跃上升25%。

这是25%规则的基础、为了检验传统观点与现实的接近程度，咨询员给出的数据计算量过去三年中每个季度的平均呼叫量.与25%规则相⽐，第四季度的季节性因⼦仅⽐第三季度搞19个百分点（然⽽第四季度的季节性因⼦⽐前三个季度的季节性因⼦的平均值0.94⾼出约25）。

尽管没有近三年以前的呼叫量数据，但可靠的销售量数据被保存下来。

通过检查前⼏年的数据，莉迪亚发现了相同的季节影响模式。

季节调整的时间序列如果先对数据进⾏去除季节因素影响的处理，再分析销售量数据，则发现新的趋势会容易的多。

实际上去除季节因素的呼叫量表⽰了如果在⼀年特定时间（圣诞采购、开学前采购等）的呼叫量平均分配到整个年度时呼叫量将会是多少。

季节调整的时间序列的波动形式（特别是最近的数据点的波动形式）对预测下⼀个数据点落在什么地⽅特别有⽤。

⽽最后⼀点是整个时间序列中最⾼的的⼀点。

这表⾯下⼀个季度的数据点会⾼于平均数7529并可能在最后⼀点8178附近甚⾄更⾼。

各种时间序列预测⽅法采⽤不同的途径来外推去除季节因素影响的时间序列的趋势⼀预测下⼀个数据点。

这⼀节降介绍主要的⼏种⽅法。

就像下⾯的概要⼀样，在得到了去除季节因素影响的预测之后，所有这些⽅法将再把预测结果转化为实际的呼叫量预测值(没有季节因素调整)。

预测呼叫量过程的概要1.选择时间序列预测⽅法。

2.将此⽅法⽤于经过季节调整的时间序列，得到下⼀个季度季节调整的呼叫量预测。

3.将这个预测值乘以相应的季节性因⼦，得到实际预测呼叫量（没有季节因素调整）。

下⾯对预测⽅法的描述集中于如何实现第⼆步，也就是如何根据给定的时间序列预测下⼀个数据点。

我们还在每⼀种⽅法中使⽤电⼦表格，以过去三年的数据完成步骤2、3，并计算MAD（平均预测误差）和MSE（平均预测误差⽅差）。

时间序列分析试题ARIMA模型与季节性调整时间序列分析被广泛应用于许多领域，如经济学、金融学、气象学等等。

它是一种研究随时间变化的数值序列的方法。

在时间序列分析中，ARIMA模型和季节性调整是常用的技术。

本文将介绍ARIMA模型和季节性调整的相关概念和应用。

一、ARIMA模型ARIMA模型是自回归移动平均模型（Autoregressive Integrated Moving Average Model）的缩写。

它是一种常用的时间序列分析方法，被广泛用于预测和建模。

ARIMA模型的核心思想是通过将时间序列分解成自回归（AR）成分、差分（I）成分和移动平均（MA）成分，来进行建模和预测。

ARIMA模型的建立包括三个步骤：确定模型阶数、估计模型参数、模型检验和预测。

1.1 确定模型阶数在确定ARIMA模型的阶数时，可以利用自相关函数（ACF）和偏自相关函数（PACF）的图形分析来寻找最佳的阶数。

ACF图可以帮助我们确定移动平均项的阶数，PACF图可以帮助我们确定自回归项的阶数。

通过观察图形，我们可以找到ACF和PACF截尾的位置，从而得到ARIMA模型的阶数。

1.2 估计模型参数在确定了模型的阶数后，我们需要估计模型的参数。

最常用的估计方法是最大似然估计法，通过最大化似然函数来估计模型的参数。

根据模型的阶数，我们可以建立ARIMA模型的估计方程，并利用时间序列数据进行参数估计。

1.3 模型检验和预测在估计了模型的参数后，我们需要对模型进行检验。

常用的检验方法有残差分析、模型拟合度检验、预测准确度检验等。

通过这些检验，我们可以评估模型的拟合效果和预测能力。

二、季节性调整很多时间序列数据都具有季节性变动的特点，这对于建模和预测带来了一定的困难。

为了解决这个问题，我们可以对时间序列进行季节性调整。

季节性调整的目标是将数据的季节性成分从原始数据中分离出来，以便更好地进行预测和分析。

常用的季节性调整方法有移动平均法、指数平滑法和X-12-ARIMA等方法。

标题：季节性预测的例题分析一、概述在日常生活和商业运营中，季节性变化是一种常见的现象。

对于零售业、农业和旅游业等行业来说，了解季节性趋势并进行准确的预测对于制定销售策略和生产计划至关重要。

在本文中，我们将以某零售企业销售数据为例，介绍季节性预测的方法和步骤。

二、收集数据我们需要收集相关的销售数据。

假设我们选择一家服装零售店为例，该店在过去几年的销售额数据。

我们需要获取每个月份或者季度的销售额数据，以便分析季节性变化的规律。

三、探索性数据分析在收集到数据之后，我们可以对数据进行探索性分析。

我们可以绘制每个月份的销售额折线图，观察是否存在季节性的波动。

我们也可以计算每年同一月份的销售额均值，观察是否存在明显的季节性趋势。

四、时间序列分解接下来，我们可以使用时间序列分解的方法，将原始数据分解为趋势、季节性和残差三个部分。

通过时间序列分解，我们可以更清晰地观察季节性的变化规律。

我们也可以通过拟合季节性模型，预测未来的季节性变化。

五、建立模型在时间序列分解的基础上，我们可以建立季节性预测模型。

常见的季节性模型包括季节性自回归移动平均模型（SARIMA）和季节性指数模型。

我们可以通过对历史数据进行拟合，选择最优的模型参数，并对模型进行诊断。

六、模型评估在建立模型之后，我们需要对模型进行评估。

我们可以使用历史数据的一部分作为训练集，另一部分作为测试集，对模型的预测精度进行评估。

常见的评估指标包括均方误差（MSE）和平均绝对误差（MAE）。

七、季节性预测我们可以利用已建立的季节性模型，对未来的销售额进行预测。

通过预测未来的季节性变化，企业可以及时调整销售策略和库存管理，以适应季节性需求的变化。

八、结论通过以上的分析和建模过程，我们可以得出对季节性预测的结论。

季节性预测可以帮助企业更好地了解市场的季节性变化规律，制定针对性的经营策略，提高销售额和效益。

结尾通过上述例题分析，我们了解了季节性预测的基本步骤和方法。

季节性预测是一种重要的商业分析工具，可以帮助企业把握市场的季节性变化规律，做出更加合理的经营决策。

应用统计硕士（时间序列分析和预测）模拟试卷1(题后含答案及解析)题型有：1. 单选选择题 3. 简答题 4. 计算与分析题单选选择题1．2003年末某市人口为120万人，2013年末达到153万人，则人口的平均发展速度为( )。

A．2．46％B．2．23％C．102．23％D．102．46％正确答案：D解析：计算平均发展速度通常采用几何平均法。

若6表示平均发展速度，n 表示环比发展速度的时期数，则：b＝，故人口的平均发展速度的计算公式为：b＝≈102．46％知识模块：时间序列分析和预测2．时间序列编制的基本原则是( )。

A．无偏性B．及时性C．完整性D．可比性正确答案：D解析：编制时间序列的目的是为了通过对各时间的变量数值进行对比，研究现象发展变化的过程和规律。

因此，保证序列中各变量数值在所属时间、总体范围、经济内容、计算口径、计算方法等方面具有充分的可比性，是编制时间序列的基本原则。

知识模块：时间序列分析和预测3．时间序列在一年内重复出现的周期性波动称为( )。

A．趋势B．季节性C．周期性D．随机性正确答案：B解析：季节性也称季节变动，它是时间序列在一年内重复出现的周期性波动。

A项趋势是时间序列在长时期内呈现出来的某种持续向上或持续下降的变动；C 项周期性也称循环波动，它是时间序列中呈现出来的围绕长期趋势的一种波浪形或振荡式变动；D项随机性也称不规则波动，它是时间序列中除去趋势、周期性和季节性之后的偶然性波动。

知识模块：时间序列分析和预测4．下列关于时点时间序列特征的描述，错误的是( )。

A．时点时间序列具有可加性B．时点时间序列是一种基本时间序列C．时点时间序列的每一项数据都是绝对数D．时点时间序列的每一项数据都是采用间断统计方法获得的正确答案：A解析：时点指标是反映现象在某一时刻上的绝对数量，由时点指标构成的时间序列就是时点时间序列，它是一种基本时间序列。

时点时间序列主要特点有：①不可加性；②指标数值的大小与时点间隔的长短一般没有直接关系；③指标值采用间断统计的方式获得。

对带有季节变动的时间序列数据的预测分析例题一：现有某地区某产品产量近三年的分月资料。

试测试该种产品2012年10月的产量解：（1）首先观察时间序列数据，具有哪些变动，进而确定选用哪种预测方法在给出的时间序列数据中我们可以明显判断出来，6月-8月销量比其他月份高出很多，而且每年都是这样，说明这列时间序列数据含有季节变动。

则应该用季节变动模型进行预测。

其次，判断整个时间序列数据是否具有趋势变动，是否是每年的平均销量均比上一年要多或者是少，第一年的均值为1y =11 第二年的均值为 2y =16 第三年的均值为3y =23 ，那么这列时间序列数据带有趋势变动。

则判断不能选用周期平均法。

最后判断是否随着年份的增加，时间序列数据的季节变动幅度在逐渐增大。

判断方法为：用每年的峰值减去均值，得到一个离差，如果每年的离差带有趋势变动，呈逐年增加或者减少，那么说明时间序列的季节变动幅度有变化。

第一年峰值为22，均值为11，离差为11.第二年峰值为29，均值为16，离差为13；第三年峰值为42，均值为23，离差为19。

判断离差在逐年增加。

说明季节变动的幅度在逐年增加。

则选择季节交乘预测模型。

也可画出散点图判断。

（2） 季节交乘预测模型为：()ˆt ya bt fi =+⨯其中fi 为季节指数；()a bt +为趋势值根据预测模型，知道预测值为预测期趋势值与预测期季节指数的乘积。

我们要预测的是2012年10月份的销售量，因此需要2012年10月份季节指数，和10月份的趋势值就可以知道10月份的销量。

而2012年10月份的季节指数是根据2011年2010年和2009年，前三年10月份的季节指数得出的。

所以首先需要求出前三年10月份的季节指数。

季节指数Ytfi Ft=; 其中Yt 代表的是观察值，Ft 代表的是趋势值。

因此首先求出，前三年10月份的趋势值。

趋势值即为，如果这列时间序列数据只有直线趋势变动，没有季节变动的时候的值。