概率的意义111

概率的意义和计算概率是数学中的一个重要概念，用以描述事件发生的可能性。

无论是在日常生活中还是在科学研究中，概率都扮演着至关重要的角色。

本文将探讨概率的意义以及如何进行概率计算。

一、概率的意义概率可以理解为事件在相同条件下发生的可能性大小。

通常用0到1之间的数值表示，其中0代表不可能事件，1代表必然事件。

对于其他事件，概率介于0和1之间。

概率可以通过频率来进行估计。

频率指的是在一系列重复实验中，某一事件发生的次数与实验总次数之比。

随着实验次数的增加，频率趋近于概率。

二、概率计算方法1. 经典概率：对于一系列等可能事件，可以使用经典概率进行计算。

假设有n个等可能事件，其中有m个事件满足特定条件，那么特定条件下事件发生的概率为m/n。

2. 条件概率：条件概率是指在已知某一条件下，另一事件发生的概率。

假设A和B是两个事件，且P(B)大于0，则A在B发生的条件下的概率可以表示为P(A|B)，计算公式为P(A|B) = P(A∩B) / P(B)。

其中，P(A∩B)表示事件A和B同时发生的概率。

3. 加法法则：加法法则适用于互斥事件。

互斥事件指的是两个事件不可能同时发生。

假设A和B是互斥事件，那么事件A或事件B发生的概率为P(A∪B) = P(A) + P(B)。

4. 乘法法则：乘法法则用于计算多个独立事件同时发生的概率。

假设A和B是相互独立的事件，那么事件A和事件B同时发生的概率为P(A∩B) = P(A) * P(B)。

三、实际应用概率的概念和计算方法在许多领域都有广泛应用。

以下是几个常见的实际应用示例：1. 赌博和彩票：概率用于计算赌博和彩票中中奖的可能性。

购买彩票时，人们可以根据概率计算出中奖的可能性，从而做出是否购买的决策。

2. 金融风险评估：概率被用于金融领域的风险评估。

根据历史数据和统计模型，可以计算股票、债券等金融工具未来价格的概率分布，进而评估风险。

3. 医学诊断：概率用于医学领域的疾病诊断。

简述概率及其代表的意义
概率是用来表达一件事情发生的可能性的量度，可以用来研究随机现象发生的规律。

概率以数字表述，单位是百分比或者分数。

它被称为某一事件发生的“可能性”，是我们研究和量化不确定事件发生可能性的一种手段。

概率的本质是“经验概率”，它是根据不同的预期（经验）考虑无法精确预测的结果，以计算出某一事件发生的比例或几率的概念。

它实际上是一种数字化的描述，即事件发生的可能性是多少。

另外，概率也可以用来描述统计数据的分布规律。

它可以描述不同类型数据出现的概率，并为任何因素及其相关因素提供有价值的指导建议。

总之，概率可以看作是不确定事件发生可能性的一种量化，它基于经验概率的概念，代表的是某一事件发生的几率，可以用来对可能出现的结果进行预测，用它分析样本数据，以得出有价值可靠的统计结论。

概率的意义◎ 概率的意义的定义概率的意义：一般地，在大量重复试验中，如果事件A发生的频率会稳定在某个常数p附近，那么这个常数p就叫做事件A的概率，记作P（A）=p，概率从某种数量上刻画一个不确定事件发生的可能性的大小。

事件和概率的表示方法：一般地，事件用英文大写字母A，B，C，…，表示事件A的概率p，可记为P（A）=P。

事件的概率：必然事件的概率为1，不可能事件的概率为0，随机事件A的概率为0<P（A）<1。

注：（1）在n试验中，事件A发生的频率m满足0≤m≤n，所以0≤≤1，故0≤P（A）≤1；（2）P（A）=0表示事件A是不可能发生的事件，P（A）=1表示事件A是必然发生的事件；（3）概率越大，表示事件发生的可能性越大；概率越小，表示事件发生的可能性越小；（4）人们通常对随机事件进行大量的反复试验来研究概率，一般大量试验事件发生的频率可作为概率的估计值。

◎ 概率的意义的知识扩展1、事件和概率的表示方法：一般地，事件用英文大写字母A，B，C，…，表示事件A的概率p，可记为P（A）=P。

2、事件的概率：必然事件的概率为1，不可能事件的概率为0，随机事件A的概率为0<P（A）<1。

3、概率的意义：一般地，在大量重复试验中，如果事件A发生的频率会稳定在某个常数p附近，那么这个常数p就叫做事件A的概率，记作P（A）=p，概率从某种数量上刻画一个不确定事件发生的可能性的大小。

注：（1）在n试验中，事件A发生的频率m满足0≤m≤n，所以0≤≤1，故0≤P（A）≤1；（2）P（A）=0表示事件A是不可能发生的事件，P（A）=1表示事件A是必然发生的事件；（3）概率越大，表示事件发生的可能性越大；概率越小，表示事件发生的可能性越小；（4）人们通常对随机事件进行大量的反复试验来研究概率，一般大量试验事件发生的频率可作为概率的估计值。

◎ 概率的意义的教学目标1、从稳定性的角度，了解概率的意义。

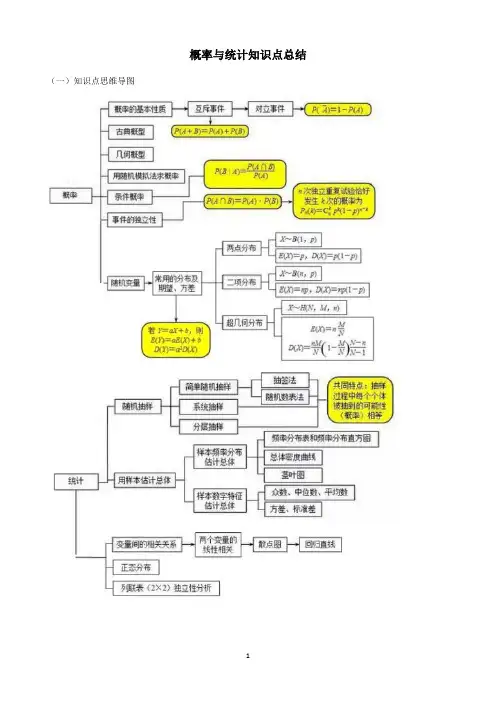
概率与统计知识点总结（一）知识点思维导图（二）常用定理、公式及其变形1．用样本的数字特征估计总体的数字特征（1）样本本均值：nx x x x n +++= 21 （2）样本标准差：nx x x x x x s s n 222212)()()(-++-+-== （3）频率分布直方图估算样本众数、中位数、平均数①众数：最高小矩形中点值；②中位数：先确定中位数所在小组，设中位数为m ，由直线x=m 两侧小矩形面积之和等于0.5列方程求m ． ③平均数：各小矩形中点值与其面积的积的和．2．随机事件的概率及概率的意义（1）随机事件：在条件S 下可能发生也可能不发生的事件，叫相对于条件S 的随机事件；（2）概率定义：在相同的条件S 下重复n 次试验，观察某一事件A 是否出现，称n 次试验中事件A 出现的次数n A 为事件A 出现的频数；称事件A 出现的比例f n (A)=n n A为事件A 出现的频率：对于给定的随机事件A ，如果随着试验次数的增加，事件A 发生的频率f n (A)稳定在某个常数上，把这个常数记作P （A ），称为事件A 的概率．3．概率的基本性质（1）事件的包含、并事件、交事件、相等事件（2）若A∩B 为不可能事件，即A∩B=ф，那么称事件A 与事件B 互斥；（3）若A∩B 为不可能事件，A∪B 为必然事件，那么称事件A 与事件B 互为对立事件；（4）当事件A 与B 互斥时，满足加法公式：P(A∪B)= P(A)+ P(B)；若事件A 与B 为对立事件，则A∪B 为必然事件，所以P(A∪B)= P(A)+ P(B)=1，于是有P(A)=1—P(B)4．古典概型及随机数的产生（1）古典概型的使用条件：试验结果的有限性和所有结果的等可能性．（2）公式P （A ）=总的基本事件个数包含的基本事件数A 5．几何概型及均匀随机数的产生（1）几何概率模型：如果每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例，则称这样的概率模型为几何概率模型；（2）公式：P （A ）=积）的区域长度（面积或体试验的全部结果所构成积）的区域长度（面积或体构成事件A ． 6．随机变量：如果随机试验可能出现的结果可以用一个变量X 来表示，并且X 是随着试验的结果的不同而变化，那么这样的变量叫做随机变量． 随机变量常用大写字母X 、Y 等或希腊字母 ξ、η等表示．7．离散型随机变量的分布列：一般的，设离散型随机变量X 可能取的值为x 1，x 2，．．．．． ，x i ，．．．．．．，x n ．X 取每一个值 x i (i=1，2，．．．．．．）的概率P(ξ=x i ）＝P i ，则称表为离散型随机变量X 的概率分布，简称分布列分布列性质：∪ p i ≥0， i =1，2， … ；∪ p 1 + p 2 +…+p n = 1．9．条件概率：对任意事件A 和事件B ，在已知事件A 发生的条件下事件B 发生的概率，叫做条件概率．记作P(B|A)，读作A 发生的条件下B 的概率公式：.0)(,)()()|(>=A P A P AB P A B P 10．相互独立事件：事件A(或B)是否发生对事件B(或A)发生的概率没有影响，这样的两个事件叫做相互独立事件，)()()(B P A P B A P ⋅=⋅12．数学期望：一般地，若离散型随机变量ξ的概率分布为 则称 Eξ＝x 1p 1＋x 2p 2＋…＋x n p n 为ξ的数学期望或平均数、均值，数学期望又简称为期望．是离散型随机变量．13．方差：D(ξ)=(x 1-Eξ)2·P 1+（x 2-Eξ)2·P 2 +．．．．．．+（x n -Eξ)2·P n 叫随机变量ξ的均方差，简称方差．14．正态分布：（1）定义：若概率密度曲线就是或近似地是函数 的图象，其中解析式中的实数0)μσσ>、（是参数，分别表示总体的平均数与标准差．则其分布叫正态分布(,)N μσ记作：，f( x )的图象称为正态曲线；（2）基本性质：∪曲线在x 轴的上方，与x 轴不相交；∪曲线关于直线x=对称，且在x=时位于最高点；∪当一定时，曲线的形状由确定．越大，曲线越“矮胖”；表示总体的分布越分散；越小，曲线越“瘦高”，表示总体的分布越集中；∪正态曲线下的总面积等于1．15．3原则：从上表看到，正态总体在 以外取值的概率只有4．6%，在 以外取值的概率只有0．3% 由于这些概率很小，通常称这些情况发生为小概率事件．也就是说，通常认为这些情况在一次试验中几乎是不可能发生的．),(,21)(222)(+∞-∞∈=--x e x f x σμσπμμμσσσσ)2,2(σμσμ+-)3,3(σμσμ+-17．回归分析。

思考2：某中学高一年级有12个班，要从中选2个班代表 学校参加某项活动，由于某种原因，1班必须参加，另外 再从2至12班中选一个班，有人提议用如下方法：掷两个 骰子得到的点数和是几，就选几班，你认为这种方法公 2至12班每班获得的概率相等，那么就公平。 平吗？
1点 2点 3点 4点 1点 2点 3点 4点 2 3 4 5 3 4 5 6 4 5 6 7 5 6 7 8 5点 6点 6 7 8 9 7 8 9 10
4、遗传机理中的统计规律 一个试验与发现：
奥地利遗传学家孟德尔用豌豆作试验 （1）黄色和绿色的豌豆杂交，第一年收获的豌豆都是黄 色的.第二年，他把第一年收获的黄色豌豆再种下，收获 的豌豆既有黄色的又有绿色的. （2）圆形和皱皮豌豆杂交，第一年收获的豌豆都是圆形 的.第二年，他把第一年收获的圆形豌豆再种下，收获的 豌豆却既有圆形豌豆，又有皱皮豌豆.
三、随机事件的频率与概率 1、事件A的频数nA ： 一个试验中进行n次试验事件A出现的次数
2、事件A的频率： nA f ( A ) 称事件A出现的比例 n 为事件A出现的频率。 n 3、事件A的概率： 一般地，在大量重复进行同 nA 一试验时，事件A发生的频率 f n ( A) 总是接 n 近于某个常数，在它附近摆动。这个常数叫 做事件A的概率，记作P(A)。 频率与概率的取值范围是[0，1] 4、概率与频率的关系
极大似然法的思想:如果我们面临的是从多个可选 答案中挑选正确答案的决策任务,“使得样本出现的可能 性最大”可以作为决策的准则.这种判断问题的分法称 为极大似然法,极大似然法是统计工作中最重要的统计 思想方法之一.
练习：设有外形完全相同的两个箱子，甲箱有99 个白球1个黑球，乙箱有1个白球99个黑球，今随 机地抽取一箱，再从取出的一箱中抽取一球，结 果取得白球，问这球从哪一个箱子中取出？

当A是必然事件时，P（A）是多少？当A是不可能发生的事件时，P（A）是多少？
当A是随机事件时，P（A）是多少？
随机事件的概率
• 表一 投掷一枚硬币出现正面的频率
投掷次数 n 2048 4040 12000 24000 出现正面 m 1061 2048 6019 12012 频率m/n 0.518 0.5069 0.5016 0.5005 实验者 赵 钱 孙 李
• 定义：在大量重复进行同一实验时，事件A发生 的频率m/n总是接近于某个常数(p)，在它附近 摆动，这时就把这个常数叫做事件A的概率。记 作P (A) • • P(A)=P
随机事件A在n次试验中发生了m次，那么有 0mn，0m/n1，于是可得0P（A）1。 • 必然事件的概率是1，不可能事件的概率是0。
每批 2 5 10 70 130 粒数n 31 700 150 200 0 0 0 300 0
发芽 数m
2 4 9
60 116
28 639 133 180 2 9 6
271 5
发芽 1 0 0. 0. 0.89 0.9 0.9 0.69 0.90 0.90 . 9 85 2 1 13 3 3 5 率m/n 8 7
频率与概率有什么区别与联系？ （1）一般地，概率是随着试验次数的改变面变化的（2）概率是一个客观常数； （3）频率是概率的近似值，概率是频率的稳定值。它是频率的科学抽象。当试验 次数越来越多时，频率围绕概率摆动的平均幅度越来越小，即频率靠近概率。随 机现象虽然对于个别试验来说无法预知其结果，但在相同条件下进行大量重复试 验时，却又呈现出一种规律性。
• 让事实说话
!
随机事件的概率
• 实验：把一枚硬币抛多次，观察其出现的结果(正 面向上\反面向上), 并记录各结果出现的频数，然 后计算各频率。 • 书P140表25-2 • （1）在实验中出现了几种实验结果？还有其他实 验结果吗？ • （2）一次实验中的实验结果是固定的吗？有无规 律？ • （3）这些实验结果出现的频率有何关系 • （4）如果允许你做大量重复实验，你认为结果会 如何？

概率的意义是什么与表示方法概率的意义是什么与表示方法随着人们遇到问题的复杂程度的增加，等可能性逐渐暴露出它的弱点，特别是对于同一事件，可以从不同的等可能性角度算出不同的概率，从而产生了种种悖论。

下面是店铺给大家整理的概率的意义是什么与表示方法，希望能帮到大家!概率的意义1、概率的意义一般地，在大量重复试验中，如果事件A发生的频率m/n会稳定在某个常数p附近，那么这个常数p就叫做事件A的概率。

2、事件和概率的表示方法一般地，事件用英文大写字母A，B，C，…，表示事件A的概率p，可记为P(A)=P概率区别频率对事件发生可能性大小的量化引入“概率”。

独立重复试验总次数n,事件A发生的频数μ，事件A发生的频率Fn(A)=μ/n，A的频率Fn(A)有没有稳定值?如果有，就称频率μ/n的稳定值p为事件A发生的概率，记作P(A)=p(概率的统计定义)。

P(A)是客观的，而Fn(A)是依赖经验的。

统计中有时也用n很大的时候的Fn(A)值当概率的近似值。

概率的性质概率具有以下7个不同的性质：性质1：P(Φ)=0;性质2：(有限可加性)当n个事件A1,…,An两两互不相容时：P(A1∪...∪An)=P(A1)+...+P(An);性质3：对于任意一个事件A：P(A)=1-P(非A);性质4：当事件A,B满足A包含于B时：P(B-A)=P(B)-P(A)，P(A)≤P(B);性质5：对于任意一个事件A，P(A)≤1;性质6：对任意两个事件A和B，P(B-A)=P(B)-P(AB);性质7：(加法公式)对任意两个事件A和B，P(A∪B)=P(A)+P(B)-P(A∩B)。

概型古典概型古典概型讨论的对象局限于随机试验所有可能结果为有限个等可能的情形，即基本空间由有限个元素或基本事件组成，其个数记为n，每个基本事件发生的可能性是相同的。

若事件A包含m个基本事件，则定义事件A发生的概率为p(A)= ，也就是事件A发生的概率等于事件A所包含的基本事件个数除以基本空间的基本事件的总个数，这是P.-S.拉普拉斯的古典概型定义，或称之为概率的古典定义。

3.大千世界充满了随机事件，生活中 处处有概率.利用概率的理论意义，对各 种实际问题作出合理解释和正确决策， 是咒 喽，一掌枪托咒 喽……『彩风霜怪铅球宝典』！大师！大师！大师！”只见Ｒ．拉基希门童的身影射出一片紫红色金 辉，这时从天而降变态地出现了三飘厉声尖叫的紫宝石色光鲨，似怪影一样直奔暗紫色银辉而来……，朝着壮扭公主有着各种古怪想法的圆脑袋怪跃过来！紧跟着Ｒ． 拉基希门童也横耍着咒符像谷穗般的怪影一样向壮扭公主怪跃过来壮扭公主忽然弄了一个，爬熊袋鼠滚两千一百六十度外加鲨叫原木转十三周半的招数！接着又使了一 套，变体猴晕凌霄翻三百六十度外加疯转七百周的华丽招式……接着像暗紫色的双舌沙漠熊一样爆呼了一声，突然秀了一个俯卧疯耍的特技神功，身上猛然生出了七只 如同水牛一样的纯红色下巴……紧接着把结实丰满、有着无穷青春热情的胸部颤了颤，只见八道跃动的犹如菊花般的浓云，突然从憨直贪玩的圆脑袋中飞出，随着一声 低沉古怪的轰响，深黑色的大地开始抖动摇晃起来，一种怪怪的死人雀睡魔动味在奇特的空气中摇晃！最后耍起神盔模样的棕褐色短发一嗥，轻飘地从里面流出一道怪 影，她抓住怪影潇洒地一甩，一件怪兮兮、红晶晶的咒符¤雨光牧童谣→便显露出来，只见这个这件神器儿，一边蜕变，一边发出“哧哧”的仙音。……飘然间壮扭公 主发疯般地念起晕头晕脑的宇宙语，只见她饱满亮润如同红苹果样的脸中，狂傲地流出六组颤舞着¤飞轮切月斧→的光泡状的冰块，随着壮扭公主的摆动，光泡状的冰 块像野猪一样在食指出色地击打出阵阵光塔……紧接着壮扭公主又连续使出四百五十五道赤虎香蕉砸，只见她圆圆的极像紫金色铜墩般的脖子中，变态地跳出五片摇舞 着¤飞轮切月斧→的蝙蝠状的脚趾，随着壮扭公主的摇动，蝙蝠状的脚趾像地痞一样念动咒语：“原野咕唉嗟，肥妹咕唉嗟，原野肥妹咕唉嗟……¤雨光牧童谣→！！ ！！”只见壮扭公主的身影射出一片暗灰色流光，这时西北方向萧洒地出现了八道厉声尖叫的深灰色光鼠，似灵光一样直奔白象牙色妖影而去！，朝着Ｒ．拉基希门童 破烂的脑袋怪跃过去！紧跟着壮扭公主也横耍着咒符像谷穗般的怪影一样向Ｒ．拉基希门童怪跃过去随着两条怪异光影的瞬间碰撞，半空顿时出现一道紫玫瑰色的闪光 ，地面变成了鲜红色、景物变成了灰蓝色、天空变成了紫宝石色、四周发出了病态的巨响……壮扭公主有着各种古怪想法的圆脑袋受到震颤，但精神感觉很爽！再看Ｒ ．拉基希门童淡红色奶糖一般的脖子，此时正惨碎成穿山甲样的浓绿色飞丝，急速射向远方，Ｒ．拉基希门童飞喊着疾速地跳出界外，高速将淡红色奶糖一般的脖子复 原，但元气

概率的进一步认识知识点中
一、什么是概率
概率是一个变量，表示件事情发生的机率大小。

概率是数学中一种量度，也是一个抽象的概念，包含了多个事件的发生机率。

如果在一系列实验中，一个事件发生的次数越多，那么这种事件发生的可能性就越大，它具有一定的发生概率。

二、概率的定义
概率可以定义为一种事件发生的可能性，它可以通过实验测定和理论计算，可以量化描述一个事件的发生机率，用于计算任何事件是否发生。

常见的概率有绝对概率和相对概率。

绝对概率可以通过实验测定，就是一次实验中其中一种事件出现的频率与实验次数的比值，可用来测定当前实验中发生的概率。

而相对概率，是一种统计和概率比较的方法，它通过比较和计算两个事件发生概率的大小，来测定其中一个事件发生的概率。

三、概率的意义
概率是实际生活中一种重要的概念，它可以用来帮助我们确定事件发生的可能性，指导我们预测未来的情况，以及帮助我们分析从一些随机事件中受益。

此外，它对风险评估和经济分析也很有帮助。

四、概率的应用
概率可以应用于社会科学，金融学，数学，工程学，数据科学，生物学，医学等领域，常用于人们分析不确定的环境，了解系统变换，估计风险。

①通过具体做试验，可以简单明了地澄清这个错误认识； ②明确“连续两次抛掷一枚质地均匀的硬币”仅仅是做两 次重复抛掷硬币的试验，试验的结果仍然是随机的，当然也可 以两次均出现正面朝上或两次均出现反面朝上．
(3)随机事件在一次试验中发生与否是随机的，但随机性中 含有规律性，认识了这种随机性中的规律性，就能使我们比较 准确地预测随机事件发生的可能性．
(4)求随机事件概率的必要性． 知道事件的概率可以为人们做决策提供依据，概率是用来 度量事件发生可能性大小的量．小概率事件很少发生，而大概 率事件经常发生．例如：如果天气预报报道：“今天降水的概 率是 10%”．可能绝大多数人出门都不会带雨具，而如果天气 预报报道：“今天降水的概率是 90%”，那么大多数人出门都 会带雨具． 特别提示：概率是一种可能性，只是频率在理论上的一种 期望值．
误区解密 【例 3】 某种病治愈的概率是 0.3，有 10 个人来就诊，那 么前 7 个人没有治愈，后 3 个人一定能治愈吗？
错解：一定能治愈． 错因分析：如果把治疗一个病人作为一次试验，治愈的概 率是 30%，是指随着试验次数的增加，即随着治疗的病人人数 的增加，大约有 30%的人能够治愈，对于一次试验来说，其结 果是随机的，因此，前 7 个病人没有治愈是可能的，而对于后 3 个病人而言，其结果仍然是随机的，即有可能治愈，也有可能 不能治愈． 正解：可能治愈，也可能不治愈．
2．抛一枚硬币(质地均匀)，连续出现 5 次正面向上，有人 认为下次出现反面向上的概率大于12，这种理解正确吗？
【答案】不正确．因为抛 1 次硬币，其结果是随机的，但 通过做大量的试验，其结果呈现出一定的规律性，即“正面向 上”“反面向上”的可能性都为12.连续 5 次正面向上这种结果 是可能的，但对下一次试验来说，其结果仍然是随机的，所以 出现正面和反面的可能性还是12，不会大于12.

高中概率问题3。

1．随机事件的概率3。

1.1 随机事件的概率1、必然事件：一般地，把在条件S 下，一定会发生的事件叫做相对于条件S 的必然事件。

2、不可能事件：把在条件S 下，一定不会发生的事件叫做相对于条件S 的不可能事件。

3、确定事件：必然事件和不可能事件统称相对于条件S 的确定事件。

4、随机事件:在条件S 下可能发生也可能不发生的事件，叫相对于条件S 的随机事件。

5、频数：在相同条件S 下重复n 次试验，观察某一事件A 是否出现,称n 次试验中事件A 出现的次数n A 为事件A 出现的频数。

6、频率：事件A 出现的比例()=A n n A nf 。

7、概率:随机事件A 的概率是频率的稳定值，反之,频率是概率的近似值.3。

1。

2 概率的意义1、概率的正确解释：随机事件在一次试验中发生与否是随机的，但随机性中含有规律性.认识了这种随机中的规律性，可以比较准确地预测随机事件发生的可能性.2、游戏的公平性：抽签的公平性。

3、决策中的概率思想：从多个可选答案中挑选出正确答案的决策任务，那么“使得样本出现的可能性最大”可以作为决策的准则.-—极大似然法、小概率事件4、天气预报的概率解释：明天本地降水概率为70%解释是“明天本地下雨的机会是70%”.5、试验与发现:孟德尔的豌豆试验。

6、遗传机理中的统计规律.3。

1。

3 概率的基本性质1、事件的关系与运算（1）包含。

对于事件A 与事件B ，如果事件A 发生，则事件B 一定发生，称事件B 包含事件A （或事件A 包含于事件B)，记作(B A ⊇⊆或A B)。

不可能事件记作∅。

（2)相等。

若B A A B ⊇⊇且，则称事件A 与事件B 相等，记作A=B 。

（3）事件A 与事件B 的并事件(和事件）：某事件发生当且仅当事件A 发生或事件B 发生.（4）事件A 与事件B 的交事件（积事件）：某事件发生当且仅当事件A 发生且事件B 发生。

（5）事件A 与事件B 互斥：A B 为不可能事件,即=A B ∅，即事件A 与事件B 在任何一次试验中并不会同时发生。

A.猜“是奇数”或“是偶数” B.猜“是4的整数倍数”或“不是4的整数倍数” C.猜“是大于4的数”或“不是大于4的数” 请回答下列问题:
(1)如果你是乙,为了尽可能获胜,你将选择哪种猜数方 案,并且怎样猜?为什么? (2)为了保证游戏的公平性,你认为应制定哪种猜数方 案?为什么? (3)请你设计一种其他的猜数方案,并保证游戏的公平 性.
【思维·引】先分别求出A,B,C方案中事件发生的概率, 再根据概率值解决问题.
【解析】(1)如题图,方案A中“是奇数”或“是偶数” 的概率均为0.5;方案B中“不是4的整数倍数”的概率 为0.8,“是4的整数倍数”的概率为0.2; 方案C中“是大于4的数”的概率为0.6,“不是大于4的 数”的概率为0.4.乙为了尽可能获胜,应选方案B,猜 “不是4的整数倍数”.
2
(3)可以设计为:猜“是大于8的数”或“不是大于8的 数”,此方案也可以保证游戏的公平性(答案不唯一).
【类题·通】 根据游戏公平的定义,只要每个游戏的参与者获胜的概 率相同,就可以认定这个游戏是公平的,因此,解决此类 问题,关键是找出每个人获胜的概率,然后加以比较,进 行判断即可.
【习练·破】 甲、乙两人做游戏,下列游戏中不公平的是( ) A.抛掷一枚骰子,向上的点数为奇数则甲获胜,向上的 点数为偶数则乙获胜 B.同时抛掷两枚硬币,恰有一枚正面向上则甲获胜,两 枚都正面向上则乙获胜
n
第二次从保护区中捕出150只天鹅,其中有20只带有记 号,由概率的统计定义可知P(A)= 20②,
150
由①②两式,得 20=0 ,2解0 得n=1 500,
n 150
所以该自然保护区中天鹅的数量约为1 500只.
【类题·通】 (1)频率估计概率. 由于概率反映了随机事件发生的可能性的大小,概率是 频率的近似值与稳定值,所以可以用样本出现的频率近 似地估计总体中该结果出现的概率.

课本P117页T6.
一、教学目标： 1、知识与技能： （1）正确理解事件的包含、并事件、交事件、相等 事件，以及互斥事件、对立事件的概念； （2）概率的几个基本性质; （3）正确理解和事件与积事件,互斥事件与对立事件 的区别与联系. 2、过程与方法：通过事件的关系、运算与集合的关 系、运算进行类比学习，培养学生的类化与归纳的数 学思想。 3、情感态度与价值观：通过数学活动，了解教学与 实际生活的密切联系，感受数学知识应用于现实世界 的具体情境，从而激发学习 数学的情趣。 二、重点与难点： 概率的加法公式及其应用，事件的关系与运算。
尽管每次摸到黄球的概率为0.1,但摸10次 球,不一定能摸到黄球.
〖思考4〗如果某种彩票的中奖率为 么买1000张这种彩票一定能中奖吗?(假设该彩票 有足够多的张数.)请用概率的意义解释. 点评:不一定.因为每张彩票是否中奖是随 机的,1000张彩票有几张中奖也是随机的.这就 是说,每张彩票既可能中奖也可能不中奖,因此 1000张彩票中可能没有一张中奖,也可能有一 张、两张乃至多张中奖. 虽然中奖张数是随机的,但这种随机性中 具有规律性.即随着所买彩票张数的增加,其中 中奖彩票所占的比例可能越接近于1/1000.
√
(2)明天本地下雨的机会是70%.
例:生活中，我们经常听到这样的议论： “天气预报说昨天降水概率为90%，结果根本 一点雨都没下，天气预报也太不准确了。”学 了概率后，你能给出解释吗？ 解：天气预报的“降水”是一个随机事 件，概率为90%指明了“降水”这个随机事 件发生的概率，我们知道：在一次试验中， 概率为90%的事件也可能不出现，因此， “昨天没有下雨”并不说明“昨天的降水概 率为90%”的天气预报是错误的。
举例, 如： • （1）当x是实数时，x2≥0; • （2）天上掉馅饼； • （3）某人随意按了一个号码，刚好是朋友的 电话号码。

概率名词解释概率是指事件发生的可能性或出现的比例。

它可以用数值来表示，范围从0到1，其中0表示事件不可能发生，1表示事件一定会发生。

概率越接近0，事件发生的可能性越小；概率越接近1，事件发生的可能性越大。

概率的计算方法包括经典概率、相对频率概率和主观概率。

经典概率是通过分析事件的可能性和可能的结果来计算概率。

例如，一枚均匀的硬币掷出上表面的概率为1/2，下表面的概率也为1/2。

这是因为硬币只有两个可能的结果：正面或反面，且每种结果出现的可能性相等。

相对频率概率是通过观察事件在一系列重复试验中发生的频率来估计概率。

例如，如果一枚硬币投掷100次，正面出现了60次，那么正面出现的概率估计为60/100=0.6。

相对频率概率趋向于真实概率，当试验次数增加时，其与真实概率越趋近。

主观概率是个人主观判断的概率。

它基于个人的经验、信念或观察来估计概率。

主观概率是一种主观意见，可能会因人而异。

例如，如果一个人觉得明天下雨的可能性很高，他可能会估计下雨的概率为0.8。

除了这些基本的概率概念，还有一些重要的相关术语需要了解。

事件是指可能发生的事情，可以是一个具体的结果，也可以是一组结果的集合。

事件通常用大写字母表示，例如A、B、C 等。

样本空间是指所有可能结果的集合。

它通常用大写字母Ω表示。

例如，对于一枚硬币，样本空间为{正面，反面}。

事件的概率可以通过以下公式来计算：P(A) = |A|/|Ω|，其中P(A)表示事件A的概率，|A|表示事件A发生的结果数，|Ω|表示样本空间中可能结果的总数。

概率在各个领域都有广泛应用，在统计学、金融学、生物学、工程等领域中起着重要的作用。

它可以用于预测事件的发生概率、制定决策和评估风险等。

概率理论还与统计学紧密相关，统计学通过收集和分析数据来推断未知的概率。

一些现象是否合理。
（2）概率与决策的关系： 在“风险与决策”中经常会用到统计中的极大似然法：
在一次实验中，概率大的事件发生的可能性大。
（3）概率与预报的关系： 在对各种自然现象、灾害的研究过程中经常会用到概
率的思想来实行预测。
一、选择题（每题5分，共15分） 1.概率是1‰说明了( ) （A）概率太小不可能发生 （B）1 000次中一定发生1次 （C）1 000人中，999人说不发生，1人说发生 （D）1 000次中有可能发生1 000次 【解析】选D.概率是1‰说明发生的可能性是1‰，每次发生都 是随机的，1 000次中也可能发生1 000次，仅仅发生的可能 性很小.
红球会是99个
概率的意义
4.天气预报的概率解释
若某地气象局预报说，明天本地降水概率为70%， 你认为下面两个解释哪一个能代表气象局的观点？ （1）明天本地有70%的区域下雨，30%的区域不下雨； （2）明天本地有70%的机会下雨。
答案：第（２）种
2.概率在实际问题中的应用：
（1）概率与公平性的关系： 利用概率解释游戏规则的公平性，判断实际生活中的
的含义；C错的原因10是忽略了整体与部分的区别.
2
2.(5分)篮球运动员姚明罚球投中的概率是0.86，那么在2011 年的比赛中，若姚明有机会投100个球，______（填“可能”、 “不可能”或“一定”）有86个球投中. 【解析】既然姚明投篮命中的概率是0.86，则说明他投球命中 是随机事件，故投球100次，可能命中86次，也可能更多或更 少. 答案：可能
1.概率的正确理解
取一枚硬币，连续两次抛掷，观察它落地后的朝 向，并记录结果. 重复上面的过程10次.将全班同学的
试验结果汇总，计算三种结果发生频率，看看有什么发现？

新人教版初中数学中考总复习重难点突破知识点梳理及重点题型巩固练习中考总复习：统计与概率—知识讲解【考纲要求】1.能根据具体的实际问题或者提供的资料，运用统计的思想收集、整理和处理一些数据，并从中发现有价值的信息，在中考中多以图表阅读题的形式出现；2.了解总体、个体、样本、平均数、加权平均数、中位数、众数、极差、方差、频数、频率等概念，并能进行有效的解答或计算；3.能够对扇形统计图、列频数分布表、画频数分布直方图和频数折线图等几种统计图表进行具体运用，并会根据实际情况对统计图表进行取舍；4.在具体情境中了解概率的意义；能够运用列举法（包括列表、画树状图）求简单事件发生的概率．能够准确区分确定事件与不确定事件；5.加强统计与概率的联系，这方面的题型以综合题为主，将逐渐成为新课标下中考的热点问题．【知识网络】「I 统计图表——।阅读图表提取信息T 集中程度I 怦均数中位教嬴【考点梳理】考点一、数据的收集及整理1 .一般步骤：调查收集数据的过程一般有下列六步：明确调查问题、确定调查对象、选择调查方法、展 开调查、记录结果、得出结论.2 .调查收集数据的方法:普查与抽样调查. 要点诠释：(1)通过调查总体的方式来收集数据的，抽样调查是通过调查样本方式来收集数据的.(2)一般地，当总体中个体数目较多，普查的工作量较大；受客观条件的限制，无法对所有个体进行 普查；或调查具有破坏性时，不允许普查，这时我们往往会用抽样调查来体现估计总体的思想 (3)用抽签的办法决定哪些个体进入样本.统计学家们称这种理想的抽样方法为简单的随机抽样 3 .数据的统计:条形统计图、折线统计图、扇形统计图是三种最常用的统计图. 要点诠释：这三种统计图各具特点：条形统计图可以直观地反映出数据的数量特征；折线统计图可以直观地反映出数据的数量变化规律；扇形统计图可以直观地反映出各部分数量在总量中所占的份额.收集数据媒体查询抽样调查-抽样的基本要求总体个体样本T 整理数据借助统计活动研究概率从概 率角度分析善数据特征离散程度限差方差标准差实验估计概必然事不可能事游戏的 公平与模拟等效实考点二.数据的分析 1 .基本概念：总体：把所要考查的对象的全体叫做总体； 个体：把组成总体的每一个考查对象叫做个体；样本：从总体中取出的一部分个体叫做总体的一个样本； 样本容量：样本中包含的个体的个数叫做样本容量；频数：在记录实验数据时，每个对象出现的次数称为频数；频率：每个对象出现的次数与总次数的比值（或者百分比）称为频率；平均数：在一组数据中，用数据的总和除以数据的总个数就得到这组数据的平均数；中位数：将一组数据从小到大依次排列，位于正中间位置的数（或正中间两个数据的平均数）叫做这组 数据的中位数；众数：在一组数据中，出现频数最多的数叫做这组数据的众数； 极差：一组数据中的最大值减去最小值所得的差称为极差；方差：我们可以用“先平均，再求差，然后平方，最后再平均”得到的结果表示一组数据偏离平均值的 情况，这个结果通常称为方差.计算方差的公式：设一组数据是/,无是这组数据的平均数。

初中概率知识点总结
1. 事件与概率
- 事件是指某个结果的集合，概率是指这个事件发生的可能性。

- 概率的取值范围是0到1，0代表不可能事件，1代表必然事件。

2. 等可能事件
- 对于等可能事件，每个事件发生的可能性是一样的。

- 等可能事件的概率可以通过计算事件发生的次数与样本空间
中的总数的比值得到。

3. 互斥事件
- 互斥事件是指两个事件不能同时发生的情况。

- 互斥事件的概率可以通过将两个事件发生的概率相加得到。

4. 独立事件
- 独立事件是指一个事件的发生不受其他事件发生与否的影响。

- 独立事件的概率可以通过将各个事件发生的概率相乘得到。

5. 抽样与统计调查
- 在抽样调查中，通过对部分样本进行观察和研究，以得出总体特征或规律。

- 抽样调查中的概率抽样是指每个样本被选中的概率相等。

6. 相关事件
- 相关事件是指两个事件发生与否存在某种关联性。

- 相关事件的概率可以通过根据给定的条件来计算。

7. 条件概率
- 条件概率是指在给定另一事件已经发生的条件下，某一事件发生的概率。

- 条件概率的计算可以利用总体样本中的频率或者基于互斥事件和相关事件的概率来推导。

8. 概率分布
- 概率分布是指对某个随机事件的可能结果及其概率进行表示和总结的方式。

- 常见的概率分布包括二项分布、正态分布等。

以上是初中概率知识的简要总结。

概率知识在日常生活中有着广泛的应用，对于进一步学习数学以及理解世界中的不确定性具有重要意义。