指数函数练习题及答案

课时 4 指数函数一 . 指数与指数幂的运算（ 1）根式的观点①假如xna, a R, x R, n 1，且 nN ，那么 x 叫做 a 的 n 次方根． 当 n 是奇数时， a 的 n 次方根用符号 na 表示；当 n 是偶数时，正数 a 的正的 n 次方根用符号na 表示，负的 n 次方根用符号na表示； 0 的 n 次方根是 0；负数 a 没有 n 次方根．②式子 n a 叫做根式，这里 n 叫做根指数， a 叫做被开方数．当n 为奇数时， a 为随意实数；当 n 为偶数时， a．③根式的性质： (na )n a ；当 n 为奇数时， n a n a ；当 n 为偶数时， n a n | a |a (a 0) ．a (a 0)（ 2）分数指数幂的观点mna m (a①正数的正分数指数幂的意义是：a n 0, m,n N , 且 n 1) ．0 的正分数指数幂等于0．②m(1m1 ) m( a正数的负分数指数幂的意义是：a n)n n (0, m, n N , 且 n1) ．0 的负分数指aa数幂没存心义． 注意口诀： 底数取倒数，指数取相反数．（ 3）分数指数幂的运算性质①a r a s a r s (a 0, r , s R)② (ar) sa rs (a 0, r , s R)③(ab)ra rb r (a0,b 0, rR)二 . 指数函数及其性质（ 4）指数函数函数名称指数函数定义函数 ya x (a 0 且 a1) 叫做指数函数a 1a 1yy a xya xy图象y1y1(0,1)(0,1)OxOx定义域 R值域（0,+ ∞）过定点 图象过定点（0,1 ），即当 x=0 时， y=1．奇偶性非奇非偶单一性在 R 上是增函数在 R 上是减函数函数值的 y ＞ 1(x ＞ 0), y=1(x=0), 0＜ y ＜ 1(x ＜ 0)y ＞ 1(x ＜ 0), y=1(x=0), 0＜ y ＜ 1(x ＞ 0)变化状况a 变化对在第一象限内， a 越大图象越高，越凑近 y 轴； 在第一象限内， a 越小图象越高，越凑近 y 轴； 图象影响在第二象限内，a 越大图象越低，越凑近x 轴．在第二象限内，a 越小图象越低，越凑近x 轴．三 .例题剖析1.设 a 、 b 知足 0<a<b<1,以下不等式中正确的选项是 ( C)A.a a <a bB.b a <b bC.a a <b aD.b b <a b 分析： A 、B 不切合底数在 (0,1) 之间的单一性 ; C 、 D 指数同样 , 底小值小 . 应选 C. 2.若 0<a<1,则函数 y=a x 与 y=(a-1)x 2 的图象可能是 (D )分析： 当 0<a<1 时 ,y=a x 为减函数 ,a-1<0, 因此 y=(a-1)x2张口向下 , 应选 D.3.设指数函数 f(x)=a x (a>0 且 a ≠ 1),则以下等式中不正确的选项是 ( D )A.f(x+y)=f(x)f(y)f (x)B.f(x-y)=f ( y)C.f(nx)= ［ f(x) ］ nD.f ［ (xy) n ］ =［ f(x) ］ n ［ f(y) ］ n (n ∈ N * )分析： 易知 A 、 B 、 C 都正确 .对于 D,f ［(xy)n］ =a (xy)n , 而［ f(x) ］ n ·［f(y) ］ n =(a x ) n ·(a y ) n =a nx+ny , 一般状况下 D 不建立 .11 34.设 a= ( 3) 3,b= ( 4)4,c= ( 3) 4,则 a 、b 、 c 的大小关系是 ( B )43 2A.c<a<b3分析： a= ( )B.c<b<aC.b<a<cD.b<c<a1 111(8133( 4)3 ( 4) 4=b, b=(4) 4)4(3) 4 =c.∴ a>b>c.3 332725.设 f(x)=4 x -2x+1,则 f -1 (0)=______1____________. 分析： 令 f -1 (0)=a, 则 f(a)=0 即有 4a -2 · 2a =0.2a · (2 a -2)=0, 而 2a >0,∴ 2a =2 得 a=1.6.函数 y=a x-3 +4(a>0 且 a ≠ 1)的反函数的图象恒过定点 ______(5,3)____________.分析： 因 y=a x 的图象恒过定点 (0,1), 向右平移 3 个单位 , 向上平移 4 个单位获得 y=a x-3 +4 的图象 , 易知恒过定点 (3,5).故其反函数过定点 (5,3).10 x 10 x.证明 f(x) 在 R 上是增函数 .7.已知函数 f(x)=x10 x10x1010x102x1,设 x 1<x 2∈ R,则f(x 1)-f(x2)=10x 1 1010x 1 10x 110x 210 x 2102 x 11 102 x 21 2(102 x 1102 x2).x 110x2 10x2 102 x1 1102 x21(102 x11)(102 x 2 1)∵ y=10 x是增函数 ,∴ 10 2x 1 10 2x 2 <0.而 10 2x 1 +1>0, 102 x 2 +1>0,故当 x <x 时 ,f(x)-f(x )<0,1212即 f(x 1)<f(x 2). 因此 f(x) 是增函数 .8.若定义运算 a b=b, ab,则函数 f(x)=3 x3-x 的值域为 ( A )a, a b,A.(0,1]B. ［ 1,+∞ )C.(0,+ ∞ )D.(- ∞ ,+∞ )分析： 当 3x ≥3-x , 即 x ≥ 0 时 ,f(x)=3-x∈(0,1 ］ ;x-x, 即 x<0 时 ,f(x)=3x∈ (0,1).3 x , x 0, 当 3<3∴ f(x)=x值域为 (0,1).3x ,0,9.函数 y=a x 与 y=-a -x (a>0,a ≠1) 的图象 ( C )A. 对于 x 轴对称B.对于 y 轴对称C.对于原点对称D.对于直线 y=-x 对称分析： 可利用函数图象的对称性来判断两图象的关系.10.当 x ∈［ -1,1］时 ,函数 f(x)=3 x-2 的值域为 _______［ -5,1 ］ ___________.3分析： f(x) 在［ -1,1 ］上单一递加 .11.设有两个命题 :(1)对于 x 的不等式 x 2+2ax+4>0对全部 x ∈ R 恒建立 ;(2) 函数 f(x)=-(5-2a) x是减函数 .若命题 (1)和 (2)中有且仅有一个是真命题 ,则实数 a 的取值范围是 _______(- ∞ ,-2)__________.分析： (1) 为真命题=(2a) 2-16<0-2<a<2. (2)为真命题 5-2a>1 a<2.若 (1) 假 (2) 真 , 则 a ∈ (- ∞ ,-2]. 若 (1) 真 (2) 假, 则 a ∈ (-2,2)∩［ 2,+ ∞］=.故 a 的取值范围为 (- ∞ ,-2).12.求函数 y=4 -x -2-x +1,x ∈［ -3,2］的最大值和最小值 .解： 设 2-x=t, 由 x ∈［ -3,2 ］得 t ∈［ 1,8 ］ , 于是 y=t 2-t+1=(t-1)2+3. 当 t= 1时 ,y3 .424有最小值 这时 x=1.当 t=8 时 ,y 有最大值57.这时 x=-3.2413.已知对于 x 的方程 2a2x-2-7a x-1 +3=0 有一个根是 2,求 a 的值和方程其他的根 . 解： ∵ 2 是方程 2a2x-2-9a x-1+4=0 的根 , 将 x=2 代入方程解得 a= 1或 a=4.2(1) 当 a= 1时 , 原方程化为 2· ( 1)2x-2-9(1) x-1 +4=0.①222x-1 2令 y=( 1) , 方程①变成 2y -9y+4=0,2解得 y 1=4,y 2= 1.∴ ( 1) x-1 =42x=-1,2( 1 ) x-1 = 1x=2.22(2) 当 a=4 时 , 原方程化为 2· 42x-2 -9 · 4x-1 +4=0. ②令 t=4 x-1 , 则方程②变成 2t 2-9t+4=0. 解得 t 1=4,t 2= 1.x-12=4x=2,∴44x-1 = 1x=- 1 .22故方程此外两根是当 a= 1时 ,x=-1;1 .2当 a=4 时 ,x=-214.函数 y= (1) 3 4xx 2的单一递加区间是 ( D )3A. ［ 1,2］B.［ 2,3］C.(-∞ ,2]D.［ 2,+∞ )分析： 由于 y=3x2-4x+3 , 又 y=3t 单一递加 ,t=x 2-4x+3 在 x ∈［ 2,+ ∞ ) 上递加 , 故所求的递加区间为［ 2,+ ∞ ).15.已知 f(x)=3 x-b (2≤ x ≤ 4,b 为常数 ) 的图象经过点 (2,1), 则 F(x)=f 2(x)-2f(x) 的值域为 ( B )A. ［ -1,+∞ )B. ［ -1,63)C.［ 0,+∞ )D.(0,63 ］分析： 由 f(2)=1, 得 32-b =1,b=2,f(x)=3 x-2.∴ F (x)= ［ f(x)-1 ］2-1=(3 x-2 -1) 2-1. 令 t=3 x-2 ,2 ≤x ≤4.2∴g(t)=(t-1) - 1,t ∈［ 1,9 ］.2.1 指数函数练习1．以下各式中建立的一项A ． ( n)71n 7 m 7B ．12 ( 3)433m3C ． 4 x 3y 3( x y) 4D ．393321111 1 52．化简 (a 3 b 2 )( 3a 2 b 3 ) ( a 6 b 6 ) 的结果3D ． 9a 2 A ． 6aB ． aC ． 9a3．设指数函数 f ( x)a x ( a 0, a1) ，则以下等式中不正确的选项是f (x) A ． f(x+y)=f(x) ·f(y)B ． f （ x y ）f ( y)C ． f (nx)[ f ( x)]n (nQ )D ． f ( xy) n [ f ( x)] n ·[f ( y)] n1 4．函数 y (x5) 0 ( x 2)2A ． { x | x 5, x 2}B ． { x | x 2}C ． { x | x 5}D ． { x | 2 x 5或 x 5}（）（）（）(n N )（ ）5．若指数函数 y a x 在 [－ 1,1]上的最大值与最小值的差是1，则底数 a 等于 （）A ．15 B ．1 5 C ．15D ．5 122 226．当 a0 时，函数 y axb 和 yb ax 的图象只可能是（）7．函数 f ( x)2 |x| 的值域是（）A ． (0,1]B ． (0,1)C ． (0, )D ． R8．函数 f ( x)2 x 1, x 0，知足 f ( x)1的 x 的取值范围1x 2 , x（）A ． ( 1,1)B ． ( 1, )C ． { x | x 0或 x2}D ． { x | x 1或 x1}9．函数 y(1) x 2x2得单一递加区间是2（）A ．[ 1,1]B ． ( , 1]C ．[2,)D ．[ 1,2]2exe x210．已知 f ( x)（）2 ，则以下正确的选项是A ．奇函数，在 R 上为增函数B ．偶函数，在 R 上为增函数C ．奇函数，在 R 上为减函数D ．偶函数，在 R 上为减函数11．已知函数 f (x)的定义域是（1， 2），则函数 f (2 x ) 的定义域是.12．当 a ＞0 且 a ≠1 时，函数 f (x)=a x －2－ 3 必过定点.三、解答题：13．求函数 y1的定义域 .x5 x 1114．若 a ＞0， b ＞ 0，且 a+b=c ，求证： (1) 当r ＞1时， a r +b r ＜ c r ； (2) 当r ＜ 1时， a r +b r ＞ c r .a x 1 15．已知函数 f ( x)(a ＞1) .a x1（ 1）判断函数 f (x) 的奇偶性；（ 2）证明 f (x)在 (－∞， +∞ )上是增函数 .xa16．函数 f(x) ＝ a (a>0 ，且 a ≠1) 在区间 [1,2] 上的最大值比最小值大2，求 a 的值．参照答案一、 DCDDD AADDA二、 11． (0,1)；12． (2，－ 2) ；三、 13． 解：要使函数存心义一定：x 1 0x 1x0 x 0x 1∴ 定义域为 ： x xR 且 x0, x 1a rrrb r此中a1,0b114． 解：ba，c rcccc.r ＞1 ，a rb ra b 1，r r r当因此+b＜ c ；时c c c crrrrr当 r ＜ 1 时， aba b1， 因此 a +b ＞c .ccc c15． 解 ：(1)是奇函数 .(2) 设x ＜x ，则 f (x 1 )ax11 ax21 。

指数函数1．指数函数的定义：函数)1(≠>=aaay x且叫做指数函数，其中x是自变量，函数定义域是R 2.指数函数的图象和性质：在同一坐标系中分别作出函数y=x2，y=x⎪⎭⎫⎝⎛21，y=x10，y=x⎪⎭⎫⎝⎛101的图象.我们观察y=x2，y=x⎪⎭⎫⎝⎛21，y=x10，y=x⎪⎭⎫⎝⎛101图象特征，就可以得到)1(≠>=aaay x且的图象和性质。

a>1 0<a<1图象00性质(1)定义域：R（2）值域：（0，+∞）（3）过点（0，1），即x=0时，y=1（4）在 R上是增函数（4）在R上是减函数指数函数是高中数学中的一个基本初等函数，有关指数函数的图象与性质的题目类型较多，同时也是学习后续数学内容的基础和高考考查的重点，本文对此部分题目类型作了初步总结，与大家共同探讨．1．比较大小例1已知函数2()f x x bx c=-+满足(1)(1)f x f x+=-，且(0)3f=，则()xf b与()x f c 的大小关系是_____．分析：先求b c ，的值再比较大小，要注意x x b c ，的取值是否在同一单调区间内．解：∵(1)(1)f x f x +=-，∴函数()f x 的对称轴是1x =．故2b =，又(0)3f =，∴3c =．∴函数()f x 在(]1-，∞上递减，在[)1+，∞上递增． 若0x ≥，则321x x ≥≥，∴(3)(2)x x f f ≥；若0x <，则321x x <<，∴(3)(2)x x f f >．综上可得(3)(2)x x f f ≥，即()()x x f c f b ≥．评注：①比较大小的常用方法有：作差法、作商法、利用函数的单调性或中间量等．②对于含有参数的大小比较问题，有时需要对参数进行讨论．2．求解有关指数不等式例2 已知2321(25)(25)x x a a a a -++>++，则x 的取值范围是___________． 分析：利用指数函数的单调性求解，注意底数的取值范围．解：∵2225(1)441a a a ++=++>≥，∴函数2(25)x y a a =++在()-+，∞∞上是增函数，∴31x x >-，解得14x >．∴x 的取值范围是14⎛⎫+ ⎪⎝⎭，∞． 评注：利用指数函数的单调性解不等式，需将不等式两边都凑成底数相同的指数式，并判断底数与1的大小，对于含有参数的要注意对参数进行讨论．3．求定义域及值域问题例3 求函数y =的定义域和值域．解：由题意可得2160x --≥，即261x -≤，∴20x -≤，故2x ≤． ∴函数()f x 的定义域是(]2-，∞．令26x t -=，则y =，又∵2x ≤，∴20x -≤． ∴2061x -<≤，即01t <≤．∴011t -<≤，即01y <≤．∴函数的值域是[)01，． 评注：利用指数函数的单调性求值域时，要注意定义域对它的影响．4．最值问题例4 函数221(01)x x y a a a a =+->≠且在区间[11]-，上有最大值14，则a 的值是_______．分析：令x t a =可将问题转化成二次函数的最值问题，需注意换元后t 的取值范围．解：令x t a =，则0t >，函数221x x y a a =+-可化为2(1)2y t =+-，其对称轴为1t =-．∴当1a >时，∵[]11x ∈-，，∴1x a a a ≤≤，即1t a a≤≤．∴当t a =时，2max (1)214y a =+-=．解得3a =或5a =-（舍去）；当01a <<时，∵[]11x ∈-，， ∴1x a a a ≤≤，即1a t a≤≤，∴ 1t a =时，2max 11214y a ⎛⎫=+-= ⎪⎝⎭， 解得13a =或15a =-（舍去），∴a 的值是3或13．评注：利用指数函数的单调性求最值时注意一些方法的运用，比如：换元法，整体代入等．5．解指数方程例5 解方程223380x x +--=．解：原方程可化为29(3)80390x x ⨯-⨯-=，令3(0)x t t =>，上述方程可化为298090t t --=，解得9t =或19t =-（舍去），∴39x =，∴2x =，经检验原方程的解是2x =．评注：解指数方程通常是通过换元转化成二次方程求解，要注意验根．6．图象变换及应用问题例6 为了得到函数935x y =⨯+的图象，可以把函数3x y =的图象（ ）．A ．向左平移9个单位长度，再向上平移5个单位长度B ．向右平移9个单位长度，再向下平移5个单位长度C ．向左平移2个单位长度，再向上平移5个单位长度2，曲线分别是指数函数 , 和 的图象,则与1的大小关系是 ( ).( 分析:首先可以根据指数函数单调性,确定,在 轴右侧令 ,对应的函数值由小到大依次为 ,故应选 .小结:这种类型题目是比较典型的数形结合的题目,第(1)题是由数到形的转化,第(2)题则是由图到数的翻译,它的主要目的是提高学生识图,用图的意识.求最值3，求下列函数的定义域与值域.(1)y ＝231-x ; (2)y ＝4x +2x+1+1.解：(1)∵x-3≠0，∴y ＝231-x 的定义域为｛x ｜x ∈R 且x ≠3｝.又∵31-x ≠0，∴231-x ≠1，∴y ＝231-x 的值域为｛y ｜y>0且y ≠1｝.(2)y ＝4x +2x+1+1的定义域为R.∵2x >0,∴y ＝4x +2x+1+1＝(2x )2+2·2x +1＝(2x +1)2>1.∴y ＝4x +2x+1+1的值域为｛y ｜y>1｝.4，已知-1≤x ≤2,求函数f(x)=3+2·3x+1-9x 的最大值和最小值解：设t=3x ,因为-1≤x ≤2，所以931≤≤t ，且f(x)=g(t)=-(t-3)2+12,故当t=3即x=1时，f(x)取最大值12，当t=9即x=2时f(x)取最小值-24。

指数函数习题及答案一．选择题1．若函数f （x ）＝()xa 1-在R 上是减函数，那么实数a 的取值范围是（ ）A ．a ＞1 且1≠aB ．１＜a ＜2C ．a ＞１且2≠aD ．a ＞０2．已知0>a ，41=--a a ，则22-+a a 的值是（ ）A ．14B ．16C ．18D ．203．一套邮票现价值a 元，每过一年都将增值00b ，则10年后其价值为（ ） A ．()00110b a + B ．()00101b a +C ．()[]10001b a + D ．()1001ba +4．设f （x ）＝x)21(，x ∈R ，那么f （x ）是（ ） A ．偶函数且在（0，＋∞）上是减函数B ．偶函数且在（0，＋∞）上是增函数C ．奇函数且在（0，＋∞）上是减函数D ．奇函数且在（0，＋∞）上是增函数 5．函数y ＝－2－x的图象一定过哪些象限（ ）A ．一、二象限B ．二、三象限C ．三、四象限D ．一、四象限 6．函数y ＝a x 在［0，1］上的最大值与最小值和为3，则函数y ＝123-⋅x a 在［0，1］上的最大值是（ ）A ．3B ．1C ．6D ．23 7．下列函数中值域为（０，＋∞）的是（ ） A ．y ＝x15B ．y ＝x )31( C ．y ＝12+-xD ．y ＝12-x8．若－1＜x ＜0，则不等式中成立的是（ ）A ．5－x ＜5x ＜0.5x B ．0.5x ＜5－x ＜5x C ．5x ＜5－x ＜0.5xD ．5x ＜0.5x ＜5－x9．当a ≠0时，函数y a x b=+和y b ax=的图象只可能是（ ）10．设指数函数)1,0()(≠>=a a a x f x，则下列等式中不正确的是（ ）A ．)()()(y f x f y x f ⋅=+B ．)()(y f x f y x f =-）（ C ．)()]([)(Q n x f nx f n∈= D ．)()]([·)]([)(+∈=N n y f x f xy f nnn二．填空题11．已知函数f （x ）＝21)31(x -，其定义域是________________．12．函数f （x ）＝a x －1＋3的图象一定过定点P ，则P 点的坐标是____________．13．函数121+⎪⎭⎫⎝⎛=x y ，[]1,2-∈x 的值域是_____________．14．函数y ＝x-3的图象与函数________________的图象关于y 轴对称． 三．解答题（共6小题，共80分） 15．（本小题12分）(1)计算：3122726141-⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛- (2)化简：2433221---÷⎪⎪⎭⎫ ⎝⎛⋅a b b a16．（12分）(1) 解不等式145-+<x x a a（a>0且a ≠1）(2)函数⎪⎩⎪⎨⎧>≤-=-0,0,12)(21x x x x f x ，求满足1)(>x f 的x 的取值范围17．(14分) 求函数2233x x y -++=的单调区间和最值(单调区间请加以证明).18．（1）已知m x f x +-=132)(是奇函数，求常数m 的值； （2）画出函数|13|-=xy 的图象，并利用图象回答：k 为何值时，方程k x=-|13|无解？有一解？有两解？19．(14分)已知函数4()42xx f x =+ （1）试求()(1)f a f a +-的值.（2）求1232007()()()()2008200820082008f f f f +++⋅⋅⋅+的值. 20．（14分）已知函数11)(+-=x x a a x f (a ＞1).（1）判断函数f (x )的奇偶性； （2）求f (x )的值域；（3）证明f (x )在(－∞，+∞)上是增函数.＜指数函数＞参考答案1—10 BCDAC CBDAD9．［－1，1］ 10．(1，4) 11．27 12．［41，2］ 13．x y 3= 14．1415．1>a 时，x>2；10<<a 时，x<2． 16．1-a17．解：单调增区间：(,1]-∞；单调减区间：[1,)+∞；值域：(,81]-∞。

[基础巩固]1．下列判断正确的是( )A ．2.52.5>2.53B ．0.82<0.83C ．π2<π 2D ．0.90.3>0.90.5解析 因为函数y ＝0.9x 在R 上为减函数，所以0.90.3>0.90.5.答案 D2．设函数f (x )＝a －|x |(a >0，且a ≠1)，若f (2)＝4，则( )A ．f (－2)>f (－1)B ．f (－1)>f (－2)C ．f (1)>f (2)D ．f (－2)>f (2) 解析 f (2)＝a －2＝4，a ＝12，f (x )＝⎝⎛⎭⎫12－|x |＝2|x |，则f (－2)>f (－1)． 答案 A3．(多选)以下关于数的大小的结论正确的是( )3．(多选)以下关于数的大小的结论正确的是( )A ．1.72.5＜1.73B ．0.8－0.1＜0.8－0.2C ．1.70.3＜0.93.1D ．⎝⎛⎭⎫13 13 ＞⎝⎛⎭⎫14 14解析 y ＝1.7x 单调递增，2.5＜3，∴1.72.5＜1.73，A 正确；y ＝0.8x 单调递减，－0.1＞－0.2，∴0.8－0.1＜0.8－0.2，B 正确；又1.70.3＞1.70＝1，0.93.1＜0.90＝1，∴1.70.3＞0.93.1，C 错误；⎣⎡⎦⎤⎝⎛⎭⎫1313 12 ＝⎝⎛⎭⎫13 4 ＝181 ， ⎣⎡⎦⎤⎝⎛⎭⎫1414 12 ＝⎝⎛⎭⎫14 3＝164 ， ∵181 ＜164，∴⎝⎛⎭⎫13 13 ＜⎝⎛⎭⎫14 14 ，D 错误． 答案 AB4．已知(a 2＋a ＋2)x >(a 2＋a ＋2)1－x ，则x 的取值范围是________．解析 ∵a 2＋a ＋2＝⎝⎛⎭⎫a ＋122＋74>1， ∴y ＝(a 2＋a ＋2)x 为R 上的增函数．∴x >1－x .即x >12. 答案 ⎝⎛⎭⎫12，＋∞ 5．已知2x ≤⎝⎛⎭⎫14x －3，则函数y ＝⎝⎛⎭⎫12x 的值域为 ________________ .解析 由2x ≤⎝⎛⎭⎫14x －3，得2x ≤2－2x ＋6， ∴x ≤－2x ＋6，∴x ≤2.∴⎝⎛⎭⎫12x ≥⎝⎛⎭⎫122＝14，即y ＝⎝⎛⎭⎫12x 的值域为⎣⎡⎭⎫14，＋∞. 答案 ⎣⎡⎭⎫14，＋∞6．已知函数.(1)若a ＝－1，求函数f (x )的单调增区间．(2)如果函数f (x )有最大值3，求实数a 的值．解析 (1)当a ＝－1时，令g (x )＝－x 2－4x ＋3＝－(x ＋2)2＋7，由于g (x )在(－2，＋∞)上递减，y ＝⎝⎛⎭⎫13x 在R 上是减函数，所以f (x )在(－2，＋∞)上是增函数，即f (x )的单调增区间是(－2，＋∞)．(2)令h (x )＝ax 2－4x ＋3，f (x )＝⎝⎛⎭⎫13h (x )，由于f (x )有最大值3，所以h (x )应有最小值－1；因此必有⎩⎪⎨⎪⎧a >0，12a －164a＝－1，解得a ＝1，即当f (x )有最大值3时，a 的值为1. [能力提升]7．已知函数f (x )＝3x －⎝⎛⎭⎫13x ，则f (x )( )A ．是奇函数，且在R 上是增函数B ．是偶函数，且在R 上是增函数C ．是奇函数，且在R 上是减函数D ．是偶函数，且在R 上是减函数解析 因为f (x )＝3x －⎝⎛⎭⎫13x ，且定义域为R ，所以f (－x )＝3－x －⎝⎛⎭⎫13－x ＝⎝⎛⎭⎫13x －3x ＝－⎣⎡⎦⎤3x －⎝⎛⎭⎫13x ＝－f (x )，即函数f (x )是奇函数． 又y ＝3x 在R 上是增函数，y ＝⎝⎛⎭⎫13x 在R 上是减函数，所以f (x )＝3x －⎝⎛⎭⎫13x 在R 上是增函数．答案 A8．若函数的值域是⎝⎛⎦⎤0，19，则f (x )的单调递增区间是________． 解析 令g (x )＝ax 2＋2x ＋3，由于f (x )的值域是⎝⎛⎦⎤0，19， 所以g (x )的值域是[2，＋∞)．因此有⎩⎪⎨⎪⎧a ＞0，12a －44a ＝2，解得a ＝1， 这时g (x )＝x 2＋2x ＋3，由于g (x )的单调递减区间是(－∞，－1]，所以f (x )的单调递增区间是(－∞，－1]．答案 (－∞，－1]9．已知函数，则f (x )的单调递增区间为________，值域为________．解析 令x 2－2x ≥0，解得x ≥2或x ≤0，∴f (x )的定义域为(－∞，0]∪[2，＋∞)，令t ＝x 2－2x －1，则其在(－∞，0]上递减，在[2，＋∞)上递增，又y ＝⎝⎛⎭⎫12t 为减函数，故f (x )的增区间为(－∞，0]．∵t ＝x 2－2x －1≥－1，∴⎝⎛⎭⎫12t ∈(0,2]．故f (x )的值域为(0,2]．答案 (－∞，0] (0,2]10．已知函数f (x )＝a －12x ＋1(x ∈R )． (1)用定义证明：不论a 为何实数，f (x )在(－∞，＋∞)上总为增函数．(2)若f (x )为奇函数，求a 的值．(3)在(2)的条件下，求f (x )在区间[1,5]上的最小值．解析 (1)因为f (x )的定义域为R ，任取x 1<x 2，所以f (x 1)－f (x 2)<0，即f (x 1)<f (x 2)．所以不论a 为何实数，f (x )在(－∞，＋∞)上总为增函数． (2)因为f (x )在R 上为奇函数，所以f (0)＝0，即a －120＋1＝0，解得a ＝12. 经检验，a ＝12时，f (x )＝12－12x ＋1是奇函数． (3)由(2)知，f (x )＝12－12x ＋1， 由(1)知，f (x )在(－∞，＋∞)上为增函数， 所以f (x )在区间[1,5]上的最小值为f (1)．因为f (1)＝12－13＝16， 所以f (x )在区间[1,5]上的最小值为16. [探索创新]11．已知函数f (x )＝a x (a ＞0且a ≠1)在[－1,1]上的最大值与最小值之差为32. (1)求实数a 的值；(2)若g (x )＝f (x )－f (－x )，当a ＞1时，解不等式g (x 2＋2x )＋g (x －4)＞0.解析 (1)当a ＞1时，f (x )max ＝a ，f (x )min ＝1a， 则a －1a ＝32，解得a ＝2， 当0＜a ＜1时，f (x )max ＝1a，f (x )min ＝a ， 则1a －a ＝32，解得a ＝12. 综上得：a ＝2或a ＝12. (2)当a ＞1时，由(1)知a ＝2，g (x )＝2x －2－x 为奇函数且在R 上是增函数，所以g (x 2＋2x )＋g (x －4)＞0⇒g (x 2＋2x )＞－g (x －4)＝g (4－x )⇒x 2＋2x ＞4－x ⇒x ＞1或x ＜－4.所以，原不等式的解集为{x |x ＞1或x ＜－4}．。

指数函数练习1. 函数（1）x y 4=； （2） 4x y =; (3） x y 4-=； (4) x y )4(-=; （5) x y π=； (6） 24x y =；(7） x x y =; （8） 1()1(>-=a a y x , 且a 1≠）中,是指数函数的是2. 函数33(0,1)x y a a a-=+>≠恒过的定点是 3. 若1()21xf x a =+-是奇函数，则a = 【答案】【解析】12(),()()2112xx x f x a a f x f x --=+=+-=--- 21121()21122112122x x x x x xa a a a ⇒+=-+⇒=-==----故 4. 若指数函数y a x =+()1在()-∞+∞，上是减函数，那么( ）A 、 01<<aB 、 -<<10aC 、 a =-1D 、 a <-15. 函数213-=x y 的定义域为6. 若函数()1222-=--aax xx f 的定义域为R ，则实数a 的取值范围 . []0,1-7. 设0x >,且1x x a b <<（0a >，0b >)，则a 与b 的大小关系是（ B ）A 1b a <<B 1a b <<C 1b a <<D 1a b <<8. 如图，指出函数①y=a x ；②y=b x ;③y=c x ；④y=d x的图象，则a,b,c,d 的大小关系是BA a 〈b 〈1〈c 〈dB b<a 〈1〈d<cC 1〈a<b 〈c 〈dD a 〈b<1〈d<c9. 下列函数图象中，函数y a a a x =>≠()01且,与函数y a x =-()1的图象只能是( C ）y y y yO x O x O x O xAB C D111110. 函数x xx x e e y e e--+=-的图像大致为( A )。

例1 已知函数2()f x x bx c =-+满足(1)(1)f x f x +=-，且(0)3f =，则()x f b 与()x f c 的大小关系是_____．分析：先求b c ，的值再比较大小，要注意x x b c ，的取值是否在同一单调区间内． 解：∵(1)(1)f x f x +=-，∴函数()f x 的对称轴是1x =．故2b =，又(0)3f =，∴3c =．∴函数()f x 在(]1-，∞上递减，在[)1+，∞上递增． 若0x ≥，则321x x ≥≥，∴(3)(2)x x f f ≥；若0x <，则321x x <<，∴(3)(2)x x f f >．综上可得(3)(2)x x f f ≥，即()()x x f c f b ≥． [f(a-x)=f(b+x)的对称轴为啥是x=(a+b)/2? 可设对称轴为x=c,不妨令a-x<c<b+x. 易知a-x 到c 的距离等于b+x 到c 的距离. 于是 c-(a-x)=(b+x)-c, 解得c=(a+b)/2. 即对称轴为x=(a+b)/2.]例2 已知2321(25)(25)x x a a a a -++>++，则x 的取值范围是___________．分析：利用指数函数的单调性求解，注意底数的取值范围．解：∵2225(1)441a a a ++=++>≥，∴函数2(25)x y a a =++在()-+，∞∞上是增函数，∴31x x >-，解得14x >．∴x 的取值范围是14⎛⎫+ ⎪⎝⎭，∞． 评注：利用指数函数的单调性解不等式，需将不等式两边都凑成底数相同的指数式，并判断底数与1的大小，对于含有参数的要注意对参数进行讨论．3.若10x =3，10y =4，则10x-y =例4 求函数y =解：由题意可得2160x --≥，即261x -≤，∴20x -≤，故2x ≤． ∴函数()f x 的定义域是(]2-，∞．令26x t -=，则y =，又∵2x ≤，∴20x -≤． ∴2061x -<≤，即01t <≤．∴011t -<≤，即01y <≤．∴函数的值域是[)01，．评注：利用指数函数的单调性求值域时，要注意定义域对它的影响．5.求下列函数的定义域与值域.(1)y ＝231-x ; (2)y ＝4x +2x+1+1.解：(1)∵x-3≠0，∴y ＝231-x 的定义域为｛x ｜x ∈R 且x ≠3｝.又∵31-x ≠0，∴231-x ≠1， ∴y ＝231-x 的值域为｛y ｜y>0且y ≠1｝.(2)y ＝4x +2x+1+1的定义域为R.∵2x >0,∴y ＝4x +2x+1+1＝(2x )2+2·2x +1＝(2x +1)2>1.∴y ＝4x +2x+1+1的值域为｛y ｜y>1｝.6．若函数是奇函数，求 的值． ．解：为奇函数， ，即，则 ， 7.求函数y ＝23231+-⎪⎭⎫ ⎝⎛x x 的单调区间. 分析 这是复合函数求单调区间的问题可设y ＝u ⎪⎭⎫ ⎝⎛31,u ＝x 2-3x+2，其中y ＝u⎪⎭⎫ ⎝⎛31为减函数 ∴u ＝x 2-3x+2的减区间就是原函数的增区间(即减减→增)u ＝x 2-3x+2的增区间就是原函数的减区间(即减、增→减)解：设y ＝u⎪⎭⎫ ⎝⎛31,u ＝x 2-3x+2,y 关于u 递减， 当x ∈(-∞，23)时，u 为减函数， ∴y 关于x 为增函数；当x ∈［23，+∞)时，u 为增函数，y 关于x 为减函数. 8.已知函数f （x ）=a －122+x （a ∈R ）， （1） 求证：对任何a ∈R ，f （x ）为增函数．（2） 若f （x ）为奇函数时，求a 的值。

2．函数f (x )＝x 2－bx ＋c 满足f (1＋x )＝f (1－x )且A ．f (b x )≤f (c x) B ．f (b x )≥f (c x) lg(a x －2x－5 ≥5 [9，(9，1，，1[1，[1，，1)上的最大值比最小值大，则234x x ---+11．(2011·银川模拟)若函数y ＝a 2x ＋2a x－1(a >0且a ≠1)在x ∈[－1,1]上的最大值为14，求a 的值．的值．12．已知函数f (x )＝3x ，f (a ＋2)＝18，g (x )＝λ·3ax －4x的定义域为[0,1]． (1)求a 的值；的值；(2)若函数g (x )在区间[0,1]上是单调递减函数，求实数λ的取值范围．的取值范围．指数函数答案指数函数答案1.1.解析：由解析：由a ⊗b ＝îïíïìa a ≤bba >b得f (x )＝1⊗2x＝îïíïì2xx，1x答案：答案：A A 2. 2. 解析：∵解析：∵f (1(1＋＋x )＝f (1(1－－x )，∴f (x )的对称轴为直线x ＝1，由此得b ＝2. 又f (0)(0)＝＝3，∴c ＝3.3.∴∴f (x )在(－∞，－∞，1)1)1)上递减，在上递减，在上递减，在(1(1(1，＋∞)上递增．，＋∞)上递增．，＋∞)上递增．若x ≥0，则3x ≥2x ≥1，∴f (3x )≥f (2x)．若x <0<0，则，则3x<2x<1<1，∴，∴f (3x)>f (2x)． ∴f (3x )≥f (2x )． 答案：答案：A A3.3.解析：由于函数解析：由于函数y ＝|2x－1|1|在在(－∞，－∞，0)0)0)内单调递减，在内单调递减，在内单调递减，在(0(0(0，＋∞)内单调递增，而函数在，＋∞)内单调递增，而函数在区间区间((k －1，k ＋1)1)内不单调，所以有内不单调，所以有k －1<0<k ＋1，解得－，解得－1<1<k <1. 答案：答案：C C4. 4. 解析：由题意得：解析：由题意得：A ＝(1,2)(1,2)，，a x －2x >1且a >2>2，由，由A ⊆B 知a x －2x>1在(1,2)(1,2)上恒成立，即上恒成立，即a x －2x －1>0在(1,2)(1,2)上恒成立，令上恒成立，令u (x )＝a x －2x －1，则u ′(x )＝a x ln a －2x ln2>0ln2>0，所以函数，所以函数u (x )在(1,2)(1,2)上单调递增，则上单调递增，则u (x )>u (1)(1)＝＝a －3，即a ≥3.≥3. 答案：答案：B B5. 5. 解析：数列解析：数列解析：数列{{a n }满足a n ＝f (n )(n ∈N *)，则函数f (n )为增函数，为增函数，注意a 8－6>(3>(3－－a )×7－)×7－33，所以îïíïìa >13－a >0a8－6－a －3，解得2<a <3.答案：答案：C C6. 6. 解析：解析：f (x )<12⇔x 2－a x <12⇔x 2－12<a x ，考查函数y ＝a x 与y ＝x 2－12的图象，的图象，当a >1时，必有a －1≥12，即1<a ≤2，≤2，当0<a <1时，必有a ≥12，即12≤a <1<1，，综上，12≤a <1或1<a ≤2.≤2.答案：答案：C C7. 7. 解析：当解析：当a >1时，y ＝a x 在[1,2][1,2]上单调递增，故上单调递增，故a 2－a ＝a 2，得a ＝32.当0<a <1时，y ＝ax 在[1,2][1,2]上单调递减，故上单调递减，故a －a 2＝a 2，得a ＝12.故a ＝12或32.答案：12或328. 8. 解析：分别作出两个函数的图象，通过图象的交点个数来判断参数的取值范围．解析：分别作出两个函数的图象，通过图象的交点个数来判断参数的取值范围．解析：分别作出两个函数的图象，通过图象的交点个数来判断参数的取值范围．曲线曲线||y |＝2x＋1与直线y ＝b 的图象如图所示，由图象可得：如果的图象如图所示，由图象可得：如果||y |＝2x＋1与直线y ＝b 没有公共点，则b 应满足的条件是b ∈[－1,1]1,1]．． 答案：答案：[[－1,1]9. 9. 解析：如图满足条件的区间解析：如图满足条件的区间解析：如图满足条件的区间[[a ，b ]，当a ＝－＝－11，b ＝0或a ＝0，b ＝1时区间长度最小，最小值为1，当a ＝－＝－11，b ＝1时区间长度最大，最大值为2，故其差为1. 答案：答案：1 110. 10. 解：要使函数有意义，则只需－解：要使函数有意义，则只需－x 2－3x ＋4≥0，即x 2＋3x －4≤0，解得－4≤x ≤1.≤1. ∴函数的定义域为∴函数的定义域为{{x |－4≤x ≤1}．≤1}． 令t ＝－x 2－3x ＋4，则t ＝－x 2－3x ＋4＝－＝－((x ＋32)2＋254，∴当－4≤x ≤1时，t max ＝254，此时x ＝－32，t min ＝0，此时x ＝－＝－44或x ＝1.∴0≤t ≤254.∴0≤－x 2－3x ＋4≤52.∴函数y ＝2341()2x x ---+的值域为的值域为[[28，1]1]．．＋)＋(≤－时，≤234()2x x ---+在，－32]－32，－32，，－32][1a，，1a ]＝1a，即(1a＋＝13或－15(或13.。

指数函数习题及答案Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】指数函数习题一、选择题1．定义运算ab＝，则函数f(x)＝12x的图象大致为( )2．函数f(x)＝x2－bx＋c满足f(1＋x)＝f(1－x)且f(0)＝3，则f(b x)与f(c x)的大小关系是( )A．f(b x)≤f(c x)B．f(b x)≥f(c x)C．f(b x)>f(c x)D．大小关系随x的不同而不同3．函数y＝|2x－1|在区间(k－1，k＋1)内不单调，则k的取值范围是( ) A．(－1，＋∞)B．(－∞，1)C．(－1,1) D．(0,2)4．设函数f(x)＝ln[(x－1)(2－x)]的定义域是A，函数g(x)＝lg(－1)的定义域是B，若AB，则正数a的取值范围( )A．a>3 B．a≥3C．a> D．a≥5．已知函数f(x)＝若数列{a n}满足a n＝f(n)(n∈N*)，且{a n}是递增数列，则实数a的取值范围是( )A．[，3) B．(，3)C．(2,3) D．(1,3)6．已知a>0且a≠1，f(x)＝x2－a x，当x∈(－1,1)时，均有f(x)<，则实数a 的取值范围是( )A．(0，]∪[2，＋∞)B．[，1)∪(1,4]C．[，1)∪(1,2]D．(0，)∪[4，＋∞)二、填空题7．函数y＝a x(a>0，且a≠1)在[1,2]上的最大值比最小值大，则a的值是________．8．若曲线|y|＝2x＋1与直线y＝b没有公共点，则b的取值范围是________．9．(2011·滨州模拟)定义：区间[x1，x2](x1<x2)的长度为x2－x1.已知函数y＝2|x|的定义域为[a，b]，值域为[1,2]，则区间[a，b]的长度的最大值与最小值的差为________．三、解答题10．求函数y＝211．(2011·银川模拟)若函数y＝a2x＋2a x－1(a>0且a≠1)在x∈[－1,1]上的最大值为14，求a的值．12．已知函数f(x)＝3x，f(a＋2)＝18，g(x)＝λ·3ax－4x的定义域为[0,1]．(1)求a的值；(2)若函数g(x)在区间[0,1]上是单调递减函数，求实数λ的取值范围．指数函数答案1.解析：由ab＝得f(x)＝12x＝答案：A2.解析：∵f (1＋x )＝f (1－x )，∴f (x )的对称轴为直线x ＝1，由此得b ＝2. 又f (0)＝3，∴c ＝3.∴f (x )在(－∞，1)上递减，在(1，＋∞)上递增． 若x ≥0，则3x ≥2x ≥1，∴f (3x )≥f (2x )． 若x <0，则3x <2x <1，∴f (3x )>f (2x )． ∴f (3x )≥f (2x )． 答案：A3.解析：由于函数y ＝|2x －1|在(－∞，0)内单调递减，在(0，＋∞)内单调递增，而函数在区间(k －1，k ＋1)内不单调，所以有k －1<0<k ＋1，解得－1<k <1. 答案：C4.解析：由题意得：A ＝(1,2)，a x －2x >1且a >2，由AB 知a x －2x >1在(1,2)上恒成立，即a x －2x －1>0在(1,2)上恒成立，令u (x )＝a x －2x －1，则u ′(x )＝a x ln a －2x ln2>0，所以函数u (x )在(1,2)上单调递增，则u (x )>u (1)＝a －3，即a ≥3. 答案：B5.解析：数列{a n }满足a n ＝f (n )(n ∈N *)，则函数f (n )为增函数， 注意a 8－6>(3－a )×7－3，所以，解得2<a <3. 答案：C6.解析：f (x )<x 2－a x <x 2－<a x ，考查函数y ＝a x 与y ＝x 2－的图象， 当a >1时，必有a －1≥，即1<a ≤2， 当0<a <1时，必有a ≥，即≤a <1， 综上，≤a <1或1<a ≤2. 答案：C7.解析：当a >1时，y ＝a x 在[1,2]上单调递增，故a 2－a ＝，得a ＝.当0<a <1时，y ＝a x 在[1,2]上单调递减，故a －a 2＝，得a ＝.故a ＝或. 答案：或8.解析：分别作出两个函数的图象，通过图象的交点个数来判断参数的取值范围．曲线|y |＝2x ＋1与直线y ＝b 的图象如图所示，由图象可得：如果|y |＝2x ＋1与直线y ＝b 没有公共点，则b 应满足的条件是b ∈[－1,1]． 答案：[－1,1]9.解析：如图满足条件的区间[a ，b ]，当a ＝－1，b ＝0或a ＝0，b ＝1时区间长度最小，最小值为1，当a ＝－1，b ＝1时区间长度最大，最大值为2，故其差为1. 答案：110.解：要使函数有意义，则只需－x 2－3x ＋4≥0，即x 2＋3x －4≤0，解得－4≤x ≤1.∴函数的定义域为{x |－4≤x ≤1}．令t ＝－x 2－3x ＋4，则t ＝－x 2－3x ＋4＝－(x ＋)2＋，∴当－4≤x ≤1时，t max ＝，此时x ＝－，t min ＝0，此时x ＝－4或x ＝1. ∴0≤t ≤.∴0≤≤.∴函数y ＝2341()2x x --+[，1]．由t ＝－x 2－3x ＋4＝－(x ＋)2＋(－4≤x ≤1)可知，当－4≤x ≤－时，t 是增函数， 当－≤x ≤1时，t 是减函数． 根据复合函数的单调性知：y ＝1()2[－4，－]上是减函数，在[－，1]上是增函数．∴函数的单调增区间是[－，1]，单调减区间是[－4，－]．11.解：令a x ＝t ，∴t >0，则y ＝t 2＋2t －1＝(t ＋1)2－2，其对称轴为t ＝－1.该二次函数在[－1，＋∞)上是增函数．①若a >1，∵x ∈[－1,1]，∴t ＝a x ∈[，a ]，故当t ＝a ，即x ＝1时，y max ＝a 2＋2a －1＝14，解得a ＝3(a ＝－5舍去)． ②若0<a <1，∵x ∈[－1,1]，∴t ＝a x∈[a ，]，故当t ＝，即x ＝－1时， y max ＝(＋1)2－2＝14. ∴a ＝或－(舍去)． 综上可得a ＝3或.12.解：法一：(1)由已知得3a ＋2＝183a ＝2a ＝log 32. (2)此时g (x )＝λ·2x －4x ， 设0≤x 1<x 2≤1，因为g (x )在区间[0,1]上是单调减函数，所以g (x 1)－g (x 2)＝(2x 1－2x 2)(λ－2x 2－2x 1)>0恒成立，即λ<2x 2＋2x 1恒成立．由于2x 2＋2x 1>20＋20＝2，所以实数λ的取值范围是λ≤2. 法二：(1)同法一．(2)此时g (x )＝λ·2x －4x ，因为g (x )在区间[0,1]上是单调减函数，所以有g ′(x )＝λln2·2x －ln4·4x ＝ln2[－2·(2x )2＋λ·2x ]≤0成立． 设2x ＝u ∈[1,2]，上式成立等价于－2u 2＋λu ≤0恒成立． 因为u ∈[1,2]，只需λ≤2u 恒成立， 所以实数λ的取值范围是λ≤2.。

2 62 指数和指数函数一、选择题 1．（3 6 a 9）4（ 6 3 a 9）4 等于（ ）（A ）a 16（B ）a 8（C ）a 4（D ）a 22. 若 a>1,b<0,且 a b+a -b=2,则 a b -a -b 的值等于（ ）（A ） （B ） ± 2（C ）-2（D ）23. 函数 f （x ）=(a 2-1)x在 R 上是减函数，则 a 的取值范围是（）（A ） a > 1 （B ） a < 2 （C ）a< （D ）1< a < 14. 下列函数式中，满足 f(x+1)= f(x)的是() 21 1 (A)(x+1)(B)x+(C)2x(D)2-x245.下列 f(x)=(1+a x )2⋅ a-x 是（ ）（A ）奇函数 （B ）偶函数（C ）非奇非偶函数（D ）既奇且偶函数1 1 11 1 16．已知 a>b,ab ≠ 0 下列不等式（1）a 2>b 2,(2)2a>2b,(3) < ,(4)a 3 >b 3 ,(5)( )a <( )ba b 3 3中恒成立的有（ ） （A ）1 个（B ）2 个 （C ）3 个 （D ）4 个2 x - 17. 函数 y=是（ ）2 x+ 1 （A ）奇函数（B ）偶函数（C ）既奇又偶函数（D ）非奇非偶函数18. 函数 y=的值域是（ ）2 x- 1（A ）（- ∞,1）（B ）（- ∞, 0） ⋃ （0，+ ∞ ）（C ）（-1，+ ∞ ） （D ）（- ∞ ，-1） ⋃ （0，+ ∞ ）9. 下列函数中，值域为 R +的是（ ）1（A ）y=5 2-xe x - e - x1（B ）y=( )1-x（C ）y= 3（D ）y= 10. 函数 y= 的反函数是（）2（A ）奇函数且在 R +上是减函数（B ）偶函数且在 R +上是减函数（C ）奇函数且在 R +上是增函数 （D ）偶函数且在 R +上是增函数11．下列关系中正确的是（ ）1 2 1 2 1 11 1 12 1 2（A ）（ ） 3 <（ ） 3 <（ ） 3（B ）（ ） 3 <（ ） 3 <（ ） 32 5 21 2 1 1 1 22 2 51 2 1 2 1 1（C ）（ ） 3 <（ ） 3 <（ ）3 （D ）（ ） 3 <（ ） 3 <（ ） 3 5 2 25 2 22 ( 1 ) x - 1 21 -2 xx 12. 若函数 y=3+2x-1的反函数的图像经过 P 点，则 P 点坐标是（）（A ）（2，5） （B ）（1，3） （C ）（5，2） （D ）（3，1）13. 函数 f(x)=3x +5,则 f -1(x)的定义域是（ ） （A ）（０，＋ ∞ ） （B ）（５，＋ ∞ ） （C ）（６，＋ ∞ ） （D ）（－ ∞ ，＋ ∞ ）14. 若方程 a x-x-a=0 有两个根，则 a 的取值范围是（ ） （A ）（1，+ ∞ ） （B ）（0，1） （C ）（0，+ ∞ ） （D ）15. 已知函数 f(x)=a x+k,它的图像经过点（1，7），又知其反函数的图像经过点（4，0），则函数 f(x)的表达式是（ ）(A)f(x)=2x +5 (B)f(x)=5x +3 (C)f(x)=3x+4(D)f(x)=4x+316. 已知三个实数 a,b=a a,c=a aa,其中 0.9<a<1,则这三个数之间的大小关系是（）（A ）a<c<b （B ）a<b<c （C ）b<a<c （D ）c<a<b17．已知 0<a<1,b<-1,则函数 y=a x+b 的图像必定不经过（ ） (A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限 二、填空题31.若 a2 <a 2 ,则 a 的取值范围是 。

2024．．．．二、多选题．函数，若对任意实数、，，则下列结论错误的是()(32log f x x x =++a b 0a b +>A ．方程有且只有6个不同的解B ．方程()()0f g x =解C ．方程有且只有5个不同的解D ．方程()()0f f x =解的零点个数为 ．()4log =-y f x x16．已知函数，若方程有4个不同的实根，，，22log (1),13()1357,322x x f x x x x ⎧-<≤⎪=⎨-+>⎪⎩()34f x =1x 2x 3x 且，则.4x 1234x x x x <<<()341211x x x x ⎛⎫++=⎪⎝⎭答案：1．C【分析】根据函数的单调性，借助中间值比较大小.【详解】因为函数在单调递增，且，所以，即，2log y x =()0,∞+π2>22log π>log 21=1a >因为函数在单调递减，且，所以，即，0.5log y x =()0,∞+π1>0.50.5log π<log 1=00b <因为函数在单调递增，且，所以，即，πxy =(),-∞+∞20-<200<ππ1-<=01c <<所以，a c b >>故选：C 2．A【分析】由提供的数据知，描述西红柿种植成本与上市时间的变化关系函数不可能是单Q t 调函数，故选取二次函数进行描述，将表格所提供的三组数据代入，即得函2Q at bt c =++Q 数解析式，进而求解.【详解】因为随着时间的增加，种植成本先减少后增加，所以函数不单调，所以选取，且开口向上，2Q at bt c =++将表格中的三组数据分别代入，2Q at bt c =++得解得116360060,8410000100,11632400180,a b c a b c a b c =++⎧⎪=++⎨⎪=++⎩0.01,2.4,224,a b c =⎧⎪=-⎨⎪=⎩即，对称轴，开口向上，20.01 2.4224Q t t =-+ 2.412020.01t -=-=⨯在对称轴处即120天时函数取最小值.∴t =西红柿种植成本最低时的上市天数是120天.∴故选：A.3．C【分析】由指数函数的性质分别对和的情况讨论单调性并求值域，从而列方程组01a <<1a >即可得到答案.【详解】函数（且）的值域为，2x y a =-0a >1,11a x ≠-≤≤5,13⎡⎤-⎢⎥⎣⎦又由指数函数的单调性可知，当时，函数在上单调递减，值域是01a <<2xy a =-[]1,1-12,2a a -⎡⎤--⎣⎦所以有，即，解得；110152321a a a -<<⎧⎪⎪-=-⎨⎪-=⎪⎩101133a a a -<<⎧⎪⎪=⎨⎪=⎪⎩13a =当时，函数在上单调递增，值域是1a >2x y a =-[]1,1-12,2a a -⎡⎤--⎣⎦所以有，即 ，解得.11152321a a a ->⎧⎪⎪-=-⎨⎪-=⎪⎩11133a a a ->⎧⎪⎪=⎨⎪=⎪⎩3a =综上所述，或.13a =3a =故选：C.4．B【分析】结合已知条件，利用抽象函数的定义域以及对数、分式的定义域求法求解即可.【详解】因为函数的定义域是，()f x [1,2022]所以对于有：，(1)()lg f x g x x +=1120220lg 0x x x ≤+≤⎧⎪>⎨⎪≠⎩解得：且，02021x <≤1x ≠故函数的定义域是，()()1ln f x g x x+=(01)(1],,2021⋃故选：B ．5．A【分析】根据题意，求得，得到，结合零点的存在性定理，3()0,(2)02f f >>3(1)()02f f ⋅<即可求解.【详解】由函数，且，可得，()348f x x x =+-()()10,30f f <>3()70,(2)2602f f =>=>所以，根据零点的存在性定理，3(1)()02f f ⋅<可得方程的近似解落在区间为.3480x x +-=31,2⎛⎫⎪⎝⎭故选：A.6．C【分析】根据给定条件，可得函数在R 上单调递增，再利用分段函数及对数函数单调性()f x 列出不等式求解即得.【详解】函数的定义域为R ，(2)1,1()log ,1a a x x f x x x --≤⎧=⎨>⎩由对任意，都有，得函数在R 上单调递增，12x x ≠1212()()f x f x x x ->-()f x 于是，解得，20130a a a ->⎧⎪>⎨⎪-≤⎩23a <≤所以实数的取值范围为.a (]2,3故选：C 7．B【分析】利用对数的换底公式和运算法则即可得解.【详解】，，，230x y k ==>Q 23log ,log x k y k ==∴11log 2,log 3k k x y ∴==，，则.12log 2log 3log 61k k k x y ∴=+=+=∴26k =6k =故选：B.8．A【分析】由函数的定义域排除C ，由函数的奇偶性排除D ，由特殊的函数值排除B ，结合奇偶性和单调性判断A.【详解】由得，则函数的定义域为，排除选项C ；30x ->33x -<<()ln 3y x =-()3,3-又，所以为偶函数，则图象关于y 轴对称，排除选项D ；()()ln 3ln 3x x --=-()ln 3y x =-当时，，排除选项B ，52x =1ln 02y =<因为为偶函数，且当时，函数单调递减，()ln 3y x =-30x >>()()ln 3ln 3y x x =-=-选项A 中图象符合.故选：A 9．ACD【分析】分析函数的奇偶性与单调性，由已知可得出，结合函数的奇偶性()f x a b >-()f x与单调性可得出合适的选项.【详解】令，对任意的，，即，()()22log 1g x x x =++x ∈R 21x x x+>≥-210x x ++>所以，函数的定义域为，()g x R 则.()()()()2222221log 1log 1log1g x x x x x g x x x⎛⎫-=+--=+-==- ⎪⎝⎭++所以，函数是定义域为的奇函数，()g x R 因为函数、为上的增函数，1u x =221u x =+[)0,∞+所以，内层函数在上为增函数，21u x x =++[)0,∞+外层函数在上为增函数，2log y u =()0,∞+所以，函数在上为增函数，()()22log 1g x x x =++[)0,∞+由于函数是定义域为的奇函数，则该函数在上为增函数，()g x R (],0-∞所以，函数在上单调递增，()()22log 1g x x x =++R 因为的定义域为，则，()f x R ()()()()()33f x x g x x g x f x -=-+-=--=-所以，函数为奇函数，()f x 又因为函数为上的增函数，所以，函数在上单调递增.3y x =R ()f x R 因为，所以，则，即，A 错B 对，0a b +>a b >-()()()f a f b f b >-=-()()0f a f b +>又、的大小不确定，故CD 错.a b 故选：ACD.方法点睛：函数的三个性质：单调性、奇偶性和周期性，在高考中一般不会单独命题，而是常将它们综合在一起考查，其中单调性与奇偶性结合、周期性与抽象函数相结合，并结合奇偶性求函数值，多以选择题、填空题的形式呈现，且主要有以下几种命题角度；（1）函数的单调性与奇偶性相结合，注意函数的单调性及奇偶性的定义，以及奇、偶函数图象的对称性．（2）周期性与奇偶性相结合，此类问题多考查求值问题，常利用奇偶性及周期性进行交换，将所求函数值的自变量转化到已知解析式的函数定义域内求解；（3）周期性、奇偶性与单调性相结合，解决此类问题通常先利用周期性转化自变量所在的区间，然后利用奇偶性和单调性求解.10．ABC【分析】根据题意，由函数的定义，只需满足集合中的每一个元素在集合中都有唯一一P Q 个元素与之对应即可，再结合选项逐一分析，即可得到结果.【详解】选项A ，，集合中的每一个元素在集合中都有唯一一个元素与之1:2f x y x→=P Q 对应，故A 正确；选项B ，，集合中的每一个元素在集合中都有唯一一个元素与之对应，故13:f x y x →=P Q B 正确；选项C ，，集合中的每一个元素在集合中都有唯一一个元素与之对应，1:2xf x y ⎛⎫→= ⎪⎝⎭P Q 故C 正确；选项D ，，集合中的1，在集合中没有元素与之对应，故D 错误；:ln f x y x →=P Q 故选：ABC 11．ABD【分析】根据奇偶性的定义即可判断A,根据基本函数的单调性即可判断BC ，根据反函数的性质即可判断D.【详解】对于A ，定义域为,关于原点对称，又由于()f x R ()()e e e e ,,22x x x xf x f x --++=-=，所以为偶函数，A 正确，()()=f x f x -()f x 对于B ，，由于函数在单调递增，所以在()e 121e 1e 1x x x f x -==-++e 1xy =+x ∈R 1e 1x y =+单调递减，因此在单调递增，B 正确，x ∈R ()21e 1xf x =-+x ∈R 对于C ，由于函数为定义域上的偶函数，当时，在区间上单调递lg y x=0x >lg y x =()0,∞+增，故C 错误，对于D ，由于函数与互为反函数，所以两者图象关于，D 正13xy ⎛⎫= ⎪⎝⎭133log log y x x ==-y x =确，故选：ABD 12．ACD【分析】令，结合图象可得有3个不同的解，，，不妨设，()t x g =()0f t =1t 2t 3t 123t t t <<则可知，，，令，结合图象可得有2个不同的解121t -<<-2t =312t <<()m f x =()0g m =，，不妨设，则可知，，再数形结合求出复合函数的解的1m 2m 12m m <121m -<<-201m <<个数.【详解】A 选项，令，结合图象可得有3个不同的解，，，()t x g =()0f t =1t 2t 3t 不妨设，则可知，，，123t t t <<121t -<<-20t =312t <<由图可知有2个不同的解，有2个不同的解，有2个不同的解，()1g x t =()2g x t =()3g x t =即有6个不同的解，A 正确；()()0f g x =B 选项，令，结合图象可得有2个不同的解，，()m f x =()0g m =1m 2m 不妨设，则可知，，12m m <121m -<<-201m <<由图可知有1个解，有3个不同的解，()1f x m =()2f x m =即有4个不同的解，B 错误；()()0g f x =C 选项，令，结合图象可得有3个不同的解，，()m f x =()0f m =1m 2m 3m 且，，，121m -<<-20m =312m <<由图可知有1个解，有3个不同的解，有1个解，()1f x m =()2f x m =()3f x m =即有5个不同的解，C 正确；()()0f f x =D 选项，令，结合图象可得有两个不同的解，()t x g =()0g t =1t2t 不妨设，则可知，，12t t <121t -<<-201t <<由图可知有2个不同的解，有2个不同的解，()1g x t =()2g x t =即有4个不同的解，D 正确．()()0g g x =故选：ACD ．13．193【分析】利用位数的定义，结合对数运算法则即可得解.k故答案为.14。

指数函数的性质与图像练习题（1）1. 下列函数中，既是偶函数又在(−∞, 0)上是单调递减的是（ ）A.y ＝−cos xB.y ＝lg |x|C.y ＝1−x 2D.y ＝e −x2. 函数f(x)=cos x x 的图象大致为（ ）A. B.C.D.3. 指数函数y ＝a x 的图象经过点(3, 27)，则a 的值是（ ）A.3B.9C.D.4. 已知a ＝(35)−13，b =(35)−14，c ＝(23)−14，则a 、b 、c 的大小关系是（ ）A.c <a <bB.a <b <cC.b <a <cD.c <b <a5. 若P =√2,Q =√6−√2，则P ，Q 中较大的数是________．6. 函数y =lg (4+3x −x 2)的单调增区间为________．7. 函数y =a x+1−2的图象恒过一定点，这个定点是________．8. 已知指数函数f(x)=(3m 2−7m +3)m x 是减函数，求实数m 的值．lg(x+1)的定义域为A，集合B={x||x|≤2}．9. 已知函数f(x)=√2−x(1)求A;(2)求A∩B.10. 已知函数f(x)＝x2+(1−a)x−a(a∈R)．（1）解关于x的不等式f(x)<0；（2）若∀a∈[−1, 1]，f(x)≥0恒成立，求实数x的取值范围．参考答案与试题解析指数函数的性质与图像练习题（1）一、选择题（本题共计 4 小题，每题 5 分，共计20分）1.【答案】B【考点】函数单调性的性质与判断函数奇偶性的性质与判断【解析】根据题意，依次分析选项中函数的奇偶性与单调性，综合即可得答案．【解答】根据题意，依次分析选项：对于A，y＝−cos x，为偶函数，但在区间(−∞, 0)上不是单调函数，不符合题意；对于B，y＝lg|x|，既是偶函数又在(−∞, 0)上是单调递减，符合题意；对于C，y＝1−x2，为偶函数，但在区间(−∞, 0)上是增函数，不符合题意；对于D，y＝e−x，不是偶函数，不符合题意；2.【答案】D【考点】函数的图象与图象的变换【解析】先判断函数的奇偶性，再判断函数值的变化趋势．【解答】f(−x)=cos(−x)−x =−cos xx=−f(x)，∴函数f(x)为奇函数，则图象关于原点对称，故排A，B，当x=π3时，f(π3)=12π3=6π3.【答案】A【考点】指数函数的单调性与特殊点【解析】此题暂无解析【解答】此题暂无解答4.【答案】D【考点】指数函数的图象与性质【解析】根据指数函数的性质判断即可．【解答】y =(35)x 是减函数，故a ＝(35)−13>b =(35)−14，而b =(35)−14>c ＝(23)−14，故c <b <a ，二、 填空题 （本题共计 3 小题 ，每题 5 分 ，共计15分 ）5.【答案】P【考点】利用不等式比较两数大小【解析】作差利用幂函数的单调性即可得出．【解答】P −Q =2√2−√6=√8−√6>0，∴ P >Q ．6.【答案】(−, 32] 【考点】复合函数的单调性【解析】函数y =lg (4+3x −x 2)的增区间即为函数y =4+3x −x 2的增区间且4+3x −x 2>0，由此即可求得．【解答】解：由4+3x −x 2>0，解得−1<x <4，所以函数的定义域为(−1, 4)．函数y =lg (4+3x −x 2)的增区间即为函数y =4+3x −x 2的增区间且4+3x −x 2>0， 因此所求增区间为(−1, 32]． 故答案为：(−1, 32]． 7.【答案】(−1, −1)【考点】指数函数的单调性与特殊点【解析】令解析式中的指数x +1=0求出x 的值，再代入解析式求出y 的值，即得到定点的坐标．【解答】解：令x +1=0解得，x =−1，代入y =a x+1−2得，y =−1，∴ 函数图象过定点(−1, −1)，故答案为：(−1, −1)．三、 解答题 （本题共计 3 小题 ，每题 5 分 ，共计15分 ）8.【答案】解：由题意得，得3m −7m +3=1，解得m =13或m =2， 又f(x)是减函数，则0<m <1，所以m =13．【考点】指数函数的单调性与特殊点【解析】由指数函数的概念得3m −7m +3=1，求出m 的值，再由指数函数的单调性和f(x)是减函数，对m 的值进行取舍．【解答】解：由题意得，得3m −7m +3=1，解得m =13或m =2，又f(x)是减函数，则0<m <1，所以m =13． 9.【答案】解：(1)据题意，得{x +1>0，2−x >0，∴ −1<x <2，∴ A =(−1,2)．(2)据(1)求解知 A =(−1,2)．又∵ B ={x||x|≤2}={x|−2≤x ≤2}，∴ A ∩B =(−1,2)．【考点】函数的定义域及其求法交集及其运算【解析】此题暂无解析【解答】解：(1)据题意，得{x +1>0，2−x >0，∴ −1<x <2，∴ A =(−1,2)．(2)据(1)求解知 A =(−1,2)．又∵ B ={x||x|≤2}={x|−2≤x ≤2}，∴ A ∩B =(−1,2)．10.【答案】不等式x 2+(1−a)x −a <0等价于(x −a)(x +1)<0，当a <−1时，不等式的解集为(a, −1)；当a ＝−1时，不等式的解集为⌀；当a >−1时，不等式的解集为(−1, a)．x 2+(1−a)x −a ＝−a(x +1)+x 2+x ，设g(a)＝−a(x +1)+x 2+x ，a ∈[−1, 1]，要使g(a)≥0在a ∈[−1, 1]上恒成立，只需{g(−1)≥0g(1)≥0， 即{x 2+2x +1≥0,x 2−1≥0,解得x ≥1或x ≤−1，所以x 的取值范围为{x|x ≤−1或x ≥1}．【考点】函数恒成立问题【解析】（1）不等式x 2+(1−a)x −a <0等价于(x −a)(x +1)<0，通过a 与−1的大小比较，求解即可．（2）x 2+(1−a)x −a ＝−a(x +1)+x 2+x ，设g(a)＝−a(x +1)+x 2+x ，a ∈[−1, 1]，要使g(a)≥0在a ∈[−1, 1]上恒成立，只需{g(−1)≥0g(1)≥0，求解即可． 【解答】不等式x 2+(1−a)x −a <0等价于(x −a)(x +1)<0，当a <−1时，不等式的解集为(a, −1)；当a ＝−1时，不等式的解集为⌀；当a >−1时，不等式的解集为(−1, a)．x 2+(1−a)x −a ＝−a(x +1)+x 2+x ，设g(a)＝−a(x +1)+x 2+x ，a ∈[−1, 1]，要使g(a)≥0在a ∈[−1, 1]上恒成立，只需{g(−1)≥0g(1)≥0， 即{x 2+2x +1≥0,x 2−1≥0,解得x ≥1或x ≤−1，所以x 的取值范围为{x|x ≤−1或x ≥1}．。

指数函数及其性质习题（含答案）一、单选题的图象可能是( ) 1．在同一坐标系内，函数y=x a(a≠0)和y=ax+1aA．B．C．D．−1，若f(a)=1，则f(−a)=（）2．已知函数f(x)=(e x+e−x)ln1−x1+xA．1B．−1C．3D．−33．已知函数f(x)=(x−a)(x−b)（其中a＞b）的图象如图所示，则函数g（x）＝a x ＋b的图象大致是( )A．B．.C．D．4．已知a=log40.7，b=log23，c=0.20.6，则a,b,c的大小关系是( )A．c<b<a B．a<c<b C．b<a<c D．a<b<c5．函数y=a x+1−3（a>0，且a≠1）的图象一定经过的点是( )A．(0，−2)B．(−1,−3)C．(0，−3)D．(−1,−2)6．在同一坐标系中，函数y=2−x与y=−log2x的图象都正确的是（）A．B．C．D ．7．设a =20.5,b =0.52,c =log 20.5，则a,b,c 的大小关系为A ． c >a >bB ． c >b >aC ． a >b >cD ． b >a >c8．若01a b <<<，则b a ， a b ， log b a ，）A ．B ．C ．D ．9．若a ，b ，c 满足2a =3，b =log 25，3c =2，则（ ）A ． c <a <bB ． b <c <aC ． a <b <cD ． c <b <a二、填空题10．已知： 12a a -+=，则22a a -+=__________．11．函数()2x f x =在[]1,3-上的最小值是__________． 12．函数y=a x+2-1(a>0且a≠1)的图象恒过定点________.13．求值：2log 323−log 3427−31+log 32=__________．14．函数f(x)=(12)−x2+2x+1的单调减区间为________． 15，.16．计算：． 17．若函数()()23x f x a =-在R 上是减函数，则实数a 的取值范围是________18．已知函数()x f x a b =+ ()0,1a a >≠的定义域和值域都是[]1,0-，则b a =__________．三、解答题19．（1）计算：(−3)−(1−0.5−2)÷(338)13；（2）已知a =log 32,3b =5用a,b 表示log 3√30．20．(1)(2)已知15a a-+=,求22a a -+和.21．计算： （1）)213013210.027163217---⎛⎫--+-+⋅ ⎪⎝⎭. （222．化简求值 (1) (827)23+(0.008)−23×225(2) 12523+(12)−2−(127)−13+10012+lg3+14lg9−lg √3lg81−lg2723．已知定义在R 上的函数f(x)=b−2x2x +a 是奇函数．⑴求a ， b 的值，并判断函数f(x)在定义域中的单调性（不用证明）；⑵若对任意的t ∈R ，不等式f(t 2−2t)+f(2t 2−k)<0恒成立，求实数k 的取值范围．24．若函数f(x)=a x −1(a >0,且a ≠1)的定义域和值域都是[0,2]，求实数a 的值.25．（本小题满分10分）已知函数f(x)=log 4(4x +1)+kx(k ∈R)是偶函数．（1）求实数k 的值;（2）设g(x)=log 4(a ⋅2x +a),若f(x)= g(x)有且只有一个实数解,求实数a 的取值范围．26．计算：(1) (−338)−23+0.002−12−10(√5−2)−1+(√2−√3)0； (2)lg 5(lg 8＋lg 1 000)＋3lg 22＋lg 16＋lg 0.06. 27．已知f(x)=4x−1−2x +5,x ∈[−2,2]．（1）求f(x)的值域．（2）若f(x)>3m 2+am +2对任意a ∈[−1,1]和x ∈[−2,2]都成立，求m 的取值范围．28．计算下列各式的值;(1)(2)参考答案1．B【解析】【分析】分两种情况讨论，利用函数的单调性，筛选排除即可得结果【详解】若a>0,y=x a在(0,+∞)递增，排除A,B选项，y=ax+1a递增，排除D；纵轴上截距为正数，排除C，即a>0时，不合题意；若a<0，y=x a在(0,+∞)递减，可排除C,D选项，由y=ax+1a递减可排除A，故选B.【点睛】本题通过对多个图象的选择考查函数的图象与性质，属于中档题.这类题型也是近年高考常见的命题方向，该题型的特点是综合性较强、考查知识点较多，但是并不是无路可循.解答这类题型可以从多方面入手，根据函数的定义域、值域、单调性、奇偶性、特殊点以及x→0+,x→0−,x→+∞,x→−∞时函数图象的变化趋势，利用排除法，将不合题意的选项一一排除.2．D【解析】分析：先化简f(a)=1得到(e a+e−a）ln1+a1−a=−2，再求f(−a)的值.详解：由题得(e a+e−a）ln1−a1+a −1=1,∴(e a+e−a）ln1−a1+a=2,∴−(e a+e−a）ln1+a1−a=2,∴(e a+e−a）ln1+a1−a=−2.所以f(−a)=(e−a+e a）ln1+a1−a−1=−2−1=−3.故答案为：D点睛：（1）本题主要考查函数求值和指数对数运算，意在考查学生对这些基础知识的掌握能力和运算能力.（2）解答本题的关键是整体代入求值.3．D【解析】【分析】根据二次函数的图象得到−1<b<0,a>1,继而得到g(x)=a x+b的图象经过一二三象限，问题得以解决.【详解】因为a,b 是二次函数的零点，由二次函数f (x )=(x −a )(x −b )（其中a >b ）的图象可知−1<b <0,a >1， 所以g (x )=a x +b 的图象经过一二三象限，只有选项D 符合题意，故选D.【点睛】函数图象的辨识可从以下方面入手：(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置．(2)从函数的单调性，判断图象的变化趋势．(3)从函数的奇偶性，判断图象的对称性．(4)从函数的特征点，排除不合要求的图象4．B【解析】【分析】利用指数与对数的单调性与中间量0，1可求得三个数大小。

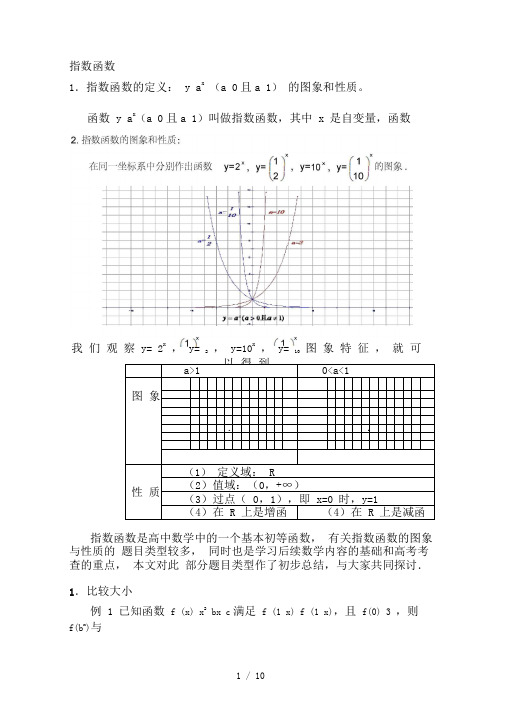
指数函数1．指数函数的定义： y a x（a 0且a 1） 的图象和性质。

a>1 0<a<1图 象111性 质（1） 定义域： R（2）值域：（0，+∞）（3）过点（ 0，1），即 x=0 时，y=1 （4）在 R 上是增函（4）在 R 上是减函指数函数是高中数学中的一个基本初等函数， 有关指数函数的图象与性质的 题目类型较多， 同时也是学习后续数学内容的基础和高考考查的重点， 本文对此 部分题目类型作了初步总结，与大家共同探讨．1．比较大小例 1 已知函数 f (x) x 2 bx c 满足 f (1 x) f (1 x)，且 f(0) 3 ，则 f(b x)与函数 y a x（a 0且a 1）叫做指数函数，其中 x 是自变量，函数定义域是 R我 们 观 察 y= 2x ， y= 2 ， y=10x， y= 10 图 象 特 征 ， 就 可 以 得 到f(c ) 的大小关系是．分析：先求b，c的值再比较大小，要注意b x，c x的取值是否在同一单调区间内．解：∵ f (1 x) f (1 x) ，∴函数 f (x) 的对称轴是x 1 ．故b 2，又f(0) 3，∴ c 3．∴函数f(x)在∞，1 上递减，在1，∞ 上递增．若x≥0，则3x≥2x≥1，∴ f(3x)≥f(2x)；若x 0，则3x 2x 1，∴ f(3x) f(2x)．综上可得f(3x)≥ f(2x)，即f(c x)≥ f(b x)．评注：①比较大小的常用方法有：作差法、作商法、利用函数的单调性或中间量等．②对于含有参数的大小比较问题，有时需要对参数进行讨论．2．求解有关指数不等式例 2 已知(a2 2a 5)3x (a2 2a 5)1 x，则x 的取值范围是_____ ．分析：利用指数函数的单调性求解，注意底数的取值范围．解：∵ a2 2a 5 (a 1)2 4≥ 4 1 ，∴函数y (a2 2a 5)x在( ∞，∞) 上是增函数，∴3x 1 x，解得x 1．∴x的取值范围是1，∞ ．44 评注：利用指数函数的单调性解不等式，需将不等式两边都凑成底数相同的指数式，并判断底数与 1 的大小，对于含有参数的要注意对参数进行讨论．3．求定义域及值域问题例 3 求函数y 1 6x 2的定义域和值域．解：由题意可得 1 6x 2≥0，即6x 2≤1，∴x 2≤0，故x≤2．∴函数 f (x)的定义域是∞，2 ．令t 6x 2，则y 1 t ，又∵ x≤2 ，∴ x 2≤ 0．∴ 0 6x 2≤1，即0 t≤1．∴ 0 ≤ 1 t 1 ，即0 ≤ y 1 ．∴函数的值域是0，1 ．评注：利用指数函数的单调性求值域时，要注意定义域对它的影响． 4．最值问题例 4 函数 y a 2x 2a x 1（a 0且a 1）在区间 [ 1，1] 上有最大值 14，则a 的值 是 ．分析：令 t a x 可将问题转化成二次函数的最值问题，需注意换元后 t 的取值 范围．解：令 t a x，则 t 0，函数 y a 2x 2a x 1可化为 y （t 1）22 ，其对称轴为 t 1 ．∴当a1 时，∵x 1，1 ，∴1≤ a x ≤ a ，即 1≤t ≤ a ． aa∴当t a 时， y max2(a 1)2214 ． 解得a 3 或a 5 （舍去） 当 0 a 1 时，∵ x 1，1 ，∴a ≤ a x≤ 1，即 a ≤ t ≤ 1， aa1 12∴ t 时， y max 1 2 14 ，aa解得a 1或a 1 （舍去），∴ a 的值是 3或1．3 5 3 评注：利用指数函数的单调性求最值时注意一些方法的运用， 比如：换元法， 整体代入等． 5．解指数方程 例 5 解方程 3x 2 32 x80 ．解：原方程可化为 9 （3x ）2 80 3x 9 0 ，令 t 3x（t 0），上述方程可化为9t 2 80t 9 0，解得 t 9或t 1 （舍去），∴ 3x 9，∴ x 2 ，经检验原方程的 9解是 x 2 ． 评注：解指数方程通常是通过换元转化成二次方程求解，要注意验根． 6．图象变换及应用问题例 6 为了得到函数 y 9 3x 5的图象，可以把函数 y 3x 的图象（ ）．A ．向左平移 9 个单位长度，再向上平移 5 个单位长度B ．向右平移 9个单位长度，再向下平移 5 个单位长度C ．向左平移 2 个单位长度，再向上平移 5 个单位长度D ．向右平移 2 个单位长度，再向下平移 5 个单位长度 分析：注意先将函数 y 9 3x5转化为t 3x 25 ，再利用图象的平移规律进 行判断．解：∵ y 9 3x5 3x 25 ，∴把函数 y 3x的图象向左平移 2 个单位长度， 再向上平移 5 个单位长度，可得到函数 y 9 3x5的图象，故选（ C ）． 评注：用函数图象解决问题是中学数学的重要方法， 利用其直观性实现数形 结合解题，所以要熟悉基本函数的图象，并掌握图象的变化规律，比如：平移、 伸缩、对称等． 习题1、比较下列各组数的大小：1）若 ，比较与2） 3） 4若 ，比较 与 ； 若 ，比较 与 ； 若 ，且 ， 若 ，且 ，故解：（1）由，此时函数比较 a 与 b ； ，比较 a 与 b ． 为减函数． 由 ，．又 ，故 （3）由 ，因 ，故 ．又而．2）由 ，故．从而 ，故．从（4）应有 ．因若 ，则．又．又因 ，故 ．从而 ， （5）应有 ．因若，则．又，故 这与已知，故这样 矛，这样有．又因 ，且 ，故 ．从而 ，这与已知矛盾．小结：比较通常借助相应函数的单调性、奇偶性、图象来求解．2，曲线分别是指数函数, 和的图象, 则与1 的大小关系是( ).(分析:首先可以根据指数函数单调性, 确定, 在轴右侧令, 由小到大依次为, 故应选.小结: 这种类型题目是比较典型的数形结合的题目由数到形的转化,第(2) 题则是由图到数的翻译,它的主要目的是提高学生识图,用图的意识. 求最值3，求下列函数的定义域与值域1(1)y ＝2 x 3; (2)y ＝4x+2x+1+1.5、设 ，求函数 的最大值和最小值．分析：注意到 ，设，利用闭区间上二次函数的值域的求法，可求得函数的最值． 解：设 ，由 知， ，函数成为 ， ，对称轴，因端点 较 距对称．6．（9 分）已知函数 y a 2x 2a x1（a 1） 在区间［－1,1］上的最大值是 14，求 a 的值.1．解： y a 2x 2a x 1（a 1）， 换元为 y t 22t 1（ t a ） ，对称轴为 t 1. a 当a 1，t a ，即 x=1 时取最大值，略 解得 a=3 （a= －5舍去 ）7．已知函数 （ 且（1）求 的最小值； （2）若 求 的取值范围．．解：（ 1） 时， 有最小值为（ 2） ，解得当 时， ； 当 时， ．28（10分）（1）已知 f （x ） x 2m 是奇函数，求常数 m 的值；3x12）画出函数 y |3x1|的图象，并利用图象回答： k 为何值时，方程 |3Ｘk 无解？有一解？有两解？，则原来的函数成为，故函数最小值为轴 远，故函数的最大值为）解： （1）常数 m=1（2）当k<0时，直线y=k 与函数 y |3x1|的图象无交点 ,即方程无解;当k=0或k 1时, 直线y=k 与函数 y |3 1| 的图象有唯一的交点，所以方程 有一解;当 0<k<1 时, 直线 y=k 与函数 y |3x 1|的图象有两个不同交点， 所以方程有 两解。

百度文库 - 让每个人平等地提升自我1．给出下列结论：② na n ＝|a|(n>1， n ∈ N * ，n 为偶数 )；④若 2x ＝16,3y＝271，则 x ＋y ＝7.其中正确的是 ( )A ．①②B ．②③C ．③④D ．②④答案 B 解析xy1∵2 ＝16，∴x ＝4，∵3 ＝27，∴y ＝－ 3. ∴x ＋ y ＝4＋(－3)＝ 1，故④错．．函数 ＝x的值域是 () 2y 16－4 A ．[0，＋∞ ) B ．[0,4] C ．[0,4)D ．(0,4)答案 C ．函数 f(x) ＝3 －x－1 的定义域、值域是 ()3 A ．定义域是 R ，值域是 RB ．定义域是 R ，值域是 (0，＋∞ )C ．定义域是 R ，值域是 (－ 1，＋∞ )D ．以上都不对答案C1 x解析f(x)＝(3) －1，∵(13)x >0，∴f(x)>－1.1 －，则 ( )4．设 y 1＝， y 2＝， y 3＝(2) A ．y 3>y 1>y 2 B ．y 2>y 1>y 3 C ．y 1>y 2>y 3 D ．y 1>y 3>y 2答案 D解析y 1 ＝， y 2 ＝， y 3＝，∵y ＝ 2x 在定义域内为增函数，∴ y 1>y 3>y 2.5．函数 f(x)＝a x －b 的图像如图，其中 a ，b 为常数，则下列结论正确的是 ()A ．a>1， b<0B ．a>1，b>0C ．0<a<1，b>0D ．0<a<1，b<0答案D6．(2014 成·都二诊 )若函数 f(x)＝(a ＋ x 1 )cosx 是奇函数，则常数 a 的值等e －1于 ()A ．－1B ．1C ．－ 12 答案D7．(2014 ·东师大附中山 ) 集合 ＝ ， ＝ a} ，集合x＋1，A {( x y)|yB ＝{( x ，y)|y ＝ b b>0， b ≠ 1} ，若集合 A ∩ B 只有一个子集，则实数 a 的取值范围是 ()A ．(－∞， 1)B ．(－∞， 1]C ．(1，＋∞ )D ．R答案 B ．函数 x －2x 在 x ∈[0，＋∞ )上的最小值是 ()8 f(x)＝3·41 A ．－12 B ．0C ．2D ．10答案 C解析 设 t ＝2x，∵ ∈ ，＋ ∞ ，∴≥1.x [0 ) t ∵y ＝ 3t 2－t(t ≥1)的最小值为 2，∴函数f(x)的最小值为 2.x －1，x>0，9．已知函数 f(x)＝ －若关于 x 的方程 f(x)＋2x － k ＝ 0 有且只2 |x|＋ 1， x ≤ 0.有两个不同的实根，则实数 k 的取值范围为 ()A ．(－1,2]B ．(－∞， 1]∪(2，＋∞ )C ．(0,1]D ．[1，＋∞ )答案 A解析 在同一坐标系中作出 y ＝f(x)和 y ＝－ 2x ＋k 的图像，数形结合即可．．函数y ＝ |x|的定义域为 [a ，b] ，值域为 [1,16] ，当 a 变化时，函数 b ＝g(a) 10 2的图像可以是 ( )答案 B解析函数 y＝ 2|x|的图像如图．当 a＝－ 4 时， 0≤b≤4；当 b＝4 时，－ 4≤a≤0.11．若函数 y＝ (a2－1)x在(－∞，＋∞ )上为减函数，则实数 a 的取值范围是________．答案(－2，－ 1)∪(1，2)解析函数 y＝(a2－1)x在(－∞，＋∞)上为减函数，则0<a2－ 1<1，解得1<a< 2或－2<a<－1.12．函数 y ＝a x 在[0,1] 上的最大值与最小值的和为 3，则 a ＝________.答案2解析∵y ＝ a x 在[0,1] 上为单调函数，∴a 0＋a 1＝3，∴a ＝2.|2x－4|1 13．(2014 ·沧州七校联考 )若函数 f(x)＝ a(a>0，a ≠1)满足 f(1)＝ ，则 f(x)9的单调递减区间是 ________．答案 [2，＋∞ )解析 f(1)＝a 2＝ 1， ＝ 1，9 a 312x 4 ， x ≥2，3－f(x)＝1 4 2x， x<2.3 －∴单调递减区间为 [2，＋ ∞)．14．若 0<a<1,0<b<1，且，则 x 的取值范围是 ________．答案 (3,4)解析 log b (x － ，∴ － ，∴3)>0 0<x 3<1 3<x<4.15．若函数 y ＝2－x ＋1＋m 的图像不经过第一象限， 则 m 的取值范围是 ______． 答案 m ≤－ 216．是否存在实数 a ，使函数 y ＝a 2x ＋2a x－1(a>0 且 a ≠1)在 [－1,1]上的最大 值是 14?1答案 a ＝3 或 a ＝3解析 令 t ＝a x ，则 y ＝t 2＋2t －1.(1)当 a>1 时，∵x ∈[－1,1]，x11∴a ∈[a ，a] ，即 t ∈[a ，a]．∴y ＝ t 2＋ 2t －1＝(t ＋1)2－2 在[ 11 )．， a] 上是增函数 (对称轴 t ＝－ 1<aa∴当t ＝a 时， y max ＝(a ＋1)2－2＝14.∴a ＝ 3 或 a ＝－ 5.∵a>1，∴a ＝3.1(2)当 0<a<1 时， t ∈[a ，a ]．∵y ＝ (t ＋ 1)2－12 在 [a ，a ]上是增函数， max12 ∴y ＝(a ＋1) －2＝14.1 11∴a ＝ 3或 a ＝－ 5.∵0<a<1，∴a ＝3.1综上， a ＝3 或 a ＝3.17． (2011 ·海上 )已知函数 f(x)＝ a ·2x ＋b ·3x ，其中 a ， b 满足 a ·b ≠ 0.(1)若 a ·b>0，判断函数 f(x)的单调性；(2)若 a ·b<0，求 f(x ＋1)>f(x)时的 x 的取值范围．答案(1)a>0， b>0 时， f(x)增函数； a<0，b<0 时， f(x)减函数(2)a<0， b>0 时， x>；a>0，b<0 时， x<解析(1)当 a>0，b>0 时，任意 x 1， x 2∈R ， x 1<x 2，∴f(x 1)－f(x 2)<0，∴函数f(x)在 R 上是增函数．当 a<0，b<0 时，同理，函数 f(x)在 R 上是减函数．(2)f(x ＋1)－ f(x)＝ a ·2x ＋2b ·3x >0.当 a<0，b>0 时， 3 x>－ a，则 x>；22b3 xa当 a>0，b<0 时， 2 <－2b ，则 x<.2x18．已知函数 f(x)＝－ 2x ＋1.(1)用定义证明函数f(x)在(－∞，＋∞ )上为减函数；(2)若 x∈[1,2] ，求函数 f(x)的值域；(3)若 g(x)＝a＋f(x)，且当 x∈[1,2] 时 g(x)≥0 恒成立，求实数 a 的取值范围．2答案 (1)略(2)[ －4 2 8 5，－3](3)a≥5(2)∵f(x)在(－∞，＋∞) 上为减函数，4 2∴f(x)的值域为 [ －5，－3] ．a 4 a 2(3)当 x∈[1,2] 时， g(x)∈[2－5，2－3] ．∵g(x)≥0 在 x∈[1,2] 上恒成立，a 4 8.∴ －≥ 0，∴a≥2 5 5。

指数函数练习题一．选择题：1．某种细菌在培育过程中，每 20 分钟分裂一次（一个分裂为两个） 。

经过 3 个小时，这类细菌由 1个可生殖成（）A.511个B.512 个C.1023个D.1024 个2．在一致平面直角坐标系中，函数f ( x)ax 与 g (x)a x 的图像可能是（）yy y y1111xoxoxoo xDABC3．设 a,b, c, d 都是不等于 1的正数， ya x , yb x , yc x , yd x 在同一坐标系中的图像yy c x如下图，则a,b, c, d 的大小次序是（）y b xyaxy dxA.a b c dB.a b d cC.b ad cD.b a c dx4.若1 x 0 ，那么以下各不等式建立的是（）oA.2 x 2 x 0.2xB.2x 0.2 x 2xC .0.2x 2 x 2 xD .2 x 2 x0.2 x5 函数 f (x)(a 2 1) x 在 R 上是减函数，则 a 的取值范围是（）A. a 1B. a 2C .a2D.1a26．函数 y1的值域是（）2 x1A.( ,1)B.(,0) (0, )C.( 1, )D .( , 1) (0, )7．当 a1 时，函数 ya x 1是（）a x1A. 奇函数B.偶函数C.既奇又偶函数D. 非奇非偶函数8．函数 ya x 21.(a 0 且 a1) 的图像必经过点（）A.(0,1)B.(1,1)C.( 2,0)D.(2,2)9．若 x 0 是方程 2x1 的解，则 x 0 （ ）xA.(0.1,0.2)B.(0.3,0.4)C.(0.5,0.7)D.(0.9,1)10．某厂 1998 年的产值为a万元，估计产值每年以n ％递加，则该厂到2010年的产值（单位：万元）是（）A.a(1 n ％ )13B.a(1n ％ )12 C .a(1 n％ )11 D.10(1n ％)129二．填空题：1．已知f (x)是指数函数，且35f ( )，则 f (3)2252．设0 a1，使不等式a x2 2 x 1a x23x 5建立的 x 的会合是3．若方程(1) x(1) x a0 有正数解，则实数 a 的取值范围是424．函数y(3x1) 082x的定义域为5．函数y2 x2x 的单一递加区间为三、解答题：x11．设0x 2 ，求函数y42 3 ? 2 x 5 的最大值和最小值。

高中数学：指数函数的概念练习及答案指数函数的概念1.下列函数中，是指数函数的是( )A．y＝2·3xB．y＝3x＋1C．y＝3xD．y＝x32.下列以x为自变量的函数中，是指数函数的是( )A．y＝(－5)xB．y＝e x(e≈2.71828)C．y＝－5xD．y＝πx＋23.函数y＝(a2－5a＋5)ax是指数函数，则有( )A．a＝1或a＝4B．a＝1C．a＝4D．a>0，且a≠14.若函数f(x)＝(a－3)·a x是指数函数，则f(2)的值为( )A．4B．8C．2D．165.函数y＝(m－2)x是指数函数，则m的取值范围是________．待定系数法求指数函数解析式6.指数函数y＝a x的图象经过点(2，16)，则a的值是( )A．B．C．2D．47.已知指数函数的图象经过点(－1，2)，则指数函数的解析式为________．8.已知f(x)是指数函数，且f(1＋)·f(1－)＝9，则f(2＋)·f(2－)的值为________．9.若指数函数f(x)的图象过点(1，)，则f(－2)＝________.指数函数的求值10.已知指数函数f(x)＝a x(a>0，且a≠1)的图象过点(3，8)，则a2.5与a2.3的大小为( )A．a2.5＝a2.3B．a2.5<a2.3C．a2.5>a2.3D．无法确定11.已知f(x)＝2x＋2－x，若f(a)＝3，则f(2a)等于( )A．5B．7C．9D．1112.已知函数f(x)＝则f[f(－4)]等于( )A．－4B．－C．4D．613.给出函数f(x)＝，则f(－1)＝________.14.若f(2x－1)＝3x－2x，则f(4)＝________.指数函数的实际应用15.设f(x)＝则f(f(－2))等于( )A．－1B．C．D．16.某种细菌经60分钟培养，可繁殖为原来的2倍，且知该细菌的繁殖规律为y＝10e kt，其中k为常数，t 表示时间(单位：小时)，y表示细菌个数，10个细菌经过7小时培养，细菌能达到的个数为( ) A．640B．1280C．2560D．512017.某环保小组发现某市生活垃圾年增长率为b，2009年该市生活垃圾量为a吨，由此可以预测2019年垃圾量为( )A．a(1＋10b)吨B．a(1＋9b)吨C．a(1＋b)10吨D．a(1＋b)9吨18.某种计算机病毒是通过电子邮件进行传播的，如果某台计算机感染上这种病毒，那么它就会在下一轮病毒发作时传播一次病毒，并感染其它20台未感染病毒的计算机．现有一台计算机被第一轮病毒感染，问被第4轮病毒感染的计算机有( )台．A．60B．400C．8000D．16000019.一种产品的成本是a元，在今后的n年内，计划成本每年比上一年降低p%，则成本随着年数变化的函数关系式是( )A．a(1－p%)n(n∈N*)B．a(p%)n(n∈N*)C．a(1－p)n%(n∈N*)D．a(1－np%)(n∈N*)20.据报道，全球变暖，使北冰洋冬季冰盖面积在最近50年内减少了5%，如果按此规律，设2000年的冬季冰盖面积为m，从2000年起，经过x年后冬季冰盖面积y与x的函数关系是( )A．y＝·mB．y＝(1－)·mC．y＝0.9550·x·mD．y＝(1－0.0550·x)·m21.某医药研究所开发一种新药，据监测，如果成人按规定的剂量服用该药，服药后每毫升血液中的含药量y(μg)与服药后的时间t(h)之间近似满足如图所示的曲线．其中OA是线段，曲线段AB是函数y＝k·at(t ≥1，a>0，k，a是常数)的图象．(1)写出服药后每毫升血液中含药量y关于时间t的函数关系式；(2)据测定：每毫升血液中含药量不少于2(μg)时治疗有效，假若某病人第一次服药为早上6：00，为保持疗效，第二次服药最迟是当天几点钟？(3)若按(2)中的最迟时间服用第二次药，则第二次服药后在过3h，该病人每毫升血液中含药量为多少μg？(精确到0.1μg)答案1.下列函数中，是指数函数的是( )A．y＝2·3xB．y＝3x＋1C．y＝3xD．y＝x3【答案】C【解析】形如y＝ax(a>0，a≠1)的函数为指数函数，y＝2·3x的3x系数不为1，y＝3x＋1的指数不是x，y＝x2是幂函数，只有y＝3x符合指数函数定义．故选C.2.下列以x为自变量的函数中，是指数函数的是( )A．y＝(－5)xB．y＝e x(e≈2.71828)C．y＝－5xD．y＝πx＋2【答案】B3.函数y＝(a2－5a＋5)ax是指数函数，则有( )A．a＝1或a＝4B．a＝1C．a＝4D．a>0，且a≠1【答案】C【解析】∵函数y＝(a2－5a＋5)ax是指数函数，∴解得a＝4.故选C.4.若函数f(x)＝(a－3)·a x是指数函数，则f(2)的值为( ) A．4B．8C．2D．16【答案】D【解析】∵函数f(x)是指数函数，∴a－3＝1，∴a＝4.∴f(x)＝4x，f(2)＝42＝16.5.函数y＝(m－2)x是指数函数，则m的取值范围是________．【答案】m>2且m≠3【解析】根据指数函数的定义，y＝ax中的底数a规定a>0且a≠1. 故此m－2>0且m－2≠1.所以m>2且m≠3.6.指数函数y＝a x的图象经过点(2，16)，则a的值是( )A．B．C．2D．4【答案】D【解析】指数函数y＝ax(a>0且a≠1)，将(2，16)代入，得16＝a2，解得a＝4，所以y＝4x，故选D.7.已知指数函数的图象经过点(－1，2)，则指数函数的解析式为________．【答案】y＝()x【解析】设指数函数的解析为：y＝ax(a>0，且a≠1)，∵函数的图象经过(－1，2)点，∴2＝a－1，∴a＝，∴指数函数的解析式为y＝()x，故答案为y＝()x.8.已知f(x)是指数函数，且f(1＋)·f(1－)＝9，则f(2＋)·f(2－)的值为________．【答案】81【解析】∵f(x)是指数函数，∴设f(x)＝ax(a>0且a≠1)，∵f(1＋)·f(1－)＝9，∴·＝a2＝9，即a＝3.∴f(2＋)·f(2－)＝·＝34＝81，故答案为81.9.若指数函数f(x)的图象过点(1，)，则f(－2)＝________.【答案】4【解析】设指数函数为f(x)＝ax(a>0且a≠1)，将(1，)代入得＝a1，解得a＝，所以f(x)＝()x，则f(－2)＝()－2＝4.故答案为4.10.已知指数函数f(x)＝a x(a>0，且a≠1)的图象过点(3，8)，则a2.5与a2.3的大小为( ) A．a2.5＝a2.3B．a2.5<a2.3C．a2.5>a2.3D．无法确定【答案】C【解析】∵指数函数f(x)＝ax(a>0，且a≠1)的图象过点(3，8)，∴a3＝8，解得a＝2.∴f(x)＝2x，且在R上单调递增，∴22.3<22.5.故选C.11.已知f(x)＝2x＋2－x，若f(a)＝3，则f(2a)等于( )A．5B．7C．9D．11【答案】B【解析】由f(a)＝3，得2a＋2－a＝3，两边平方得，22a＋2－2a＋2＝9，即22a＋2－2a＝7，∴f(2a)＝7.选B项．12.已知函数f(x)＝则f[f(－4)]等于( )A．－4B．－C．4D．6【答案】C【解析】f[f(－4)]＝f[()－4]＝f(16)＝＝4.13.给出函数f(x)＝，则f(－1)＝________.【答案】9【解析】f(－1)＝f(1)＝f(3)＝32＝9.14.若f(2x－1)＝3x－2x，则f(4)＝________.【答案】21【解析】令2x－1＝4，得x＝3，将其代入f(2x－1)＝3x－2x，得f(4)＝33－2×3＝21.15.设f(x)＝则f(f(－2))等于( )A．－1B．C．D．【答案】C【解析】因为f(－2)＝2－2＝，所以f(f(－2))＝f()＝1－＝1－＝，故答案选C.16.某种细菌经60分钟培养，可繁殖为原来的2倍，且知该细菌的繁殖规律为y＝10e kt，其中k为常数，t 表示时间(单位：小时)，y表示细菌个数，10个细菌经过7小时培养，细菌能达到的个数为( ) A．640B．1280C．2560D．5120【答案】B【解析】设原来的细菌数为a.由题意可得，在函数y＝10e kt中，当t＝1时，y＝2a.∴2a＝10e k即e k＝.当a＝10时，e k＝2，y＝10e kt＝10·2t，若t＝7，则可得此时的细菌数为y＝10×27＝1280，故选B.17.某环保小组发现某市生活垃圾年增长率为b，2009年该市生活垃圾量为a吨，由此可以预测2019年垃圾量为( )A．a(1＋10b)吨B．a(1＋9b)吨C．a(1＋b)10吨D．a(1＋b)9吨【答案】C【解析】2009年该市生活垃圾量为a吨，所以2010年产生的垃圾量是a(1＋b)吨，2011年产生的垃圾量是a(1＋b)(1＋b)＝a(1＋b)2吨，…由此可以预测2019年垃圾量为a(1＋b)10吨．故选C.18.某种计算机病毒是通过电子邮件进行传播的，如果某台计算机感染上这种病毒，那么它就会在下一轮病毒发作时传播一次病毒，并感染其它20台未感染病毒的计算机．现有一台计算机被第一轮病毒感染，问被第4轮病毒感染的计算机有( )台．A．60B．400C．8000D．160000【答案】C【解析】由题意可得，每一轮感染的计算机数量构成以1为首项，以20为公比的等比数列，故第4轮病毒感染的计算机数量为1×203＝8000台，故选C.19.一种产品的成本是a元，在今后的n年内，计划成本每年比上一年降低p%，则成本随着年数变化的函数关系式是( )A．a(1－p%)n(n∈N*)B．a(p%)n(n∈N*)C．a(1－p)n%(n∈N*)D．a(1－np%)(n∈N*)【答案】A【解析】设成本经过x年降低到y元，第一年为y＝a(1－p%)，第二年为y＝a(1－p%)(1－p%)＝a(1－p%)2，第三年为y＝a(1－p%)(1－p%)(1－p%)＝a(1－p%)3，…则随着年数n变化的函数关系式是y＝a(1－p%)n(n∈N*)．故选A.20.据报道，全球变暖，使北冰洋冬季冰盖面积在最近50年内减少了5%，如果按此规律，设2000年的冬季冰盖面积为m，从2000年起，经过x年后冬季冰盖面积y与x的函数关系是( )A．y＝·mB．y＝(1－)·mC．y＝0.9550·x·mD．y＝(1－0.0550·x)·m【答案】A【解析】设北冰洋冬季冰盖面积的年平均变化率为p，则p50＝0.95，∴p＝，∴设2000年的冬季冰盖面积为m，从2000年起，经过x年后冬季冰盖面积y与x的函数关系是：y＝·m. 故选A.21.某医药研究所开发一种新药，据监测，如果成人按规定的剂量服用该药，服药后每毫升血液中的含药量y(μg)与服药后的时间t(h)之间近似满足如图所示的曲线．其中OA是线段，曲线段AB是函数y＝k·at(t ≥1，a>0，k，a是常数)的图象．(1)写出服药后每毫升血液中含药量y关于时间t的函数关系式；(2)据测定：每毫升血液中含药量不少于2(μg)时治疗有效，假若某病人第一次服药为早上6：00，为保持疗效，第二次服药最迟是当天几点钟？(3)若按(2)中的最迟时间服用第二次药，则第二次服药后在过3h，该病人每毫升血液中含药量为多少μg？(精确到0.1μg)【答案】(1)当0≤t<1时，y＝8t；当t≥1时，把A(1，8)、B(7，1)代入y＝kat，得解得故y ＝(2)设第一次服药后最迟过t小时服第二次药，则解得t＝5，即第一次服药后5h服第二次药，也即上午11：00服药．(3)第二次服药3h后，每毫升血液中含第一次服药后的剩余量为：y1＝8()8＝μg，含第二次服药量为：y2＝8()3＝4μg，所以此时两次服药剩余的量为＋4≈4.7μg，故该病人每毫升血液中的含药量为4.7μg.11/11。

专题4.2 指数函数1、指数函数的概念：一般地，函数x y a = 叫做指数函数，其中x 是自变量，函数的定义域为R ．注意：指数函数的底数的取值范围，底数不能是负数、零和1．即 a>0且a ≠12、指数函数的图象和性质0<a<1a>1图像定义域R , 值域（0，+∞）（1）过定点（0，1）,即x=0时，y=1(2)在R 上是减函数(2)在R 上是增函数性质（3）当x>0时,0<y<1;当x<0时,y>1（3）当x>0时,y>1;当x<0时,0<y<1图象特征函数性质向x 轴正负方向无限延伸函数的定义域为R 函数图象都在x 轴上方函数的值域为R +图象关于原点和y 轴不对称非奇非偶函数共性函数图象都过定点（0，1）过定点（0，1）自左向右看，图象逐渐下降减函数在第一象限内的图象纵坐标都小于1当x>0时,0<y<1;在第二象限内的图象纵坐标都大于1当x<0时,y>10<a<1图象上升趋势是越来越缓函数值开始减小极快，到了某一值后减小速度较慢；自左向右看，图象逐渐上升增函数在第一象限内的图象纵坐标都大于1当x>0时,y>1;在第二象限内的图象纵坐标都小于1当x<0时,0<y<1a>1图象上升趋势是越来越陡函数值开始增长较慢，到了某一值后增长速度极快；注意： 指数增长模型：y=N(1+p)x 指数型函数： y=ka x 3 考点：（1）a b =N, 当b>0时，a,N 在1的同侧；当b<0时，a,N 在1的 异侧。

（2）指数函数的单调性由底数决定的，底数不明确的时候要进行讨论。

掌握利用单调性比较幂的大小，同底找对应的指数函数，底数不同指数也不同插进1(=a 0)进行传递或者利用（1）的知识。

（3）求指数型函数的定义域可将底数去掉只看指数的式子，值域求法用单调性。

2023届高考数学---指数与指数函数综合练习题（含答案解析）1、已知a ，b ∈(0，1)∪(1，＋∞)，当x ＞0时，1＜b x ＜a x ，则( ) A ．0＜b ＜a ＜1 B ．0＜a ＜b ＜1 C ．1＜b ＜aD ．1＜a ＜bC [∵当x ＞0时，1＜b x ，∴b ＞1.∵当x ＞0时，b x ＜a x ，∴当x ＞0时，(ab )x ＞1. ∴ab ＞1，∴a ＞b .∴1＜b ＜a ，故选C.]2、设f (x )＝e x ，0＜a ＜b ，若p ＝f (ab )，q ＝f (a ＋b2)，r ＝f （a ）f （b ），则下列关系式中正确的是( )A ．q ＝r ＜pB ．p ＝r ＜qC ．q ＝r ＞pD ．p ＝r ＞qC [∵0＜a ＜b ，∴a ＋b 2＞ab ，又f (x )＝e x 在(0，＋∞)上为增函数，∴f (a ＋b2)＞f (ab )，即q ＞p .又r ＝f （a ）f （b ）＝e a e b ＝e a ＋b2＝q ，故q ＝r ＞p .故选C.]3、已知函数f (x )＝a x (a ＞0，a ≠1)在[1，2]上的最大值比最小值大a2，则a 的值为________．12或32 [当0＜a ＜1时，a －a 2＝a 2， ∴a ＝12或a ＝0(舍去)． 当a ＞1时，a 2－a ＝a2， ∴a ＝32或a ＝0(舍去)． 综上所述，a ＝12或32.]4、已知定义域为R 的函数f (x )＝－2x ＋b2x ＋1＋a是奇函数．(1)求a ，b 的值；(2)若对任意的t ∈R ，不等式f (t 2－2t )＋f (2t 2－k )＜0恒成立，求k 的取值范围． [解] (1)因为f (x )是定义在R 上的奇函数，所以f (0)＝0，即－1＋b2＋a＝0，解得b ＝1，所以f (x )＝－2x ＋12x ＋1＋a.又由f (1)＝－f (－1)知－2＋14＋a ＝－－12＋11＋a， 解得a ＝2.(2)由(1)知f (x )＝－2x ＋12x ＋1＋2＝－12＋12x ＋1，由上式易知f (x )在R 上为减函数，又因为f (x )是奇函数，从而不等式f (t 2－2t )＋f (2t 2－k )＜0等价于f (t 2－2t )＜－f (2t 2－k )＝f (－2t 2＋k )．因为f (x )是R 上的减函数，由上式推得t 2－2t ＞－2t 2＋k . 即对一切t ∈R 有3t 2－2t －k ＞0， 从而Δ＝4＋12k ＜0，解得k ＜－13. 故k 的取值范围为(－∞，－13)．5、设y ＝f (x )在(－∞，1]上有定义，对于给定的实数K ，定义f K (x )＝⎩⎨⎧f （x ），f （x ）≤K ，K ，f （x ）＞K .给出函数f (x )＝2x ＋1－4x ，若对于任意x ∈(－∞，1]，恒有f K (x )＝f (x )，则( )A ．K 的最大值为0B ．K 的最小值为0C ．K 的最大值为1D ．K 的最小值为1D [根据题意可知，对于任意x ∈(－∞，1]，若恒有f K (x )＝f (x )，则f (x )≤K 在x ≤1上恒成立，即f (x )的最大值小于或等于K 即可．令2x ＝t ，则t ∈(0，2]，f (t )＝－t 2＋2t ＝－(t －1)2＋1，可得f (t )的最大值为1，所以K ≥1，故选D.]6、已知函数f (x )＝14x －λ2x －1＋3(－1≤x ≤2)．(1)若λ＝32，求函数f (x )的值域；(2)若函数f (x )的最小值是1，求实数λ的值． [解] (1)f (x )＝14x －λ2x －1＋3＝(12)2x －2λ·(12)x ＋3(－1≤x ≤2)． 设t ＝(12)x ，得g (t )＝t 2－2λt ＋3(14≤t ≤2)． 当λ＝32时，g (t )＝t 2－3t ＋3 ＝(t －32)2＋34(14≤t ≤2)．所以g (t )max ＝g (14)＝3716，g (t )min ＝g (32)＝34. 所以f (x )max ＝3716，f (x )min ＝34， 故函数f (x )的值域为[34，3716]． (2)由(1)得g (t )＝t 2－2λt ＋3 ＝(t －λ)2＋3－λ2(14≤t ≤2)，①当λ≤14时，g (t )min ＝g (14)＝－λ2＋4916， 令－λ2＋4916＝1，得λ＝338＞14，不符合，舍去； ②当14＜λ≤2时，g (t )min ＝g (λ)＝－λ2＋3，令－λ2＋3＝1，得λ＝2(λ＝－2＜14，不符合，舍去)；③当λ＞2时，g(t)min＝g(2)＝－4λ＋7，令－4λ＋7＝1，得λ＝32＜2，不符合，舍去．综上所述，实数λ的值为 2.一、选择题1．设a＞0，将a2a·3a2表示成分数指数幂的形式，其结果是()A．a 12B．a 5 6C．a 76D．a32C[a2a·3a2＝a2a·a23＝a2a53＝a2a56＝a2－56＝a76.故选C.]2．已知函数f(x)＝4＋2a x－1的图像恒过定点P，则点P的坐标是()A．(1，6) B．(1，5)C．(0，5) D．(5，0)A[由于函数y＝a x的图像过定点(0，1)，当x＝1时，f(x)＝4＋2＝6，故函数f(x)＝4＋2a x－1的图像恒过定点P(1，6)．]3．设a＝0.60.6，b＝0.61.5，c＝1.50.6，则a，b，c的大小关系是()A．a＜b＜c B．a＜c＜bC．b＜a＜c D．b＜c＜aC[y＝0.6x在R上是减函数，又0.6＜1.5，∴0.60.6＞0.61.5.又y＝x0.6为R上的增函数，∴1.50.6＞0.60.6，∴1.50.6＞0.60.6＞0.61.5，即c＞a＞b.]4．函数y ＝xa x|x |(0＜a ＜1)的图像的大致形状是( )A BC DD [函数的定义域为{x |x ≠0}，所以y ＝xa x |x |＝⎩⎨⎧a x，x ＞0，－a x ，x ＜0，当x ＞0时，函数是指数函数y ＝a x ，其底数0＜a ＜1，所以函数递减；当x ＜0时，函数y ＝－a x 的图像与指数函数y ＝a x (0＜a ＜1)的图像关于x 轴对称，所以函数递增，所以应选D.]5．已知函数f (x )＝⎩⎨⎧1－2－x ，x ≥0，2x －1，x ＜0，则函数f (x )是( )A ．偶函数，在[0，＋∞)上单调递增B ．偶函数，在[0，＋∞)上单调递减C ．奇函数，且单调递增D ．奇函数，且单调递减C [易知f (0)＝0，当x ＞0时，f (x )＝1－2－x ，－f (x )＝2－x －1，此时－x ＜0，则f (－x )＝2－x －1＝－f (x )；当x ＜0时，f (x )＝2x －1，－f (x )＝1－2x ，此时，－x ＞0，则f (－x )＝1－2－(－x )＝1－2x ＝－f (x )．即函数f (x )是奇函数，且单调递增，故选C.]二、填空题1、若函数f (x )＝a |2x －4|(a ＞0，a ≠1)满足f (1)＝19，则f (x )的单调递减区间是________．[2，＋∞) [由f (1)＝19得a 2＝19，所以a ＝13或a ＝－13(舍去)，即f (x )＝(13)|2x －4|.由于y ＝|2x －4|在(－∞，2]上单调递减，在[2，＋∞)上单调递增， 所以f (x )在(－∞，2]上单调递增，在[2，＋∞)上单调递减．] 2、不等式2－x 2＋2x＞(12)x ＋4的解集为________．(－1，4) [原不等式等价为2－x 2＋2x＞2－x －4，又函数y ＝2x 为增函数，∴－x 2＋2x ＞－x －4， 即x 2－3x －4＜0，∴－1＜x ＜4.]3、若直线y 1＝2a 与函数y 2＝|a x －1|(a ＞0且a ≠1)的图像有两个公共点，则a 的取值范围是________．(0，12) [(数形结合法)当0＜a ＜1时，作出函数y 2＝|a x －1|的图像，由图像可知0＜2a ＜1， ∴0＜a ＜12；同理，当a ＞1时，解得0＜a ＜12，与a ＞1矛盾． 综上，a 的取值范围是(0，12)．] 三、解答题4、已知函数f (x )＝(13)ax 2－4x ＋3.(1)若a ＝－1，求f (x )的单调区间； (2)若f (x )有最大值3，求a 的值； (3)若f (x )的值域是(0，＋∞)，求a 的值． [解] (1)当a ＝－1时，f (x )＝(13)－x 2－4x ＋3，令u ＝－x 2－4x ＋3＝－(x ＋2)2＋7.则u 在(－∞，－2)上单调递增，在(－2，＋∞)上单调递减，而y ＝(13)u 在R 上单调递减，所以f (x )在(－∞，－2)上单调递减，在(－2，＋∞)上单调递增，即函数f (x )的单调递增区间是(－2，＋∞)，单调递减区间是(－∞，－2)．(2)令h (x )＝ax 2－4x ＋3，则f (x )＝(13)h (x )，由于f (x )有最大值3，所以h (x )应有最小值－1.因此必有⎩⎪⎨⎪⎧a ＞0，12a －164a ＝－1，解得a ＝1，即当f (x )有最大值3时，a 的值为1.(3)由f (x )的值域是(0，＋∞)知，函数y ＝ax 2－4x ＋3的值域为R ，则必有a ＝0. 5、已知函数f (x )＝b ·a x (其中a ，b 为常量，且a ＞0，a ≠1)的图像经过点A (1，6)，B (3，24)．(1)求f (x )的表达式；(2)若不等式(1a )x ＋(1b )x －m ≥0在(－∞，1]上恒成立，求实数m 的取值范围． [解] (1)因为f (x )的图像过A (1，6)，B (3，24)， 所以⎩⎨⎧b ·a ＝6，b ·a 3＝24. 所以a 2＝4，又a ＞0，所以a ＝2，b ＝3. 所以f (x )＝3·2x .(2)由(1)知a ＝2，b ＝3，则x ∈(－∞，1]时，(12)x ＋(13)x －m ≥0恒成立，即m ≤(12)x ＋(13)x 在(－∞，1]上恒成立．又因为y ＝(12)x 与y ＝(13)x 均为减函数，所以y ＝(12)x ＋(13)x也是减函数，所以当x＝1时，y＝(12)x＋(13)x有最小值56.所以m≤56.即m的取值范围是(－∞，56]．本课结束。