折射和反射定律、菲涅耳公式
- 格式:ppt
- 大小:2.12 MB
- 文档页数:39

物理光学折射与反射公式整理折射与反射是物理光学中的基本现象,它们描述了光在不同介质间传播时的行为。
在本文中,我们将整理折射与反射公式,以便更好地理解和应用这些概念。
1. 反射公式当光线从一种介质射向另一种介质的界面时,一部分光线会发生反射,即光线回射到原来的介质中。
反射公式用于计算反射角和入射角之间的关系。
根据反射定律,入射角(θ₁)等于反射角(θ₂):θ₁ = θ₂这个公式适用于所有类型的反射,无论是在光滑的表面上还是在粗糙的表面上。
2. 折射公式当光线从一种介质射入另一种介质时,光线会发生偏折,即光线改变传播方向。
折射公式用于计算入射角和折射角之间的关系。
根据斯涅尔定律(也称为折射定律),入射角(θ₁)和折射角(θ₂)满足以下关系:n₁sin(θ₁) = n₂sin(θ₂)其中,n₁和n₂分别代表两个介质的折射率。
折射率是介质中光传播速度与真空中光传播速度的比值。
3. 全反射临界角当光线从光密介质射向光疏介质时,当入射角大于一个特定的角度(临界角),发生全反射。
此时,光线完全反射回原介质,不再折射入另一介质。
临界角可以通过折射公式计算得出。
当折射角(θ₂)等于90度时,入射角(θ₁)即为临界角(θc)。
此时,折射公式可以简化为:n₁sin(θc) = n₂如果入射角小于临界角,则出射角将变大,并根据折射公式计算。
4. 光的菲涅尔公式菲涅尔公式用于计算光线从一个介质射向另一个介质时的反射和透射的强度。
反射分为平行极化光和垂直极化光两种情况。
对于平行极化光,反射系数(r₁)由以下公式给出:r₁ = (n₁cos(θ₁) - n₂cos(θ₂)) / (n₁cos(θ₁) + n₂cos(θ₂))对于垂直极化光,反射系数(r₂)由以下公式给出:r₂ = (n₂cos(θ₁) - n₁cos(θ₂)) / (n₂cos(θ₁) + n₁cos(θ₂))透射系数(t)由以下公式给出:t = 2n₁cos(θ₁) / (n₁cos(θ₁) + n₂cos(θ₂))这些公式描述了反射和透射光的幅度与入射角、折射角以及介质折射率之间的关系。

菲涅尔方程式
菲涅耳方程式(Fresnel Equations)是用来描述光在两种介质界面上反射和透射的现象和规律的方程式。
它由奥古斯汀·菲涅耳(Augustin-Jean Fresnel)在19世纪提出,并成为光学领域中的重要理论工具。
菲涅耳方程式分为反射方程和透射方程,分别描述了光在界面上的反射和折射(透射)行为。
这些方程式基于电磁波的传播和边界条件,可以通过麦克斯韦方程和边界条件进行推导。
反射方程描述了入射光波在介质界面上的反射行为。
对于垂直入射的光,反射系数(反射光强与入射光强之比)可以通过下述菲涅耳反射方程计算:
r = (n1 - n2) / (n1 + n2)
其中,n1和n2分别是两种介质的折射率,r是反射系数。
透射方程描述了入射光波通过介质界面的折射行为。
同样对于垂直入射的光,透射系数(透射光强与入射光强之比)可以通过下述菲涅耳透射方程计算:
t = 2n1 / (n1 + n2)
其中,n1和n2分别是两种介质的折射率,t是透射系数。
需要注意的是,菲涅耳方程式仅适用于垂直入射的光,并且忽略了光在界面上的散射和吸收行为。
在实际应用中,还需要考虑光的入射角度、极化状态和表面特性等因素,并结合其他衍射、干涉等现象来对界面上的光行为进行更全面的描述。
菲涅耳方程式在材料科学、光学器件设计和表面反射控制等领域中具有广泛的应用,并能解释和预测光在界面上的反射和透射现象。

光线传播的四个基本定律光是一种电磁波,它在空气、水和其他介质中传播时,遵循着一些基本的定律。
这些定律可以帮助我们理解光的传播和反射,也为光学领域的实践应用提供了重要的基础。
本文将介绍光线传播的四个基本定律,分别是折射定律、反射定律、菲涅尔公式和全反射定律。
一、折射定律当光线从一种介质进入另一种介质时,它会发生折射。
折射定律规定了光线在两种介质之间传播时的方向和角度关系。
具体来说,它表明:入射角和折射角的正弦之比在两种介质中是一个常量,这个常量被称为折射率。
这个定律可以用来解释很多现象,比如为什么水中的物体看起来更小,为什么眼镜的镜片可以矫正视力等。
二、反射定律当光线从一种介质射向另一种介质的边界时,一部分光线会被反射回去。
反射定律规定了反射光线的方向和角度关系。
具体来说,它表明:入射角和反射角的大小相等,方向相反,且在同一平面内。
这个定律可以用来解释为什么镜子能够反射图像,为什么光可以在光学器件中进行反射等。
三、菲涅尔公式菲涅尔公式是用来计算反射和折射光线的强度的公式。
它基于电磁波在边界处的边界条件,将电磁波的振幅、相位和入射角考虑在内,可以精确地预测光线的反射和折射情况。
这个公式在光学领域的应用非常广泛,比如用于设计反光镜、光学镜头等。
四、全反射定律当光线从一个介质射向另一个介质时,如果入射角大于某个临界角,就会发生全反射。
全反射定律规定了这个临界角的大小和折射光线的存在性。
具体来说,它表明:入射角大于临界角时,光线将完全反射回去,没有折射光线存在。
临界角的大小取决于两个介质的折射率,可以用折射定律计算得出。
这个定律在光纤通信、光学器件等领域的应用非常广泛。
总结光线传播的四个基本定律是折射定律、反射定律、菲涅尔公式和全反射定律。
它们分别描述了光线在不同介质之间传播时的方向、角度和强度关系,为我们理解光学现象和应用光学技术提供了重要的基础。
在实践中,我们可以根据这些定律来设计光学器件、计算光线的传播和反射等,以实现各种光学应用。

菲涅耳原理
菲涅耳原理指的是一个波从一个介质传播到另一介质时,会发生折射和反射,而这些现象可以通过一组简单的公式进行描述。
这个原理是由法国科学家菲涅耳(Augustin-Jean Fresnel)在19世纪初期提出的,他研究的主要是光的传播和衍射。
后来,这个原理也被推广至其他波动领域。
入射角是波的传播方向与介质界面法线的夹角。
假设波从一般介质A传入到另一介质B,那么入射角就是这个波与介质A表面法线的夹角。
这些参数可以用以下公式计算:
折射角 = 反射角 = i
其中r为反射系数,n1和n2分别是介质A和介质B的折射率,i为入射角。
关于折射率,我们可以根据介质的光密度来计算。
光密度是指在介质中传播的光线数量,它通常与介质的折射率成正比。
菲涅耳原理可以帮助我们理解许多光学现象,例如透明物体、反光镜、玻璃表面的反射、水面反射等等。
总的来说,菲涅耳原理揭示了波在介质间的传播规律和相互作用,使我们能够更加深入地理解和利用波的性质。

玻璃的反射率可以通过菲涅尔公式来计算。
菲涅尔公式描述了光线从介质1射入介质2时的反射和折射现象。
对于垂直入射的光线,菲涅尔公式可以表示为:
反射率R = ((n1 - n2) / (n1 + n2))^2
其中,n1是入射介质的折射率,n2是出射介质的折射率。
对于平行入射的光线,菲涅尔公式可以表示为:
反射率R = ((n1 * cosθ2 - n2 * cosθ1) / (n1 * cosθ2 + n2 * cosθ1))^2
其中,θ1是入射角,θ2是折射角,n1和n2分别是入射介质和出射介质的折射率。
需要注意的是,菲涅尔公式只适用于光线从一个介质射入另一个介质的情况,且假设介质是均匀的。
在实际应用中,还需要考虑光线的波长、入射角度等因素。

fresnel公式Fresnel公式是描述光在两种介质之间传播时发生反射和折射的规律。
它由奥古斯汀·让·菲涅耳在19世纪初提出。
Fresnel公式分为反射和折射两个部分,分别描述了光的入射、反射和透射的振幅和相位之间的关系。
根据Fresnel公式,入射光线在介质界面上会发生一部分反射,另一部分则会折射进入下一个介质。
对于垂直入射的光线,反射系数和折射系数可以按以下公式计算:反射系数R = |(n1 - n2) / (n1 + n2)|^2折射系数T = 1 - R其中,n1和n2分别为上一个介质和下一个介质的折射率。
反射系数表示入射光线被反射的比例,折射系数表示入射光线被折射的比例。
对于非垂直入射的光线,Fresnel公式还包括极化方向的影响。
在这种情况下,入射光线可以分为垂直极化(s极化)和平行极化(p极化)两部分。
对于s极化,反射和折射系数分别为:反射系数Rs = |(n1*cos(θ1) - n2*co s(θ2)) / (n1*cos(θ1) + n2*cos(θ2))|^2折射系数Ts = 1 - Rs其中,θ1和θ2分别为入射角和折射角。
对于p极化,反射和折射系数分别为:反射系数Rp = |(n2*cos(θ1) - n1*cos(θ2)) / (n2*cos(θ1) + n1*cos(θ2))|^2折射系数Tp = 1 - RpFresnel公式在光学领域和光学器件设计中具有广泛应用。
例如,它可以被用来优化反射镜、透镜和光学薄膜的性能,以及研究光在介质中的传播和吸收等现象。
总结来说,Fresnel公式描述了光线在介质界面上的反射和折射行为,它提供了计算反射和折射系数的数学表达式,便于研究光的传播和相位的变化。



菲涅尔积分公式
菲涅尔积分公式是光学和工程学中非常重要的公式之一,它用于描述光在两种不同介质之间反射和折射的过程。
这个公式是由物理学家和数学家奥古斯特·菲涅尔在19世纪初提出的,它基于光的波动理论,描述了光波在两种不同介质之间的传播行为。
菲涅尔积分公式包含两个部分:反射系数和折射系数。
反射系数用于描述光在两种不同介质之间的反射行为,而折射系数用于描述光在两种不同介质之间的折射行为。
这两个系数都与入射角、反射角和折射角有关,同时也与两种介质的折射率有关。
反射系数和折射系数的具体形式如下:
1. 反射系数R = (n2 * sinθi - n1 * sinθt) / (n2 * sinθi + n1 * sinθt),其中n1 和n2 分别是两种介质的折射率,θi 和θt 分别是入射角和反射角。
2. 折射系数T = 2 * n1 * sinθi / (n2 * sinθt + n1 * sinθi),其中n1 和n2 分别是两种介质的折射率,θi 和θt 分别是入射角和折射角。
在光学和工程学中,菲涅尔积分公式被广泛应用于计算光在各种不同介质之间的反射和折射行为。
这个公式对于光学设计、成像系统分析、光学仪器制造等领域非常重要。
除了菲涅尔积分公式外,还有许多其他公式和定理用于描述光的行为,例如斯涅尔定律、反射定理、折射定理等。
这些公式和定理都是基于光的波动理论或量子理论,是光学和工程学领域的重要工具。
综上所述,菲涅尔积分公式是一个重要的公式,用于描述光在两种不同介质之间反射和折射的行为。
它基于光的波动理论,包含反射系数和折射系数两个部分,对于光学设计和工程学领域非常重要。
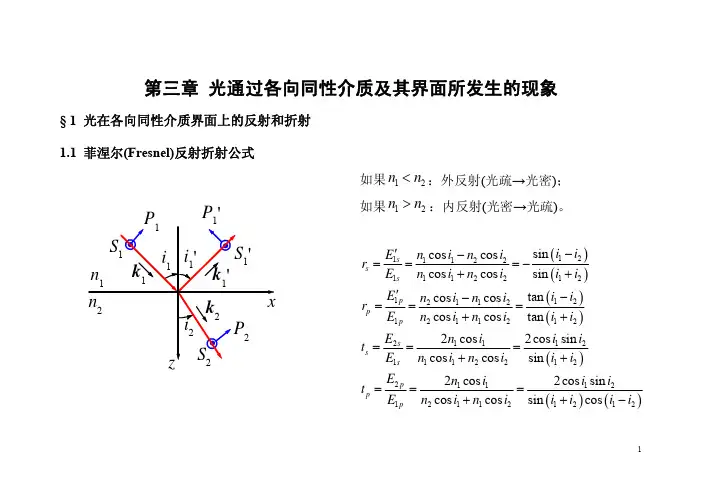
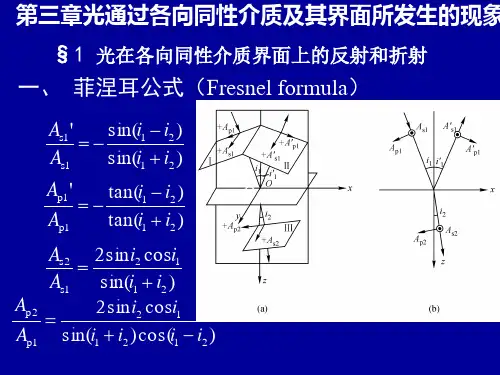
光在介质膜界面的反射率一、光垂直入射介质界面时的反射率光在介质界面反射、折射时的菲涅耳公式为:式中r s 、r p 分别为s分量、p分量振幅反射系数, t s 、t p 分别为s分量、p分量振幅透射系数.二、单层膜的反射率首先计算单层膜反射率的多光束干涉形式. 也就是说, 上述计算单层薄膜反射率的双光束干涉形式仅是近似的处理方法.如图, 假定在折射率为n 2 的光学基板上有一层厚度均匀的薄膜, 膜折射率为n 1 , 膜的几何厚度为d 1 , 入射介质的折射率为n 0 , 当光束照射到薄膜上表面时, 光束在薄膜两表面上要多次反射, 因而产生一组反射光束1, 2, 3,……, 和一组透射1’,2’,3’,……,如果入射光的振幅为E 0 , 则各反射光束的振幅为这里的分别表示在两个界面上的反射系数和透射系数(图2).由斯托克斯定律可知, .式(1)中的为膜的位相厚度,即两相邻光束间的位相差为.反射光的合振幅E R 为于是我们得到单层膜的反射系数为从上式可见, 单层膜的反射系数是一个复数,故上式可写成上式中可通过菲涅尔公式求得为膜的位相厚度. 为反射光相移,表示反射光波的位相落后于入射光波的值.单层膜的反射率R 为从上面的结果我们可以看出,单层膜的两个界面可以用一个等效界面来代替.如图3所示,膜的折射率为nk,入射介质的折射率为nk-1,出射介质(或基板玻璃)的折射率为nk+1,膜的位相厚度是k,设单层膜上界面的反射系数为rk,下界面的反射系数为rk+1,于是这个单层膜的等效界面的反射系数为,综上求得:三、多层膜的反射率经过这样处理和理解以后, 我们可以将单层膜的反射率计算推广应用到多层膜场合. 首先从与基片相邻的底层膜开始, 将底层膜的两个界面等效成一个界面, 然后再将这个等效界面与上一个界面等效为一个界面, 依次往上递推到膜系的顶层的第一个界面, 如图由之前的结果可知:根据折射定律, 有因此可以得到各层膜中光的入射和折射角i对各层膜有,根据菲涅尔公式计算出各层的菲涅尔系数,对p分量,对s分量最后求出反射率四、增透膜,增反膜为了减少光在光学元件表面上的反射损失,可利用薄膜上、下表面反射光的相消干涉来减少反射光. 因此常在光学元件的表面镀制介质薄膜———增透膜.为了提高反射率, 常在玻璃上镀制增反膜, 增反膜的折射率比玻璃的高, 称为高膜。