(浙江专用)高考数学专题五数列第37练数列的前n项和及求法练习

温馨提示：此套题为Word版，请按住Ctrl,滑动鼠标滚轴，调节合适的观看比例，答案解析附后。

关闭Word文档返回原板块。

核心素养测评三十六等比数列及其前n项和(30分钟60分)一、选择题(每小题5分,共25分)1.已知数列a,a(1-a),a(1-a)2,…是等比数列,则实数a满足的条件是( )A.{a|a≠1}B.{a|a≠0或a≠1}C.{a|a≠0}D.{a|a≠0且a≠1}【解析】选D.由等比数列定义可知a≠0且1-a≠0,即a≠0且a≠1.2.已知数列{a n}的首项a1=2,数列{b n}为等比数列,且b n=,若b10b11=2,则a21=( ) A.29 B.210 C.211 D.212【解析】选C.由b n=,且a1=2,得b1==,a2=2b1;b2=,a3=a2b2=2b1b2;b3=,a4=a3b3=2b1b2b3;…;a n=2b1b2b3…b n-1,所以a21=2b1b2b3…b20,又{b n}为等比数列,所以a21=2(b1b20)(b2b19)…(b10b11)=2(b10b11)10=211.3.(2020·丽水模拟)设等比数列{a n}的前n项和为S n,下列结论一定成立的是( ) A.a1+a3≥2a2 B.a1+a3≤2a2C.a1S3>0D.a1S3<0【解析】选C.选项A,数列-1,1,-1为等比数列,但a1+a3=-2<2a2=2,故A 错误;选项B,数列1,-1,1为等比数列,但a1+a3=2>2a2=-2,故B错误;选项D,数列1,-1,1为等比数列,但a1S3=1>0,故D错误;对于选项C,a1(a1+a2+a3)=a1(a1+a1q+a1q2)=(1+q+q2),因为等比数列的项不为0,故>0,而1+q+q2=+>0,故(1+q+q2)>0,即a1S3>0.【变式备选】已知方程(x2-mx+2)(x2-nx+2)=0的四个根组成以为首项的等比数列,则等于( )A. B.或C. D.以上都不对【解析】选B.设a,b,c,d是方程(x2-mx+2)(x2-nx+2)=0的四个根,不妨设a<c<d<b,则a·b=c·d=2,a=,故b=4,根据等比数列的性质,得到:c=1,d=2,则m=a+b=,n=c+d=3或m=c+d=3,n=a+b=,则=或=.4.(2020·宁波模拟)在单调递减的等比数列{a n}中,若a3=1,a2+a4=,则a1=( ) A.2 B.4 C. D.2【解析】选B.在等比数列{a n}中,a2a4==1,又a2+a4=,数列{a n}为递减数列,所以a2=2,a4=,所以q2==,所以q=(负值舍去),a1==4.【变式备选】已知数列{a n}的前n项和S n=Aq n+B(q≠0),则“A=-B”是“数列{a n}是等比数列”的 ( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【解析】选B.若A=B=0,则S n=0,故数列{a n}不是等比数列;若数列{a n}是等比数列,则a1=Aq+B,a2=Aq2-Aq,a3=Aq3-Aq2,由=,得A=-B.5.已知数列{a n}满足a1,,,…,是首项为1,公比为2的等比数列,则a101=( ) A.22 020 B.22 525 C.2101 D.25 050【解析】选D.因为数列{a n}满足a1,,,…,是首项为1,公比为2的等比数列,所以a1=1,=2n-1,n≥2,所以a n=a1···…·=1×2×22×…×2n-1==,当n=1时,a1=1满足上式,故a n=,所以a101==25 050.【变式备选】在递增的等比数列{a n}中,已知a1+a n=34,a3·a n-2=64,且前n项和S n=42,则n等于( )A.3B.4C.5D.6【解析】选A.因为{a n}为等比数列,所以a3·a n-2=a1·a n=64.又a1+a n=34,所以a1,a n是方程x2-34x+64=0的两根,解得或又因为{a n}是递增数列,所以由S n===42,解得q=4.由a n=a1q n-1=2×4n-1=32,解得n=3.二、填空题(每小题5分,共15分)6.已知等比数列{a n}的前n项和为S n,若=2a3a6,S5=-62,则a1的值是________,公比为________.【解析】设{a n}的公比为q.由=2a3a6得(a1q4)2=2a1q2·a1q5,所以q=2,所以S5==-62,a1=-2.答案:-2 2【变式备选】在等比数列{a n}中,已知a1=-1,a4=64,则q=________,S4=________.【解析】因为a4=a1·q3,所以q3=-64,q=-4,S4===51. 答案:-4517.(2019·全国卷Ⅰ)记S n为等比数列{a n}的前n项和.若a1=,=a6,则S5=________.【解析】设等比数列的公比为q,由已知a1=,=a6,所以=q5,又q≠0,所以q=3,所以S5===.答案:【变式备选】等比数列{a n}的各项均为实数,其前n项和为S n.已知S3=,S6=,则a8=________.【解析】设等比数列{a n}的公比为q,则由S6≠2S3得q≠1,则S3==,S6==,解得q=2,a1=,则a8=a1q7=×27=32. 答案:328.若等比数列{a n}的各项均为正数,且a10a11+a9a12=2e5,则ln a1+ln a2+…+ln a20=________. 世纪金榜导学号【解析】因为数列{a n}为等比数列,且a10a11+a9a12=2e5,所以a10a11+a9a12=2a10a11=2e5,所以a10a11=e5,所以ln a1+ln a2+…+ln a20=ln(a1a2…a20)=ln(a10a11)10=ln(e5)10=lne50=50.答案:50三、解答题(每小题10分,共20分)9.(2018·全国卷Ⅲ)等比数列中,a1=1,a5=4a3.(1)求的通项公式.(2)记S n为的前n项和.若S m=63,求m.【解析】(1)设{a n}的公比为q,由题设得a n=q n-1.由已知得q4=4q2,解得q=0(舍去),q=-2或q=2.故a n=(-2)n-1或a n=2n-1.(2)若a n=(-2)n-1,则S n=.由S m=63得(-2)m=-188,此方程没有正整数解.若a n=2n-1,则S n=2n-1.由S m=63得2m=64,解得m=6.综上,m=6.10.(2020·郑州模拟)已知等比数列{a n}的公比q>0,其前n项和为S n,且S5=62,a4,a5的等差中项为3a3.(1)求数列{a n}的通项公式.(2)设b n=,求数列{b n}的前n项和T n. 世纪金榜导学号【解析】(1)因为a4+a5=6a3,所以a1q3+a1q4=6a1q2,即q2+q-6=0,解得q=2或q=-3(舍去).所以S5==31a1=62,a1=2,所以a n=2·2n-1=2n.(2)因为b n===,所以T n=b1+b2+…+b n====-.(20分钟40分)1.(5分)中国古代数学名著《九章算术》中有这样一个问题:今有牛、马、羊食人苗,苗主责之粟五斗.羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟.羊主人说:“我的羊所吃的禾苗只有马的一半.”马主人说:“我的马所吃的禾苗只有牛的一半.”打算按此比率偿还,他们各应偿还多少?已知牛、马、羊的主人各应偿还粟a升,b升,c升,1斗为10升,则下列判断正确的是( )A.a,b,c成公比为2的等比数列,且a=B.a,b,c成公比为2的等比数列,且c=C.a,b,c成公比为的等比数列,且a=D.a,b,c成公比为的等比数列,且c=【解析】选D.由题意可得,a,b,c成公比为的等比数列,b=a,c=b,三者之和为50升,故4c+2c+c=50,解得c=.【变式备选】已知等比数列{a n}的公比q=2,前100项和为S100=90,则其偶数项a2+a4+…+a100为( )A.15B.30C.45D.60【解析】选D.S100=a1+a2+…+a100=90,设S=a1+a3+…+a99,则2S=a2+a4+…+a100,所以S+2S=90,S=30,故a2+a4+…+a100=2S=60.2.(5分)在等比数列{a n}中,a3,a15是方程x2-6x+8=0的根,则=( )A.2B.2C.1D.-2【解析】选A.由题知,a3+a15=6>0,a3a15=8>0,则a3>0,a15>0,由等比数列的性质知a1a17=a3a15=8=⇒a9=±2.设等比数列{a n}的公比为q,则a9=a3q6>0,故a9=2,故==2.3.(5分)(2019·全国卷Ⅰ)记S n为等比数列{a n}的前n项和.若a1=1,S3=,则S4=________.【解析】设等比数列的公比为q,由已知S3=a1+a1q+a1q2=1+q+q2=,即q2+q+=0,解得q=-,所以S4===.答案:【变式备选】设{a n}是公比为q的等比数列,S n是它的前n项和,若{S n}是等差数列,则q为________.【解析】若q=1,则S n=na1,所以{S n}是等差数列;若q≠1,则当{S n}是等差数列时,一定有2S2=S1+S3,所以2·=a1+,即q3-2q2+q=0,故q(q-1)2=0,所以q=0或q=1,而q≠0,q≠1,所以此时不成立.综上可知,q=1.答案:14.(12分)已知正项数列{a n}满足a1+a2+a3+…+a n=.世纪金榜导学号(1)求数列{a n}的通项公式.(2)设b n=2n·a n,求数列{b n}的前n项和T n.【解题指南】(1)式中令n=1,求得a1=1,n用n-1代,得a1+a2+a3+…+a n-1=,两式作差化简可得a n-a n-1=2,进而可求得a n. (2)由(1)可得b n=·2n,由错位相减法可求和.【解析】(1)设数列{a n}的前n项和为S n.当n=1时, a1=,所以a1=1,当n≥2时,4S n=,所以4S n-1=,两式相减得4a n=+2a n--2a n-1,即(a n+a n-1)(a n-a n-1-2)=0,又a n>0,所以a n-a n-1=2,所以数列{a n}是首项为1,公差为2的等差数列,即a n=2n-1.(2)因为b n=(2n-1)·2n,所以T n=1×21+3×22+5×23+…+(2n-1)×2n,①2T n=1×22+3×23+5×24+…+(2n-3)×2n+(2n-1)×2n+1,②①-②得-T n=2+2(22+23+…+2n)-(2n-1)×2n+1=2-8+2n+2-(2n-1)×2n+1=-6+2n+1(2-2n+1)=-6+2n+1(3-2n),所以T n=6+2n+1(2n-3).5.(13分)已知数列{a n}的前n项和为S n,且a n=(n∈N*).(1)若数列{a n+t}是等比数列,求t的值.(2)求数列{a n}的通项公式. 世纪金榜导学号【解析】(1)当n=1时,由a1==得a1=1;当n≥2时,a n=S n-S n-1=2a n-n-2a n-1+(n-1),即a n=2a n-1+1,所以a2=3,a3=7. 依题意得(3+t)2=(1+t)(7+t),解得t=1,当t=1时,a n+1=2(a n-1+1),n≥2,即{a n+1}为等比数列成立,故实数t的值为1.(2)由(1)知当n≥2时,a n+1=2(a n-1+1),又因为a1+1=2,所以数列{a n+1}是首项为2,公比为2的等比数列,所以a n+1=2×2n-1=2n,所以a n=2n-1. 【变式备选】已知首项为的等比数列{a n}的前n项和为S n(n∈N*),且-2S2,S3,4S4成等差数列.(1)求数列{a n}的通项公式.(2)证明:S n+≤(n∈N*).【解析】(1)设等比数列{a n}的公比为q,因为-2S2,S3,4S4成等差数列,所以2S3=4S4-2S2,即S3=2S4-S2,即S4-S3=S2-S4,可得2a4=-a3,于是q==-.又a1=,所以等比数列{a n}的通项公式为a n=×=(-1)n-1·.(2)由(1)知,S n=1-,S n+=1-+=当n为奇数时,S n+随n的增大而减小,所以S n+≤S1+=.当n为偶数时,S n+随n的增大而减小,所以S n+≤S2+=.故对于n∈N*,有S n+≤.1.“十二平均律”是通用的音律体系,明代朱载堉最早用数学方法计算出半音比例,为这个理论的发展做出了重要贡献.十二平均律将一个纯八度音程分成十二份,依次得到十三个单音,从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于.若第一个单音的频率为f,则第八个单音的频率为( ) 世纪金榜导学号A. fB. fC. fD. f【解析】选D.这13个单音构成了一个以f为首项,为公比的等比数列,所以a n=a1q n-1=f·()n-1,即a8= f.2.(2020·郑州模拟)设首项为1的数列{a n}的前n项和为S n,且a n=若S m>2 020,则正整数m的最小值为( )世纪金榜导学号A.15B.16C.17D.18【解析】选C.由题意知a2k=a2k-1+1,a2k+1=2a2k+1,所以a2k+1=2(a2k-1+1)+1=2a2k-1+3,即a2k+1+3=2(a2k-1+3).又a1+3=4,所以数列是以4为首项,2为公比的等比数列, 所以a2k-1=4·2k-1-3,a2k=4·2k-1-2,所以S奇=a1+a3+…+a2k-1=-3k=2k+2-4-3k,S偶=a2+a4+…+a2k=2k+2-4-2k,所以S2k=S奇+S偶=2k+3-8-5k.当k=8时,S16=2 000<2 020.又a17=1021,所以S17=3 021>2 020,故正整数m的最小值为17.关闭Word文档返回原板块快乐分享，知识无界！感谢您的下载!由Ruize收集整理！。

求数列前N 项和的七种方法1. 公式法等差数列前n 项和：特别的，当前n 项的个数为奇数时，211(21)k k S k a ++=+，即前n 项和为中间项乘以项数。

这个公式在很多时候可以简化运算。

等比数列前n 项和： q=1时，1n S na =()1111n n a q q S q-≠=-，，特别要注意对公比的讨论。

其他公式： 1、)1(211+==∑=n n k S nk n 2、)12)(1(6112++==∑=n n n k S nk n3、213)]1(21[+==∑=n n k S nk n[例1] 已知3log 1log 23-=x ，求⋅⋅⋅++⋅⋅⋅+++n x x x x 32的前n项和.[例2] 设S n ＝1+2+3+…+n，n ∈N *,求1)32()(++=n nS n S n f 的最大值.2. 错位相减法这种方法是在推导等比数列的前n 项和公式时所用的方法，这种方法主要用于求数列{a n · b n }的前n 项和，其中{ a n }、{ b n }分别是等差数列和等比数列. [例3] 求和：132)12(7531--+⋅⋅⋅++++=n n x n x x x S ………………………①[例4] 求数列⋅⋅⋅⋅⋅⋅,22,,26,24,2232n n 前n 项的和.练习： 求：S n=1+5x+9x 2+······+(4n -3)xn-13. 分组法求和有一类数列，既不是等差数列，也不是等比数列，若将这类数列适当拆开，可分为几个等差、等比或常见的数列，然后分别求和，再将其合并即可.[例5] 求数列的前n 项和：231,,71,41,1112-+⋅⋅⋅+++-n aa a n ，…[例6] 求数列{n(n+1)(2n+1)}的前n 项和.解：设kk k k k k a k ++=++=2332)12)(1(∴∑=++=nk n k k k S 1)12)(1(＝)32(231k k k n k ++∑=将其每一项拆开再重新组合得S n＝kk k nk nk nk ∑∑∑===++1213132（分组）＝)21()21(3)21(2222333n n n +⋅⋅⋅++++⋅⋅⋅++++⋅⋅⋅++＝2)1(2)12)(1(2)1(22++++++n n n n n n n（分组求和）＝2)2()1(2++n n n练习：求数列∙∙∙+∙∙∙),21(,,813,412,211n n 的前n 项和。

专题7.3 等比数列及其前n 项和1．（2021·全国高考真题（文））记n S 为等比数列{}n a 的前n 项和.若24S =，46S =，则6S =（ ）A ．7B ．8C ．9D ．10【答案】A 【解析】根据题目条件可得2S ，42S S -，64S S -成等比数列，从而求出641S S -=，进一步求出答案.【详解】∵n S 为等比数列{}n a 的前n 项和，∴2S ，42S S -，64S S -成等比数列∴24S =，42642S S -=-=∴641S S -=，∴641167S S =+=+=.故选：A.2．（2021·山东济南市·）已知S n 是递增的等比数列{a n }的前n 项和，其中S 3＝72，a 32＝a 4，则a 5＝（ ）A ．116B ．18C ．8D ．16【答案】C 【解析】设等比数列的公比为q ，根据题意列方程，解出1a 和q 即可.【详解】解：设递增的等比数列{a n }的公比为q ，且q >1，∵S 3＝72，234a a =，∴1a （1+q +q 2）＝72，21a q 4＝1a q 3，解得1a ＝12，q ＝2；1a ＝2，q ＝12（舍去）．练基础则5a ＝4122⨯=＝8．故选：C ．3．（2021·重庆高三其他模拟）设等比数列{}n a 的前n 项和为271,8,4n S a a =-=，则6S =（ ）A ．212-B ．152C ．212D ．632【答案】C 【解析】设等比数列{}n a 公比为q ，由572a a q =结合已知条件求q 、1a ，再利用等比数列前n 项和公式求6S .【详解】设等比数列{}n a 公比为q ，则572a a q =，又2718,4a a =-=，∴12q =-，故116a =，又1(1)1-=-nn a q S q ，即666311616[1()]216421321()22S ⨯⨯--===--.故选：C4．（2021·合肥市第六中学高三其他模拟（理））若等比数列{}n a 满足12451,8a a a a +=+=，则7a ＝（ ）A ．643B ．643-C ．323D ．323-【答案】A 【解析】设等比数列{}n a 的公比为q ，根据等比数列的通项公式建立方程组，解之可得选项.【详解】设等比数列{}n a 的公比为q ，则345128a a q a a +==+，所以2q =，又()11121+11,3a a a a q =+==，所以6671123643a a q ==⨯⨯=，故选：A.5.（2020·河北省曲阳县第一高级中学高一期末）中国古代数学著作《算法统宗》中记载了这样一个问题：“三百七十八里关，初行健步不为难，次日脚痛减一半，六朝才得到其关，要见次日行里数，请公仔细算相还.”其大意为：有一个人走了378里路，第一天健步行走，从第二天起因脚痛每天走的路程为前一天的一半，走了6天后到达目的地，问此人第二天走了（ ）A ．6里B ．24里C ．48里D ．96里【答案】D 【解析】根据题意，记每天走的路程里数为，可知是公比的等比数列，由，得，解可得，则；即此人第二天走的路程里数为96；故选：D ．6．（2021·江苏南通市·高三其他模拟）已知等比数列{}n a 的公比为q ，前n 项和为n S ，则“1q >”是“112n n n S S S -++>”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】D 【解析】由112n n n S S S -++>可得出1n n a a +>，取10a <，由101n n q a a +<⇔，进而判断可得出结论.【详解】若112n n n S S S -++>，则11n n n n S S S S +-->-，即1n n a a +>，所以，数列{}n a 为递增数列，若10a <，101n n q a a +<<⇔>，所以，“1q >”是“112n n n S S S -++>”的既不充分也不必要条件.故选：D.7．（2021·黑龙江大庆市·大庆实验中学高三其他模拟（文））在数列{}n a 中，44a =，且22n n a a +=，则{}n a {}n a 12q =6378S =6161[1()]2378112-==-a S 1192a =211192962a a q =⨯=⨯=21nni a==∑___________.【答案】122n +-【解析】由44a =，22n n a a +=，得到22a =且22n na a +=，得出数列{}2n a 构成以2为首项，以2为公比的等比数列，结合等比数列的求和公式，即可求解.【详解】由22n n a a +=，可得22n na a +=，又由44a =，可得4224a a ==，所以22a =，所以数列{}2n a 构成以2为首项，以2为公比的等比数列，所以1212(12)2212n nn n i a +=-==--∑.故答案为：122n +-.8．（2021·浙江杭州市·杭州高级中学高三其他模拟）已知数列{}n a 满足21n n S a =-，则1a =_____，n S =_______．【答案】1 21n -【解析】利用1n n n a S S -=-求通项公式，再求出n S .【详解】对于21n n S a =-，当n =1时，有1121S a =-，解得：1a =1；当2n ≥时，有1121n n S a --=-，所以()112121=n n n n n a S S a a ----=--，所以1=2nn a a -，所以数列{}n a 为等比数列，111=2n n n a a q--=，所以122112nn n S -==--.故答案为：1，21n -.9.（2021·浙江杭州市·杭州高级中学高三其他模拟）已知数列{}n a 满足21n n S a =-，则3a =________，n S =________．【答案】4 21n -【解析】根据11,1,2n n n S n a S S n -=⎧=⎨-≥⎩，求出数列的通项公式，再代入求出n S ．【详解】解：因为21n n S a =-当1n =时，1121S a =-，解得11a =；当2n …时，1121n n S a --=-，所以111(21)(21)22n n n n n n n a S S a a a a ---=-=---=-，即12n n a a -=于是{}n a 是首项为1，公比为2的等比数列，所以12n n a -=．所以34a =，11212212n nn n S a -=-⨯-==-故答案为：4；21n -；10.（2018·全国高考真题（文））等比数列{a n }中，a 1=1 ， a 5=4a 3．（1）求{a n }的通项公式；（2）记S n 为{a n }的前n 项和．若S m =63，求m ．【答案】（1）a n =(―2)n―1或a n =2n―1 .（2）m =6.【解析】（1）设{a n }的公比为q ，由题设得a n =q n―1．由已知得q 4=4q 2，解得q =0（舍去），q =―2或q =2．故a n =(―2)n―1或a n =2n―1．（2）若a n =(―2)n―1，则S n =1―(―2)n3．由S m =63得(―2)m =―188，此方程没有正整数解．若a n =2n―1，则S n =2n ―1．由S m =63得2m =64，解得m =6．综上，m =6．1．（辽宁省凌源二中2018届三校联考)已知数列为等比数列，且，则（ ）A.B.C.D. 【答案】B【解析】由等比数列的性质可得： ，，结合可得： ，结合等比数列的性质可得： ，即：本题选择B 选项.2．（2021·全国高三其他模拟（文））如图，“数塔”的第i 行第j 个数为12j -(其中i ，*j N ∈，且i j ≥).将这些数依次排成一列1，1，2，1，2，4，1，2，4，8，1，2，4，8，16，…，记作数列{}n a ，设{}n a 的前n 项和为n S .若1020n S =，则n =（）A ．46B ．47C ．48D ．49【答案】C 【解析】{}n a 2234764a a a a =-=-46tan 3a a π⎛⎫⋅= ⎪⎝⎭32343364,4a a a a a ==-∴=-4730a a q =<2764a =78a =-463732a a a a ==463222tan tan tan 10tan 3333a a πππππ⎛⎫⎛⎫⎛⎫⋅==+== ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭练提升根据“数塔”的规律，可知第i 行共有i 个数，利用等比数列求和公式求出第i 行的数字之和，再求出前m 行的和，即可判断1020n S =取到第几行，再根据每行数字个数成等差数列，即可求出n ；【详解】解：“数塔”的第i 行共有i 个数，其和为211212222112i i i --++++==-- ，所以前m 行的和为()()()123121222222212m m m m m m +-++++-=-=-+- 故前9行所有数学之和为102111013-=，因此只需要加上第10行的前3个数字1,2,4，其和为10131241020+++=，易知“数塔”前m 行共有()12m m +个数，所以9103482n ⨯=+=故选：C3．（2021·江苏高三其他模拟）已知数列{}n a 满足11a =，()1lg 1091n an a +=++，其前n 项和为n S ，则下列结论中正确的有（ ）A ．{}n a 是递增数列B ．{}10n a +是等比数列C ．122n n n a a a ++>+D ．(3)2n n n S +<【答案】ACD 【解析】将递推公式两边同时取指数，变形得到1110109n n a a +-=+，构造等比数列可证{}1010n a+为等比数列，求解出{}n a 通项公式则可判断A 选项；根据()()()2132101010a a a ++≠+判断B 选项；根据{}n a 的通项公式以及对数的运算法则计算()122n n n a a a ++-+的正负并判断C 选项；将{}n a 的通项公式放缩得到()lg 2101n n a n <⨯<+，由此进行求和并判断D 选项.【详解】因为()1lg 1091n an a +=++，所以()11lg 109n an a +-=+，从而1110109n n a a +-=+，110101090n n a a +=⨯+，所以()11010101010n n a a ++=⨯+，所以11010101010n na a ++=+，又1101020a +=，{}1010n a +是首项为20，公比为10的等比数列，所以110102010210n a n n -+=⨯=⨯，所以1021010n a n =⨯-，即()lg 21010nn a =⨯-，又因为21010n y =⨯-在[)1,,*n n N ∈+∞∈时单调递增，lg y x =在定义域内单调递增，所以{}n a 是递增数列，故A 正确；因为1231011,10lg19010lg1911,10lg199010lg19911a a a +=+=+=++=+=+，所以()()()()()222213101010lg191111lg19911lg 1922lg1911lg199a a a +-++=+-+=+-，所以()()()2222213361101010lg 1911lg1911lg199lg 1911lg0199a a a +-++=+-=+>，所以()()()2132101010a a a ++≠+，所以{}10n a +不是等比数列，故B 错误.因为()()()()121222lg 21010lg 21010lg 21010n n n n n n a a a ++++-+=⨯--⨯--⨯-()()()()()()2211211210102101 lglg210102101021012101n n n n n n +++-+⨯-⨯-=⨯-⨯-⨯-⨯-=，而()()()211221121012101210141041014102102101n n n nnn n n -++-⨯--⨯-⨯-=⨯-⨯+-⨯+⨯+⨯-20100.21041016.2100nnnn=⨯+⨯-⨯=⨯>，从而()()()211210121012101nn n -+⨯->⨯-⋅⨯-，于是，122n n n a a a ++>+，故C 正确.因为()()lg 21010lg 210lg 21nnn n a n =⨯-<⨯=+<+，所以()()21322nn n n n S +++<=，故D 正确.故选：ACD.4. （2019·浙江高三期末）数列的前n 项和为，且满足，Ⅰ求通项公式；Ⅱ记，求证：．【答案】Ⅰ；Ⅱ见解析【解析】Ⅰ，当时，，{}n a n S 11a =()11.n n a S n N ++=+∈()n a ()12111n n T S S S =++⋯+31222n n T -≤<(1) 2n n a -=()(1)1n n a S +=+Q ①∴2n ≥11n n a S -=+②得，又，，数列是首项为1，公比为2的等比数列，；证明：Ⅱ，，时，，，同理：，故：．5．（2021·河北衡水中学高三三模）已知数列{}n a 的前n 项和为n S ，且满足13a =，()122n n a xa n n -=+-≥，其中x ∈R .（1）若1x =，求出n a ；（2）是否存在实数x ，y 使{}n a yn +为等比数列？若存在，求出n S ，若不存在，说明理由.【答案】（1）2382n n n a -+=；（2）存在，()21242n n n n S ++=--.【解析】（1）将1x =代入，由递推关系求出通项公式，并检验当1n =时是否满足，即可得到结果；（2）先假设存在实数x ，y 满足题意，结合已知条件求出满足数列{}n a yn +是等比数列的实数x ，y 的值，运用分组求∴-①②()122n n a a n +=≥2112a S =+=Q 212a a ∴=∴{}n a 12n n a -∴=(1)2nn a += 21n n S ∴=-2n ≥Q 111122n n n S -≤≤1121111113142112212n n n n T S S S -⎛⎫- ⎪⎝⎭∴=++⋯+≥+=--11111221221212n n n T -⎛⎫- ⎪⎝⎭≤+=-<-31222n n T -≤<和法求出n S 的值.【详解】（1）由题可知：当1x =时有：12n n a a n --=-，当2n ≥时，()()()()()()121321213012232n n n n n a a a a a a a a n ---=+-+-+⋅⋅⋅+-=++++⋅⋅⋅+-=+，又13a =满足上式，故()()22138322nn n n n a ---+=+=.（2）假设存在实数x ，y 满足题意，则当2n ≥时，由题可得：()()111n n n n a yn x a y n a xa xy y n xy --+=+-⇔=+--⎡⎤⎣⎦，和题设12n n a xa n -=+-对比系数可得：1xy y -=，22xy x -=-⇔=，1y =.此时121n n a na n -+=+-，114a +=，故存在2x =，1y =使得{}n a yn +是首项为4，公比为2的等比数列.从而()()1112121224122nn n n n n nn n a n a n S a a a ++-++=⇒=-⇒=++⋅⋅⋅+=--.所以()21242n n n n S ++=--.6．（2021·辽宁本溪市·高二月考）已知数列{}n a ，满足11a =，121n n a a n +=+-，设n n b a n =+，n n c a n λ=+（λ为实数）．（1）求证：{}n b 是等比数列；（2）求数列{}n a 的通项公式；（3）若{}n c 是递增数列，求实数λ的取值范围．【答案】（1）证明见解析；（2）2nn a n =-；（3）()1,-+∞．【解析】（1）由121n n a a n +=+-，变形为()11222n n n a n a n a n +++=+=+，再利用等比数列的定义证明；（2）由（1）的结论，利用等比数列的通项公式求解；（3）根据{}n c 是递增数列，由10n n c c +->,*n N ∈恒成立求解.【详解】（1）因为121n n a a n +=+-，所以()11222n n n a n a n a n +++=+=+，即12n n b b +=，又因为11120b a =+=≠，所以0n b ≠，所以12n nb b +=，所以{}n b 是等比数列．（2）由1112b a =+=，公比为2，得1222n n n b -=⋅=，所以2nn n a b n n =-=-．（3）因为()21nn n c a n n λλ=+=+-，所以()()11211n n c n λ++=+-+，所以1122121n n n n n c c λλ++-=-+-=+-，因为{}n c 是递增数列，所以*10,n n c c n N +->∈成立，故210n λ+->，*n N ∈成立，即12n λ>-，*n N ∈成立，因为{}12n-是递减数列，所以该数列的最大项是121-=-，所以λ的取值范围是()1,-+∞．7．（2021·河南商丘市·高二月考（理））在如图所示的数阵中，从任意一个数开始依次从左下方选出来的数可组成等差数列，如：2，4，6，8，…；依次选出来的数可组成等比数列，如：2，4，8，16，….122344468858121616记第n 行第m 个数为(),f n m .（Ⅰ）若3n ≥，写出(),1f n ，(),2f n ，(),3f n 的表达式，并归纳出(),f n m 的表达式；（Ⅱ）求第10行所有数的和10S .【答案】（Ⅰ）(),1f n n =，()(),221f n n =-，()(),342f n n =-，()()12,1m m m f n n --+=；（Ⅱ）102036=S .【解析】（I ）由数阵写出(),1f n n =，()(),221f n n =-，()(),342f n n =-，由此可归纳出()()12,1m m m f n n --+=.（II ）()()()()1010,110,210,310,10S f f f f =++++ 291029282 1 =+⨯+⨯++⨯ ，利用错位相减法求得结果.【详解】（Ⅰ）由数阵可知：(),1f n n =，()(),221f n n =-，()(),342f n n =-，由此可归纳出()()12,1m m m f n n --+=.（Ⅱ）()()()()1010,110,210,310,10S f f f f =++++ 291029282 1 =+⨯+⨯++⨯ ，所以231010220292821S =+⨯+⨯++⨯ ，错位相减得291010102222S =-+++++ ()102121012-=-+-2036=.8．（2021·山东烟台市·高三其他模拟）已知数列{}n a 的前n 项和为n S ，且满足11a =，12n n S na +=，*n ∈N .（1）求{}n a 的通项公式；（2）设数列{}n b 满足11b =，12nn n b b +=，*n ∈N ，按照如下规律构造新数列{}n c ：123456,,,,,,a b a b a b ，求{}n c 的前2n 项和.【答案】（1）n a n =，*n ∈N ；（2）数列{}n c 的前2n 项和为1222++-n n .【解析】（1）由()12n n n a S S n -=-≥可得1(2)1n na a n n n+=≥+可得答案；（2）由12nn n b b +=得1122n n n b b +++=，两式相除可得数列{}n b 的偶数项构成等比数列，再由（1）可得数列{}n c 的前2n 项的和.【详解】（1）由12n n S na +=，12(1)(2)n n S n a n -=-≥，得12(1)n n n a na n a +=--，所以1(2)1n na a n n n +=≥+.因为122S a =，所以22a =，所以212n a an ==，(2)n a n n =≥.又当1n =时，11a =，适合上式.所以n a n =，*n ∈N .（2）因为12nn n b b +=，1122n n n b b +++=，所以*22()n nb n b +=∈N ，又122b b =，所以22b =.所以数列{}n b 的偶数项构成以22b =为首项､2为公比的等比数列.故数列{}n c 的前2n 项的和()()21321242n n n T a a a b b b -=+++++++ ，()122212(121)22212nn n n n T n +-+-=+=+--所以数列{}n c 的前2n 项和为1222++-n n .9．（2019·浙江高考模拟）已知数列中，， （1）令，求证：数列是等比数列；{}n a ()110,2*n n a a a n n N +==+∈+11n n n b a a =-+{}n b（2）令 ，当取得最大值时，求的值.【答案】（I ）见解析（2）最大，即【解析】（1）两式相减，得 ∴即：∴ 数列是以2为首项，2为公比的等比数列（2）由（1）可知， 即也满足上式令，则 ，3nn n a c =n c n 3,n n c =3k =121221n n n n a a n a a n +++=+=++Q ，211221n n n n a a a a +++-=-+()211121n n n n a a a a +++-+=-+12n nb b +=21120a b ==≠Q 又，{}n b 2nn b =121nn n a a +-=-2121a a -=-23221a a -=-⋅⋅⋅⋅⋅⋅()11212n n n a a n ---=-≥()211222121n n n a a n n -∴-=++⋅⋅⋅+--=--2,21n n n a n ∴≥=--11,0n a ∴==21n n a n ∴=--111212233n n n n n n n n c c +++----=∴=11112221212333n n nn n n n n n n n c c ++++----+-∴-=-=()212nf n n =+-()11232n f n n ++=+-()()122n f n f n ∴+-=-∴ 最大，即10.（2021·浙江高三其他模拟）已知数列{}n a 满足112a =，123n n a a ++=，数列{}n b 满足11b =，()211n n nb n b n n +-+=+.（1）数列{}n a ，{}n b 的通项公式；（2）若()1n n n n c b b a +=-，求使[][][][]1222021n c c c c +++⋅⋅⋅+≤成立([]n c 表示不超过n c 的最大整数)的最大整数n 的值.【答案】（1）112nn a ⎛⎫=+- ⎪⎝⎭，2n b n =；（2）最大值为44.【解析】（1）由题得数列{}1n a -是等比数列，即求出数列{}n a 的通项；由题得{}n b n 是一个以111b=为首项，以1为公差的等差数列，即得数列{}n b 的通项公式；（2）先求出[]()*1,16,2,2,21,21,22n n n c k N n n k n n k =⎧⎪=⎪=∈⎨=+⎪⎪+=+⎩，再求出[][][][]()2*12221,1,3,2,231,2122n n c c c c n n n k k N n n n k ⎧⎪=⎪⎪++++=+=∈⎨⎪⎪+-=+⎪⎩即得解.【详解】解：（1）由123n n a a ++=得()11112n n a a +-=--，所以数列{}1n a -是等比数列，公比为12-，()()()()()()12,234f f f f f f n ∴=>>>⋅⋅⋅>()()()()1210,310,3,0f f f n f n ==>=-<∴≥<Q 123345...c c c c c c ∴>，3,n n c =3k =解得112nn a ⎛⎫=+- ⎪⎝⎭.由()211n n nb n b n n +-+=+，得111n nb b n n+-=+，所以{}n b n 是一个以111b=为首项，以1为公差的等差数列，所以1(1)1n bn n n=+-⨯=，解得2n b n =.（2）由()1n n n n c b b a +=-得()12121121(1)22n nn n n c n n ⎛⎫+⎛⎫=++-=++- ⎪ ⎪ ⎪⎝⎭⎝⎭，记212n n n d +=，1112321120222n n n n n n n nd d +++-++-=-=<，所以{}n d 为单调递减且132d =，254d =，3718d =<，所以[]()*1,16,2,2,21,21,22n n n c k N n n k n n k =⎧⎪=⎪=∈⎨=+⎪⎪+=+⎩，因此[][][][]()2*12221,1,3,2,231,2122n n c c c c n n n k k N n n n k ⎧⎪=⎪⎪++++=+=∈⎨⎪⎪+-=+⎪⎩，当2n k =时，2320212n n +≤的n 的最大值为44；当2+1n k =时，231202122n n +-≤的n 的最大值为43；故[][][][]1222021n c c c c +++⋅⋅⋅+≤的n 的最大值为44.1．（2021·全国高考真题（理））等比数列{}n a 的公比为q ，前n 项和为n S ，设甲：0q >，乙：{}n S 是递增数列，则（）A ．甲是乙的充分条件但不是必要条件练真题B ．甲是乙的必要条件但不是充分条件C ．甲是乙的充要条件D ．甲既不是乙的充分条件也不是乙的必要条件【答案】B 【解析】当0q >时，通过举反例说明甲不是乙的充分条件；当{}n S 是递增数列时，必有0n a >成立即可说明0q >成立，则甲是乙的必要条件，即可选出答案．【详解】由题，当数列为2,4,8,--- 时，满足0q >，但是{}n S 不是递增数列，所以甲不是乙的充分条件．若{}n S 是递增数列，则必有0n a >成立，若0q >不成立，则会出现一正一负的情况，是矛盾的，则0q >成立，所以甲是乙的必要条件．故选：B ．2.（2020·全国高考真题（文））记S n 为等比数列{a n }的前n 项和．若a 5–a 3=12，a 6–a 4=24，则nnS a =（ ）A ．2n –1B ．2–21–n C ．2–2n –1D ．21–n –1【答案】B 【解析】设等比数列的公比为q ，由536412,24a a a a -=-=可得：421153111122124a q a q q a a q a q ⎧-==⎧⎪⇒⎨⎨=-=⎪⎩⎩，所以1111(1)122,21112n nn n n n n a q a a qS q ----=====---，因此1121222n n n n n S a ---==-.故选：B.3.（2019·全国高考真题（文））已知各项均为正数的等比数列的前4项和为15，且，则（ ）{}n a 53134a a a =+3a =A ．16B ．8C ．4D ．2【答案】C 【解析】设正数的等比数列{a n }的公比为，则，解得，，故选C ．4．（2019·全国高考真题（文））记S n 为等比数列{a n }的前n 项和.若，则S 4=___________．【答案】.【解析】设等比数列的公比为，由已知，即解得，所以．5．（2020·海南省高考真题）已知公比大于1的等比数列{}n a 满足24320,8a a a +==．（1）求{}n a 的通项公式；（2）求112231(1)n n n a a a a a a -+-+⋯+-.【答案】（1）2nn a =；（2）2382(1)55n n +--【解析】(1) 设等比数列{}n a 的公比为q (q >1)，则32411231208a a a q a q a a q ⎧+=+=⎨==⎩，整理可得：22520q q -+=，11,2,2q q a >== ，q 2311114211115,34a a q a q a q a q a q a ⎧+++=⎨=+⎩11,2a q =⎧⎨=⎩2314a a q ∴==13314a S ==，58q 223111314S a a q a q q q =++=++=2104q q ++=12q =-441411()(1)521181()2a q S q ---===---数列的通项公式为：1222n n n a -=⋅=.(2)由于：()()()1121111122112n n n n n n n n a a --++-+=-⨯⨯=--，故：112231(1)n n n a a a a a a -+-+⋯+-35791212222(1)2n n -+=-+-+⋯+-⋅()()3223221282(1)5512n n n +⎡⎤--⎢⎥⎣⎦==----.6．（2021·浙江高考真题）已知数列{}n a 的前n 项和为n S ，194a =-，且1439n n S S +=-.（1）求数列{}n a 的通项；（2）设数列{}n b 满足*3(4)0()n n b n a n N +-=∈，记{}n b 的前n 项和为n T ，若n n T b λ≤对任意N n *∈恒成立，求实数λ的取值范围.【答案】（1）33(4nn a =-⋅；（2）31λ-≤≤.【解析】（1）由1439n n S S +=-，结合n S 与n a 的关系，分1,2n n =≥讨论，得到数列{}n a 为等比数列，即可得出结论；（2）由3(4)0n n b n a +-=结合(1)的结论，利用错位相减法求出n T ，n n T b λ≤对任意N n *∈恒成立，分类讨论分离参数λ，转化为λ与关于n 的函数的范围关系，即可求解.【详解】（1）当1n =时，1214()39a a a +=-，229272749,4416a a =-=-∴=-，当2n ≥时，由1439n n S S +=-①，得1439n n S S -=-②，①-②得143n na a +=122730,0,164n n n a a a a +=-≠∴≠∴=，又213,{}4n a a a =∴是首项为94-，公比为34的等比数列，1933(3(444n n n a -∴=-⋅=-⋅；（2）由3(4)0n n b n a +-=，得43(4)(34n n n n b a n -=-=-，所以234333333210(4)44444nn T n ⎛⎫⎛⎫⎛⎫⎛⎫=-⨯-⨯-⨯⨯++-⋅ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎝+⎭⎭ ，2413333333321(5)(4)444444n n n T n n +⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-⨯-⨯-⨯++-⋅+-⋅ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ ，两式相减得234113333333(4)4444444n n n T n +⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-⨯++++--⋅ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭1193116493(4)34414n n n -+⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭⎢⎥⎛⎫⎣⎦=-+-- ⎪⎝⎭-111993334(4)44444n n n n n +++⎛⎫⎛⎫⎛⎫=-+---⋅=-⋅ ⎪⎪⎪⎝⎭⎝⎭⎝⎭，所以134()4n n T n +=-⋅，由n n T b λ≤得1334((4)(44n nn n λ+-⋅≤-⋅恒成立，即(4)30n n λ-+≥恒成立，4n =时不等式恒成立；4n <时，312344n n n λ≤-=----，得1λ≤；4n >时，312344n n n λ≥-=----，得3λ≥-；所以31λ-≤≤.。

浙江省高考数学提分专练：第5题数列（选择_填空题）姓名:________ 班级:________ 成绩:________一、真题演练 (共6题；共22分)1. （5分） (2019高三上·广东月考) 已知数列满足，，则等于（）A .B .C .D .2. （5分）在等差数列中，，则前13项之和等于（）A . 13B . 26C . 52D . 1563. （5分）等比数列{an}中，a4=4，则a2•a6等于（）A . 4B . 8C . 16D . 324. （5分） (2020高一下·萍乡期末) 已知数列中，其前n项和，数列的前n项和，若对恒成立，则实数取值范围是（）A .B .C .D .5. （1分）(2019·厦门模拟) 在等比数列中，，，则 ________．6. （1分） (2017·延边模拟) 已知等差数列{an}的首项为a1 ，公差为d，其前n项和为Sn ，若直线y=a1x+m 与圆x2+（y﹣1）2=1的两个交点关于直线x+y﹣d=0对称，则数列（）的前100项的和为________．二、模拟实训 (共14题；共67分)7. （5分）等差数列{an}的通项公式为an＝2n＋1，其前n项的和为Sn ，则数列的前10项的和为（）．A . 120B . 70C . 75D . 1008. （5分）(2019·贵州模拟) 设等比数列的前项和为，若，，则（）A . -60B . -40C . 20D . 409. （2分） (2019高二上·丽水月考) 等差数列的前n项和为，若，则（）A .B .C .D .10. （5分）已知数列中，，则的通项公式为（）A .B .C .D .11. （5分）(2017·厦门模拟) 递增数列{an}的前n项和为Sn ，若（2λ+1）Sn=λan+2，则实数λ的取值范围是________．12. （5分） (2020高一下·滦县期中) 设等比数列的前n项和为，且，则（）A . 255B . 375C . 250D . 20013. （5分）(2019·湖南模拟) 已知等差数列的前项和为，，，则数列的前2018项和为（）A .B .C .D .14. （5分） (2015高二上·潮州期末) 等差数列{an}的前n项和是Sn ，若a1+a2=5，a5+a6=13，则S6的值为（）A . 18B . 27C . 36D . 4615. （5分）为等差数列的前项和，，则（）A .B . 27C . 54D . 10816. （5分）设为等差数列的前n项和，若a1=1，公差d=2，Sk+2 Sk=24，则k=（）A . 8B . 7C . 6D . 517. （5分）已知公差不为零的等差数列与公比为q的等比数列有相同的首项，同时满足，，成等比，，，成等差，则=（）A .B .C .D .18. （5分）(2018·广元模拟) 若正项递增等比数列满足，则的最小值为（）A .B .C .D .19. （5分） (2019高一下·合肥期中) 已知数列中，，，则数列的通项公式为________.20. （5分） (2019高三上·上海月考) 已知数列前n项和为，满 ( 为常数)，且，设函数，则数列的前17项和为________.参考答案一、真题演练 (共6题；共22分)1-1、2-1、3-1、4-1、5-1、6-1、二、模拟实训 (共14题；共67分)7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、15-1、16-1、17-1、18-1、19-1、20-1、。

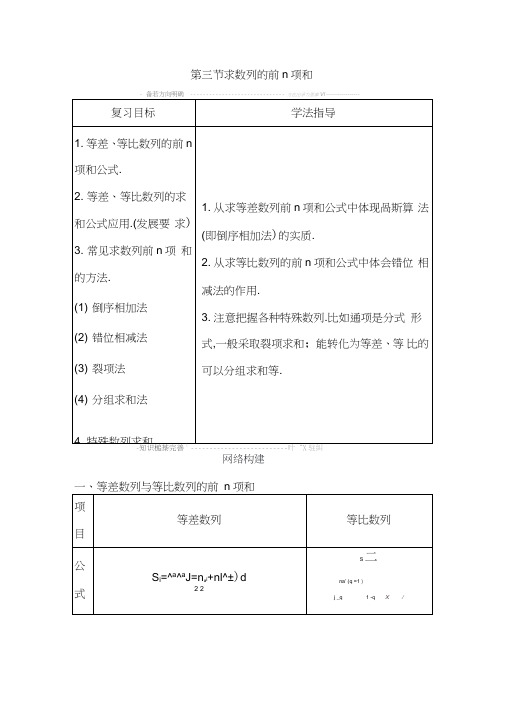
第三节求数列的前n项和方也出爭为里事网络构建一、等差数列与等比数列的前n项和二、求前n项和1. 求和问题的切入口：对通项公式的分析研究，首先要准确识别出是等差数列还是等比数列.(1) 从通项公式上识别，若a n是关于n的一次函数，则数列｛a n｝是等差数列.(2) 从前n项和公式上识别，若S是关于n的无常数项的二次函数，则数列｛a n｝是等差数列；若S是关于n的有非零常数项的二次函数，则从第二项起｛a n｝为等差数列；若S是关于n的指数型函数与常数项之和，且指数型函数的系数与常数项互为相反数，则数列｛a n｝为等比数列.2. 三种常见求和类型(1) 若数列的通项公式是由等差数列与等比数列之积构成的，常用错位相减法求和.(2) 若数列的通项公式是由等差数列和等比数列之和构成的，常用拆项分组法求和.⑶若数列的通项是分式结构，分母所含因式是等差数列中相邻项时，常用裂项相消法求和.三、与等差、等比数列相关联的结论1. 在等差数列中，若n为偶数，则S 偶-S奇二罗；若n为奇数，则S奇-S偶=a 中(中间项).2. 在等比数列中，若数列项数为2n,则鱼=q.s 奇3.1+2+3+ …+n=J.224.2+4+6+ …+2n=n+n.25.1+3+5+7+…+2n-1=n . 四、数列求和的基本思路1. 一般的数列求和，应从通项入手，若无通项,则先求通项，然后通过 对通项变形，转化为与特殊数列有关或具有某种方法适应特点的形式 从而选择合适的方法求和.2. 解决非等差、等比数列的求和，主要有两种思路：一是转化的思想, 即将一般数列设法转化为等差或等比数列，这一思想方法往往通过通 项分解或错位相减来完成；二是不能转化为等差或等比数列的数列， 往往通过裂项相消法、错位相减法、倒序相加法等来求和.等价转换思想是解决数列求和问题的基本思想方法，它可将复杂的数列转化为 等差、等比数列问题来解决.1. 数列｛a n ｝的前 n 项和 S n =1-2+3-4+ …+(-1) n-1 • n,则 S7等于(A ) (A)9(B)8(C)17(D)16解析:S 仃=1-2+3-4+5-6+ …+ 15-16+17 = 1+(-2+3)+(-4+5)+ …+(-14+15)+(-16+17) = 1 + 1 + 1 +…+ 1=9. 故选A.2. 已知等差数列｛a n ｝的前n 项和为S,a 5=5,S 5=15,则｛ — ｝的前100a n an+1项和为(A )（A ）罟（B ）洛（C ）益 © IS解析:设数列｛a n ｝的首项为a 1,公差为d,因为所以 所以 所以 所以 所以 S °0=(1- 1)+( 2-3)+…+(禽诘) ' 2' '21 100=1- —101 101故选A.3.3 x 2-1+4X 2-2+5X 2-3+…+(n+2) • 2-n =解析：设 S n =3x 2-1+4X 2-2+5X 2-3+…+(n+2) • 2-n , *S=3X 2-2+4X 2-3+5X 2-4+…+(n+2) • 2-(n+1), 则*S=3X 2-1+2-2+2-3+…+2-n -(n+2) • 2-(n+1) 1 -丄 =1 + 2 £ -(n+2) • 2 -2 -n-1=2-1 -(n+2) • 2-n-1S=4-n 2=4-J 42n2n 44.(2017 n 1:一 —= k上S 解析：因为比勺•全国H 卷）等差数列｛a n ｝的前n 项和为S,a 3=3,S 4=10,则所以 a1 2d =3,4a^6d =10,解得ai 二|d二1,所以a n =n,S n 二字 所以丄二-^=2(1-S nn (n 书) n所以 <1=2(1- !+!■ =2(1-丄) ' n +1 丿 =2nn 1答案：空n +1高频考点突破考点一分组法求和【例 1 ] 已知数列｛a n｝,｛b n｝满足 a i=5,a n=2a n-i+3n-1 (n > 2,n € N ),b n =a n -3 n (n € N).(1) 求数列｛b n ｝的通项公式；⑵求数列｛a n｝的前n 项和S n.解:(1)因为 a n =2a -1+3- (n € N,n >2), 所以 a n -3n =2(a n-1-3n-1), 所以 b n =2b n-1(n € N *,n >2). 因为 b 1=a 1-3=2 工 0, 所以b n 工0(n > 1), 所以电=2(n > 2),bi _L所以｛b n ｝是以2为首项,2为公比的等比数列禽),]+•.. +3T 在训练中掌握方法卜所以b n=2 • 2n-1=2n.⑵由(1)知a n=b+3n=2n+3：所以S=(2+22+…+2n)+(3+32+…+3n)=21一2" +31'"1 -2 1-3=才+32-72 2丘思旧网分组法求和的常见类型(1)若a n = b n± C n,且｛b n｝,｛C n｝为等差或等比数列，可采用分组法求® n｝的前n项和.⑵通项公式为a n=::为奇数，的数列,其中数列｛b n｝,｛c n｝是等比数列或等差数列，可采用分组法求和.L迂移迪箋在数列｛a n｝中,a 1=2,a n+1=2a n-n+1(n € N),数列｛a n｝的前n 项和为S.(1)证明：数列｛a n-n｝是等比数列，并求数列｛a n｝的通项公式；⑵求S;⑶证明:S n+1>S+2n+n.(1) 证明：因也!_L = 2ai -2n =2,故数列｛a n-n｝是公比为2的等比数列.a n - n Oi —n又因a1-1=1,故a n-n=2n-1,a n二n+21-1.(2) 解:S n=(1+20)+(2+2 1)+(3+2 2)+ …+(n+2n-1)=(1+2+3+ …0 1 2 n-1+n)+(2 +2+2+…+2 )= n(n If2 '⑶证明：由⑵得S n+1= n ^n 2 +2n+1-1,故S+1-(S n+2n+n)= n 2+2n+1-1- -2 n+1-2n-n.二n1 n：-n n 1+(2n+1-2 x 2n)-n=1>0, 故S+i>S+2 + n. S+i-(S n+2n+n)考点二错位相减法求和【例2】数列｛a n｝的前n项和为S n,对于任意的自然数2a n>0,4S n = (a n+1).(1) 求证：数列｛a n｝是等差数列，并求通项公式；(2) 设b n二聖,求和T n二b l + b2+…+b n.3(1) 证明：令n=1,4S i=4a i=(a i+1)2,解得a i=1,2由4S n=(a n+1),得4S+1 = (a n+l + 1)；两式相减得4a n+1 = (a n+l + 1) 2-(a n+1)2,整理得(a n+1+a n)(a n+1-a n-2) = 0,因为a n>0,以a n+1-a n = 2,则数列｛a n｝是首项为1,公差为2的等差数列，a n=1+2( n-1)=2 n-1.⑵解:由(1)得b n二辛，3T n=4+3+2+…+ 欝, ①3 3 3 3则3T n=l+|+3^+- +黑,②3 3 3 3 3①-②得_2 2n 2=3-于-，所以 T n = 1-2_J .理a (1)新数列｛c n ｝=｛a n • b n ｝,其中数列｛a n ｝是等差数列，数列｛b n ｝ 是等比数列，求数列｛C n ｝前n 项和分三步：①写出数列｛c n ｝的前n 项和S=C l +C 2+C 3+…+C n ；②把上述和式等号左右各项都乘以等比数列 ｛b n ｝的 公比q 得qS 二qc i +qc 2+qa+…+qC n ；③把所得两式相减，注意等号右边要 错位相减,错位相减部分恰好组成一个等比数列的若干项的和式 ，然 后整理化简.(2)错位相减法求数列的前n 项和是一种重要方法.在应用这种方法 时,一定要抓住数列的特征：数列的项可以看作是由一个等差数列和 一个等比数列对应项相乘所得的数列.所谓“错位”，就是要找“同类 项”相减，要注意的是相减后得到部分等比数列的和，此时一定要查清其项数.错位相减法在使用时由于运算量较大，易出现因运算不准确而致错的问题，所以在求解过程中要注意在“两式相减” “结果整理” 这些环节上的检查，最后可将n=1和n=2代入所得表达式进行检验(2018 •浙江卷)已知等比数列｛a n ｝的公比q>1,且a 3+Q+a 5=28,a 4+2是 a 3,a 5的等差中项.数列｛b n ｝满足b 1=1,数列｛(b n+1-b n )a n ｝的前n 项和为 2 2n +n. =1+2X 33"1+2(2n -1(1)求q的值；⑵求数列｛b n｝的通项公式.解:(1)由a4+2是a3,a5的等差中项,得a3+a5=2a4+4,所以a3+a4+a5=3a4+4=28,解得a4=8.由a3+a5=20,得8(q+1)=20, q解得q=2或q=l.2因为q>1,所以q=2.(2) 设C n = (b n+1-b n)a n,数列｛C n｝的前n项和为Sn _2.解得C n=4n-1.由(1)可得a n=2n-1,所以b n+i-b n=(4n-1) x (1)n-1,故b n-b n-1=(4n-5) x (1)n-2,n >2,b n-b 1=(b n-b n-1 )+(b n-1-b n-2)+ …+少3七2)+(b 2-b 1)=(4n-5) x (舟)"2+(4门-9) x (丄)n-3+…+7X !+3.设T n=3+7x 1+11 x (1)2+…+(4n-5) x (丄)n-2,n >2,2 2 2则2T n=3x 1+7x(2)2+…+(4 n-9) x(2)n-2+(4 n-5) x (期-1, 所以1T n=3+4x 1+4x(1) 2+ …+4x (丄)n-2-(4n-5) x (1)n-1,2 2 2 2 2 因此T n=14-(4n+3) • (f )n-2,n >2, 又b1=1,所以b n=15-(4 n+3) •(f)：考点三裂项相消法求和【例3】数列｛a n ｝的前n 项和为S,a n 是S 和1的等差中项，等差数列 ｛b n ｝满足 b i +S 4=0,b 9=a i .(1)求数列｛a n ｝,｛b n ｝的通项公式；⑵若6二 1 ,求数列｛c n ｝的前n 项和W(b n +16 ]b n +18 )' I J解：(1)因为a n 是S 和1的等差中项，所以 2a n =S n +1,所以 S=2a-1.当n 》2时，a n =S-S nj =(2a n -1)-(2a n-1 -1)=2a n -2a n-1,所以 a n =2a>1,当 n=1 时,a 1=S=2a/,所以a 1=1,所以a n 工0(n € N ),空=2,a n 丄所以数列｛a n ｝是以a 1=1为首项，2为公比的等比数列所以 an =2n-1, S=a 〔+a 2+…+a n =2 -1,设｛b n ｝的公差为 d,b 1=-S 4=-15,b 9=-15+8d=1,所以d=2.所以b n =-15+(n-1) x 2=2n-17. (2)c n = 1 1 12n -1 =丄 X (— ------ —)2n 1 2 ' 2n -1 2n 1 7_J ______ )]= J =^^2n -1 2n 1 2 4n 2 2n 1 '所以娇丄[(匚丄)+ ( 1-打+…+(2°'13丿\3 5/ '(i )裂项相消法一般适用分式数列求和.把数列的通项分解 为两项的差是这种方法使用的关键所在.使用裂项相消法求和时，要 注意正负项相消时消去了哪些项，保留了哪些项，切不可漏写未被消 去的项,未被消去的项有前后对称的特点，实质上造成正负相消是此 法的根源与目的. ⑵裂项相消法的基本思想是把数列的通项 a n 分拆成a n 二b n+1-b n 或者 a n 二b n -b n+1或者a n = b n+2-b n 等,从而达到在求和时逐项相消的目的，在解 题中要善于根据这个基本思想变换数列｛a n ｝的通项公式，使之符合裂 项相消的条件•(3) 常见的裂项方法有：① a n= - =1- —,a n =-=丄(丄-丄); n (n 出)n n +1 n (n +k ) k n n +k ② a n = - =丄(丄-—)；(2n -1 ]2n 北)2 ' 2n —1 2n +1③ a n 二 ------ _1 = J n +1-伍, "n g n 也④ a n =1 =丄[亠-1— n (n +1]n +2) 2「n(n 也)(n 也][n +2 ⑤ a n =』^ •丄=GL — •丄n fn 州、 2 n f n 十1 \ 2匚迂移训练已知正项数列｛a n ｝满足:4S n 二a"2a-3,其中S 为数列｛a n ｝的前n 项和.(1)求数列｛a n ｝的通项公式；an =^hTn =1(E -耐 i严[(' 汩-(缶尙兀1_ 1 n n . ・ n ■ n 2 - n 1 2⑵设b n二亠,求数列｛b n｝的前n项和T n. 3i -1解:(1)令n=1 得4a1=a：+2a1-3,且a n>0,解得a1=3.当n》2 时,4S n-4S n-i = a；- a n 1 +2ch-2a n-i,即4a n= a；- a；丄+2a-2a n-i,整理得(a n + a n-i)(a n-a n-1-2) = 0,因为a n>0,以a n-a n-1 =2,所以数列｛a n｝是首项为3,公差为2的等差数列，故a n=3+(n-1) x 2=2n+1.⑵由(1)知：^=亠=丄 =1=丄(丄-丄)，0, -1 4n2 +4n 4n(n +1)4 ' n n+1，所以T n=b1+b2+- +b n=!(1- 1+[-〕+••• +丄-丄)=1(1-丄)二4' 2 2 3 n n+1， 4' n+1， 4n+4考点四含绝对值数列求禾口【例4】在公差为d的等差数列｛a n｝中，已知a1=10,且a,2a2+2,5a3 成等比数列.(1)求d,a n；(2) 若d<0,求|a 1|+|a 2|+|a 3|+ …+|a n|.解:(1)由已知得&+2 j =5aa3? 4®+d 刑=50(a1+2d)?(11+d) 2=25(5+d)121+22d+d=125+25d? d2-3d-4=0 ? f =4' 或a n =4n 十6 f n =11 —n.(2)由(1)知,当d<0 时,a n=11-n,所以|a n| = 11 -n,1 _n _11, n -11,n _12.①当1< n w 11时, a n> 0,6所以 |a i |+|a 2|+|a 3|+ …+|a n |=a i +Q+a3 — &=n 10「_n = n 2；」.②当n 》12时，因为a n < 0,所以 |a i |+|a 2|+|a 3|+ …+|a n |=a i +G+a 3+…+a^-(a i2+a ；3+ …+a n )=2(a i +a 2+a3 — a ii )-(a11 科21 _11 n(21 -n )= n 2 /1n+2202 2 2综上所述,n 21 _n2 口”n 2 _21n 220“ n _12 I. 2 ' 有些数列是因项的正负分布不同而产生分段.对于这种数列,我们就要按参加求和的项是否是同一种符号的项分为两类来求 和.需要注意的是该数列的项是按照什么规律进行分类的，只有准确 把握项的正负分类才能正确地求解.(2)有些数列是因奇数项和偶数项分别按照不同规律而产生分段 .对 于这种数列，我们就要按参加求和的奇数项和偶数项的个数是否相同 分为两类来求和•在每一类中，要注意奇数项和偶数项分别有多少，避 免 因 分 类 不 清 而 致 错 的 现 象 产生.［应移迪箋已知每一项都是正数的数列｛a n ｝满足a 1=1,a n+1=2(n € N *).12a n(1) 用数学归纳法证明:a 2n+1<a 2n-1 ；(2) 证明:丄 < a n < 1;i +a 2+a 3+…+a n )=2 x |a i |+|a 2|+|a 3|+ …+|a n | =(3) 记S n为数列｛|a n+i-a n|｝的前n项和,证明:S n<6(n € N).证明:(1)由题知,a 1=1>0,a n+1=y >0(n € N).12&①当 n=1 时,a i =1,a 2=a ^1 =-'c- 612a 1 "證=^，a 3Va 1 成立；②假设n=k 时，结论成立，即a 2k+i <a 2k-i ,a2n 1 因为 a 2n+1=a2n12a212a 2n:n J_12 .a^12a2n 113已2 n 丄'：1 12 a ■ 1以 a 2k+3-a 2k+i=13a 2k + +1 12 a 2k 1 1即n 二k+1时也成立， 13a 2 k 丄■ 1 =a 2k i - a 2k 丄 — vO.12 a 2k 丄 1a 2k 1 1 冬丄 1由①②可知对于n € N,都有a 2n+i <a 2n-i 成立. (2)由(1)知,a 2n+1 <a 2n-1 , 所以 仁a i >…>a 2n-1 >a 2n+1 ,同理由数学归纳法可证a 2n <a 2n+2, 1a 2n >a 2n-2>°°° >32=—.6 猜测:a 2n V 1<a 2n-1 ,下证这个结论.3丄-1〕 因为 a n+1- 1= 3-,34a n所以a n+1- 1与a n -1异号.33注意到 a 1- 1 >0,知 a 2n-1 - - >0,a 2n - - <0,333即卩 a 2n < 1 <a 2n-1 .3所以有a 1> …>a 2n-1 >a 2n+1>1 >a 2n >a 2n-2 >••• >a 2,3=6 •(6)n '所以害专a n+i -a n |.所以 |a n+i -a n | w — |a n -a n-i | w ( 6) |a n-i -a n-21 w …w (—) |a 2-a 11(3)|a n+2-a n+i |=| ^!^- — |=a n i-an<i2a n ii2a n 'i2a “a n i务 iS= a 2 -a ^-|a ^a 2I ：j a4 _a 3 • • a n i -a n=5[i 埒+()+…+(；)n-i ]=5 X 76i_6 7<35<36=66【例题】 等比数列.裂项相消及错位相减法求和 已知等差数列｛a n ｝的公差为2,前n 项和为S,且S,S 2,S 4成(i)求数列｛a n ｝的通项公式;n-ia n an⑵令b n= (-i)d ,求数列｛b n ｝的前n 项和T n .解:(1)d=2,S i =a i ,S 2=2a i +d,S 4=4ai +6d,因为S,S 2,S 4成等比数列，所以s ；=SS. 解得 a i =1,所以 a n =2n-1. n-ia.%(2)b n =(-i) n-i Q =(-i) n-i (当n 为偶数时, T n =(i+i )-( 3+i )+ …+(*+*)-(羔计)所以 T n = i- i _ 2n2n i 2n i当n 为奇数时，T n =(i + [)-(丄+丄)+…-(丄 +丄)+(丄 +亠) 33 52n —3 2n —i2n —i 2n +i所以T n = i+丄二沁.2n +i 2n,n 为偶数，所以T n = 2n 1 叱,n 为奇数.2n 1解题规范斗|规范要求:(1)对b n 中的符号易忽视讨论，当n 为偶数时和当n 为奇数 时和是不 同的；⑵裂项相消时，要注意消去了哪些项，余下哪些项；n 1(3) 最后结果要用分段形式表达或写成兀=2「「-1匚形式.2n -1温馨提示：(1)第1问实质是基本量的计算，对等差数列的通项公式及 前n 项和公式要得心应手；⑵ 把b n拆项成(-1) n-1(丄+丄)是本题之关键，正负抵消要看清剩2n -1 2n北余的项.【规范训练1】(2017 •山东卷)已知｛X n ｝是各项均为正数的等比数列且 X 1+X 2=3，X 3-X 2 = 2. (1)求数列｛X n ｝的通项公式；⑵ 如图，在平面直角坐标系xOy 中，依次连接点P 1(X 1, 1)，P 2(X22)，…，P n+1(X n+1, n+1)得到折线P P 2-P n+1,求由该折线与直线 y=0，X=X 1,X =X n+1所围成的区域的面 积T n .解:(1)设数列｛x n ｝的公比为q,2n n 为偶数,由题意得X12WXiq _x’q =2,所以3q2-5q-2=0.由已知得q>0,所以q=2,x i=1,因此数列｛x n｝的通项公式为*=2：⑵过P l,P2,…,P n+1向X轴作垂线,垂足分别为Qd …,Q n+1.由(1)得X n+1-X n r?"”'/1,记梯形P n P n+1Q+1Q的面积为b n.由题意得b n=l寸丄x 2n-1=(2n+1) x 2n-2,所以T n=b1+b2+…+b n=3x 2-1+5X 2°+7X 夕+…+(2n-1) x 2n-3+(2n+1) x 2：①又2T n=3x 2°+5x 21+7x 22+…+(2n-1) x 2n-2+(2n+1) x 2n-1.②①-②得r n 1-T n=3x 2-1+(2+22+…+2n-1 )-(2n+1) x 2n-1=£ + 2：：_ -(2n+1) x 2n-1,所以T n=2n-1 2n M.2【规范训练2】已知数列｛a n｝和｛b n｝满足a1=2,b1=1,a n+1=2a(n € N), 4+52+口3+…+^b n = bn+1-1(n € N*).2 3 n(1)求a n 与b n；⑵记6二—-—,求数列｛c n｝的前n项和T n.44+ b n b n +解:(1)由a1=2,a n+1=2a n,得a n=2n(n € N*).由题意知，当n=1 时,b 1=b2-1,故b2=2,当 n 》2 时,b 1+- b 2 -------------------------------------------------------------b n-l + - b n = b n+1-1,两式相减得-b n =b n+1-b n整理得虹=冬类型一分组法求和1.已知数列｛a n ｝满足 a i =1,a n+i • a n =2n (n € N ),则 S o-6 等于(B ) (A)2 2 016-1(B)3 • 21 008-3(C)3 • 21 008-1 (D)3 • 21 007-2n 1解析:a 1=1,a 2=-=2,又 an 2 an 1 =牛=2.a 1an + a n2所以也=2.所以a 1,a s ,a 5,—成等比数列 砂砂小，一成等比数列, 所以 S 016=a 1+a 2+a 3+a 4+a 5+a 6—+a 2 015 +a 2 016=(a 1+a s +a s+—a ? 015 )+(a 2+a 4+a s —+a ? 016)故选B.2.有穷数列1,1+2,1+2+4,…,1+2+4+- +2n-1所有项的和 为 _______ .b i + - b 2+— + b n-i =b n -1,2n _12n -1 n所以 b n =n(n € N). -3.解析：由题意知所求数列的通项为—n=2n-1,1_2故由分组求和法及等比数列的求和公式可得和为2血-n=2n+1-n-2.1_2答案：2n+1-n-2类型二错位相减法求和3. 已知数列｛a n｝的前n项和为S n且a n=n • 2n,则S n= ____________________ .解析:S n=1 • 2+2 • 22+3 • 23+…+n • 2n, ①2S=1 •22+2 •23+…+(n-1) •2n+n •2n+1,②①-②得-S n=2+2+2 — 2-n • 2 1=-2(1-2 n)-n • 2n+1=-2+2n+1-n • 2n+1=-2-( n-1) • 2n+1,所以S=2+(n-1) • 2n+1.答案:2+( n-1) • 2n+14. 已知数列｛a n｝,且a n=(2n+1) • 3n-1,则其前n项和S二 _____ . 解析:S n=3+5X 3+7X 32+—+(2n+1) x 3n-1, ①3S=3X 3+5X 32+—+(2n-1) x 3n-1+(2n+1) x 3n,②①-②得-2S n=3+2X 3+2X 32+—+2x 3n-1-(2n+1) x 3n=3+2x ^=^-(2n+1) • 3n=-2n x 3n,所以S=n • 3n.答案:n • 3n类型三裂项相消法求和S=£则n 等于(B ) (A)6(B)7(C)8 (D)9解析：因为数列｛a n ｝的通项公式a n =1,那么要求解数列的前n2n -1 2n 1项和问题,主要是分析通项公式的特点.因为因此可知,S=a 1+a 2+a 3—+&=!(1- 1 )2 2n 1=n2n 1'所以丄=7,所以n=7.2n 比 15故可知n 的值为7,故选B.6.已知数列｛a n ｝满足a n=^ ' n ,则数列｛丄｝的前n 项和 na nan +为 _______ .n2贝 y =4=4(—anS 1 n 1 n 2n 15.已知数列｛a n ｝的通项公式a n = .若数列｛a n ｝的前n 项和a n =1 2n -11 2n 1)，=2[(1- 1)+(3-5)+(112n -1)]解析:a n =1 2 d 川u 1匕) 2n 1所以 s=4[( 1-1)+( 1-^)+ …+( —— )]=4(丄-丄)二亘 2334n 1 n 22n 2 n 2答案:2n n 28.(2016 •浙江卷)设数列｛a n ｝的前n 项和为S,已知S 2=4,a n+1=2S+1,n*€ N.(1) 求通项公式a n ；(2) 求数列｛|a n -n-2|｝的前n 项和. 解:(1)由题意得a1 a2 S 则a1乩 I s t =2日 1 1. a 2 =3. 又当 n 》2 时,由 a n+1-a n =(2S n +1)-(2S n-1 +1) = 2a n , 彳得 a n+1=3a n .^又 a 2=3a 1,所以,数列｛a n ｝的通项公式为a n =3n-1 ,n € N. ⑵ 设 b n =|3n-1-n-2|,n € N,b 1=2,b 2=1. 当n 》3时，由于 3n-1>n+2,故 b n =3n-1-n-2,n 》3.设数列｛b n ｝的前n 项和为T n , 7.若已知数列的前四项是亠 1 +2 尢，羔，宀，则数列的前n 项和 解析：因为通项a n^^=1(1n (n +2)2 n则数列的前n 项和Si (1-1 + 1-1+1-1 +…+丄-丄+丄-丄), 2、1 3 2 4 3 5 n_1 n+1 n n+2 八1 - 1 - 1 )= 3 - 2n +32 n 1 n 2 4 2 n 1 n 2 2n 32 n 1 n 2 含绝对值数列求和 s=1(1+ 2 1 答案：3 -4 类型四 n^)，则T1=2,T2=3.当n》3时，+9(1护(n+7ji n_2]=3n_n2_5n+11Tn=31」 2 2 ' |2,n =1，所以T i= 3n _n2 _5n 11,n 亠2.2。

第五篇 数列及其应用 专题5.3 等比数列及其前n 项和【考纲要求】1.理解等比数列的概念．2.掌握等比数列的通项公式与前n 项和公式．3．能在具体的问题情境中识别数列的等比关系，并能用等比数列的有关知识解决相应的问题． 4.了解等比数列与指数函数的关系. 【命题趋势】1.利用公式求等比数列指定项、前n 项和；利用定义、通项公式证明数列为等比数列．2.利用等比数列性质求等比数列指定项、公比、前n 项和. 【核心素养】本讲内容主要考查数学运算、逻辑推理的核心素养. 【素养清单•基础知识】 1．等比数列的有关概念(1)定义：如果一个数列从第2项起，每一项与它的前一项的比等于同一常数(不为零)，那么这个数列就叫做等比数列．这个常数叫做等比数列的公比，通常用字母q 表示，定义的表达式为a n ＋1a n ＝q .(2)等比中项：如果a ，G ，b 成等比数列，那么G 叫做a 与b 的等比中项．即G 是a 与b 的等比中项⇔a ，G ，b 成等比数列⇒G 2＝ab . 只有当两个数同号且不为0时，才有等比中项，且等比中项有两个. 2．等比数列的有关公式 (1)通项公式：a n ＝a 1q n －1.(2)前n 项和公式：S n ＝⎩⎪⎨⎪⎧na 1，q ＝1，a 1(1－q n)1－q ＝a 1－a n q 1－q ，q ≠1.3．等比数列与指数型函数的关系当q >0且q ≠1时，a n ＝a 1q ·q n 可以看成函数y ＝cq x ，其是一个不为0的常数与指数函数的乘积，因此数列{a n }各项所对应的点都在函数y ＝cq x的图象上；对于非常数列的等比数列{a n }的前n 项和S n ＝a 1(1－q n )1－q ＝－a 11－q q n ＋a 11－q ，若设a ＝a 11－q ，则S n ＝－aq n＋a (a ≠0，q ≠0，q ≠1)．由此可知，数列{S n }的图象是函数y ＝－aq x ＋a 图象上一系列孤立的点．对于常数列的等比数列，即q ＝1时，因为a 1≠0，所以S n ＝na 1.由此可知，数列{S n }的图象是函数y ＝a 1x 图象上一系列孤立的点． 【素养清单•常用结论】设数列{a n }是等比数列，S n 是其前n 项和． (1)通项公式的推广：a n ＝a m ·q n －m (n ，m ∈N *)．(2)若m ＋n ＝p ＋q ，则a m a n ＝a p a q ；若2s ＝p ＋r ，则a p a r ＝a 2s ，其中m ，n ，p ，q ，s ，r ∈N *.(3)a k ，a k ＋m ，a k ＋2m ，…仍是等比数列，公比为q m (k ，m ∈N *)．(4)若数列{a n }，{b n }是两个项数相同的等比数列，则数列{ba n }，{pa n ·qb n }和⎩⎨⎧⎭⎬⎫pa n qb n 也是等比数列．(5)若数列{a n }的项数为2n ，则S 偶S 奇＝q ；若项数为2n ＋1，则S 奇－a 1S 偶＝q . 【真题体验】1.【2019年高考全国III 卷理数】已知各项均为正数的等比数列的前4项和为15，且，则（ ）A ．16B ．8C ．4D ．22.【2019年高考全国I 卷理数】记S n 为等比数列{a n }的前n 项和．若，则S 5=___________．3.【2018年高考浙江卷】已知成等比数列，且．若，则（ ）A ．B ．C ．D ．4.【2017年高考全国II 卷理数】我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层共有灯（ ） A ．1盏 B ．3盏 C ．5盏D ．9盏5．【2017年高考全国III 卷理数】等差数列的首项为1，公差不为0．若a 2，a 3，a 6成等比数列，则前6项的和为（ ）A ．B ．C ．3D ．86.【2018年高考全国I 卷理数】记为数列的前项和，若，则___________．【考法拓展•题型解码】考法一 等比数列基本量的求解归纳总结：解决等比数列有关问题的常用思想方法(1)方程的思想：等比数列中有五个量a 1，n ，q ，a n ，S n ，一般可以“知三求二”，通过列方程(组)求出关键量a 1和q ，问题便可迎刃而解．(2)分类讨论的思想：等比数列的前n 项和公式涉及对公比q 的分类讨论，将q 分为q ＝1和q ≠1两种情况进行讨论．【例1】 (2018·全国卷Ⅲ)等比数列{a n }中，a 1＝1，a 5＝4a 3. (1)求{a n }的通项公式；(2)记S n 为{a n }的前n 项和，若S m ＝63，求m . 考法二 等比数列的性质及应用 归纳总结(1)等比数列性质的应用可以分为三类：通项公式的变形、等比中项的变形、前n 项和公式的变形．根据题目条件，认真分析，发现具体的变化特征即可找出解决问题的突破口．(2)在应用相应性质解题时，要注意性质成立的前提条件，有时需要进行适当变形．此外，解题时注意设而不求思想的运用．【例2】 (1)已知等比数列{a n }满足a 1＝14，a 3a 5＝4(a 4－1)，则a 2＝( ) A ．2 B ．1 C. 12 D. 18(2)设等比数列{a n }中，前n 项和为S n ，已知S 3＝8，S 6＝7，则a 7＋a 8＋a 9＝( ) A. 18 B ．－18 C. 578 D. 558(3)已知等比数列{a n }中，a 4＋a 8＝－2，则a 6(a 2＋2a 6＋a 10)的值为( ) A ．4 B ．6C ．8D ．－9 考法三 等比数列的判定与证明 解题技巧:等比数列的四种常用判定方法(1)定义法：若a n ＋1a n ＝q (q 为非零常数，n ∈N *)或a na n －1＝q (q 为非零常数且n ≥2，n ∈N *)，则{a n }是等比数列． (2)等比中项法：若数列{a n }中，a n ≠0且a 2n ＋1＝a n ·a n ＋2(n ∈N *)，则{a n }是等比数列． (3)通项公式法：若数列{a n }的通项公式可写成a n ＝c ·q n －1(c ，q 均是不为0的常数，n ∈N *)，则{a n }是等比数列．(4)前n 项和公式法：若数列{a n }的前n 项和S n ＝k ·q n －k (k 为常数且k ≠0，q ≠0,1)，则{a n }是等比数列． 【例3】 (2018·全国卷Ⅰ改编)已知数列{a n }满足a 1＝1，na n ＋1＝2(n ＋1)a n ，设b n ＝a n n . (1)求b 1，b 2，b 3；(2)判断数列{b n }是否为等比数列，并说明理由； (3)求{b n }的前10项和S 10. 【易错警示】易错点 忽视等比数列的一些基本条件【典例】 设等比数列{a n }的公比为q ，前n 项和S n ＞0(n ＝1,2,3，…)，求q 的取值范围．【错解】：因为a 1＝S 1＞0，S n ＝a 1(1－q n )1－q ＞0，所以⎩⎪⎨⎪⎧ 1－q ＞0，1－q n ＞0或⎩⎪⎨⎪⎧1－q ＜0，1－q n ＜0，所以－1＜q ＜1或q ＞1，故所求q 的取值范围为(－1,1)∪(1，＋∞)．【错因分析】本题中出现两个基本错误：一是q ≠0这一隐含条件被忽视，二是对于前n 项和没有分q ＝1和q ≠1两种情况进行讨论，故而解答出现错误．【正解】：因为数列{a n }为等比数列，S n ＞0，所以a 1＝S 1＞0，q ≠0.当q ＝1时，S n ＝na 1＞0；当q ≠1时，S n＝a 1(1－q n )1－q ＞0，即1－q n 1－q ＞0，所以⎩⎪⎨⎪⎧ 1－q ＞0，1－q n ＞0或⎩⎪⎨⎪⎧1－q ＜0，1－q n ＜0，所以－1＜q ＜1或q ＞1.综上，q 的取值范围为(－1,0)∪(0，＋∞)．【误区防范】：等比数列中的三个易误点 (1)特别注意q ＝1时，S n ＝na 1这一特殊情况．(2)由a n ＋1＝qa n ，q ≠0，并不能立即断言{a n }为等比数列，还要验证a 1≠0.(3)在运用等比数列的前n 项和公式时，必须注意对q ＝1与q ≠1分类讨论，防止因忽略q ＝1这一特殊情形而导致解题失误．【跟踪训练】 等比数列{a n }中，a 1＝2，前n 项和为S n ，若数列{a n ＋1}也是等比数列，则S n ＝( ) A ．2n ＋1－2 B ．3n C ．2n D ．3n －1 【递进题组】1．在等比数列{a n }中，a 2，a 16是方程x 2＋6x ＋2＝0的根，则a 2a 16a 9＝( )A ．－2＋22 B ．－ 2 C. 2 D ．－2或 22．已知数列{a n }是等比数列，S n 为其前n 项和，若a 1＋a 2＋a 3＝4，a 4＋a 5＋a 6＝8，则S 12＝( ) A ．40 B ．60 C ．32 D ．503．(2017·全国卷Ⅱ)已知等差数列{a n }的前n 项和为S n ，等比数列{b n }的前n 项和为T n ，a 1＝－1，b 1＝1，a 2＋b 2＝2.(1)若a 3＋b 3＝5，求{b n }的通项公式； (2)若T 3＝21，求S 3.4．(2019·西安一中月考)已知数列{a n }的前n 项和为S n ，且a n ＝S n ＋n2(n ∈N *)． (1)若数列{a n ＋t }是等比数列，求t 的值； (2)求数列{a n }的通项公式． 【考卷送检】 一、选择题1．等比数列x,3x ＋3,6x ＋6，…的第四项等于( ) A ．－24 B ．0 C ．12 D ．242．(2018·北京卷)“十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例．为这个理论的发展做出了重要贡献．十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于122.若第一个单音的频率为f ，则第八个单音的频率为( )A.32fB.322fC.1225fD.1227f3．在等比数列{a n }中，若a 3，a 7是方程x 2＋4x ＋2＝0的两根，则a 5的值是( ) A ．－2 B ．－ 2 C ．±2 D. 24．已知等比数列{a n }的前n 项和为S n ，且a 1＋a 3＝52，a 2＋a 4＝54，则S na n ＝( ) A ．4n －1 B ．4n －1 C ．2n －1 D ．2n －15．(2019·潍坊重点高中联考)设等比数列{a n }的前n 项和为S n ，若S 6S 3＝3，则S 9S 6＝( ) A ．2 B.73 C. 83 D ．36．(2019·湖南师大附中月考)已知各项不为0的等差数列{a n }满足a 6－a 27＋a 8＝0，数列{b n }是等比数列，且b 7＝a 7，则b 2·b 8·b 11＝( ) A ．1 B ．2 C ．4 D ．8 二、填空题7．等比数列的各项均为正数，且a 1a 5＝4，则log 2a 1＋log 2a 2＋log 2a 3＋log 2a 4＋log 2a 5＝________. 8．(2017·江苏卷)等比数列{a n }的各项均为实数，其前n 项和为S n .已知S 3＝74，S 6＝634，则a 8＝________. 9．(2019·杭州期中)设数列{a n }满足a 1＝23，且对任意的n ∈N *，满足a n ＋2－a n ≤2n ，a n ＋4－a n ≥5×2n ，则a 2 017＝________. 三、解答题10．设数列{a n }的前n 项和为S n ，a 1＝1，且数列{S n }是以2为公比的等比数列． (1)求数列{a n }的通项公式； (2)求a 1＋a 3＋…＋a 2n ＋1.11．(2019·河南实验中学质检)数列{b n }满足b n ＋1＝2b n ＋2，b n ＝a n ＋1－a n ，且a 1＝2，a 2＝4. (1)求数列{b n }的通项公式；(2)求数列{a n }的前n 项和S n .12．已知在正项数列{a n }中，a 1＝2，点A n (a n ，a n ＋1)在双曲线y 2－x 2＝1上，数列{b n }中，点(b n ，T n )在直线y ＝－12x ＋1上，其中T n 是数列{b n }的前n 项和． (1)求数列{a n }的通项公式； (2)求证：数列{b n }是等比数列．13．(2019·焦作一中月考)定义在(－∞，0)∪(0，＋∞)上的函数f (x )，如果对于任意给定的等比数列{a n }，{f (a n )}仍是等比数列，则称f (x )为“保等比数列函数”．现有定义在(－∞，0)∪(0，＋∞)上的如下函数：①f (x )＝x 2；②f (x )＝2x；③f (x )＝|x |；④f (x )＝ln |x |.则其中是“保等比数列函数”的f (x )的序号为________．。

【步步高】（浙江专用）2017年高考数学 专题五 数列 第37练 数列的前n 项和及求法练习一、选择题1．已知数列{a n }的前n 项和为S n ＝n 2－6n (n ∈N *)，则{|a n |}的前n 项和T n 等于( )A ．6n －n 2B ．n 2－6n ＋18 C.⎩⎪⎨⎪⎧ 6n －n2，1≤n≤3，n2－6n ＋18，n>3 D.⎩⎪⎨⎪⎧ 6n －n2，1≤n≤3，n2－6n ，n>3 2．若数列{a n }的通项公式是a n ＝(－1)n (2n －1)，则a 1＋a 2＋a 3＋…＋a 100等于( )A ．－200B ．－100C ．200D ．100 3．已知等比数列{a n }中，a 1＝1，q ＝2，则T n ＝1a1a2＋1a2a3＋…＋1anan ＋1的结果可化为( )A ．1－14nB ．1－12n C.23(1－14n) D.23(1－12n ) 4．已知函数f (x )＝x 2＋2bx 过(1,2)点，若数列{1f(n)}的前n 项和为S n ，则S 2 016的值为( )A.2 0162 015 B.2 0152 016 C.2 0172 016 D.2 0162 0175．设函数f (x )＝12＋log 2x 1－x ，定义S n ＝f (1n )＋f (2n )＋…＋f (n －1n)，其中，n ∈N *，n ≥2，则S n 等于( )A.n(n －1)2B.n －12－log 2(n －1)C.n －12D.n －12＋log 2(n －1) 二、填空题6．若数列{a n }是1，(1＋12)，(1＋12＋14)，…，(1＋12＋14＋…＋12n －1)，…，则数列{a n }的前n 项和S n ＝________.7．已知数列{a n }满足a 1＝2，a n ＋1＝5an －133an －7(n ∈N *)，则数列{a n }的前100项和为________．8．(2015·贵阳一模)已知等差数列{a n }的前n 项和为S n ，a 4＝4，S 4＝10，则数列{1anan ＋1}的前2 015项和为________．9．设{a n }是等比数列，公比q ＝2，S n 为{a n }的前n 项和．记T n ＝17Sn －S2n an ＋1，n ∈N *.设Tn 0为数列{T n }的最大项，则n 0＝________.三、解答题10．数列{a n }满足a 1＝1，a n ＋1＝2a n (n ∈N *)，S n 为其前n 项和，数列{b n }为等差数列，且满足b 1＝a 1，b 4＝S 3.(1)求数列{a n }，{b n }的通项公式；(2)设c n ＝1bn·log2a2n＋2，数列{c n }的前n 项和为T n ，证明：13≤T n <12.答案解析1．C [由S n ＝n 2－6n 得{a n }是等差数列，且首项为－5，公差为2.所以a n ＝－5＋(n －1)×2＝2n －7，所以n ≤3时，a n <0；n >3时，a n >0.所以T n ＝⎩⎪⎨⎪⎧ 6n －n2，1≤n≤3，n2－6n ＋18，n>3.]2．D [由题意知，a 1＋a 2＋a 3＋…＋a 100＝－1＋3－5＋7＋…＋(－1)100(2×100－1)＝(－1＋3)＋(－5＋7)＋…＋(－197＋199)＝2×50＝100，选D.]3．C [依题意，a n ＝2n －1，1anan ＋1＝12n －1·2n ＝122n －1＝12×14n －1， 所以T n ＝12[1－(14)n]1－14＝23[1－(14)n ]，故选C.] 4．D [由已知得b ＝12，所以f (n )＝n 2＋n ， 所以1f(n)＝1n2＋n ＝1n(n ＋1)＝1n －1n ＋1， 所以S 2 016＝1－12＋12－13＋…＋12 016－12 017＝1－12 017＝2 0162 017.故选D.] 5．C [因为f (1n )＋f (n －1n)＝1， 所以2S n ＝[f (1n )＋f (n －1n )]＋[f (2n )＋f (n －2n )]＋…＋[f (n －1n )＋f (1n)]＝n －1. 故S n ＝n －12.] 6．2n －2＋12n －1解析 a n ＝1＋12＋14＋…＋12n －1＝1－(12)n 1－12＝2(1－12n )， 所以S n ＝2[(1－12)＋(1－122)＋…＋(1－12n)] ＝2[(1＋1＋ (1)n 个－(12＋122＋ (12))] ＝2[n －12(1－12n )1－12] ＝2[n －(1－12n)] ＝2n －2＋12n －1. 7．200 解析 设S n 为数列{a n }的前n 项和，由递推公式可得a 1＝2，a 2＝3，a 3＝1，a 4＝2，a 5＝3，a 6＝1，…所以数列{a n }是周期为3的周期数列，∴S 100＝33(a 1＋a 2＋a 3)＋a 1＝200. 8.2 0152 016解析 设等差数列{a n }的公差为d ，则a 4＝a 1＋3d ＝4，S 4＝4a 1＋6d ＝10，联立解得a 1＝d ＝1，所以a n ＝a 1＋(n －1)d ＝n ，1anan ＋1＝1n(n ＋1)＝1n －1n ＋1， 所以数列{1anan ＋1}的前 2 015项和为(1－12)＋(12－13)＋…＋(12 015－12 016)＝1－12 016＝2 0152 016. 9．4解析 由等比数列的公比q ＝2得S n ＝a1[1－(2)n]1－2， a n ＝a 1·(2)n －1，∴T n ＝17·a1[1－(2)n]1－2－a1[1－(2)2n]1－2a1·(2)n＝17[1－(2)n]－[1－(2)2n](1－2)·(2)n＝16－17·(2)n ＋(2)2n (1－2)·(2)n ＝16(2)n ＋(2)n －171－2≤8－171－2＝9(2＋1)． 当且仅当(2)2n ＝16，即n ＝4时，等号成立，即T 4为数列{T n }的最大项，此时n 0＝4.10.(1)解 因为数列{a n }满足a 1＝1，a n ＋1＝2a n (n ∈N *)， 所以数列{a n }是等比数列，公比为2，首项为1， 所以a n ＝1×2n －1＝2n －1.设等差数列{b n }的公差为d ，满足b 1＝a 1，b 4＝S 3， 所以b 1＝1，b 1＋3d ＝1＋2＋22，解得d ＝2，所以b n ＝1＋2(n －1)＝2n －1， 所以a n ＝2n －1，b n ＝2n －1.(2)证明 c n ＝1bn·log2a2n＋2＝1(2n －1)·log222n＋1＝1(2n －1)(2n ＋1)＝12(12n －1－12n ＋1)， 所以数列{c n }的前n 项和为T n ＝12[(1－13)＋(13－15)＋…＋(12n －1－12n ＋1)] ＝12(1－12n ＋1)，因为数列{1－12n ＋1}为单调递增数列， 所以T 1＝13≤T n <12， 所以13≤T n <12.。

专题01 数列求通项（n S 法、n T 法）(典型例题+题型归类练)一、必备秘籍1对于数列{}n a ，前n 项和记为n S ； ①1231n n n S a a a a a -=++++；②11231(2)n n S a a a a n --=+++≥①-②：1(2)n n n S S a n --=≥2对于数列{}n a ，前n 项积记为n T ； ①1231n n n T a a a a a -=；②11231(2)n n T a a a a n --=≥①÷②：1(2)nn n T a n T -=≥二、典型例题n S 法：角度1：用1n n S S --，得到n a例题1．（2022·湖北·黄冈中学二模）数列{}n a 的前n 项和为n S ，11a =，()12N n n a S n *+=∈.求数列{}n a 的通项n a ；感悟升华（核心秘籍）1、使用n S 法注意两步：①1n =②2n ≥2、在本例中化简1n n S S --后，得到13(2)n na n a +=≥，特别提醒，在化简后需跟上（2n ≥），此时需要验证1n =是否符合，如本例2123a a =≠，则此时，数列{}n a 是从第二项开始成以3为公比的等比数列【答案】(1)21,123,2n n n a n -=⎧=⎨⋅≥⎩①当时，思路点拨：根据题意：，已知与的关系，用②当时，；又由题意知作 差，又因为：所以，数列从第二项开始成以为公比的等比数列，则，下结论解答：解：当1n =时，2122a S ==，当2n ≥时，由12n n a S +=可得12n n a S -=，上述两个等式作差得12n n n a a a +=-，可得13n n a a +=，且213a a ≠，所以，数列{}n a 从第二项开始成以3为公比的等比数列，则223n n a -=⋅，因为11a =不满足223n n a -=⋅，故21,123,2n n n a n -=⎧=⎨⋅≥⎩.n S 法：角度2：将题意中的n a 用1n n S S --替换例题2．（2022·全国·模拟预测）已知首项为1的数列{}n a 的前n 项和为()*n S n ∈N ，且11n n n S a S ++=-．求数列{}n a 的通项公式；由思路点拨：根据题意：，已知与的关系，用替换题目中的由约分，所以是首项为1，公差为1的等差数列，所以，当时，，又当时，也满足上式，所以解答过程化简再用作差法感悟升华（核心秘籍）1、已知1n a +与1n n S S ++，使用n S 法时，用1n n S S +-替换1n a +作为核心秘籍记忆；2、当遇到1(2)n n n a S S n -=≥，使用n S 法时，用1n n S S --替换n a 作为核心秘籍记忆；【答案】21n a n =-依题意，111n n n n n S S a S S ++++==-，故()()111n n n nn n S S S S S S ++++=-+，因为10n n S S ++>，所以11n n S S +-=，又111S a ==，所以{}n S 是首项为1，公差为1的等差数列，所以n S n =，2n S n =．当2n ≥时，()221121n n n a S S n n n -=-=--=-， 又当n ＝1时，11a =也满足上式，所以21n a n =-．n S 法：角度3：已知等式中左侧含有：1ni i i a b =∑例题3．（2022·湖北十堰·三模）已知数列{}n a 满足()()1233521131n n a a a n a n ++++-=-+.求{}n a 的通项公式；①当时思路点拨：根据题意：，用类似作差法②当时：，所以.又因为当时，上式也成立，所以的通项公式为.解答过程检验 作差感悟升华（核心秘籍）已知等式中左侧含有：1ni i i a b =∑，如本例：()()1233521131n n a a a n a n ++++-=-+解题密码类似“1n n S S --”；【答案】13-=n n a 解：因为()()1233521131n n a a a n a n ++++-=-+，① 当1n =时11a =，当2n ≥时，()()112313523231n n a a a n a n --++++-=-+，②①-②得()()()()()11211312312132n n n n n a n n n n --⎡⎤⎡⎤-=-+--+=-≥⎣⎦⎣⎦.所以()132-=≥n n a n .又因为当1n =时，上式也成立，所以{}n a 的通项公式为13-=n n a .n T 法：角度1：已知n T 和n 的关系例题4．（2022·湖北·模拟预测）已知数列{}n b 的前n 项之积()(1)*22N n n n T n +=∈.求{}nb 的通项公式.感悟升华（核心秘籍）使用n T 法本质：1(2)nn n T a n T -=≥其中： ①1231n n n T a a a a a -=；②11231(2)n n T a a a a n --=≥①当时，思路点拨：根据题意：，已知与的关系，用②当时，；当时，上式也成立，所以.检验解答过程【答案】2nn b =解：由(1)22n n nT +=，当1n =时，112b T ==， 当2n ≥时，12n nn n T T b -==， 当1n =时，上式也成立，所以2nn b =.n T 法：角度2：已知n T 和n a 的关系例题5．（2022·贵州毕节·模拟预测（理））已知数列{}n a 的前n 项积为n T ，且121n na T +=.求数列{}n T 的通项公式；【答案】21n T n =+，*n N ∈ 当1n =时，113T a == 当2n ≥时，1n n n T a T -=∴11n n nT a T -= 由121n n a T +=得121n n nT T T -+=即12n n T T -+= ∴12n n T T --=，∴{}n T 是以3为首项，2为公差的等差数列，∴21n T n =+，*n N ∈ ①当时，思路点拨：根据题意：，已知和的关系，用替换题目中②当时，∴代入已知条件，得即解答过程下结论∴12n n T T --=∴{}n T 是以3为首项，2为公差的等差数列， ∴21n T n =+，*n N ∈三、题型归类练1．（2022·青海·大通回族土族自治县教学研究室二模（文））数列{}n a 满足31232n a n a a a +++=+()121n n -⋅+，则7a =（ ）A ．64B ．128C ．256D ．512【答案】A当2n ≥时，由31232n a n a a a +++=+()121n n -⋅+，①得()1231231n a a a n a -++++-=()1221n n --⋅+，②①－②，得()121n n na n ⎡⎤=-⋅+⎣⎦()1221n n -⎡⎤--⋅+⎣⎦12n n -=⋅()2n ≥，所以()122n n a n -=≥，则764a =．故选：A ．2．（2022·辽宁实验中学高二期中）设数列{}n a 满足123211111222n n a a a a n -+++⋅⋅⋅+=+，则{}n a 的前n 项和（ ） A ．21n - B ．21n + C ．2n D ．121n +-【答案】C解：当1n =时，12a =，当2n ≥时，由1231221111112222n n n n a a a a a n ---+++⋅⋅⋅++=+得123122111222n n a a a a n --+++⋅⋅⋅+=，两式相减得，1112n n a -=，即12n na ，综上，12,12,2n n n a n -=⎧=⎨≥⎩所以{}n a 的前n 项和为()11212224822212n n n ---+++++=+=-，故选：C.3．（2022·全国·模拟预测）若数列{}n a 前n 项和为123n n S a =+，则数列{}n a 的通项公式是n a =______．【答案】1132n -⎛⎫⋅- ⎪⎝⎭123n n S a =+①，当1n =时，11123a a =+，解得：13a =，当2n ≥时，11123n n S a --=+②，①-②得：11133n n n a a a -=-，解得：112n n a a -=-， 所以{}n a 是首项为3，公比是12q =-的等比数列，所以1132n n a -⎛⎫=⋅- ⎪⎝⎭，经检验，符合要求故答案为：1132n n a -⎛⎫=⋅- ⎪⎝⎭4．（2022·江苏江苏·三模）已知数列{}n a 的前n 项和为n S ，各项均为正数的数列{}n b 的前n 项积为n T ，且21n n S a =-，11b a =，()n n n n T a b =.(1)求{}n a 的通项公式； (2)证明：{}n b 为等比数列. 【答案】(1)12n na (2)证明见解析(1)解：当1n =时，1121a a =-，11a =，当2n ≥时，()()111212122n n n n n n n a S S a a a a ---=-=---=-， 所以12n n a a -=，所以数列{}n a 是以1为首项，2为公比的等比数列， 所以12n na ；(2)证明：1110a b ==≠，()12nn n n T b -=，当2n ≥时，()()122112111222nn n nn n n n n n n n n n b T b b T b b --------===，则122112n n n n n b b ----=， 由于0n b >，则()1124n n b b n -=≥，所以数列{}n b 是等比数列.5．（2022·黑龙江·哈师大附中高二期中）已知数列{}n a 的前n 项和为n S ，且对任意正整数n ，22n n a S -=成立.求证：数列{}n a 是等比数列，并求{}n a 的通项公式； 【答案】(1)证明见解析，n a n =； 在22n n a S -=中令1n =得12a =．因为对任意正整数n ，22n n a S -=成立，所以1122n n a S ++-=， 两式相减得120n n a a +-=，所以12n n a a +=，即12n na a +=，所以{}n a 为等比数列， 所以1222n nn a -=⋅=.6．（2022·福建福州·高二期中）设各项均为正数的数列{}n a 的前n 项和为n S ，满足2412n n n S a a -=+．求数列{}n a 的通项公式； 【答案】(1)21n a n =-当1n =时，由2412n n n S a a -=+得2111412a a a -=+，11a =． 当2n ≥时，由2412n n n S a a -=+得2111412n n n S a a ----=+，两式相减可得2211422n n n n n a a a a a --=+--，化简得()()1120n n n n a a a a --+--=，由条件得10n n a a ->+，故()122n n a a n -=+≥， 得数列{}n a 是以1为首项，2为公差的等差数列， 从而数列{}n a 的通项公式为21n a n =-．7．（2022·浙江绍兴·模拟预测）已知等差数列{}n a 的首项为11a =，且1533+=+a a a ，数列{}n b 满足1122(21)31,2n n n n a b a b a b n *-⋅++++=∈N ．求n a 和n b ；【答案】(1)n a n =；123n n b -=⋅因为{}n a 是等差数列，设其公差为d .因为1533+=+a a a ，所以111342a d d a a +=+++． 因为11a =，所以等差数列{}n a 的公差1d =， 所以1(1)n a a n d n =+-=． 因为1122(21)312n n n n a b a b a b -⋅++++=，所以112a b =，所以12b =．当2n ≥时，11(21)31(23)312322---⋅+-⋅+=-=⋅n n n n n n n a b n ， 结合n a n =可知123n n b -=⋅．经检验：12b =也适合上式.所以123n n b -=⋅．8．（2022·湖北·模拟预测）已知各项均为正数的数列{}n a 的前n 项和为)*1,1,,2n n S a a n N n =∈≥.求证；数列是等差数列，并求{}n a 的通项公式；【答案】(1)证明见解析，21n a n =-因为n a 所以当2n ≥时，1n n S S --=即=而0n a >0>()12n =≥所以数列1=为首项，公差为1的等差数列； ()111n n +-⨯=，则2,n S n =当2n ≥时，121n a n n n =+-=-，又11a =满足上式， 所以{}n a 的通项公式为21n a n =-.9．（2022·广东·测试·编辑教研五高二阶段练习）数列{}n a 满足2313123n na a a a n++++=-．求n a ； 【答案】(1)123n n a n -=⋅解：因为2313123n na a a a n++++=-， 当1n =时，11312a =-=，当2n ≥时，1231131231n n a a a a n --++++=--， 两式相减得113323n n n na n--=-=⋅， 所以123(2)n n a n n -=⋅≥，又12a =符合上式，所以123n n a n -=⋅．10．（2022·四川省通江中学高二阶段练习（理））已知正项数列{}n a 的前n 项和为n S ，且)12,N,2n a a n n =∈≥ ；(1)求数列{}n a 的通项公式；【答案】(1)2,123,2,N n n a n n n *=⎧⎪=⎨+≥∈⎪⎩由题意正项数列{}n a 的前n 项和为n S ， 当2n ≥时，1n n n a S S -=- ，故1n n n a S S -=-=22=-，1=，所以 1为公差的等差数列，(1)1n n -= ，所以11123,(2)n a n n n n =+-=+≥ ，即23n a n =+，但12a =不适合上式，故2,123,2,N n n a n n n *=⎧⎪=⎨+≥∈⎪⎩； 11．（2022·全国·高二课时练习）已知各项均为正数的数列{}n a 的前n 项和为n S ，且满足11S =，2n a =（2N*n n ≥∈， ），求数列{}n a 的通项公式n a ； 【答案】11882n n a n n =⎧=⎨-≥⎩，， ∵an ＞0，当2n ≥时，∵2n a =，∴2n a ==Sn ﹣Sn ﹣1=，∴2， 又∵1=，∴是首项为1，公差为2的等差数列，∴1+2（n ﹣1）＝2n ﹣1，∴()221n S n =- ，当2n ≥ 时，()()221212388n n n a S S n n n -=-=---=- ，111a S == 不满足该式，∴an 11882n n n =⎧=⎨-≥⎩，，； 12．（2022·广东·高三阶段练习）已知正项数列{}n a 满足11,a =前n 项和n S满足*22,)n a n n N =≥∈.求数列{}n a 的通项公式；【答案】(1)1,121,24n n a n n =⎧⎪=⎨+≥⎪⎩由*22,)n a n n N =≥∈可得)*22,n a n n N =≥∈ 即：())*122,n n S S n n N --=≥∈ 0n a >0n S ∴>，0>2=12，∴1=为首项，公差为12的等差数列211,22nn nS++⎛⎫= ⎪⎝⎭当2n≥时，1214n n nna S S-+=-=当1n=时，11a=所以：1,121,24nna nn=⎧⎪=⎨+≥⎪⎩13．（2022·湖北恩施·高二期中）记n b为数列{}n a的前n项积，已知13a=，121n na b+=.证明：数列{}n b是等差数列.由题意可得1(2)nnnba nb-=，因为121n na b+=，所以121(2)nn nbnb b-+=，即12(2)n nb b n-+=，所以12(2)n nb b n--=.又11121a b+=，13a=，所以13b=，故{}n b是以3为首项，2为公差的等差数列.14．（2022·新疆·乌市八中高二期中（理））设数列{}n a的前n项积为n T，且()*22n nT a n=-∈N.求证数列1nT⎧⎫⎨⎬⎩⎭是等差数列；因为数列{}n a的前n项积为n T，且()*22n nT a n=-∈N，∴当n=1时，11122T a a==-，则123a=，1132T=.当n≥2时，1121222nnn n nTTT T T--=-⇒=-，∴11112n nT T--=，所以1nT⎧⎫⎨⎬⎩⎭是以1132T=为首项，12为公差的等差数列；15．（2021·湖北黄冈市·黄冈中学高三其他模拟）在数列{}n a中，若12a=-且12(2)n n na S S n-=≥.求数列{}n a的通项公式。

第四节 数列求和1．公式法(1)等差数列的前n 项和公式： S n ＝n (a 1＋a n )2＝na 1＋n (n －1)2d ；(2)等比数列的前n 项和公式：S n ＝⎩⎨⎧na 1，q ＝1，a 1－a n q 1－q ＝a 1(1－q n)1－q ，q ≠1.2．分组转化法把数列的每一项分成两项或几项，使其转化为几个等差、等比数列，再求解． 3．裂项相消法(1)把数列的通项拆成两项之差，在求和时中间的一些项可以相互抵消，从而求得其和．(2)裂项时常用的三种变形： ①1n (n ＋1)＝1n －1n ＋1；②1(2n －1)(2n ＋1)＝12⎝⎛⎭⎪⎫12n －1－12n ＋1； ③1n ＋n ＋1＝n ＋1－n .4．错位相减法如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的，这个数列的前n 项和可用错位相减法求解．5．倒序相加法如果一个数列{a n }的前n 项中与首末两端等“距离”的两项的和相等或等于同一个常数，那么求这个数列的前n 项和即可用倒序相加法求解．6．并项求和法一个数列的前n项和中，可两两结合求解，则称之为并项求和．形如a n＝(－1)n f(n)类型，可采用两项合并求解．例如，S n＝1002－992＋982－972＋…＋22－12＝(100＋99)＋(98＋97)＋…＋(2＋1)＝5 050.1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)(1)如果数列{a n}为等比数列，且公比不等于1，则其前n项和S n＝a1－a n＋11－q.()(2)当n≥2时，1n2－1＝12⎝⎛⎭⎪⎫1n－1－1n＋1.()(3)求S n＝a＋2a2＋3a3＋…＋na n之和时只要把上式等号两边同时乘以a即可根据错位相减法求得．()(4)如果数列{a n}是周期为k(k为大于1的正整数)的周期数列，那么S km＝mS k.()．[答案](1)√(2)√(3)×(4)√2．(教材改编)数列{a n}的前n项和为S n，若a n＝1n(n＋1)，则S5等于()A．1 B.5 6C.16 D.130B[∵a n＝1n(n＋1)＝1n－1n＋1，∴S5＝a1＋a2＋…＋a5＝1－12＋12－13＋…－16＝56.]3．(2016·杭州学军中学3月模拟)已知等比数列{a n}中，a2·a8＝4a5，等差数列{b n}中，b4＋b6＝a5，则数列{b n}的前9项和S9等于()A．9 B．18C．36 D．72B [∵a 2·a 8＝4a 5，即a 25＝4a 5，∴a 5＝4，∴a 5＝b 4＋b 6＝2b 5＝4，∴b 5＝2， ∴S 9＝9b 5＝18，故选B.]4．若数列{a n }的通项公式为a n ＝2n ＋2n －1，则数列{a n }的前n 项和S n ＝__________. 【导学号：51062174】2n ＋1－2＋n 2 [S n ＝2(1－2n)1－2＋n (1＋2n －1)2＝2n ＋1－2＋n 2.]5．3·2－1＋4·2－2＋5·2－3＋…＋(n ＋2)·2－n ＝__________. 4－n ＋42n [设S ＝3×12＋4×122＋5×123＋…＋(n ＋2)×12n ， 则12S ＝3×122＋4×123＋5×124＋…＋(n ＋2)×12n ＋1.两式相减得12S ＝3×12＋⎝ ⎛⎭⎪⎫122＋123＋…＋12n －n ＋22n ＋1.∴S ＝3＋⎝ ⎛⎭⎪⎫12＋122＋…＋12n －1－n ＋22n ＝3＋12⎣⎢⎡⎦⎥⎤1－⎝ ⎛⎭⎪⎫12n －11－12－n ＋22n ＝4－n ＋42n.]已知{a n }是等差数列，{b n }是等比数列，且b 2＝3，b 3＝9，a 1＝b 1，a 14＝b 4.(1)求{a n }的通项公式；(2)设c n ＝a n ＋b n ，求数列{c n }的前n 项和．[解] (1)设等比数列{b n }的公比为q ，则q ＝b 3b 2＝93＝3，所以b 1＝b 2q ＝1，b 4＝b 3q ＝27，所以b n ＝3n －1(n ＝1,2,3，…).3分 设等差数列{a n }的公差为d .因为a 1＝b 1＝1，a 14＝b 4＝27，所以1＋13d ＝27，即d ＝2. 所以a n ＝2n －1(n ＝1,2,3，…).6分 (2)由(1)知a n ＝2n －1，b n ＝3n －1. 因此c n ＝a n ＋b n ＝2n －1＋3n －1.10分 从而数列{c n }的前n 项和S n ＝1＋3＋…＋(2n －1)＋1＋3＋…＋3n －1 ＝n (1＋2n －1)2＋1－3n 1－3＝n 2＋3n －12.14分[规律方法] 分组转化法求和的常见类型(1)若a n ＝b n ±c n ，且{b n }，{c n }为等差或等比数列，则可采用分组求和法求{a n }的前n 项和．(2)通项公式为a n ＝⎩⎪⎨⎪⎧b n ，n 为奇数，c n ，n 为偶数的数列，其中数列{b n }，{c n }是等比数列或等差数列，可采用分组求和法求和．易错警示：注意在含有字母的数列中对字母的分类讨论．[变式训练1] (2016·浙江高考)设数列{a n }的前n 项和为S n ，已知S 2＝4， a n ＋1＝2S n ＋1，n ∈N *.(1)求通项公式a n ；(2)求数列{|a n －n －2|}的前n 项和．[解] (1)由题意得⎩⎪⎨⎪⎧ a 1＋a 2＝4，a 2＝2a 1＋1，则⎩⎪⎨⎪⎧a 1＝1，a 2＝3.2分又当n ≥2时，由a n ＋1－a n ＝(2S n ＋1)－(2S n －1＋1)＝2a n ，得a n ＋1＝3a n ， 所以数列{a n }的通项公式为a n ＝3n －1，n ∈N *.7分 (2)设b n ＝|3n －1－n －2|，n ∈N *，则b 1＝2，b 2＝1.当n ≥3时，由于3n －1>n ＋2，故b n ＝3n －1－n －2，n ≥3.10分 设数列{b n }的前n 项和为T n ，则T 1＝2，T 2＝3，当n ≥3时，T n ＝3＋9(1－3n －2)1－3－(n ＋7)(n －2)2＝3n －n 2－5n ＋112，所以T n ＝⎩⎪⎨⎪⎧2， n ＝1，3n －n 2－5n ＋112， n ≥2，n ∈N *.14分(2017·绍兴二诊)若An 和B n 分别表示数列{a n }和{b n }的前n 项的和，对任意正整数n ，a n ＝2(n ＋1)，3A n －B n ＝4n .(1)求数列{b n }的通项公式； (2)记c n ＝2A n ＋B n，求{c n }的前n 项和S n . 【导学号：51062175】 [解] (1)由于a n ＝2(n ＋1)，∴{a n }为等差数列，且a 1＝4.2分 ∴A n ＝n (a 1＋a n )2＝n (4＋2n ＋2)2＝n 2＋3n ，∴B n ＝3A n －4n ＝3(n 2＋3n )－4n ＝3n 2＋5n ， 当n ＝1时，b 1＝B 1＝8，当n ≥2时，b n ＝B n －B n －1＝3n 2＋5n －[3(n －1)2＋5(n －1)]＝6n ＋2.由于b 1＝8适合上式，∴b n ＝6n ＋2.7分(2)由(1)知c n ＝2A n ＋B n＝24n 2＋8n＝14⎝ ⎛⎭⎪⎫1n －1n ＋2，9分 ∴S n ＝14⎣⎢⎡⎝ ⎛⎭⎪⎫11－13＋⎝ ⎛⎭⎪⎫12－14＋⎝ ⎛⎭⎪⎫13－15＋⎦⎥⎤⎝ ⎛⎭⎪⎫14－16＋…＋⎝ ⎛⎭⎪⎫1n －1－1n ＋1＋⎝⎛⎭⎪⎫1n －1n ＋2＝14⎝ ⎛⎭⎪⎫1＋12－1n ＋1－1n ＋2 ＝38－14⎝ ⎛⎭⎪⎫1n ＋1＋1n ＋2.14分[规律方法] 1.裂项相消法求和就是将数列中的每一项裂成两项或多项，使这些裂开的项出现有规律的相互抵捎，要注意消去了哪些项，保留了哪些项，从而达到求和的目的．2．消项规律：消项后前边剩几项，后边就剩几项，前边剩第几项，后边就剩倒数第几项．[变式训练2] (2017·宁波一模)已知等差数列{a n }中，2a 2＋a 3＋a 5＝20，且前10项和S 10＝100.(1)求数列{a n }的通项公式； (2)若b n ＝1a n a n ＋1，求数列{b n }的前n 项和． [解] (1)由已知得⎩⎨⎧2a 2＋a 3＋a 5＝4a 1＋8d ＝20，10a 1＋10×92d ＝10a 1＋45d ＝100，解得⎩⎪⎨⎪⎧a 1＝1，d ＝2，3分所以数列{a n }的通项公式为a n ＝1＋2(n －1)＝2n －1.6分 (2)b n ＝1(2n －1)(2n ＋1)＝12⎝⎛⎭⎪⎫12n －1－12n ＋1，10分 所以T n ＝12⎝ ⎛⎭⎪⎫1－13＋13－15＋…＋12n －1－12n ＋1 ＝12⎝ ⎛⎭⎪⎫1－12n ＋1＝n2n ＋1.14分已知数列{an }的前n 项和S n ＝3n 2＋8n ，{b n }是等差数列，且a n ＝b n＋b n ＋1.(1)求数列{b n }的通项公式；(2)令c n ＝(a n ＋1)n ＋1(b n ＋2)n ，求数列{c n }的前n 项和T n .[解] (1)由题意知当n ≥2时，a n ＝S n －S n －1＝6n ＋5. 当n ＝1时，a 1＝S 1＝11，符合上式． 所以a n ＝6n ＋5.2分 设数列{b n }的公差为d .由⎩⎪⎨⎪⎧ a 1＝b 1＋b 2，a 2＝b 2＋b 3，即⎩⎪⎨⎪⎧11＝2b 1＋d ，17＝2b 1＋3d ， 解得⎩⎪⎨⎪⎧b 1＝4，d ＝3.所以b n ＝3n ＋1.6分(2)由(1)知c n ＝(6n ＋6)n ＋1(3n ＋3)n＝3(n ＋1)·2n ＋1.8分 又T n ＝c 1＋c 2＋…＋c n ，得T n ＝3×[2×22＋3×23＋…＋(n ＋1)×2n ＋1]， 2T n ＝3×[2×23＋3×24＋…＋(n ＋1)×2n ＋2]，9分两式作差，得－T n ＝3×[2×22＋23＋24＋…＋2n ＋1－(n ＋1)×2n ＋2]＝3×⎣⎢⎢⎡⎦⎥⎥⎤4＋4(1－2n )1－2－(n ＋1)×2n ＋2 ＝－3n ·2n ＋2， 所以T n ＝3n ·2n ＋2.14分[规律方法] 1.如果数列{a n }是等差数列，{b n }是等比数列，求数列{a n ·b n }的前n 项和时，可采用错位相减法求和，一般是和式两边同乘以等比数列{b n }的公比，若{b n }的公比为参数，应分公比等于1和不等于1两种情况讨论．2．在书写“S n ”与“qS n ”的表达式时应特别注意将两式“错项对齐”，即公比q 的同次幂项相减，转化为等比数列求和．[变式训练3] (2017·湖州第三次模拟)已知等差数列{a n }的前n 项和S n 满足S 3＝6，S 5＝15.(1)求{a n }的通项公式；(2)设b n ＝a n2a n，求数列{b n }的前n 项和T n .[解] (1)设等差数列{a n }的公差为d ，首项为a 1. ∵S 3＝6，S 5＝15，∴⎩⎪⎨⎪⎧3a 1＋12×3×(3－1)d ＝6，5a 1＋12×5×(5－1)d ＝15，即⎩⎪⎨⎪⎧a 1＋d ＝2，a 1＋2d ＝3，解得⎩⎪⎨⎪⎧a 1＝1，d ＝1.4分∴{a n }的通项公式为a n ＝a 1＋(n －1)d ＝1＋(n －1)×1＝n .6分 (2)由(1)得b n ＝a n 2a n＝n2n ，8分∴T n ＝12＋222＋323＋…＋n －12n －1＋n 2n ，①①式两边同乘12， 得12T n ＝122＋223＋324＋…＋n －12n ＋n2n ＋1，② ①－②得12T n ＝12＋122＋123＋…＋12n －n 2n ＋1＝12⎝ ⎛⎭⎪⎫1－12n 1－12－n 2n ＋1＝1－12n －n 2n ＋1，12分 ∴T n ＝2－12n －1－n2n .14分[思想与方法]解决非等差、等比数列的求和，主要有两种思路：(1)转化的思想，即将一般数列设法转化为等差或等比数列，这一思想方法往往通过通项分解或错位相减来完成．(2)不能转化为等差或等比数列的数列，往往通过裂项相消法、倒序相加法等来求和．[易错与防范]1．直接应用公式求和时，要注意公式的应用范围，如当等比数列公比为参数(字母)时，应对其公比是否为1进行讨论．2．利用裂项相消法求和的注意事项：(1)抵消后并不一定只剩下第一项和最后一项，也有可能前面剩两项，后面也剩两项．(2)将通项裂项后，有时需要调整前面的系数，使裂开的两项之差与系数之积与原通项相等．如：若{a n }是等差数列，则1a n a n ＋1＝1d ⎝ ⎛⎭⎪⎫1a n －1a n ＋1，1a n a n ＋2＝12d ⎝ ⎛⎭⎪⎫1a n －1a n ＋2. 课时分层训练(二十九) 数列求和A 组 基础达标(建议用时：30分钟)一、选择题1．数列112，314，518，7116，…，(2n －1)＋12n ，…的前n 项和S n 的值等于( )A ．n 2＋1－12nB ．2n 2－n ＋1－12nC ．n 2＋1－12n －1D ．n 2－n ＋1－12nA [该数列的通项公式为a n ＝(2n －1)＋12n ，则S n ＝[1＋3＋5＋…＋(2n －1)]＋⎝ ⎛⎭⎪⎫12＋122＋…＋12n ＝n 2＋1－12n .]2．(2017·金华十校3月联考)在数列{a n }中，a n ＋1－a n ＝2，S n 为{a n }的前n 项和．若S 10＝50，则数列{a n ＋a n ＋1}的前10项和为( )A ．100B ．110C ．120D ．130C [{a n ＋a n ＋1}的前10项和为a 1＋a 2＋a 2＋a 3＋…＋a 10＋a 11＝2(a 1＋a 2＋…＋a 10)＋a 11－a 1＝2S 10＋10×2＝120.故选C.]3．(2017·浙江名校2月联考)中国古代数学著作《算法统宗》中有这样一个问题：“三百七十八里关，初行健步不为难，次日脚痛减一半，六朝才得到其关，要见次日行里数，请公仔细算相还．”其意思为：有一个人走378里路，第一天健步行走，从第二天起脚痛每天走的路程为前一天的一半，走了6天后到达目的地，请问第二天走了( )A ．192里B ．96里C ．48里D ．24里B [由题意，知每天所走路程形成以a 1为首项，公比为12的等比数列，则a 1⎝ ⎛⎭⎪⎫1－1261－12＝378，解得a 1＝192，则a 2＝96，即第二天走了96里．故选B.] 4．(2017·浙江五校联考)已知数列5,6,1，－5，…，该数列的特点是从第二项起，每一项都等于它的前后两项之和，则这个数列的前16项之和S 16等于( )A ．5B ．6C ．7D ．16C [根据题意这个数列的前8项分别为5,6,1，－5，－6，－1,5,6，发现从第7项起，数字重复出现，所以此数列为周期数列，且周期为6，前6项和为5＋6＋1＋(－5)＋(－6)＋(－1)＝0.又因为16＝2×6＋4，所以这个数列的前16项之和S 16＝2×0＋7＝7.故选C.]5．已知函数f (x )＝x a 的图象过点(4,2)，令a n ＝1f (n ＋1)＋f (n )，n ∈N *，记数列{a n }的前n 项和为S n ，则S 2 017＝( ) A. 2 016－1 B. 2 017－1 C. 2 018－1 D. 2 018＋1 C [由f (4)＝2得4a ＝2，解得a ＝12，则f (x )＝x 12.∴a n ＝1f (n ＋1)＋f (n )＝1n ＋1＋n ＝n ＋1－n ，S 2 017＝a 1＋a 2＋a 3＋…＋a 2 017＝(2－1)＋(3－2)＋(4－3)＋…＋( 2 018－ 2 017)＝ 2 018－1.]二、填空题6．设数列{a n }的前n 项和为S n ，且a n ＝sin n π2，n ∈N *，则S 2 016＝__________.【导学号：51062176】0 [a n ＝sin n π2，n ∈N *，显然每连续四项的和为0.S 2 016＝S 4×504＝0.]7．对于数列{a n }，定义数列{a n ＋1－a n }为数列{a n }的“差数列”，若a 1＝2，{a n }的“差数列”的通项公式为2n ，则数列{a n }的前n 项和S n ＝__________.2n ＋1－2 [∵a n ＋1－a n ＝2n ，∴a n ＝(a n －a n －1)＋(a n －1－a n －2)＋…＋(a 2－a 1)＋a 1＝2n －1＋2n －2＋…＋22＋2＋2＝2－2n 1－2＋2＝2n －2＋2＝2n . ∴S n ＝2－2n ＋11－2＝2n ＋1－2.] 8．(2017·杭州二中综合测试(二))设数列{a n }的前n 项和为S n ，若a 2＝12，S n ＝kn 2－1(n ∈N *)，则数列⎩⎨⎧⎭⎬⎫1S n 的前n 项和为__________． n 2n ＋1[令n ＝1得a 1＝S 1＝k －1，令n ＝2得S 2＝4k －1＝a 1＋a 2＝k －1＋12，解得k ＝4，所以S n ＝4n 2－1，1S n ＝14n 2－1＝1(2n ＋1)(2n －1)＝12⎝ ⎛⎭⎪⎫12n －1－12n ＋1，则数列⎩⎨⎧⎭⎬⎫1S n 的前n 项和为12⎝ ⎛⎭⎪⎫11－13＋12⎝ ⎛⎭⎪⎫13－15＋…＋12⎝ ⎛⎭⎪⎫12n －1－12n ＋1＝12⎝ ⎛⎭⎪⎫1－12n ＋1＝n 2n ＋1.] 三、解答题9．(2017·温州二诊)已知数列{a n }中，a 1＝1，又数列⎩⎨⎧⎭⎬⎫2na n (n ∈N *)是公差为1的等差数列．(1)求数列{a n }的通项公式a n ；(2)求数列{a n }的前n 项和S n .[解] (1)∵数列⎩⎨⎧⎭⎬⎫2na n 是首项为2，公差为1的等差数列， ∴2na n＝2＋(n －1)＝n ＋1，4分 解得a n ＝2n (n ＋1).6分 (2)∵a n ＝2n (n ＋1)＝2⎝ ⎛⎭⎪⎫1n －1n ＋1， ∴S n ＝2⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1－12＋⎝ ⎛⎭⎪⎫12－13＋…＋⎝ ⎛⎭⎪⎫1n －1n ＋1＝2⎝⎛⎭⎪⎫1－1n ＋1＝2n n ＋1.14分 10．等差数列{a n }中，a 3＋a 4＝4，a 5＋a 7＝6.(1)求{a n }的通项公式；(2)设b n ＝[a n ]，求数列{b n }的前10项和，其中[x ]表示不超过x 的最大整数，如[0.9]＝0，[2.6]＝2. 【导学号：51062177】[解] (1)设数列{a n }的首项为a 1，公差为d ，由题意有⎩⎪⎨⎪⎧ 2a 1＋5d ＝4，a 1＋5d ＝3，解得⎩⎨⎧ a 1＝1，d ＝25.4分所以{a n }的通项公式为a n ＝2n ＋35.6分(2)由(1)知，b n ＝⎣⎢⎡⎦⎥⎤2n ＋35. 当n ＝1,2,3时，1≤2n ＋35＜2，b n ＝1；当n ＝4,5时，2≤2n ＋35＜3，b n ＝2；10分当n＝6,7,8时，3≤2n＋35＜4，b n＝3；当n＝9,10时，4≤2n＋35＜5，b n＝4.所以数列{b n}的前10项和为1×3＋2×2＋3×3＋4×2＝24.14分B组能力提升(建议用时：15分钟)1．已知等比数列{a n}的各项都为正数，且当n≥3时，a4a2n－4＝102n，则数列lg a1,2lg a2,22lg a3,23lg a4，…，2n－1lg a n，…的前n项和S n等于() A．n·2n B．(n－1)·2n－1－1C．(n－1)·2n＋1 D．2n＋1C[∵等比数列{a n}的各项都为正数，且当n≥3时，a4a2n－4＝102n，∴a2n＝102n，即a n＝10n，∴2n－1lg a n＝2n－1lg 10n＝n·2n－1，∴S n＝1＋2×2＋3×22＋…＋n·2n－1，①2S n＝1×2＋2×22＋3×23＋…＋n·2n，②∴①－②得－S n＝1＋2＋22＋…＋2n－1－n·2n＝2n－1－n·2n＝(1－n)·2n－1，∴S n＝(n－1)·2n＋1.]2．(2017·浙江嘉兴第一中学期中)数列{a n}的前n项和为S n＝n2－6n，则a2＝________；数列{|a n|}的前10项和|a1|＋|a2|＋…＋|a10|＝________.－358[当n＝1时，a1＝S1＝－5，当n≥2时，a n＝S n－S n－1＝n2－6n－(n－1)2＋6(n－1)＝2n－7，∴a2＝2×2－7＝－3，∴|a1|＋|a2|＋…＋|a10|＝5＋3＋1＋1＋3＋…＋13＝9＋1＋132×7＝9＋49＝58.]3．(2017·杭州学军中学测试(二))设S n是数列{a n}的前n项和，已知a1＝3，a n＋1＝2S n＋3(n∈N*)．(1)求数列{a n }的通项公式；(2)令b n ＝(2n －1)a n ，求数列{b n }的前n 项和T n .[解] (1)当n ≥2时，由a n ＋1＝2S n ＋3得a n ＝2S n －1＋3， 两式相减，得a n ＋1－a n ＝2S n －2S n －1＝2a n ，∴a n ＋1＝3a n ，∴a n ＋1a n＝3. 当n ＝1时，a 1＝3，a 2＝2S 1＋3＝2a 1＋3＝9，则a 2a 1＝3.5分 ∴数列{a n }是以a 1＝3为首项，公比为3的等比数列． ∴a n ＝3×3n －1＝3n .6分(2)法一：由(1)得b n ＝(2n －1)a n ＝(2n －1)·3n ，7分 ∴T n ＝1×3＋3×32＋5×33＋…＋(2n －1)·3n ，① 3T n ＝1×32＋3×33＋5×34＋…＋(2n －1)·3n ＋1，② ①－②得－2T n ＝1×3＋2×32＋2×33＋…＋2×3n －(2n －1)·3n ＋1 ＝3＋2×(32＋33＋…＋3n )－(2n －1)·3n ＋1＝3＋2×32(1－3n －1)1－3－(2n －1)·3n ＋1 ＝－6－(2n －2)·3n ＋1.14分∴T n ＝(n －1)·3n ＋1＋3.15分法二：由(1)得b n ＝(2n －1)a n ＝(2n －1)·3n .7分 ∵(2n －1)·3n ＝(n －1)·3n ＋1－(n －2)·3n ， ∴T n ＝b 1＋b 2＋b 3＋…＋b n＝(0＋3)＋(33＋0)＋(2×34－33)＋…＋[(n －1)·3n ＋1－(n －2)·3n ] ＝(n －1)·3n ＋1＋3.15分。

高中数学-数列求和方法汇总及经典练习（含答案）一、公式法:利用以下公式求数列的和 1.d n n na a a n Snn 2)1(2)(11-+=+=({}n a 为等差数列)2.qqa a q q a Sn n n --=--=11)1(11 (1≠q )或)1(1==q na Sn ({}n a 为等比数列) 3.6)12)(1(3212222++=+⋅⋅⋅⋅⋅⋅⋅+++n n n n4.23333]2)1([321+=+⋅⋅⋅⋅⋅⋅⋅+++n n n 等公式例已知数列{}n a ，其中()12111,3,22n n n a a a a a n +-===+≥，记数列{}n a 的前n 项和为n S ，数列{}ln n S 的前n 项和为n U ，求n U 。

解：由题意，{}n a 是首项为1，公差为2的等差数列 前n 项和()211212n n S n n ++-=⋅=，2ln ln 2ln n S n n ==()()2ln1ln 2ln 2ln !n U n n =+++=L二、分组求和法对于数列{}n a ，若⋅⋅⋅⋅⋅⋅±±=n n n C b a 且数列{}n b 、{}n c ……都能求出其前n 项的和，则在求{}n a 前n 项和时，可采用该法例如：求和：321999.09999.0999.099.09.0个n Sn ⋅⋅⋅+⋅⋅⋅⋅⋅⋅++++= 解：设n n na --=⋅⋅⋅⋅⋅⋅=10199.0943421个 n a a a a a Sn +⋅⋅⋅⋅⋅⋅++++=∴4321)101()101()101()101()101(4321n------+⋅⋅⋅⋅⋅⋅+-+-+-+-=)1010101010()111(43211n n -----+⋅⋅⋅⋅⋅⋅++++-+⋅⋅⋅⋅⋅⋅++=4434421相加个 )101(91n n ---= 三、倒序相加法（或倒序相乘法）将一个数列倒过来排列（反序），再把它与原数列相加，就可以得到n 个)(1n a a +，S n 表示从第一项依次到第n 项的和，然后又将S n 表示成第n 项依次反序到第一项的和，将所得两式相加，由此得到S n 的一种求和方法。