新北师大版九年级数学上册《反比例函数的图像》学案

课题 6.2.1反比例函数的图象与性质课型新授教学目标（知识与技能、过程与方法、情感态度与价值观）1、知识与技能：进一步熟悉作函数图象的主要步骤，会作反比例函数的图象，逐步提高从函数图象中获取信息的能力，探索并掌握反比例函数的主要性质.2、过程与方法: 通过学生自己动手列表、描点、连线，提高学生的作图能力；通过观察图象，概括反比例函数的有关性质，训练学生的概括、总结能力.3.情感态度与价值观:让学生积极参与到数学学习活动中，增强他们对数学学习的好奇心与求知欲.教学重点画反比例函数的图象；并从函数图象中获取信息，探索并研究反比例函数的主要性质.教学难点反比例函数的图象特点及性质的探究. 辅助教具电子白板、多媒体课件学习方法自主学习、合作探究、总结归纳教学过程一、复习导入1．什么是反比例函数？一般地，形如( k是常数, k ≠0 ) 的函数叫做反比例函数。

2．反比例函数的定义中需要注意什么？（1）k 是非零常数；（2）三种形式: ; y =kxˉ1 ; xy = k二、探究新知反比例函数(k≠0)的图象是什么样子呢？例1．画出函数的图象。

思考：（1）画函数图象的三个步骤是什么？列表、描点、连线。

注意：①x≠0；②列表时自变量取值易于计算,易于描点补充、修正、体会kyx=kyx=xy4=你认为作比例函数图象时应注意哪些问题？1.列表时,选取的自变量的值,既要易于计算,又要便于描点,尽量多取一些数值(取互为相反数的一对一对的数),多描一些点,这样既可以方便连线，又可以使图象精确。

2 .描点时要严格按照表中所列的对应值描点，绝对不能把点的位置描错。

3.一定要养成按自变量从小到大的顺序依次画线,连线时必须用光滑的曲线连接各点,不能用折线连接。

4.图像是延伸的，注意不要画成有明确端点。

5.曲线的发展趋势只能靠近坐标轴,但不能和坐标轴相交.练习1．画出函数的图象(直接画在课本上)观察：函数和的图象,有什么相同点和不同点？相同点:1.图象分别都是由两支曲线组成.它们都不与坐标轴相交2.两个函数图象自身都是轴对称图形,它们各有两条对称轴.3.两个函数图象自身都是中心对称图形,对称中心是坐标原点.不同点: 两支曲线分别位于第一、三象限内; 两支曲线分别位于第二、四象限内，形状：图像分别都是由两支曲线组成，因此称反比例函数的图象为双曲线。

新北师大版九年级数学上册《反比例函数的图像》导学案1．作函数图象的一般步骤是：__列表，描点，连线__．2．反比例函数y ＝kx的图象是由__两支曲线__组成的．当k >0时，两支曲线分别位于第__一、三__象限内；当k <0时，两支曲线分别位于第__二、四__象限内．3．反比例函数的图象既是__轴对称__图形，又是__中心对称__图形，其对称轴为直线__y ＝x 或y ＝－x __，其对称中心为__原点__．知识点一：反比例函数的图象1．(2014·淮安)若反比例函数y ＝kx的图象经过点(5，－1)，则双曲线位于( B )A ．第一、三象限B ．第二、四象限C ．第一、四象限D ．第二、三象限2．(2014·兰州)若反比例函数y ＝k －1x的图象位于第二、四象限，则k 的取值可以是( A )A ．0B ．1C ．2D ．以上都不是3．已知反比例函数y ＝m －1x的图象的一支位于第一象限，则常数m 的取值范围是__m>1__．4．画出反比例函数y ＝6x 和y ＝－6x的图象．解：略知识点二：根据图象确定反比例函数的表达式5．如图是我们学过的反比例函数，它的函数表达式可能是( B )A ．y ＝x 2B ．y ＝4xC ．y ＝－3xD ．y ＝12x,第5题图) ,第6题图)6．如图，已知OA ＝6，∠AOB ＝30°，则经过点A 的反比例函数的表达式为( B )A ．y ＝－93xB ．y ＝93xC ．y ＝9xD ．y ＝－9x7．(2014·怀化)已知点A(－2，4)在反比例函数y ＝kx(k ≠0)的图象上，则k 的值为__－8__．知识点三：利用反比例函数求点的坐标8．若反比例函数y ＝8x的图象经过点(－2，m )，则m 的值是( C )A.14 B ．－14C ．－4D ．4 9．反比例函数y ＝－6x的图象是轴对称图形，它的对称轴有( B )A ．1条B ．2条C ．3条D ．4条10．反比例函数y ＝kx(k >0)的图象与经过原点的直线l 相交于A ，B 两点，已知A 点的坐标为(2，1)，那么B 点的坐标为__(－2，－1)__．11．当x >0时，函数y ＝－5x的图象在( A )A ．第四象限B ．第三象限C ．第二象限D ．第一象限12．(易错题)已知函数y ＝(m ＋1)xm 2－5是反比例函数且图象位于第二、四象限内，则m 的值为( B )A ．2B ．－2C ．±2D ．－1213．(2014·聊城)如图，一次函数y 1＝k 1x ＋b 的图象和反比例函数y 2＝k 2x的图象交于A(1，2)，B(－2，－1)两点，若y 1<y 2，则x 的取值范围是( D )A ．x <1B ．x <－2C ．－2<x <0或x >1D ．x <－2或0<x <114．已知一个函数图象与y ＝6x 的图象关于y 轴对称，则这个函数的表达式为__y ＝－6x__．15．如图，在平面直角坐标系xOy 中，正比例函数y ＝kx 的图象与反比例函数y ＝2x的图象有一个交点A (m ，2)．(1)求m 的值；(2)求正比例函数y ＝kx 的表达式；(3)试判断点B (－2，－1)是否在反比例函数的图象上，并说明理由．解：(1)m ＝1(2)正比例函数y ＝kx 的表达式为y ＝2x (3)点B (－2，－1)在反比例函数图象上，∵当x ＝－2时，y ＝2－2＝－1，∴点B (－2，－1)在双曲线y ＝2x上16．如图，一次函数y ＝kx ＋b 的图象与反比例函数y ＝mx的图象相交于A (－2，1)，B (1，n )两点．(1)求反比例函数与一次函数的表达式；(2)根据图象写出当一次函数的值大于反比例函数的值时，x 的取值范围．解：(1)把A (－2，1)代入y ＝m x ，得m ＝－2.即反比例函数为y ＝－2x ，则n ＝－21＝－2.即B (1，－2)．把A (－2，1)，B (1，－2)代入y ＝kx ＋b ，求得k ＝－1，b ＝－1.∴一次函数的表达式为y ＝－x －1 (2)x<－2或0<x<117．已知，反比例函数y ＝kx和一次函数y ＝2x －1，其中一次函数的图象经过点(k ，5)．(1)试求反比例函数的表达式；(2)若点A 在第一象限，且同时在上述两函数的图象上，求A 点的坐标．解：(1)一次函数y ＝2x －1的图象经过点(k ，5)，∴5＝2k －1，解得k ＝3.所以反比例函数的表达式为y ＝3x (2)把y ＝3x 代入y ＝2x －1得3x ＝2x －1，解得x 1＝－1(因为点A 在第一象限，故舍去)，x 2＝32.当x ＝32时，y ＝2，∴A 点坐标为(32，2)18．如图，点A (1，a )在反比例函数y ＝3x(x >0)的图象上，AB 垂直于x 轴，垂足为点B ，将△ABO 沿x 轴向右平移2个单位长度，得到Rt △DEF ，点D 落在反比例函数y ＝kx(x >0)的图象上．(1)求点A 的坐标； (2)求k 的值．解：(1)∵点A (1，a )在y ＝3x 的图象上，∴a ＝31＝3.∴点A (1，3) (2)∵△ABO 向右平移2个单位长度，得到△DEF ，∴D (3，3)．∵点D 在y ＝k x (x>0)的图象上，∴3＝k3.∴k ＝9第2课时 反比例函数的性质1．反比例函数y ＝kx，当k >0时，图象的两个分支分别位于第__一、三__象限，在每个象限内，y 随x 的增大而__减小__；当k <0时，图象的两个分支分别位于第__二、四__象限，在每个象限内，y 随x 的增大而__增大__．2．过反比例函数y ＝kx图象上任意一点P (x ，y )作x 轴，y 轴的垂线，所得矩形的面积为__|k|__．知识点一：反比例函数图象的性质1．如果反比例函数y ＝kx(k ≠0)，当x >0时，y 随x 的增大而增大，则反比例函数的图象经过( B )A ．第一、三象限B ．第二、四象限C ．第一、四象限D ．第二、三象限2．(2014·随州)关于反比例函数y ＝2x的图象，下列说法正确的是( D )A ．图象经过点(1，1)B ．两个分支分布在第二、四象限C ．两个分支关于x 轴对称D ．当x <0时，y 随x 的增大而减小3．(2014·天津)已知反比例函数y ＝10x，当1<x<2时，则y 的取值范围是( C )A ．0<y <5B ．1<y <2C ．5<y <10D ．y >104．点(2，y 1)，(3，y 2)在函数y ＝－2x的图象上，则y 1__<__y 2.(填“>”“<”或“＝”)5．已知反比例函数y ＝m －2x的图象上有两个点A (x 1，y 1)，B (x 2，y 2)且0<x 1<x 2时，y 1>y 2，则m 的取值范围是__m>2__．6．反比例函数y ＝(2m －1)xm 2－2，当x >0时，y 随x 的增大而增大，求m 的值． 解：根据题意，m 2－2＝－1，解得m ＝±1.∵当x>0时，y 随x 的增大而增大，∴2m－1<0.解得m<12.∴m ＝－1知识点二：反比例函数图象中比例系数k 的几何意义7．如图，正方形OABC ，正方形ADEF 的顶点A ，D ，C 在坐标轴上，顶点F 在AB 上，顶点B ，E 在函数y ＝1x(x >0)的图象上，则点E 的坐标是( A )A ．(5＋12，5－12)B ．(3＋52，3－52)C ．(5－12，5＋12)D ．(3－52，3＋52)8．(2014·黔东南)如图，正比例函数y ＝x 与反比例函数y ＝2x的图象相交于A ，B 两点，BC ⊥x 轴于点C ，则△ABC 的面积为( B )A ．1B ．2C ．3D ．4,第8题图) ,第9题图)9．如图，点A 在双曲线y ＝kx上，AB ⊥x 轴于点B ，△ABO 的面积是2，则k ＝__－4__．10．(2014·怀化)已知一次函数y ＝kx ＋b 的图象如图，那么正比例函数y ＝kx 和反比例函数y ＝kx在同一坐标系中的图象大致是( B )11．(2014·湘潭)如图，点A ，B 在双曲线y ＝4x上，分别经过A ，B 两点向坐标轴作垂线段，已知S 阴影＝1，则S 1＋S 2＝( D )A ．3B ．4C ．5D ．612．(易错题)已知点A(1，y 1)，B(2，y 2)，C(－3，y 3)都在反比例函数y ＝6x的图象上，则y 1，y 2，y 3的大小关系是( D )A ．y 3<y 1<y 2B ．y 1<y 2<y 3C ．y 2<y 1<y 3D ．y 3<y 2<y 113．已知(x 1，y 1)，(x 2，y 2)为反比例函数y ＝kx图象上的点，当x 1<x 2<0时，y 1<y 2，则k的一个值可为__－1(只要k<0即可)__．(只需写出符合条件的一个k 的值)14．如图，一次函数y ＝x ＋b 与反比例函数y ＝kx在第一象限的图象交于点B ，且点B的横坐标为1，过点B 作y 轴的垂线，C 为垂足，若S △BCO ＝32，求一次函数和反比例函数的表达式．解：∵一次函数y ＝x ＋b 过点B ，且点B 的横坐标为1，∴y ＝1＋b ，即B (1，1＋b )．∵BC ⊥y 轴，且S △BCO ＝32，∴12×OC ×BC ＝12×1×(b ＋1)＝32，解得b ＝2.∴B (1，3)，∴一次函数的表达式为y ＝x ＋2.又∵y ＝k x 过点B ，∴k ＝3.∴反比例函数的表达式为y ＝3x15．(2014·苏州)如图，已知函数y ＝kx(x>0)的图象经过点A ，B ，点A 的坐标为(1，2)，过点A 作AC ∥y 轴，AC ＝1(点C 位于点A 的下方)，过点C 作CD ∥x 轴，与函数的图象交于点D ，过点B 作BE ⊥CD ，垂足E 在线段CD 上，连接OC ，OD.(1)求△OCD 的面积；(2)当BE ＝12AC 时，求CE 的长．解：(1)y ＝kx(x>0)的图象经过点A (1，2)，∴k ＝2，∵AC ∥y 轴，AC ＝1，∴点C 的坐标为(1，1)．∵CD ∥x 轴，点D 在函数图象上，∴点D 的坐标为(2，1)．∴S △OCD ＝12×1×1＝12 (2)∵BE ＝12AC ，∴BE ＝12，∴B (43，32)，∴CE ＝43－1＝1316．(2014·遂宁)已知：如图，反比例函数y ＝kx的图象与一次函数y ＝x ＋b 的图象交于点A(1，4)，点B(－4，n)．(1)求一次函数和反比例函数的表达式； (2)求△OAB 的面积；(3)直接写出一次函数值大于反比例函数值的自变量x 的取值范围．解：(1)把点A (1，4)分别代入反比例函数y ＝kx ，一次函数y ＝x ＋b ，得k ＝1×4，1＋b ＝4，解得k ＝4，b ＝3，反比例函数的表达式是y ＝4x，一次函数表达式是y ＝x ＋3 (2)当x ＝－4时，y ＝－1，B (－4，－1)，当y ＝0时，x ＋3＝0，x ＝－3，设直线AB 交x 轴于点C ，C (－3，0)，S △AOB ＝S △AOC ＋S △BOC ＝12×3×4＋12×3×1＝152(3)∵B (－4，－1)，A (1，4)，∴根据图象可知：当x>1或－4<x<0时，一次函数值大于反比例函数值专题(十五) 反比例函数与不等式1．已知A (－1，y 1)，B (2，y 2)两点在双曲线y ＝3＋2mx上，且y 1>y 2，则m 的取值范围是( D )A ．m <0B ．m >0C ．m >－32D ．m <－322．(2014·黔西南)已知如图，一次函数y ＝ax ＋b 和反比例函数y ＝kx的图象相交于A ，B两点，不等式ax ＋b>kx的解集为( B )A ．x <－3B ．－3<x <0或x >1C ．x <－3或x >1D ．－3<x <13．(2014·南充)如图，一次函数y 1＝kx ＋b 的图象与反比例函数y 2＝mx的图象相交于点A(2，5)和点B ，与y 轴相交于点C(0，7)．(1)求这两个函数的表达式； (2)当x 取何值时，y 1<y 2.解：(1)∵反比例函数y 2＝m x 的图象过点A (2，5)，∴5＝m2，m ＝10，即反比例函数的表达式为y ＝10x，∵一次函数y 1＝kx ＋b 的图象过点A (2，5)和C (0，7)，∴b ＝7，k ＝－1，即一次函数表达式为y ＝－x ＋7(2)解方程组⎩⎪⎨⎪⎧y ＝－x ＋7，y ＝10x ，得⎩⎨⎧x 1＝2，y 1＝5，或⎩⎨⎧x 2＝5，y 2＝2，∴另一交点B 的坐标为(5，2)，根据图象可知，当0<x<2或x>5时，y 1<y 24．(2014·巴中)如图，在平面直角坐标系xOy 中，已知四边形DOBC 是矩形，且D(0，4)，B(6，0)．若反比例函数y ＝k 1x(x>0)的图象经过线段OC 的中点A ，交DC 于点E ，交BC于点F.设直线EF 的表达式为y ＝k 2x ＋b.(1)求反比例函数和直线EF 的表达式； (2)求△OEF 的面积；(3)请结合图象直接写出不等式k 2x ＋b －k 1x>0的解集．解：(1)∵四边形DOBC 是矩形，且D (0，4)，B (6，0)，∴C 点坐标为(6，4)，∵点A为线段OC 的中点，∴A 点坐标为(3，2)，∴k 1＝3×2＝6，∴反比例函数表达式为y ＝6x，把x ＝6代入y ＝6x 得x ＝1，则F 点的坐标为(6，1)，把y ＝4代入y ＝6x 得x ＝32，则E 点坐标为(32，4)，把F (6，1)，E (32，4)代入y ＝k 2x ＋b 得⎩⎪⎨⎪⎧6k 2＋b ＝1，32k 2＋b ＝4，解得⎩⎪⎨⎪⎧k 2＝－23，b ＝5∴直线EF 的表达式为y ＝－23x ＋5 (2)△OEF 的面积＝S 矩形BCDO －S △ODE －S △OBF －S △CEF ＝454 (3)不等式k 2x ＋b －k 1x >0的解集为32<x<65．(2014·德阳)已知一次函数y 1＝x ＋m 的图象与反比例函数y 2＝6x的图象交于A ，B 两点．已知当x>1时，y 1>y 2；当0<x<1时，y 1<y 2.(1)求一次函数的表达式；(2)已知反比例函数图象在第一象限上有一点C 到y 轴的距离为3，求△ABC 的面积． 解：(1)一次函数表达式为：y 1＝x ＋5 (2)由题意得C (3，2)，联立⎩⎪⎨⎪⎧y ＝x ＋5，y ＝6x解得⎩⎨⎧x 1＝1，y 1＝6，⎩⎨⎧x 2＝－6，y 2＝－1，∴B (－6，－1)，作CD ∥x 轴交AB 于点D ，则点D 的坐标为(－3，2)，CD ＝3－(－3)＝6，∴S △ABC ＝S ADC ＋S △BDC ＝12×6×4＋12×6×3＝21专题(十六) 反比例函数与一次函数的综合一、反比例函数与正比例函数1．(2014·益阳)正比例函数y ＝6x 的图象与反比例函数y ＝6x的图象交点位于( D ) A ．第一象限 B ．第二象限C ．第三象限D ．第一、三象限2．已知直线y ＝kx (k >0)与双曲线y ＝3x交于点A (x 1，y 1)，B (x 2，y 2)两点，则x 1y 2＋x 2y 1的值为( A )A ．－6B ．－9C ．0D ．9二、反比例函数与一次函数3．(2014·咸宁)如图，双曲线y ＝m x与直线y ＝kx ＋b 交于点M ，N ，并且点M 的坐标为(1，3)，点N 的纵坐标为－1，根据图象信息可得关于x 的方程m x＝kx ＋b 的解为( A ) A ．－3，1 B ．－3，3C ．－1，1D ．－1，34．如图，在平面直角坐标系xOy 中，函数y ＝4x(x >0)的图象与一次函数y ＝kx －k 的图象的交点为A (m ，2)．(1)求一次函数的表达式；(2)设一次函数y ＝kx －k 的图象与y 轴交于点B ，与x 轴交点为C ，若点P 是x 轴上一点，且满足△P AB 的面积是4，直接写出P 点的坐标．解：(1)将A (m ，2)代入y ＝4x(x>0)得，m ＝2，则A 点坐标为A (2，2)，将A (2，2)代入y ＝kx －k 得2k －k ＝2，解得k ＝2，则一次函数表达式为y ＝2x －2 (2)∵一次函数y ＝2x －2与x 轴的交点为C (1，0)，与y 轴的交点为B (0，－2)，S △ABP ＝S △ACP ＋S △BPC ，∴12×2CP ＋12×2CP ＝4，解得CP ＝2，则P 点坐标为(3，0)，(－1，0)5．(2014·广东)如图，已知A(－4，12)，B(－1，2)是一次函数y ＝kx ＋b 与反比例函数y ＝m x(m ≠0，m<0)图象的两个交点，AC ⊥x 轴于点C ，BD ⊥y 轴于点D. (1)根据图象直接回答：在第二象限内，当x 取何值时，一次函数大于反比例函数的值？(2)求一次函数表达式及m 的值；(3)P 是线段AB 上的一点，连接PC ，PD ，若△PCA 和△PDB 面积相等时，求点P 坐标．解：(1)由图象可知，当－4<x<－1时，一次函数大于反比例函数的值 (2)y ＝kx ＋b 的图象过点(－4，12)，(－1，2)，则⎩⎪⎨⎪⎧－4k ＋b ＝12，－k ＋b ＝2，解得⎩⎨⎧k ＝12，b ＝52，一次函数的表达式为y ＝12x ＋52，反比例函数y ＝m x的图象过点(－1，2)，m ＝－1×2＝－2 (3)连接PC ，PD ，如图，设P (x ，12x ＋52)．由△PCA 和△PDB 面积相等得12×12×(x ＋4)＝12×1×(2－12x －52)，得x ＝－52，y ＝12x ＋52＝54，∴P 点坐标为(－52，54)。

第2课 反比例函数的图象与性质(1)课前预习◆知识点 反比例函数的图象与性质 1.用描点法画出反比例函数y ＝4x 的图象．解：列表：x … －8 －4 －2 －1 1 2 4 8 … y ＝4x …－1－2－4421…描点、连线：2.画出反比例函数y ＝－6x 的图象．解：列表：x … －6 －3 －2 －1 1 2 3 6 … y ＝－6x…1236－6－3－2－1…描点、连线：小结反比例函数的图象与性质：反比例函数y ＝kx (k ≠0)的图象是双曲线图象k _>__0k __ <__0性质(1)图象在第一、三象限；(2)在每个象限内，y 随x 的增大而Y 31Y ＋＋＋减小(1)图象在第二、四象限；(2)在每个象限内，y 随x 的增大而Y 31Y ＋＋＋增大对称性：图象既是Y 31Y ＋＋＋轴对称图形，又是Y 31Y ＋＋＋中心对称图形◆知识点 反比例函数图象与性质的简单应用3.反比例函数y ＝6x 的图象在第一、三象限，在每一个象限内，y 随x 的增大而减小., 4.若函数y ＝k －1x 的图象在第一、三象限内，则k 的取值范围是k ＞1.5.如图，双曲线过点A ． (1)求双曲线的表达式；(2)判断点B (4，－2)，C (3，－3)是否在此双曲线上？6.已知反比例函数y ＝k ＋1x 的图象经过点A (2，－2)．(1)求k 的值及函数的表达式；(2)判断点B (4，1)，C (－2，2)是否在此函数的图象上？强化训练1.反比例函数y ＝2 023x的大致图象是( )A B C D 2.关于双曲线y ＝3x ，下列说法错误的是( )A ．当x >0时，y 随x 的增大而增大B ．图象在第一、三象限C ．点(－1，－3)在此双曲线上D ．双曲线的两支关于原点对称3.反比例函数y ＝－1x 的图象位于第二、四象限．在每一象限内，y 随x 的增大而增大.4.点(2，6)在反比例函数y ＝kx的图象上，则k ＝12，图象位于第一、三象限．5.已知反比例函数y ＝1－2kx，当x >0时，y 随x 的增大而增大，则k 的取值范围是k ＞ .6.已知某个反比例函数，它在每个象限内，y 随x 的增大而减小，则这个反比例函数可以是y ＝ (答案不唯一)(写出一个即可)．7.若正比例函数y ＝k 1x 的图象与反比例函数y ＝k 2x 的图象的一个交点的坐标是(－2，4)．(1)k 1＝－2，k 2＝－8；(2)这两个函数图象的另一个交点的坐标为(2，－4).,8.在同一平面直角坐标系中，函数y ＝kx ＋1与y ＝－kx(k ＞0)的图象大致是( )A B C D。

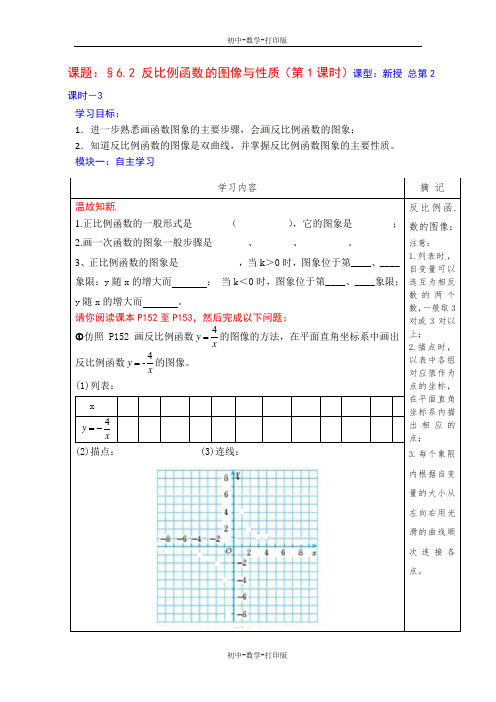
课题：§6.2 反比例函数的图像与性质（第1课时）课型：新授 总第2课时－3 学习目标：1．进一步熟悉画函数图象的主要步骤，会画反比例函数的图象；2．知道反比例函数的图像是双曲线，并掌握反比例函数图象的主要性质。

模块一：自主学习学习内容摘 记 温故知新1.正比例函数的一般形式是______ （__________），它的图象是________；2.画一次函数的图象一般步骤是_______、_______、_________。

3、正比例函数的图象是____________，当k ＞0时，图象位于第____、____象限；y 随x 的增大而 ； 当k ＜0时，图象位于第____、____象限；y 随x 的增大而 。

请你阅读课本P152至P153，然后完成以下问题： 仿照P152画反比例函数x y 4=的图像的方法，在平面直角坐标系中画出反比例函数x y 4-=的图像。

(1)列表： xx y 4-= (2)描点： (3)连线：反比例函数的图像： 注意：1.列表时，自变量可以选互为相反数的两个数，一般取3对或3对以上；2.描点时，以表中各组对应值作为点的坐标，在平面直角坐标系内描出相应的点；3.每个象限内根据自变量的大小从左向右用光滑的曲线顺次连接各点。

模块二：交流研讨模块三：巩固内化研讨内容摘 记内容一：小组成员之间交换讲学稿，交换答案，看看与你的有什么不同。

把你的修改意见在讲学稿上直接标注。

并按照组长的分工，每位同学选择一个内容向全组同学进行交流。

如有不同意见，直接提出或质疑。

内容二：判断下列函数的图像是否正确？若错误，请说明理由。

（1）x y 4=（2）xy 4= 内容三：观察x4y =和x4-y =的图象，回答下列问题。

(1)反比例函数是中心对称图形吗？如果是，请找出对称中心。

(2)反比例函数是轴对称图形吗？如果是，请找出对称轴。

(3)写出两个反比例函数的相同点和不同点；(4)反比例函数x4y =和x4-y =的图象分别在哪两个象限,由什么确定？注意：(1) 0x ≠；(2)连线时不能用折线，必须用光滑的曲线连接各点；(3)反比例函数的图像不是直线，不能用“两点法”作图； 图象是延伸的，不要画成有明确端点； (4)曲线的发展趋势是无限靠近坐标轴,但不和坐标轴相交。

北师大版数学九年级上册《反比例函数的图象》教学设计1一. 教材分析《反比例函数的图象》是北师大版数学九年级上册的一章，主要介绍了反比例函数的图象特点及其应用。

本章内容是在学生已经掌握了函数的概念、一次函数和二次函数的图象与性质的基础上进行的。

通过本章的学习，使学生能理解反比例函数的概念，掌握反比例函数的图象特征，提高学生解决实际问题的能力。

二. 学情分析九年级的学生已经具备了一定的函数知识，对于一次函数和二次函数的图象与性质有一定的了解。

但学生在学习过程中，可能对反比例函数的理解和图象的把握存在一定的困难。

因此，在教学过程中，需要教师引导学生从实际问题出发，激发学生的学习兴趣，引导学生主动探究，从而提高学生的学习效果。

三. 教学目标1.知识与技能：使学生理解反比例函数的概念，掌握反比例函数的图象特征，能运用反比例函数解决实际问题。

2.过程与方法：通过观察、分析、归纳等方法，引导学生探索反比例函数的图象特点，培养学生的逻辑思维能力和归纳总结能力。

3.情感态度与价值观：激发学生学习数学的兴趣，培养学生的团队合作意识和自主学习能力。

四. 教学重难点1.反比例函数的概念及其图象特征。

2.反比例函数在实际问题中的应用。

五. 教学方法1.情境教学法：通过设置实际问题，激发学生的学习兴趣，引导学生主动探究。

2.直观教学法：利用多媒体课件，展示反比例函数的图象，使学生直观地理解反比例函数的特点。

3.小组合作学习：引导学生分组讨论，培养学生的团队合作意识和沟通能力。

4.归纳总结法：在教学过程中，引导学生总结反比例函数的图象特征，提高学生的归纳总结能力。

六. 教学准备1.多媒体课件：制作反比例函数的图象展示课件。

2.教学素材：准备一些实际问题，用于引导学生应用反比例函数解决实际问题。

3.学案：为学生准备学习任务单，引导学生有序学习。

七. 教学过程1.导入（5分钟）教师通过展示实际问题，引导学生思考反比例函数的应用，激发学生的学习兴趣。

6.2反比例函数的图像和性质（一）导学案学习目标1、进一步熟悉作函数图象的主要步骤，会作反比例函数的图象；2、体会函数的三种表示方法的互相转换，探索并掌握反比例函数的主要性质； 学习重点：画反比例函数的图象，探索并研究反比例函数的主要性质.学习难点：反比例函数的图象特点及性质的探究知识回顾1、画函数图像的主要步骤是什么？ 、 、 。

2、下列等式中，哪个等式表示y 是x 的反比例函数 （ ）（A ） k y x = （B ） 23y x = （C ） 121y x =+ （D ） 21xy -= 知识探究一、探索一：试着作反比例函数y ＝x 4的图象： 思考：（1）这个函数中自变量的取值范围是什么？ （2）画函数图象的三个步骤是什么？二、议一议：你认为作反比例函数图像时应注意什么？三、完成课本P152,作反比例函数y ＝x4-的图象. 四、 观察y ＝x 4和y ＝x4-的图象，它们有什么相同点和不同点? 反比例函数的图象是两支 ，当k>0时，图象的两支曲线在第 象限内；当k<0时，两支曲线分别位于第 象限.五、你能画出反比例函数y=x 5 和y=x 5-的大致图象吗?知识反馈基础题： 1、完成随堂练习2、双曲线k y x=经过点(2-，3)，则_____=k ； 3、已知函数1k y x +=的图象两支分布在第二、四象限内，则k 的范围是_________ 4、反比例函数 2k y x= (0≠k )的图象的两个分支分别位于 （ ） （A ） 第一、二象限 （B ） 第一、三象限（C ） 第二、四象限 （D ） 第一、四象限提高题：1、如图，反比例函数k y x=的图象经过点A ， 则k 的值是（A ） 2 （B ） 1.5 （C ） 3- （D ） 32-2、点A 为反比例函数图象上一点，它到原点的距离为5，到x 轴的距离为3，若点A 在第二象限内.则这个反比例函数的解析式为 （ ）（A ） 12y x = （B ） 12y x =- （C ） 112y x = （D ） 112y x=- 创新题：在同一坐标系中，函数 和y=k 2x+b 的图像大致如下，则 k 1 、k 2、b 各应满足什么条件？说明理由。

九年级数学上册6.2.1反比例函数的图象和性质教案（新版）北师大版课题：6.2反比例函数的图像与性质教学目标：1.经历探索反比例函数的性质的过程，体会函数的三种表示方法的相互转换，对函数进行认识上的整合.2.会作反比例函数的图象，进一步掌握画函数图象的主要步骤.3.培养学生从函数图象中获取信息的能力，初步探索反比例函数的性质.教学重点与难点：重点：画反比例函数图象并认识图象的特点.难点：体会函数的三种表示方法的相互转换．课前准备：多媒体课件．教学过程:一、复习回顾，导入新课活动内容：（多媒体出示）创设问题情景.问题：1.什么叫做反比例函数？2.反比例函数的定义中需要注意什么？（此时老师板书反比例函数的表达式.）3.函数有几种表达形式？4.大家还记得一次函数图象是什么？那反比例函数的图象又会是什么样？处理方式：1.问题1,2由学生口答完成后，教师板书反比例函数的表达式.2.学生口答完函数的表达形式有列表法、图像法、关系式法之后，教师追问：如何用表格法和图像法表示反比例函数？接着教师引导学生根据反比例函数关系式可以列表格，再根据表格描点可以得到反比例函数的图像，体会函数三种表示方法可以相互转化.3. 最后老师继续追问：一次函数图象是什么？那反比例函数的图象又会是什么样？从而引出本节课课题，导入新课.设计意图：通过问题串引导学生回归复习反比例的定义，通过追问让学生回忆根据关系式可以列表格，根据表格描点可以得到反比例函数的图像，既复习了函数图像的定义，又让学生体会三种表示方法可以相互转化.二、探究学习，感悟新知活动内容1：例1.画出xy 4 的图象.处理方式：1.让学生独立思考、尝试，然后小组之间交流.学生充分交流后教师利用投影或者课件展示以下错例.2.教师逐步引导学生思考（1）他们做的对吗？为什么？同学会发现图一选取的自变量的值太少，导致图象不具代表性；图二，取自变量的值时，取值以偏带全导致只画出一支曲线．（2）教师追问怎样取值才全面？图三画成有明确端点，图像应是延伸的，连线时习惯用线段，导致出现“硬转弯”的折线图.（3）教师继续发问，为什么图像应是延伸的？适时点拨：我们根据函数图象的定义x 可取无数个值，相应函数值y 可得无数个值，所以图象不要画成如图三．（4）你认为作反比例函数图象时应注意哪些问题？设计意图：先让学生按自己的理解尝试画反比例函数xy 4=的图象，在作图过程中学生会出现各种各样的问题，通过学生的讨论、交流，和教师的点拨让学生理解错误的原因，通过问题串的形式，逐步引导学生思考探究画图象的步骤，并且对于其中出现的错误及时纠正，然后通过对比师生共同总结作反比例函数图象注意的问题.同时在这一过程中让学生积累数学活动经验.活动内容2：看老师如何画出xy 4=图象的（几何画板演示步骤）处理方式：1.教师利用几何画板本演示画图的步骤及过程.2.教师强调作图时应注意以下问题(1)列表时,选取的自变量的值,既要易于计算,又要便于描点,尽量多取一些数值(取互为相反数的一对一对的数),多描一些点,这样既可以方便连线，又可以使图象精确.（2）连线时必须用光滑的曲线连接各点,不能用折线连接.（3）图像是延伸的，注意不要画成有明确端点.（4）曲线的发展趋势只能靠近坐标轴,但不能和坐标轴相交.（5）描点时一定要养成按自变量从小到大的顺序依次画线, 从中体会函数的增减性. 设计意图：教师利用几何画板本演示画图的步骤，体现步骤的严密性，规范性．三、由此及彼，应用新知活动内容1：现在我们已经知道当K 取正数时，我们画出了反比例函数的图像，当K 取负数时它的图像又是什么形状呢?请同学们继续下面的练习. 练习：大家用同样的方法作反比例函数xy 4-= 的图象. 处理方式：然后让学生试着自己作图.教师根据学生的作图情况，期间需要做出必要引导，多媒体出示正确的作图过程，让学生参考，让学生修改自己的解题过程.设计意图：让学生进一步熟悉画函数图像的主要步骤，并在巩固训练中积累素材，通过观察发现K 决定了图象所在的象限等性质做准备．活动内容2：议一议：（1）观察 x y 4=和x y 4-= 的图象，它们有什么相同点和不同点？（2）反比例函数图像是中心对称图形吗？如果是，请找出对称中心，反比例函数是轴对称图形吗？如果是请指出它的对称轴.处理方式：(1)让学生先独立思考后再与同桌交流答案，最后师生共同小结反比例函数的性质.（教师板书）反比例函数y = x k 有下列性质：反比例函数的图象y = xk 是由两支曲线组成的。

最新北师大版九年级数学上册《反比例函数的图像》学案我的疑问 4. 在一个反比例函数图象上任取两点P，Q，过点P，Q分别作x、轴，y轴的平行线，与坐标【学习目标】1.经历抽象反比例函数概念的过程、领会反比例函数的意义，理解反比例函数的概念.2.会作反比例函数的图象，并探索和掌握反比例函数的主要性质.3.会从函数图象中获取信息，解决实际问题.。

[来源学科网]【学习重难点】重点：反比例函数的概念，会画反比例函数的图象，并掌握其性质.反比例函数的应用 难点：探索反比例函数的主要性质.反比例函数的应用.【使用说明与学法指导】1.认真阅读课本内容自主探究本节中知识重点。

2．认真完成导学案的问题，并把自己的疑问写出来，最后小组交流并解决。

[来源:]【自主学习】（一）试建立本章知识结构图（二）知识点填空反比例函数图象的性质有：1.反比例函数的图象是两支双曲线，当k>0时，图象分别位于第 象限；当k<0时，图象分别位于第 象限.2.当k>0时.在每一个象限内，y 随x 的增大而 ；当k<0时，在每一个象限，y 随x 的增大而 .[来源:学科网]3.因为在y=x k( k ≠0)中，x 不能为0，y 也不能为0，所以反比例函数的图象 与X 轴不相交，也 与y 轴相交.5.一次函数ｙ＝ｋｘ＋ｂ的图象与反比例函数ｙ＝－x 2的图象交于Ａ，Ｂ两点，且点Ａ的横坐标与点Ｂ的横坐标分别是方程022=-+x x 的两个根，求一次函数的解析式。

轴围成的矩形面积为S 1，S 2则5. 反比例函数的图象既是轴对称图形，又是中心对称图形，它有 条对称轴，对称中心是【合作探究】1．对于函数y=x 2，当x>0时，y_______0，这部分图象在第______象限；对于y ＝-x2，当x<0时，y____0，这部分图象在第_____象限.2..函数y=x10的图象在第____象限内，在每一个象限内，y 随x 的增大而______. 3.根据下列条件，分别确定函数y ＝xk的表达式(1)当x=2时，y ＝-3； (2)点(-31,21-)在双曲线y ＝x k上.4．在函数xy 3=的图象上任取一点P ，过P 分别作x 轴、y 轴的平行线，与坐标轴围成的矩形面积是多少? . 59.已知：如图5-11，反比例函数y = k2x和一次函数y = 2x -1, 其中一次函数图像经过（a ，b )，(a +1，b + k )两点.【课后检测】.1.下列函数中，其图象位于第一、三象限的有哪些?在其图象所在象限内，y 的值随x 值的增大而增大的是哪些 ( )(1)x y 31=(3)x y 2.0= (2)x y 10-= (4)x y 1007-=2. 函数y kx =-与y kx =（k ≠0）的图象的交点个数是（ ） A. 0 B. 1 C. 2 D. 不确定 3. 若函数y x =4与y x =1的图象有一个交点是（12，2），则另一个交点坐标是（ ）。

6.2 反比例函数的图象与性质第1课时 反比例函数的图象【学习目标】1．进一步熟悉画函数图象的主要步骤，会画反比例函数的图象。

2．体会函数三种表示方法的相互转换，对函数进行认识上的整合。

3．逐步提高从函数图象中获取信息的能力，探索并掌握反比例函数的主【学习方法】利用导学案，采用学生自学和小组讨论的方式进行合作探究式学习。

【学习重点】掌握反比例函数的画图【学习难点】反比例函数三种表示方法的相互转换二、【学习过程】1、画出一次函数y=2x+1的图象，解：（1）列表： (2)描点、连线2、画函数图象的步骤是： ， ， 。

3、画出反比例函数y=x6的图象 x ... -6 -3 -2 -1 1 2 3 6 … y=x6思考：1、列表时所选取的数值不同，图象的形状相同吗？x 0 y 02、连线时能否连成折线，为什么必须用光滑的曲线连接各点3、曲线的发展趋势如何？那么你在今后画图象时，应注意那些问题?画出反比例函数y=-x6的图象 x ... … y=-x6三、【总结提升】 1、请同学们观察y=x 6和y=-x6的图象，回答问题： （1）你能发现它们的共同特点吗？（2）每个函数的图象分别位于哪几个象限？（3）在每个象限内，y 随x 的变化如何变化？说说你的理由。

如果把“在每个象限内”这几个字去掉，你同意吗？为什么？（4）每个函数的双曲线会与坐标轴相交吗？为什么？（5）比例函数y=x 6与y=-x6的图象有什么关系？你是如何得出的？2、反比例函数y=xk（k 为常数且k ≠0）图象与性质： （1）反比例函数y=xk的图象是 ； （2）反比例函数y=xk（k 为常数且k ≠0）性质： k>0时，双曲线的两支分别位于第_________象限，在每个象限内______________________________________________. k<0时，双曲线的两支分别位于第_________象限，在每个象限内_____________________________________________.五、反思升华。

北师大版数学九年级上册5.2《反比例函数的图象与性质》教学设计1一. 教材分析《反比例函数的图象与性质》是北师大版数学九年级上册第五章第二节的内容。

本节内容是在学生已经掌握了函数的概念、正比例函数的图象与性质的基础上，进一步学习反比例函数的图象与性质。

通过本节课的学习，使学生能够理解反比例函数的概念，掌握反比例函数的图象与性质，并能够运用反比例函数解决一些实际问题。

二. 学情分析九年级的学生已经具备了一定的函数知识，对正比例函数的图象与性质有一定的了解。

但是，对于反比例函数的理解可能会存在一定的困难，因此，在教学过程中，需要引导学生从实际问题出发，逐步理解反比例函数的概念，掌握反比例函数的图象与性质。

三. 教学目标1.知识与技能目标：使学生能够理解反比例函数的概念，掌握反比例函数的图象与性质，能够运用反比例函数解决一些实际问题。

2.过程与方法目标：通过观察、分析、归纳等方法，使学生能够自主探索反比例函数的图象与性质，提高学生的数学思维能力。

3.情感态度与价值观目标：培养学生对数学的兴趣，使学生能够积极主动地参与数学学习活动。

四. 教学重难点1.反比例函数的概念。

2.反比例函数的图象与性质。

五. 教学方法1.情境教学法：通过创设生活情境，引导学生从实际问题中抽象出反比例函数模型。

2.自主探索法：鼓励学生自主探究反比例函数的图象与性质，培养学生的创新能力。

3.合作交流法：引导学生通过小组合作、讨论，共同解决问题，提高学生的团队协作能力。

六. 教学准备1.准备一些与反比例函数相关的实际问题，如广告费用、速度与时间等问题。

2.准备反比例函数的图象与性质的课件，以便于学生更好地理解反比例函数。

七. 教学过程1.导入（5分钟）教师通过展示一些实际问题，引导学生从实际问题中抽象出反比例函数模型，激发学生的学习兴趣。

2.呈现（10分钟）教师通过课件展示反比例函数的图象与性质，引导学生观察、分析，从而归纳出反比例函数的性质。