当前位置：文档之家 › 大学物理-圆周运动

大学物理-圆周运动

  • 格式：ppt
  • 大小：404.50 KB
  • 文档页数：14

下载文档原格式

  / 14

合集下载

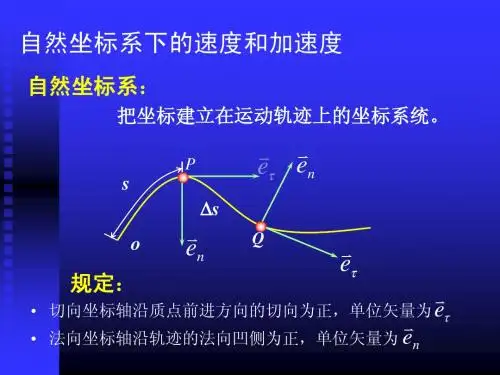
大学物理01_2圆周运动

大学物理01_2圆周运动

2
讨论
det dt
O
Δ
et et (t t ) - et (t )
当： t 0 , 0 有 e t e t 方向
et t t
s
P 1
P2
et t
et et
et
et t t
自然坐标系下的速度和加速度
自然坐标系：
把坐标建立在运动轨迹上的坐标系统。 s o
P
e en
s
Q
en
•
•
切向坐标轴沿质点前进方向的切向为正，单位矢量为 e 法向坐标轴沿轨迹的法向凹侧为正，单位矢量为 en
规定：
e
s
P
s en
e
Q
o
e
v
质点位置： s st 路程：
（2 ）
at an
解得
b R t c c
at r (2) 0.2 0.4 m s 2
1
v
an r 2 0.2(2 1 4) 2 0.8 m s 2
2 a at2 an 0.89 m s 2
1 an 1 0.8 tan tan 63.4 at 0.4
2 n
2 t
速度的方向（以与切线方向的夹角表示）：
an arctan a
例：抛体运动
an

at
g
2 v d a = et + v e n = at + a n R dt
讨论:
v d et 的产生是由于 1. 切向加速度 at = dt 速度 v 大小的变化。 2 v 法向加速度 a n = e n 的产生是由于 R 速度 v 方向的变化。 只有速度方向的改变，所以加速度为 v 2 R

大学物理102 第一章第二节 圆周运动

大学物理102 第一章第二节 圆周运动

• 速度与角速度的矢量关系式
dr dθ r dθ v dt dt dt 大小 v r (标量式) 方向
k r ω r ω r (由右手法则确定)
• 加速度与角加速度的矢量关系式
dr dv d(ω r ) dω a r ω β r ω v dt dt dt dt ω 第一项 r aτ 大小 a r
解：
本题涉及：
风、地、车上人
V风对人 V风对地 V地对人
西
★人感到风是从西北方向吹来
北
y
东
x
V风对人
南
例3 一个带篷子的卡车，篷高为h=2 m ，当它停在马路边时， 雨滴可落入车内达 d=1 m ，而当它以15 km/h 的速率运动 时，雨滴恰好不能落入车中。 求 雨滴的速度矢量。
v K 2 2 4 s 3 t Rt
2

当t 0.5s v R 4 Rt
2
4t
2
dv 2 a 8 Rt 8 . 0 ( m/s ) v 4 Rt 2.0(m/s) τ dt v2 2 2 2 2 an 2.0(m/s ) a an a 8.25(m/s ) R an arctan( ) 13.6 a
解 根据速度变换定理
va vr ve
ve
h
d
va
画出矢量图
h arctan 63.4 d
ve 15 va 33.5km/h 9.3 m/s cos α cos
2. 适当画出矢量图，有助于分析问题。

大学物理圆周运动

大学物理圆周运动

引言：大学物理中，圆周运动是一个重要的概念和题目，是建立在基础的运动学知识上的一个重要应用。

本文将详细介绍大学物理中的圆周运动（二），包括角速度、角加速度、牛顿定律在圆周运动中的应用以及相关的数学推导和实践应用。

概述：圆周运动是指物体在一个固定圆轨道上运动的情况。

在这种运动中，物体以一个恒定的速度绕着圆心旋转。

圆周运动是一种重要的运动形式，广泛应用于物理学、工程学和天文学等领域。

本文将着重介绍圆周运动中的角速度、角加速度以及相关的应用和推导。

正文：1.角速度的定义和计算1.1角速度的定义1.2圆周运动中的角速度计算方法1.3角速度与线速度的关系2.角加速度的定义和计算2.1角加速度的定义2.2圆周运动中的角加速度计算方法2.3角加速度与线加速度的关系3.牛顿定律在圆周运动中的应用3.1牛顿第一定律在圆周运动中的应用3.2牛顿第二定律在圆周运动中的应用3.3牛顿第三定律在圆周运动中的应用4.圆周运动相关的数学推导4.1圆周运动中的位移、速度和加速度的关系4.2圆周运动中的周期和频率的关系4.3圆周运动中的力学能量守恒定律5.圆周运动的实践应用5.1汽车在转弯时的圆周运动5.2行星围绕太阳的圆周运动5.3粒子加速器中的圆周运动总结：圆周运动是大学物理中一个重要的概念和题目，掌握相关的知识和应用对于深入理解物体的运动学特性和动力学规律具有重要意义。

本文通过对角速度、角加速度、牛顿定律在圆周运动中的应用以及相关的数学推导和实践应用的详细阐述，希望能够对读者加深对圆周运动的认识和理解，提高解题能力和应用能力。

在实践应用中，圆周运动的概念和方法也被广泛应用于各个领域，为相关领域的发展和进步做出了重要贡献。

大学物理-运动学

大学物理-运动学

x
矢量OM 的端点 M 所画的圆叫参考圆。 矢量 OM 0 是 t = 0 时刻的位置，它与 x 轴的夹角φ叫初相位。 简谐振动的参考圆和矢量表示方法十分形 象，有很广泛的应用。
M M0
A
ω
ωt
O
φ x P
X
M
A
P x
A
P
M
x
注意：旋转矢量在第 1 象限 速度v < 0
A
P
M
x
注意：旋转矢量在第 1 象限 速度v < 0
第五节 抛体运动
第五节
抛体运动
将一质点以仰角θ抛射出 去，其初 速度为 v0，不计 空气阻力，此质点有一垂直 向下的恒加速度 g，研究质 点的运动情况。 解: 设 x 轴平行于水平面，
y 轴垂直向上，质点在 t = 0 时位于原点被抛出。 v0 在X轴和Y轴上的投影分别是 V0x=V0cosθ, V0y=V0sinθ 物体的加速度为: a = g = -g j 在水平方向加速度分量为零，物体作匀速运动，在垂 直方向加速度分量为-g 物体作垂直上抛运动, 因此 Vx=V0cosθ , Vy=V0sinθ - g t
A2
φ2
A1
φ1
x
振动 1 滞后振动 2 若周相差Δ Φ = 0 称两振动同步
0
A1 A2
相位差的问题 x 1= A cos( t +φ 1 ) ω x 2 = A cos ( t +φ 2 ) ω 若周相差Δ Φ = φ 2 φ 1 ＞ 0 0 称振动 2 超前振动 1
A2
φ2
A1
φ1
x
振动 1 滞后振动 2 若周相差Δ Φ = 0 称两振动同步 若周相差Δ Φ = π 称两振动反相

大学物理-圆周运动

大学物理-圆周运动
§1-6 圆周运动
圆周运动是曲线运动的一个重要特例 圆周运动中质点的速度的大小和方向都在改变
存在两个加速度
法向加速度（速度方向变化引起） 用 an 表示 切向加速度（速度大小变化引起） 用 at 表示
一．匀速率圆周运动
质点作匀速率圆周运动时，速
度大小不变，方向改变，只有 法向加速度用 an
a
a
lim v lim sv
解：v dS / dt b ct
a dv / dt c t
a b ct2 / R n
根据题意： at= an
c b ct2 / R
t Rb cc
三、一般曲线运动
总加速度
a
a
n
a
t
v2 R
e
n
dv
dt
e
t
用曲率半径 代替R
在曲线上某一点找到一个 和它内切的半径最大的圆， 这个圆的半径就定义为曲 率半径。
v vn vt
lim
vn
lim
v t
t t 0
t t 0
a a
n
t
法向加速度
an
v2 RΒιβλιοθήκη v2 v1or
v vt v2vn v1
切向加速度
at
lim vt t vt
t 0
t
dv dt
a t 大小
at
dv dt
a t 方向
v 当 v2 v1 时, a t 与 方向一致
v2 v1
o
r
v 当 v2 v1 时, a t 与 方向相反
总加速度
aa a
n
t
v2
e
dv
e
R n dt t

物理必修二圆周运动知识点总结

物理必修二圆周运动知识点总结

物理必修二圆周运动知识点总结一、圆周运动的基本概念定义：质点以某点为圆心，半径为r在圆周上运动，其轨迹是圆周或圆弧的运动称为圆周运动。

圆周运动是曲线运动的一种，因此它一定是变速运动。

分类：圆周运动可分为匀速圆周运动和变速圆周运动。

匀速圆周运动指的是线速度大小处处相等的圆周运动，尽管线速度大小不变，但由于方向时刻改变，因此匀速圆周运动仍然是变速运动。

二、描述圆周运动的物理量线速度：描述质点沿圆周运动的快慢的物理量，其方向是质点在圆周上某点的切线方向。

在匀速圆周运动中，线速度大小不变，但方向时刻改变。

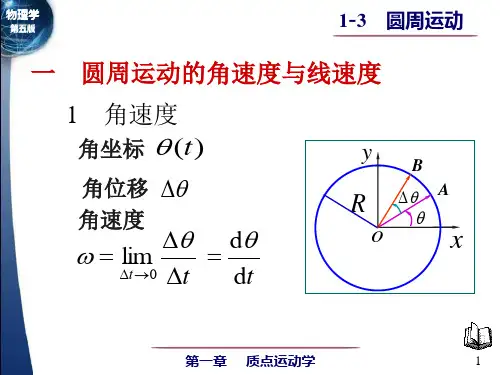
角速度：描述质点绕圆心转动的快慢的物理量，是矢量，其方向用右手螺旋定则确定。

在匀速圆周运动中，角速度大小和方向都不变。

周期和频率：周期是质点完成一次圆周运动所需的时间，频率是周期的倒数，表示单位时间内完成圆周运动的次数。

在匀速圆周运动中，周期和频率都不变。

向心力：使质点沿圆周运动的力，方向始终指向圆心。

向心力的大小与线速度、角速度和半径有关，其作用是改变质点的速度方向，使质点能够持续沿圆周运动。

三、圆周运动的规律和应用牛顿第二定律在圆周运动中的应用：通过向心力表达式，可以推导出圆周运动的线速度、角速度、周期等物理量之间的关系。

圆周运动在日常生活和科技领域中的应用：例如电动机转子、车轮、皮带轮等的运动都是圆周运动。

此外，人造卫星、行星运动等天体运动也可以视为圆周运动。

四、离心运动做圆周运动的物体，由于惯性，总有沿着切线方向飞去的倾向。

一旦受力突然消失或合力不足以提供所需的向心力时，物体就会做离心运动。

以上是物理必修二中关于圆周运动的主要知识点总结。

这些知识点是理解和分析圆周运动的基础，对于后续学习物理的其他部分以及应用物理知识解决实际问题具有重要意义。

大学物理之 圆周运动

大学物理之 圆周运动
第一章 质点运动学
13
物理学
第五版
1-3
v 0 R 0 0 . 50 18 . 8 9 . 42 m / s
圆周运动
解：（1）吊扇翼尖P原来的转动角速度为
v
则翼尖的线速度为
0 2 n
2 180 60 18 .8 rad / s
P at an aθ ω
R
2
方向
tan
1 a t an
tan
1
0 . 105 2 . 16
2 . 78

第一章
质点运动学
15
物理学
第五版
作业
1-3
圆周运动
• P36-38
1.6 1.12 1.16
结束
第一章
质点运动学
16
物理学
第五版
1-3
圆周运动
例 一歼击机在高空 A vA 点A时的水平速率为1 940 B km·-1 ,沿近似圆弧曲线俯 r h 冲到点B，其速率为2 192 -1 , 经历时间为3 s , km· h vB o 设 AB 的半径约为 3.5 km , 飞机从A到B过程视为匀变速率圆周运动，不 计重力加速度的影响，求：(1) 飞机在点B的 加速度；(2)飞机由点A到点B所经历的路程.
4
物理学
第五版
1-3
圆周运动
• 所以，
法向加速度
v
det dt
v e n
2
那么，
a n v R dv v a e v e 2
dt
t n
v
(v )n
at an
第一章 质点运动学
(v )t

物理圆周运动总结归纳

物理圆周运动总结归纳

物理圆周运动总结归纳物理学中，圆周运动是一个重要的概念。

它涉及到物体在一个固定半径的圆形轨道上运动的问题。

在本文中，我们将对物理圆周运动进行总结归纳，探讨其相关理论和应用。

一、基本概念圆周运动是指物体在固定半径的圆形轨道上运动，维持在此轨道上的力称为向心力。

向心力的大小与物体质量成正比，与物体的速度的平方成正比，与物体运动半径的倒数成正比。

圆周运动的速度大小恒定，而速度的方向则始终朝向圆心。

同时，圆周运动还存在一个与速度大小相对的概念，即角速度。

二、角速度与角加速度角速度是描述物体在圆周运动中旋转快慢的物理量。

它的大小等于物体绕圆心转动的角度的变化率。

使用符号ω表示，单位为弧度/秒。

公式为：ω = Δθ / Δt其中，Δθ是物体绕圆心转动的角度变化量，Δt是时间的变化量。

角加速度则是描述物体在圆周运动中转速变化的物理量。

它的大小等于角速度随时间的变化率。

使用符号α表示，单位为弧度/二次方秒。

公式为：α = Δω / Δt三、牛顿第二定律在圆周运动中的应用牛顿第二定律是物理学中最基本的定律之一，它在圆周运动中也有重要的应用。

当物体受到向心力作用时，可以利用牛顿第二定律来推导物体的运动方程。

假设质量为m的物体在半径为r的圆形轨道上运动，并受到向心力F_c的作用。

根据牛顿第二定律，物体的向心加速度a_c与向心力的关系为：F_c = m * a_c由于向心加速度与角加速度之间存在关联，可以推导出物体在圆周运动中的运动方程为：a_c = r * α将上述两个等式结合，可以得到：F_c = m * r * α四、应用领域1. 行星公转行星公转是天体运动中的一种圆周运动。

行星沿着围绕恒星的轨道运动，即围绕一个公共圆心进行圆周运动。

该应用领域研究行星的轨道、速度以及力学规律，对于了解天体运动和星际空间探索具有重要的意义。

2. 粒子加速器粒子加速器是一种利用电磁场加速高能粒子的装置，广泛应用于粒子物理学和核物理学领域。

大学物理圆周运动教案

大学物理圆周运动教案

课时：2课时教学目标：1. 理解圆周运动的概念，掌握匀速圆周运动和变速圆周运动的特点。

2. 掌握线速度、角速度、周期、频率等物理量的定义和计算方法。

3. 理解向心力的概念，掌握向心力公式及其应用。

4. 能够运用圆周运动的知识解决实际问题。

教学重点：1. 线速度、角速度、周期、频率等物理量的定义和计算方法。

2. 向心力的概念及其应用。

教学难点：1. 向心力的来源和作用。

2. 圆周运动中的能量守恒。

教学过程：第一课时一、导入1. 回顾物体运动的基本形式，引入圆周运动的概念。

2. 提出问题：什么是圆周运动？圆周运动有哪些特点？二、新课讲授1. 圆周运动的概念：物体沿圆周轨迹运动的现象。

2. 匀速圆周运动的特点：线速度大小不变，方向时刻改变；角速度大小不变，方向始终指向圆心。

3. 线速度、角速度、周期、频率的定义和计算方法。

- 线速度：物体在单位时间内沿圆周轨迹所通过的弧长。

- 角速度：物体在单位时间内绕圆心转过的角度。

- 周期：物体完成一周圆周运动所需的时间。

- 频率：单位时间内物体完成的圆周运动次数。

4. 线速度、角速度、周期、频率之间的关系：v = ωr，T = 1/f，n = 1/T。

三、课堂练习1. 计算匀速圆周运动中物体在某一时刻的线速度和角速度。

2. 根据线速度和角速度的关系，计算匀速圆周运动中物体的半径。

第二课时一、复习导入1. 回顾匀速圆周运动的特点和物理量的计算方法。

2. 提出问题：匀速圆周运动中物体受到的向心力是什么？二、新课讲授1. 向心力的概念：使物体沿圆周轨迹运动的力。

2. 向心力公式：F = mω²r，其中m为物体质量，ω为角速度，r为半径。

3. 向心力的来源：物体受到的合外力。

4. 向心力的应用：- 计算向心力的大小。

- 分析向心力对物体运动的影响。

三、课堂练习1. 计算匀速圆周运动中物体所受的向心力。

2. 分析向心力对物体运动的影响。

四、总结1. 回顾圆周运动的特点和物理量的计算方法。

大学物理12圆周运动

大学物理12圆周运动
S系 (Oxyz)
基本参考系
S'系(O' x' y' z')
运动参考系
u是S’系相对S系
运动的速度
1-3 相对运动
yy'
P P'
*
oo'
xx'
t0
y
o
P
y'
D
r
P'
uQ
r'
xx'
ut o' t t
第一章 质点运动学
22
物理学
第五版
位移关系
r r'D 或 r r'ut
速度变换
r r' u t t v v'u
理解伽利略速度变换式, 并会用它求简 单的质点相对运动问题．
第一章 质点运动学
2
物理学
第五版
质点运动的自然坐标描述
自然坐标系 —— 坐标原点固接 于质点, 坐标轴沿质点运动轨道
1-2 圆周ev运t 动 evt B
的切向和法向的坐标系，叫做自
然坐标系。切向以质点前进方向 A
为 侧正方，向记 为做 正，ev记t ，做法ev向n以。曲线凹
y
A
r
二 圆周运动的角速度
❖ 角坐标 (t)
o
❖角位移
y
xx
B
❖ 角速度
lim
d
t0 t dt
r A
o
x
单位：rad·s-1
第一章 质点运动学
4
物理学
第五版
1-2 圆周运动
❖ 速率 v lim Δs r lim Δθ
Δt0 Δt
Δt0 Δt

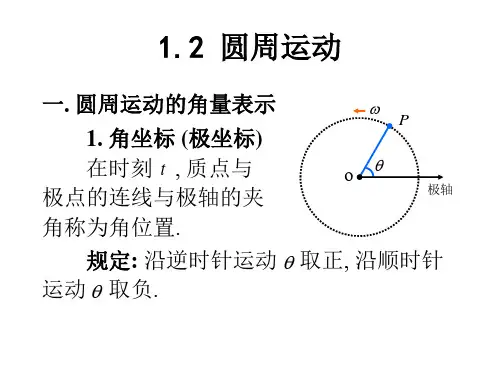
大学物理第1章第2节-圆周运动

大学物理第1章第2节-圆周运动
2 v v lim P Q an r t 0 t r
v2 an an n n r
称为法向加速度.
(2) at lim(vt t )
方向: 当 t 0 时,
0 vt v1 vt v at 沿平行于 v
lim | OA || v1 |
n v | v |
v
O
v2
| OA || v1 |
A
vt
Q
称为切向加速度
v 2 dv a an at n r dt
加速度的大小
a a a
2 n 2 t
P
an
O
v2
A
v2
作| OA || v1 | , 记 PA vn , AQ vt , v vn vt
v a lim t 0 t vn vt v v v lim lim t 0 t t 0 t
例1.6 某发动机工作时, 主轴边缘一点 做圆周运动的方程为 t 3 4t 3 (SI). 求: (1) t 2s 时, 该点的角速度和角加速度 为多大? (2) 若主轴直径 D 40cm , 则时 t 1s , 该 点的速率和加速度. 解 (1) 已知运动方程求角速度和角加速 度是微分问题.
t 0
v1
P
O
| OA || v1 |
vn
v
vt
Q
A
v2
(即 v1 ) 的方向.
大小:
| vv | t1 | at | lim t 0 t O
| vt | v2 v1 t 0

圆周运动的基本概念与公式推导

圆周运动的基本概念与公式推导

圆周运动的基本概念与公式推导一、圆周运动的基本概念1.圆周运动：物体沿着圆周轨道运动的现象称为圆周运动。

2.圆心：圆周运动的中心点，通常用O表示。

3.半径：从圆心到圆周上任意一点的线段，用r表示。

4.角速度：描述圆周运动快慢的物理量，表示单位时间内物体绕圆心转过的角度，用ω表示。

5.周期：圆周运动一次完整往返所需要的时间，用T表示。

6.频率：单位时间内圆周运动的次数，与周期互为倒数，用f表示。

二、圆周运动的公式推导1.线速度公式：线速度（v）= 半径（r）× 角速度（ω）2.角速度与周期的关系：角速度（ω）= 2π / 周期（T）即ω = 2π / T3.向心加速度公式：向心加速度（a）= 半径（r）× 角速度的平方（ω²）即a = rω²4.向心力公式：向心力（F）= 质量（m）× 向心加速度（a）即F = ma = mrω²三、圆周运动的分类1.匀速圆周运动：角速度恒定的圆周运动。

2.非匀速圆周运动：角速度变化的圆周运动。

四、圆周运动的应用1.匀速圆周运动的应用：2.非匀速圆周运动的应用：–匀速圆周运动的加速器五、注意事项1.在研究圆周运动时，要区分角速度、线速度、向心加速度和向心力等概念，并理解它们之间的关系。

2.注意圆周运动的分类，掌握匀速圆周运动和非匀速圆周运动的特点及应用。

3.在实际问题中，要根据题目条件选择合适的公式进行分析。

习题及方法：1.习题：一个物体在半径为2m的圆形轨道上做匀速圆周运动，角速度为2rad/s，求物体的线速度和向心加速度。

根据线速度公式v = rω，将给定的半径 r = 2m 和角速度ω = 2rad/s 代入公式，得到物体的线速度：v = 2m × 2rad/s = 4m/s根据向心加速度公式a = rω²，将给定的半径 r = 2m 和角速度ω = 2rad/s 代入公式，得到物体的向心加速度：a = 2m × (2rad/s)² = 8m/s²答案：物体的线速度为4m/s，向心加速度为8m/s²。

圆周运动总结知识要点

圆周运动总结知识要点

圆周运动问题是高考考查的热点，物体在竖直面内的圆周运动中临界条件的考查在高考中多有出现圆周运动的特点：物体所受外力在沿半径指向圆心的合力才是物体做圆周运动的向心力，因此利用矢量合成的方法分析物体的受力情况同样也是本单元的基本方法；只有物体所受的合外力的方向沿半径指向圆心，物体才做匀速圆周运动。

另外，由于在具体的圆周运动中，物体所受除重力以外的合外力总指向圆心，与物体的运动方向垂直，因此向心力对物体不做功，所以物体的机械能守恒。

（一）匀速圆周运动1. 定义：做圆周运动的质点，若在相等的时间内通过的圆弧长度相等，这种运动就叫做匀速圆周运动。

2. 运动学特征：v 大小不变，T 不变，ω不变，向a 大小不变；v 和向a 的方向时刻在变，匀速圆周运动是加速度不断改变的变速运动。

3. 动力学特征：合外力大小恒定，方向始终指向圆心。

（二）描述圆周运动的物理量 1. 线速度（1）物理意义：描述质点沿圆周运动的快慢。

（2）方向：质点在圆弧某点的线速度方向沿圆弧该点的切线方向。

（3）大小：（s 是t 时间内通过的弧长）。

2. 角速度 （1）物理意义：描述质点绕圆心转动的快慢。

（s /rad ），ϕ是连接质点（2）大小：和圆心的半径在t 时间内转过的角度。

3. 周期T ，频率f 做匀速圆周运动的物体运动一周所用的时间叫做周期。

做匀速圆周运动的物体单位时间内沿圆周绕圆心转过的圈数，叫做频率，也叫转速。

4. v 、ω、T 、f 的关系f 1T =f 2T 2π=π=ωω=π=r r T 2v5. 向心加速度（1）物理意义：描述线速度方向改变的快慢。

（2）大小：=a 0222222v r T 4r f 4r r v ω=π=π=ω=（3）方向：总是指向圆心（三）向心力向F1. 作用效果：产生向心加速度，不断改变质点的速度方向，维持质点做圆周运动，但不改变速度的大小。

2. 大小：rm r mv F 22ω==向3. 来源：向心力是按效果命名的力，可以由某个力提供，也可以由几个力的合力提供或由某个力的分力提供，如同步卫星的向心力由万有引力提供，圆锥摆摆球所受向心力由重力和绳上的拉力的合力提供4. 匀速圆周运动中向心力就是合外力，而在非匀速圆周运动中，向心力是合外力沿半径方向的一个分力，合外力的另一个分力沿切线方向，用来改变线速度的大小。

《大学物理》圆周运动

《大学物理》圆周运动

得切向加速度与角加速度的关系为a r
dt
而法向加速度an
v2 r
dt r 2
质点作匀变速圆周运动时的角速度、角位移与角加速度的关系式
为：
ω ω0 t
θ θ0 ω0t t 2 / 2
ω2 ω02 2 (θ θ0 )
v v0 at
x
x0
v0t
at2 / 2
v2
v02
2a( x
(R
sin
ti
R
c
ostj )
a(t)
dv(dtt)
2 (R
costi
R 2
sin tj)
dt
速度、加速度也可以用其在x、y方向上的分量来表示
二、自然坐标系下的描述
自然坐标系：以动点为坐标原点，以动点所在轨道处的切线和 法线为坐标轴（切向指向前进方向，法向指向曲率中心），、n 为切、法向的单位矢量。
1-16.飞轮作匀减速转动 , 在 5 秒内角速度由 40πrad/s 减到 10πrad/s , 则飞轮在这 5秒内总共转过了多少圈?飞轮再经过多 少时间才能停止转动?
课后习题 1-8 1-9 1-10
（2）如
匀变速直线运动
（3）如 a 0,a；则0 质点作
n
t
匀速直线运动
（4）如
a n
0,
a t
0；, 质 点 c作
一般曲线运动
（5）如 a 0, a 0；, 质点c作
n
t
变速圆周运动
（6）如
a n
0,
a t
c；, 质点c作
匀变速圆周运动
（7）如 a 0, a 0；, 质点c作
dt dt
dt dt

大学物理圆周运动.ppt

大学物理圆周运动.ppt
2
y
a
an
v

a
e
大小 a
a n 方向 θ tan a
1
a a
2
2 n
o
A e n
x
切向加速度(速度大小变化) 法向加速度(速度方向变化)
dv a e d t2 v an en r
利用自然坐标, 一切运动可以 根据切向、法向加速度来分类：
a
an
角量与线量的关系 v 速度与角速度的关系
s d θ v r r ω lim t d t t 0
v 加速度与角速度和角加速度的关系
s r
s P r
o
Q

x (极轴 )
vr ad d t

v 2 a v r n r
2
例1一质点作半径为0.1m 的圆周运动，已知运动学方程为
2 4 t( r a d )
3
求 (1) t = 2s 时，质点的切向加速度和法向加速度的大小; (2) t = 2s 时，质点的加速度。 解 (1)由运动学方程可得角速度和角加速度
d d 3 2 ( 2 4) t 1 2 t d t d t d d 2 ( 1 2 t ) 2 4 t d t d t
依据材料概括晚清中国交通方式的特点，并分析其成因。
提示：特点：新旧交通工具并存(或：传统的帆船、独轮车， 近代的小火轮、火车同时使用)。 原因：近代西方列强的侵略加剧了中国的贫困，阻碍社会发 展；西方工业文明的冲击与示范；中国民族工业的兴起与发展；
政府及各阶层人士的提倡与推动。
[串点成面· 握全局]
2 2 4
任意时刻，质点的切向加速度和法向加速度的大小

大学物理圆周运动ppt讲解

大学物理圆周运动ppt讲解
1 – 3 圆周运动
物理学教程 （第二版）
平面极坐标
设一质点在 Oxy 平面内
运径动r，与某时x刻轴它之位间于的点夹A角.矢
为 . 于是质点在点 A 的位
置可由 A(r, ) 来确定 .
y

o
A
r
x
以 (r, ) 为坐标的参考系为平面极坐标系 .
它与直角坐标系之间的变换关系为
x r cos y r sin
第一章 质点运动学
1 – 3 圆周运动
一 圆周运动的角速度和角加速度
角坐标 (t)
角速度 (t) d (t)
dt
速率
vltim0st rltim0t
v

ds dt
v(t) r(t)
角加速度 d
dt
第一章 质点运动学
物理学教程 （第二版）
y
B
r A
v2
en
et
v1
o r
v2vt v vv1n

1 – 3 圆周运动
a atet anen
物理学教程
a 与 et 夹角
（第二版）


tan1
an at
an 0 0 π
切向加速度
at

dv dt

r
0, 0 π2, v 增大

o
x
1 – 3 圆周运动
二 匀速率圆周运动
v
v


ddstret
vr
加速度大小 a


vet
v t
lim
ret
v r r t
v v2
t0 t r

大学物理(1.3.1)--圆周运动与一般平面曲线运动

大学物理(1.3.1)--圆周运动与一般平面曲线运动

v

lim
t 0
s t

ds dt
v

v

ds dt

( et , n en )
3
二、圆周运动中的加速度
速 度: 加速度 :
v
a


v
d dt

v
ds dt


dv dt


v
d dt
其 中 : d d n d n
2 、切向加速度与角加速 a R
度 3 、 法向加速度与角速度
an

v2 R
v

R 2
4 、速度分量式
vx

dx dt

d dt
(R cos
t)

R
sin
t
vy

dy dt

d dt
(R sin
t)

R
cos
t
v
vx2

v
2 y

R
5
、速度矢量式 v

1 2
t
2

2

2 0

2 (
0
)
与匀变速率直线运动类比
v v0 at s s0 v0t
1 2
at
2
v2 v02 2a(s s0 )
※ 一般平面曲线运动
曲率半径是变化的，通常用 来表示 。a a an a ann
a

a
7
五、匀变速率圆周运动
常量， 故 at r，an r 2


dω dt

大学物理 第一章 第二节圆周运动与一般平面曲线运动

大学物理 第一章 第二节圆周运动与一般平面曲线运动

2、角加速度
lim
t 0 t
d
dt
d 2
dt 2
方向？
四、 圆周运动中线量和角量的关系 1、线速度与角速度 v R
角速度 的方向:
按“右旋规则”确定 角加速度 的方向: 加速时与方向相同 减速时与方向相反
y
R
o
x
2、切向加速度与角加速度 3、 法向加速度与角速度
a R
an
v2 R
v
R 2
4、速度分量式
（1）可将抛体运动分解为 沿x和y 两个方向的独立运动。
立进行的运动迭加而成。
※
抛体运动方程的矢量形式
v
(v0cos )i
(v0
sin
gt)
j
v0t
r
1
gt
2
2
v dr dt
r
t vdt
0
t 0
(vxi
vy
j )dt
(v0t
cos
)i
(v0t
sin
1 2
gt2 )
j
（2）也可将抛体运动分解为沿初速度方向的匀速直线运动和
t
a a
ax2
a
2 y
R 2
7
五、匀变速率圆周运动
常量， 故 at r，an r 2
dω 常量，
dt
又
dω dt d dt，
如 t 0 时, 0 ， 0
可得：
0 t θ θ0 0t
1 2
t
2
2
2 0
2 (
0)
匀变速率圆周运动
0 t
θ
θ0
0t
1 2
t

大学物理圆周运动

大学物理圆周运动

圆周运动的分类
总结词
圆周运动可以根据不同的分类标准进行分类，如匀速圆周运动和变速圆周运动。
详细描述
匀速圆周运动是指物体在转动过程中角速度保持不变的运动，其特点是线速度的 大小不变，只有方向改变。变速圆周运动是指物体在转动过程中角速度发生变化 的运动，其特点是线速度的大小和方向都可能改变。
02
匀速圆周运动
ቤተ መጻሕፍቲ ባይዱ 匀速圆周运动的定义
总结词
匀速圆周运动是指物体沿着圆周路径做等速运动，即线速度大小恒定，方向时刻改变。
详细描述
匀速圆周运动是圆周运动的一种特殊形式，其特点是线速度的大小恒定，方向始终沿着圆周的切线方 向。匀速圆周运动中，物体的加速度大小恒定，方向始终指向圆心，即向心加速度的大小恒定，方向 始终与线速度垂直并指向圆心。
圆周运动的描述
总结词
圆周运动可以通过角速度、角加速度、转速等物理量进行描述。
详细描述
角速度是描述圆周运动快慢的物理量，单位为弧度/秒，其值等于物体转动一周所需的时间。角加速度是描述圆 周运动加速度的物理量，单位为弧度/秒²，表示物体转动过程中角速度的变化率。转速是描述圆周运动频率的物 理量，单位为转/分，表示物体每分钟转动的圈数。
03
非匀速圆周运动
非匀速圆周运动的定义
特点
加速度不指向圆心，存在 切向加速度和法向加速度 。
非匀速圆周运动
与匀速圆周运动相对，速 度大小或方向发生变化的 圆周运动。
切向加速度
改变速度大小，不改变速 度方向。
法向加速度
改变速度方向，不改变速 度大小。
非匀速圆周运动的描述
描述参数
线速度、角速度、周期、频率、向心加速 度等。
离心力的计算

《圆周运动》精美版课件

《圆周运动》精美版课件

v
速运动,“匀速”是指速率不
变 匀速圆周运动是指：速率、角
v
o
速度、周期、频率、转速都不
变的运动
v
描述圆周运动各物理量的关系
∆s
在任何相等的1时.间线里速，连度接物与体角和圆速心的度半的径转关过的系角度都相等
rΔθ
知道角速度的物理意义、定义式及单位，了解转速和周期的意义。
题1 ［2019•北京师范大学附属中学高一期末］关于角速度和线速度，下列说法正确的是（ ）
Δs θ 8π rad/s D. v = = =ωr 分析时可暂时不考虑周期性，表示出一个周期的情况，再根据圆周运动的周期性，在转过的角度上再加上2nπ，具体n的取值应视情况 Δt Δt 而定。 r 左侧是一轮轴，大轮半径为4r，小轮半径为2r，b点在小轮上，到小轮中心的距离为r。
Δ 【b点解和析d】点的根线2据速.v线度=之ω速r比可为知度1，∶与半4 径周一定期时(，频角速率度)与的线速关度成系正:比(；转动一周)
弧长 l
=
=
半径 r
3.转速n (r/s):单位时间内转过的圈数 转速越大物体运动得越快
4.周期T (s):转过一周所用的时间 周期越大运动得越慢,周期越小运动得越快
描述圆周运动快慢的物理量:线速度v、角速度w、转速n
匀速圆周运动
物体沿着圆周运动,并且线速度的大小
处处相等.
注意:匀速圆周运动是一种变
TA = rA TB rB
2.同轴转(相等时间里转过的角度相等) 动
用时间Δt 的比值 当Δt 趋近零时,弧长Δl就等于物体的位移,v 就是瞬时速度. 地球上的物体随着地球一起饶地轴自转。 能在具体的情境中确定线速度和角速度与半径的关系。 题2［2019•云南文山州二中高一检测］［多选］对于做匀速圆周运动的物体，下列说法中正确的是（ ） ◆解决圆周运动多解问题的方法 角速度与周期(频率)的关系:(转动一周) 题7［2019·沈阳高一检测］［多选］如图所示，为一皮带传动装置，右轮半径为r，a为其边缘上的一点； 半径一定时，角速度与线速度成反比 半径一定时，角速度与线速度成正比 角速度一定时，线速度与半径成正比。 (5)弧度制:用弧长与半径的比值表示角的大小 （1）摩擦传动时，两轮边缘的线速度大小相等。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
v1
o

r
v 2 v 1 时,
v 2 v 1 时,
at 与 v 方向一致 at 与 v 方向相反
v d v 总加速度 a a n a t e e
2
R
n
dt
t
a at an
2 2
a tan an t
1
an 0 0 π
v1
o

t 0
t 0
an at
r
法向加速度
v an R
2
v t v n
v
v1
v2
vt t vt dv 切向加速度 a t l i m t 0 t dt
at 大小 at 方向
当 当
dv at dt
v2
Ｒ
v sv a a n lim lim t 0 t t 0 Rt
红三角形与蓝三角形相似
o Ｒ

v
v
v v s R
v v s R
v
v

2 v sv v l i m s v a a n l i m lim R R t 0 t t 0 t t 0 Rt
0, 0 π , v 增大 2 π 0 , , v 常量 at 2 0, π π , v 减小 2
a
y
v
en
et
o a x a
质点作半径为R的变速圆周运动时的加速度大小为
(v表示任一时刻质点的速率)
（A） dv
dt
v2 （B） R
§1-6 圆周运动
圆周运动是曲线运动的一个重要特例
圆周运动中质点的速度的大小和方向都在改变
存在两个加速度 法向加速度（速度方向变化引起） 用 a 表示 n 切向加速度（速度大小变化引起） 用 at 表示
一．匀速率圆周运动
质点作匀速率圆周运动时，速 度大小不变，方向改变，只有 法向加速度用 an
v
2
dv v （C） dt R
dv v （D） 2 dt R
2 4
1/ 2
答案D
例1. 一质点沿半径为R的圆周运动．质点所经过
的弧长与时间的关系为Biblioteka 1 2 S bt ct 2
其中b、
c是大于零的常量，求从开始到切向加速度与法向 加速度大小相等时所经历的时间． 解： v dS / dt b ct
法向加速度 方向指向圆心 原因
v an R
2
v
v

v
t 0 0 v与速度v垂直
二．变速率圆周运动
v v v n v t a lim t 0 t v v lim lim t t
n
t
v2
a t dv / dt c
根据题意：
an b ct / R
2
at= an
R b c c
c b ct / R
2
t
三、一般曲线运动 总加速度
v dv a an at e e
2
R
n
dt
t
用曲率半径
代替R
在曲线上某一点找到一个 和它内切的半径最大的圆， 这个圆的半径就定义为曲 率半径。
Q(t t )
s P(t ) R
o
dv dR at R dt dt
v 2 R 2 2 an R R
参考方向
R
2
d dt d dt
d x at 0 dt an g
由
o

0

an g
x
an
v
2

得
(v 0 cos ) v an g
2
2
#
四、圆周运动的角量描述
1.角位移
单位: 弧度 rad 单位: 弧度 rad/s 单位: 弧度 rad/s2
d 2.角速度 dt d 3.角加速度 dt
a 方向
质点作加速运动
at 与 v 方向一致
a与
v1
an

a
a t v2
v 之间的夹角
2
质点作减速运动
at 与 v 方向相反
a与
v1
a an
at

v2
v 之间的夹角
2
例1求如图所示的抛体轨道顶点处的曲率半径 解：在轨道顶点 y 0
y
v v x v 0 cos
Q(t t )

P(t )
o

参考方向 如圆周运动
圆周运动时，由于轨迹确定，用这套物理量较为方便
匀速率圆周运动
常数 0 t
1 2 0 t t 2
变速率圆周运动
0 t
4. 圆周运动的线量和角量关系
s R d R v lim lim R t 0 t 0 t t dt