自动控制原理课后答案2 西工大版

第1章习题答案1-1 解：自动控制系统：被控对象和控制装置的总体；被控对象：要求实现自动控制的机器、设备和生产过程；扰动：除给定值之外，引起被控制量变化的各种外界因素；给定值：作用于控制系统输入端，并作为控制依据的物理量；反馈：将输出量直接或间接的送到输入端，并与之相比较，使系统按其差值进行调节，使偏差减小或消除。

1-2 解：开环控制有洗衣机的洗衣过程，闭环控制有抽水马桶的蓄水控制、电冰箱制冷系统等。

1-3 解：1-4 解：a与d相连，b与c相连即可；系统原理框图如下所示：1-5 解：系统原理框图如下所示：1-6 解：对控制系统的基本要求是稳定性、准确性和快速性：稳定性是系统正常工作的前提条件；准确性反映控制系统的控制精度，要求过渡过程结束后，系统的稳态误差越小越好；快速性是要求系统的响应速度快，过渡过程时间短，超调量小。

1-7 解：该系统的任务是使工作机械（被控对象）的转角θc（被控量）自动跟踪手柄给定角度θr（给定量）的变化。

该系统的工作原理是：检测电位计与给定电位计的电气特性相同，工作机械的转角θc经检测电位计转换成电压u c，手柄给定角度θr经给定电位计转换成给定电压u r，u c与u r接入放大器前端的电桥。

当工作机械转角θc没有跟踪手柄给定角度θr时，u c与u r两者不相等而产生偏差Δu=u r-u c，Δu经过放大器放大，使电动机转动，通过减速器使得负载产生减小偏差的转动。

当检测电位计检测并转换的u c与u r相等，此时Δu=u r-u c=0,电动机不转，工作机械停在当前位置。

其原理框图如下图所示。

1-8 解：谷物湿度控制系统原理框图如下。

该系统的被控量是谷物湿度，给定量是希望的谷物湿度。

谷物加湿后的实时湿度经湿度检测后送到调节器，若与希望的湿度产生偏差，则通过调节器控制给水阀门的开大或关小，以减小两者的偏差。

谷物在入口端的湿度由前馈通道输入到调节器。

这样若入口处谷物湿度较大，则会使得偏差减小，从而减小阀门的开度；若谷物干燥，会增大偏差，从而加大阀门的开度。

第2章 控制系统的数学模型习题及解答2-1 已知质量-弹簧系统如题2-1图所示，图中标明了质量和弹簧的弹性系数。

当外力F (t )作用时，系统产生运动，如果在不计摩擦的情况下，以质量m 2的位移y (t )为输出，外力F (t )为输入，试列写系统的运动方程。

解： 设 质量m 1的位移量为x (t ),根据牛顿第二定律有y k y x k dt yd m 21222-)(−= ①)(1221y x k F dtxd m −−= ②①式可以写作y k k x k dtyd m )(211222+−= ③由①式也可以得到y k dtyd m y x k 22221)(+=− ④③式两端同时求二阶导数，可得2221221442)(dty d k k dt x d k dt yd m +−= ⑤将②、③式代入⑤式中，整理可得F m k y m k k dty d m k m k m m dt y d m 1112122122121442)(=−++++ 2-2 求题2-2图中由质量-弹簧-阻尼器组成的机械系统，建立系统的运动方程。

其中，x (t )为基底相对于惯性空间的位移，y (t )为质量相对于惯性空间的位移。

z (t )= y (t )- x (t )为基底和质量之间的相对位移，z (t )由记录得到， x (t )和z (t )分别为输入量和输出量。

解：应用牛顿第二定律可得dtt dz f kz dt y d m )(22−−= 将z (t )= y (t )- x (t )代入上式，整理可得2222dtx d m kz dt dz f dt z d m −=++题2-2图题2-1图解：（a ）引入中间变量u c (t)表示电容器两端的电压。

根据基尔霍夫电流定律有o c c u R u R dt du C2111=+ 根据基尔霍夫电压定律有o i c u u u −=联立消去中间变量，可得描述输入量u i (t )和输出量u o (t )之间关系的微分方程为i i o o u R dt du C u R R R R dt du C121211+=++ （b ）引入回路电流i (t )和电容器两端的电压u c (t)作为中间变量，根据基尔霍夫电压定律有i o u u i R =+1 另有电容元件的元件约束关系方程dtdu Ci c =和i R u u o c 2−=联立求解，消去中间变量可得i i o o u R dt du C u R R R R dt du C121211+=++（c ）设电容器C 2两端的电压为u c 2(t)，根据基尔霍夫电流定律有dtduC u u R dt u u d C c o i o i 2211)(1)(=−+− ①求导可得22221221)(1)(dtu d C dt u u d R dt u u d C c o i o i =−+− ② 另有输出支路电压方程o c c u u dtdu C R =+2222 等式两边求导有dtdu dt du dt u d C R oc c =+222222 ③将①、②代入③式，整理可得i ii ooo u C R dt du C R C R C R dt u d C R u C R dt du C R C R C R C R dt u d C R 2121221121221212122112121122+++=++++2-4 试求题2-4图所示有源RC 电路的微分方程，其中u i (t )为输入量，u o (t )为输出量。

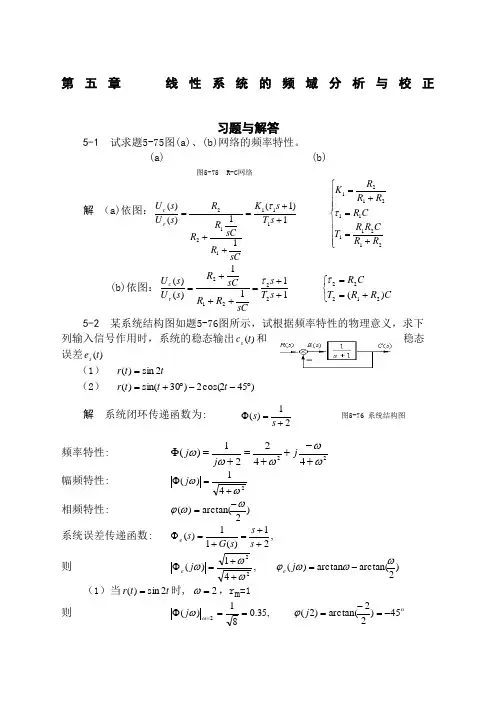
第五章 线性系统的频域分析与校正习题与解答5-1 试求题5-75图(a)、(b)网络的频率特性。

(a) (b)图5-75 R-C 网络解 （a)依图：⎪⎪⎪⎩⎪⎪⎪⎨⎧+==+=++=++=2121111212111111221)1(11)()(R R C R R T C R RR R K s T s K sC R sC R R R s U s U r c ττ (b)依图：⎩⎨⎧+==++=+++=C R R T CR s T s sCR R sC R s U s U r c)(1111)()(2122222212ττ 5-2 某系统结构图如题5-76图所示，试根据频率特性的物理意义，求下列输入信号作用时，系统的稳态输出)(t c s 和稳态误差)(t e s（1） t t r 2sin )(=（2） )452cos(2)30sin()(︒--︒+=t t t r 解 系统闭环传递函数为: 21)(+=Φs s 图5-76 系统结构图 频率特性: 2244221)(ωωωωω+-++=+=Φj j j 幅频特性: 241)(ωω+=Φj相频特性: )2arctan()(ωωϕ-=系统误差传递函数: ,21)(11)(++=+=Φs s s G s e 则 )2arctan(arctan )(,41)(22ωωωϕωωω-=++=Φj j e e（1）当t t r 2sin )(=时, 2=ω，r m =1 则 ,35.081)(2==Φ=ωωj ο45)22arctan()2(-=-=j ϕ（2） 当 )452cos(2)30sin()(︒--︒+=t t t r 时: ⎩⎨⎧====2,21,12211m m r r ωω5-3 若系统单位阶跃响应 试求系统频率特性。

解 ss R s s s s s ss C 1)(,)9)(4(3698.048.11)(=++=+++-= 则 )9)(4(36)()()(++=Φ=s s s s R s C 频率特性为 )9)(4(36)(++=Φωωωj j j5-4 绘制下列传递函数的幅相曲线：解 ()()()12G j K j K e j ==-+ωωπ幅频特性如图解5-4(a)。

自动控制原理卢京潮主编课后习题答案西北工业大学出版社SANY标准化小组 #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#第五章 线性系统的频域分析与校正习题与解答5-1 试求题5-75图(a)、(b)网络的频率特性。

(a) (b)图5-75 R-C 网络解 （a)依图：⎪⎪⎪⎩⎪⎪⎪⎨⎧+==+=++=++=2121111212111111221)1(11)()(R R C R R T C R RR R K s T s K sC R sC R R R s U s U r c ττ (b)依图：⎩⎨⎧+==++=+++=C R R T CR s T s sCR R sC R s U s U r c)(1111)()(2122222212ττ 5-2 某系统结构图如题5-76图所示，试根据频率特性的物理意义，求下列输入信号作用时，系统的稳态输出)(t c s 和稳态误差)(t e s（1） t t r 2sin )(=（2） )452cos(2)30sin()(︒--︒+=t t t r 解 系统闭环传递函数为: 21)(+=Φs s 图5-76 系统结构图 频率特性: 2244221)(ωωωωω+-++=+=Φj j j 幅频特性: 241)(ωω+=Φj相频特性: )2arctan()(ωωϕ-=系统误差传递函数: ,21)(11)(++=+=Φs s s G s e 则 )2arctan(arctan )(,41)(22ωωωϕωωω-=++=Φj j e e（1）当t t r 2sin )(=时, 2=ω，r m =1则 ,35.081)(2==Φ=ωωj 45)22arctan()2(-=-=j ϕ （2） 当 )452cos(2)30sin()(︒--︒+=t t t r 时: ⎩⎨⎧====2,21,12211m m r r ωω5-3 若系统单位阶跃响应 试求系统频率特性。

自动控制原理第二章到第七章课后习题答案第二章2-1试求下图所示电路的微分方程和传递函数。

解：（a ）根据电路定律，列写出方程组：001Li R c L R C di L u u dtu R i i dt Ci i i ⋅+==⋅==+⎰消除中间变量可得微分方程：20002i d u du L L C u u dt R dt⋅⋅+⋅+=对上式两边取拉氏变换得：2000()()()()i LL C U s s U s s U s U s R⋅⋅⋅+⋅⋅+= 传递函数为022()1()()1i U s R G s L U s R Ls LCRs s LCs R ===++++ （b ）根据电路定律，列写出方程组：12011()i i u i R R idt C u u i R =++-=⎰消除中间变量可得微分方程：121012i R R Ru u idt R R C+=-⎰ 对上式两边取拉氏变换得：2012()(1)()(1)i U s R Cs U s R Cs R Cs +=++传递函数为0212()1()()1i U s R CsG s U s R Cs R Cs+==++2-3求下图所示运算放大器构成的电路的传递函数。

解：（a ）由图（a ），利用等效复数阻抗的方法得22111(s)1(s)()1o i R U R Cs Cs G U s R R Cs ++==-=-+（b ）由图（b ），利用等效复数阻抗的方法得222121211221211111(s)()1(s)1()1o i R U C s R R C C s R C R C s G U s R C s R C s R C s++++==-=-+2-5试简化下图中各系统结构图，并求传递函数()()C s R s 。

2-6试求下图所示系统的传递函数11()()C s R s ，21()()C s R s ，12()()C s R s 及22()()C s R s 。

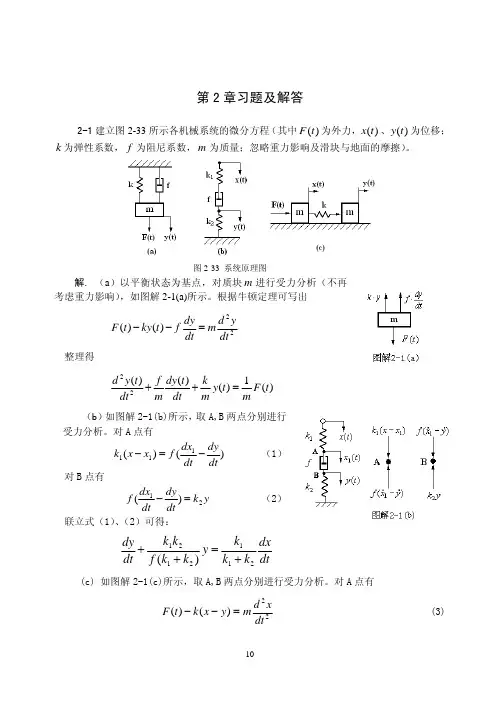
第二章习题及答案2-1 试建立题2-1图所示各系统的微分方程 [其中外力)(t F ，位移)(t x 和电压)(t u r 为输入量；位移)(t y 和电压)(t u c 为输出量；k （弹性系数），f （阻尼系数），R （电阻），C （电容）和m （质量）均为常数]。

解（a ）以平衡状态为基点，对质块m 进行受力分析（不再考虑重力影响），如图解2-1(a)所示。

根据牛顿定理可写出22)()(dty d m dt dy f t ky t F =-- 整理得)(1)()()(22t F m t y m k dt t dy m f dtt y d =++（b ）如图解2-1(b)所示，取A,B 两点分别进行受力分析。

对A 点有 )()(111dtdydt dx f x x k -=- （1） 对B 点有 y k dtdydt dx f 21)(=- （2） 联立式（1）、（2）可得：dtdx k k k y k k f k k dt dy2112121)(+=++ (c) 应用复数阻抗概念可写出)()(11)(11s U s I csR cs R s U c r ++= （3）2)()(R s Uc s I =（4） 联立式（3）、（4），可解得： CsR R R R Cs R R s U s U r c 212112)1()()(+++=微分方程为: r r c c u CR dt du u R CR R R dt du 121211+=++(d) 由图解2-1（d ）可写出[]Css I s I s I R s U c R R r 1)()()()(++= （5） )()(1)(s RI s RI Css I c R c -= （6） []Css I s I R s I s U c R c c 1)()()()(++= （7）联立式（5）、（6）、（7），消去中间变量)(s I C 和)(s I R ，可得：1312)()(222222++++=RCs s C R RCs s C R s U s U r c 微分方程为 r r r c c c u RC dt du CR dt du u R C dt du CR dt du 222222221213++=++2-2 试证明题2-2图中所示的力学系统(a)和电路系统(b)是相似系统（即有相同形式的数学模型）。

自动控制原理第二章课后习题答案（免费）离散系统作业注明：*为选做题2-1 试求下列函数的Z 变换 （1）()E z L =();n e t a = 解：01()[()]1k k k z E z L e t a z z z aa∞-=====--∑ （2） ();at e t e -= 解：12211()[()][]1...1atakT k aT aT aTaT k z E z L e t L ee z e z e z z e e z∞----------=====+++==--∑2-2 试求下列函数的终值：（1）112();(1)Tz E z z --=-解： 11111()(1)()1lim lim lim t z z Tz f t z E z z---→∞→→=-==∞- （2）2()(0.8)(0.1)z E z z z =--。

解：211(1)()(1)()0(0.8)(0.1)lim lim limt z z z z f t z E z z z →∞→→-=-==-- 2-3* 已知()(())E z L e t =,试证明下列关系成立：（1）[()][];n z L a e t E a =证明：0()()nn E z e nT z∞-==∑00()()()()[()]n n n n n n z z E e nT e nT a z L a e t a a ∞∞--=====∑∑ （2）()[()];dE z L te t TzT dz=-为采样周期。

证明：11100[()]()()()()()()()()()nn n n n n n n n n L te t nT e nT zTz ne nT z dE z de nT z dz dz e nT n zne nT z ∞∞---==∞-=∞∞----======-=-∑∑∑∑∑所以：()[()]dE z L te t Tzdz=- 2-4 试求下图闭环离散系统的脉冲传递函数()z Φ或输出z 变换()C z 。

西工大821自动控制原理第二章 控制系统的数学模型习题及答案2-1 试建立图2-27所示各系统的微分方程。

其中外力)(t F ，位移)(t x 和电压)(t u r 为输入量；位移)(t y 和电压)(t u c 为输出量；k （弹性系数），f （阻尼系数），R （电阻），C （电容）和m （质量）均为常数。

解（a ）以平衡状态为基点，对质块m 进行受力分析（不再考虑重力影响），如图解2-1(a)所示。

根据牛顿定理可写出22)()(dty d m dt dy f t ky t F =-- 整理得)(1)()()(22t F m t y m k dt t dy m f dt t y d =++（b ）如图解2-1(b)所示，取A,B 两点分别进行受力分析。

对A 点有 )()(111dtdydt dx f x x k -=- （1） 对B 点有 y k dtdydt dx f 21)(=- （2） 联立式（1）、（2）可得：dtdx k k k y k k f k k dt dy2112121)(+=++ (c) 应用复数阻抗概念可写出)()(11)(11s U s I cs R cs R s U c r ++= （3） 2)()(R s Uc s I = （4）联立式（3）、（4），可解得： CsR R R R Cs R R s U s U r c 212112)1()()(+++=微分方程为: r r c c u CR dt du u R CR R R dt du 121211+=++(d) 由图解2-1（d ）可写出[]Css I s I s I R s U c R R r 1)()()()(++= （5） )()(1)(s RI s RI Css I c R c -= （6） []Css I s I R s I s U c R c c 1)()()()(++= （7）联立式（5）、（6）、（7），消去中间变量)(s I C 和)(s I R ，可得：1312)()(222222++++=RCs s C R RCs s C R s U s U r c 微分方程为 r r r c c c u RC dt du CR dt du u R C dt du CR dt du 222222221213++=++2-2 试证明图2-28中所示的力学系统(a)和电路系统(b)是相似系统（即有相同形式的数学模型）。

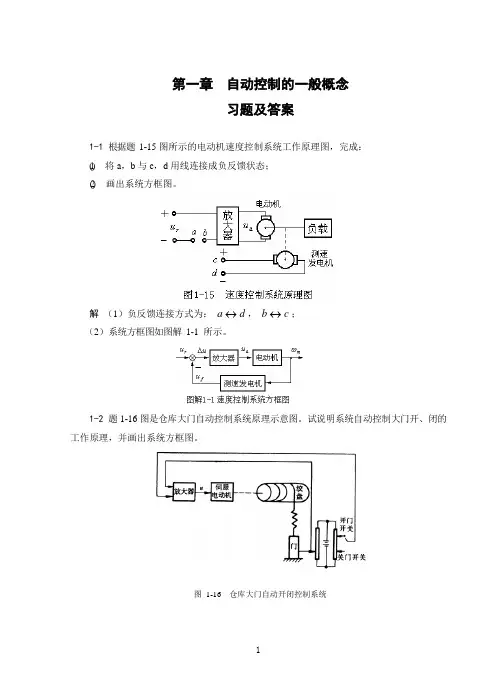
第一章自动控制的一般概念习题及答案1-1 根据题1-15图所示的电动机速度控制系统工作原理图，完成：(1)将a，b与c，d用线连接成负反馈状态；(2)画出系统方框图。

解（1）负反馈连接方式为：a↔d，b↔c；（2）系统方框图如图解1-1所示。

1-2 题1-16图是仓库大门自动控制系统原理示意图。

试说明系统自动控制大门开、闭的工作原理，并画出系统方框图。

图1-16仓库大门自动开闭控制系统1解当合上开门开关时，电桥会测量出开门位置与大门实际位置间对应的偏差电压，偏差电压经放大器放大后，驱动伺服电动机带动绞盘转动，将大门向上提起。

与此同时，和大门连在一起的电刷也向上移动，直到桥式测量电路达到平衡，电动机停止转动，大门达到开启位置。

反之，当合上关门开关时，电动机带动绞盘使大门关闭，从而可以实现大门远距离开闭自动控制。

系统方框图如图解1-2所示。

1-3 图1-17为工业炉温自动控制系统的工作原理图。

分析系统的工作原理，指出被控对象、被控量和给定量，画出系统方框图。

图1-17 炉温自动控制系统原理图解加热炉采用电加热方式运行，加热器所产生的热量与调压器电压u c的平方成正比，u c 增高，炉温就上升，u c的高低由调压器滑动触点的位置所控制，该触点由可逆转的直流电动机驱动。

炉子的实际温度用热电偶测量，输出电压u f。

u f作为系统的反馈电压与给定电压u r进行比较，得出偏差电压u e，经电压放大器、功率放大器放大成u a后，作为控制电动机的电枢电压。

在正常情况下，炉温等于某个期望值T°C，热电偶的输出电压u f正好等于给定电压u r。

此时，u e=u r−u f=0，故u1=u a=0，可逆电动机不转动，调压器的滑动触点停留在某个合适的位置上，使u c保持一定的数值。

这时，炉子散失的热量正好等于从加热器吸取的热量，形成稳定的热平衡状态，温度保持恒定。

当炉膛温度T°C由于某种原因突然下降(例如炉门打开造成的热量流失)，则出现以下2的控制过程：控制的结果是使炉膛温度回升，直至T°C的实际值等于期望值为止。

《自动控制原理》（第2版）习题答案1第2章2-1 （1）t e t ett23sin 3123cos122--+- （2）6 + 3t（3）)334(322+++---t t e e t t （4）t t ωωωsin 1132-2-2 （1）2351853tt e e --+-（2）t e 2-（3）t e a b t ae n t nnn t n n ωωζωωζωζωsin cos --++（4）t a Aa t a A e b a A atωωωωωωωsin cos 222222++++⎪⎭⎫ ⎝⎛++- 2-3 （a ）)()()(2110f f ms f s X s X i ++=（b ）212110)()()(k k s k k f fsk s X s X i ++=2-4 （a ）)()()(t u t kx t xm =+ （b ）)()()(2121t u t x k k k k t x m =++ 2-5 （a ）)()()()()(2212121t u R dt t du C R R t u R R dt t du CR R r r c c +=++ （b ）)()()()()()(22121221t u R t u R R dt t du C R R L dt t u d LC R r c c c =++++ 2-6 252312)14(100)()(2+++=s s s s R s C 2523125231210)()(22++++⋅=s s s s s R s E 2-7 t t e e t c 2241)(--+-= 2-8 )1)(2(23)(+++=s s s s G t t e e t h ---=24)(22-9 （a ）1)(1)()(32213+++⋅-=s R R C s CR R R s U s U r c （b ）13221)()()(R R R s R CR s U s U r c ++-= 2-10 （a ）))((1)()(432121G G G G G G s R s C -+++=（b ）)(1)1()()(21221H H G G G s R s C -++=（c ）331311321332123113211)()(H G H G H G G G G H G G H G G H G G G G s R s C ++++++=2-11 （a ）32211)()(G G G G s R s C ++=（b ）H G H H G s R s C 111)1()()(+--=（c ）121223121)()()(H G G H G G G G s R s C +++=2-12 （a ）))((1)1()()(23111232123111134321H G H G H H G G G H G H G H G G G G G G s R s C --++++++=))((1)1(1)()(2311123212311123423H G H G H H G G G H G H G H H G G H G s R s E --++++-+⋅=（b ）21212121312)()(G G G G G G G G s R s C ++-++-= 21212131)1(1)()(G G G G G G s R s E ++-+⋅=2-13 （a ）12121211)()(H G G G G G G s R s C ++= 121211211)1(1)()(H G G G G H G G s R s E +++⋅=12121231211)1(1)()(H G G G G G G H G G s D s C ++++⋅-=12121231211)1(1)()(H G G G G G G H G G s D s E ++-+⋅= （b ）434242143421)()(G G G G G G G G G G G s R s C ++++= 434242111)()(G G G G G G G s R s E ++-=434241)()(G G G G G s D s C ++= 434241)()(G G G G G s D s E ++-=32-14 （a ）))((1)(23113343321231134321H G H G H G G H G G G H G H G G G G G G s G -+++-++=（b ）3541432326543211)(H G G H G G H G G G G G G G G s G +-+=（c ） 15.1 （d ）))((1)1()(ch af ehgf ch gb af gb ed abcd s G +----++=45σ % = 56.2% t p = 1.006 t s = 63-13 0 < K < 0.75 3-14 （1）0（2）1 3-16 （1）∞ ∞6分离点：d = -0.8857（4） 渐近线：σa = -1 ϕa = ± 60︒，180︒与虚轴的交点：K = 3 s = ± j1.414分离点：d = -0.423 根迹图略（5） 渐近线：σa = -2/3 ϕa = ± 60︒，180︒与虚轴的交点：K = 4 s = ± j1.414（6）渐近线：σa = -1.5 ϕa = ± 45︒，± 135︒起始角：ϕ1 = -63.4︒根迹图略 （7）（8）894-9 零度根轨迹。

自动控制原理第二版课后习题参考答案2-1 (a)()()1121211212212122112+++⋅+=+++=CS R R R R CS R R R R R R CS R R R CS R R s U s U (b)()()1)(12221112212121++++=s C R C R C R s C C R R s U s U 2-2 (a)()()RCs RCs s U s U 112+=(b) ()()141112+⋅-=Cs R R R s U s U (c)()()⎪⎭⎫⎝⎛+-=141112Cs R R R s U s U 2-3 设激磁磁通f f i K =φ恒定()()()⎥⎦⎤⎢⎣⎡++++=Θφφπφm e a a a a m a C C f R s J R f L Js L s C s U s 2602 2-4()()()φφφπφm A m e a a a a m A C K s C C f R i s J R f L i Js iL C K s R s C +⎪⎭⎫⎝⎛++++=260232-5 ()2.0084.01019.23-=⨯--d d u i 2-8 (a)()()()()3113211G H G G G G s R s C +++=(b)()()()()()31243212143211H G H G G G H G G G G G G s R s C +++++=2-9 框图化简中间结果如图A-2-1所示。

图A-2-1 题2-9框图化简中间结果()()()()52.042.018.17.09.042.07.023++++++=s k s k s s s R s C 2-10()()4232121123211G H G G H G G H G G G G s R s C ++-+=2-11 系统信号流程图如图A-2-2所示。

图A-2-2 题2-11系统信号流程图()()()()2154214212654212215421421321111H H G G G G G G G H G G G G G s R s C H H G G G G G G G G G G s R s C -++=-++=2-12 (a)()()()adgi abcdi agdef abcdef cdhs R s C +++-=11(b)()()()1221211222112++++=s C R C R C R s C R C R R s R s C 2-13 由选加原理,可得()()()()()()[]s D H G G s D G s D G s R G G G H G H s C 3121221221221111--+++=第三章3-1 分三种情况讨论 (a) 当1>ζ时()()()()()⎥⎥⎦⎤⎢⎢⎣⎡-+----+-=-+-=---=⎪⎭⎫ ⎝⎛-+-⎪⎭⎫ ⎝⎛---221221222211112121,122ζζζζωζωζωζζωζζωζζωζζt t n n nn n n e e t t c s s (b) 当10<<ζ时()()()⎪⎪⎭⎫⎝⎛-----+-=---+---=-+-=---=---22222222222121121sin 1121sin 1211cos 221,1ζζζωζωζωζωζωζζωζωζωζωζζωζζζωζωζωarctg t et t e t et t c j s j s n tnnn t nn tnnn n n n n(c) 当1=ζ时设系统为单位反馈系统,有()()()()()2222nn n r s s s s R s c s R s E ωζωζω+++=-= 系统对单位斜坡输入的稳态误差为 ()nn n n s sr s s s s s s im e ωζωζωζω22212220=+++⋅⋅=→ 3-2 (1) 0,0,50===a v p K K K (2) 0,,==∞=a v p K K K K(3) 10,,K K K K a v p =∞=∞= (4) 0,200,==∞=a v p K KK K 3-3 首先求系统的给定误差传递函数()⎪⎭⎫ ⎝⎛++-=-=-t e t t c s n t n n nn 21222,1ωωωωω()101.0)11.0()(11)()(2+++=+==Φs s s s s G s R s E s e 误差系数可求得如下()()()0)101.0()12.0(20)101.0(2lim lim 1.0)101.0()12.0(10lim lim 0101.0)11.0(lim lim 32220220222001200=+++-++=Φ==+++=Φ==+++=Φ=→→→→→→s s s s s s ds d C s s s s ds d C s s s s s C s e s s e s s e s(1) 0)(R t r =，此时有0)()(,)(0===t r t r R t r s s s ，于是稳态误差级数为()0)(0==t r C t e s sr ，0≥t(2) t R R t r 10)(+=，此时有0)(,)(,)(110==+=t r R t r t R R t r s s s ，于是稳态误差级数为()1101.0)()(R t rC t r C t e s s sr =+= ，0≥t (3) 221021)(t R t R R t r ++=，此时有t R R t rt R t R R t r s s 212210)(,21)(+=++= ，2)(R t r s = ，于是稳态误差级数为())(1.0)(!2)()(21210t R R t r C t rC t r C t e s s s sr +=++= ，0≥t 3-4 首先求系统的给定误差传递函数()5001.0)11.0()(11)()(2+++=+==Φs s s s s G s R s E s e 误差系数可求得如下()()()232220220222001200050098)5001.0()12.0(1000)5001.0(100lim lim 5001)5001.0()12.0(500lim lim 05001.0)11.0(lim lim =+++-++=Φ==+++=Φ==+++=Φ=→→→→→→s s s s s s ds d C s s s s ds d C s s s s s C s e s s es s e stt r t t rt t r s s s 5sin 25)(5cos 5)(5sin )(-===稳态误差级数为()[][][]tt tC t C C t e sr 5cos 1015sin 109.45cos 55sin 25224120 -⨯++⨯=-⨯+⎥⎦⎤⎢⎣⎡+⨯-=- 3-5 按技术条件（1）~（4）确定的二阶系统极点在s 平面上的区域如图A-3-1 (a) ~ (d)的阴影区域。