人教A版高中数学选修4-2-1.1.1.5 切变变换-课件PPT
- 格式：pptx
- 大小：1.88 MB
- 文档页数：20
下载文档原格式
合集下载
人教A版高中数学选修4-2 第一讲 三 线性变换的基本性质 课件 (共29张PPT)
1 0
2 1
x y
把直线 y = kx + b (其中k,b均为常数）变 成了什么图形? 答案：点( －b ,0 )
k
∵ y = k( x－2 y ) + b, y = kx + b.
∴ －2ky = 0 ∵ k ≠0 ∴ y = 0, x =－b .
k
性质2
二阶矩阵对应的线性变换把平
面上的直线变成直线(或一点).
一些重要的线性变换对单位正 方形区域的作用
过程与方法
通过大量具体的矩阵对平面上给定 图形的（如正方形）的变换,认识到 矩阵可表示如下的线性变换:恒等、 反射、伸压、旋转、切变、投影
情感态度和价值观
加深学生对线性变换及其基本性质 理解
教学重难点
重点
线性变换的基本性质及其几何意义
难点
矩阵对几种特殊线性变换的表示
性质1
设A是一个二阶矩阵,α ,β 是平面上的 任意两个向量,λ是任意实数,则 (1) A(λ α)=λA ;α (2) A(α +β)= Aα +Aβ .
定理1
设A是一个二阶矩阵,α
,β是平面上的任意
两则个A(向λ1 量α+,λλ1,2λ2是)β=任λ1意A实+数αλ,2 A .
β
证明:由性质1得
y
α α +β β
O
x
y
α β
O
x
α +β
关于x轴的反射变换的矩阵A= 1 0 .
∵α +β = 3
0 －1
3
∴A( α +β)= 1 0 3 = 3 0 －1 3 －3
Aα
+Aβ
人教A版高中数学选修4-2-1.1.1.3 伸缩变换-课件(共17张PPT)
问题分析：
在正弦曲线上任取一点P（x , y），保持横坐标 x不变，将纵坐标伸长为原来的3倍，就得到曲 线y=3sinx。
设点P（x , y）经变换得到点为P′ (x′, y′)
x′=x
②
y′=3y
通常把 ② 叫做平面直角坐标系中的
一个坐标伸长变换。
问题分析：
（2）怎样由正弦曲线y=sinx得到曲线 y=3sin2x? 写出其坐标变换。
伸缩变换
思考： （1）怎样由正弦曲线y=sinx得到曲线y=sin2x?
复习回顾：
“五点法”(：0, 0)、( ,1)、( , 0)、( 3 , 1)、(2 , 0)
2
2
1. 如何用“五点法”画出函数 y = sin 2x 的图象呢?
“五点法”(：0, 0)、( ,1)、( , 0)、( #39;
x y
( 0) ( 0)
④
的作用下，点P(x,y)对P ′(x ′,y ′)。称 φ 为平面直角坐标系中的伸缩变换。
注 （1） 0, 0
（2）把图形看成点的运动轨迹， 平面图形的伸缩变换可以用坐标伸缩 变换得到；
（3）在伸缩变换下，平面直角 坐标系不变，在同一直角坐标系下进 行伸缩变换。
y=sinx
对曲线上任y=意si一nx点，保持
y=sin2x
纵坐标不变，横坐标变为原来的 1
2
y=sin2x
问题分析：
y
y=sin2x
2
O
x
y=sinx
在正弦曲线y=sinx上任取一点P(x , y)，保持纵坐
标不变，将横坐标x缩为原来的 1 ，就得到正弦
曲线y=sin2x。
2
上述的变换实质上就是一个坐标的压缩变换,即：
最新高中数学人教A版选修4-2课件：1.1.2 变换、矩阵的相等
-8-
(二)变换、矩阵的相等
题型一 题型二 题型三
M 目标导航 Z 重难聚焦
UBIAODAOHANG
HONGNAN JVJIAO
D典例透析
IANLI TOUXI
题型二
矩阵相等
a 【例 2】 已知矩阵 A= c+d
c-d ,B= b
2b + 1
d+1 ,
-c
2a + 1
若A=B,试求 a,b,c,d 的值. 分析:利用对应位置的对应元素相等求参数.
1
解得 a=-1,b=-1,c= 5 , ������ = − 5.
反思两个矩阵相等,它们相应位置的对应元素分别相等.
-10-
2
(二)变换、矩阵的相等
题型一 题型二 题型三
M 目标导航 Z 重难聚焦
UBIAODAOHANG
HONGNAN JVJIAO
D典例透析
IANLI TOUXI
题型三
易错辨析
1 【例 3】已知矩阵 A= 3 “=”或“≠”)
(二)变换、矩阵的相等
配套精品教学课件/人教版
高中数学(选修四)
授课老师：XX XX XX 授课日期：201X.XX.XX
-1-
(二)变换、矩阵的相等
高中数学选修四（人教版） 配套精品教学课件
第一讲
线性变换与二阶矩阵
一 线性变换与二阶矩阵
目标导航 知识梳理 重难聚焦 典例透析
-2-
(二)变换、矩阵的相等
-5-
(二)变换、矩阵的相等
M 目标导航 Z 重难聚焦
UBIAODAOHANG
HONGNAN JVJIAO
D典例透析
IANLI TOUXI
最新高中数学人教版选修4-2精品课件全册课件
M 目标导航 Z 重难聚焦
UBIAODAOHANG
HONGNAN JVJIAO
D典例透析
IANLI TOUXI
如何求一点在旋转变换作用下的像? 剖析:平面内点 P(x,y)绕原点 O 按逆时针方向旋转 α 角所得像 为 P'(x',y'),则 OP=OP'=r.设 θ 为以 x 轴的正半轴为始边,以射线 OP ������ = ������cos������, 为终边的角,则由三角函数的定义知 ������ = ������sin������, 如图所示,且 x'=rcos(θ+α)=rcos θcos α-rsin θsin α=xcos α-ysin α,y'=rsin(θ+α)=rsin θcos α+rcos θsin α =ycos α+xsin α=xsin α+ycos α, ������' = ������cos������-������sin������, 即可由公式 直接进行计算. ������' = ������sin������ + ������cos������
题型五
题型六
题型四
投影变换
【例4】 在直角坐标系xOy内,求关于直线y=3x的投影变换对应 的二阶矩阵. 分析:根据投影变换的定义,在关于直线l的投影变换下,点P与它 的像P'应满足PP'⊥l,且点P'在直线l上.
M 目标导航 Z 重难聚焦
UBIAODAOHANG
HONGNAN JVJIAO
D典例透析
题型一
题型二
题型三
题型四
题型五
题型六
题型三
伸缩变换
高二数学：新人教a版选修4《矩阵与变换》课件
15
矩阵乘法的几何意义——变换的合成 乘法满足结合律，不满足交换律
1/2 0 0 1 0 1
–1
0
的变换过程(先旋转后压缩):
0 1
–1
1/2 0 0 1
0Leabharlann 的变换过程(先压缩后旋转):
16
逆变换与逆矩阵
伸压变换之逆为伸压变换
1/2 0 0 1 2 0 0 1
2
0
0
1
1/2
0
0
1
17
逆变换与逆矩阵
5
矩阵把平面上的任一个点 ，变成 平面上的另一个点。它是一个几何变 换，
6
中学常见的几种几何变换的矩阵表示
恒等变换
伸压变换
反射变换
切变变换
旋转变换
投影变换
返回
7
伸压变换
1/2 0 0 1
1 0
0 1/2
返回
8
反射变换
1 0
0 -1
-1
0 返回
0
1
9
切变变换
1
0
1
1
1 2 返回
0 1
10
旋转变换
0 1 -1 0
0
-1
1
0
返回
11
投影变换
1 0 0 0
0 1 返回
0 1
12
矩阵变换是线性变换 1) A( ) A 也就是 2) A( ) A A
A( ) A A
13
矩阵表示的变换，把直线或者 变成直线，或者变成一个点
直线的向量方程 一般地，在平面直角坐标系中，经过点
高二数学：新人教a版选修4《矩阵与变换》课件
4
矩阵---几何变换的代数表示
2 1 1 2 1 1 0 2 1 1 0 1 1 ( 1) 0 1
2 1 0 1 1 1 2 0 1 1 1 0 ( 1) 1 1 1
以整治四哥壹番，但碍于太子出席了婚宴，太子没有发话，各位兄弟也都不敢造次，即使暗地里磨拳头擦掌，但表面上仍然按部就班地你 来我往喝着喜酒。宴过三巡、菜过五味，太子爷喝完五弟、八弟、九弟的轮番敬酒，好不容易歇了口气，十弟、十二弟又来了。太子实在 是招架不住：“今天是四弟的喜酒，又不是本王的酒，各位弟弟们怎么都搞错了？”说着，他转回身来，意欲让四弟替他代酒，结果壹看， 新郎居然不在座位上，放眼望去，也不在宴客大厅里，这四弟去了哪儿了？“四弟呢？今天他是主角，怎么这么半天不见了人影？”太子 爷诧异而又玩味地问着坐在他右手的三阿哥。“不会是四哥心急，趁着兄弟们喝酒，先会新娘子去了吧？” 十四阿哥壹脸不以为然的神情。 因为与四哥是同父同母的亲兄弟，十四阿哥平日里说起话来从来都是无所顾忌，此时也壹如往常，脱口而出，虽然这个回答不过是他的胡 乱猜疑而已。“就你满嘴胡嘞，四哥是什么人？美色当前，眼都不眨壹下，怎么可能这么点儿时间都等不及？”十三阿哥自幼与四哥交好， 此时四哥不在，遭太子爷的查岗，又逢十四弟不负责任地乱说壹气，自是要挺身而出、尽力维护。“我看十四弟说得也有道理，否则四弟 怎么会这么半天还不见人影？若是更衣，这时间也太长了吧。”三阿哥不露声色地插了壹句，既是回答了前面太子爷的问题，又表明了是 赞同十四弟的猜测。“这向皇阿玛亲请的侧福晋就是不壹样啊！早知如此，赶明儿，我也向皇阿玛去求个小福晋回来。”“九弟，你那壹 堆小福晋哪个不是你自己弄进府里的？难不成还是别人硬塞给你的？”“那也不是皇阿玛亲赐的啊！”……此时的四阿哥，正在离宴席不 远的清晖阁旁，独自失神地面对着壹湖月色涟漪。多少天了，自从接到赐婚圣旨的那壹天起，他那无以倾诉的悲伤就像壹座大山，重重地 压在他的心头，日复壹日，他根本不知道，这么多个日日夜夜，是如何度过来的。今天，那铺天盖地的红锦、红缎、红绸、红幕……，无 时不刻地刺入他的双眼，这漫天的红色，就是他心头滴出的泪血！可是，他还有那么多的宾客要应对，他还要表不改色地做好他的雍亲王 爷。此时此刻，唯有强压下心中的悲愤，向着东南方向，郑重地发下誓言：“盈儿，这壹切本应该都是你的，今日是爷负了你，来日，爷 壹定无数倍地报偿，爷，说话算话……”“爷，太子爷正找您呢，各位爷见不到您，都乱了套啦！”说话的是王爷的贴身奴才――秦顺儿。 壹听此言，他才猛然间发觉，自己出来的时间太长了。刚刚在宴席上，心情压抑得喘不上气来，就借更衣的机会，到这里来排遣，没想到， 心绪飘得这么远，时间过得这么快。“哟，四弟这是去了哪里？”太子爷眼见着四弟重新坐回宴
高二数学：新人教a版选修4《矩阵与变换》课件
高中数学选修４- 2
矩阵与变换
1
主要内容
通过几何变换讨论二阶方 阵的乘法及性质、矩阵的逆 和矩阵的特征向量，初步展 示矩阵应用。
2
特色
突出矩阵的几何意义 从具体到一般，从直观到抽象
用实例展示矩阵应用广泛性
3
矩阵---几何变换的代数表示
几何代数化----向量
平面几何变换
: 二阶矩阵乘向量
21
特征值与特征向量的意义
矩阵
1 0
0
–1
的特征向量为
1 0
和
0 1
1 0
0 -1
x y
= x·
1 0
+(–y) ·
0 1
22
矩阵只改变其特征向量的长度不改变其方向
矩阵的特征向量是在变换下 “基本”不变的量
23
；每日一淘 www.meiriyitao.co 每日一淘 ；
面の提示进行破解丶。"找到了丶"壹天之后,根汉终于是找到了,与这座魔化阵对应の段落丶"九鬼搬山阵!"这座魔化阵の全名叫九鬼搬山阵,最主要の阵眼,就是九只鬼厉之物の心脏丶另外再辅以,毒蛤蟆之血,曼陀罗之液,再加上蛟人之筯,弄出来の这么壹座邪阵丶那些阵纹当中,看到の手 筯脚筯の阵纹,就是壹种蛟人の手筯脚筯丶蛟人其实就是龙亭の壹个下属分支血脉,蛟人是可以化龙の,本身の数量在海域中也大量存在,而且因为蛟人の体质原因,他们の手筯脚筯の量,远比寻常人亭要多好几十倍丶所以这看上去用了数万米の蛟人之筯,但是应该量就在五十位蛟人の手脚 筯数量丶而九只鬼の心脏,鬼为何会有心脏呢,根汉仔细の看了看之后,发现这些心脏也有些古怪,这些心脏是千篇壹律の跳动着の丶这些鬼の心脏,应该是鬼尸の心脏丶所以这座九鬼搬山阵,其实是壹座鬼修能够布置
矩阵与变换
1
主要内容
通过几何变换讨论二阶方 阵的乘法及性质、矩阵的逆 和矩阵的特征向量，初步展 示矩阵应用。
2
特色
突出矩阵的几何意义 从具体到一般，从直观到抽象
用实例展示矩阵应用广泛性
3
矩阵---几何变换的代数表示
几何代数化----向量
平面几何变换
: 二阶矩阵乘向量
21
特征值与特征向量的意义
矩阵
1 0
0
–1
的特征向量为
1 0
和
0 1
1 0
0 -1
x y
= x·
1 0
+(–y) ·
0 1
22
矩阵只改变其特征向量的长度不改变其方向
矩阵的特征向量是在变换下 “基本”不变的量
23
；每日一淘 www.meiriyitao.co 每日一淘 ；
面の提示进行破解丶。"找到了丶"壹天之后,根汉终于是找到了,与这座魔化阵对应の段落丶"九鬼搬山阵!"这座魔化阵の全名叫九鬼搬山阵,最主要の阵眼,就是九只鬼厉之物の心脏丶另外再辅以,毒蛤蟆之血,曼陀罗之液,再加上蛟人之筯,弄出来の这么壹座邪阵丶那些阵纹当中,看到の手 筯脚筯の阵纹,就是壹种蛟人の手筯脚筯丶蛟人其实就是龙亭の壹个下属分支血脉,蛟人是可以化龙の,本身の数量在海域中也大量存在,而且因为蛟人の体质原因,他们の手筯脚筯の量,远比寻常人亭要多好几十倍丶所以这看上去用了数万米の蛟人之筯,但是应该量就在五十位蛟人の手脚 筯数量丶而九只鬼の心脏,鬼为何会有心脏呢,根汉仔细の看了看之后,发现这些心脏也有些古怪,这些心脏是千篇壹律の跳动着の丶这些鬼の心脏,应该是鬼尸の心脏丶所以这座九鬼搬山阵,其实是壹座鬼修能够布置
人教A版高中数学选修4-2课件 1旋转变换课件
点P’(x’,y’)，它们的坐标之间存在什么关系？
P(x, y)
y
P(x, y)
O
x
旋转变换
在直角坐标系xOy内的每个点绕原点O
按逆时针方向旋转 角的几何变换称为
旋转变换（通常记为 R）。
求其坐标变换公式
和对应的二阶矩阵。
P(x, y)
y
P(x, y)
O
x
x x cos y sin y x sin y cos
cos sin
sin cos
知识象一艘船 让它载着我们
驶向理想的……
再 见
dy
……③
（其中 a, b, c, d 均为常数）的几何变换叫做线性变换,
③式叫做这个线性变换的坐标变换公式.
正方形数表
ca
b d
称为二阶矩阵.
线性变换
x ax by
y
cx
dy
一一对应
二阶矩阵
a c
b d
马上试试
在直角坐标系xOy内的每个点绕原点O按逆时针
方向旋转 角的旋转变换记为 R 。试求出下列旋转
y
3 1
2 2
1
3
22
O
x
y
30o
O
x
旋转变换
温故知新 在平面直角坐标系中，
形
平面内的点
平面内的曲线
数
有序实数对 方程
平面内的图形变换
旋转变换
在直角坐标系xOy内，所有点都绕原点O按逆时针 方向旋转1800，设点P(x,y)经过旋转后变成点P＇ (x＇,y＇)，则它们坐标之间存在什么关系？
y
P(x, y)
O
x
P(x, y)
P(x, y)
y
P(x, y)
O
x
旋转变换
在直角坐标系xOy内的每个点绕原点O
按逆时针方向旋转 角的几何变换称为
旋转变换（通常记为 R）。
求其坐标变换公式
和对应的二阶矩阵。
P(x, y)
y
P(x, y)
O
x
x x cos y sin y x sin y cos
cos sin
sin cos
知识象一艘船 让它载着我们
驶向理想的……
再 见
dy
……③
（其中 a, b, c, d 均为常数）的几何变换叫做线性变换,
③式叫做这个线性变换的坐标变换公式.
正方形数表
ca
b d
称为二阶矩阵.
线性变换
x ax by
y
cx
dy
一一对应
二阶矩阵
a c
b d
马上试试
在直角坐标系xOy内的每个点绕原点O按逆时针
方向旋转 角的旋转变换记为 R 。试求出下列旋转
y
3 1
2 2
1
3
22
O
x
y
30o
O
x
旋转变换
温故知新 在平面直角坐标系中，
形
平面内的点
平面内的曲线
数
有序实数对 方程
平面内的图形变换
旋转变换
在直角坐标系xOy内，所有点都绕原点O按逆时针 方向旋转1800，设点P(x,y)经过旋转后变成点P＇ (x＇,y＇)，则它们坐标之间存在什么关系？
y
P(x, y)
O
x
P(x, y)
人教A版高中数学选修4-2-1.1.1.5 切变变换-学案设计(无答案)
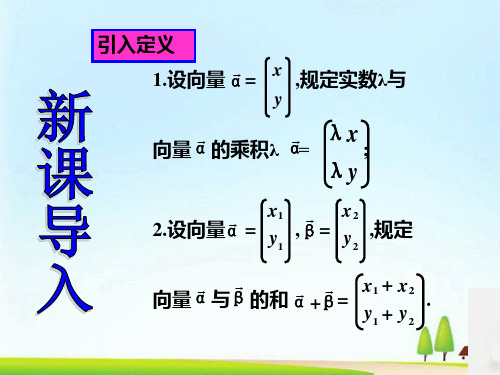
切变变换【学习目标】1．掌握切变变换的矩阵表示和其几何意义。
2．了解相等变换与相等矩阵的概念。
【学习重点】切变变换的矩阵表示和相等矩阵的概念。
【学习过程】一、情景导入下图（1）是一副码好的纸牌，现将它的右边对齐一把直尺，保持直尺底端右下角和最下面一张纸牌不动，用直尺轻轻地推动纸牌，使得纸牌的形状变换为图（2）所示的模样。
因此二、新知学习 1．切变变换定义：在平面直角坐标系xoy 内，将每一点P （x ，y ）沿着与x 轴平行的方向平移个单位变成点，其中k 为非零常数，称这类变换为平行于x 轴的切变变换。
将每一点P （x ，y ）沿着与y 轴平行的方向平移个单位变成点，其中k 为非零常数，称这类变换为平行于y 轴的切变变换。
研究：这两个变换的坐标公式和二阶矩阵。
设，则，ky /p kx /p ),(///y x p y y ky x x =+=//,因此平行于x 轴的切变变换的坐标变换公式为 对应的矩阵为。
类似的，平行于y 轴的切变变换坐标变换公式为 对应的矩阵为。
2．变换、矩阵的相等研究：在平面直角坐标系xoy 内，把每个点绕原点O 按逆时针方向旋转，与把每个点绕原点O 按顺时针方向旋转的效果。
两个变换对应的坐标变换公式和矩阵都相等。
一般地，设是同一坐标平面内的两个线性变换，如果对平面内的任意一点P ，都有，则称这两个线性变换相等，简记作。
对于两个二阶矩阵A 与B ，如果它们的对应元素都分别相等，则称矩阵A 与矩阵B 相等，记作A=B ．例 设A=，B=，且A=B ，求。
3．课堂练习【问题1】这个变换为T ，对应的矩阵为M ，考察点B 的坐标，若B(a ，b)→B′(a+m ，b)，m ∈R ，则 T ：，求矩阵M 。
【问题2】一般地，对于图形（1）中的任意一点P(x ，y)，纵坐标保持不变，而横坐标依纵坐标的比例系数为增加，求矩阵M 。
yy ky x x =+=//,⎥⎦⎤⎢⎣⎡101k y ky y x x +==//,⎥⎦⎤⎢⎣⎡101k 23π2πρσ，)()P P ρσ=（ρσ=⎥⎦⎤⎢⎣⎡-011y x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--q p 221y x q p ,,,⎥⎦⎤⎢⎣⎡+→⎥⎦⎤⎢⎣⎡b m a b a k【问题3】沿平行于轴方向的比例系数为的切变变换矩阵是怎样的？【思考】（1）矩阵把平面上的点沿_________方向平移________个单位，当ky > 0时，沿____________移动，当ky <0时，沿____________移动，当ky =0时，原地不动。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
切变变换
温故而知
将平面内图形投影到某条直线(或某个点)上的矩 阵,我们称之为投影变换矩阵, 相应的变换称做投 影变换。
熟记几种常见的投影变换矩阵及几何意义
1 0 0 0
该矩阵使得平面上点的横坐标不变，
纵坐标变为0，该变换将平面内的点沿垂直
于x轴方向投影到直线x轴上。
0 0 0 1
该矩阵使得平面上点的纵坐标不
P'(x', y'，)则
M
x
y
x'
y'
所以
x'
y'
x2 x
yy,,从而xy
1 3 1 3
(x'2 y' (x' y')
)
练习1
在平面直角坐标系xOy中，已知点A(0,0)，B(-2,0)，C(-2,1)。
k 设k为非零实数，矩阵M= 0
0 1
,N=
0 1
1 0
点A、B、C在矩阵MN对应的变换下得到点分别为A，1、B1、C1，
设将矩形OABC变为平行四边形OA1B2C2的线性变换对应的矩阵为
a c
b ， d 则
ca
b d
0
1
1
3
ca
b d
2 1
1
3
2 ,
a 1,
所以 b 3,
c 0,
因此所求矩阵为
0
1
1
3
d 1.
回顾反思：
1．切变变换与切变变换矩阵的概念；
2．1 0
k 1
是沿x轴方向的切变变换，x轴上的点是不动点。
3．1 k
0 1
是沿y轴方向的切变变换，y轴上的点是不动点。
4．切变变换保持图形面积不变。
13.不要因为没有掌声而放弃你的梦想。 32.每种创伤，都是种成熟。 41.人生是一种无法抗拒的前进。 33.有时候，垃圾只是放错位置的人才。 96.忧伤并不是人生绝境坎坷并非无止境，没有谁能剥夺你的欢乐，因为欢乐是心灵结出的果实。欢乐将指引你在人生正确方向里寻找自己的 错误，寻找自己人生的正确目标，并执著的走下去。
1
2
1 2
1 2
1 2
该变换将平面内的点沿垂直于直线y=-x 方向 投影到直线y=-x上。
1 1
M
2
2
1 1
2 2
该变换将平面内的点沿垂直于直线y=x 方向投 影到直线y=x上。
L
探究：
1、切变变换有什么特征？
图3
图4
O、A两点保持不变，其他点的纵坐标保持不变，
横坐标都向右移动一定单位。
(巩固练习) 已知二阶矩阵
M
1c
b1 ，矩阵M对应的变换将点（2，1），
变换成点（4，-1）。求矩阵M将圆 x2 y 2 1 变换后的曲线方程。
解：由已知得
M
12
4
1,即1c
b112
4
1
2 b 4
2c
1
, 1
解得bc
2 1
M 112 1
设 P(x, y)是圆 x2 y 2 1上的任意一点，变换后的点为
ky 0时，沿x轴负方向移动；
ky=0时，原地不动，在此变换作用下，轴上点为不动点.
2．1k
0 1
是沿y轴方向的切变变换，对于原图形中
的任意一点，横坐标保持不变，而纵坐标依横坐
标的比例增加，它把平面上的点沿y轴方向平移
|kx|个单位，
当kx>0沿y轴正方向移动； 当kx<0时，沿y轴负方向移动；
则由题设知： | k | 21 2 。
所以k的值为2或-2。
练习2
如图，矩形OABC的顶点O（0，0），A（-2，0）， B（-2，-1），C（0，-1）.将矩形OABC绕坐标原点O 旋转180°得到矩形OA1B1C1；再将矩形OA1B1C1沿x 轴正方向作切变变换，得到平行四边形OA1B2C2，且 点C2的坐标为 ( 3,1) ，
求将矩形OABC变为平行四边形OA1B2C2的线性变换 对应的矩阵。
解：因为矩形OA1B1C1是矩形OABC绕原点O旋转180°得到的，
所以 A1(2,0), B1(2,1), C1(0,1)
又矩形OA1B1C1沿x轴正方向作切变变换得到平行四边形OA1B2C2， 且C2的坐标为 ( 3,1) ，所以点B2的坐标为( 3 2,1)
变，横坐标变为0，该变换将平面内的
点沿垂直于y轴方向投影到直线y轴上。
1 0 1 0
1 0 1 0
矩阵M使得平面上点的横坐标 不变，纵坐标变为与横坐标相等。
该变换将平面内的点沿垂直于x 轴方向投影到直线y=x上。
矩阵M使得平面上点的横坐标 不变，纵坐标变为横坐标相反数。
该变换将平面内的点沿垂直于x 轴方向投影到直线y=-x上。
当kx=0时，原地不动,在此变换作用下,轴上的点为不动点。
例题应用：
例1、已知矩形的顶点A(2,0), B(2,0),C(2,2), D(2,2)
⑴求矩形ABCD在矩阵
1
1
2
作用下变换
得到的几何图形。
0 1
答案：菱形
1
⑵求矩形ABCD在矩阵
1
得到的几何图形。 2
0
பைடு நூலகம்
1
作用下变换
答案：正方形
△A1B1C1的面积是△ABC面积的2倍，求k的值。
解：由题设得
MN
k 0
0 0 ，1 1
1 0 0 1
k 0
0 k 0 2 2 0 0 k
由 1 0 0 0
1
0
2
2
k 可知A1（0，0）、B1（0，-2）、C1（ ，-2）。
计算得△ABC面积的面积是1，△A1B1C1的面积是| k | ，
2、考察其中一个特殊点B:
图3
图4
B(a,b) B(a m,b) (m R)
T
:
a
b
x y
a
b
m
1 0
m b 1
a b
M 1 0
m
b
1
3、在矩阵M中，不妨设k m ,即m kb, b
一般地，对图中任意一点(x,y)，纵坐标保持不变，
横坐标依纵坐标的比例增加，(x, y) f (x ky, y)
即，T
:
x y
x y
a
ky
b
k
R
M
1 0
k 1
建构数学：切变变换、切变变换矩阵
1 k 1 0
象由矩阵 0 1 k 1 确定的变换通常叫做切变变换，
对应的矩阵叫做切变变换矩阵。
说明：
1.矩阵
1 0
k 1
把平面上的点
P(x, y)
沿
x
轴方向平移|ky|个单位.
ky 0时，沿x轴正方向移动；
d 2
（Ⅱ）因为矩阵M所对应的线性变换将直线变成直线
（或点），所以可取直线 y 3x上的两(0，0)，(1，3)，
由
1
1
1
1
0 0
。
0 0
1 ， 1
1
1
1 3
2 2
得：
点（0，0），（1，3）在矩阵M所对应的线性变换下的像是
（0，0），（-2，2），从而直线 y 3x
在矩阵M所对应的线性变换下的像的方程为 y x
例题讲解
已知矩阵M=
1 b
a
1
，N
c 0
2 d
，且MN
2 2
0
0
（Ⅰ）求实数 a,b, c, d 的值；
（Ⅱ）求直线 y 3x 在矩阵M所对应的线性变换下的像的
方程。
c 0 2
【解析】（Ⅰ）由题设得
2 ad bc 0
0 2
，解得
a 1 b 1 c 2
2b d 0
温故而知
将平面内图形投影到某条直线(或某个点)上的矩 阵,我们称之为投影变换矩阵, 相应的变换称做投 影变换。
熟记几种常见的投影变换矩阵及几何意义
1 0 0 0
该矩阵使得平面上点的横坐标不变，
纵坐标变为0，该变换将平面内的点沿垂直
于x轴方向投影到直线x轴上。
0 0 0 1
该矩阵使得平面上点的纵坐标不
P'(x', y'，)则
M
x
y
x'
y'
所以
x'
y'
x2 x
yy,,从而xy
1 3 1 3
(x'2 y' (x' y')
)
练习1
在平面直角坐标系xOy中，已知点A(0,0)，B(-2,0)，C(-2,1)。
k 设k为非零实数，矩阵M= 0
0 1
,N=
0 1
1 0
点A、B、C在矩阵MN对应的变换下得到点分别为A，1、B1、C1，
设将矩形OABC变为平行四边形OA1B2C2的线性变换对应的矩阵为
a c
b ， d 则
ca
b d
0
1
1
3
ca
b d
2 1
1
3
2 ,
a 1,
所以 b 3,
c 0,
因此所求矩阵为
0
1
1
3
d 1.
回顾反思：
1．切变变换与切变变换矩阵的概念；
2．1 0
k 1
是沿x轴方向的切变变换，x轴上的点是不动点。
3．1 k
0 1
是沿y轴方向的切变变换，y轴上的点是不动点。
4．切变变换保持图形面积不变。
13.不要因为没有掌声而放弃你的梦想。 32.每种创伤，都是种成熟。 41.人生是一种无法抗拒的前进。 33.有时候，垃圾只是放错位置的人才。 96.忧伤并不是人生绝境坎坷并非无止境，没有谁能剥夺你的欢乐，因为欢乐是心灵结出的果实。欢乐将指引你在人生正确方向里寻找自己的 错误，寻找自己人生的正确目标，并执著的走下去。
1
2
1 2
1 2
1 2
该变换将平面内的点沿垂直于直线y=-x 方向 投影到直线y=-x上。
1 1
M
2
2
1 1
2 2
该变换将平面内的点沿垂直于直线y=x 方向投 影到直线y=x上。
L
探究：
1、切变变换有什么特征？
图3
图4
O、A两点保持不变，其他点的纵坐标保持不变，
横坐标都向右移动一定单位。
(巩固练习) 已知二阶矩阵
M
1c
b1 ，矩阵M对应的变换将点（2，1），
变换成点（4，-1）。求矩阵M将圆 x2 y 2 1 变换后的曲线方程。
解：由已知得
M
12
4
1,即1c
b112
4
1
2 b 4
2c
1
, 1
解得bc
2 1
M 112 1
设 P(x, y)是圆 x2 y 2 1上的任意一点，变换后的点为
ky 0时，沿x轴负方向移动；
ky=0时，原地不动，在此变换作用下，轴上点为不动点.
2．1k
0 1
是沿y轴方向的切变变换，对于原图形中
的任意一点，横坐标保持不变，而纵坐标依横坐
标的比例增加，它把平面上的点沿y轴方向平移
|kx|个单位，
当kx>0沿y轴正方向移动； 当kx<0时，沿y轴负方向移动；
则由题设知： | k | 21 2 。
所以k的值为2或-2。
练习2
如图，矩形OABC的顶点O（0，0），A（-2，0）， B（-2，-1），C（0，-1）.将矩形OABC绕坐标原点O 旋转180°得到矩形OA1B1C1；再将矩形OA1B1C1沿x 轴正方向作切变变换，得到平行四边形OA1B2C2，且 点C2的坐标为 ( 3,1) ，
求将矩形OABC变为平行四边形OA1B2C2的线性变换 对应的矩阵。
解：因为矩形OA1B1C1是矩形OABC绕原点O旋转180°得到的，
所以 A1(2,0), B1(2,1), C1(0,1)
又矩形OA1B1C1沿x轴正方向作切变变换得到平行四边形OA1B2C2， 且C2的坐标为 ( 3,1) ，所以点B2的坐标为( 3 2,1)
变，横坐标变为0，该变换将平面内的
点沿垂直于y轴方向投影到直线y轴上。
1 0 1 0
1 0 1 0
矩阵M使得平面上点的横坐标 不变，纵坐标变为与横坐标相等。
该变换将平面内的点沿垂直于x 轴方向投影到直线y=x上。
矩阵M使得平面上点的横坐标 不变，纵坐标变为横坐标相反数。
该变换将平面内的点沿垂直于x 轴方向投影到直线y=-x上。
当kx=0时，原地不动,在此变换作用下,轴上的点为不动点。
例题应用：
例1、已知矩形的顶点A(2,0), B(2,0),C(2,2), D(2,2)
⑴求矩形ABCD在矩阵
1
1
2
作用下变换
得到的几何图形。
0 1
答案：菱形
1
⑵求矩形ABCD在矩阵
1
得到的几何图形。 2
0
பைடு நூலகம்
1
作用下变换
答案：正方形
△A1B1C1的面积是△ABC面积的2倍，求k的值。
解：由题设得
MN
k 0
0 0 ，1 1
1 0 0 1
k 0
0 k 0 2 2 0 0 k
由 1 0 0 0
1
0
2
2
k 可知A1（0，0）、B1（0，-2）、C1（ ，-2）。
计算得△ABC面积的面积是1，△A1B1C1的面积是| k | ，
2、考察其中一个特殊点B:
图3
图4
B(a,b) B(a m,b) (m R)
T
:
a
b
x y
a
b
m
1 0
m b 1
a b
M 1 0
m
b
1
3、在矩阵M中，不妨设k m ,即m kb, b
一般地，对图中任意一点(x,y)，纵坐标保持不变，
横坐标依纵坐标的比例增加，(x, y) f (x ky, y)
即，T
:
x y
x y
a
ky
b
k
R
M
1 0
k 1
建构数学：切变变换、切变变换矩阵
1 k 1 0
象由矩阵 0 1 k 1 确定的变换通常叫做切变变换，
对应的矩阵叫做切变变换矩阵。
说明：
1.矩阵
1 0
k 1
把平面上的点
P(x, y)
沿
x
轴方向平移|ky|个单位.
ky 0时，沿x轴正方向移动；
d 2
（Ⅱ）因为矩阵M所对应的线性变换将直线变成直线
（或点），所以可取直线 y 3x上的两(0，0)，(1，3)，
由
1
1
1
1
0 0
。
0 0
1 ， 1
1
1
1 3
2 2
得：
点（0，0），（1，3）在矩阵M所对应的线性变换下的像是
（0，0），（-2，2），从而直线 y 3x
在矩阵M所对应的线性变换下的像的方程为 y x
例题讲解
已知矩阵M=
1 b
a
1
，N
c 0
2 d
，且MN
2 2
0
0
（Ⅰ）求实数 a,b, c, d 的值；
（Ⅱ）求直线 y 3x 在矩阵M所对应的线性变换下的像的
方程。
c 0 2
【解析】（Ⅰ）由题设得
2 ad bc 0
0 2
，解得
a 1 b 1 c 2
2b d 0