分析力学答案

分析力学参考答案分析力学参考答案引言：分析力学是物理学的一个重要分支，研究物体在力的作用下的运动规律。

在学习分析力学的过程中，参考答案是一个非常重要的工具，可以帮助学生巩固知识，理解问题的解决方法。

本文将分析力学的一些典型问题，并给出参考答案，帮助读者更好地掌握分析力学的基本原理和解题技巧。

一、牛顿第二定律问题牛顿第二定律是分析力学的基础，描述了物体在力的作用下的加速度。

以下是一个典型的牛顿第二定律问题：问题：一个质量为m的物体在水平面上受到一个恒定的力F作用，求物体的加速度和受力大小的关系。

解答：根据牛顿第二定律的公式F=ma，我们可以得到物体的加速度a等于受力F除以物体的质量m，即a=F/m。

因此，物体的加速度与受力大小成反比。

二、动量守恒问题动量守恒是分析力学中的一个重要原理，描述了系统在没有外力作用下动量的守恒。

以下是一个典型的动量守恒问题：问题：两个质量分别为m1和m2的物体在水平面上碰撞，碰撞前物体1的速度为v1，物体2的速度为v2，碰撞后物体1的速度为v'1，物体2的速度为v'2，求碰撞前后两个物体的动量是否守恒。

解答：根据动量守恒定律，系统在没有外力作用下，动量守恒。

即m1v1 +m2v2 = m1v'1 + m2v'2。

因此，两个物体的动量在碰撞前后保持不变，动量守恒。

三、角动量问题角动量是分析力学中的一个重要概念，描述了物体绕某一点旋转的特性。

以下是一个典型的角动量问题：问题：一个质量为m的物体绕固定点O以角速度ω旋转，求物体的角动量L 与角速度ω的关系。

解答：根据角动量的定义L=Iω，其中I为物体对固定点O的转动惯量。

对于一个质量为m的物体，其转动惯量I等于mr^2，其中r为物体到固定点O的距离。

因此，物体的角动量L与角速度ω成正比，L=mr^2ω。

结论：通过以上的分析力学问题及其参考答案，我们可以看出分析力学的基本原理和解题技巧。

牛顿第二定律描述了物体在力的作用下的加速度，动量守恒原理描述了系统在没有外力作用下动量的守恒，角动量则描述了物体绕某一点旋转的特性。

第一章分析力学基础答案1-1 图a自由度数为1；图b自由度数为2。

1-2广义力不都具有力的量纲，可以是力，也可以是力矩，还可以是其他量。

广义力与广义坐标的虚增量之积等于虚功。

1-3分别对图示系统写出其势能表达式，求一阶与二阶导数，由稳定性判别依据可得图a所示系统为不稳定平衡状态，图b所示系统为稳定平衡状态。

1-4只要内力作功就应该计入内力所作的功。

1-5将摩擦力看作为“主动力”，即可应用动力学普遍方程或拉格朗日方程。

1-6刚体平面运动有3个自由度，选质心坐标和转角为广义坐标，写出系统的动能，刚体所受力系向质心简化，此即为3个广义力，代入拉格朗日方程运算即可。

1-7在证明拉格朗日两个恒等式时，在推导以广义坐标表示的动力学普遍方程时。

第二章非惯性系中的质点动力学答案2-1找不到作用处；不成立。

2-2略。

2-3A对。

2-4向右面；（2）向左面；（3）与南、北半球情况相同。

2-5 略。

第三章碰撞答案3-1按恢复因数定义结合动量守恒定理求解。

时，基本按原速返回，基本不动；时，停止运动，以速度前进；时，以速度继续前进，以速度2前进。

3-2一般情况下，难以积分；碰撞过程中，可看为常量，容易积分。

3-3弹性碰撞时变形不能全部恢复，机械能损耗难以计算，不适宜用动能定理；恢复因数e=1时，是完全弹性碰撞，无机械能损失，可以用动能定理。

3-4恢复因数定义为碰撞后与碰撞前物体接触点处法向速度的比值；补充动力学方程以解决机械能损耗难以计算的困难。

3-5棒球击于球棒的撞击中心且与球棒垂直时，不震手；反之，手握棒处有碰撞冲量，有碰撞力，震手。

3-6用撞击中心的概念解释；撞击中心趋于无穷远处，无意义。

3-7均可用动量定理和对质心的动量矩定理求解。

作用于距质心l/6长度处。

第四章机械振动基础答案4-1 弹簧固有频率与弹簧松紧程度无关；不可以。

4-2不同，水平放置重力不是恢复力，铅直放置重力为恢复力。

如果在无重力场，固有频率与放置方式无关。

图2-1-7图2-2-2高一物理力学受力分析1如图2-1-7所示，甲、乙球通过弹簧连接后用绳悬挂于天花板，丙、丁球通过细绳连接后也用绳悬挂天花板．若都在A 处剪断细绳，在剪断瞬间，关于球的受力情况，下面说法中正确的是（ ）A ．甲球只受重力作用B ．乙球只受重力作用C ．丙球受重力和绳的拉力作用D ．丁球只受重力作用分析：当在A 处剪断时两球看作一个整体，整体加速度为g ，此时弹簧中的力不变，对A B 球都会有力的作用故A B 错，绳在松弛状态不能提供力，假设绳中有拉力，则丁的加速度会大于g 而丙的加速度会小于g ，则两球会相互靠近，绳则松弛，假设不成立，故绳中无拉力2．如图2-2-8所示，物体a 、b 和c 叠放在水平桌面上，水平力F b =5N 、F c =10N 分别作用于物体b 、c 上，a 、b 和c 仍保持静止．以F 1、F 2、F 3分别表示a 与b 、b 与c 、cA ．F 1=5N ，F 2=0，F 3=5NB ．F 1=5N ，F 2=5N ，F3=0 C ．F 1=0，F 2=5N ，F 3=5ND ．F 1=0，F 2=10N ，F 3=5N 分析：（分析方法从简单到复杂）因为a 、b 、c 均保持静止，故加速度，合外力都为0。

先分析a 只受b 对a 的支持力，以及重力故F1=0，再分析b ，b 受到重力、a 对b 的压力、c 对b 的支持力、Fb 、以及c 对b 的摩擦力，c 对b 的摩擦力为水平方向，故需水平方向的力来平衡，故F2=Fb=5，方向向右。

同理在对c 分析3如图2-2-1所示，A 、B 两物体叠放在水平面上，水平力F 作用在A 上，使两者一起向右作匀速直线运动，下列判断正确的是（ ）A ．A 、B 间无摩擦力 B ．A 对B 的静摩擦力大小为F ，方向向右C ．B 对地面的动摩擦力的大小为F ，方向向右D ．B 受到了向右的静摩擦力和向左的滑动摩擦力分析：两者一起向右作匀速直线运动，则加速度都为0，处于平衡状态。

力学参考答案解析力学参考答案解析力学是物理学的一个重要分支，研究物体在受到外力作用下的运动和相互作用。

学习力学需要掌握一系列的基本概念和定律，并能够应用这些知识解决实际问题。

在学习过程中，参考答案解析是一个重要的辅助工具，它能够帮助我们理解问题的解题思路和方法。

首先，我们来看一个力学问题的例子：一个质量为m的物体以初速度v0沿着水平方向匀速运动，经过时间t后速度变为v。

求物体受到的合外力F。

解答这个问题的关键在于应用牛顿第二定律，即F=ma，其中F表示物体受到的合外力，m表示物体的质量，a表示物体的加速度。

根据题目中给出的条件，物体在时间t内的加速度为a=(v-v0)/t。

将这个加速度代入牛顿第二定律的公式中，可以得到F=m(v-v0)/t。

通过这个例子，我们可以看出参考答案解析的作用。

首先，它告诉我们解答这个问题的关键在于应用牛顿第二定律，这是我们解决力学问题的基本原理。

其次，它给出了具体的计算步骤和公式，帮助我们进行问题的求解。

最后，它给出了最终的答案，即物体受到的合外力为F=m(v-v0)/t。

在学习力学的过程中，参考答案解析不仅仅是为了得到正确的答案，更重要的是理解解题的思路和方法。

通过分析解答过程，我们可以看到问题的关键点和解题思路。

在解答问题的过程中，我们需要注意以下几点。

首先，要仔细阅读问题，理解问题的要求和条件。

在解答问题之前，我们需要明确问题的目标和所给的限制条件。

只有明确了问题的要求，我们才能有针对性地选择合适的解题方法和公式。

其次，要善于运用物理学的基本原理和定律。

力学是建立在牛顿力学定律基础上的，所以我们在解答力学问题时，需要熟练掌握牛顿力学的基本原理和定律。

只有掌握了这些基本概念和定律，我们才能够正确地应用它们解决实际问题。

再次，要注意问题的逻辑推理和计算过程。

在解答问题的过程中，我们需要进行逻辑推理和计算。

逻辑推理是为了找到问题的解题思路和方法，计算过程是为了得到最终的答案。

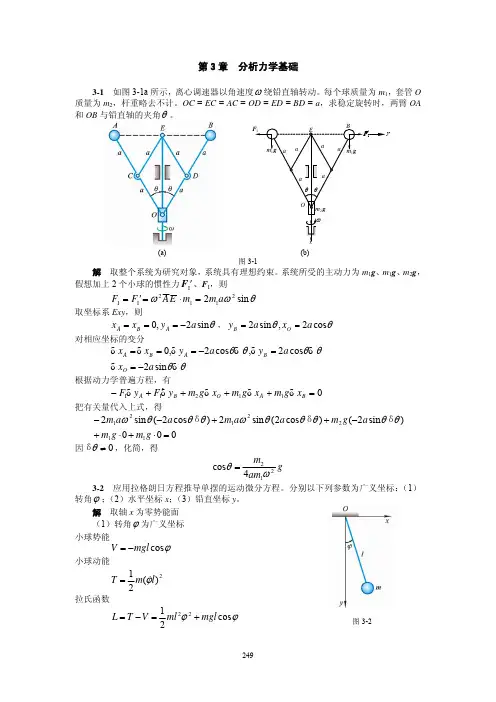
《理论力学》第五章分析力学一、单选题（共6题）1、广义坐标必须是:()A、笛卡儿坐标B、独立的位置变量C、角坐标或弧坐标;D、任何位置变量正确答案：B2、关于虚位移下列表述中不正确的是:()A、与约束有关;B、与时间无关;C、与主动力有关;D、一般不唯一正确答案：C解析：虚位移不是真实发生的位移,而是想象中可能发生的位移,它只取决于质点在此时刻的位置和加在它上面的约束,而不是由于时间的改变所引起的。

3、保守系的拉格朗日函数等于系统的:()A、总动能加总势能;B、总动能减总势能;C、总势能减总动能;D、广义速度的二次式正确答案：B解析：L=T-V。

4、分析力学中哈密顿正则变量为:()A、广义速度和广义坐标;B、广义速度和广义动量;C、广义动量和广义坐标;D、广义能量和广义动量.正确答案：C5、关于分析力学中的概念,找出错误的说法()A、拉格朗日方程是S个二阶常微分方程组成的方程组;B、哈密顿正则方程是2S个一阶常微分方程组成的方程组;C、拉格朗日函数和哈密顿函数的变量不同;D、拉格朗日方程和哈密顿正则方程是分析力学中两个基本的方程,不能相互推演。

正确答案：D解析：A、拉格朗日方程为,是由S个二阶常微分方程组成的方程组;B、哈密顿正则方程为,是由2S个一阶常微分方程组成的方程组;C、;D拉格朗日方程和哈密顿正则方程是分析力学中两个基本的方程，可以互相推演。

6、一质点质量为m,速度v,势能为Ep,则其拉格朗日函数为:____正确答案：B解析：L=T-V.二、填空题（共7题）1、一个不受任何约束的系统,由n个质点组成,该系统的独立坐标个数为____个;若该系统受k个完整约束,m个非完整约束,则该系统的自由度数目变为____个;独立坐标(广义坐标)个数变为____个。

正确答案：第1空:3n第2空:3n-k-m第3空:3n-k2、虚位移是____允许的所有位移,与时间____。

正确答案：第1空:稳定约束第2空:无关3、理想完整系统是指只受____、____的系统。

第五章思考题5.1虚功原理中的“虚功”二字作何解释？用虚功原理理解平衡问题，有何优点和缺点？ 答：作.用于质点上的力在任意虚位移中做的功即为虚功，而虚位移是假想的、符合约束的、无限小的.即时位置变更，故虚功也是假想的、符合约束的、无限小的.且与过程无关的功，它与真实的功完全是两回事.从∑⋅=ii i r F W δδ可知：虚功与选用的坐标系无关，这正是虚功与过程无关的反映；虚功对各虚位移中的功是线性迭加，虚功对应于虚位移的一次变分.在虚功的计算中应注意：在任意虚过程中假定隔离保持不变，这是虚位移无限小性的结果. 虚功原理给出受约束质点系的平衡条件，比静力学给出的刚体平衡条件有更普遍的意义；再者，考虑到非惯性系中惯性力的虚功，利用虚功原理还可解决动力学问题，这是刚体力学的平衡条件无法比拟的；另外，利用虚功原理解理想约束下的质点系的平衡问题时，由于约束反力自动消去，可简便地球的平衡条件；最后又有广义坐标和广义力的引入得到广义虚位移原理，使之在非纯力学体系也能应用，增加了其普适性及使用过程中的灵活性.由于虚功方程中不含约束反力.故不能求出约束反力，这是虚功原理的缺点.但利用虚功原理并不是不能求出约束反力，一般如下两种方法：当刚体受到的主动力为已知时，解除某约束或某一方向的约束代之以约束反力；再者，利用拉格朗日方程未定乘数法，景观比较麻烦，但能同时求出平衡条件和约束反力.5.2 为什么在拉格朗日方程中，a θ不包含约束反作用力？又广义坐标与广义力的含义如何？我们根据什么关系由一个量的量纲定出另一个量的量纲?答 因拉格朗日方程是从虚功原理推出的，而徐公原理只适用于具有理想约束的力学体系虚功方程中不含约束反力，故拉格朗日方程也只适用于具有理想约束下的力学体系，αθ不含约束力；再者拉格朗日方程是从力学体系动能改变的观点讨论体系的运动，而约束反作用力不能改变体系的动能，故αθ不含约束反作用力，最后，几何约束下的力学体系其广义坐标数等于体系的自由度数，而几何约束限制力学体系的自由运动，使其自由度减小，这表明约束反作用力不对应有独立的广义坐标，故αθ不含约束反作用力.这里讨论的是完整系的拉格朗日方程，对受有几何约束的力学体系既非完整系，则必须借助拉格朗日未定乘数法对拉格朗日方程进行修正.广义坐标市确定质点或质点系完整的独立坐标，它不一定是长度，可以是角度或其他物理量，如面积、体积、电极化强度、磁化强度等.显然广义坐标不一定是长度的量纲.在完整约束下，广义坐标数等于力学体系的自由度数；广义力明威力实际上不一定有力的量纲可以是力也可以是力矩或其他物理量，如压强、场强等等，广义力还可以理解为；若让广义力对应的广义坐标作单位值的改变，且其余广义坐标不变，则广义力的数值等于外力的功由W q r F s i ni i δδθδααα==⋅∑∑==11 知，ααδθq 有功的量纲，据此关系已知其中一个量的量纲则可得到另一个量的量纲.若αq 是长度，则αθ一定是力，若αθ是力矩，则αq 一定是角度，若αq 是体积，则αθ一定是压强等.5.3广义动量a p 和广义速度a q 是不是只相差一个乘数m ？为什么a p 比a q 更富有意义？答 αp 与αq 不一定只相差一个常数m ，这要由问题的性质、坐标系的选取形式及广义坐标的选用而定。

分析⼒学思考题解答第五章思考题5.1虚功原理中的“虚功”⼆字作何解释？⽤虚功原理理解平衡问题，有何优点和缺点？答：作.⽤于质点上的⼒在任意虚位移中做的功即为虚功，⽽虚位移是假想的、符合约束的、⽆限⼩的.即时位置变更，故虚功也是假想的、符合约束的、⽆限⼩的.且与过程⽆关的功，它与真实的功完全是两回事.从∑?=ii i r F W δδ可知：虚功与选⽤的坐标系⽆关，这正是虚功与过程⽆关的反映；虚功对各虚位移中的功是线性迭加，虚功对应于虚位移的⼀次变分.在虚功的计算中应注意：在任意虚过程中假定隔离保持不变，这是虚位移⽆限⼩性的结果. 虚功原理给出受约束质点系的平衡条件，⽐静⼒学给出的刚体平衡条件有更普遍的意义；再者，考虑到⾮惯性系中惯性⼒的虚功，利⽤虚功原理还可解决动⼒学问题，这是刚体⼒学的平衡条件⽆法⽐拟的；另外，利⽤虚功原理解理想约束下的质点系的平衡问题时，由于约束反⼒⾃动消去，可简便地球的平衡条件；最后⼜有⼴义坐标和⼴义⼒的引⼊得到⼴义虚位移原理，使之在⾮纯⼒学体系也能应⽤，增加了其普适性及使⽤过程中的灵活性.由于虚功⽅程中不含约束反⼒.故不能求出约束反⼒，这是虚功原理的缺点.但利⽤虚功原理并不是不能求出约束反⼒，⼀般如下两种⽅法：当刚体受到的主动⼒为已知时，解除某约束或某⼀⽅向的约束代之以约束反⼒；再者，利⽤拉格朗⽇⽅程未定乘数法，景观⽐较⿇烦，但能同时求出平衡条件和约束反⼒.5.2 为什么在拉格朗⽇⽅程中，a θ不包含约束反作⽤⼒？⼜⼴义坐标与⼴义⼒的含义如何？我们根据什么关系由⼀个量的量纲定出另⼀个量的量纲?答因拉格朗⽇⽅程是从虚功原理推出的，⽽徐公原理只适⽤于具有理想约束的⼒学体系虚功⽅程中不含约束反⼒，故拉格朗⽇⽅程也只适⽤于具有理想约束下的⼒学体系，αθ不含约束⼒；再者拉格朗⽇⽅程是从⼒学体系动能改变的观点讨论体系的运动，⽽约束反作⽤⼒不能改变体系的动能，故αθ不含约束反作⽤⼒，最后，⼏何约束下的⼒学体系其⼴义坐标数等于体系的⾃由度数，⽽⼏何约束限制⼒学体系的⾃由运动，使其⾃由度减⼩，这表明约束反作⽤⼒不对应有独⽴的⼴义坐标，故αθ不含约束反作⽤⼒.这⾥讨论的是完整系的拉格朗⽇⽅程，对受有⼏何约束的⼒学体系既⾮完整系，则必须借助拉格朗⽇未定乘数法对拉格朗⽇⽅程进⾏修正.⼴义坐标市确定质点或质点系完整的独⽴坐标，它不⼀定是长度，可以是⾓度或其他物理量，如⾯积、体积、电极化强度、磁化强度等.显然⼴义坐标不⼀定是长度的量纲.在完整约束下，⼴义坐标数等于⼒学体系的⾃由度数；⼴义⼒明威⼒实际上不⼀定有⼒的量纲可以是⼒也可以是⼒矩或其他物理量，如压强、场强等等，⼴义⼒还可以理解为；若让⼴义⼒对应的⼴义坐标作单位值的改变，且其余⼴义坐标不变，则⼴义⼒的数值等于外⼒的功由W q r F s i ni i δδθδααα==?∑∑==11 知，ααδθq 有功的量纲，据此关系已知其中⼀个量的量纲则可得到另⼀个量的量纲.若αq 是长度，则αθ⼀定是⼒，若αθ是⼒矩，则αq ⼀定是⾓度，若αq 是体积，则αθ⼀定是压强等.5.3⼴义动量a p 和⼴义速度a q 是不是只相差⼀个乘数m ？为什么a p ⽐a q 更富有意义？答αp 与αq 不⼀定只相差⼀个常数m ，这要由问题的性质、坐标系的选取形式及⼴义坐标的选⽤⽽定。

分析⼒学试题与标答武汉理⼯⼤学考试试题纸（ A 卷）课程名称分析⼒学专业班级⼯⼒0901、02、1001、备注: 学⽣不得在试题纸上答题(含填空题、选择题等客观题)⼀、试推导质点系理想约束情况下的动⼒学普遍⽅程，并写出解析表达式。

(10分)⼆、已知均质杆A 1B 1和A 2B 2杆重为P 1和P 2，不计各处摩擦，试⽤虚位移原理求平衡时α、β⾓应满⾜的关系。

（20分）三、均质圆柱体半径R ，质量为M ，沿直线轨道做⽆滑动滚动，在圆⼼⽤铰链连接⼀长为l 的刚性杆OA ，不计杆的质量，杆的A 端有⼀质量为m 的⼩球，构成⼀单摆。

试⽤拉格朗⽇⽅程求系统的运动微分⽅程，并写出其初积分。

（30分）四、具有⽔平轨道的管⼦可绕铅直轴转动，质量为m 的⼩球⽆摩擦地沿管⼦滑动。

管⼦的转动惯量为J =mR 2，作⽤在⼩球上的⼒具有势函数V (r )。

试⽤哈密顿正则⽅程建⽴系统的运动微分⽅程。

（15分）五、质量为m 的物体放在光滑⽔平⾯上，刚性系数为k 的弹簧⽔平放置，⼀端与物块相连，另⼀端固结在竖直墙⾯上，试由哈密顿原理求物体的振动微分⽅程。

（10分）六、图⽰均质杆OA 长l =3m ，质量为m =2kg ；O 为铰链，A 端连⼀弹簧，刚度系数为k =4N/m 。

弹簧原长为l 0=1.2m ，h =3.6m 。

试⽤势⼒场质点系的平衡条件求平衡时的⾓度θ，并讨论平衡的稳定性。

（15分）21 xA武汉理⼯⼤学教务处试题标准答案及评分标准⽤纸课程分析⼒学（ A 卷）1、解：质系n 个质点，第i 个质点质量m i ，主动⼒合⼒F i ，约束反⼒F Ni ，惯性⼒F gi =-ma i由达朗伯原理 0=++gi Ni i F F F（3分）给质点系⼀虚位移，第i 质点的虚位移为i rδ，由虚位移原理 0)(=?++i gi Ni i r F F Fδ（3分）对上式求和0)(=?++∑i gi Ni i r F F Fδ理想约束情况下 0=?∑i Ni r Fδ（2分）于是有0)(=?+∑i gi i r F Fδ或0)(=?-∑i i i i r a m Fδ（1分）解析表达式为0)()()(=?-+?-+?-∑i i i i i i i i i i i iz z m Z y y m Y x x m Xδδδ（1分）2、解：以系统为研究对象，单⾃由度，以α为⼴义坐标。