指派问题例题
- 格式:ppt
- 大小:193.50 KB
- 文档页数:6
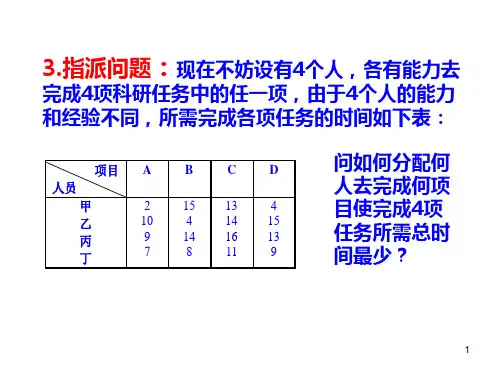
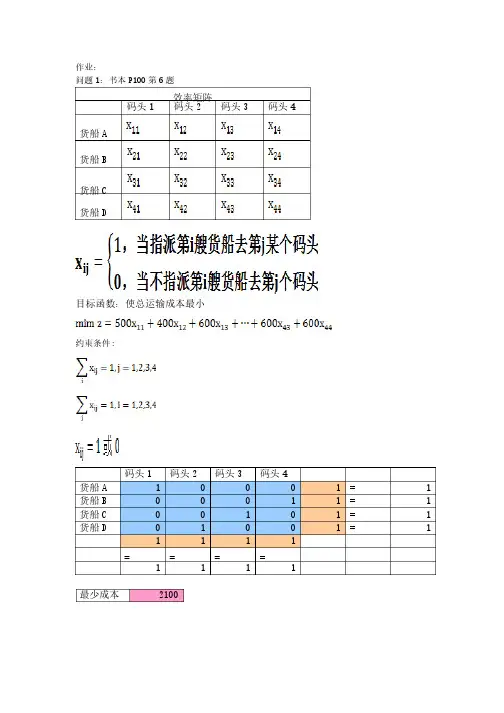
作业:作业:问题1:书本P100第6题效率矩阵效率矩阵码头1 码头2 码头3 码头4货船A货船B货船C货船D目标函数:使总运输成本最小目标函数:使总运输成本最小约束条件约束条件: :码头1 码头2 码头3 码头4货船A 1 0 0 0 1 = 1 货船B 0 0 0 1 1 = 1 货船C 0 0 1 0 1 = 1 货船D 0 1 0 0 1= 11 1 1 1 ====1 1 1 1最少成本最少成本2100问题问题 2: 2: 2: 书本书本书本P101P101P101第第7题效率矩阵效率矩阵A B C D E甲乙丙丁目标函数:使总花费时间最小目标函数:使总花费时间最小约束条件约束条件: :方案矩阵方案矩阵AB C D E甲 2.22E-16 1 0 0 0 1 <= 1 <= 2 乙 0 0 1 1 2.22E-16 1 <=2 <= 2 丙 0 1.11E-16 0 0 1 1 <=1 <=2 丁 1 0 0 4.44E-16 0 1 <=1 <=2 1 11 1 1= == ==11 1 1 1时间最少时间最少131问题3:五人翻译五种外文的速度(印刷符号:五人翻译五种外文的速度(印刷符号//小时)如下表所示:小时)如下表所示: 语种语种语种 人 英 俄俄 日日 德德 法法 甲甲乙 丙 丁 戊900 400 600 800 500 800 500 900 1000 600 900 700 300 500 800400 800 600 900 5001000 500 300 600 800若规定每人专门负责一个语种的翻译工作,那么,试解答下列问题:若规定每人专门负责一个语种的翻译工作,那么,试解答下列问题: (1)应如何指派,使总的翻译效率最高?应如何指派,使总的翻译效率最高?效率矩阵效率矩阵英俄 日 德 法 甲 乙 丙 丁目标函数:使翻译效率最高目标函数:使翻译效率最高约束条件约束条件: :方案矩阵方案矩阵英俄 日 德 法甲0 011 =1乙0 1 0 0 0 1 = 1 丙0 0 0 1 0 1 = 1丁 1 0 0 0 0 1 = 1 戊0 0 1 0 0 1 = 11 1 1 1 1= = = = =1 1 1 1 1效率最高 2200效率最高若甲不懂德文,乙不懂日文,其他数字不变,则应如何指派?(2)若甲不懂德文,乙不懂日文,其他数字不变,则应如何指派?方案矩阵方案矩阵英俄日德法甲0 1 0 0 0 1 = 1 乙0 0 0 0 1 1 = 1 丙0 0 0 1 0 1 = 1 丁 1 0 0 0 0 1 = 1 戊0 0 1 0 0 1 = 11 1 1 1 1= = = = =1 1 1 1 1。




4、运输问题和指派问题案例1:P&T公司的配送问题家族经营的小公司,加工蔬菜罐头并分销到各地:–三个食品厂,四个分销仓库面临的问题:运输成本不断攀升目前的运输策略:–首先考虑最偏远的厂,先将其产品充分满足距它最近的仓库,再运至次之的仓库;–再考虑最偏远的仓库,优先从距其最近的工厂进货;–距离居中的工厂用于补充不足的部分。
问题:如何改进运输策略以降低成本?CANNERY 1BellinghamCANNERY 2EugeneWAREHOUSE 1 Sacramento WAREHOUSE 2Salt Lake CityWAREHOUSE 3Rapid CityWAREHOUSE 4AlbuquerqueCANNERY 3Albert Lea最偏远的厂最偏远的仓库300合计100Albert Lea 125Eugene 75Bellingham 产量(车)工厂Albert Lea5Eugene 75Bellingham 工厂SacramentoFrom\To运费995Albert Lea352Eugene $464Bellingham 工厂Sacramento From\To 总运费:Total shipping cost = 75($464) + 5($352) + 65($416) + 55($690)运输问题的基本术语P&T 公司问题罐头罐头厂仓库罐头厂的产量各仓库的需求量每车运费Ì运输问题是物流中的一个重要问题,即如何以尽可能小的成本把货物从一系列出发地(如工厂、仓库)运输到一系列目的地(如仓库、顾客)。
需求假设:–每个出发地都有一个固定的供应量,且所有供应量均须配送到目的地;–每个目的地都有一个固定的需求量,且所有需求量均须被满足可行解特征:–运输问题有可行解,当且仅当供应量总和等于需求量总和(供求平衡) 成本假设:–从任一出发地到任一目的地的配送成本与所配送的货物量成正比,即配送成本等于单位配送成本乘以配送量供应量、需求量和单位成本提供了运输问题所需的一切数据整数解:–运输问题通常以运送的车数作为计量单位,因此其解一般为整数整数解性质:只要运输问题的供应量和需求量都是整数,任何有可行解的运输问题必然有使所有决策变量都是整数的最优解。

指派问题
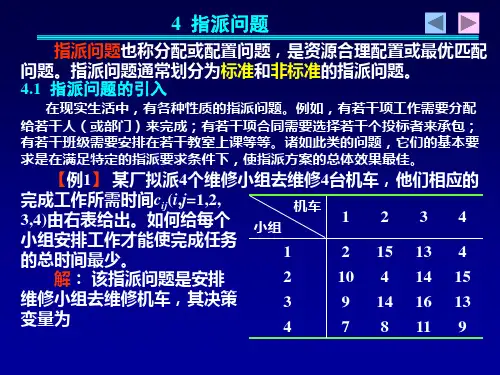
例3、某工厂有4个工人甲、乙、丙、丁,他们都可以从事4种不同的工作A,B,C,D,但每个人在不同的岗位创造的产出是不同的,见下表。
现给每个工人分配一个岗位,求如何安排才能使产出最
大?
解:
这是一个求最大值的问题,因此首先对系数矩阵
进行变换,表中的系数矩阵最大值是10,因此
bij=M-cij=10-cij,然后就可以按照匈牙利法德步
骤进行求解,具体过程如下:
注意:设分配问题中人数为m,任务数为n,当m>n时虚拟m-n项任务,对应的效率为零;当m<n 时,虚拟n-m个人,对应的效率为零,转化为人数与任务数相等的平衡问题后再求解。
如有5个人分配做3项工作,效率矩阵变化如下,。
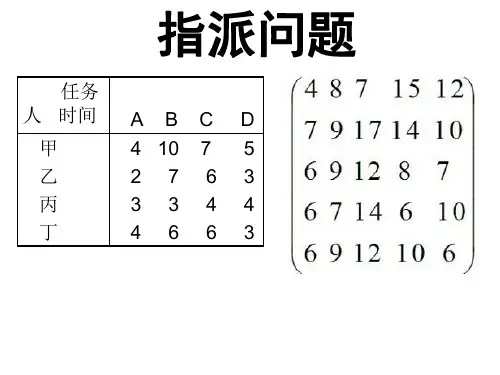

练习一:有四个工人,要分别指派他们完成四项不同的工作,每人做各项工作所消耗的时间如下表所示,问应如何指派工作,才能使总的消耗时间为最少。
最优解如下********************************************起至销点发点 1 2 3 4-------- ----- ----- ----- -----1 0 1 0 02 1 0 0 03 0 0 1 04 0 0 0 1此运输问题的成本或收益为: 70此问题的另外的解如下:起至销点发点 1 2 3 4-------- ----- ----- ----- -----1 1 0 0 02 0 0 0 13 0 0 1 04 0 1 0 0 此运输问题的成本或收益为: 70练习二:现有4份工作,6个人应聘,由于个人的技术专长不同,他们承担各项工作所需时间如下表所示,且规定每人只能做一项工作,每一项工作只能由一个人承担,试求使总时间最少的分派方案。
解析最优解如下********************************************起至销点发点 1 2 3 4 5 6 -------- ----- ----- ----- ----- ----- -----1 0 0 0 0 1 02 0 0 0 0 0 13 0 0 0 1 0 04 1 0 0 0 0 05 0 0 1 0 0 06 0 1 0 0 0 0 此运输问题的成本或收益为: 20练习三:某商业公司计划开办五家新商店。
为了尽早建成营业,商业公司决定由3家建筑公司分别承建。
已知第A i(i=1,2,3)个建筑公司对第B j(j=1,2,3,4,5)家新商店的建造费用的报价如下表,为保证工程进度,每家建筑公司最多只能承建两个商店,且由于某种原因,第B3家商店不能由第A1个建筑公司承办,求使总费用最少的指派方案解析:最优解如下********************************************起至销点发点 1 2 3 4 5-------- ----- ----- ----- ----- -----1 1 0 0 0 02 0 0 0 0 13 0 0 1 0 04 0 1 0 0 05 0 0 0 0 06 0 0 0 1 0此运输问题的成本或收益为: 42注释:总供应量多出总需求量 1第5个产地剩余 1此问题的另外的解如下:起至销点发点 1 2 3 4 5 -------- ----- ----- ----- ----- -----1 1 0 0 0 02 0 0 0 0 13 0 0 0 1 04 0 1 0 0 05 0 0 0 0 06 0 0 1 0 0 此运输问题的成本或收益为: 42注释:总供应量多出总需求量 1第5个产地剩余 1练习四:某人事部门拟招聘4人任职4项工作,对他们综合考评的 得分如下表(满分100分),如何安排工作使总分最多85927390958778958283799086908088C ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦甲乙=丙丁 解析: 最优解如下********************************************起 至 销点发点 1 2 3 4 -------- ----- ----- ----- ----- 1 0 1 0 0 2 1 0 0 0 3 0 0 0 1 4 0 0 1 0 此运输问题的成本或收益为: 357。
