齿轮结构设计和校核

齿轮强度校核的新方法(图文)论文导读：使用有限元分析软件ANSYS对齿轮进行强度分析，可对齿轮的强度设计提供可靠的根据，实现变速器齿轮的计算机辅助设计，能够加快设计进程、缩短研制周期、提高设计质量。

本文应用了APDL，即ANSYS参数化设计语言（ANSYSParametricDesignLanguage），设计直齿圆柱齿轮模块与应用ANSYS有限元软件进行有限元分析方面，做一些初步的探索。

关键词：ANSYS，直齿圆柱齿轮，接触应力，齿根弯曲应力0引言齿轮作为在机械结构中经常用到的重要的传动零件，其强度直接影响到整个机械结构的工作性能与寿命，然而在传统齿轮设计中，齿轮的强度校核过程与设计过程要紧是通过人工设计完成，计算繁琐，设计周期长且难以实现优化设计。

本文使用有限元分析法对渐开线标准圆柱直齿轮进行接触应力与齿根弯曲应力进行分析计算。

同时在有限元分析中,对AYSYS[1]软件进行二次开发，即应用了APDL[2]语言，自动实现了齿轮的参数精确建模，自习惯网格划分与有限元强度分析。

最后与传统经典方法进行了对比分析,证明了本方法的准确性。

具有实际操作性与推广价值。

论文发表。

1.齿轮强度分析的基本要求在机械专业中，减速机是要紧的重要的传动机构，而齿轮传动是其中最常见的实现方式。

论文发表。

因此齿轮零件的设计就显得尤为重要。

其中齿轮应力强度校核是齿轮结构设计的前提，只有相互啮合的齿轮通过了接触与弯曲强度校核计算，才能进行齿轮结构设计。

当然相互啮合的齿轮种类十分繁杂。

这里我们为方便起见，只考虑渐开线标准圆柱直齿轮的问题。

传统的应力强度校核计算十分烦琐，需要查阅机械设计手册中大量的数据（包含图形与图表）。

而传动机构中往往是多对齿轮啮合，其中有一对不符合要求，整个计算就得重来，耗费了设计者大量的精力。

因此借助计算机及相应软件完成对齿轮的优化设计十分必要。

使用有限元分析软件ANSYS对齿轮进行强度分析，可对齿轮的强度设计提供可靠的根据，实现变速器齿轮的计算机辅助设计，能够加快设计进程、缩短研制周期、提高设计质量。

齿轮设计校核齿轮作为机械传动的基础部件之一，在工业生产领域中应用广泛。

然而，由于工作条件的不同，齿轮的类型、尺寸及负载等参数不尽相同，因此在齿轮的设计时需要进行严格的校核才能确保其在实际使用中的安全可靠性。

一、齿轮参数设计1、齿轮类型根据使用的具体条件和要求，可以选择不同的齿轮类型，如圆柱齿轮、锥齿轮、螺旋齿轮、斜齿轮等。

不同类型的齿轮具有不同的传动效率、负载能力、精度要求等特点，应根据实际需要进行选择。

2、齿轮尺寸齿轮的尺寸包括齿数、模数、齿轮宽度等参数。

这些参数的选取应考虑到齿轮的负载、转速等因素，以便使齿轮的数据计算精确，并满足使用要求。

3、齿轮材料齿轮的材料需要具有良好的强度、硬度、韧性、耐磨性等特性，以满足工作条件下的负载和磨损要求。

通常选择的材料有合金钢、低碳钢、不锈钢、铜合金等。

模数是齿轮设计的关键参数之一，它与齿轮的齿数、圆径有关。

在设计时，需要根据负载情况、转速、尺寸等因素计算出具体的模数值。

齿数计算是齿轮设计中重要的部分，它直接影响到齿轮的传动比、噪声、载荷分布等性能。

在计算中，应考虑到齿轮传动的要求，并保证齿轮的强度和使用寿命。

3、齿轮载荷计算齿轮设计中的负载计算是根据齿轮所受的载荷和转矩计算得出的。

在设计中，应考虑到齿轮所受的载荷和转矩的不同作用方式，以及齿轮在使用过程中所承受到的动、静载荷等因素。

齿轮精度计算是指齿轮的基本圆直径、齿距误差等参数的计算。

在设计中，应考虑到齿轮传动的要求，以及齿轮间的配合情况，选取合适的精度要求。

齿轮设计校核是指针对齿轮设计过程中的各项计算进行检验和验证。

在校核中需要考虑到齿轮所承受的负载、强度、精度、磨损等因素，确保齿轮的设计参数满足使用要求。

1、强度校核强度校核是指对齿轮材料的强度、载荷、应力等因素进行检验和验证，以确保齿轮的强度能够满足工作要求和使用寿命。

精度校核是指对齿轮的齿距误差、跳动等参数进行检验和验证，以确保齿轮的精度符合设计要求，并满足传动的精度要求。

齿轮校核:软齿面齿轮按接触疲劳强度设计，按弯曲疲劳强度校核；硬齿面齿轮按弯曲疲劳强度设计，按接触疲劳强度校核。

齿轮:齿轮是指轮缘上有齿轮连续啮合传递运动和动力的机械元件。

齿轮在传动中的应用很早就出现了。

19世纪末，展成切齿法的原理及利用此原理切齿的专用机床与刀具的相继出现，随着生产的发展，齿轮运转的平稳性受到重视。

发展起源:历史在西方，公元前300年古希腊哲学家亚里士多德在《机械问题》中，就阐述了用青铜或铸铁齿轮传递旋转运动的问题。

希腊著名学者亚里士多德和阿基米德都研究过齿轮，希腊有名的发明家古蒂西比奥斯在圆板工作台边缘上均匀地插上销子，使它与销轮啮合，他把这种机构应用到刻漏上。

这约是公元前150年的事。

在公元前100年，亚历山人的发明家赫伦发明了里程计，在里程计中使用了齿轮。

公元1世纪时，罗马的建筑家毕多毕斯制作的水车式制粉机上也使用了齿轮传动装置。

到14世纪，开始在钟表上使用齿轮。

东汉初年（公元1世纪）已有人字齿轮。

三国时期出现的指南车和记里鼓车已采用齿轮传动系统。

晋代杜预发明的水转连磨就是通过齿轮将水轮的动力传递给石磨的。

史书中关于齿轮传动系统的最早记载，是对唐代一行、梁令瓒于725年制造的水运浑仪的描述。

北宋时制造的水运仪象台（见中国古代计时器）运用了复杂的齿轮系统。

明代茅元仪著《武备志》（成书于1621年）记载了一种齿轮齿条传动装置。

1956年发掘的河北安午汲古城遗址中，发现了铁制棘齿轮，轮直径约80毫米，虽已残缺，但铁质较好，经研究，确认为是战国末期（公元前3世纪）到西汉(公元前206～公元24年)期间的制品。

1954年在山西省永济县蘖家崖出土了青铜棘齿轮。

参考同坑出土器物，可断定为秦代(公元前221～前206)或西汉初年遗物，轮40齿，直径约25毫米。

关于棘齿轮的用途，迄今未发现文字记载，推测可能用于制动，以防止轮轴倒转。

1953年陕西省长安县红庆村出土了一对青铜人字齿轮。

根据墓结构和墓葬物品情况分析，可认定这对齿轮出于东汉初年。

2齿轮的设计及校核齿轮是一种常见的动力传递装置，广泛应用于机械传动中。

齿轮的设计和校核是确保齿轮传动系统正常工作的重要环节。

本文将从齿轮的设计和校核两个方面进行分析，详细介绍其原理和方法。

齿轮的设计是根据传动的要求和工作条件，确定齿轮的尺寸、型号、齿数等参数的过程。

首先需要确定传动的速比、转矩要求等。

然后根据这些参数，计算出齿轮的模数、齿轮的宽度、齿轮的材料等。

根据实际情况，可以选择使用标准齿轮或定制齿轮。

齿轮的校核是验证设计参数的合理性和齿轮传动系统的可靠性的过程。

主要包括以下几个方面：1.齿轮强度校核。

根据所选用的齿轮材料，计算其强度参数，并与设计需求进行比较。

常用的齿轮强度计算方法有弗赖德、路中曼等。

2.齿面接触强度校核。

通过计算齿轮齿面接触应力和接触应力分布，判断齿面接触是否能满足传动要求。

根据计算结果，可以调整齿轮的齿形和齿数等参数。

3.齿轮轴承能力校核。

根据齿轮传动的工作转矩，计算齿轮轴承的最大受力，并与轴承的额定负载进行比较。

如果超过了轴承的额定负载，需要重新选择适合的轴承。

4.齿轮的热强度校核。

计算齿轮的热强度参数，判断齿轮在长时间高速工作时的热强度能否满足要求。

如果不能满足，可能需要进行降速设计或采取散热措施。

5.齿轮的动态特性校核。

根据齿轮的质量、转动惯量等参数，计算齿轮系统的固有频率和谐振现象，并进行分析和校核。

如果存在谐振问题，需要采取减振措施。

在齿轮的设计和校核过程中，需要使用一些专业软件和标准规范进行计算和判断。

一般常用的计算软件有Ansys、AutoCAD等，相关的标准规范有GB/T 3456.2-2024等。

总之，齿轮的设计和校核是确保齿轮传动系统正常运行的关键步骤。

只有在设计和校核过程中充分考虑到齿轮的强度、接触、轴承、热强度和动态特性等方面的要求，才能保证齿轮传动系统的可靠性和稳定性。

齿轮强度校核的基本原则齿轮强度校核的基本原则主要包括以下几点：1.遵循国家标准和行业规范：在开展齿轮强度校核工作时，应严格遵循我国相关的国家标准和行业规范，确保校核结果的准确性和可靠性。

目前，我国有关齿轮设计及强度校核的主要标准有GB/T3478.1-1995《齿轮设计手册》和GB/T10095.1-2001《圆柱齿轮精度等级》等。

2.采用合理的计算方法：在进行齿轮强度校核时，应采用合理的计算方法，如有限元分析法、传统设计方法等。

其中，有限元分析法具有较高的计算精度，可有效模拟齿轮在工作过程中的受力情况，为强度校核提供可靠依据。

而传统设计方法则主要依据经验公式和图表进行计算，虽然过程较为简便，但精度相对较低。

3.考虑齿轮组合的强度平衡：在齿轮强度校核过程中，应充分考虑齿轮组合的强度平衡，确保各齿轮的强度足够且匹配合理。

此外，还需注意齿轮材料的选用，使其具有较高的强度和耐磨性。

4.遵循简化原则：为了便于计算和分析，可以在强度校核过程中对齿轮结构进行简化。

例如，将直齿锥齿轮传动中的齿数比、锥距等参数进行合理简化，以便于进行强度计算。

5.考虑齿轮传动的稳定性：在强度校核过程中，还需考虑齿轮传动的稳定性，避免因传动比过大或过小导致的齿轮失效。

此外，还需注意齿轮传动机构的润滑和防尘设计，以降低齿轮磨损和故障风险。

6.结合实际工况进行校核：齿轮强度校核应结合实际工况进行，充分考虑齿轮在工作过程中承受的载荷、转速、振动等因素。

此外，还需注意齿轮在安装和维护过程中的强度损失，确保校核结果的可靠性。

7.留有一定的安全系数：为了保证齿轮在使用过程中的安全性能，在校核强度时，应适当留有一定的安全系数。

安全系数的选取应根据实际工况和设计要求进行，一般取2~3较为合适。

综上所述，齿轮强度校核的基本原则包括遵循国家标准和行业规范、采用合理的计算方法、考虑齿轮组合的强度平衡、遵循简化原则、考虑齿轮传动的稳定性、结合实际工况进行校核以及留有一定的安全系数。

© R =1/3直齿锥齿轮传动是以大端参数为标准值的。

在强度计算时，则以齿宽中 点处的当量齿轮作为计算的依据。

对轴交角 刀=90。

的直齿锥齿轮传动，其齿数 比u 、锥距&图＜直齿锥齿轮传动的几何参数 ＞）、分度圆直d i , d 2、平均分度圆直 径d mi, d m2当量齿轮的分度圆直径d vi , d v2之间的关系分别为：連 1 d] u = — = = cot O| =tanfi 2 = = = — — — — —V 22 2 2九i gR-O.Sb h d x d 2 R R 令© R =b/R,称为锥齿轮传动的齿宽系数，通常取 © R =0.25-0.35,最常用的值为 ⑷由右图可 找出当量 直齿圆柱 齿轮得分 度圆半径r v 与平均 分度圆直 径d m 的关 系式为d mJ =十 -------------------------------------- ⑷ZCOSD现以g 表示当量直齿圆柱齿轮的模数，亦即锥齿轮平均分度圆上轮齿 的模数（简称平均模数），则当量齿数 Z v 为直齿锥齿轮传动的几何参数显然，为使锥齿轮不至发生根切，应使当量齿数不小于直齿圆柱齿轮的根切齿数。

另外，由式(d)极易得出平均模数mm和大端模数m的关系为111^=111(1-0.5^)--------------------------------------------------------- (h)、直齿圆锥齿轮的背锥及当量齿数为了便于设计和加工，需要用平面曲线来近似球面曲线，如下图OAB为分度圆锥，J和：为轮齿在球面上的齿顶高和齿根高，过点A作直线AO丄AQ与圆锥齿轮轴线交于点O,设想以OO为轴线, OA为母线作一圆锥QAB,称为直齿圆锥齿轮的背锥。

由图可见A B附近背锥面与球面非常接近。

因此，可以用背锥上的齿形近似地代替直齿圆锥齿轮大端球面上的齿形。

从而实现了平面近似球面。

齿轮齿条的设计计算与校核1. 引言齿轮齿条是一种常见的传动装置，广泛应用于机械设备中。

它们通过齿轮和齿条之间的啮合来传递运动和力量。

在设计齿轮齿条传动系统时，需要进行一系列的计算与校核，以确保其可靠性和性能满足要求。

本文将介绍齿轮齿条传动系统的设计计算与校核方法，包括齿轮参数的选择、传动比的计算、齿轮强度的校核等。

2. 齿轮参数的选择在设计齿轮齿条传动系统时，首先需要选择合适的齿轮参数。

齿轮参数包括模数、齿数、压力角等。

2.1 模数的选择模数是指齿轮齿条的齿数与圆直径之比。

模数的选择应根据齿轮传动的要求和可用的标准模数进行匹配。

一般情况下，应选择尽可能大的模数，以提高齿轮的强度和寿命。

2.2 齿数的选择齿数的选择主要考虑齿轮传动的传动比和齿轮的工作条件。

传动比是指齿轮输入轴的转速与输出轴的转速之比。

2.3 压力角的选择压力角是指齿轮齿条啮合面上法线与齿轮轴线之间的夹角。

压力角的选择应根据齿轮传动的要求和可用的标准压力角进行匹配。

一般情况下，应选择尽可能小的压力角，以减小齿轮齿条的侧向力和噪声。

3. 传动比的计算传动比是齿轮齿条传动系统中重要的性能指标之一，它影响着输出轴的转速和扭矩。

传动比的计算可以根据齿轮齿数的比值来确定。

4. 齿轮强度的校核齿轮强度是齿轮齿条传动系统设计中关键的校核指标之一，它决定了齿轮的承载能力和寿命。

齿轮强度的校核可以通过齿轮的材料强度和几何参数来确定。

4.1 齿轮模数的校核齿轮模数的校核可以通过计算齿轮的接触应力和弯曲应力来进行。

应保证齿轮的接触应力和弯曲应力不超过齿轮材料的强度极限。

4.2 齿轮齿数的校核齿轮齿数的校核可以通过计算齿轮的接触比和模数来进行。

应保证齿轮的接触比和模数满足设计要求。

4.3 齿轮强度的校核齿轮强度的校核可以通过计算齿轮的接触疲劳寿命来进行。

应保证齿轮的接触疲劳寿命不低于设计要求。

5. 结论齿轮齿条的设计计算与校核是确保齿轮齿条传动系统可靠性和性能的重要环节。

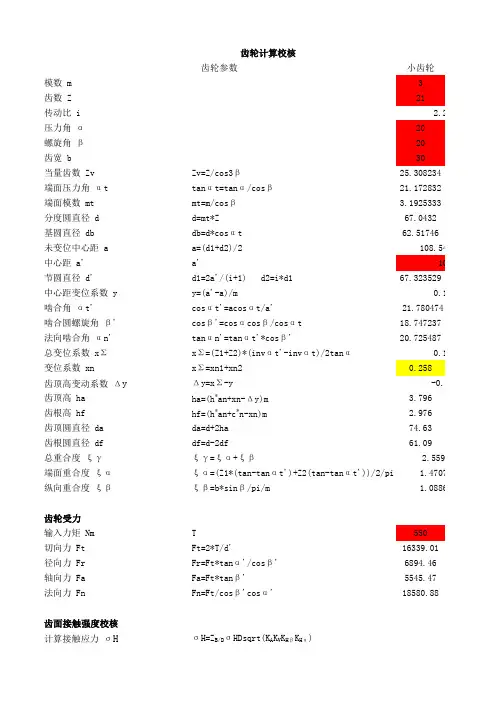
小齿轮模数 m3齿数 Z21传动比 i压力角 α20螺旋角 β20齿宽 b30当量齿数 ZvZv=Z/cos3β25.308234端面压力角 αttan αt=tan α/cos β21.172832端面模数 mtmt=m/cos β 3.1925333分度圆直径 dd=mt*Z 67.0432基圆直径 dbdb=d*cos αt 62.51746未变位中心距 aa=(d1+d2)/2中心距 a'a'节圆直径 d'd1=2a'/(i+1) d2=i*d167.323529中心距变位系数 yy=(a'-a)/m 啮合角 αt'cos αt'=acos αt/a'21.780474啮合圆螺旋角 β'cos β'=cos αcos β/cos αt 18.747237法向啮合角 αn'tan αn'=tan αt'*cos β'20.725487总变位系数 x Σx Σ=(Z1+Z2)*(inv αt'-inv αt)/2tan α变位系数 xnx Σ=xn1+xn20.258齿顶高变动系数 ΔyΔy=x Σ-y 齿顶高 haha=(h *an+xn-Δy)m 3.796齿根高 hfhf=(h *an+c *n-xn)m 2.976齿顶圆直径 dada=d+2ha 74.63齿根圆直径 dfdf=d-2df 61.09总重合度 ξγξγ=ξα+ξβ端面重合度 ξαξα=(Z1*(tan-tan αt')+Z2(tan-tan αt'))/2/pi 纵向重合度 ξβξβ=b*sin β/pi/m 齿轮受力输入力矩 NmT 550切向力 FtFt=2*T/d'16339.01径向力 FrFr=Ft*tan α'/cos β'6894.46轴向力 FaFa=Ft*tan β'5545.47法向力 FnFn=Ft/cos β'cos α'18580.88齿面接触强度校核计算接触应力 σHσH=Z B/D σHDsqrt(K A K V K H βK H α)许用接触应力 σHP σHP=σHG/S Hmin齿轮计算校核齿轮参数 2.2381.4707051.0886832.559389-0.007108.54611090.1510.144啮合系数 Z B Z D使用系数 K A 1.25动载系数 K V接触强度计算的齿向载荷分布系数 K Hβ接触强度计算的齿间载荷分布系数 K Hα计算接触应力基本值 σHDσHD=Z H Z E ZαZβsqrt(Ft(i+1)/(d1*b*i))节点区域系数 Z H弹性系数 Z E重合度系数 Zα螺旋角系数 Zβ计算齿轮接触极限应力 σHGσHG=σHlim Z NT Z L Z V Z R Z W Z X实验齿轮接触疲劳极限 σHlim接触强度计算寿命系数 Z NT润滑剂系数 Z L速度系数 Z V粗糙度系数 Z R工作硬化系数 Z W接触强度计算尺寸系数 Z X接触强度最小安全系数 S Hmin 1.25齿根弯曲强度校核计算齿根应力 σFσF=σFDK A K V K FβK Fα许用齿根应力 σFPσFP=σFG/S Fmin齿根应力基本值 σFDσFD=FtY F Y S Yβ/bm弯曲强度计算的齿向载荷分布系数 K Fβ弯曲强度计算的齿间载荷分布系数 K Fα齿形系数 Y F应力修正系数 Y S螺旋角系数 Yβ计算齿轮弯曲极限应力 σFGσFG=σFlimY ST Y NT Yδrel T Y Rrel Y X实验齿轮弯曲疲劳极限 σFlim试验齿轮应力修正系数 Y ST弯曲强度计算寿命系数 Y NT齿根圆角敏感系数 YδrelT齿根表面状况系数 Y Rrel弯曲强度计算尺寸系数 Z X弯曲强度最小安全系数 S Fmin角度转弧度RADIAN弧度转角度DEGR 大齿轮平方POWER3472.23820203056.64223921.1728323.1925333150.04907139.92003.5461328109150.676470.15121.78047418.74723720.7254870.144-0.1140.0072.6804.092155.41141.87593893970705461886839291230.9516339.016894.465545.4718580.88。