信号处理基础 何子述版 第三章仿真题

3.7 用一个时间常数未0.35S 的一阶装置去测量周期分别为1S 、2S 、5S 的正弦信号，问A （ω）误差为多少？解：τ1 =1S, τ2 =2S, τ3 =5Sω1 =2π/1=2 , ω2 =2π/2= , ω3 =2π/5由式（3.16） A(ω)=1)(12+τω 得幅值比：A 1(ω)=1)1/235.0(12+⨯π =0.413A 2(ω)=1)2/235.0(12+⨯π =0.673A 3(ω)= 1)5/235.0(12+⨯π =0.915误差1 = [1-A 1(ω)]×100%=(1-0.41) ×100% = 58.6%误差2 = [1- A 2(ω)]×100%=（1-0.67）×100% = 32.7%误差3 = [1- A 3(ω)]×100%=(1-0.92) ×100% = 8.5%3.8 求周期信号x(t)=0.5cos10t +0.2cos(100t-45°)通过传递函数为 H(s) = 1005.01+S 的装置后所得到的稳态响应。

解：把原信号分成两个信号：x 1( t ) = 0.5 cos10t , x 2 ( t ) = 0.2cos(100t-45°)ω1= 10S -1, ω2=100S -1由一阶系统的幅频特性 A(ω)=1)(12+τω , 知第一个信号的幅值比 A 1(ω)=1)10005.0(12+⨯ = 0.99875输出幅值A 0=A 1(ω) ×0.5 = 0.99875×0.5 = 0.499第二个信号的幅值比：A 2(ω) =1)100005.0(12+⨯ =0.89443φ1(ω)= -arc tan τω1= -arc tan(10×0.005)= - 2.86° .φ2(ω)= -arc tan τω2= -arc tan(100×0.005)= 26.57°所以，周期信号的稳态响应为：x (t) = 0.499cos(10 t - 2.86°)+0.179cos(100 t - 71.57°)3.9 想用一个一阶系统作100Hz 正弦信号的测量，如要求限制振幅误差在5%以内。

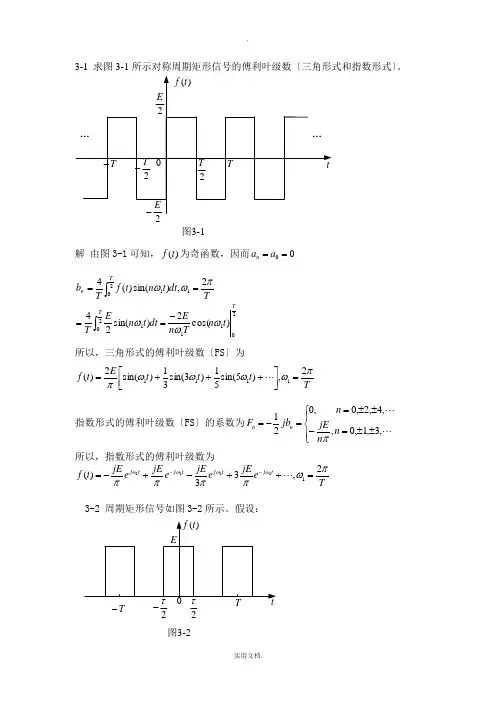
3-1 求图3-1所示对称周期矩形信号的傅利叶级数〔三角形式和指数形式〕。

图3-1解 由图3-1可知，)(t f 为奇函数，因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以，三角形式的傅利叶级数〔FS 〕为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数〔FS 〕的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以，指数形式的傅利叶级数为T e jE e jE e jE e jE t f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。

假设：图3-22τT-2τ-重复频率kHz f 5= 脉宽 s μτ20=幅度 V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。

解 对于图3-2所示的周期矩形信号，其指数形式的傅利叶级数〔FS 〕的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n那么的指数形式的傅利叶级数〔FS 〕为∑∑∞-∞=∞-∞=⎪⎭⎫⎝⎛==n tjn n tjn ne n Sa TE eF t f 112)(1ωωτωτ 其直流分量为T E n Sa T E F n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω 将各参数的值代入，可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 假设周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示，)(1t f 的参数为s μτ5.0=，s T μ1= ，V E 1=； )(2t f 的参数为s μτ5.1=，s T μ3= ，V E 3=，分别求：〔1〕)(1t f 的谱线间隔和带宽〔第一零点位置〕，频率单位以kHz 表示； 〔2〕)(2t f 的谱线间隔和带宽； 〔3〕)(1t f 与)(2t f 的基波幅度之比； 〔4〕)(1t f 基波与)(2t f 三次谐波幅度之比。

数字信号处理习题解答 第二章 数据采集技术基础2.1 有一个理想采样系统，其采样角频率Ωs =6π，采样后经理想低通滤波器H a (j Ω)还原，其中⎪⎩⎪⎨⎧≥Ω<Ω=Ωππ30321)(，，j H a 现有两个输入，x 1(t )=cos2πt ，x 2(t )=cos5πt 。

试问输出信号y 1(t )，y 2(t )有无失真？为什么？分析：要想时域采样后能不失真地还原出原信号，则采样角频率Ωs 必须大于等于信号谱最高角频率Ωh 的2倍，即满足Ωs ≥2Ωh 。

解：已知采样角频率Ωs =6π，则由香农采样定理，可得 因为x 1(t )=cos2πt ，而频谱中最高角频率πππ32621=<=Ωh ，所以y 1(t )无失真；因为x 2(t )=cos5πt ，而频谱中最高角频率πππ32652=>=Ωh ，所以y 2(t )失真。

2.2 设模拟信号x (t )=3cos2000πt +5sin6000πt +10cos12000πt ，求：（1） 该信号的最小采样频率；（2） 若采样频率f s =5000Hz ，其采样后的输出信号； 分析：利用信号的采样定理及采样公式来求解。

○1采样定理 采样后信号不失真的条件为：信号的采样频率f s 不小于其最高频率f m 的两倍，即f s ≥2f m○2采样公式 )()()(s nT t nT x t x n x s===解：（1）在模拟信号中含有的频率成分是f 1=1000Hz ，f 2=3000Hz ，f 3=6000Hz∴信号的最高频率f m =6000Hz由采样定理f s ≥2f m ，得信号的最小采样频率f s =2f m =12kHz （2）由于采样频率f s =5kHz ，则采样后的输出信号⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛====n n n n n n n n n n n f n x nT x t x n x s s nTt s522sin 5512cos 13512cos 10522sin 5512cos 35112cos 105212sin 5512cos 3562cos 10532sin 5512cos 3)()()(πππππππππππ 说明：由上式可见，采样后的信号中只出现1kHz 和2kHz 的频率成分，即kHzf f f kHzf f f ss 25000200052150001000512211======，，若由理想内插函数将此采样信号恢复成模拟信号，则恢复后的模拟信号()()t t t f t f t y ππππ4000sin 52000cos 132sin 52cos 13)(21-=-=可见，恢复后的模拟信号y (t ) 不同于原模拟信号x (t )，存在失真，这是由于采样频率不满足采样定理的要求，而产生混叠的结果。

第三章习题基础题3.1 证明cos t , cos(2)t , …,cos()nt (n 为正整数)，在区间(0,2)π的正交集。

它是否是完备集?解：(积分???)此含数集在(0,2)π为正交集。

又有sin()nt 不属于此含数集02sin()cos()0nt mt dt π=⎰，对于所有的m和n 。

由完备正交函数定义所以此函数集不完备。

3.2 上题的含数集在(0,)π是否为正交集？解：由此可知此含数集在区间(0,)π是正交的。

3.3实周期信号()f t 在区间(,)22T T -的能量定义为222()TT E f t dt -=⎰。

如有和信号12()()f t f t +(1)若1()f t 与2()f t 在区间(,)22T T-相互正交，证明和信号的总能量等于各信号的能量之和;(2)若1()f t 与2()f t 不是相互正交的，求和信号的总能量。

解：(1)和信号f(t)的能量为[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰（少乘以2）由1()f t 与2()f t 在区间正交可得2122()()0T T f t f t dt -=⎰则有 22221222()()T T T T E f t dt f t dt --=+⎰⎰即此时和信号的总能量等于各信号的能量之和。

和信号的能量为(2)[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰（少乘以2吧？）由1()f t 与2()f t 在区间(,)22T T-不正交可得 2122()()0T T f t f t dt K -=≠⎰则有2222222212122222()()()()T T T T T T T T E f t dt f t dt K f t dt f t dt ----=++≠+⎰⎰⎰⎰即此时和信号的总能量不等于各信号的能量之和。

第三章习题基础题3.1 证明cos t , cos(2)t , …,cos()nt (n 为正整数)，在区间(0,2)π的正交集。

它是否是完备集?解：(积分???)此含数集在(0,2)π为正交集。

又有sin()nt 不属于此含数集02sin()cos()0nt mt dt π=⎰，对于所有的m和n 。

由完备正交函数定义所以此函数集不完备。

3.2 上题的含数集在(0,)π是否为正交集？解：由此可知此含数集在区间(0,)π是正交的。

3.3实周期信号()f t 在区间(,)22T T -的能量定义为222()TT E f t dt -=⎰。

如有和信号12()()f t f t +(1)若1()f t 与2()f t 在区间(,)22T T-相互正交，证明和信号的总能量等于各信号的能量之和;(2)若1()f t 与2()f t 不是相互正交的，求和信号的总能量。

解：(1)和信号f(t)的能量为[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰（少乘以2）由1()f t 与2()f t 在区间正交可得2122()()0T T f t f t dt -=⎰则有 22221222()()T T T T E f t dt f t dt --=+⎰⎰即此时和信号的总能量等于各信号的能量之和。

和信号的能量为(2)[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰（少乘以2吧？）由1()f t 与2()f t 在区间(,)22T T-不正交可得 2122()()0T T f t f t dt K -=≠⎰则有2222222212122222()()()()T T T T T T T T E f t dt f t dt K f t dt f t dt ----=++≠+⎰⎰⎰⎰即此时和信号的总能量不等于各信号的能量之和。

现代数字信号处理何子述课后现代数字信号处理是一门极为重要的学科，它对于现代通信、信息处理乃至于音视频处理都具有非常重要的意义。

何子述教授的课程内容涵盖广泛，是掌握现代数字信号处理知识的必修课程，下面就以何子述课后为主题展开论述。

第一步：认识现代数字信号处理的基础知识现代数字信号处理的基础知识主要包括数字信号、数字系统等。

数字信号是指通过离散化时间和幅度的信号，它可以进行数字系统的处理。

数字系统是通过数字信号处理电路实现数字信号的转换、处理以及存储等。

要掌握现代数字信号处理的知识，首先需要对这些基础知识有一个全面的认识。

第二步：了解数字信号处理的处理流程数字信号处理的处理流程主要包括采样、量化、编码、传输等过程。

采样是指将连续时间的模拟信号转换为离散信号的过程。

量化是指将连续的模拟信号转换为离散的数值，编码是将离散的数值转换为符号。

传输是指将数字信号传输至接收端。

只有了解了数字信号处理的处理流程，才能更好地理解数字信号处理的具体实现。

第三步：学习数字信号处理的具体技术数字信号处理的技术主要包括滤波器设计、时域处理、频域处理、自适应处理等。

滤波器设计是数字信号处理中的基础，其目的是去除或改变信号中的某些成分。

时域处理是指直接对信号进行处理，如加减乘除等。

频域处理是指对信号进行傅里叶变换，对其在频域上进行处理。

自适应处理是另一种常用的数字信号处理技术，其目的是通过自适应反馈，让系统自适应其输入和输出之间的关系。

第四步：实践数字信号处理的实际应用数字信号处理的实际应用十分广泛，涵盖通信、音视频处理乃至于医学影像等领域。

在实践数字信号处理的实际应用过程中，需要根据具体的应用场景选择不同的数字信号处理技术，进行系统设计和实现。

以上就是关于现代数字信号处理何子述课后的分步骤解析。

通过学习该课程，可了解数字信号处理的基本知识，理解数字信号处理的处理流程，掌握数字信号处理的技术和应用，为将来在相关领域进行数字信号处理提供基础和指引，是一门非常有价值的课程。

信号处理基础仿真作业学号：S*********姓名：***3.17在计算机上用如下方法产生随机信号()u n的观测样本：首先产生一段零均值、方差为2σ的复高斯白噪声序列()v n；然后在()v n上叠加三个复正弦信号，它们的归一化频率分别是f1=0.15，f2=0.17和f3=0.26。

调整2σ和正弦信号的幅度，使在f1、f2和f3处得信噪比分别为30dB、30dB和27dB。

（1）令信号观测样本长度N=32，试用3.1.1节讨论的基于FFT的自相关函数快速计算方法估计出自相关函数^()0mr，并与教材式（3.1.2）估计出的自相关函数^()mr做比较。

产生零均值、方差为1的复高斯白噪声序列y >> y=randn(1,32);>> y=y-mean(y);>> y=y/std(y);>> a=0;>> b=sqrt(2);>> y=a+b*y产生三个复正弦信号并产生观察样本：>> N=32;>> f1=0.15;>> f2=0.17;>> f3=0.26;>> SNR1=30;>> SNR2=30;>> SNR3=27;>> A1=10^(SNR1/20);>> A2=10^(SNR2/20);>> A3=10^(SNR3/20);>> signal1=A1*exp(j*2*pi*f1*(0:N-1));>> signal2=A2*exp(j*2*pi*f2*(0:N-1));>> signal3=A3*exp(j*2*pi*f3*(0:N-1));>> un=signal1+signal2+signal3+y基于FFT的自相关函数快速计算方法：N=32;>> Uk=fft(un, 2*N);Sk=(1/N)* abs(Uk).^2;r0=ifft(Sk);r1=[r0(N+2:2*N),r0(1:N)];>> figure(1);>> stem(real(r1));>> figure(2);>> stem(imag(r1))输出结果为：图 1 基于FFT的自相关函数快速计算实部：虚部：教材中式（3.1.2）估计自相关函数>> r=xcorr(un, N-1,'biased');>> figure(1);>> stem(real(r))>> figure(2);>> stem(imag(r))输出结果为：图 2 教材式（3.1.2）估计的自相关函数实部：虚部：（2）令信号观测样本长度N=256，试用BT法和周期图法估计()u n的功率谱，这里设BT法中所用自相关函数的单边长度M=64。

第三章 用直接型及正准型结构实现以下传递函数1．(1)321213315.025)(-----+++-+-=z z z z z z H x(n) -5 y(n) x(n) -5 y(n)直接型 正准型(2)3213212323234152238.0234)5223(8.0)(------++++=++++++=z z z z z z z z z z z z z H x(n) 0.8 3 y(n) x(n) 0.8 3 y(n)直接型 正准型(3)212128/34/112813282)(------+-=--+-=zz z z z z z z H x(n) 1/8 y(n) x(n) 1/8 y(n)2．用级联型结构实现以下传递函数)81.02728.11)(5.01()4142.11)(1(5)(211211------+--+--=z z z z z z z H 一共能有几种级联型网络？解：x(n) 5 y(n)级联型之一共有2！*2！=4种级联型网络。

3．用级联型及并联型实现以下传递函数：解：(1)2111211211223115.012)1)(5.01(35.235.313)5.0)(1(5.25.33)(---------+--+-=+--+-=-+-+-=zz z z z z z z z z z z z z z z H x(n) 3 y(n) 2级联型之一 并联型(2)21112234142.11)7071.01(27071.012)7071.0)(14142.1(8284.24)(----+--++=++-+-=z z z z z z z z z z z H x(n) 4 y(n) 2级联型之一 并联型4．设滤波器差分方程为：)2(81)1(43)1(31)()(---+-+=n y n y n x n x n y 用直接I 型，II 型以及全部一阶节的级联型，并联型结构实现它。

解：传递函数为：112114113721131081431311)(-------+-=+-+=z z z z z z H x(n) y(n) x(n) y(n) 直接I 型 直接II 型x(n) y(n) x(n) y(n)x(n) y(n) x(n) y(n)级联型10/3 -7/3并联型5．求以下结构的差分方程及传递函数：x(n) y(n) x(n) )(1n y )(2n y 2 y(n)(a) (b)解：(a)21183411412)()2(83)1(41)1(41)(2)(---+-+=---+-+=z z z z H n y n y n x n x n y (b)54321543212121111133112111221212113311221212113233111321211108.062.098.026.05.118.08.71.55.164.46)()()()8.02.01)(5.05.11()24)(25.01()()()()()2.01)(5.05.11(25.01)()()()(8.02.0124)()()(2.011)()()(,)()(5.05.1125.01)()()(2)()2(8.0)1(2.0)2(2)1()(4)()1(2.0)()()2(5.0)1(5.1)2(2)1(5.0)()(-----------------------------------+-+++++==+---++++==+--++==+-++==+===--++=+=---+-+-+=--=-+-+-+-+=z z z z z z z z z z z X z Y z H z z z z z z z z z X z Y z H z H z z z z z z X z Y z H z H z z z z z Y z Y z H z z Y z Y z H z X z Y z z z z z H n y n y n y n y n y n y n y n y n y n y n y n y n y n y n x n x n x n yy(n)=6x(n)+4.4x(n-1)+16.5x(n-2)+5.1x(n-3)+7.8x(n-4)+0.8x(n-5)+1.5y(n-1)-0.26y(n-2)+0.98y(n-3)+0.62y(n-4)+0.08y(n-5)6．求以下结构的差分方程及传递函数：解：设变量4321,,,u u u u有：⎪⎪⎩⎪⎪⎨⎧=+==-+=--134423112421cos sin sin cos z u u u r r u u z u u u r u r x u θθθθ )2()1(cos 2)1(sin )(cos 21sin )(cos 21sin 22211322113---+-=+-=∴=+-=------n y r n y r n x r n y z r z r zr z H u Y z r z r z r x u θθθθθθ(b)设变量：321,,u u u有：33133213233123212211212211211111,u Y u z a u z a u u z a u z a u z a u x u z a u z a u =⎪⎩⎪⎨⎧+=++=++=-------用矩阵表示：[])(001)1()1()1(00)()()(:001,001003213332232221121132132131211133322322211211321n x n u n u n u a a a a a a a n u n u n u u u u Y x u z u z u z a a a a a a a u u u ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---即其中：⎪⎪⎩⎪⎪⎨⎧--=--++=++==322311332112332211233221123322331122113322113212a a a a a a a a a D a a a a a a a a a a C a a a B a a A7．已知滤波器单位脉冲响应为⎩⎨⎧≤≤=nn n h n 其他,050,2.0)(，横截型结构。

数字信号处理习题解答 第二章 数据采集技术基础2.1 有一个理想采样系统，其采样角频率Ωs =6π，采样后经理想低通滤波器H a （j Ω)还原，其中⎪⎩⎪⎨⎧≥Ω<Ω=Ωππ30321)(，，j H a 现有两个输入，x 1(t )=cos2πt ,x 2(t )=cos5πt 。

试问输出信号y 1（t )，y 2（t )有无失真？为什么？分析：要想时域采样后能不失真地还原出原信号，则采样角频率Ωs 必须大于等于信号谱最高角频率Ωh 的2倍,即满足Ωs ≥2Ωh 。

解:已知采样角频率Ωs =6π，则由香农采样定理，可得 因为x 1（t ）=cos2πt ，而频谱中最高角频率πππ32621=<=Ωh ,所以y 1（t )无失真；因为x 2（t ）=cos5πt ，而频谱中最高角频率πππ32652=>=Ωh ，所以y 2（t ）失真.2.2 设模拟信号x (t )=3cos2000πt +5sin6000πt +10cos12000πt ，求：（1） 该信号的最小采样频率；（2） 若采样频率f s =5000Hz ，其采样后的输出信号； 分析：利用信号的采样定理及采样公式来求解。

错误!采样定理采样后信号不失真的条件为:信号的采样频率f s 不小于其最高频率f m 的两倍，即f s ≥2f m错误!采样公式)()()(s nT t nT x t x n x s===解：（1）在模拟信号中含有的频率成分是f 1=1000Hz ，f 2=3000Hz ，f 3=6000Hz∴信号的最高频率f m =6000Hz由采样定理f s ≥2f m ，得信号的最小采样频率f s =2f m =12kHz （2）由于采样频率f s =5kHz ，则采样后的输出信号⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛====n n n n n n n n n n n f n x nT x t x n x s s nTt s522sin 5512cos 13512cos 10522sin 5512cos 35112cos 105212sin 5512cos 3562cos 10532sin 5512cos 3)()()(πππππππππππ 说明：由上式可见,采样后的信号中只出现1kHz 和2kHz 的频率成分，即kHzf f f kHzf f f ss 25000200052150001000512211======，，若由理想内插函数将此采样信号恢复成模拟信号,则恢复后的模拟信号()()t t t f t f t y ππππ4000sin 52000cos 132sin 52cos 13)(21-=-=可见，恢复后的模拟信号y （t ） 不同于原模拟信号x （t ），存在失真，这是由于采样频率不满足采样定理的要求,而产生混叠的结果.第三章 傅里叶分析I. 傅里叶变换概述3.1 ［习题3.2］设序列x （n )=δ(n-m ），求其频谱X (e j ω），并讨论其幅频和相频响应分析:求解序列的频谱有两种方法:○，1先求序列的z 变换X （z )，再求频谱ωωj e z j z X e X ==)()(,即X （e j ω）为单位圆上的z 变换；错误!直接求序列的傅里叶变换∑∞-∞=-=n nj j en x e X ωω)()(解：对序列x （n )先进行z 变换,再求频谱，得m z m n ZT n x ZT z X -=-==)]([)]([)(δ则ωωωjm e z j e z X e X j -===)()(若系统的单位采样响应h （n ）=x (n ），则系统的频率响应)}(exp{)(1)()(ωϕωωωωωj e H e e e X e H j jm jm j j ====--•故其幅频和相频响应(如图)分别为幅频响应 1)(=ωj e H 相频响应 ωωϕm -=)(由图可见,该系统的频率响应具有单位幅值以及线性相位的特点。