计量经济学第三章作业

姓名:汪宝班级:七班学号:68已知我国29个省、直辖市、自治区１９９４年城镇居民人均生活费支出Ｙ，可支配收入Ｘ的截面数据见下表。

（１）：用等级相关数据和戈德菲尔特——夸特方法检验支出模型的扰动项是否存在异方差性。

支出模型是Ｙｉ＝Ｂ０＋Ｂ１Ｘｉ＋ｕｉ（２）：无论ｕｉ是否存在异方差性，用ＥＶｉｅｗｓ练习加权最小二乘法估计模型，并用模型进行预测。

解：（１）按照斯皮尔曼等级相关检验的步骤，现将Ｘ的样本观测值从小到大排列并划分等级，计算Ｘｉ的等级与相应产生的ｅｉ的等级差ｄｉ及ｄｉ２，具体解法见下面：①对X进行排序:②在对原有数据进行obls回归得到resid.接着对abs(resid)进行排名。

③:计算斯皮尔曼等级相关系数r=1-∑(dt*dt)/(N3-N)=1-(6*2334)/(293-29)=1-0.5749=0.4251 等级相关系数检验，提出原假设与备选假设H0:P=0 H1≠Pr～N(0,1/(n-1))=(0,1/28)构造Z的统计量Z=r/(1/√28)=0.4251/0.189=2.249给定显著水平a=0.05，查正态分布表，得Z a/2=1.96，因为Z=2.249>１．９６，所以应拒绝Ｈ０，接受Ｈ１，即等级相关系数是显显著，说明支出模型的扰动是存在异方差的。

按着戈德菲尔特－夸特方法检验支出模型的扰动项是否存在异方差。

将Ｘ的样本观测值按升序排列，Ｙ的样本观测值按原来与Ｘ样本观测值的对应关系进行排列，具体计算过程如下①对Ｘ进行排序：对Ｙ进行排序：略去中心７个样本观测值，将２２个样本观测值分成容量相等的两个样本，每个子样本的样本观测值个数均为１１。

用第一个子样本估计模型，由上面的表格知第一个子样本的估计模型，得Ｙ＝－２８７．１８７２＋０．９７４７５１Ｘ残差平方和∑ｅｉ１２＝２１６８８．８９第二个子样本估计模型：由上面的表格可知：Ｙ＝－２７．６８３４５＋０．８２０３３７Ｘ残差平方和∑ｅｉ２２＝４３７０２．６５提出原假设：Ｈ０：Ｈ１：构造Ｆ统计量Ｆ＝∑ｅｉ２２／∑ｅｉ１２＝４３７０２．６５／２１６８８．８９≈２．０１５给定显著性水平ａ＝０．０５，查Ｆ分布表ｖ１＝ｖ２＝１１－２＝９，Ｆ０．０５（９,９）＝３．１８，因为Ｆ＝２．０１５>１．９６，所以应接受备择假设，即支出扰动模型存在异方差．（２）用加权最小二乘法估计模型由该表格可知：Ｙ＝１６．６６＋０．８１４Ｘ，又由于原来的模型的拟合优度９８．５％，又由于加权后的拟合优度为９９．７％。

计量经济学第三章练习题及参考全部解答第三章练习题及参考解答3.1为研究中国各地区入境旅游状况，建立了各省市旅游外汇收入（Y ，百万美元）、旅行社职工人数（X1，人）、国际旅游人数（X2，万人次）的模型，用某年31个省市的截面数据估计结果如下：ii i X X Y 215452.11179.00263.151?++-= t=(-3.066806)(6.652983) (3.378064)R 2=0.934331 92964.02=R F=191.1894 n=31 1)从经济意义上考察估计模型的合理性。

2)在5%显著性水平上，分别检验参数21,ββ的显著性。

3)在5%显著性水平上，检验模型的整体显著性。

练习题3.1参考解答:(1)由模型估计结果可看出：从经济意义上说明，旅行社职工人数和国际旅游人数均与旅游外汇收入正相关。

平均说来，旅行社职工人数增加1人，旅游外汇收入将增加0.1179百万美元；国际旅游人数增加1万人次，旅游外汇收入增加1.5452百万美元。

这与经济理论及经验符合，是合理的。

（2）取05.0=α，查表得048.2)331(025.0=-t 因为3个参数t 统计量的绝对值均大于048.2)331(025.0=-t ，说明经t 检验3个参数均显著不为0，即旅行社职工人数和国际旅游人数分别对旅游外汇收入都有显著影响。

（3）取05.0=α，查表得34.3)28,2(05.0=F ，由于34.3)28,2(1894.19905.0=>=F F ，说明旅行社职工人数和国际旅游人数联合起来对旅游外汇收入有显著影响，线性回归方程显著成立。

3.2 表3.6给出了有两个解释变量2X 和.3X 的回归模型方差分析的部分结果：表3.6 方差分析表1）回归模型估计结果的样本容量n 、残差平方和RSS 、回归平方和ESS 与残差平方和RSS 的自由度各为多少?2）此模型的可决系数和调整的可决系数为多少? 3）利用此结果能对模型的检验得出什么结论?能否确定两个解释变量2X 和.3X 各自对Y 都有显著影响?练习题3.2参考解答:(1) 因为总变差的自由度为14=n-1，所以样本容量：n=14+1=15 因为TSS=RSS+ESS 残差平方和RSS=TSS-ESS=66042-65965=77 回归平方和的自由度为：k-1=3-1=2 残差平方和RSS 的自由度为：n-k=15-3=12（2）可决系数为：2659650.99883466042ES R TSS S === 修正的可决系数：222115177110.998615366042i i e n R n k y --=-=-?=--∑∑（3）这说明两个解释变量2X 和.3X 联合起来对被解释变量有很显著的影响，但是还不能确定两个解释变量2X 和.3X 各自对Y 都有显著影响。

詹姆斯·斯托克,马克·沃森计量经济学第三章实证练习stata答案⼀、Two-sample t test with equal variancesGroup Obs Mean Std.Err. Std.Dev. 95% Conf. Interval1992 7,612 11.62 0.0644 5.619 11.49 11.742012 7,440 19.80 0.124 10.69 19.56 20.04combined 15,052 15.66 0.0770 9.442 15.51 15.81diff -8,183 0.139 -8.455 -7.911 diff = mean(1992) - mean(2012) t = -58.9871Ho: diff = 0 degrees of freedom = 15050Ha: diff < 0 Ha: diff != 0 Ha: diff > 0Pr(T < t) = 0.0000 Pr(|T| > |t|) = 0.0000 Pr(T > t) = 1.0000⼆、Two-sample t test with equal variancesGroup Obs Mean Std.Err. Std.Dev. 95% Conf. Interval 1992 7,612 15.64 0.0867 7.564 15.47 15.81 2012 7,440 19.80 0.124 10.69 19.56 20.04 combined 15,052 17.69 0.0772 9.471 17.54 17.85 diff -4.164 0.151 -4.459 -3.869diff = mean(1992) - mean(2012) t = -27.6423Ho: diff = 0 degrees of freedom = 15050Ha: diff < 0 Ha: diff != 0 Ha: diff > 0Pr(T < t) = 0.0000 Pr(|T| > |t|) = 0.0000 Pr(T > t) = 1.0000三、第⼆题根据通货膨胀率进⾏了调整，反映了购买⼒的变化，所以可⽤利⽤第⼆题的结果进⾏分析。

（3） = TSS
RSS 480 = = 750 2 1− R 1 − 0.36
7. 答： （1） cov( = x, y )
1 2 2 ( xt − x )( y = r σx σ y ＝ 0.9 × 16 ×10 ＝11.38 ∑ t − y) n −1
∑ ( x − x )( y − y )=
即表明截距项也显著不为 0，通过了显著性检验。 （3）Yf=2.17+0.2023×45＝11.2735
2 1 (x f − x ) 1 (45 − 29.3) 2 ˆ 1+ + = × × + = 4.823 t0.025 (8) × σ 1.8595 2.2336 1+ n ∑ ( x −x ) 2 10 992.1
3
2
五、综合题 1. 答： （1）建立深圳地方预算内财政收入对 GDP 的回归模型，建立 EViews 文件，利用地方预 算内财政收入（Y）和 GDP 的数据表，作散点图
可看出地方预算内财政收入（Y）和 GDP 的关系近似直线关系，可建立线性回归模型：
Yt = β1 + β 2 GDPt + u t
第 3 章参考答案
一、名词解释 1. 高斯－马尔可夫定理：在古典假定条件下，OLS 估计量是模型参数的最佳线性无偏估计 量，这一结论即是高斯－马尔可夫定理。 2. 总变差（总离差平方和） ：在回归模型中，被解释变量的观测值与其均值的离差平方和。 3. 回归变差（回归平方和） ：在回归模型中，因变量的估计值与其均值的离差平方和，也就 是由解释变量解释的变差。 4. 剩余变差（残差平方和） ：在回归模型中，因变量的观测值与估计值之差的平方和，是不 能由解释变量所解释的部分变差。 5. 估计标准误差：在回归模型中，随机误差项方差的估计量的平方根。 6. 样本决定系数：回归平方和在总变差中所占的比重。 7. 拟合优度：样本回归直线与样本观测数据之间的拟合程度。 8. 估计量的标准差：度量一个变量变化大小的测量值。 9. 协方差：用 Cov（X，Y）表示，度量 X,Y 两个变量关联程度的统计量。 10. 显著性检验：利用样本结果，来证实一个虚拟假设的真伪的一种检验程序。 11. 拟合优度检验：检验模型对样本观测值的拟合程度，用 R 2 表示，该值越接近 1，模型 对样本观测值拟合得越好。 12. t 检验：是针对每个解释变量进行的显著性检验，即构造一个 t 统计量，如果该统计量 的值落在置信区间外，就拒绝原假设。 13. 点预测：给定自变量的某一个值时，利用样本回归方程求出相应的样本拟合值，以此作 为因变量实际值均值的估计值。

第三章、经典单方程计量经济学模型：多元线性回归模型一、内容提要本章将一元回归模型拓展到了多元回归模型，其基本的建模思想与建模方法与一元的情形相同。

主要内容仍然包括模型的基本假定、模型的估计、模型的检验以及模型在预测方面的应用等方面。

只不过为了多元建模的需要，在基本假设方面以及检验方面有所扩充。

本章仍重点介绍了多元线性回归模型的基本假设、估计方法以及检验程序。

与一元回归分析相比，多元回归分析的基本假设中引入了多个解释变量间不存在（完全）多重共线性这一假设；在检验部分，一方面引入了修正的可决系数，另一方面引入了对多个解释变量是否对被解释变量有显著线性影响关系的联合性F检验，并讨论了F检验与拟合优度检验的内在联系。

本章的另一个重点是将线性回归模型拓展到非线性回归模型，主要学习非线性模型如何转化为线性回归模型的常见类型与方法。

这里需要注意各回归参数的具体经济含义。

本章第三个学习重点是关于模型的约束性检验问题，包括参数的线性约束与非线性约束检验。

参数的线性约束检验包括对参数线性约束的检验、对模型增加或减少解释变量的检验以及参数的稳定性检验三方面的内容，其中参数稳定性检验又包括邹氏参数稳定性检验与邹氏预测检验两种类型的检验。

检验都是以F检验为主要检验工具，以受约束模型与无约束模型是否有显著差异为检验基点。

参数的非线性约束检验主要包括最大似然比检验、沃尔德检验与拉格朗日乘数检验。

它们仍以估计无约束模型与受约束模型为基础，但以最大似然χ分布为检验统计原理进行估计，且都适用于大样本情形，都以约束条件个数为自由度的2量的分布特征。

非线性约束检验中的拉格朗日乘数检验在后面的章节中多次使用。

二、典型例题分析例1．某地区通过一个样本容量为722的调查数据得到劳动力受教育的一个回归方程为36.0.+=-10+094medufedu.0sibsedu210131.0R2=0.214式中，edu为劳动力受教育年数，sibs为该劳动力家庭中兄弟姐妹的个数，medu与fedu分别为母亲与父亲受到教育的年数。

计算r得，
(10*204200-1680*1110)/((10*315400-1680*1680)*(10*133300-1110*1110))^0.5=0.968748122
3.22表3 -7给出1974-2006年向美国的黄金价格、消费者价格指数(CPl)和纽约证券交易所指数(NYSE lndex)数据. NYSE指数包括在NYSE上市的1 500多种股票中的大多数.
解：a、在同一个散点图中描绘黄金价格、CPI和NYSE指数
b.CPI衡量通货膨胀，如果假设成立，则要求 不小于1。
拟合得Gold pricet=215.286+1.038CPIt+ui
NYSEt=-3444.992+50.297CPIt+ui
所以，股票市场比黄金更能对付通货膨胀，实现保值。
首先用MATLAB生成随机数，ui服从均值为0方差为9的正态分布。得到：
b.求β2与ɑ2的估计量，它们是否相同?它们的方差是否相同?
c.如果模型11比模型I好，好在哪里?
a. ，
，
所以它们的估计量不同,方差也不相等。
b.
所以它们的估计值和方差都相等。
c.当X较大时使用模型II更好，因为计算相对简单，运行速度更快。
3.14在总体回归模型中，每个X都乘2，或都加2，对Y的残差和拟合值有什么影响。
cov(Yi,Yj)=E(ui,uj)
=E(ui)E(uj)
=0
（3）var（Yi|Xi）=E[Yi-E(Yi)]2
=E（ui2）
=var(ui|Xi)
=σ2
3.3
3.3 PRF是Yi=β1+β2Xi+ui，
①：β1=0，β2=1且E（ui）=0，从而E（Yi/Xi）=Xi。

《计量经济学》第3章习题一、单项选择题1．多元线性回归模型的“线性”是指对（ ）而言是线性的。

A ．解释变量B ．被解释变量C ．回归参数D ．剩余项 2．多元线性回归模型参数向量β最小二乘估计式的矩阵表达式为（ ）A ．'1'ˆ()XX X Y β-= B ．'1'ˆ()X X X Y β-= C ．'1ˆ()XX XY β-= D ．'1'ˆ()XX XY β-= 3．ˆβ的方差－协方差矩阵ˆ()Var Cov β-为（ ） A ．2'1()X X σ- B ． 2'1()XX σ- C ．'12()XX σ- D ． '12()X X σ- 4．修正可决系数与未经修正的多重可决系数之间的关系为（ ）A ．2211(1)n R R n k -=--- B ．221(1)1n kR R n -=--- C ．2211n k R R n -=-- D ．2211n R R n k-=--5．多重可决系数R 2是指（ ）A ．残差平方和占总离差平方和的比重B ．总离差平方和占回归平方和的比重C ．回归平方和占总离差平方和的比重D ．回归平方和占残差平方和的比重 二、多项选择题1．多元线性回归模型的古典假定有（ ）A ．零均值假定B ．同方差和无自相关假定C ．随机扰动项与解释变量不相关假定D ．无多重共线性假定E ．正态性假定2．对模型01122i i i i Y X X u βββ=+++进行总体显著性检验，如果检验结果总体线性关系显著，则可能有（ ）A ．1β＝2β＝0B ．1β≠0，2β=0C ．1β≠0，2β≠0D ．1β＝0，2β≠0E ．1β＝2β≠0 3．残差平方和是指（ ）A ．被解释变量观测值与估计值之间的变差B ．被解释变量回归估计值总变差的大小C ．被解释变量观测值总变差的大小D ．被解释变量观测值总变差中未被列入模型的解释变量解释的那部分变差E．被解释变量观测值总变差中由多个解释变量作出解释的那部分变差4．关于多重可决系数，说法正确的有（）A．多重可决系数越大，表示回归方程与样本拟合得越好B．多重可决系数与模型中解释变量的数目有关，一般而言，解释变量越多，多重可决系数就越大C．实际应用中，使用修正的可决系数判断依据。

出参数估计量，所要求的最小样本容量为（ ）
A n ≥ k +1 B n ≤ k +1 C n ≥ 30 D n ≥ 3(k +1)
6. 对于 Yi =βˆ0 + βˆ1Xi +ei ，以σˆ 表示估计标准误差，r 表示相关系数，则有（ ） A σˆ＝0时，r=1
B σˆ＝0时，r=-1
C σˆ＝0时，r=0
7. 简述变量显著性检验的步骤。 8. 简述样本相关系数的性质。 9. 试述判定系数的性质。
五、综合题
1. 为了研究深圳市地方预算内财政收入与国内生产总值的关系，得到以下数据：
年份
地方预算内财政收入 Y
国内生产总值(GDP)X
（亿元）
（亿元）
1990
21.7037
171.6665
1991
27.3291
184.7908
1436.0267
2000
225.0212
1665.4652
2001
265.6532
1954.6539
要求：
（1）建立深圳地方预算内财政收入对 GDP 的回归模型；
（2）估计所建立模型的参数，解释斜率系数的经济意义；
（3）对回归结果进行检验；
（4）若是 2005 年的国内生产总值为 3600 亿元，确定 2005 年财政收入的预测值和预
）
A 可靠性
B 合理性
C 线性
D 无偏性
E 有效性
5. 剩余变差是指（
）
A 随机因素影响所引起的被解释变量的变差
B 解释变量变动所引起的被解释变量的变差
C 被解释变量的变差中，回归方程不能做出解释的部分
D 被解释变量的总变差与回归平方和之差

计量经济学第三章作业1、家庭消费支出（y）、可支配收入（x1）、个人个财富（x2）设定模型下：yi=β0+β1x1i+β2x2i+μi回归分析结果为：ls//dependentvariableisydate:18/4/02time:15:18sample:110includedobservations:10variablecoefficientstd.errort-statisticprob.c24.40706.9973________0.01010.5002x2-0.34010.4785________x20.08230.04580.1152r-squared________meandependentvaradjustedr-squared111.12560.9504s.d.dependentvar31.42894.1338s.e.ofregression________akaikeinfocriterionsumsquaredresid342.5486schwartzcriterion4.2246loglikelihood-31.8585f-statistic87.33392.4382prob(f-statistic)0.0001durbin-watsonstat补齐表中划线部分的数据（保留四位小数）；并写出回归分析报告。

24.4070t==3.48816.9973ˆβ-0.34011t1===-0.71080.4785se(β1)ˆβ0.08232t2===1.79690.0458se(β2)2=1-(1-r2)n-1n-k(k=3)∴r2=1-(1-2)n-kn-1由表中所述，2=0.9504故r2=1-(1-0.9504)10-3=0.961410-1ˆ=σrss342.5486==6.5436n-210-2重回分析报告如下：由以上结果整理得：ˆ=24.4070-0.3401yx1+0.0823x2(6.9973)(0.4785)(0.0458)t=3.4481-0.71081.7969r2=0.9614n=10从重回结果来看，r2=0.9614，2=0.9504，f=87.3339,比较小，则模型的插值优度不是较好.模型说明当可支配收入每增加１元，平均说来家庭消费支出将减少0.3401元，当个人财富每增加１元，平均来说家庭消费支出将增加0.0823元。

第三章练习题及参考解答3.1进入21世纪后，中国的家用汽车增长很快。

家用汽车的拥有量受到经济增长、公共服务、市场价格、交通状况、社会环境、政策因素，都会影响中国汽车拥有量。

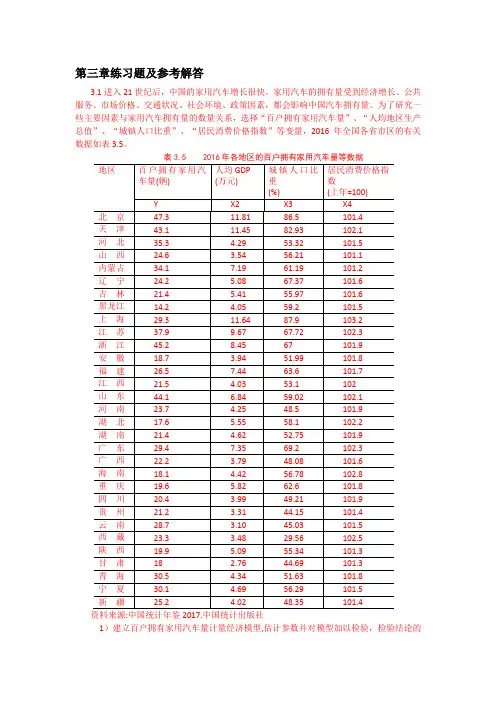
为了研究一些主要因素与家用汽车拥有量的数量关系，选择“百户拥有家用汽车量”、“人均地区生产总值”、“城镇人口比重”、“居民消费价格指数”等变量，2016年全国各省市区的有关数据如表3.5。

表3.5 2016年各地区的百户拥有家用汽车量等数据资料来源:中国统计年鉴2017.中国统计出版社1）建立百户拥有家用汽车量计量经济模型,估计参数并对模型加以检验，检验结论的依据是什么?。

2)分析模型参数估计结果的经济意义,你如何解读模型估计检验的结果? 3) 你认为模型还可以如何改进?【练习题3.1 参考解答】：1)建立线性回归模型: 1223344t t t t t Y X X X u ββββ=++++ 回归结果如下:由F 统计量为14.69998, P 值为0.000007，可判断模型整体上显著, “人均地区生产总值”、“城镇人口比重”、“居民消费价格指数”等变量联合起来对百户拥有家用汽车量有显著影响。

解释变量参数的t 统计量的绝对值均大于临界值0.025(27) 2.052t =,或P 值均明显小于0.05α=，表明在其他变量不变的情况下,“人均地区生产总值”、“城镇人口比重”、“居民消费价格指数”分别对百户拥有家用汽车量都有显著影响。

2）X2的参数估计值为4.8117,表明随着经济的增长,人均地区生产总值每增加1万元,平均说来百户拥有家用汽车量将增加近5辆。

由于城镇公共交通的大力发展,有减少家用汽车的必要性,X3的参数估计值为-0.4449,表明随着城镇化的推进,“城镇人口比重”每增加1%,平均说来百户拥有家用汽车量将减少0.4449辆。

汽车价格和使用费用的提高将抑制家用汽车的使用, X4的参数估计值为-5.7685,表明随着家用汽车使用成本的提高, “居民消费价格指数”每增加1个百分点,平均说来百户拥有家用汽车量将减少5.7685辆。

一、单项选择题（每题2分）1、多元线性回归模型的“线性”是指对（）而言是线性的。

（A ）解释变量（B）被解释变量（C）回归参数（D）剩余项2、多元样本线性回归函数是（）（A）Y=B i+%X2i+B3X3i+H|+P kXki+Ui（B）Y? = f? + J?2x2i+險3 +…+隊X ki （C ）E（Y|X2i,X3i,^X ki）二时jX2i」X3i 小」X ki（D）Y=X B +U3、多元总体线性回归函数的矩阵形式为（）(A) ?=(XX')」X'Y(B) ? =(x'x)」xY(C) ? = (XX')」XY(D) ? = (XX，)」XY'5、?的方差一协方差矩阵Var - Cov（ ?）为（）(A 2(X'X)4(B)二2(XX')J（C）（xx'）.26随机扰动项方差的估计式是（）Z e2；(D) (X'X)七2(B)廿n—2送e2(C)二n —k送e2(D)Cjjn —k7、残差平方和RSS的是（）2（A）、（Y -Y）(B)、(Y -Y?)2（A）Y=X B +U'）Y = X B4、多元线性回归模型参数向量（B）Y=X ? + e（D）Y=X B + e1最小二乘估计式的矩阵表达式为（n -1 R 211、 多重可决系数R 2是指（）（A ）（B ） （C ） （D ） 12、 在由n=30的一组样本估计的、包含 的多重可决系数为0.8500,则修正的可决系数为（ （A ） 0.8603 （ B ） 0.8389 （C ） 0.8655 （ D ） 0.8327 13、 设k 为模型中的参数个数，则回归平方和是指（8、 修正可决系数与未经修正的多重可决系数之间的关系为（ （A ） R 2"_g （1_R 2） （B ） R 2 “一口 n —k（C ） R 2“_S R 2n —19、 回归方程的显著性检验的F 检验量为（） ESS/ （A ） F ----k 1RSS n — k ESS（C ） F =n kRSS ,n —110、 F 统计量与可决系数R 2之间的关系为 (D) (B )(D)R 2) (1-R 2) n -1亠1R 2n —kESS n —1 n — k ESS ■ n _k RSS(B) F(D)F・1 R2残差平方和占总离差平方和的比重总离差平方和占回归平方和的比重 回归平方和占总离差平方和的比重 回归平方和占残差平方和的比重3个解释变量的线性回归模型中，计算 ） n(A ) (y ii ± -y)2(B) n工(比-？)2iTn(C )(?i i斗-y)2(D)14、用一组有30个观测值的样本估计模型':o:2x 2i u i 后，在 0.05(D )M-Y)(C )(Y?-Y )的显著性水平下对打的显著性做t检验，则1显著地不等于零地条件是其统计量大于等于（）（A）t0.05 （30）（B）t0.025（28）(C) to.025 (27) (D) F O.025 (1, 28)15、在模型古典假定满足的条件下，多元线性回归模型的最小二乘估计是( ) 估计(A)WIND ( B)OLS(C)BLUE (D)GREEN二、多项选择题1、多元样本线性回归函数是( )(A) Y=E1+P2X2i+B3X3i+lil+B kX ki+u(B) Y? = fV%X2i…+氏X ki ( C )E(Y|X2i,X3i,小X ki)二」：2X2i \X3i 小「k X kiA A A A(D)Y i = -1 ~2X2i * -3 X3i * | * -k X ki ' e i2、多元总体线性回归函数的矩阵形式为( )(A) Y=X B +U ( B) Y=X ? + eA A(C) Y = X B (D) E(Y) = X B3、多元线性回归模型的古典假定有( )(A)零均值假定(B)同方差和无自相关假定(C)随机扰动项与解释变量不相关假定(D)无多重共线性假定(E)正态性假定4、对模型％=0。

第三、四章习题09国贸1班张继云 1403.31）为分析家庭书刊年消费支出（Y）对家庭月平均收入（X）与户主受教育年数（T）的关系，做如图所示的线形图。

建立多元线性回归模型为Y i=β1+β2X+β3T+μi2) 假定所建立模型中的随机扰动项μi满足各项古典假设，用OLS法估计其参数，得到的回归结果如下。

可用规范形式将参数估计和检验结果写为Y = -50.01638+0.086450X+52.37031T（49.46026）（0.029363）（5.202167）t=（-1.011244）（2.944186）（10.06702）R2=0.951235 F=146.2974 n=183）对回归系数β3的t检验：针对H0：β3=0和H1：β3≠0，由回归结果中还可以看出，估计的回归系数β3的标准误差和t值分别为：SE(β3)= 5.202167, t(β3)= 10.6702。

当α=0.05时，查t分布表得自由度n-3=18-3=15的临界值t0.025（15）=2.131。

因为t(β1)= 10.6702> t0.025（16）=2.131,所以应该拒绝H0：β2=0。

这表明户主受教育年数对家庭书刊年消费支出有显著性影响。

4）所估计的模型的经济意义是当户主受教育年数保持不变时，家庭月平均收入每增加一元时将导致家庭书刊年消费支出增加0.086450元。

而当家庭月平均收入保持不变时，户主受教育年数每增加一年时将导致家庭书刊年消费支出增加52.37031元。

此模型可用于预测将来的家庭书刊年消费支出。

4.31）假定所建立模型中的随机扰动项μi满足各项古典假设，用OLS法估计其参数，得到的回归结果如下。

可用规范形式将参数估计和检验结果写为LnY t = -3.060638+1.056682lnGDP t－1.656536lnCPI t（0.337331）(0.092174) （0.214570）t = (-9.073096) (17.97182) （-4.924656）R2=0.992222 F=1275.739 n=232）数据中有多重共线性，居民消费价格指数的回归系数的符号不能进行合理的经济意义解释，且其简单相关系数呈现正向变动。

1. 回归分析Dependent Variable: LOG(Y) Method: Least Squares Date: 03/18/15 Time: 22:46 Sample: 1 31Included observations: 31Variable Coefficient Std. Error t-Statistic Prob.C 1.153994 0.727611 1.586004 0.1240 LOG(K) 0.609236 0.176378 3.454149 0.0018 LOG(L)0.3607960.201591 1.7897410.0843R-squared0.809925 Mean dependent var 7.493997 Adjusted R-squared 0.796348 S.D. dependent var 0.942960 S.E. of regression 0.425538 Akaike info criterion 1.220839 Sum squared resid 5.070303 Schwarz criterion 1.359612 Log likelihood -15.92300 F-statistic 59.65501 Durbin-Watson stat0.793209 Prob(F-statistic)0.0000002. 方程视图Estimation Command: ===================== LS LOG(Y) LOG(K) LOG(L) CEstimation Equation: =====================LOG(Y) = C(1)*LOG(K) + C(2)*LOG(L) + C(3)Substituted Coefficients: =====================LOG(Y) = 0.6092355345*LOG(K) + 0.360796487*LOG(L) + 1.153994406解：（1）对模型方程左右两边同时取对数得 ln Y =C +αln K +βln L C =ln A +μln e 按上式回归，得方程：ln(Y)= 0.6092355345*ln(K) +0.360796487*ln(L) + 1.1539944068099.02=R7963.02=-R 66.59=F回归变化的结果表明ln(Y)变化的81.0%可由其他两个变量的变化来解释。

第三章 一元经典线性回归模型的基本假设与检验问题3.1 TSS,RSS,ESS 的自由度如何计算？直观含义是什么？答：对于一元回归模型，残差平方和RSS 的自由度是(2)n -，它表示独立观察值的个数。

对于既定的自变量和估计量1ˆβ和2ˆβ，n 个残差 2ˆˆˆi i i iu Y X ββ=-- 必须满足正规方程组。

因此，n 个残差中只有(2)n -个可以“自由取值”，其余两个随之确定。

所以RSS 的自由度是(2)n -。

TSS 的自由度是(1)n -：n 个离差之和等于0，这意味着，n 个数受到一个约束。

由于TSS=ESS+RSS ，回归平方和ESS 的自由度是1。

3.2 为什么做单边检验时，犯第一类错误的概率的评估会下调一半？答：选定显著性水平α之后，对应的临界值记为/2t α，则双边检验的拒绝区域为/2||t t α≥。

单边检验时，对参数的符号有先验估计，拒绝区域变为/2t t α≥或/2t t α≤-，故对犯第I 类错误的概率的评估下下降一半。

3.3 常常把高斯-马尔科夫定理简述为：OLS 估计量具有BULE 性质，其含义是什么？ 答：含义是：（1）它是线性的（linear ）：OLS 估计量是因变量的线性函数。

（2）它是无偏的（unbiased ）：估计量的均值或数学期望等于真实的参数。

比如22ˆ()E ββ=。

（3）它是最优的或有效的（Best or efficient ）：如果存在其它线性无偏的估计量，其方差必定大于OLS 估计量的方差。

3.4 做显著性检验时，针对的是总体回归函数（PRF ）的系数还是样本回归函数（SRF ）的系数？为什么？答：做显著性检验时，针对的是总体回归函数（SRF ）的系数。

总体回归函数是未知的，也是研究者所关心的，所以只能利用样本回归函数来推测总体回归函数，后者是利用样本数据计算所得，是已知的，无需检验。

（习题）3.5 以下陈述正确吗？不论正确与否，请说明理由。

3.2解答：（1）因为自由度df=n-1=14,则样本容量n=15因为有 总变差平方和=参差平方和+回归平方和 ，即TSS=RSS+ESS 则残差平方和RSS=TSS-ESS=66042-65965=77因为有两个解释变量2X 和3X ，则k=3，回归平方和ESS 的自由度为：df=k-1=3-1=2 残差平方和RSS 的自由度为：df=n-k=15-3=12 （2）模型的可决系数为：2659650.99883466042ESS R TSS === 调整后的修正可决系数为：22221111i i e n n R R n k y n k--=-=---∑∑ 15110.9988340.9986153-=-⨯=- （3）从模型的可决系数20.998834R =及修正可决系数20.9986R =可以说明整个模型可以较好的解释被解释变量，即两个解释变量2X 和.3X 联合起来对被解释变量有很显著的影响，但是这并不能确定两个解释变量2X 和.3X 各自对Y 都有显著影响。

要确定每个变量分别对Y 的影响，需要做回归参数的显著性检验（t 检验）。

3.4解答：（１）．建立的模型为t t t t u X X Y +++=33221βββ 经过EViews 软件的处理，可以得到回归分析报告：Dependent Variable: Y Method: Least Squares Date: 03/14/12 Time: 21:32 Sample: 1970 1982 Included observations: 13Variable Coefficient Std. Error t-Statistic Prob. C 7.105975 1.618555 4.390321 0.0014 X2 -1.393115 0.310050 -4.493196 0.0012 R-squared0.872759 Mean dependent var 7.756923 Adjusted R-squared 0.847311 S.D. dependent var 3.041892 S.E. of regression 1.188632 Akaike info criterion 3.382658 Sum squared resid 14.12846 Schwarz criterion 3.513031 Log likelihood -18.98728 F-statistic 34.29559 Durbin-Watson stat2.254851 Prob(F-statistic)0.000033则该模型的估计为：23tˆ7.105975+-1.393115X 1.480674X t t Y =+ 经济学的说明：实际通货膨胀率受到失业率和预期通货膨胀率的共同影响，在预期通货膨胀率不变的前提下，失业率每提高1%，实际通货膨胀率就会平均下降1.393115%；在失业率不变的前提下，预期通货膨胀率每提高1%，实际通货膨胀率就会升高1.480674%。

4、解： （1）不一定，因为题目未告知是否通过了经 济意义检验。猜测为：X1为学生数量，X2 为附近餐厅的盒饭价格，X3为气温，X4为 校园内食堂的盒饭价格； （2）理由是被解释变量应与学生数量成正比， 并且应该影响显著；被解释变量应与本食 堂盒饭价格成反比，这与需求理论相吻合； 被解释变量应与附近餐厅的盒饭价格成正 比，因为彼此有替代作用；被解释变量应 与气温的变化关系不是十分显著，因为大 多数学生不会因为气温变化不吃饭。
6、解： （1）方程B更合理些。 原因是：方程B中的参数估计值的符号与现实更接 近些，如与日照的小时数同向变化，天长则慢跑 的人会多些；与第二天需交学期论文的班级数成 反向变化。 （2）解释变量的系数表明该变量的单位变化，在方 程中其他解释变量不变的条件下，对被解释变量 的影响，由于在方程A和方程B中选择了不同的解 释变量，方程A选择的是“该天的最高温度”， 而方程B选择的是“第二天需交学期论文的班级 数”，造成了与这两个变量之间关系的不同，所 以用相同的数据估计相同的变量得到了不同的符 号。
7、解： （1） 在降雨量不变时,每亩增加1千克肥料将使当年的玉米 产量增加0.1吨/亩;在每亩施肥量不变的情况下,每增加1毫 米的降雨量将使当年的玉米产量增加5.33吨/亩。 （2） 在种地的一年中不施肥也不下雨的现象同时发生的可 能性很小,所以玉米的负产量不可能存在.事实上,这里的截 距无实际意义。 （3） 如果的真实值为0.40,则表明其估计值与真实值有偏误, 但不能说的估计是有偏估计.理由是0.1是的一个估计值,而 所谓估计的有偏性是针对估计的期望来说的,即如果取遍 所有可能的样本,这些参数估计值的平均值与0.4有偏误的 话,才能说估计是有偏的。 （4） 不一定。即便该方程并不满足所有的经典模型假设， 不是最佳线性无偏估计量，的真实值也有等于5.33的可能 性。因为有偏估计意味着参数估计的期望不等于参数本身， 并不排除参数的某一估计值恰好等于参数的真实值的可能 性。

计量经济学第三章练习1．根据我国某省22年的数据估计出下列回归方程其中，Yt ＝第t 年的小麦产量（吨/亩）；HFt ＝第t 年的化肥施用量（公斤/亩）；JRt ＝第t 年的降雨量（寸）。

请分析变量HF 和JR 能否通过拟合优度、F 检验和t 检验，显著性水平为5％ 。

2、考虑以下方程（括号内为估计标准差）其中，Wt ——第t 年员工工资；Pt ——第t 年物价水平；Ut ——第t 年失业率。

（1）该模型是否能通过经济意义的检验？(2)试评价可决系数的值，并在给定显著性水平为5％的情况下，对解释变量进行显著性检验；（3）讨论Pt-1在理论上的正确性，讨论Pt-1在本模型中是否应该删除？为什么？3、假定以校园内食堂每天卖出的盒饭数量作为被解释变量，盒饭价格、气温、附近餐厅的盒饭价格、学校当日的学生数量（单位：千人）作为解释变量，进行回归分析；假设不管是否有假期，食堂都营业。

不幸的是，食堂内的计算机被一次病毒侵犯，所有的存储丢失，无法恢复，你不能说出独立变量分别 代表着哪一项！下面是回归结果（括号内为t 检验值）：被解释变量：每天卖出的盒饭数量解释变量：盒饭价格、气温、附近餐厅的盒饭价格、学校当日的学生数量试判断每项结果对应哪个解释变量？并说明理由。

4、假设要求你建立一个计量经济模型来说明在学校跑道上慢跑一英里或一英里以上的人数，以便决定是否修建第二条跑道以满足所有的锻炼者。

你通过整个学年收集数据，得到两个可能的解释性方程：2800.12 4.985.82)(6.02)0.92.. 1.971197.23t t tY H F JR t R D W F ∧=-++===值:（--128.60.3640.004-2.560(0.08)(0.072)(0.658)0.873,19t t t tW P P U R n ∧=++==12342ˆ10.628.412.70.61 5.9(10.92) (2.02) (1.01) (-0.99) R 0.63,35i i i i iY X X X X n =+++-==方程A ：其中：y —某天慢跑者的人数 ,X1—该天降雨的英寸数,X2—该天日照的小时数， X3—该天的最高温度方程B ：y —某天慢跑者的人数 ,X1—该天降雨的英寸数,X2—该天日照的小时数，x4—第二天需课程作业的班级数 问题：（1）你认为哪个模型更合理？为什么？（2）两个模型都选择日照数为解释变量，为什么得到的系数符号不一样呢？5、课本104页，第4题6、下面的方程式考察工作与休息之间的替代关系，模型设定如下其中，sleep 、work 是每周休息和工作时间（单位分钟），edu 表示受教育的年数，age 为年龄。