电力系统简单计算
- 格式:ppt
- 大小:401.50 KB
- 文档页数:29

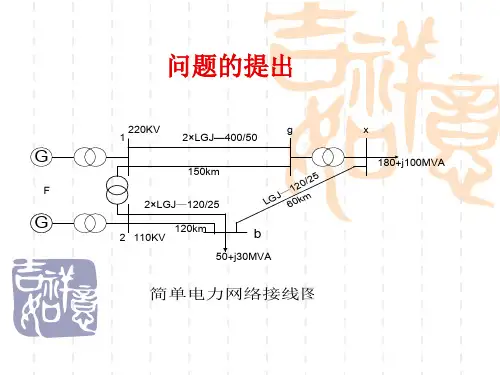

简单电力系统的潮流计算电力系统的潮流计算是电力系统规划和运行中非常重要的一环。
潮流计算的目的是通过计算各节点的电压幅值和相角来确定电力系统中各分支的有功功率和无功功率的分配情况,以便评估系统的稳态运行。
首先,需要建立电力系统的拓扑结构。
拓扑结构描述了电力系统中各组分之间的连接关系。
可以使用节点法或支路法来表示电力系统的拓扑结构。
节点法将电力系统抽象为节点和支路的组成,而支路法则将电力系统抽象为支路和节点的组成。
建立电力系统的拓扑结构后,可以将电力系统表示为节点间的导纳矩阵。
接下来,需要确定各组分的参数。
电力系统中的各组分包括发电机、变压器和负荷。
发电机的参数包括发电机的等值电路参数、有功功率和无功功率等。
变压器的参数包括变压器的等值电路参数、变压器的变压比等。
负荷的参数包括负荷的有功功率和无功功率等。
然后,可以进行潮流计算。
潮流计算的基本原理是根据电力系统的拓扑结构和组分的参数来计算各节点的电压幅值和相角。
计算公式基于功率平衡方程和电流平衡方程。
功率平衡方程表示电力系统中有功功率和无功功率的平衡情况,即输入功率等于输出功率。
电流平衡方程表示电力系统中潮流经过节点和支路的平衡情况。
通过求解这些方程组可以得到电力系统各节点的电压幅值和相角。
最后,可以对潮流计算结果进行分析和评估。
分析和评估的目的是判断系统的稳态运行情况,包括节点电压的稳定性、线路的过载情况等。
根据分析和评估的结果,可以采取相应的措施来改善系统的稳态运行情况,如增加发电容量、改造变压器等。
综上所述,简单电力系统的潮流计算是一个基于电力系统的拓扑结构和组分参数的计算过程,通过计算各节点的电压幅值和相角来确定电力系统中各分支的有功功率和无功功率的分配情况,以评估系统的稳态运行情况。
潮流计算对于电力系统的规划和运行具有重要的意义。


简单电力系统分析潮流计算电力系统潮流计算是电力系统分析中的一项重要任务。
其目的是通过计算各个节点的电压、电流、有功功率、无功功率等参数,来确定系统中各个元件的运行状态和互相之间的相互影响。
本文将介绍电力系统潮流计算的基本原理、计算方法以及应用。
潮流计算的基本原理是基于电力系统的节点电压和支路功率之间的网络方程。
通过对节点电压进行迭代计算,直到满足所有支路功率平衡方程为止,得到系统的运行状态。
潮流计算的基本问题可以表示为以下方程组:P_i = V_i * (G_i * cos(θ_i - θ_j ) + B_i * sin(θ_i -θ_j )) - V_j * (G_i * cos(θ_i - θ_j ) - B_i * sin(θ_i -θ_j )) (1)Q_i = V_i * (G_i * sin(θ_i - θ_j ) - B_i * cos(θ_i -θ_j )) - V_j * (G_i * sin(θ_i - θ_j ) + B_i * cos(θ_i -θ_j )) (2)其中,P_i为节点i的有功功率注入;Q_i为节点i的无功功率注入;V_i和θ_i分别为节点i的电压幅值和相角;V_j和θ_j分别为节点j的电压幅值和相角;G_i和B_i分别为支路i的导纳的实部和虚部。
对于一个电力系统,如果知道了节点注入功率和线路的导纳,就可以通过潮流计算求解出各节点的电压和功率。
这是一种不断迭代的过程,直到系统达到平衡状态。
潮流计算的方法有多种,常见的有高斯-赛德尔迭代法、牛顿-拉夫逊迭代法等。
其中,高斯-赛德尔迭代法是最常用的一种方法。
高斯-赛德尔迭代法的思想是从已知节点开始,逐步更新其他节点的电压值,直到所有节点的电压值收敛为止。
具体步骤如下:1.初始化所有节点电压的初始值;2.根据已知节点的注入功率和节点电压,计算其他节点的电压值;3.判断节点电压是否收敛,如果收敛则结束计算,否则继续迭代;4.更新未收敛节点的电压值,返回步骤2高斯-赛德尔迭代法的优点是简单有效,但其收敛速度较慢。


计算题:1、单母线线路停送电的操作过程:倒闸操作:断路器和隔离开关操作遵循先通后断的原则:切除WL1(断电)拉开 QF3 → QS4 → QS3投入WL1(送电)合上 QS3 → QS4 → QF3基本的操作原则是:操作QS必须是在QF断开的时候进行投入QS时,从电源侧往负荷侧合上QS退出QS时,从负荷侧往电源侧拉开QS第二章作业题:(1)请写出下图中 G1,G2,QS1,QS2,QS3,QS4,QS5,QF1,QF2,QF3 的名称。
答: G1/G2:电源(发电机) QS1/QS2:电源隔离开关 QS3:母线隔离开关 QS4:线路隔离开关 QF1/QF2:电源断路器 QF3:出线断路器 QS5:接地开关(2)请写出线路 WL1 送电,倒闸操作的顺序。
答:合上 QS3 → QS4 → QF3(3)请写出线路 WL1 停电,倒闸操作的顺序。
答: 拉开 QF3 → QS4 → QS32、手算潮流解题思路:(1)求功率:由末端向始端逐点、逐支路推算功率损耗。
(2)求电压:用末端数据,计算阻抗上的电压损耗,得到始端电压一.已知:末端电压 ,末端功率 ,求始端电压 ,始端功率 。
取 为参考方向,则 ,负荷以滞后功率因数运行。
(如何表达负荷以超前功率因数运行?)(1)支路末端导纳支路的功率损耗为:2U 222~jQ P S+=1U 111~jQ P S +=2U 222U U U *==222222222222y y Y Y 2211G j B P j Q 22y y U S I U U U ***∆==⨯=⨯=-=∆-∆ )22222y 22y y 22(2)S S S P jQ P j Q P jQ '''=+∆=++∆-∆=+222222222(3))33()3Z Z ZZZZ ZSI I Z I P Q S Z R jX P j Q U U ***∆==='''+==+=∆+∆ 122211(4)Z Z Z S S S P j Q P jQ P jQ ''''''=∆+=∆+∆++=+ 111221111(5)22y y y S GU j BU P j Q ∆=-=∆-∆ 111111111(6)y y y S S S P jQ P j Q P jQ '''=+∆=++∆-∆=+222222222()()Z S P jQ dU R jX U P R Q X P X Q R j U j UU U δ*'''-===+''''+-=+=∆+二、如果已知始端电压和始端功率,如何求末端电压和末端功率?相量图如何?(老师上课总结过与作业题类似) 三、末端空载时12212221222dU=U+j U U dU+U U U+j U U UarctgU UP R+Q X U U U=U U δδδδ∆==+∆==+∆''=+∆+近似计算:222121~~0~.0,0222222222222222BRU U BXU U X Q R P U BU Q BU j S S jQ P S G R y =<-='-'=∆='⇒-=∆='=+===δ末端空载,则:已知:几个概念:电压降落是指电力线路两端电压的相量差电压损耗是指电力线路两端电压的有效值之差,即U1-U2,电压损耗是一个标量,一般可近似认为U1-U2≈△U ,电压损耗常以百分数表示,即电压偏移是指电力线路两端电压与电力线路额定电压的数值差,电压偏移也常以百分数表示,电力线路两端电压偏移百分数为:电压调整是指电力线路末端空载与负载时电压的数值差,电压调整也常以百分数表示:输电效率是衡量电力线路经济效益的重要指标,是指电力线路末端输出的有功功率P2与电力线路始端输入的有功功率P1之比,其百分数为:第四章作业题:1、负荷由发电厂母线经110kV 单回线供电,线路长80公里,km s b km x km r /1065.2,/429.0,/33.06111-⨯=Ω=Ω=。
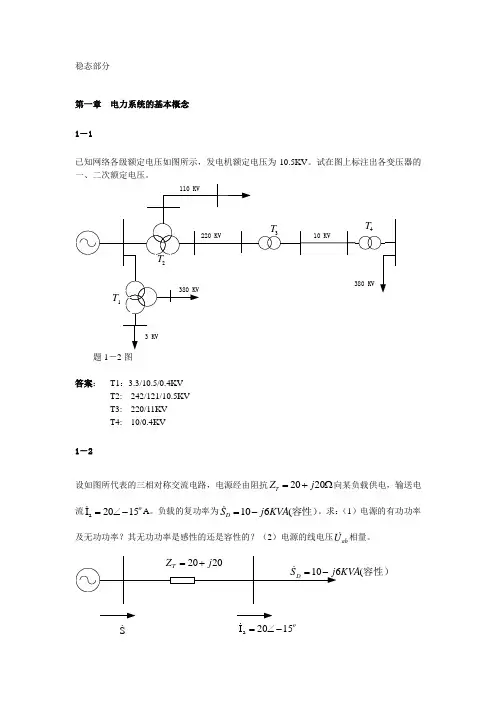
稳态部分第一章 电力系统的基本概念 1-1已知网络各级额定电压如图所示,发电机额定电压为10.5KV 。
试在图上标注出各变压器的一、二次额定电压。
题1-2图答案: T1:3.3/10.5/0.4KV T2: 242/121/10.5KV T3: 220/11KVT4: 10/0.4KV 1-2设如图所代表的三相对称交流电路,电源经由阻抗2020T Z j =+Ω向某负载供电,输送电流a I 2015o =∠-A 。
负载的复功率为106(D S j KVA =-容性)。
求:(1)电源的有功功率及无功功率?其无功功率是感性的还是容性的?(2)电源的线电压ab U 相量。
So1520I a -∠= 容性)(KVA题1-2图答案: (1) 34+j18 即发出有功34KW ,感性无功18Kvar(2)09.421.1∠KV1-3过激运行的三相同步电动机,它的电流I 可以领先电压U ,应用它可以改进功率因数。
设同步电动机的线电压30000ab U =∠V ,线电流50030a I =∠A ,求它的有功功率、无功功率。
它吸收的无功功率是感性的还是容性的? 答案: 1299-j2250(KV A) 1-4如图单相电路,1E 2200=∠V ,2E 22060=∠-V,111Z j =-Ω,336Z j =+Ω, 用复功率概念求:(1)各阻抗消耗功率P 及Q(2)各个电源发出的功率P 1,Q 1,P 2,Q 2(3)分别求出负荷消耗的总功率P L 、Q L 和电源发出的功率电Ps 、Qs ,并检验计算结果。
1E 2E 答案: (1)各阻抗消耗: S1=484-j484(V A ) S2=968+j1452(V A ) S3=1452+j2904(V A ) (2)电源发出: Se1=4805-j579(V A ) Se2=-1901+j4451(V A )(3)总发出的有功:2904W 无功: 3872(Var )可验证有功无功均平衡(或者近似平衡,与计算误差有关) 第二章 电力系统元件参数和等值电路 2-1正三角形排列的架空输电线,若无架空地线。

电力系统分析计算公式1.电力系统潮流计算电力系统潮流计算是一种用于确定电力系统各个节点电压和功率的方法。
常用的电力系统潮流计算公式包括:- 节点功率方程:P = V * I * cos(theta) + V * U * sin(theta) - 节点电流方程:I = V * I * sin(theta) - V * U * cos(theta)其中,P为节点有功功率,V为节点电压,I为节点电流,theta为节点相角,U为无功功率系数。
2.短路电流计算短路电流计算是用于评估电力系统短路故障时电流的大小和方向的方法。
常用的短路电流计算公式包括:- 对称短路电流公式:Isc = V / Zs其中,Isc为短路电流,V为电压,Zs为短路阻抗。
3.电力系统电压稳定性计算电力系统电压稳定性计算是为了评估电力系统节点电压的稳定性。
常用的电力系统电压稳定性计算公式包括:-V/Q稳定器灵敏度公式:dV/dQ=-Ry*dQ/dP+Xy*(dQ/dQ+dV/dV)其中,V为节点电压,Q为节点无功功率,P为节点有功功率,Ry为负荷灵敏度,Xy为发电机灵敏度。
4.功率系统频率计算功率系统频率计算是为了评估电力系统频率的稳定性。
常用的功率系统频率计算公式为:- 系统频率变化率公式:df/dt = (P - Pd) / (2 * H)其中,df/dt为频率变化率,P为实际功率,Pd为负荷功率,H为系统等效惯量。
5.电力系统稳定裕度计算电力系统稳定裕度计算是为了评估电力系统在各种故障情况下的稳定性。
常用的电力系统稳定裕度计算公式包括:- 稳定裕度指标公式:S ω = (δmax - δmin) / δfc其中,Sω为稳定裕度指标,δmax为最大转子转角,δm in为最小转子转角,δfc为临界转子转角。
以上是一些常用的电力系统分析计算公式,这些公式是电力系统工程师进行电力系统设计和运行评估的重要依据。
电力系统分析计算的结果可以帮助工程师评估电力系统的稳定性,指导运维工作,并制定相应的措施以确保电力系统的安全、可靠和高效运行。


电力系统电量计算在电力系统中,电量是一个重要参数,用于衡量电能的消耗和供给。
电力系统电量的计算涉及到电力的功率、时间和效率等因素。
本文将按照合适的格式,简洁明了地介绍电力系统电量计算的相关内容。
一、电力系统基本概念电力系统是由发电站、输电网和配电网组成的,其主要功能是将发电站产生的电能输送到各个用户。
电力系统中的电量是指通过一定时间间隔的电流电量的累加。
电量的单位是千瓦时(kWh),表示一定时间内的电能消耗或供给。
二、电量计算公式电量的计算公式可以根据不同情况进行推导和应用。
以下是一些常见的电量计算公式:1. 单相电路电量计算公式:电量(kWh)= 电压(V) ×电流(A) ×使用时间(h) ×功率因数2. 三相电路电量计算公式:电量(kWh)= √3 × 电压(V) ×电流(A) ×使用时间(h) ×功率因数其中,功率因数是指电路中有功功率和视在功率之间的比值,通常为0到1之间的小数。
三、电量计算实例下面我们通过一个实例来演示电量的计算过程,并使用合适的格式来展示。
假设某家庭使用一台功率为2000瓦的电视机,每天使用5小时。
使用的电压为220伏,功率因数为0.9。
根据单相电路的电量计算公式:电量(kWh)= 220(V) × 2(A) × 5(h) × 0.9= 1980(W) × 5(h) × 0.9= 8910(Wh)= 8.91(kWh)因此,该电视机每天消耗的电量为8.91千瓦时。
四、电量计算的重要性电量的准确计算对于电力系统的管理和资源规划非常重要。
合理估计和控制电量的消耗对于提高能源效率、降低能源浪费具有重要意义。
电量计算可以用于评估设备的能耗情况,优化电力使用方式,减少不必要的能源开支。
五、电量计算的应用领域电量计算广泛应用于各个领域,例如:1. 工业生产:工厂和生产线的电量计算可以帮助评估设备和机器的能耗状况,优化生产过程,提高生产效率。
电力系统的参数计算随着社会的发展和电力需求的增加,电力系统的建设和运行成为人们关注的焦点。
作为电力系统的基本要素和核心部分之一,电力系统的参数计算对于电网的稳定运行和安全性非常重要。
本文将介绍电力系统的参数计算方法、计算过程以及参数计算的应用。
一、电力系统参数的定义和分类电力系统的参数是指用于描述电力系统特性和性能的各种物理量。
根据不同的需求和目的,电力系统参数可以分为静态参数和动态参数两类。
1. 静态参数:指在稳态条件下,电力系统的各种特性和性能所对应的参数。
主要包括:- 电阻(R):用于描述电路中电流通过时的电阻性质;- 电抗(X):用于描述电路中电流通过时的电抗性质;- 电导(G):用于描述电流通过时的电导性质;- 电纳(B):用于描述电流通过时的电纳性质。
2. 动态参数:指在电力系统发生变化或运行过程中,描述电力系统特性和性能所对应的参数。
主要包括:- 暂态电阻(Rt):用于描述电力系统在暂态过程中电流通过时的电阻性质;- 暂态电抗(Xt):用于描述电力系统在暂态过程中电流通过时的电抗性质;- 稳态电阻(Rd):用于描述电力系统在稳态过程中电流通过时的电阻性质;- 稳态电抗(Xd):用于描述电力系统在稳态过程中电流通过时的电抗性质。
二、电力系统参数的计算方法电力系统的参数计算是通过测量电网中的各种物理量,并根据相关的理论和公式进行计算得出的。
常用的电力系统参数计算方法包括:1. 电流计算方法:- 欧姆定律:通过测量电压和电阻,利用欧姆定律计算电流大小;- 电压法:通过测量电流和电阻,利用欧姆定律计算电压大小;- 功率法:通过测量电压和电流,利用功率公式计算功率大小。
2. 电阻和电抗计算方法:- 直流电阻计算:利用直流电压和电流的比值计算直流电阻;- 交流电阻计算:利用交流电压和电流实部的比值计算交流电阻;- 电感计算:通过测量交流电路上的电压和电流,利用复数法计算电感大小。
3. 短路电流计算方法:- 对称分量法:通过对称分量的计算,将不对称短路电流转化为对称短路电流进行计算;- 滑差法:通过测量转子滑差,利用滑差法计算短路电流。
—线路的电压降落和功率损耗—变压器的电压降落和功率损耗—辐射网潮流计算—环网潮流计算*电力系统潮流计算是指节点电压和支路功率分布的计算。
详细地讲,电力系统潮流计算就是根据给定的某些运行条件(比如:有功、无功负荷,发电机的有功出力,发电机母线电压大小等)和电力系统接线方式,求解电网中各母线的电压、各条线路和各台变压器中的功率及功率损耗。
*标志电网电压运行水平的指标(1)电压降落—指线路始、末两端电压的相量差即:(2)电压损耗(或电压损失)—指线路始、末两端电压的数量差,即:U1–U2或(3)电压偏移—指线路始端或末端电压与线路额定电压的数值差,即:U1–U N 及 U2–U N或*线路的电压降落和功率损耗取,则电压降落为:相量图:如果取,则当采用Π型等值电路时,必须考虑并联导纳支路的功率:电压降落:三相功率损耗:注意:公式中的功率为三相功率,并且为直接流入或流出阻抗的功率;电压为线电压。
如果功率为容性,即,则有关公式中的无功功率符号要改变,为:*变压器的电压降落和功率损耗与线路的计算类似。
比如,已知功率和电压则:*放射式电网的潮流计算放射式电网可以简化为末端有一个集中负荷时的线路(或包括变压器):首先作等值电路:或如果已知末端功率和电压,则如果已知末端功率和首端电压,则可以先假设末端电压为U2=U N,由末端起求电网的功率损耗和功率分布,然后用U1和功率分布从始端起求末端节点的电压。
在第六、八讲的习题中,已知线路末端功率为10 MW,cosφ2=0.95滞后或超前,这时的无功功率即为感性或容性。
滞后:φ2 = cos-10.95 =18.195°Q2 = P2tgφ2 = 3.287 Mvar超前:*树枝式电网的潮流计算对于树枝式(或链式、主干式)电网,也仍然需要作等值电路:树枝式电网往往已知末端功率和首端电压,求潮流时可以先假设全网电压为额定电压U N,由末端起求电网的功率损耗和功率分布,最后用U1和功率分布从始端起求其它各节点的电压。
电力系统分析计算公式1. 意义和应用场景电力系统分析是电力系统工程中的重要环节,它主要研究电力系统的稳态和暂态问题,通过分析计算系统中的电压、电流、功率等参数,从而评估系统的稳定性和可靠性,指导电力系统的设计和运行。
在电力系统规划、设计、运行和维护中,我们常常需要用到一些分析计算公式,以便更好地理解和优化电力系统。
本文档将介绍一些常见的电力系统分析计算公式,包括电流计算公式、功率计算公式和电压计算公式。
这些公式可以用于分析电力系统的各种问题,比如短路计算、电能损耗计算等。
2. 电流计算公式2.1 直流电流计算公式直流电流计算公式用于计算直流电路中的电流。
根据欧姆定律,直流电流可以通过电压和电阻来计算,其公式为:I = V / R其中,I 表示电流,V 表示电压,R 表示电阻。
2.2 交流电流计算公式交流电流计算公式用于计算交流电路中的电流。
在纯电阻电路中,电流可以通过电压和电阻来计算,其公式为:I = V / Z其中,I 表示电流,V 表示电压,Z 表示电阻。
在交流电路中,电阻可以用复阻抗表示,复阻抗由电阻和电感或电容的阻抗组成。
3. 功率计算公式3.1 有功功率计算公式有功功率是电路中用于产生功率的部分,可以通过电压、电流和功率因数来计算。
其公式为:P = V * I * cos(θ)其中,P 表示有功功率,V 表示电压,I 表示电流,θ 表示功率因数。
3.2 无功功率计算公式无功功率是电路中储存和释放能量的部分,可以通过电压、电流和功率因数来计算。
其公式为:Q = V * I * sin(θ)其中,Q 表示无功功率,V 表示电压,I 表示电流,θ 表示功率因数。
3.3 视在功率计算公式视在功率是无功功率和有功功率的平方和的平方根,可以通过电压和电流来计算。
其公式为:S = sqrt(P^2 + Q^2)其中,S 表示视在功率,P 表示有功功率,Q 表示无功功率。
4. 电压计算公式4.1 直流电压计算公式直流电压计算公式用于计算电路中的电压。