两因素方差分析检验讲解学习

两因素重复测量方差分析，史上最详细SPSS教程！一、问题与数据研究者想知道短期(2周)高强度锻炼是否会减少C反应蛋白(C-Reactive Protein, CRP)的浓度。

研究者招募了12名研究对象，并让研究对象参与两组试验：对照试验和干预试验。

在对照试验中，研究对象照常进行日常活动；在干预试验中，研究对象每天进行45分钟的高强度锻炼，每组试验持续2周，两组试验中间间隔足够的时间。

CRP的浓度在每组试验中共测量了3次：试验开始时的CRP浓度、试验中的CRP浓度(1周)和试验结束时的CRP浓度(2周)。

这三个时间点代表了受试者内因素“时间”的三个水平，因变量是CRP的浓度，单位是mg/L。

con_1、con_2和con_3分别代表对照试验开始时、对照试验中和对照试验结束时研究对象的CRP浓度，int_1、int_2和int_3分别代表干预试验开始时、干预试验中和结束时研究对象的CRP浓度。

部分数据如下：二、对问题的分析使用两因素重复测量方差分析(Two-way Repeated Measures Anova)进行分析时，需要考虑5个假设。

对研究设计的假设：假设1：因变量唯一，且为连续变量；假设2：有两个受试者内因素（Within-Subject Factor），每个受试者内因素有2个或以上的水平。

注：在重复测量的方差分析模型中，对同一个体相同变量的不同次观测结果被视为一组，用于区分重复测量次数的变量被称为受试者内因素，受试者内因素实际上是自变量。

对数据的假设：假设3：受试者内因素的各个水平，因变量没有极端异常值；假设4：受试者内因素的各个水平，因变量需服从近似正态分布；假设5：对于受试者内因素的各个水平组合而言，因变量的方差协方差矩阵相等，也称为球形假设。

三、思维导图（点击图片看清晰大图）四、SPSS操作两因素重复测量方差分析的操作1. 在主菜单下点击Analyze > General Linear Model > Repeated measures...，如下图所示：2. 出现Repeated Measures Define Factor(s)对话框，如下图所示：3. 在Within-Subject Factor Name:中将“factor1”更改为treatment，因为研究对象共进行了2组试验，在Number of Levels：中填入2；4. 点击Add，出现下图：5. 在Within-Subject Factor Name:中填入time，因为研究对象的CRP水平在每组试验中共测量了3次，在Number of Levels：中填入3，点击Add；6. 点击Define，出现下图Repeated Measures对话框；7. 如下图所示，Within-Subjects Variables后面的括号内是受试者内因素的名字，将左侧六个变量均选入右侧框中，如下图所示：8. 点击Plots，出现Repeated Measures: Profile Plots 对话框，如下图所示：9. 将time选入Horizontal Axis：框中，将treatment选入Separate Lines：框中；10. 点击Add，出现下图，点击Continue；11. 点击Save，出现Repeated Measures: Save对话框；12. 在Residuals下方选择Studentized，如下图所示，点击Continue；13. 点击Options，出现Repeated Measures: Options对话框；14. 将treatment、time和treatment*time选入Display Means for：中，下方Compare main effects为勾选状态，在Confidence interval adjustment：下选择Bonferroni，在Display下方勾选Descriptive statistics 和Estimates of effect size，点击Continue，点击OK。

双因素方差分析结果解读双因素方差分析（Two-wayANOVA）是一种分析数据的统计方法，它可以检验同一总体的两个或多个变量之间的差异。

双因素方差分析的一个重要特点是它可以检验基于不同组别、不同资源或者不同情况下同一个总体上的差异。

它可以检验在多个组别之间存在差异、或者在不同组别之间存在偏差的情况。

本文将通过介绍双因素方差分析的原理、分析方法、结果解读方法，帮助读者更好地解读双因素方差分析的结果。

首先，双因素方差分析的原理是涉及两个不同的自变量，即因变量和一个或多个自变量。

因变量是一个连续的响应变量，而自变量则分为定类的自变量和定序的自变量，根据不同的实验需求采用不同的变量。

例如，定类的自变量可以用于比较基于性别或不同药物治疗后被试者的反应，定序的自变量则可用于比较基于疗程的不同反应。

其次，双因素方差分析需要构建一个双因素的实验单元，即一个自变量和一个因变量的实验设计，它可以确定每个组别之间的比较，比如在不同性别和不同处方药物治疗下被试者的反应。

双因素方差分析可以检验两个或多个因变量是否相对独立，以及独立或不独立的因变量是否存在差异。

最后，双因素方差分析的结果解读是比较重要的一步，它可以有效地解释出双因素实验单元下的差异或偏差，帮助研究者更好地做出他们的决策。

通常，根据双因素方差分析的结果可以检测出两个或多个自变量的差异，以及基于性别、时间、处方药物治疗等不同情况下的被试者的反应等。

只有当双因素方差分析的F值超过某一显著性水平的时候（通常为0.05或0.01），双因素方差分析的结果才被认为是显著的，可以通过结果解释和决策。

综上所述，双因素方差分析是一种非常有用的统计方法，可以检验同一总体的两个或多个变量之间的差异。

其中双因素方差分析原理，分析方法，以及结果解读方法都非常重要，有助于我们在解决实际问题时更好地解读双因素方差分析的结果，识别出不同组别，或者在不同组别之间存在的差异，从而发现新的实验结果，增加研究的学术价值。

双因素方差分析一、双因素方差分析的含义和类型（一）双因素方差分析的含义和内容在实际问题的研究中，有时需要考虑两个因素对实验结果的影响。

例如上一节中饮料销售量的例子，除了关心饮料颜色之外，我们还想了解销售地区是否影响销售量，如果在不同的地区，销售量存在显著的差异，就需要分析原因，采用不同的推销策略，使该饮料品牌在市场占有率高的地区继续深入人心，保持领先地位，在市场占有率低的地区，进一步扩大宣传，让更多的消费者了解，接受该产品。

在方差分析中，若把饮料的颜色看作影响销售量的因素A，饮料的销售地区看作影响因素B。

同时对因素A和因素B进行分析，就称为双因素方差分析。

双因素方差分析的内容包括：对影响因素进行检验，究竟一个因素在起作用，还是两个因素都起作用，或是两个因素的影响都不显著。

双因素方差分析的前提假定：采样地随机性，样本的独立性，分布的正态性，残差方差的一致性。

（二）双因素方差分析的类型双因素方差分析有两种类型：一个是无交互作用的双因素方差分析，它假定因素A 和因素B的效应之间是相互独立的，不存在相互关系；另一个是有交互作用的双因素方差分析，它假定因素A和因素B的结合会产生出一种新的效应。

例如，若假定不同地区的消费者对某种品牌有与其他地区消费者不同的特殊偏爱，这就是两个因素结合后产生的新效应，属于有交互作用的背景；否则，就是无交互作用的背景。

有交互作用的双因素方差分析已超出本书的范围，这里介绍无交互作用的双因素方差分析。

1.无交互作用的双因素方差分析。

无交互作用的双因素方差分析是假定因素A和因素B的效应之间是相互独立的，不存在相互关系；2.有交互作用的双因素方差分析。

有交互作用的双因素方差分析是假定因素A和因素B的结合会产生出一种新的效应。

例如，若假定不同地区的消费者对某种颜色有与其他地区消费者不同的特殊偏爱，这就是两个因素结合后产生的新效应，属于有交互作用的背景，否则，就是无交互作用的背景。

二、数据结构方差分析的基本思想：通过分析研究中不同来源的变异对总变异的贡献大小，从而确定可控因素对研究结果影响力的大小。

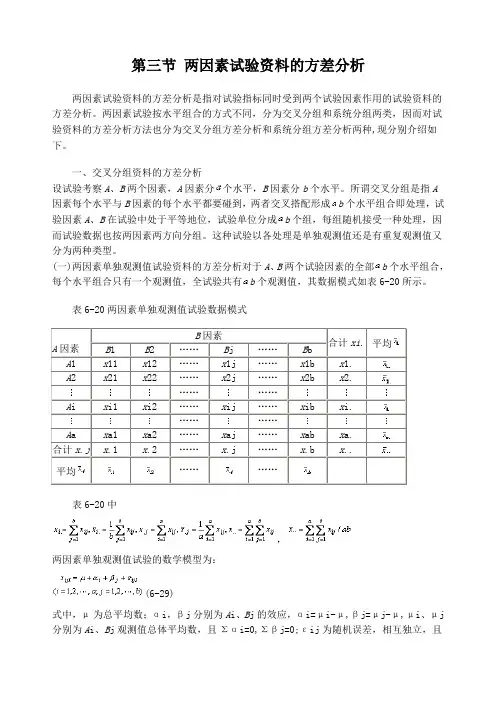
第三节两因素试验资料的方差分析两因素试验资料的方差分析是指对试验指标同时受到两个试验因素作用的试验资料的方差分析。

两因素试验按水平组合的方式不同，分为交叉分组和系统分组两类，因而对试验资料的方差分析方法也分为交叉分组方差分析和系统分组方差分析两种,现分别介绍如下。

一、交叉分组资料的方差分析设试验考察A、B两个因素，A因素分个水平，B因素分b个水平。

所谓交叉分组是指A因素每个水平与B因素的每个水平都要碰到，两者交叉搭配形成b个水平组合即处理，试验因素A、B在试验中处于平等地位，试验单位分成b个组，每组随机接受一种处理，因而试验数据也按两因素两方向分组。

这种试验以各处理是单独观测值还是有重复观测值又分为两种类型。

(一)两因素单独观测值试验资料的方差分析对于A、B两个试验因素的全部b个水平组合，每个水平组合只有一个观测值，全试验共有b个观测值，其数据模式如表6-20所示。

表6-20两因素单独观测值试验数据模式平均平均表6-20中，两因素单独观测值试验的数学模型为：(6-29)式中，μ为总平均数；αi，βj分别为A i、B j的效应，αi=μi-μ,βj=μj-μ,μi、μj 分别为A i、B j观测值总体平均数，且Σαi=0,Σβj=0;εij为随机误差，相互独立，且服从N(0，σ2)。

交叉分组两因素单独观测值的试验，A因素的每个水平有b次重复，B因素的每个水平有次重复，每个观测值同时受到A、B两因素及随机误差的作用。

因此全部b个观测值的总变异可以剖分为A因素水平间变异、B因素水平间变异及试验误差三部分；自由度也相应剖分。

平方和与自由度的剖分式如下：(6-30)各项平方和与自由度的计算公式为矫正数总平方和A因素平方和B因素平方和(6-31)误差平方和SS e=SS T-SS A-SS B总自由度dfT=ab-1A因素自由度dfA=a-1B因素自由度dfB=b-1误差自由度dfe=dfT-dfA-dfB=(a-1)(b-1)相应均方为【例6.5】为研究雌激素对子宫发育的影响，现有4窝不同品系未成年的大白鼠，每窝3只，随机分别注射不同剂量的雌激素，然后在相同条件下试验，并称得它们的子宫重量，见表6-21，试作方差分析。

两因素重复方差测量结果解读重复方差分析（RFA）是统计学中常用的一种分析方法，用于研究两种或多种因素变量之间的相互作用效果。

近年来，重复方差分析的应用越来越广泛，已成为社会科学研究领域中最常用的分析方法之一。

本文将针对重复方差分析中两因素的情形，对重复方差分析的概念、意义以及其在社会科学研究中的应用进行深入分析，最终提供一种有效的解释方案。

一、重复方差分析概述重复方差分析（RFA）是一种统计学方法，用于研究两个因素或多个因素之间的相互作用效果，常用来检验一个因素对另一个因素的影响程度，或者多个因素是否同时影响一个结果。

重复方差分析的基本原理是，将可以解释总变差的部分拆解成各个自变量和共同变量，以便研究它们之间的关系。

重复方差分析关注的是总变差的分配，以及那些变差是由自变量引起而不是其他因素引起。

二、两因素重复方差分析原理两因素重复分析（RFA）是其中一种重复分析方法，被认为是社会科学研究中最常用的分析方法之一。

两因素重复方差分析是指将总变差分解成自变量和共同变量的影响，仅使用两个因素：一个主要因素和一个控制变量，来检验假设模型的差异。

两因素重复方差分析可以用来检验主要变量对被观察变量的影响，以及它们之间的交互作用效果是否具有显著性。

三、两因素重复方差分析在社会科学研究中的应用重复方差分析不仅可以检验参与者之间的因素和变量之间的关系，也可以检验因素和变量之间的交互作用是否对结果有重要影响。

由于重复方差分析方法具有完整性和便捷性，因此在社会科学研究中被广泛用于各种社会和心理学概念的研究，以进一步了解影响变量的影响力以及它们之间的关系。

四、解释重复方差分析的措施重复方差分析的解释依赖于该研究的实际意义和研究设计，以利用上述因素和变量之间的关系提供准确的解释。

重复方差分析的解释包括以下几个方面：（1）检验双方变量；（2）检验主要变量的影响；（3）验双方变量的交互作用；（4）使用多元分析确定变量的重要性。