小升初数学—大小比较讲解及试题

小升初六年级数学比和比例专题讲解第二讲比和比例教学目标：1、比例的基本性质2、熟练掌握比例式的恒等变形及连比问题3、能够进行各种条件下比例的转化，有目的的转化；4、单位“1”变化的比例问题5、方程解比例应用题知识点拨：比例与百分数作为一种数学工具在人们日常生活中处理多组数量关系非常有用，这一部分内容也是小升初考试的重要内容.通过本讲需要学生掌握的内容有：一、比和比例的性质性质1：若a:b=c：d，则(a+c)：(b+d)=a：b=c：d；性质2：若a:b=c：d，则(a-c)：(b-d)=a：b=c：d；性质3：若a:b=c：d，则(a+xc)：(b+xd)=a：b=c：d；(x 为常数)性质4：若a:b=c：d，则a×d=b×c；(即外项积等于内项积) 正比例：如果a÷b=k(k为常数)，则称a、b成正比；反比例：如果a×b=k(k为常数)，则称a、b成反比．二、主要比例转化实例xaabybxy①；；；XXXxamxaxma②(其中m)；；XXXxaxax ya bx ya b③。

ybx ya bx ya bxaxaycxac④，；x:y:zXXXcdadbc⑤x的等于y的，则x是y的，y是x的．abbcad三、按比例分配与和差关系⑴按比例分配例如：将x个物体按照a:b的比例分配给甲、乙两个人，那么实际上甲、乙两个人各自分配到的物体数量与x axbx的比分别为a:a b和b:a b，以是甲分派到个，乙分派到个.a ba b⑵两组物体的数量比和数量差，求各个种别数量的问题ax比方：两个种别A、B，元素的数量比为a:b(这里a b)，数量差为x，那么A的元素数量为，B的a bbx元素数量为，以是解题的关键是求出a b与a或b的比值．a b四、比例题目常用解题方式和思路解答分数应用题关键是正确理解、运用单位“l”。

题中如果有几个不同的单位“1”，必须根据具体情况，将不同的单位“1”，转化成统一的单位“1”，使数量关系简单化，达到解决问题的效果。

第9讲比较大小第一关整数的大小比较【学问点】1.整数的大小比较：位数越多的整数越大，假如位数相同，则从最高位起依次比较各位数字大小，相同位上数字越大的整数越大．2.特殊方法：①放缩法：依据分子不变分母转变或者分母不变分子转变，对分数进行肯定的处理，得到形式简洁的、大小介于两者之间的数，参与比较，简化比较过程．②倒数法：倒数越大，数越小．某些分子分母之间的关系相差不大的分数作比较时，假如分数结构简单不适合通分解决，取它们的倒数是比较有效的方法，但必需对分数有特定要求．③等值放缩比较法：两个分数比较，分母或者分子相差肯定的倍数时，使用通分法将分母或者分子放缩为相近的数，然后比较得到的结果．④归一法：假如相比较的两个分数结构简单，但是分子分母相差很小，即分数值与1很接近，则将问题转化为比较两个分数与1的差的大小．【例1】在8050、8505、8500、8005这四个数中，最接近8000的是__________。

【答案】8005【例2】A=123456789，B=98765432，最接近1亿的数是__________。

【答案】B【例3】比较大小：A=9876543×3456789，B=9876544×3456788。

【答案】A【例4】把下列数量从小到大排列：10.5公顷10公顷50平方米10.5亩10500平方米．【答案】10.5亩＜10500平方米＜10公顷50平方米＜10.5公顷【例5】北京到西安的飞机票价是每张960元．张老师想从网上订购一张从北京到西安的飞机票．海蓝票务中心的机票以九五折出售，但每张票要加收30元送票费；云天票务中心的机票不打折，但免费送票．张老师从__________票务中心购买飞机票更省钱．（填“海蓝”或“云天”）【答案】海蓝【例6】对于两个数，M=1998×19991999，N=1999×19981998．小王说，M比N大；小张说，N比M 大；小李说，M和N相等．你认为说对的是____________。

数字比大小的数学题数字比大小是我们在数学学习中最早接触到的概念之一，也是非常基础且重要的一部分。

从幼儿园的小朋友开始认识数字，到小学生逐步掌握加减法，再到更高年级学习复杂的数学运算，数字比大小都贯穿始终。

当我们面对两个或多个数字时，要判断它们的大小关系，其实有一些简单而直观的方法。

比如，对于个位数来说，1 比 0 大，2 比 1 大，以此类推，9 是最大的个位数。

这是我们最初对数字大小的直观感受。

当数字变得稍微大一些，比如两位数 12 和 21，我们可以先比较十位上的数字。

十位上数字大的那个数就大，如果十位上的数字相同，再比较个位上的数字。

所以在 12 和 21 中，十位上 2 大于 1，所以 21大于 12 。

再看三位数，比如 123 和 231 。

还是先比较百位，百位上 2 大于 1，所以 231 大于 123 。

如果百位相同，就接着比较十位，十位也相同再比较个位。

对于正数和负数的比较，这可能会稍微有点复杂。

正数是大于 0 的数，负数是小于 0 的数。

所以所有的正数都大于负数。

比如 5 大于－5 。

当两个负数比较大小时，数字越大的反而越小。

例如－2 和－5 ，虽然 5 大于 2 ，但因为是负数，所以－2 大于－5 。

在实际生活中，数字比大小也有很多的应用。

比如说在购物的时候，我们会比较不同商品的价格。

如果一件商品的价格是 50 元，另一件是80 元，我们就能很容易地判断出 50 元的商品更便宜。

在比赛的计分中，比如篮球比赛，球队的得分有高有低，通过比较得分的大小来判断哪支球队更优秀。

在测量身高体重时，我们也会用到数字比大小。

比如小明的身高是150 厘米，小红的身高是 145 厘米，我们能得出小明比小红高。

在数学的学习中，数字比大小不仅仅是一个简单的操作，它还为我们后续学习更复杂的数学知识打下了基础。

比如在学习不等式、函数的单调性等内容时，都需要我们对数字大小的关系有清晰的认识和准确的判断。

在解决数字比大小的数学题时，我们要仔细观察数字的特点，选择合适的比较方法。

比和比例⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧→→⎭⎬⎫→→⎪⎩⎪⎨⎧⎩⎨⎧⎭⎬⎫→⎪⎭⎪⎬⎫→⎩⎨⎧→→→应用意义正、反比例解比例性质意义比例比例尺按比例分配求未知数化简比性质求未知数求比值比与除法、分数的关系意义比比和比例一、本章概念： 比：比的意义：两个数相除，又叫做两个数的比。

比值：比的前项除以后项所得的商，叫作比值。

比值相等的两个比相等。

比、分数、除法的关系：)0(:≠÷==b b a bab a比的基本性质：比的前项和后项同时乘以或除以相同的数（0除外），比值不变。

按比例分配：在工农业生产和日常生活中，常常需要把一个数量按照一定的比例进行分配。

比例：比例的意义：表示两个比相等的式子叫作比例。

比例的基本性质：在比例里，两个外项的积等于两个内项的积。

解比例：根据比例的基本性质，如果已知比例中的任何三项，就可以求出这个比例中的另一个未知项。

求比例中的未知项，叫做解比例。

比例尺：图上距离和实际距离的比，叫做这幅图的比例尺。

比例尺分为数值比例尺和线段比例尺。

正比例的意义：两种相关联的量，一种量变化，另一种也随着变化，如果这两种量中相对应的两个量的比值（也就是商）一定，这两种量叫做成正比例的量，它们的关系叫作正比例关系。

如果用字母x 和y 分别表示两种相关联的量，用k 表示它们的比值，正比例关系的式子可表示为：（一定）k xy =。

反比例的意义：两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量对应的两个量积一定，这两种量就叫作反比例的量，它们的关系叫作反比例关系。

如果用字母x 和y 分别表示两种相关联的量，用k 表示它们的积，反比例关系可以用式子表示为：（一定）k xy =。

二、先关概念的比较1.比和比例的意义、形式、组成和基本性质的区别意义 形式 各部分名称 组成 基本性质比两个数相除由两项组成（前项、后项）项后号比：项前↓↓↓7149任意两个数都可以组成比（同类量或不同类量） 比的前项和后项同时乘以或除以相同 的数（0除外），比值不变比例两个比相等的式子由四项组成（内项、外项各两个）任意四个数不一定能组成比例 在比例里，两个外项的积等于两个内项的积2.比、分数和除法的区别和联系相当部分区别比（bab a 或:） 前项 比号（：） 后项 比值 两个数的倍比关系分数（ba ） 分子 分数线（—） 分母 分数值 一个数值 除法（b a ÷）被除数除号（÷）除数商一种运算3.求比值和化简的区别意义一般方法结果求比值 前项除以后项所得的商根据比值的意义，用前项除以后项是一个商，可以是整数、小数或分数化简比把两个数的比化成最简单的整数比 根据比的基本性质，比的前项和后项同时乘以或除以相同的数（0除外）；有时也可以用求比值的方法来化简比 是一个比，它的前项和后项都是整数，而且公因数只有1 注意：当同类量的两个数相比，前项和后项单位不同时，要先化成相同的单位，然后再求比值或者化简比。

小升初——10、比较分数的大小知识要点：1、通分，同分子或同分母比较。

2、标准法：两个分数都接近一个数，可分别求出它们与1的差，比较差的大小，差小的那个分数反而大。

3、倒数法：倒数小的那个分数反而大。

4、一个最简真分数的分子、分母同时加上相同的数，所得的分数比原分数大；一个比1大的假分数的分子、分母同时加上相同的数，所得的分数比原分数小。

例1：比较 89 和 56 的大小。

例2：将下列三个分数按照从小到大的顺序排列起来。

20202017，9087，20192016例3：将下列分数按照从小到大的顺序排列起来。

2321，8984，1312，3128，1514例4：比较6666555和666665555的大小。

例5：将0.••15 、32 、0.5•1 、 95 、0.518 、4724这些数从大到小排列起来。

例6：已知b a 是一个最简分数，并且b a >1。

那么ba 与19981998++b a 哪一个大？例7：2000199819981997（ ）194920001998194919981997−−练习：一、比较下面各组中两个分数的大小。

1、8785 （ ） 10199 2、 98761234 （ ） 98751233 3、5557777 （ ） 5555777773、2312 （ ） 24114、338 （ ） 7865、4998979649999897++（ ）9897969998977、3421 （ ） 5534 9、88888898888887和 9999994999999110、399299（ ） 40230211、15829（ ）9817二、将下列各分数按照从小到大的顺序排列起来。

！）75，1712，2920，89602）2002200220012001，2004200420032003，2003200320022002三、在157、0.••564、2512、0.47中最小的一个数是多少？四、填空：〈32〈（ ）（ ）〈（ ）（ ）43。

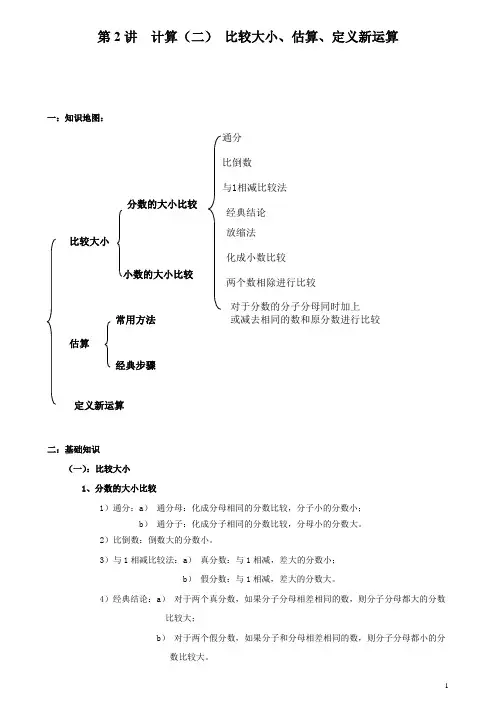
第2讲 计算（二） 比较大小、估算、定义新运算一：知识地图：二：基础知识（一）：比较大小1、分数的大小比较1）通分：a ） 通分母：化成分母相同的分数比较，分子小的分数小；b ） 通分子：化成分子相同的分数比较，分母小的分数大。

2）比倒数：倒数大的分数小。

3）与1相减比较法：a ）真分数：与1相减，差大的分数小；b ） 假分数：与1相减，差大的分数大。

4）经典结论：a ） 对于两个真分数，如果分子分母相差相同的数，则分子分母都大的分数比较大；b ） 对于两个假分数，如果分子和分母相差相同的数，则分子分母都小的分比较大小 分数的大小比较 通分 比倒数 与1相减比较法 经典结论 放缩法 化成小数比较 两个数相除进行比较 对于分数的分子分母同时加上 或减去相同的数和原分数进行比较 小数的大小比较 估算 常用方法 经典步骤 定义新运算对于分数的分子分母同时加上或减去相同的数和原分数进行比较：（a b >，且,,a b c 为非零自然数时）（1）,b b c b b c a a c a a c+-<>+- 即“真分数越加越大，越减越小”（0a c -≠）如331331,551551+-<>+-； （2）,a a c a a c b b c b b c+->>+-即“假分数越加越小，越减越大”。

5）放缩法。

6）化成小数比较：小数比较大小的关键是小数点对齐，从高位比起。

切记！7）两个数相除进行比较。

如：34和57，352114720÷=>，所以3547>。

2、小数的大小比较常用方法：将小数排成一个竖列，并在它们的末尾添上适当的“0”，使它们都变成小数位数相同的小数，然后比较。

（二）估算问题1、常用方法1） 放缩法：为求出某数的整数部分，设法放大或缩小，将结果确定在两个接近数之间，从而估算出结果。

2）变换结构：将算式变形为便于估算的形式。

2、经典步骤估算和式整数部分：a ） 令和式结果等于A ；b ） 最小的数×个数＜A ＜最大的数×个数；c ） 求A 。

小升初分班考数学：比较大小如果a=2020/2021 b=2021/2022 则a、b中比较大的数是？法1：直接比较。

统分，这时候要注意，不要着急化简，特别是分母并不影响这这个数与零大小的比较，更不能算出来。

a-b=2020/2021 -2021/2022 =（2020×2022-2021×2021）/2021×2022看分母即可：2020×2022-2021×2021=（2021-1）×（2021+1）-2021×2021 =-1＜0所以a＜b法2：观察到a、b与1都很接近，故我们可以将a、b与1比较大小后，再进行相应的比较。

1-a=1-2020/2021=1/20211-b=1-2021/2022=1/2022因为1/2021＞1/2022 所以1-a＞1-b 即-a＞-b 即b＞a法3：倒数法。

显然a＞0，b＞0，若1/a ＞1/b ，则b＞a1/a=2021/2020 =1+ 1/20201/b=2022/2021 =1+ 1/2021所以1/a ＞1/b 所以 b＞a法4：生活中的事情来理解。

（其实这在高中叫“糖水不等式”）简单说就是如果溶液的质量为a，溶质的质量为b，则浓度为 b/a若再往这瓶溶液中加入溶质m克（假设可以完全溶解），则浓度变为（b+m）/（a+m）因为加入溶质，从而浓度一定是增大了，也就是后来的浓度大于先前的浓度，也就是有以下不等式成立：（b+m）/（a+m）＞ b/a对于本题来说，若溶液1的密度为2020/2021 加入1个单位溶质后，变成溶液2的密度为2021/2022易知溶液2的密度大于溶液1的密度，也就是2021/2022 ＞2020/2021就是b＞a小升初/分班考数学：解方程小升初/分班考数学：简便运算几题小升初数学：求阴影部分面积：探究、归纳、化归为何被3整除的数，其各个位上的数字之和能被3整除？小升初数学：简便运算——拆分、重组小升初数学：简便运算-不着急计算出结果，带分数进行计算小升初数学：简便运算——整体代换回答上次留的作业题小升初/分班考数学：分橘子练习：a=1/3 +1/4 b=1/5+1/6+1/7 则a、b中较大的数是。

PC 第02讲分数的大小比较与运算教学目标：1、使学生理解分数的意义，通过"分数墙"对分数的大小比较和加减计算进行整理，直观建立起分数大小比较和加减计算的统一模型，对相等的分数进行直观探究；2、培养学生观察能力、归纳总结能力、推理判断能力和初步逻辑思维能力；3、让学生在学习过程中养成互相帮助、团结协作的良好品德。

教学重点：建立分数大小比较和加减法计算的统一模型。

教学难点：发现和探究大小相等的分数。

教学过程：【温故知新】1、整体分成若干份，其中的一份或几份用分数表示，分数由分母、分数线、分子组成；分母表示一个整体被平均分成的份数，分子表示有这样的几份；2、几分之一：把一个整体（总数）平均分成若干份，取其中的一份，就是几分之一，几分之几：几个几分之一就是几分之几；一个整体被平分成几个部分，每一个部分就是整体的几分之一。

3、数形结合表示分数。

【巩固作业1】生活中有很多时候需要大家做出判断，袋鼠老师给大家出了很多道判断题，同学们，大家一起判断下面的说法是否正确（用“√”和“×”表示）。

（1）分数线下面的数叫分子。

（）（2）将一张纸对折、对折、再对折后折纸面的大小是原来的13。

（）（3）8个小朋友分吃一个蛋糕，每人吃18。

（）（4）20千克糖平均装在10个盒子里，每盒装了这些糖的110。

（）（5）小明吃了一个苹果的一半的一半，他吃了这个苹果的18。

（）解析部分：让学生回顾这些问题，分数是由哪些部分组成的？平均分是什么意思？分数线下面的叫分母，上面的叫分子；大家动动手，将一张纸对折、对折、再对折后是原来的18；8个小朋友分吃一个蛋糕，如果平均分，那么每人吃了这个蛋糕的18；小明吃了一个苹果的一半的一半，他吃了这个苹果的14。

给予新学员的建议：教师给学生补充分数的组成部分；哈佛案例教学法：鼓励学生独立完成，课堂上分享解题方法。

参考答案：（1）×，（2）×，（3）×，（4）√，（5）×。

第6讲 比较数的大小1、考察范围：分数与小数的大小比较。

2、考察重点：异分母分数大小比较，分数小数百分数之间的转化。

3、命题趋势：多以选择填空为主，考察分数、小数之间的大小比较。

1、常用方法. ★同分母的分数，分子越大，分数值越大。

同分子的分数，分母越大，分数值越小。

★异分母的分数，先通分母，再运用同分母分数大小比较的方法。

（或通分子）★分数、小数、百分数之间比较大小，可统一转化成分数或小数进行比较。

★分子和分母差一定时，分子或分母越大的分数，其值越大。

2、特殊方法.★基准数法：确定一个标准，使所有分数都和它比较。

★着商法：用一个数除以另一个数，把得数和1进行比较。

★着差法：用一个数减去另一个数，把得数和0进行比较。

★倒数法：利用倒数比较大小，然后确定原数的大小。

【例1】 在1912，2315，9760三个数中，最大的是 ，最小的是 。

【变式练习】1、把下面几个数按照从大到小的顺序排列：95，1910，3715，6130。

2、把下面几个数按照从大到小的顺序排列：74，116，178，2312，5324。

考点解读知识梳理典例剖析【例2】 把下面几个数按照从小到大的顺序排列：53，1，85，π，14.3，722。

【变式练习】1、某超市有甲、乙、丙三种餐巾纸，甲种1元钱3包，乙种2元钱5包，丙种3元钱8包， 种纸每包价格最贵。

2、已知10＜＜x ，将x ，x1，2x 按从小到大的顺序排列。

【例3】 比较1666333=A 和16633=B 的大小。

【变式练习】1、比较7777777和777777777的大小。

【例4】 比较99988887=A 和66655554=B 的大小。

【变式练习】1、比较335234=A ，22352134=B ，890789=C 三个数的大小。

2、比较100710022=A ，89842=B ，34292=C 三个数的大小。

【例5】 比较6868686813131313和6813的大小。

小升初比的典型练习题一．选择题（共22小题）1．把10克糖容在100克水中，水与糖水的比是（）A．1：10B．1：11C．9：10D．10：112．把5克盐溶于100克水中，盐与盐水的重量比是（）A．1：19B．1：20C．1：213．把10克盐溶解在100克水中，盐与盐水的重量比是（）A．1：10B．1：11C．10：114．圆柱体的侧面展开图是一个正方形，底面直径与高的比是（）A．1：πB．1：2πC．1：4 πD．2：π5．甲比乙多2倍，乙比丙多1/2，则甲：乙：丙=（）A．3：1：2B．2：1：3C．3：1：6D．9：3：26．一种糖水，糖占25%，糖与水的比是（）A．1：4B．1：3C．4：1D．25：1007．李师傅做一批零件，以前要1小时完成，现在提前了1/6小时，现在的工效与原来工效之比是（）A．6：5B．5：6C．6：18．笔筒里红铅笔和黑铅笔一共有12支，红铅笔与黑铅笔的比不可能是（）A．1：2B．1：3C．1：4D．无选项9．如果A×2=B÷3，那么A：B=（）A．2：3B．6：1C．1：610．一项工作，甲单独完成要12天，乙单独完成要10天，甲和乙工作效率的比是（）A．6：5B．12：10C．1/10:1/12 D．5：611．15：28也可以写成15/28，读作（）A．二十八分之十五B．15比28C．28比1512．比的前项是3，比值是1/5，后项是（）A．15B．1/15 C．3/513．3：5的后项增加10，要使比值不变，比的前项应（）A．加上10B．乘2C．加6D．都不对14．A÷B＝1/2（A、B都不为0），那么A（）B．A．＞B．＜C．=15．比的前项相当于分数中的（）A．分子B．分母C．分数线16．甲、乙两数的比是7：5，甲数比乙数多（）A．40%B．5/7 C．2/717．某校男教师与女教师人数的比是5：3，以下说法不正确的是（）A．女教师比男教师少40%B．女教师占全校教师人数的37.5%C．男教师比女教师少全校教师的40%D．男教师是女教师的5/318．“16/( )=（）÷40=0.8=（）成”这道题中，依次应填入哪三个数？（）A．40、16、0.8B．20、5、8C．20、32、819．桃树的棵数比李树多1/5，桃树棵数和李树棵数的比是（）A．1：5B．5：6C．6：520．甲数除以乙数，商是0.4，甲数与乙数的最简整数比是（）A．5：2B．4：1C．2：5D．4：1021．甲数除以乙数，商是0.4．甲数与乙数的最简整数比是（）A．0.4：1B．5：2C．4：10D．2：522．一本故事书已看的页数和未看页数的比是2：3，下面说法错误的是（）23．A．已看的页数是未看页数的2/3 B．已看的页数比未看的页数少1/2C．已看了全书页数的2/5 D．全书还有3/5没有看1．两个数的比值是1.2，如果比的前项扩大2倍，后项缩小两倍，比值是（）A．1.2B．2.4C．4.8D．9.62．化简比的依据是（）A．除法的运算B．分数的基本性质C．比的基本性质3．比的前项扩大10倍，后项缩小10倍，比值就（）A．不变B．扩大10倍C．扩大100倍D．缩小100倍4．比的前项扩大2倍，后项缩小2倍，比值（）A．扩大2倍B．扩大4倍C．缩小2倍5．5/7的前项和后项都扩大3倍，比值是（）A．15：21B．5：7C．1:2/5D．5/7 6．5：9的前项加上10，要使比值不变，后项应加上（）A．10B．27C．18D．367．4：5的前项增加16，要使比值不变，后项应该（）A．加上25B．乘16C．加上5D．乘58．一个比的比值是7/8，如果把它的前项和后项同时扩大3倍，这时的比值（）A．不变B．扩大3倍C．扩大9倍9．在2：5中，如果前项加上4，要使比值不变，后项应加上（）A．10B．4C．1510．3：10的前项加上6，如果要使比值不变，后项应该（）A．加上20B．加上6C．扩大2倍11．在a/12=1/3中，a的值是（）A．2B．4C．6D．812．解比例：x/3=2：1，x=（）A．6B．1.5C．0.7D．913．80：2=200：x，那（）A．800B．5C．80D．0.514．2：x=1/2：1/4，x=（）A．40B．4C．0.4D．115．如果a÷7/8=b×7/8（a、b都不等于零），那么（）A．a＞bB．a=bC．a＜b16．在2、3、5/6这三个数中插入第四个数X，使得这四个数能组成比例，那么X最小是（）A．5/6 B．36/5 C．5/9 D．5/417．2：x=12：24 x=（）A．40B．4C．0.4D．118．1/3：1/5=x：9的正确的解是（）A．x=15B．x=1/15 C．x=3/519．x=5/4是比例（）的解．A．2.6：x=1：8B．3：6=x：8C．5/2：x=2/5:1/5 20．如果11/18和m/12相等，则m等于（）A．22/3 B．32/11 C．17/2 D．33/6 21．若X、Y、Z都是不为零的自然数，且2/3X=3/4Y=1/2Z，则它们的大小关系是（）A．X＞Y＞ZB．Y＞Z＞XC．Z＞Y＞XD．Z＞X＞Y22．x、y、z是三个非零自然数，且x×6/5=y×8/7=z×10/9，那么x、y、z按照从大到小的顺序排列应是（）A．x＞y＞zB．z＞y＞xC．y＞x＞zD．y＞z＞x23．从甲地到乙地，客车和货车所用的时间比是4：5，那么它们的速度之比是（）A．5：4B．1/5:1/4 C．4：524．在比例尺是1：6000000的地图上，量得南京到北京的距离是15厘米，南京到北京的实际距离大约是（）千米．A．800千米B．90千米C．900千米25．小正方形和大正方形边长的比是2：7，小正方形和大正方形面积的比是（）A.2：7B．6：21C．4：49D．7：226．一台拖拉机，前轮直径是后轮的1/2，前轮转动8圈，后轮转（）圈．A．8B．16C．4D．627．把一块三角形的地画在比例尺是1：500的图纸上，量得图上三角形的底是12厘米，高8厘米，这块地实际面积是（）A．480平方米B．240平方米C．1200平方米28．a，b，c 三个数均大于零，当a×1=b×1/12=c×5/4时，则 a，b，c中最大的是（）A．aB．bC．c30．同学们做广播体操，每行站20人，正好站18行．如果每行站24人，可以站多少行．列成比例式（）A．20/18=24/x B．20×18=24ΧC．18：20=Χ：2431．一杯牛奶，喝去20%，加满水摆匀，再喝去1/2，再加满水，这时杯中牛奶与水的比是（）A．3：7B．2：5C．2：3D．1：132．甲数是乙数的2/3，乙数是丙数的4/5，甲、乙、丙三数的比是（）A．4：5：8B．4：5：6C．8：12：15D．12：8：1533．一个直角三角形中，已知一个锐角与直角的度数比是3：5，那么两个锐角的度数比是（）A．2：5B．5：3C．3：234．甲、乙两个粮仓各有若干袋大米，若乙拿出它的1/5给甲，则两仓大米袋数相等．原来甲、乙两仓大米袋数的比是（）A．4：5B．3：5C．5：335．如图，阴影部分的面积相当于甲圆面积的1/6，相当于乙圆面积的1/5，那么乙与甲两个圆的面积比是（）A．6：1B．5：1C．5：6D．6：536．甲比乙多2倍，乙比丙多1/2，则甲：乙：丙=（）A．3：1：2B．2：1：3C．3：1：6D．9：3：237．一根绳子对折2次后的长度和另一根绳子对折3次后的长度相等，那么这两根绳子原来长度的比是（）A．2：3B．1：2C．4：338.一项工程，单独做甲队要8天，乙队要10天．甲队和乙队的工效比是（）A．8：10B．5：4C．1/10:1/8 D．4：539．一种糖水，糖占25%，糖与水的比是（）A．1：4B．1：3C．4：1D．25：10040．两个数的比值是1.2，如果比的前项扩大2倍，后项缩小两倍，比值是（）A．1.2B．2.4C．4.8D．9.641．比的前项扩大2倍，后项缩小2倍，比值（）A．扩大2倍B．扩大4倍C．缩小2倍42.一个比的前项是20，如果前项增加40，要使比值不变，后项应该（）A．增加40B．减少40C．扩大到原来的2倍D．除以1/343．甲数比乙数少25%，甲数比乙数的最简整数比是（）A．1：4B．4：1C．3：4D．4：344．甲数除以乙数的商是1.2，那么甲数与乙数的最简整数比是（）A．5：6B．6：5C．10：12D．1：1.21．把一根绳子剪成两段，第一段长是2/9米，第二段占全长的4/9，则（）A．第一段长B．第二段长C．两段一样长2．一个三角形与一个平行四边形的面积和底部都相等，这个三角形与平行四边形高的比是（）A．2：1B．1：2C．1：1D．3：1二．填空题（共7小题）1．甲走的路程比乙走的路程多1/3，乙用的时间比甲多1/4，那么甲乙的速度比是．2．已知六（2）班男生人数的3/7与女生人数的6/11相等，这个班的男生与女生人数的最简整数比是，如果女生有22人，全班有人．3．÷15=4/5=1.2：= %= （小数）= 成．4．在含盐率30%的盐水中，加入3克盐和7克水，这时盐水中盐和水的比是．5．3/8与0.8的最简单的整数比是，它们的比值是6．两箱苹果，如果从甲箱取出1/6,放入乙箱后，两箱苹果正好一样重，原来两箱苹果重量的最简比是．7．一个长方体的所有棱长之和为1.8米，长、宽、高的比是6：5：4．把这个长方体截成两个小长方体，表面积最多可以增加平方米．8．2/5：0.375化成最简整数比是，比值是．9．王老师要做一个长方体模型的教具．他先用一根长24分米的铁丝做一个长方体框架，使它的长、宽、高的比是5：4：3；然后在这个长方体框架外面糊一层纸．那么，王老师所做的长方体模型的体积是分米3，他至少需要准备分米2的纸．10．按下面的方法摆58个图形，最后一个是图形，一共有个△．△△○○△○△△○○△○△△…11．一个零件如图阴影部分，它的周长是厘米，面积是平方厘米．12．一个分数的分子、分母之和是38，如果把分子与分母各加上3，则分子与分母的比是4：7，原分数是．13．如图，平行四边形ABCD的边长BC为10厘米，直角三角形BCE的直角边EC为8厘米，已知阴影部分的面积比三角形EFG的面积大4.8平方厘米，则CF的长是厘米．14．在比例尺是1:200000的一幅地图上，量得甲乙两地相距10厘米，甲乙两地实际距离是千米．15．在5：6中，5是比的，是比的后项，比值是16．1/8=9÷ = ：56=( )/40= （小数）17．甲数是乙数的5/7，乙数与甲乙总数的比是，乙数比甲数多18．2：3可以读作三分之二．．（判断对错）19．组成比例的四个数叫做比例的，中间的两个数叫做比例的，两端的两个数叫做比例的20．4：5读作4比5，也可写作4/5（判断对错）三．解答题1．一个比的前项缩小到原来的1/3，后项缩小到原来的1/6，比是2：5，这个比原来的比值是多少？2．用120厘米长的铁丝做一个长方体框架，长、宽、高的比是3：2：1，这个长方体的长、宽、高各是多少？3．张师傅加工一批零件，第一天完成的个数与零件的总个数的比是1：3．如果再加工15个，就可以完成这批零件的一半．这批零件共有多少个？4．修一条公路，甲队修了全长的1/3，乙队和丙队修路的比是3：5，已知甲队比乙队多修24米，这条公路全长多少米？5．六年级参加体育兴趣小组的人数与年级总人数的比是1：4，如果算上合唱的72人，占全年级总人数的1/3，六年级参加体育兴趣小组的有多少人？6．上下两层书架，如果从上层取出15本放入下层，这时下层的书正好是上层的5/7．已知下层原来有书35本，上层原来有书多少本？7．工地有一批水泥，第一天用了14吨，第二天用去的是第一天5/7，这时用去的水泥与剩下的比是3：5．这批水泥原有多少吨？8．一个长方体棱长总和是220厘米，长与宽的比是2：1，宽与高的比例是3：2，这个长方体体积是多少立方厘米？9．学校图书馆购进科技书，文艺书和故事书共400本．科技书占30%，文艺书和故事书的本数比是4：3，文艺书有多少本？10．把一条路按3：5：9分给甲、乙、丙三个修路队去修．已知甲队比乙队少修16km，这条路全长是多少千米？11．一堆煤，第一天运走的吨数与总吨数的比是1：3，第二天运走4.5吨后，两天正好运走了总数的一半，这堆煤有多少吨？12．工程队修一条路，上半月修好的米数与全长的比是1：5．如果再修360米，就正好修了这条路的一半．这条路全长多少米？13．甲仓原来存粮是乙仓的4/5，后来甲仓增加存粮88吨，这时乙仓与甲仓存粮吨数的比是6：7，乙仓有存粮多少吨？14．甲、乙两队人数的比是7：8，如果从甲队派30人去乙队，那么甲、乙两队人数的比是2：3．甲、乙两队原来各有多少人？。

2020年通用版小升初数学冲A提高集训分数问题—专题01《分数的大小比较》一．选择题1．（2014春•肥城市期末）在20042005，20052006，20062007中，最小的分数是()A．20042005B．20052006C．20062007D．无法比较【分析】用1减去每个分数后结果分别是12005，12006，12007，根据分子相同时，分母小的分数就大可知1 2005最大，所以20042005最小，据此解答即可．【解答】解：因为：20041120052005-=20051120062006-=20061120072007-=111200520062007>>根据被减数相同，差大的，减数就小，所以：200420052006200520062007<<故选：A．2．下面算式中，()得数最大．A．2015220169⨯B．2015220169÷C．2015920164⨯【分析】先把选项B根据分数除法的计算方法：除以一个不为零的数等于乘上这个数的倒数，把除法变成乘法，再根据一个因数相同(0除外）另一个因数越大，积越大进行比较．【解答】解：2015220159 2016920162÷=⨯；这样三个算式都有一个相同的因数，299942<<所以：2015220169÷的结果最大．故选：B ．3．在下面几个算式中，第( )个式子的得数最大．A ．11()201719+⨯B ．11()302429+⨯C ．11()403137+⨯D ．11()504147+⨯ 【分析】分数乘整数，分母不变，分子乘以整数．两个加数的和乘一个整数，等于每个加数分别乘这个整数，然后求和．分别计算四个算式，然后进行比较．【解答】解：（1）11()201719+⨯20201719=+3121719=++9325157=++；（2）11()302429+⨯30302429=+ 6122429=++9323687=++；（3）11()403137+⨯40403137=+9323137=++；（4）11()504147+⨯50504147=+9324147=++； 结果中都有2，只要比较分数部分即可：分子相同，分母小的分数反而大，31364151<<<，37475787<<<，可以得出（3）式最大．答：在下面四个算式中，最大的得数是C ．故选：C ．4．已知：5321150%653a b c d ⨯=⨯=÷=-，并且a 、b 、c 、d 都不等于0，则a 、b 、c 、d 中最小的数是( )A ．aB ．bC ．cD ．d 【分析】首先根据5321150%653a b c d ⨯=⨯=÷=-，可得：5331150%652a b c d ⨯=⨯=⨯=-，然后判断出56、315、32的大小关系，即可推出a 、b 、c 的大小关系，进而判断出a 、b 、c 、d 中最小的数是哪个即可． 【解答】解：因为5321150%653a b c d ⨯=⨯=÷=-， 所以5331150%652a b c d ⨯=⨯=⨯=-， 因为5331625<<，所以b c a <<； 因为31150%5b d d ⨯=-<，所以b d <，所以a 、b 、c 、d 中最小的数是b ．故选：B ．5．在2008200720092008,,,2007200820082009这四个数中，最大的数是( ) A ．20072008 B ．20082007 C ．20092008 D ．20082009【分析】首先观察这四个分数，排除掉分母比分子大的20072008和20082009，剩下20082007和20092008，它们的共同点在于都可以把它们看作“1+分数单位”的形式，如20081120072007=+，20091120082008=+，它们的不同点在于两者的分母一个大一个小，然后根据“分子相同，分母大的反而小，分母小的反而大”，做出判定． 【解答】解：因为200712008<，200812009<，200812007>，200912008>，因此20072008和20082009应排除；20081120072007=+，20091120082008=+，1120072008>，因此2008200920072008>． 最大数是20082007．故选：B ．6．（2014•深圳自主招生）下面各组中的两个分数都是最简真分数，你能否在“〇”里填上“>”或“<” (a 和b 表示被墨汁盖掉了数字）310〇3a 3b 〇4(5) A ．>，> B ．>，< C ．<，< D ．无法确定【分析】两个分数都是最简真分数，那么ab 都是非0的自然数，然后根据异分母分数比较大小，先依据分数的基本性质化成同分母分数或者同分子的分数，再比较大小即可．【解答】解：（1）391030=10330a a =a 是非0的自然数，所以910a <，那么9103030a < 那么3103a <；（2）3124b b =412515= 因为3b 是最简真分数，所以4b …，4416⨯=， 4b 最小是16，1615>，所以415b > 即：345b <． 故选：C ．7．若217173A <<，式中A 最多可能表示( )个不同的自然数．A ．6B ．7C ．8D ．9 【分析】把217173A <<，分成2177A <，1713A <两个不等式来解，据此解答． 【解答】解：2177A <2717A <⨯2119A <59.5A <1713A <173A >⨯51A >所以5159.5A <<在51和59.5之间的自然数有52、53、54、55、56、57、58、59共8个；故选：C ．8．如果a b <，b c >，a c >，且a 、b 、c 都不等于0，那么在2a 、2b 、2c 三个分数中，最小的一个分数是( )A ．2aB ．2bC ．2c【分析】根据分数大小比较方法，分子相同时分母大的分数反而小．【解答】解：因为a b <，b c >，a c >，且a 、b 、c 都不等于0，所以a ，b ，c 中，c 最小，其次是a ，最大是b ，所以b a c >>，然后根据分子大小比较的方法即可得：222c a b >>； 故选：B ．9．（2019•长沙）已知a 、b 、c 三个数均大于0，且a b c >>，下列式子正确的是( )A ．1a b c >+B ．1a b c >-C ．1a b c <⨯D ．1a b c<+ 【分析】观察选项，发现是一些分数与1比较大小，如果是一个分子大于分母的假分数，那么这个数就大于1，如果是分子小于分母的真分数这个数就小于1，所以只要比较每个分数的分子与分母的大小关系即可判断．【解答】解：因为只知道a b c >>，所以无法比较a 与b c +的大小；即：选项A 、D 中a b c +与1的大小关系无法比较； 同理也无法得出a 与b c ⨯的大小关系；选项C 中ab c ⨯与1的大小关系无法比较；a 最大，那么a 一定大于bc -的差；即：a b c -的分子大于分母，1a b c >-是正确的．故选：B ．二．填空题10．（2014•郑州）有一个算式： 1.372511++≈W W W 算式左边的□里都是整数，右边答案只写出了四舍五入的近似值，则算式□中的数依次分别是 1，3，3 ．【分析】因为算式的值为近似值，且其介于1.365和1.374之间，又因□里的数是整数，从而可推算□的值． 【解答】解： 1.372511++≈W W W ， 所以1.365 1.3742511++W W W 剟， 通分得1.365… 1.374…，于是有150.1555⨯…□22+⨯□10+⨯□151.14…，由于□里的数是整数，所以，55⨯□22+⨯□10+⨯□151=，只有551223103151⨯+⨯+⨯=，故□里数字依次填1，3，3．11．（2013•长沙模拟）把下列分数按大小顺序排列：23，58，1523，1017，1219 2151251032319817>>>> ． 【分析】把分数的分子都化为相同的数，而2，5，15，10，12的最小公倍数是60，根据分数的基本性质，分子扩大多少倍，分母就扩大多少倍，再利用分子相同时，分母大的分数反而小即可．【解答】解：因为：223060333090⨯==⨯551260881296⨯==⨯15154602323492⨯==⨯101066017176102⨯==⨯12125601919595⨯==⨯且90929596102<<<< 所以：2151251032319817>>>> 故答案为：2151251032319817>>>>． 12．（1）717105()7<< （2）3()754010<<． 【分析】（1）分子通分，可得11901190119085070()833<<⨯，依此可得( )为12； （2）分母通分，可得24()28404040<<，依此可得( )的取值范围，从而求解． 【解答】解：（1）717105()7<< 则11901190119085070()833<<⨯， 则( )为12；（2）3()754010<<， 则24()28404040<<， 24(< )28<，则( )为27，26，25中任选一个．13．三个分数244245，344345，544545按从大到小的顺序排列为 544344244545345245>> ． 【分析】根据这三个分数的特点先求出1与这三个分数的差，再比较差的大小，根据差大原分数就小，进而解答． 【解答】解：34411345345-=，24411245245-=，54411545545-=， 因为111245345545>>， 所以544344244545345245>>． 故答案为：544344244545345245>>． 14．6181.4160739A B C D E ⨯=⨯=÷=⨯=÷把A ，B ，C ，D ，E 按从大到小的顺序排列是 E C B D A >>>> ． 【分析】令6181.41601739A B C D E ⨯=⨯=÷=⨯=÷=，分别求出A ，B ，C ，D ，E 的值，比较大小后，即可按从大到小的顺序排列． 【解答】解：令6181.41601739A B C D E ⨯=⨯=÷=⨯=÷=， 则57A =，76B =，113C =，98D =，60E =， 因为17956013687>>>>， 所以E C B D A >>>>．故答案为：E C B D A >>>>．15．（2012秋•慈溪市期末）比较大小：998875998877 > 889975889977；100201 150301． 【分析】（1）把两个分数通过变形，即998875998877221998877998877998877-==-，889975889977221889977889977889977-==-，因为减号后面的数越大这个数就越小，反之越大，据此解答；（2）100201和150301可化成小数，再进行比较． 【解答】解：（1）998875998877221998877998877998877-==-， 889975889977221889977889977889977-==-， 因为22998877889977<，所以998875889975998877889977>． （2）因为1000.4975201≈，1500.49833301≈， 因此100150201301<． 故答案为：>，<．16．（2013秋•贵阳校级期中）在 上填上“<”、“ =”、“ >”：5157⨯< 15 317⨯ 37 2167÷ 16． 【分析】（1）一个因数57比1小，积比另一个因数15小； （2）一个因数等于1，积就等于另一个因数37；（3）除数27小于1，商大于被除数16；由此做出选择． 【解答】解：515()157⨯<；331()77⨯=；216()167÷>．故答案为：<，=，>．17．（2011•高阳县）在56%、311、58、513这四个数中，大于12的数是 58和56% ． 【分析】几个不同形式的数比较大小，一般把这些数都化成小数再比较．【解答】解：56%0.56=，30.27311≈，50.6258=，50.38513≈，10.52=， 所以大于12的数是58和56%． 故答案为：58和56%．18．比较大小．38613862 > 59715974． 【分析】因为13861138623862-=，35971159745974-=，所以要比较比较38613862与59715974的大小，只比较13862与35974的大小即可． 【解答】解：因为13861138623862-=，35971159745974-=， 而133********= 33115865974< 所以3311115865974->- 所以3861597138625974> 故答案为：>．19．（2018•长沙）若11333a =，1113333b =，111133333c =，则a 、b 、c 中最大的是 c ，最小的是 ． 【分析】求出这三个数的倒数，然后比较这三个数的倒数，倒数越大，原来分数就越小，由此求解． 【解答】解：11333的倒数是330111113333的倒数是330111111133333的倒数是3301111333303030111111111>>， 那么111111111333333333333<<，即最大数是c ，最小的数是a ．故答案为：c ，a ．20．（2014秋•海安县期末）比较大小．33338888 < 22225555． 【分析】观察两个分数发现分子分母都含有公因数1111，所以先把两个分数约分成最简分数，再化成小数比较大小即可 【解答】解：333330.37588888==，222220.455555==，0.3750.4<，所以3333222288885555<． 故答案为：<．三．应用题21．快乐提升 比较1415、1516、1617的大小． 【分析】观察1415、1516、1617这三个数，它们的分子和分母相差1，只要用1减去这三个分数，求出差，差越大，那么这个数就越小，由此求解， 【解答】解：14111515-= 15111616-= 16111717-= 111151617>> 所以：141516151617<<． 四．解答题22．（2012•郑州模拟）已知1234731511515.214.89934574A B C D ⨯⨯=⨯÷⨯=⨯÷=⨯⨯．A 、B 、C 、D 四个数中最大的是 B ．【分析】利用分数大小的比较方法即可求解．先将题目中的分数化为同分母分数，分子大的分数值就大，则字母的值就越小． 【解答】解：1234731511515.214.89934574A B C D ⨯⨯=⨯÷⨯=⨯÷=⨯⨯， 100245151515.214.699334A B C D ⨯⨯=⨯⨯⨯=⨯⨯=⨯， 5004073193335A B C D ⨯=⨯=⨯=⨯， 2500220031352409165165165165A B C D ⨯=⨯=⨯=⨯， 由此可知：31352500240922001165165165165>>>>， 则C A D B <<<．故答案为：B ．23．比一比，1a a +与12a a ++哪个大？ 12a a ++ > ． 【分析】将1a a +与12a a ++进行变形，1111a a a =-++，11122a a a +=-++，因为12a a +<+，所以1112a a >++，111112a a -<-++，所以112a a a a +<++． 【解答】解：，1111a a a =-++，11122a a a +=-++ 因为12a a +<+ 所以1112a a >++，111112a a -<-++， 所以112a a a a +<++． 故答案为：12a a ++，1a a +．24．已知20032008a =，20042009b =，是比较a 与b 的大小． 【分析】两个分数分母进行通分数字太大，不利于比较；那么通过观察发现，两个分数都比1少一个自身的分数单位，那么我们就可以通过比较它们与1之间的差的方法进行比较，哪个与1的差大，这个数就越小．通过比较发现20032008与1的差数小，所以较大的数字就是20042009． 【解答】解：20035120082008-=，20045120092009-=， 分子相同时，分母越大，分子越小， 所以5520082009>， 所以2003200420082009<．答：a b <．25．1357992468100⨯⨯⨯⨯⋯⨯与110相比，哪个更大？为什么？ 【分析】相乘的这些分数的特点是分母都是偶数，分子都是奇数；再写出一道分数相乘，使它们分子都是偶数，分母都是奇数(1100)-，把这两道算式相乘，得出积为1100，由此进一步再做比较． 【解答】解：假设1357992468100A =⨯⨯⨯⨯⋯⨯，24681003579101B =⨯⨯⨯⨯⋯⨯， 因为1223<、3445<、5667<⋯，99100100101<， 所以A B <， 又因为1100A B ⨯=，1100A A ⨯<， 所以110A <． 答：110大一些．26．你会用简单的方法比较2653、1735、111223的大小吗？ 【分析】根据题意，2653、1735、111223这三个分数的分子都接近分母的一半，分别用12减去这三个分数，可得1106、170、1446，根据同分子分数分母大的反而小，可得11170106446>>，再根据被除数相同，除数大的差就小，可得11126172235335>>． 【解答】解：1261253106-=；117123570-=；111112223446-=； 因为11170106446>>； 所以，11712611112352532223->->-； 因此，11126172235335>>． 27．四个连续自然数的倒数之和等于1920，求这四个自然数的两两乘积之和． 【分析】设这四个连续自然数分别为a ，1a +，2a +，3a +，则11111912320a a a a +++=+++，所以1911111111420123a a a a a a a a a =+++<+++=+++，4419a <．1a =，2，4都不合题意，所以3a =，这四个自然数为3，4，5，6，其两两乘积之和为343536454656119⨯+⨯+⨯+⨯+⨯+⨯=．【解答】解：设这四个连续自然数分别为a ，1a +，2a +，3a +，则11111912320a a a a +++=+++， 所以1911111111420123a a a a a a a a a =+++<+++=+++，4419a <． 易知1a =，2，4均不合题意，故3a =，这四个自然数为3，4，5，6其两两乘积之和为：343536454656119⨯+⨯+⨯+⨯+⨯+⨯=．答：这四个自然数的两两乘积之和是119．28．（2015春•大同期末）李晓在比较分数大小时发现这样一条规律：一个真分数的分子与分母加上相同的数，(0除外）这个新分数大于原来的真分数．你认为这条规律正确吗？（1）举例：在横线上填上>、<、或=．34 < 45，512 118，59 37 你的例子： ⋯（2）思考：34 和45相比， 更接近1； 和 相比， 更接近1；⋯ （3）你的结论：（4）联想：假分数符合这个规律吗？有理有据的思考并简要写出你的推想过程．【分析】（1）根据题干中的规律比较两个真分数的大小，真分数与假分数比较大小，真分数小于假分数，并举出例子；（2）根据分数的意义可知，分数的分子分母相差1时，分子分母大的更接近1；（3）根据前两题的解答得出结论；（4）假分数不符合这个规律，举例解答即可．【解答】解：（1）3445<，511128<，5397> 再如：4556<，6778<，⋯（2）思考：34 和45相比，45更接近1；67和78相比，78更接近1；⋯（3）我的结论：一个真分数的分子与分母加上相同的数(0除外），这个新分数大于原来的真分数．（4）联想：假分数不符合这个规律， 假设这个假分数是11，分子和分母同时加上1是22，分数值相等于原分数；假设这个假分数是32，分子和分母同时加上1是43，4332<，分数值小于原分数； 综上可知：一个假分数的分子与分母加上相同的数(0除外），则分数值不大于原分数．故答案为：<、<、>，4556<、6778<，45、67、78、78，一个真分数的分子与分母加上相同的数(0除外），这个新分数大于原来的真分数．29．（2014•台湾模拟）在1618[]4n <<的[]中，可以填入的整数有多少个？ 【分析】设中间数的分母为x ，然后进行通分，再根据分子的大小确定x 的值．【解答】解：设中间数的分母为x ，则通分后最小公倍数为8x ，那么三个分数的关系通分后可以化为482888x x x x x <<因为分母相同，所以482x x <<，可知x 最大整数是47，最小整数是25，共23个．故答案为：23．30．（1）四个数：20112010，20102011，20122011，20112012，其中最大的数是 20112010，最小的数是 ． （2）一个分数，分子加上分母等于168；分子，分母都减去6，分数变成57，原来的分数是 ． 【分析】（1）首先判断出201112010>，201012011<，201212011>，201112012<，然后判断出20112010，20122011的大小关系，即可判断出最大的数是多少；最后判断出20102011，20112012的大小关系，即可判断出最小的数是多少． （2）首先设这个分数的分母是x ，则分子是168x -，然后根据分子，分母都减去6，分数变成57，可得1686567x x --=-；然后解方程，求出x 的值是多少，即可判断出原来的分数是多少． 【解答】解：20111)12010>，201012011<，201212011>，201112012<，因为2011201120102012⨯>⨯， 所以2011201220102011>， 所以最大的数是20112010；因为2010201220112011⨯<⨯， 所以2010201120112012<， 所以最小的数是20102011．综上，可得 最大的数是20112010，最小的数是20102011．（2）设这个分数的分母是x ，则分子是168x -， 所以1686567x x --=- 5(6)7(1686)x x -=--53011347x x -=-121164x =1212116412x ÷=÷97x =1689771-=， 所以原来的分数是7197． 故答案为：20112010；20102011；7197． 31．比较下面这组分数的大小．553555 和442444． 【分析】根据题意，5535552=-，所以，553555221555555555-==-，同理44221444444=-，然后再比较2555与2444的大小，然后再进一步解答即可． 【解答】解：553555221555555555-==-； 442444221444444444-==-； 2555与2444的分子都是2，由于555444>，所以，22555444<； 因此，2211555444->-； 由此，553442555444>．。

【总结】本题考查了分数比较大小．
【例 20】 把下列每组中的分数通分，并比较大小：
（1） 5 ， 7 ； 14 16
（2） 6 ， 16 ； 17 51
（3） 3 ， 4 ， 5 ； 4 20 8
（4） 7 ， 13 ， 19 ． 12 18 24
6 【解析】由已知得：四月份用水 150+30=180（吨），故 150 5 ．
180 6
【总结】本题考查了占比问题及约分．
【例 10】 （1）把 5 克糖溶解在水中形成 40 克糖水，那么糖占糖水的几分之几？水占糖 水 的 几 分
之几？
（2）把 5 克糖溶解在 40 克水中形成糖水，那么糖占糖水的几分之几？水占糖水的几分之几？【ຫໍສະໝຸດ 识结构】模块一：分数的约分
1、 约分 把一个分数的分子与分母的公因数约去的过程，称为约分．
2、 最简分数 分子和分母互素的分数，叫做最简分数． 将分数化为最简分数，可以将分子、分母分别除以它们的最大公因数，也可以不断的约分，直到分
子、分母互素为止．
【例 1】将分数 16 、 105 约分，并化为最简分数． 24 180
b
28
28
故无法确定，选择 D．
【总结】本题考查了对分数约分概念的理解．
【例 5】下列说法中，不正确的个数为（ ）
○1 分子和分母都是奇数的分数，一定是最简分数；
第 2 页 共 19 页
○2 分子和分母都是素数的分数，一定是最简分数；
○3 最简分数一定比 1 小；
○4 约分后的分数比原来的分数小；
45 ． 54
【解析】约分不改变分数的大小，故将 3 的分子分母同时乘以 18 得到 54 ；
4
72

小数比大小题目100道一、题目1. 比较0.5和0.3的大小。

2. 0.7与0.9哪个大？3. 比较1.2和1.5。

4. 0.45和0.54谁大？5. 2.1和2.05比大小。

6. 0.8与0.78哪个大？7. 比较3.56和3.6。

8. 0.12和0.21谁大？9. 4.01和4.1比大小。

10. 0.99与1.01哪个大？11. 比较0.67和0.76。

12. 0.33和0.3哪个大？13. 5.2和5.18比大小。

14. 0.09和0.1谁大？15. 6.05和6.5比大小。

16. 0.56与0.65哪个大？17. 比较7.12和7.2。

18. 0.81和0.9谁大？19. 8.03和8.3比大小。

20. 0.25与0.35哪个大？二、解析1. 对于0.5和0.3，先比较整数部分，都是0，再比较十分位，5 > 3，所以0.5>0.3。

2. 0.7和0.9，整数部分都是0，十分位7 < 9，所以0.9 > 0.7。

3. 1.2和1.5，整数部分都是1，十分位2<5，所以1.5 > 1.2。

4. 0.45和0.54，整数部分都是0，十分位4 < 5，所以0.54 > 0.45。

5. 2.1和2.05，整数部分都是2，十分位1 > 0，所以2.1>2.05。

6. 0.8和0.78，整数部分都是0，十分位8 > 7，所以0.8 > 0.78。

7. 3.56和3.6，整数部分都是3，十分位5 < 6，所以3.6 > 3.56。

8. 0.12和0.21，整数部分都是0，十分位1 < 2，所以0.21 > 0.12。

9. 4.01和4.1，整数部分都是4，十分位0 < 1，所以4.1 > 4.01。

10. 0.99和1.01，先比较整数部分，0 < 1，所以1.01 > 0.99。

11. 0.67和0.76，整数部分都是0，十分位6 < 7，所以0.76 > 0.67。

A.a>b>c
B.b>c>a
c
a
C.c>a>b
D.b>a>c
b
在数轴上表示的两个数,右边的数总比左边的数大。
比较有理数的大小
运用法则比较有理数的大小


> −
1、比较大小：- _________

两个负数比较大小的步骤是：
绝对值
大小
（1）先求_______________;（2）再比较绝对值的____________；
绝对值大的数反而小
（3）最后比较负数的大小：___________________.
2.比较大小：
>
ሷ
（2）-1.38____________-1.384
<
（2）-______________
− 3.14
比较有理数的大小
两个负数之间如何比较大小？
（1）正数大于0，负数小于0，正数大于负数；
（2）两个负数，绝对值大的反而小．
21
解：（3）∵|−
而
7
5
3 3
3 3
8
8
3 3 9
|= ，|− |= = .（4）∵|− 5 |=5，|− 4|=4，
21 21
7 7 21
8
9
＜ ，
21 21
即 |−
∴−
4
而
8
3
|＜|− |
21
7
8
3
＞−
21
7
.
，
3
3
＜ ，
5
4
3
5
3
4
即 |− |＜|− |，

一 、单选题（本大题共15小题，共30分）1.3.70和3.7两个小数（ ）A. 3.70大于3.7B. 一样大并且小数位数一样C. 一样大只是意义不一样2.把下面各组数量按从大到小的顺序排列正确的是（ ）。

A. 0.65千克、65千克、0.00065吨B. 0.0065吨、0.65千克、65克C. 65克、0.65千克、0.0065吨3.在下面大小比较中，正确的是（ ）A. 0.8=0.800B. 32个0.01＞4个十分之一C. 95﹣29+21＜95-（29+21）4.到哪个商店买毛巾最便宜？（ ）A. 小熊商店每条3.82元B. 小狗商店每条4.00元C. 小兔商店每条4.12元5.数a （非0自然数）先乘100，再把小数点向左移三位得到数b ．则a 与b 的大小关系是（ ）。

A. a ＞bB. a ＜bC. a=bD. 不能确定6.下面排列正确的一组是( )。

A. 1.5米＞0.15千米＞15厘米B. 3.5元＞34角＞3元C. 2.07吨＞2吨7千克＞21700千克7.0.1与0.10比较，它们的（ ）。

A. 大小不等单位不同B. 大小相等单位不同C. 大小相等单位相同8.下面各数中最大的数是( )。

A. 0.517517…B. 51.7%C. 0.517 数与代数—多位小数的大小比较（二）小升初总复习专项RJ9.李红体重的1.09倍等于王华体重乘0.98，李红和王华谁重？（）A. 一样重B. 李红重C. 王华重D. 无法比较10.0.2和0.9之间有（）个一位小数．A. 6B. 7C. 无数11.下面说法正确的有（）。

A. 小数都比整数小B. 6.7t等于6t 70kgC. 等腰三角形是轴对称图形12.2.7与2.70（）。

A. 大小相同，意义相同B. 大小相同，意义不相同C. 大小不相同，意义相同D. 大小、意义都相同13.7．□4＞7.3，符合条件的数字有（）个．A. 7个B. 无数C. 8个14.7.□4＞7.3，符合条件的数字有（）个．A. 7个B. 无数C. 8个15.下面各数中和“5”最接近的数是( )。

分数大小比较方法引导一、通化分子法看到两个分数或几个分数比较大小时，看看这几个分数的分子或分母的大小。

如果每个分数的分子都比分母小时，或都容易把分子化成相同的分数时，则把分子化成相同的分数。

这样来比较大小。

“分子相同的两个分数，分母小的分数比较大”。

如4/7和5/9则可化成分子相同的分数20/35和20/36，则可判断20/35＞20/36。

由然可断定，4/7＞5/9。

二、简化小数法这一方法很简单，只要把两个分数化成小数，然后就可以进行比较大小了。

如，5/9和4/10。

先把5/9化成小数等于0.5……，4/10化成小数是0.4，0.5＞0.4，所以5/9＞4/10。

三、比例相乘法就是根据比例的关系，把第一个分数的分子与第二个分数的分母相乘的积当作第一个分数的相对值；把第二个分数的分子与第一个分数的分母相乘的积当作第二个分数的相对值，则通过两个相对值的大小然后比较大的分数大小的方法。

如5/11和7/12。

5/11的相对应的值就是比的内项积：60；7/12的相对应的值就是比的外项积：77。

60＞77，所以5/11＞7/12。

四、运用倒数法比较两个分数大小时，可以通过比较两个分数倒数的大小，倒数较小的分数，原分数较大；倒数较大的分数，原分数较小。

这个方法要灵活地运用，可与其它方法综合使用。

在5/12和3/7两个分数中，倒数12/5＞7/3，所以3/7＞5/12。

这两个分数比较时，可以把化成倒数的分数化成小数进行比较。

然后进行原分数的比较。

五、相乘化整法就是将两个分数同时乘其中一个分数的分母，把其中一个分数化为整数，然后再进行这两个分数的比较。

如，9/12和11/13两个分数进行比较大小，可先将9/12乘以12等于9，11/13乘以12等于132/13。

可见132/13＞9，所以11/13＞9/12。

六、运用相约法在比较两个分数之前，先将要比较的两个分数进行约分，化成最简分数，然后再比较最简分数的大小，最简分数大的原分数大；最简分数小的原分数小。

比较大小【知识、方法梳理】我们已经掌握了基本的比较整数、小数、分数大小的方法。

本周将进一步研究如何比较一些较复杂的数或式子的值的大小。

解答这种类型的题目，需要将原题进行各种形式的转化，再利用一些不等式的性质进行推理判断。

如：a＞b＞0，那么a的平方＞b的平方；如果a＞b＞0，那么1a＜1b；如果ab＞1，b＞0，那么a＞b等等。

比较大小时，如果要比较的分数都接近1时，可先用1减去原分数，再根据被减数相等（都是1），减数越小，差越大的道理判断原分数的大小。

如果两个数的倒数接近，可以先用1分别除以这两个数。

再根据被除数相等，商越小，除数越大的道理判断原数的大小。

除了将比较大小转化为比差、比商等形式外，还常常要根据算式的特点将它作适当的变形后再进行判断。

【典例精讲】例1：比较777773777778和888884888889的大小。

这两个分数的分子与分母各不相同，不能直接比较大小，使用通分的方法又太麻烦。

由于这里的两个分数都接近1，所以我们可先用1分别减去以上分数，再比较所得差的大小，然后再判断原来分数的大小。

因为1－777773777778=5777778，1－888884888889=58888895777778＞5888889所以777773777778＜888884888889。

练习1：1、比较77777757777777和66666616666663的大小。

2、将9876598766，98769877，987988，9899按从小到大的顺序排列出来。

3、比较235861235862和652971652974的大小。

例2：比较1111111和111111111哪个分数大？可以先用1分别除以这两个分数，再比较所得商的大小，最后判断原分数的大小。

因为1÷1111111＝1111111＝1011111÷111111111＝111111111＝1011111101111＞1011111所以1111111＜111111111练习2：1、比较A＝3331666和B＝33166的大小2、比较111111110222222221和444444443888888887的大小3、比较88888878888889和99999919999994的大小。